HLODs Remain Powerful Tools for Detection of Linkage in the Presence of Genetic Heterogeneity

To the Editor:

Recently, Whittemore and Halpern (2001) investigated whether one can meaningfully estimate the admixture parameter α (their p) in the admixture LOD score (i.e., “HLOD”) when certain assumptions of HLODs are violated. They argued that such estimates of α are fundamentally problematic, a conclusion with which we agree. However, they then went on to suggest that, in such circumstances, investigators should not use HLODs to detect linkage in the presence of suspected heterogeneity (i.e., should not treat α as a “nuisance parameter”) but should, instead, use “nonparametric” methods. Unfortunately, they do not cite any evidence to support this final recommendation.

We are writing this letter because, in fact, there is a fair body of evidence, from numerous simulation studies, supporting the use of HLODs to detect linkage, even when the assumed heterogeneity model is incorrect. Some of these studies have been published; others are currently in press and were not available to Whittemore and Halpern (2001) when they did their work. We summarize some of these studies.

Several already-published studies have investigated various violations of HLOD model assumptions: Goldin (1992) compared the magnitude of HLODs to the magnitude of two-locus (2L) LODs in data sets in which many families were segregating both the linked and unlinked forms of the disease (these are called “mixed” families). The assumptions made by the 2L analyses exactly matched the reality, whereas the assumptions of the HLODs did not, because the latter assume, incorrectly, that every family has either the linked form or the unlinked form but not both. Goldin found that the HLODs were almost as high as the “correct” 2L LODs. This finding, in conjunction with the work of Abreu et al. (in press; see below), implies, in turn, that the power of the HLOD is also almost as good as the power of analyses performed under the correct model. Durner et al. (1992) made similar comparisons, in data sets with varying proportions of “mixed” families, but under generating models different than those which Goldin had used, and found similar results. Vieland et al. (2001) and Huang and Vieland (2001a) considered yet another violation of HLOD assumptions—namely, that proportions of linked families may differ across different data sets. They showed that, for affected-sib-pair (ASP) data, a simple adaptation of the HLOD maintained higher power than did both the homogeneity LOD and certain nonparametric tests (the ASP mean test, as well as Risch’s [1990] maximum LOD score under Holmans’s [1993] “possible triangle” constraint) in these situations.

We would also like to bring to readers’ attention several relevant just-published or not-yet-published studies: Greenberg and Abreu (in press) show that the multipoint HLOD has excellent power to detect linkage—and better power than that of the nonparametric NPL statistic of GENEHUNTER (Kruglyak et al. 1996). Their simulations include generating models, such as epistatic and additive models, that violate the assumptions of the HLOD. Vieland and Logue (in press) focus on another way in which the assumptions of the HLOD are commonly violated when the genetic models at the linked and unlinked loci differ. Their work shows, in agreement with that of Whittemore and Halpern (2001), that estimates of α are problematic, but simultaneously it indicates that the maximum HLOD provides a directly interpretable and powerful measure of the strength of evidence for linkage in a data set, despite the problems with α. Abreu et al. (in press) demonstrate that one does not pay much of a price in type I error by using HLODs to detect linkage—in most cases, considerably less than even “half” a degree of freedom to the corresponding asymptotic χ² statistic; also see the work of Faraway (1993) and Huang and Vieland (2001b).

Of necessity, our list of studies is not exhaustive, and our summaries of the papers’ findings are oversimplified. For more details, interested readers can consult the papers. Also, we have mentioned only those papers that use HLODs. Another body of published work demonstrates that simple single-locus LOD scores have better power than nonparametric methods do—even without inclusion of the admixture parameter (e.g., see Durner and Greenberg 1992; Goldin and Weeks 1993; Abreu et al. 1999; Durner et al. 1999).

One more point: Whittemore and Halpern (2001) also advocate looking for heterogeneity by using “subgroup analyses”—that is, subdividing the families on the basis of known attributes that might be genetically relevant (e.g., age at onset, ethnic background, etc.) We agree wholeheartedly that this is a valuable approach when one has some idea of how to subdivide families. This approach has been dubbed the “predivided-sample,” as opposed to the “admixture” approach (Hodge et al. 1983; Ott 1983). But in a situation in which one suspects genetic heterogeneity but in which this heterogeneity does not appear to fall along ethnic and other lines, the admixture approach provides an essential tool. Whittemore and Halpern’s suggestion of waiting until we have identified the gene before concerning ourselves with heterogeneity does not take into account the effect of heterogeneity on identifying the gene’s location in the first place.

In conclusion, this letter should not be misconstrued as attacking Whittemore and Halpern’s (2001) findings concerning estimation of the admixture parameter. We agree with Whittemore and Halpern that interpretation of 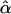is problematic in many circumstances. However, as we have summarized here, despite the well-known and -recognized problems with parameter estimation, a good deal of evidence indicates that the HLOD can provide a robust and powerful tool for detection of linkage in the presence of heterogeneity, even when the assumptions of the HLOD are violated. Whittemore and Halpern (2001, p. 457) stated that “nevertheless, we do not recommend the use of parametric heterogeneity models in linkage analysis, even merely as a tool for increasing the statistical power to detect linkage. … because the assumptions required by these models cannot be verified, and their violation could actually decrease power.” Violation of assumptions “could” decrease power, but so far all the evidence is that the power is still greater than that of nonparametric methods. There may well be situations in which such a power loss could be serious, but so far we have not seen these situations, in contrast to numerous demonstrations that simple LOD scores, especially when they incorporate admixture, have good power to detect linkage in the presence of heterogeneity, including situations in which many different assumptions of the model are violated. Whittemore and Halpern’s recommendation not to use HLODs to detect linkage in these circumstances may have seemed reasonable in the light of the problems in interpretation of α, but that recommendation is not, in fact, supported by the evidence available so far. Certainly, this topic of robustness of HLODs could use more research. However, given the difficulties in dealing with complex diseases, as well as our need for as many good analytic tools as we can find, it would be a shame if readers of Whittemore and Halpern avoided this particular useful tool, the HLOD, unnecessarily.