Optimized shear wave generation using hybrid beamforming methods

Abstract

Elasticity imaging is a medical imaging modality that measures tissue elasticity to aid in diagnosis of certain diseases. Shear wave-based methods have been developed to perform elasticity measurements in soft tissue. These methods often utilize the radiation force mechanism of focused ultrasound to induce shear waves in soft tissue such as liver, kidney, breast, thyroid, and skeletal muscle. The efficiency of the ultrasound beam for producing broadband extended shear waves in soft tissue is very important for widespread use of this modality. Hybrid beamforming combines two types of focusing, conventional spherical and axicon focusing, to produce a beam for generating a shear wave that has increased depth-of–field (DOF) so that measurements can be made with a shear wave with a consistent wave front. Spherical focusing is used in many applications to achieve high lateral resolution, but has low DOF. Axicon focusing, with a cone- shaped transducer can provide good lateral resolution with large DOF. We present our linear aperture design and beam optimization performed using angular spectrum simulations. A large parametric simulation study was performed which included varying the focal depth for the spherical focusing portion of the aperture, the number of elements devoted to spherical and axicon focusing portions of the aperture, and the opening angle used for axicon focusing. The hybrid beamforming method was experimentally tested in two phantoms and the shear wave speed measurement accuracy as well as the DOF for each hybrid beam was evaluated. We compared our results with shear waves generated using only spherical focusing. The results of this study show that hybrid beamforming is capable of producing a beam with increased DOF over which accurate shear wave speed measurements can be made for different size apertures and at different focal depths.

Introduction

Characterizing the mechanical properties of the tissue based on shear elasticity is one of the noninvasive methods which help to understand the state of the tissue health (Sarvazyan et al. 1998). In an isotropic, homogeneous, and elastic medium, the shear modulus is

$$\mu =\rho c_s^2$$ (1)

where, c_s, is the shear wave propagation speed, and ρ is density which can be assumed 1000 kg/m³ for soft tissues. Acoustic radiation force resulting from focused ultrasound has the ability to generate shear waves within the tissue (Zhao et al. 2011). Sarvazyan, et al., proposed a method called Shear Wave Elastography Imaging (SWEI) (Sarvazyan et al. 1998) using the acoustic radiation force to generate a shear wave. Nightingale, et al., applied impulsive acoustic radiation force to create shear wave (Nightingale et al. 2001) . Bercoff, et al., developed a new method called Supersonic Shear Imaging (SSI) which creates a shear wave from the combination of several separate radiation force pushes that are moved through depth. The resulting wave in SSI has a sharp wave front (Bercoff et al. 2004) . Chen, et al., proposed a new method called Shearwave Dispersion Ultrasound Vibrometry (SDUV) (Chen et al. 2009) using shear wave propagation speed measured in tissue at multiple frequencies to solve quantitatively for both tissue elasticity and viscosity. These techniques use focused ultrasound beams to generate the shear waves. The focusing is implemented by adjusting the time delays applied to the signals for each element in an array transducer. These time delays are computed to focus much like a physical spherical lens would if placed on a flat transducer. Throughout the rest of the paper, we will refer to this technique as spherical focusing.

McAleavey, et al., applied a spatially modulated acoustic radiation force (SMURF) to generate a radiation force pattern of known spatial frequency to determine the shear modulus of an elastic material (McAleavey et al. 2007). This spatial modulation was accomplished using a complicated apodization function. Hoyt, et al., reported using shear waves generated by axicon focal beams for an elasticity measurement method (Hoyt et al. 2012).

In most shear wave-based measurement methods it is assumed that the shear wave is a cylindrical wave (Chen et al. 2004) and has a portion of the wave that is flat, that is, a wave that arrives at a consistent time at lateral locations as evaluated through depth. If the shear wave front is not perpendicular to the direction of speed estimation as may occur with focused beams with a low f-number, a bias can be introduced in the speed estimation. Using either the SSI technique or an unfocused beam provides a relatively flat wave front (Bercoff et al. 2004), (Zhao et al. 2012) over a large depth-of-field. Maximizing this depth-of-field (DOF) of an ultrasound beam used for shear wave generation should provide more stable and accurate shear wave speed estimation.

In pulse-echo imaging, axicon focusing is advantageous because the beams maintain a constant width of main lobe over the length of the beam, allowing for a large depth-of-focus (Patterson and Foster 1982), (C. B. Burckhardt 1973). The axicon has been typically been implemented using a conical transducer in keeping with the implementation of the axicon lens in the field of optics (Patterson and Foster 1982), (C. B. Burckhardt 1973). The conical transducer is characterized by the opening angle of the transducer. The waves originating from the inner part of the axicon focus intersect the axis of the axicon close to the transducer while the waves produced at the outer part of the axicon will intersect the axis farther away from the transducer surface. The interaction of the waves form a line source along the axis of the transducer (C. B. Burckhardt 1973). However, there is considerable side lobe energy beyond the main axis that has prevented practical use of axicon focusing in pulse-echo imaging (Hooi et al. 2010). As a result, Hooi, et al., proposed using a hybrid beamforming technique to improve pulse-echo imaging by combining spherical and axicon focusing to improve DOF in B-mode imaging (Hooi et al. 2010). In that study, an optimization technique was used to maximize the DOF and reduce side lobes.

In this study, we describe a novel hybrid beamforming method to improve upon spherical beamforming utilizing a linear ultrasound transducer. We propose a method of optimizing an aperture that combines the spherical and axicon focusing to produce a transmit beam with an extended depth-of-focus while suppressing much of the side lobe. We used an angular spectrum-based method to simulate the intensity distributions for many different realizations of the hybrid beamforming to find optimal configurations. We implemented these configurations experimentally with a linear array transducer and tested them in two elastic phantoms. We analyzed the motion and the shear wave speed estimates to evaluate the shear wave speed accuracy with depth. We conclude with discussion of the results.

Methods

First, we describe the theory of hybrid beamforming and its ability to extend the DOF of the ultrasound beam used for shear wave generation. With the focusing time-delays derived from the theory, we use an angular spectrum simulation method for different configurations to find the most optimal configurations, that is, maximizing the depth-of-field of the ultrasound beam. We implemented the optimized simulated configurations experimentally and applied them on two phantoms with different shear moduli to estimate the shear wave speed accuracy with depth produced by the new methods to show that increasing the DOF, which is the goal in this study, does not have any detrimental effect on speed measurement accuracy.

Theory

The purpose of hybrid beamforming is to use both spherical focusing and axicon focusing to produce a beam for making a shear wave with increased DOF so that shear wave measurements can be made over a range of depths with a flat shear wave. This kind of focusing not only elongates the beams, but also it helps to minimize the side lobes and preserve the beam width. The focusing time delays at the edges between the spherical and axicon parts of the aperture are matched carefully to decrease the phase distortion effects (Hooi et al. 2010).

Assuming a linear array transducer with N elements, we devote 2N_s elements for what we call spherical focusing or traditional focusing. We also use 2N_ax elements for axicon focusing. The total number of elements is

$$N=2N_S+2N_{ax}.$$ (2)

We determine the time delays for half of the aperture and apply the resulting time delays symmetrically. The lateral extent, X₁ in Fig. 1, for the spherical focusing portion of the transducer is

$$X_1=w∕2+w{N}_S,$$ (3)

where w is the pitch of the elements. This represents the transition point from spherical focusing to axicon focusing. The end of the axicon focusing occurs at

$$X_2=w∕2+w(N_S+N_{ax}).$$ (4)

Figure 1.

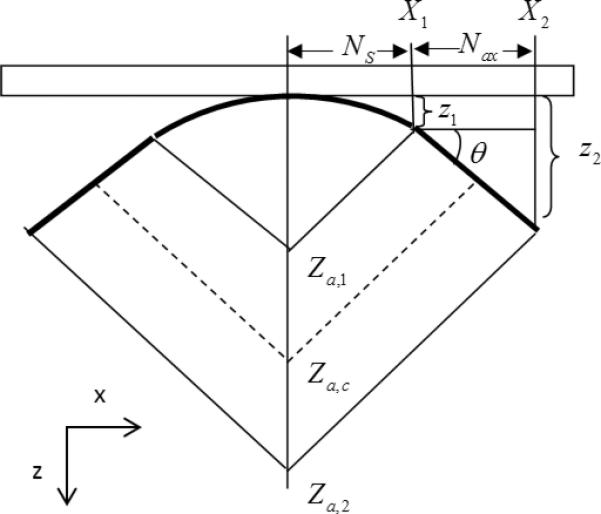
Geometrical diagram for calculating time-delays for hybrid beamforming. N_s is the number of elements allocated to spherical part, N_ax is the number of elements allocated to axicon part, θ is the axicon angle. The parameters Z_a,1, Z_a,2, Z_a,c indicate the beginning, end, and center of the axicon beam formed, respectively.

The spherical focusing delay can be calculated for focusing at a depth of z_f along the central axis by using

$$t_s\left(x_n\right)=(z_f-\sqrt{z_f^2+x_n^2})∕c,$$ (5)

where c is the speed of sound in the medium and x_n is the lateral position of the center of the nth element.

Patterson and Foster studied conical radiators and described the geometry for frustrum-shaped lens that we will use for this derivation (Patterson and Foster 1982). If we use the analogy in which the delays are like a physical lens on an unfocused transducer then we want to find the physical position that corresponds to the transition point between the spherical and axicon focusing. This can be represented by the point (X₁,Z₁) where

$$Z_1=c{t}_s\left(X_1\right)$$ (6)

The axicon is defined by an angle θ as defined in Fig. 1. Following the derivation described by Patterson and Foster (Patterson and Foster 1982), the position of the end of the axicon focusing element is given by

$$Z_2=Z_1+(X_2-X_1)\tan \left(\theta \right)=Z_1+w{N}_{ax}\tan \left(\theta \right).$$ (7)

We can determine key points on the central axis related to the axicon focusing. The depths of the start, center, and end of the axicon focusing occurs at Z_a,1 = Z₁/sin²(θ), Z_a,c = (Z₁ + Z₂)/2sin²(θ), Z_a,2 = Z₂/sin²(θ), respectively. The time delays due to the axicon can be found using a linear fitting by,

$$t_{ax}\left(x_n\right)=\frac{1}{c}\left(\frac{Z_2-Z_1}{X_2-X_1}{x}_n+Z_1-\frac{Z_2-Z_1}{X_2-X_1}{X}_1\right).$$ (8)

The complete set of time delay is

$$t_d=\left\{\begin{array}{cc}\hfill (z_f-\sqrt{z_f^2+x_n^2})∕c,& x_n=\mid [w∕2,w∕2+w{N}_S]\mid \hfill \\ \hfill \frac{1}{c}\left(\frac{Z_2-Z_1}{X_2-X_1}{x}_n+Z_1-\frac{Z_2-Z_1}{X_2-X_1}{X}_1\right),& x_n=\mid [w∕2+w{N}_S,w∕2+w(N_S+N_{ax})]\mid \hfill \end{array}\right\}.$$ (9)

To make the delays all positive and the delays at the edge of the arrays identically zero, that is, the outer elements have zero delay, we apply the rule

$$t_d=t_d-t_d(w∕2+w(N_S+N_{ax})).$$ (10)

Simulations

We used the angular spectrum method to simulate the hybrid beamforming results (Vecchio et al. 1994). We simulated the intensity distributions because the radiation force is proportional to the intensity (F = 2αI/c, where α is the ultrasound attenuation) (Nightingale et al. 2001). To choose the optimal cases, we defined a window of 2 mm × 20 mm (in x- and z-directions, respectively, as shown in Fig. 1 centered about the designated focal distance to analyze the results quantitatively within this window.

Our goal is to produce a beam that is maximally long in terms of depth-of-field or resolution in the z-direction, R_z. We also desire a beam that has intensity that is maximally uniform having the highest mean value, I_m, over the length of the beam. We varied the number of active elements in aperture, N, number of axicon elements for a half aperture configuration, N_ax, axicon angle, θ, the spherical focusing depth, z_f. We simulated the x-z plane for each combination of these parameters. For each prescribed focal depth, we found the configuration which maximizes the R_z and the intensity-depth product of I_m·R_z. The product I_m·R_z emphasizes both the geometry of the formed beam as well as the intensity magnitude. To define the R_z resolution cell we used a cutoff level of −6 dB.

We studied three different aperture sizes of active elements, N = 64, 96 and 128. For each case we set the spherical focus value, z_f, from 10 mm to 40 mm in 5 mm increments. The number of axicon elements, N_ax, also increased from 0, which results in a spherical focusing aperture, to half of the number of active elements, which represents the full axicon focusing case. The increment used for N_ax was 4 elements. The axicon angle, θ, was varied from 0° to 40° in 2° increments.

The linear array that is used is modeled after the one used for experiments. The elements in this array have a height of 7 mm, width of 0.288 mm, and pitch of 0.308 mm (kerf = 0.020 mm). We use an ultrasound frequency of 4.09 MHz and assumed medium parameters of ρ = 1000 kg/m³, c = 1540 m/s, and an ultrasound attenuation of 0.5 dB/cm/MHz.

Phantom studies

A Verasonics ultrasound system (Verasonics, Inc. Redmond, WA) was used in this study to make shear wave speed measurements with a linear array transducer (L7-4, Philips Healthcare, Andover, MA). The center frequency used for push and detection was 4.09 MHz. The propagation of the shear wave was monitored by the L7-4 probe using compounded plane wave imaging (Zhao et al. 2012). We used three angle compounding with angles −4°, 0°, and +4° (Montaldo et al. 2009). The imaging rate for each angle was 10 kHz and so the effective frame rate for the compounded frame was 3.33 kHz. Tissue velocity due to shear wave motion was calculated from in-phase/quadrature (IQ) data, using a one-dimensional autocorrelation method (Kasai 1986). The beam was focused in the middle of the transducer aperture. We applied a directional filter on the data to isolate only right-traveling waves on the right side of the focus and vice versa for the left-propagating waves (Manduca et al. 2003). The motion was averaged using 1.54 mm windows. A Radon transform algorithm was applied to measure the propagation shear wave velocity for each window (Urban and Greenleaf 2012). In brief, a full Radon transform of the shear wave motion is taken as opposed to a Radon sum that was previously reported by Rouze, et al (Rouze et al. 2010). The angle at which there is a peak in the Radon transform space is identified and used to calculate the shear wave speed. The angle is related to the time and space dimensions of the image representation of the shear wave propagation.

We tested the optimal configurations in two custom made elastic phantoms (CIRS, Inc., Norfolk, VA) with shear wave speeds of 1.48 and 3.96 m/s. We made measurements in each phantom at five different locations, and the results are presented as means and standard deviations of these data.

The shear wave speed in the softer phantom (P1) used in this study has been compared to measurements made with Magnetic Resonance Elastography (MRE) and Transient Elastography (TE) (Zhao et al. 2012). The results from the unfocused beam study showed very good consistency through depth and good agreement with the MRE and TE results. As a result, we regarded the unfocused push method as a validated, in-house method to make measurements in other phantoms. The stiffer phantom (P2) was evaluated with unfocused beams as discussed by Zhao, et al. (Zhao et al. 2012), For P1, the push length was 400 μs and for P2 the push length was set to 600 μs because P2 is stiffer. For consistency, we performed measurements with unfocused beams in the two phantoms at five different locations and found mean and standard deviations of the shear wave speed of 1.48 ± 0.04 m/s for P1 and 3.96 ± 0.11 m/s for P2. These values were used for our reference values for evaluating shear wave speed accuracy.

The DOF for accurate shear wave velocity measurements was evaluated by finding the number of averaged data sets through depth that had speed within a range of 1.48 ± 0.15 m/s for P1 and 3.96 ± 0.11 m/s for P2. Then, we multiplied the number of the data sets within these speed ranges by 1.54 mm. The points evaluated for the DOF were only included if they were contiguous with other points. The optimal configurations from the simulated results based on maximizing R_z and I_m·R_z, were tested on phantoms with the known shear wave speeds in order to understand the relationship between optimizing the intensity distribution and its effects on the accuracy of shear wave speed estimation. To evaluate this we made measurements of shear wave velocity and the DOF over which these shear wave velocities were accurate within the tolerances given above.

Results

Figure 2 shows optimal simulated intensity beam shapes for cases of N = 64, 96, and 128 elements, in the three rows, respectively, at focal depths of z_f = 15, 25, 35 mm in the three columns, respectively. The optimal settings found using the R_z criteria for the different beams are specified in Fig. 2 and Tables 1, 2, and 3 for the cases of N = 64, 96, and 128 elements, respectively. Each of the beam shapes are plotted on a linear scale.

Figure 2.

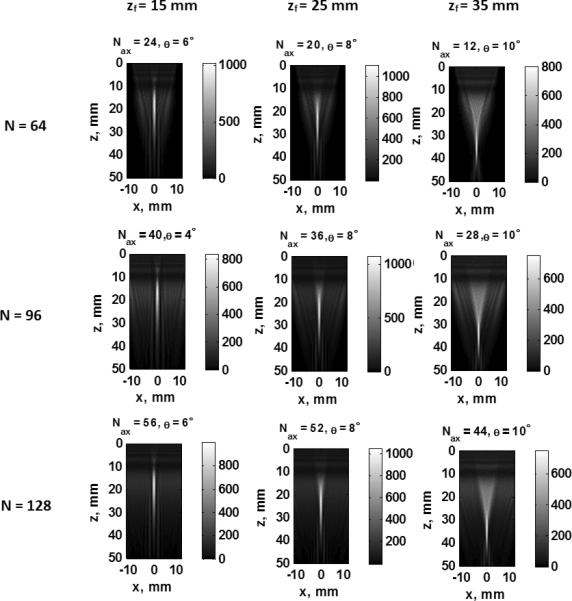
Simulation results for optimal beams using the R_z optimization criteria. The rows are arranged with N = 64, 96, and 128 elements, respectively, and the three columns have z_f = 15, 25, and 35 mm, respectively.

Table 1.

Simulation and experimental results using N = 64 elements. All R_z and R_z,D measurements are made in mm.

Focal Depth, mm	Spherical Simulation	Hybrid Simulation						Spherical Experiment		Hybrid Experiment
		Rz			Im·Rz					Rz		Im·Rz
								P1	P2	P1	P2	P1	P2
	Rz	Nax	θ	Rz	Nax	θ	Rz	Rz,D	Rz,D	Rz,D	Rz,D	Rz,D	Rz,D
10	1.03	20	2°	9.03	20	10°	8.33	9.16	17.32	12.60	25.41	19.92	23.51
15	1.98	24	6°	15.27	24	6°	15.27	7.82	19.93	18.48	20.67	18.48	20.67
20	3.19	28	4°	18.38	24	8°	15.03	12.84	18.45	19.33	21.70	17.96	22.76
25	4.53	20	8°	15.59	20	8°	15.59	18.46	18.66	20.91	22.39	20.91	22.39
30	6.08	16	8°	18.16	16	8°	18.16	22.87	19.03	20.93	22.18	20.93	22.18
35	7.96	12	6°	16.26	12	10°	15.23	25.81	20.68	19.54	19.33	23.02	21.21
40	9.71	8	8°	19.17	8	8°	19.17	25.69	22.36	21.81	20.98	21.81	20.98

Table 2.

Simulation and experimental results using N = 96 elements. All R_z and R_z,D measurements are made in mm.

Focal Depth, mm	Spherical Simulation	Hybrid Simulation						Spherical Experiment		Hybrid Experiment
		Rz			Im·Rz					Rz		Im·Rz
								P1	P2	P1	P2	P1	P2
	Rz	Nax	θ	Rz	Nax	θ	Rz	Rz,D	Rz,D	Rz,D	Rz,D	Rz,D	Rz,D
10	1.03	36	0°	8.67	36	12°	7.64	11.55	17.76	12.10	23.29	19.79	26.43
15	1.98	44	2°	16.39	40	4°	14.84	7.44	19.79	16.15	20.96	18.02	20.52
20	3.19	44	4°	18.00	40	6°	17.82	10.95	19.31	18.01	20.04	19.65	20.23
25	4.53	36	8°	16.43	36	8°	16.43	17.03	19.59	21.25	22.78	21.25	22.78
30	6.08	32	10°	15.21	32	10°	15.21	24.18	22.19	24.26	21.94	24.26	21.94
35	7.96	28	10°	15.57	28	10°	15.57	30.49	23.55	24.27	21.61	24.27	21.61
40	9.71	20	8°	13.72	20	8°	13.72	31.58	25.12	24.55	21.66	24.55	21.66

Table 3.

Simulation and experimental results using N = 128 elements. All R_z and R_z,D measurements are made in mm.

Focal Depth, mm	Spherical Simulation	Hybrid Simulation						Spherical Experiment		Hybrid Experiment
		Rz			Im·Rz					Rz		Im·Rz
								P1	P2	P1	P2	P1	P2
	Rz	Nax	θ	Rz	Nax	θ	Rz	Rz,D	Rz,D	Rz,D	Rz,D	Rz,D	Rz,D
10	0.58	52	2°	8.89	52	10°	8.41	8.53	16.69	12.10	27.18	18.10	24.25
15	0.88	64	2°	15.29	56	6°	15.25	7.98	19.51	15.69	18.15	20.02	21.75
20	1.23	56	6°	17.58	56	6°	17.58	12.63	19.45	20.74	19.60	20.74	19.6
25	1.63	52	8°	16.97	52	8°	16.97	17.14	20.05	20.51	19.88	20.51	19.88
30	2.11	48	10°	13.80	48	10°	13.80	25.69	22.39	23.15	21.34	23.15	21.34
35	2.65	44	10°	16.18	44	10°	16.18	31.03	25.21	22.38	20.76	22.38	20.76
40	3.23	40	10°	15.83	40	10°	15.83	35.22	26.18	24.05	22.28	24.05	22.28

Figure 3 shows a comparison between the spherical focusing method and the hybrid focusing method. In this case, N = 96 for both cases and the z_f = 30 mm. For the hybrid case, N_ax = 32, θ = 10° are the parameters for the optimized configuration. Figures 3(a) and 3(d) are simulated intensity results from the spherical and hybrid focusing, respectively, with yellow contours related to the −6 dB cutoff levels of the beams. Figures 3(b) and 3(e) represent the spherical and hybrid beamforming results, respectively, in P1 0.34 ms after applying the radiation force push. Figures 3(c) and 3(f) show the shear wave motion produced by the spherical and hybrid beamforming, respectively, in P1 4.5 ms after applying the radiation force push. These simulation and experimental results illustrate the larger depth-of-field with a flat wavefront with the hybrid beamforming technique.

Figure 3.

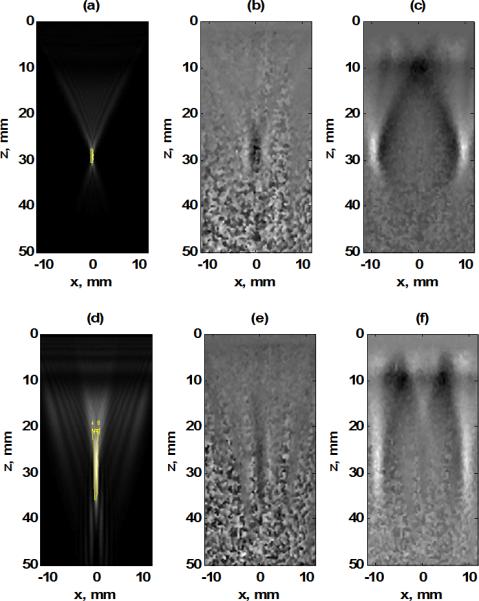
Comparison of spherical and hybrid beamforming methods with N = 96 elements and z_f = 30 mm, (a) Simulated intensity result for spherical focusing and contour for -6 dB level (colored yellow), (b) Shear wave particle velocity from spherical focus 0.34 ms after the radiation force push. (c) Shear wave particle velocity from spherical focus 4.5 ms after the radiation force push, (d) Simulated intensity result for hybrid focusing and contour for −6 dB level (colored yellow), (e) Shear wave particle velocity from hybrid focus 0.34 ms after the radiation force push, (f) Shear wave particle velocity from hybrid focus 4.5 ms after the radiation force push.

Tables 1-3 include the simulation and experimental results for comparison for N = 64, 96, 128, respectively. For each aperture size and each value of z_f, we listed the configurations (N_ax, θ) for the optimized beams for the R_z and I_m·R_z criteria when evaluating with a cutoff of −6 dB. The R_z values for each of the simulated cases are shown. To compare with the simulated values of R_z, we computed the beam resolution of the experimental data based on the displacement peak amplitude and found the R_z,D based on a −6 dB cutoff. The displacement is proportional to the force, which is proportional to the intensity produced by the simulations. The values were tabulated in Tables 1-3 for the spherical and hybrid beamforming results for phantoms P1 and P2.

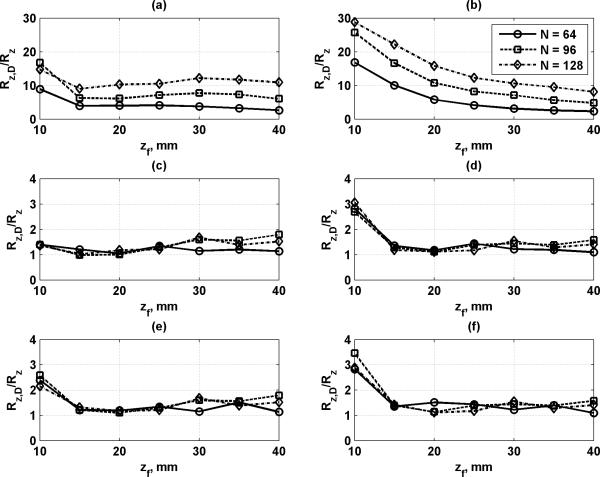
Figure 4 shows the ratio of the values of R_z,D and R_z from the experiments and simulations, respectively. When this ratio is close to 1, then the experimental displacement beam resolution is similar to that found in the simulations. This is indicative that the simulations can reliably predict the size of the wavefront of the induced shear wave.

Figure 4.

Comparison of R_z,D and R_z values from Tables 1-3. The ratio of R_z,D and R_z is plotted for N = 64, 96, and 128 elements. (a) Spherical focusing, P1, (b) spherical focusing, P2, (c) hybrid focusing, R_z optimization criteria, P1, (d) hybrid focusing, R_z optimization criteria, P2, (e) hybrid focusing, I_mR_z optimization criteria, P1, (f) hybrid focusing, I_mR_z optimization criteria, P2.

Figures 5(a) and 5(b) illustrate a comparison between the shear wave speeds measured using hybrid and spherical focusing through depth in P1 and Figures 5(c) and 5(d) show the same comparison in P2. In all figures horizontal lines are drawn to show the true shear wave speed and low and high tolerance levels which were 1.48 ± 0.15 m/s for P1 and 3.96 ± 0.15 m/s for P2. For both cases N = 96, z_f = 30 mm, and in the hybrid case N_ax = 32 and θ = 10°. The large shear wave speeds close to transducer surface are probably artifacts due to ill-defined peaks used for shear wave speed estimation.

Figure 5.

Comparison of shear wave speed between spherical and hybrid beam forming methods with N = 96 and z_f = 30 mm in phantoms P1 and P2. In all the plots the mean and standard deviations from five measurements are shown, (a) P1 results for spherical focusing case with true speed of 1.48 m/s and ±0.15 m/s threshold, (b) P1 results for hybrid focusing case with true speed of 1.48 m/s and ±0.15 m/s threshold, (c) P2 results for spherical focusing case with true speed of 3.96 m/s and ±0.15 m/s threshold, (d) P2 results for hybrid focusing case with true speed of 3.96 m/s and ±0.15 m/s threshold.

Figure 6 shows the experimental results for the DOF measured in P1and P2 for all three values of N related to all spherical and hybrid focusing schemes. For the hybrid cases we show the result from either the R_z or I_m·R_z optimization criteria which gives the maximum DOF value. The DOF in almost all cases are larger for the hybrid focusing compared to the spherical focusing for P1 (20 out of 21 configurations). For the results of P2, the hybrid DOF is better than the spherical DOF in a majority of cases (14 out of 21 configurations). The DOF also increases with greater focal distance in P1, but the maximum DOF values occur at z_f = 30 mm in P2.

Figure 6.

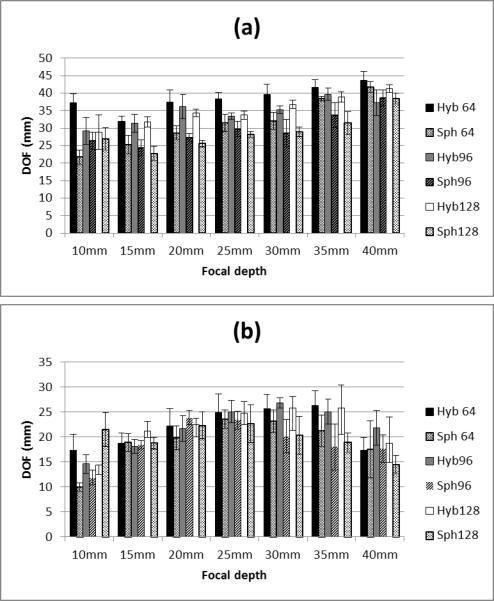
Comparison of DOF for different types of focusing at values of z_f in phantoms P1 and P2. The plotted values are the mean and standard deviations from five measurements, (a) Comparison of hybrid and spherical focusing DOF results for N = 64, 96 and 128 elements in P1, (b) Comparison of hybrid and spherical focusing DOF results for N = 64, 96 and 128 elements in P2.

Figure 7 shows the measurements of shear wave speed for the spherical and hybrid focusing in P1 over the DOF for different number of elements, parts (a), (b), and (c) refers to N = 64, 96, and 128 elements, respectively. The true mean shear wave speed for P1 is 1.48 m/s. We report the mean speed found for the hybrid focusing over the hybrid DOF (Hyb), and the spherical focusing over the spherical DOF (Sph). Within the defined DOF for each focusing technique, the shear wave speed estimates are similar for both methods. As the focal depth increases, the error is reduced. In Fig. 8 we plotted similar DOF metrics for results in P2 where the true mean shear wave speed is 3.96 m/s. The layout for Fig. 8 is similar to that of Fig. 7. The shear wave speeds for the hybrid and spherical focusing were close to the true shear wave speed.

Figure 7.

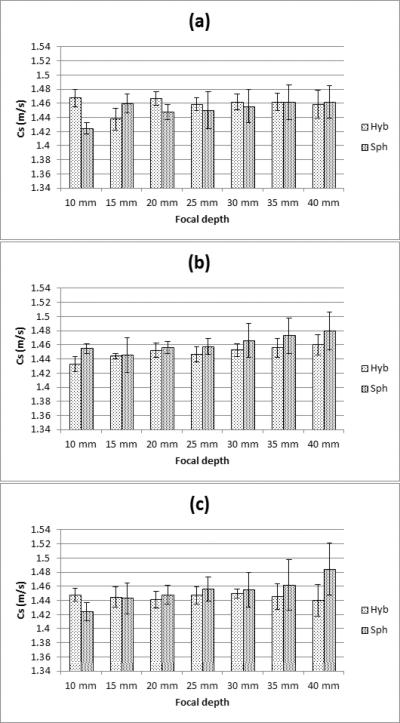
Comparison of the shear wave velocity measurement in P1 using the hybrid focusing (Hyb), the spherical focusing (Sph). The plotted values are the mean and standard deviations from five measurements, (a) N = 64 elements, (b) N = 96 elements, (c) N = 128 elements.

Figure 8.

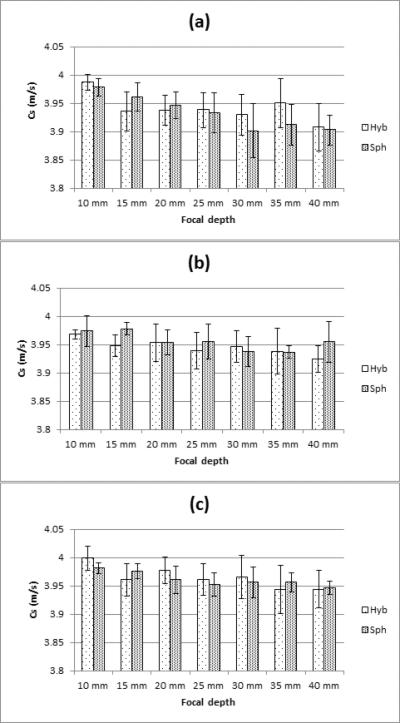
Comparison of the shear wave velocity measurement in P2 using the hybrid focusing (Hyb), the spherical focusing (Sph). The plotted values are the mean and standard deviations from five measurements, (a) N = 64 elements, (b) N = 96 elements, (c) N = 128 elements.

Discussion

The proposed hybrid beamforming method is the result of combining spherical and axicon focusing and has the capability to increase depth-of-field of the resulting ultrasound beam. We used a simulation approach to determine optimal hybrid focusing configurations and implemented them for experimental evaluation.

We confirmed that the hybrid beamforming scheme can produce beams with a larger portion of the shear wave front that is flat compared to conventional spherical focusing using the same aperture size and focal depth. This is illustrated both from simulation and experimental results in Fig. 3. Figure 5 depicted the variation of shear wave speed through depth measured using the spherical and hybrid focusing approaches. These plots demonstrate the degree to which the shear wave speed estimates vary from the accepted values for the phantoms. The values found using the hybrid beamforming are closer to the real shear wave speed when compared to the spherical method. These shear waves speed results are more stable through the depth especially when it comes to the stiffer phantom the fluctuation in shear wave speed values for hybrid case is smaller than the spherical case.

The data tabulated in Tables 1-3 compare the simulation results for the optimized hybrid focusing beams and the spherical focusing results. Also contained in these tables are the experimental results from the measured displacement in P1 and P2. The values from the simulations, R_z, and experiments, R_z,D, were in fairly good agreement for the hybrid beamforming configurations, but the R_z,D values are much larger for the spherical focusing when comparing to the simulation R_z values. The plots in Fig. 4 show that the ratios of R_z,D/ R_z are close to 1 in many cases except for the hybrid focusing with z_f = 10 mm and for the spherical focusing cases. This increased measured motion could be due to boundary conditions in the experiments that are not accounted for in the simulations such as shear wave propagation near the surface of transducer because the focal zone is close to the surface of the phantom. In the spherical focusing case, there may be significant motion in the near-field before the specified focal depth that increases the values of R_z,D.

We used two different optimization criteria, R_z and I_m·R_z in this study. To a great degree both optimization criteria provide the same parameters, particularly at larger focal depths. The experimental results showed that when the beams were different, the I_m·R_z beam provided a slightly higher R_z,D value at shallow focal depths and with N = 96 and 128 elements.

Figure 6 demonstrates that the DOF values obtained with the hybrid beamforming technique are larger than those produced with spherical focusing. In the softer P1, which had a shear modulus similar to healthy liver (Chen et al. 2009), the DOF increased with focal depth largely because the effective f/number increased. However, the stiffer P2, which had a shear modulus similar to relaxed skeletal muscle (Zhao et al. 2012), (Gennisson et al. 2010), yielded DOF values that were largest at focal depths from 25-30 mm. This may be due to reduced shear wave amplitude produced at the deeper focal depths. It should be noted that both phantoms had similar ultrasound attenuation.

In Fig. 6(a), showing the results in the softer phantom, the mean DOF in the case of 64 elements is larger for the hybrid method compared to the spherical one. The best results for N = 64 elements occur at the shallower focal depths. For the case of N = 96 elements the same trend is repeated. At 40 mm, the spherical focusing result provides a slightly higher DOF. For N = 128 elements in all cases the hybrid method produces a beam that has the longer depth of field compared to spherical cases. When using 64 elements the hybrid gives a larger DOF difference at focal depths of 10, 15, and 20 mm, while the 128 element configuration provides larger differences at focal depths of 20, 25, 30, and 35 mm. The hybrid method had a higher mean DOF in 20 of 21 configurations.

The results are different in the stiffer phantom as shown in Fig. 6(b). The mean DOF was larger for the hybrid method in 14 of 21 configurations. The hybrid method had higher mean DOF for focal depths of 25, 30, and 35 mm for all aperture sizes. In the stiffer material, the shear wave amplitude may not be as high when using the hybrid method as compared to the conventional spherical focusing, and as a result a valid shear wave measurement cannot be made at certain locations.

When it comes to the stiffer phantom P2, the spherical method could be more advantageous due to higher concentration of energy in this case compared to hybrid case. These results provide guidance to use the most relevant configuration to gain adequate data to make a valid measurement. It should be noted that in most of the cases where the spherical focusing did have a higher mean DOF, the values of DOF were fairly close.

Figures 7 and 8 demonstrate that the two methods generally produce accurate measurements of shear wave speed within the DOF found from the experiments. In both phantoms, the mean shear wave speeds underestimated the reference shear wave speeds, but the values were within one standard deviation of the reference measurements. It is fundamentally important for clinical applications to make accurate shear wave speed measurements so if the range over which accurate shear wave speed measurements can be extended, more tissue can be investigated in one acquisition. These figures also confirm that hybrid beamforming has the capability to measure the shear wave speed over a large area covered by the hybrid beam with a high accuracy while when using spherical focusing case the area covered by the beam is much smaller for similar levels of accuracy. To obtain the same DOF with spherical focusing, multiple acquisitions would be necessary to match that of the hybrid beamforming DOF.

We have found optimal beam configurations for different focal depths and different size apertures. These optimal configurations could be stored in a look-up table for different applications such as thyroid, breast, and musculoskeletal shear wave measurements.

There are a few limitations for this proposed method. Because the energy in the beam is being distributed over a larger area in the hybrid focusing case as compared to the more concentrated deposition of energy with spherical focusing the peak motion amplitude is reduced so the shear waves may not propagate as far from the push location before being attenuated to a level below where reliable measurements can be made. This may limit the lateral extent for analysis of the shear waves produced by hybrid focusing in real tissues.

An added advantage to distributing the energy that was concluded by Hazard et al. (Hazard et al. 2012) was that increasing depth-of-field may help to deposit more energy while the peak energy is maintained at a lower level in order to satisfy regulatory limits such as those made for the mechanical index (Herman and Harris 2002). If the system has sufficient power capabilities, higher intensity could be generated while still falling under the acoustic output limits imposed by the Food and Drug Administration. The SSI technique also produces a shear wave with a large depth-of-field, but uses spherically focused beams that are stepped in depth at a fast rate. Therefore, the hybrid beamforming method may not be as limited in acoustic output as the SSI method may be. Another optimization metric for the hybrid beamforming method could be used in the future could relate to the maximum energy that can be deposited.

The hybrid beamforming method produces a beam with a large DOF. The methods that most closely compare with this large DOF are SSI and using an unfocused beam. The main advantage of using the hybrid beamforming method compared to other methods like SSI is that in hybrid beamforming we apply just one push and cover a large area but using SSI the same area is interrogated by applying different pushes at successively different times. In most cases, the resulting displacement when using SSI is higher than when using hybrid beamforming, but as the results show in this study, the shear wave produced by the hybrid beamforming resulted in sufficient displacement for shear wave speed estimation.

For an unfocused beam, the energy deposition is lower because fewer elements are used and there is no gain from focusing. The shear wave may be better defined at shallower depths using the unfocused push as some of the fields produced by hybrid beamforming can be complicated in the 10 mm closest to the transducer. However, hybrid beamforming can be used for deeper depths where unfocused pushes are only effective up to about 35 mm. A more systematic study would have to be conducted to evaluate how these three methods truly compare in terms of shear wave amplitude, DOF, and accuracy of shear wave speed estimation.

In future studies we will explore the frequency characteristics of shear waves produced by hybrid beamforming technique to assess the ability for viscoelastic tissue characterization. Additionally, we will explore using this beam for shear wave imaging applications because the hybrid beam offers a beam with large depth-of-field.

Conclusion

One of the emerging quantitative, noninvasive modalities that can help clinicians to understand different disease processes is to measure the tissue elasticity with ultrasound. By combining the spherical and axicon focusing we introduce a new beam forming methods called hybrid beamforming for shear wave generation. The unique characteristic of this method is to generate a shear wave which has increased depth-of-field. In this paper we presented the aperture design and beam optimization performed using angular spectrum methods. We tested this new method to evaluate the shear wave speed measurement accuracy as well as the DOF for each hybrid beam in two different phantoms with different shear moduli. These results were compared with measurements made using spherical focusing. We found that hybrid beamforming can increase the depth-of-field most significantly when the desired focal depth ranged from 15-35 mm for different aperture sizes in two different elastic phantoms.