Bias in Estimates of Quantitative-Trait–Locus Effect in Genome Scans: Demonstration of the Phenomenon and a Method-of-Moments Procedure for Reducing Bias

Abstract

An attractive feature of variance-components methods (including the Haseman-Elston tests) for the detection of quantitative-trait loci (QTL) is that these methods provide estimates of the QTL effect. However, estimates that are obtained by commonly used methods can be biased for several reasons. Perhaps the largest source of bias is the selection process. Generally, QTL effects are reported only at locations where statistically significant results are obtained. This conditional reporting can lead to a marked upward bias. In this article, we demonstrate this bias and show that its magnitude can be large. We then present a simple method-of-moments (MOM)–based procedure to obtain more-accurate estimates, and we demonstrate its validity via Monte Carlo simulation. Finally, limitations of the MOM approach are noted, and we discuss some alternative procedures that may also reduce bias.

Introduction

When the linkage of genetic markers to quantitative traits is tested, two classes of tests are commonly used. One class selects extremely concordant and/or extremely discordant pairs of relatives and tests for deviations between the distribution of identity-by-descent (IBD) scores and the distribution that was expected under the null hypothesis (Risch and Zhang 1995, 1996). Another class tests whether there is an association between the number of alleles that a relative pair shares IBD and the degree of phenotypic similarity for any given type of biological relation. This latter class of tests includes several least-squares implementations of the Haseman-Elston (HE) test (e.g., see Haseman and Elston 1972; Elston et al. 2000), maximum-likelihood (ML) testing (e.g., see Hopper 1993; Amos 1994; Fulker and Cherny 1996), and robust methods (e.g., see Guerra et al. 1999). If the phenotypes are standardized to unit variance and if we assume the recombination fraction between the marker and the QTL to be zero, then each of these testing procedures involves the modeling of a parameter that directly estimates the proportion of variance that is explained by the QTL. When the sample is randomly ascertained—and, in some cases, when it has not been randomly ascertained (Dolan et al. 1999)—it is possible to obtain nearly unbiased estimators of the QTL effects. However, several factors in the common practice of genome scanning can lead to marked biases in these estimates.

One minor factor is that it is common practice to constrain variance components to lie within their theoretical boundaries of 0.0 and 1.0 (when components are expressed as a proportion of total variance). For example, in the case of the second version of the HE test (Elston et al. 2000), which we denote as “HE2,” this would involve either setting the QTL-effect estimate to 0.0 if the ordinary-least-squares (OLS) estimate of the slope were <0.0 or, in case the phenotypes had been standardized to unit variance before analysis, setting the QTL-effect estimate to 1.0 if the OLS estimate of the slope were >1.0. In the ML framework, this involves the constraint of both the QTL variance and any other variance components in the model to remain nonnegative. This is analogous to the case of multiple regression, in which adjusted R² values must be allowed to go below 0.0 to obtain unbiased estimation of the population R², even though R² values theoretically cannot go below zero. Constraint of the estimates to lie within their theoretical boundaries can lead to small upward biases for true effects near the lower boundary and small downward biases for true effects near the upper boundary. However, such constraints usually lead to estimates with smaller mean-square errors (MSEs), which is desirable (McCulloch and Searle 2000).

A second source of bias can be quite dramatic. It involves the fact that QTL effects are generally estimated or presented only when a significant result is obtained. For example, in a genome scan by Pratley et al. (1998), results are only reported for markers with LOD scores ⩾1.2. Given such selection, even if an estimator is completely unbiased when considered across all markers tested, there will be marked upward biases when estimation is performed or presented only at significant loci. This bias has been demonstrated in the literature on multiple testing in general (Thomas 1985) and in the context of QTL detection in experimental crosses (Beavis 1998; Kearsey and Farquhar 1998; Melchinger et al. 1998; Utz et al. 2000) but has not been studied in detail for QTL mapping in humans.

Similarly, in the context of a genome scan, when a region is detected where there is a statistically significant QTL effect, there may be several loci within the region at which results are statistically significant. However, the putative effect is generally presented only at the peak (i.e., the point within the region where the evidence of linkage is strongest), even though, in some cases, the QTL may lie within the identified region but not at the exact point of the peak. That is, not only do genetics researchers tend to report only estimates that are statistically significant, but, within regions, they tend to report only the largest of all significant results. This selection process may exacerbate the problems of biased estimation; however, we will not consider this issue specifically. Rather, for the sake of simplicity, we simulated conditions in which only statistically significant results are used to estimate a single QTL effect. Therefore, our simulations have a conditional selection process similar to that of a genome scan. Furthermore, any newly proposed method needs to be analyzed under less restrictive conditions before its performance can be evaluated under more-complicated circumstances.

Using simulation, Beavis (1998) showed that QTL-effect estimates obtained in genome scans with experimental crosses are likely to be marked overestimates for many realistic scenarios. (He also showed that the number of true QTLs is often markedly underestimated.) The degree of overestimation is inversely related to the power of the study, with small QTL effects yielding more-severe overestimation. However, he offered no solution. Göring et al. (2001) provided an analytical expression for this bias and demonstrated that the estimate of the QTL effect is essentially independent of the true underlying QTL effect. However, they only presented studies from an ML-estimation approach, which have certain distributional assumptions.

Here we show that this problem of overestimation can also be of large magnitude in studies of QTL mapping in humans. We then consider potential solutions and show how a method-of-moments (MOM) procedure, which does not have stringent distributional assumptions, can offer far more accurate and unbiased estimation. The MOM procedure that we developed has the advantage of conceptual simplicity and, at least in certain cases, can be implemented retroactively, for published genome scans, even in the absence of the raw data. However, it also has certain disadvantages, and we therefore discuss potential alternative approaches.

Methods

Notation and Terminology

In this article, we refer to the estimate of a QTL effect from any method that tests and estimates each QTL effect individually as a “preliminary estimate.” In addition, we will use the following notation:

• σ²_QTL = the proportion of variance in the phenotype explained by the QTL under study (i.e., the effect to be estimated);

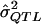• = a preliminary estimator of σ²_QTL;

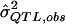• = a specific realization of the random variable 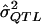(i.e., the 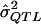value that one observes in one’s sample for a specific locus);

• α = the prespecified level (test size) for the probability of a type I error;

• P = the observed probability value from the statistical test of the QTL effect.

Statistical Test

In this article, we demonstrate both the problem and the MOM approach by use of HE2 (Elston et al. 2000). Although we illustrate the MOM approach by use of HE2 applied to independent sibling pairs, an important advantage of this approach is that it is easily generalized to other preliminary methods of QTL estimation and other pedigree structures. Denoting the phenotypes of the first and second siblings in the jth sibling pair as “Y_1,j” and “Y_2,j,” respectively, and the proportion of alleles that the pair shares IBD as “π_j,” Elston et al. (2000) developed HE2, a least-squares implementation of a variance-components test in the style of the implementations proposed by Amos (1994) and, subsequently, Fulker and Cherny (1996). In this test, we fit the regression equation

where 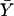is the sample mean of Y for the first and second siblings combined—that is, 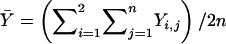. It is assumed that siblings are ordered randomly within pairs. We test the significance of the estimate of β with a one-tailed test in which only positive β values are considered to be indicative of linkage. Given random sampling and complete linkage, the expectation of the sample estimate of β is σ²_QTL—that is, 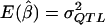, and, therefore, in the context of HE2, .

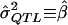The MOM Approach

The MOM approach is among the simplest and earliest of general methods for the derivation of estimators of population parameters. In brief, if a distribution function involves a parameter of interest, one finds a population moment that is a function of the parameter, equates the sample estimate of that moment to the function, and then solves for the parameters (Mood 1950; Ross 1987). This method is limited only by the ability to derive and to solve the functions. However, computer simulation makes this a tractable task, even in complex situations (Pakes and Pollard 1989; Gallant and Tauchen 1999). An advantage of MOM estimators is that, unlike ML estimators, they do not require assumptions about the higher-order moments of data. Therefore, MOM estimates are free from distributional assumptions about the data.

Because, in the context of the genome scan, we usually present only significant results, we are sampling from a truncated distribution of 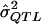. The MOM procedure identifies the truncated distribution of 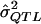, which is determined by the underlying genetic model such that 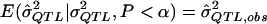. In essence, by using the MOM procedure, we are asking, “What σ²_QTL value has an expected QTL estimate of 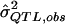among only those results that are statistically significant?” We then use that value as the MOM estimate of σ²_QTL. To determine the truncated distribution of 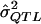, many features of the underlying genetic model may be specified, including σ²_QTL, mode of inheritance, and allele frequency, as well as the sampling scheme, the sample size, and the preliminary estimation procedure used. Therefore, additional assumptions about the σ²_QTL value are not necessary to perform this analysis. For this reason, if the genetic model is complex and includes several unlinked loci, then we will still obtain unbiased estimates of σ²_QTL, owing to the flexibility of the MOM procedure

In some cases, it will be feasible to analytically derive a function to answer this question. For example, in the case of HE2, the sampling distribution of 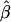is asymptotically normal, and formulae for the expected value of a truncated normal are well established (e.g., see Cohen 1949). However, in virtually all cases, it will be possible to simulate 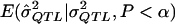(i.e., the expected 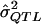value given an assumed σ²_QTL value and given that the observed P value is less than the α level). Such simulations can accommodate any specifiable sampling scheme—as well as any phenotypic distribution, any genetic model, and any preliminary estimation procedure—whereas the derivation of analytic expressions for expected values under truncation in all of these situations may be impractical. One can simulate data under an exhaustive range of values for σ²_QTL until one obtains the σ²_QTL value that empirically minimizes the quantity 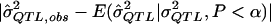, a function of σ²_QTL. By drawing on simulation, the method, although somewhat computationally demanding, is adaptable to virtually any sampling scheme, any pedigree structure, and any initial method of testing and estimating σ²_QTL. Hence, this should not be limited to HE testing, sibling pairs, or random sampling. Yet, for convenience, we focus on these conditions in the current study.

Simulation Parameters and Methods

Several simulation experiments were run. In each experiment, we evaluated both the bias and the MSE of all estimators considered. Bias was estimated as the average of the signed differences between the parameter and its estimator. MSE was estimated as the average of the squared differences between the parameter and its estimator. We simulated QTLs with effects expressed by σ²_QTL values from 0.0 (i.e., no linkage) to 0.99 of the phenotypic variance at increments of 0.01. Note that we do not claim that true QTL effects >0.75 are particularly plausible, but we include them for completeness. Thus, a total of 100 genetic models were used. The residual (within-genotype) distribution was assumed to be normal, and the sibling correlation conditional on genotype (i.e., the residual correlation) was set to zero. Thus, all variance in our simulation is due to major genetic or nongenetic nonshared sources. Each simulated data set consisted of 200 sibling pairs from independent families. Again, these conditions were selected to evaluate MOM-estimation procedures under simple conditions before more-complex issues could be addressed.

Although the genome-scan context is of interest and is slightly more complex, we simulated data at only a single locus. This is because, for QTLs located at unlinked loci, the QTL effects will be uncorrelated, and, therefore, the process that we simulated at a single point would only be replicated at multiple points. That is, for QTLs at unlinked loci, the simulation of a whole-genome scan would be just “more of the same.” For multiple true QTLs within a linkage group, there are substantial unsolved problems with estimation that go far beyond the truncation process we are considering herein, and, thus, such a situation is beyond the scope of this paper. For a single true QTL within a linkage group with QTL effects that are estimated at each point within the linkage group, estimates would be expected to be correlated. The process of selecting the highest point within a region for which there is a significant QTL effect to be the point at which one estimates that QTL effect should increase still further the bias that is herein demonstrated.

In experiment 1, QTL effects were estimated for all data sets, regardless of their significance. In this simulation, 1,000 data sets were generated for each genetic model. In the situation of no selection on the basis of significance, the HE2 procedure was expected to produce approximately unbiased estimates of QTL effects for true effects ∼0.50 and small upward and downward biases for true QTL effects near zero and one, respectively. Thus, this experiment plays a primarily illustrative role.

In experiment 2, data sets were generated, and we concluded that we had identified a QTL if the associated P value from the HE2 test was <.01 (i.e., if the LOD score was ⩾1.2). We generated sample data sets until 1,000 data sets with statistically significant results were generated. The α level of 0.01 (rather than a more stringent level) was used, to minimize the simulation time. The QTL-effect estimates from these 1,000 data sets were then used to illustrate the bias that ordinary estimation have when only significant data sets are selected. This conditional use of only statistically significant results is similar to the selection process that is often used in genome scans in which the researchers declare linkage for a region (or regions) where the LOD score exceeds some predefined critical value.

These same data were then used to illustrate the MOM approach. Specifically, for each data set generated, a MOM estimate of the QTL effect, 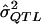, was obtained by (a) the examination of all 100,000 simulated data sets (i.e., 1,000 data sets for each QTL value from 0.00 to 0.99) and (b) the selection of the σ²_QTL value that empirically minimizes the quantity 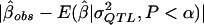, which is a function of σ²_QTL.

In experiment 3, a fresh set of 1,000 significant results for each genetic model were generated as in experiment 2, and we computed the MOM estimates by use of the 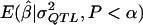values that were obtained in experiment 2. This was done both to check that the apparently desirable performance of the MOM estimators in experiment 2 was not merely due to simulation that was conditional on the specific data from each replicate and to ensure that experiment 4 would be meaningful.

In experiment 4, we address the problem in which the investigator may not know either the true mode of inheritance or the allele frequency when the simulations to estimate 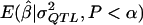are conducted. Here we generated 1,000 data sets with statistically significant results for each σ²_QTL value from 0.0 to 0.99 in increments of 0.01. This was done for each of three combinations of modes of inheritance and allele frequencies:

• Model A. 

  The increasor allele acts dominantly, and the allele frequency is 0.5;

• Model B. 

  The increasor allele acts recessively, and the allele frequency is 0.1;

• Model C. 

  The increasor allele acts recessively, and the allele frequency is 0.9.

For these models, the proportions of σ²_QTL that were attributable to the additive variance (Liu 1998) were 0.67, 0.18, and 0.95, respectively. The MOM estimator was then applied, but with the 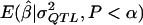values that were derived in experiment 2 by the additive model. This study was performed to determine how much the bias and the MSE of the MOM estimator would be increased by use of a “default,” but incorrect, genetic model.

Results

Experiment 1: No Selection

One thousand data sets were generated, and the QTL effects were estimated in the usual way—that is, by using 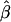from equation (1) and by setting values <0.0 and >1.0 to 0.0 and 1.0, respectively. Results are plotted in figure 1 and are presented, with further details, in table 1. As can be seen, we obtain the expected relatively minor upward biases in the estimates for QTL effects <0.50 and relatively minor downward biases in the estimates for QTL effects >0.50. It should be noted that the bias near the endpoints (0.0 and 1.0) is larger than expected, owing to the fixing of the minimum and maximum values at 0.0 and 1.0, respectively.

Figure 1.

Estimated versus true QTL effects, without selection of only significant results. All analyses included 200 independent sibling pairs and used HE2 to provide the QTL estimates.

Table 1.

Results for the Additive Model with No Selection/Random Sampling (Experiment 1) or Only Significant Results Selected (Experiment 3)

				Only Significant Results
	No Selection/Random Sampling			Ordinary Estimator			MOM Estimator
σ2QTL	Mean	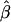Bias	MSE	Mean	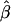Bias	MSE		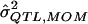Bias	MSE
.00	.08	.08	.02	.52	.52	.28	.05	.05	.01
.01	.09	.08	.02	.53	.52	.27	.05	.04	.01
.05	.11	.06	.03	.56	.51	.27	.08	.03	.02
.10	.14	.04	.03	.59	.49	.25	.11	.01	.02
.15	.19	.04	.04	.62	.47	.23	.16	.01	.03
.20	.21	.01	.04	.66	.46	.22	.22	.02	.04
.25	.26	.01	.05	.69	.44	.21	.27	.02	.04
.30	.32	.02	.05	.72	.42	.19	.31	.01	.05
.35	.35	.00	.06	.75	.40	.17	.37	.02	.06
.40	.40	.00	.06	.77	.37	.16	.42	.02	.07
.45	.45	.00	.08	.81	.36	.15	.50	.05	.08
.50	.50	.00	.08	.83	.33	.13	.55	.05	.08
.55	.54	−.01	.08	.86	.31	.11	.61	.06	.08
.60	.59	−.01	.08	.89	.29	.09	.67	.07	.08
.65	.62	−.03	.09	.91	.26	.08	.72	.07	.08
.70	.66	−.04	.08	.93	.23	.06	.77	.07	.07
.75	.70	−.05	.07	.94	.19	.04	.81	.06	.06
.80	.71	−.09	.08	.95	.15	.03	.84	.04	.05
.85	.75	−.10	.08	.96	.11	.02	.87	.02	.04
.90	.79	−.11	.07	.97	.07	.01	.91	.01	.03
.95	.81	−.14	.08	.98	.03	.00	.93	−.02	.02
.99	.83	−.16	.08	.99	.00	.00	.94	−.05	.02

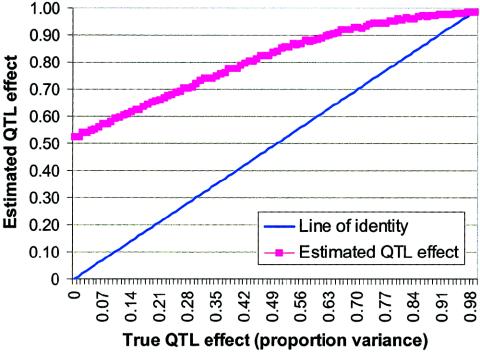
Experiment 2: Selection of Only Significant Results

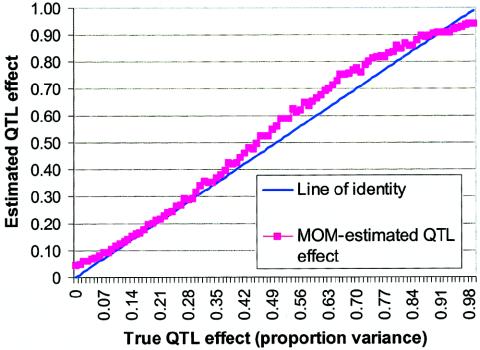
Data sets were generated until 1,000 data sets with statistically significant values were obtained. Results are plotted in figure 2. As can be seen, among results selected for significance, even when there is a true QTL effect, such an effect is substantially overestimated by 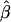unless the true QTL effect is unrealistically high (i.e., σ²_QTL>0.90). In contrast, when the MOM estimator is used, the biases are nearly eliminated for virtually all values of σ²_QTL as portrayed in figure 3. Not only is the bias reduced but the MSE associated with the MOM estimator also is significantly lower than that of the preliminary (ordinary) estimator. Therefore, the MOM approach provides not only an unbiased estimate but also a more consistent estimate. Furthermore, we investigated the use of the median of the MOM estimate, to examine bias in parameter estimation. Owing to the truncation of the distribution of significant results, the median estimates were lower than the mean estimates, which in turn yields less conservative MOM estimates. That is, MOM estimates based on the median (which is a quantile, not a moment) would not fully reduce the bias that is under consideration herein.

Figure 2.

Estimated versus true QTL effects, with selection of only significant results. All analyses included 200 independent sibling pairs and used HE2 as the preliminary test with a one-tailed α level of 0.01.

Figure 3.

MOM estimates of QTL effect versus true QTL effect, with selection of only significant results from experiment 2. All analyses included 200 independent sibling pairs and used HE2 as the preliminary test with a one-tailed α level of 0.01.

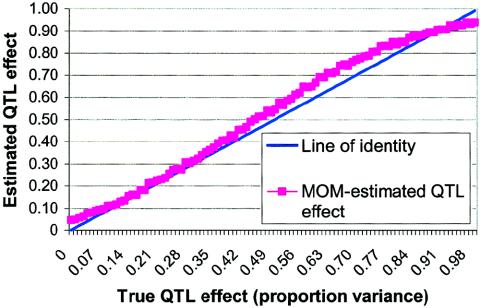
Experiment 3: Independent Check on Experiment 2

A fresh set of 1,000 data sets with statistically significant values of 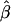were generated for each genetic model. The MOM estimates were computed by use of the 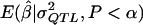values obtained in experiment 2 to check that the apparently desirable performance of the MOM estimators that we used (as shown in fig. 3) was not an artifact of the sample statistic to the population parameter function being derived from the same data to which the MOM-estimation procedure was applied. The results of experiment 3 are plotted in figure 4 and shown, for selected σ²_QTL values, in table 1. As can be seen, the results shown in figures 3 and 4 are virtually identical, indicating that the excellent performance of the MOM estimators that was observed in experiment 2 was not an artifact. As shown in table 1, for all σ²_QTL values >0.95, the MOM estimator dramatically reduces bias. Equally important, for all σ²_QTL values less than the perhaps implausibly large 0.65, the MOM estimator dramatically reduces the MSE of the QTL estimate.

Figure 4.

MOM estimates of QTL effect versus true QTL effect, with selection of only significant results from experiment 3. All analyses included 200 independent sibling pairs and used HE2 as the preliminary test with a one-tailed α level of 0.01.

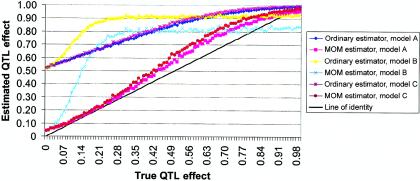
Experiment 4: Effects of Assuming Incorrect Model

We used four different nonadditive models to evaluate the extent to which having based the MOM estimator on an incorrect default genetic model (i.e., additivity with an allele frequency of 0.5) affected the bias and/or the MSE of the MOM estimator. In terms of bias, results are displayed graphically in figure 5, and more details are given for both bias and MSE in table 2, for values of σ²_QTL in increments of 0.05. As can be seen, although the MOM estimator (table 3) markedly reduces the bias in QTL estimation in these cases, the degree of reduction is far from complete and is significantly less than that observed in the case in which the true model is additive. This incomplete reduction occurs because the selection-induced bias decreases monotonically with increasing power and because power is affected by variables such as the proportion of the QTL variance that is nonadditive variance, the allele frequency, and the mode of inheritance. Thus, depending on one’s perspective, one could adopt various principles. The adoption of an additive model with an allele frequency of 0.5 should lead to liberal MOM estimates (i.e., probably biased high) that do not overcorrect the selection bias. In contrast, the adoption of a recessive model with a very low allele frequency should lead to conservative MOM estimates (i.e., possibly biased low) that do not undercorrect the selection bias.

Figure 5.

Simulations with nonadditive models, but with MOM estimates calculated assuming additivity. Note that the true QTL effects, as well as the preliminary (ordinary) estimates, include both the additive component and the dominance component. All analyses included 200 independent sibling pairs and used HE2 as the preliminary test with a one-tailed α level of 0.01. For details of nonadditive models, see the “Simulation Parameters and Methods” subsection.

Table 2.

Results for the Nonadditive Models (Experiment 4) with Only Significant Results Selected and Ordinary Estimator Used^[Note]

	Model A			Model B			Model C
σ2QTL	Mean	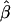Bias	MSE	Mean	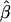Bias	MSE	Mean	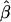Bias	MSE
.00	.52	.52	.28	.52	.52	.28	.52	.52	.52
.01	.53	.52	.27	.52	.51	.27	.53	.52	.52
.05	.56	.51	.26	.59	.54	.30	.56	.51	.51
.10	.59	.49	.25	.71	.61	.40	.59	.49	.49
.15	.62	.47	.23	.81	.66	.46	.64	.49	.49
.20	.67	.47	.23	.87	.67	.48	.66	.46	.46
.25	.69	.44	.20	.90	.65	.45	.69	.44	.44
.30	.73	.43	.20	.90	.60	.40	.74	.44	.44
.35	.75	.40	.18	.90	.55	.34	.77	.42	.42
.40	.79	.39	.17	.92	.52	.29	.80	.40	.40
.45	.82	.37	.15	.91	.46	.24	.83	.38	.38
.50	.85	.35	.14	.92	.42	.20	.87	.37	.37
.55	.88	.33	.12	.92	.37	.16	.89	.34	.34
.60	.91	.31	.10	.91	.31	.13	.91	.31	.31
.65	.92	.27	.08	.93	.28	.10	.94	.29	.29
.70	.93	.23	.06	.92	.22	.07	.96	.26	.26
.75	.95	.20	.05	.91	.16	.05	.97	.22	.22
.80	.96	.16	.03	.92	.12	.04	.98	.18	.18
.85	.97	.12	.02	.92	.07	.03	.98	.13	.13
.90	.98	.08	.01	.93	.03	.02	.99	.09	.09
.95	.99	.04	.00	.93	−.02	.02	.99	.04	.04
.99	.99	.00	.00	.93	−.06	.03	1.00	.01	.01

Note.— For details of nonadditive models, see “Simulation Parameters and Methods” subsection.

Table 3.

Results for the Nonadditive Models (Experiment 4) with Only Significant Results Selected and MOM Estimator Used

	Model A			Model B			Model C
σ2QTL		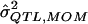Bias	MSE		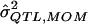Bias	MSE		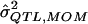Bias	MSE
.00	.05	.05	.01	.05	.05	.01	.05	.05	.01
.01	.05	.04	.01	.05	.04	.01	.05	.04	.01
.05	.07	.02	.01	.12	.07	.03	.08	.03	.01
.10	.11	.01	.02	.34	.24	.15	.12	.02	.02
.15	.16	.01	.03	.53	.38	.27	.18	.03	.03
.20	.23	.03	.04	.69	.49	.39	.22	.02	.04
.25	.26	.01	.04	.76	.51	.40	.27	.02	.04
.30	.33	.03	.06	.78	.48	.36	.34	.04	.05
.35	.38	.03	.06	.78	.43	.32	.41	.06	.07
.40	.46	.06	.08	.81	.41	.29	.47	.07	.08
.45	.51	.06	.08	.80	.35	.25	.54	.09	.09
.50	.59	.09	.09	.81	.31	.22	.62	.12	.09
.55	.64	.09	.09	.80	.25	.19	.68	.13	.09
.60	.71	.11	.08	.80	.20	.17	.72	.12	.08
.65	.75	.10	.08	.83	.18	.14	.79	.14	.08
.70	.79	.09	.06	.82	.12	.13	.85	.15	.07
.75	.84	.09	.06	.80	.05	.13	.88	.13	.05
.80	.87	.07	.04	.82	.02	.11	.91	.11	.04
.85	.90	.05	.03	.81	−.04	.12	.93	.08	.03
.90	.93	.03	.02	.82	−.08	.11	.95	.05	.02
.95	.95	.00	.01	.83	−.12	.12	.96	.01	.01
.99	.96	−.03	.01	.83	−.16	.13	.97	−.02	.01

Example

As an example, consider the study of human obesity by Walder et al. (2000). Walder et al. conducted a genome scan for linkage analysis by use of both the original HE method, which we denote as “HE1,” and a maximum-likelihood variance-components (MLVC) approach among 1,199 sibling pairs from 239 families and considered any findings with LOD scores >1.2 (corresponding to a one-tailed P value of .00937) as significant. They detected a LOD score of 2.1 with the MLVC approach when using serum leptin level as the phenotype and estimated the QTL effect to account for 22% of the phenotypic variance. It is noteworthy that Walder et al. estimated the total additive heritability for this trait to be only 21%. That the QTL effect accounts for essentially all of the heritable variance strongly suggests the possibility of overestimation.

Additional information regarding this example was provided by R. L. Hanson (personal communication). Specifically, the pairwise sibling-sibling correlation for leptin was 0.10. Expressing the phenotype in unit variance, the slope of the HE1 regression was −0.80 at the point where the QTL effect was estimated, which means that the preliminary estimate of the QTL effect from the HE procedure is ∼0.40 (i.e., −0.80/−2). The total variance of the squared sibling-pair differences was 5.979, and the HE1 test had 495 df after adjustment to account for nonindependent pairs. Of course, it is impossible for us to simulate Walder et al.’s (2000) exact situation (i.e., exact distribution of sibship sizes, exact phenotypic distribution, etc.) without access to the raw data. However, using only the information provided, we can still conduct a reasonable simulation to get a sense of what a more accurate QTL estimate might be in this case. To do so, we simulated data sets consisting of 497 sibling pairs (495 df + 2) from a population with a phenotypic sibling correlation of 0.10. For each σ²_QTL value from 0.00 to 0.20, we simulated data under an additive model until 1,000 significant results were obtained, using the HE1 test (Haseman and Elston 1972). (The upper bound was set at 0.20, because, under complete additivity, the maximum QTL effect possible is twice the sibling correlation.) The threshold for significance was set at α=0.00937 (one tailed). For each σ²_QTL value from 0.00 to 0.40, we also simulated data under a recessive model with an allele frequency of 0.10, until 1,000 significant results were obtained. (The upper bound was set at 0.40, because, under complete nonadditivity, the maximum QTL effect possible is four times the sibling correlation.) Using the data obtained, we found the σ²_QTL values for which the expected value of the slope under the HE1 test is −0.80. Interestingly, for both the additive model and the recessive model, the MOM estimate was 0.00. To find a range of plausible values for the QTL effect, 95% confidence intervals that contained −0.80 were constructed. The QTL value that had −0.80 as the 5th percentile of its sampling distribution of slopes (i.e., minimum plausible value of the confidence interval) was 0.04 for the additive model (0.03 for the recessive model). This suggests that estimates of the proportion of variance in leptin levels, attributed to the locus detected by Walder et al., between 0 and 0.04 may be more-reasonable estimates than are the estimates of 0.21 by the ML method and 0.40 by the HE method. Although it seems odd that the MOM estimate of a significant locus is nearly zero, unbiased estimators can sometimes produce odd estimates for specific cases. Again, we use the example of adjusted R², which is an unbiased estimator of the population R² but occasionally takes on negative values for specific cases. In those cases, although the estimate of R² cannot be correct, the use of adjusted R² guarantees that, over the course of many studies, the estimate will be right on average. Similarly, we cannot say with certainty that the QTL effect in the population that was sampled in this study is between 0 and 0.04. Rather, we can say that, if many studies are done and if we estimate QTL effects in this way, then we will be right on average. In a larger study, the MOM adjustment would be smaller than that which we found in this situation. Thus, this particular example shows the effect that a small sample size can have on the bias estimation when only significant results are presented (Beavis 1998).

Discussion

Advantages and Disadvantages of the MOM Approach

Although our simulation studies were presented when only a single position was considered, they are relevant to genome scans. In a genome scan, one searches for genetic effects over intervals and declares linkage for a region (or regions) for which the LOD score exceeds some predefined critical value. If QTL effects are evaluated across multiple chromosomes and different linkage groups, then estimated effects should be independent. Thus, for these situations, the problem of truncated estimation is just a recapitulation of the same problem. That is, we have multiple independent areas in which we are conducting tests and then generating estimates only when the tests are significant. Each independent area simply recapitulates the process we have simulated herein. Within linkage groups, QTL-effect estimates will be correlated. Here the general practice is to simply provide the estimate at the point where the evidence is maximal. As mentioned above, this may further exacerbate the biasing effects of the truncation process. In theory, this could be added to the MOM-estimation process that we have illustrated; however, we have not done so at this time.

The MOM approach that we have described has certain advantages. First, it is conceptually very simple. Second, by relying on simulation, it offers great flexibility (Pakes and Pollard 1989; Gallant and Tauchen 1999). Although it is possible to analytically derive the MOM estimators in some situations, we chose not to, in part, to preserve this flexibility. Thus, it was easy for us to switch from our initial simulations with HE2 to the example that we considered that used the HE1 test. The MOM-simulation approach allows adaptation to any pedigree structure, any sampling scheme, and any test statistic, as long as that pedigree structure, that sampling scheme, and that test statistic are incorporated in the simulation. Moreover, although we used a normal distribution for the within-genotype phenotypic distribution in our simulations, investigators faced with nonnormal data could adapt the simulation phase of the MOM estimation process to accommodate the nonnormality (although in many situations a normalizing transformation of the observed phenotypic data prior to analysis may be preferable). By use of the generalized λ distribution described by Karian and Dudewicz (2000), it is possible to simulate nonnormal data to accommodate almost any observed distribution. Third, as we have illustrated, the MOM approach has the potential to essentially eliminate the bias that is imposed by the selection of only significant results for estimation. Although this requires further empirical investigation, the results of this study are promising in that the MOM estimation procedure is flexible, and thus, its ability to reduce bias could be generalized to more complex conditions.

However, the MOM approach also has some disadvantages. First, if one implements the MOM approach by relying on simulation, the computational demand can be high. This is because, at the low power levels that occur with small sample sizes and low QTL levels, one must generate and test many samples to obtain a sufficient number (e.g., 1,000) that yield statistically significant QTL estimates. Second, because every study is different, implementation may require rewriting simulation code or rederiving analytic formulae for 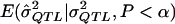if an analytical approach is used. Third, to derive 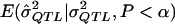, one must first assume some underlying model, and, as we saw in experiment 4 above, the assumption of the incorrect model can lead to biased estimates. In certain estimation procedures, it is common practice to report only the additive component of variance in genome scans, which suggests that, in these cases, the MOM procedure with an additive assumption may be applied to most of the results that are presented. The results of the current study show that, even if an incorrect model is assumed, then the MOM approach still yields less-biased estimates. However, one could also apply the MOM approach to study both additive and dominance components to minimize model assumptions. Fourth, it is somewhat unclear how to place confidence intervals around the MOM estimates. One could use bootstrap methods (Chernick 1999), but this requires further computation to ensure enough replicates to provide a reliable coverage interval. Fifth, MOM estimators are less efficient than some competing estimators (Stuart et al. 1999). Göring et al. (2001) presented studies from an ML-estimation approach that is efficient when distributional assumptions are met. However, when these distributional assumptions are not tenable, this ML method may be more biased than the proposed MOM method, which does not necessarily require distributional assumptions. Finally, as seen in the example above, the MOM approach can potentially leave one in the curious position of having declared a QTL effect to be statistically significant on that basis of the P value and then having stated that the best estimate of the effect, based on the MOM approach, is zero. Despite some shortcomings, the MOM approach has the advantage of being easy to implement and being robust to distributional assumptions.

Potential Alternatives to the MOM Approach

Because the MOM approach may not be fully efficient in some cases, we discuss two alternative procedures. The first alternative involves simultaneous ML estimation of all QTL effects in a genome scan. For linkage analysis, one approach to estimation and inference that explicitly acknowledges that individual locus effects are estimated in the context of a genome scan consists of the joint modeling of effects from two or more loci that are initially determined to be significant on the basis of a genome scan that first considers each locus separately (e.g., see Blangero and Almasy 1997; Almasy and Blangero 1998). This approach may be expected to reduce the upward biases in the effect sizes but may not eliminate it, because one would still be providing estimates only for significant QTL. An approach that might, theoretically, provide better estimates than this would jointly model the effects of all loci (whether significant or not) simultaneously. Such simultaneous estimation would presumably impose (a) severe constraints on the magnitude that any one QTL-effect estimate could take and/or (b) severe limitations on the number of loci that could be estimated not to have extremely small effects. Rather than requiring that the sum (in terms of proportion of phenotypic variance explained) not exceed 1.0, one can impose even-more-severe constraints on the estimates by requiring that the sum not exceed four times the sibling correlation. The upper bound was set at 0.40, because, under complete nonadditivity, the maximum QTL effect possible is four times the sibling correlation (see the “Example” section). However, finite sample sizes and computational resources may make the literal modeling of all QTL effects simultaneously impractical. Thus, it may be important to combine this approach with model-selection techniques such as, for example, those illustrated by Li and Nyholt (2001) in a related context.

A second alternative is the use of empirical Bayes approaches (Morris 1983; Carlin and Louis 2000a, 2000b). The empirical Bayes approach permits the joint incorporation of results from the entire genome scan, to allow the investigator to assign a prior distribution of QTL-effect sizes throughout the genome. This approach would have the effect of smoothing the results from the genome scan and so reduce upward bias in QTL-effect estimates at the regions most strongly suggestive of linkage.

Until recently, most methodological efforts addressing linkage analysis for quantitative traits were directed at simply detecting effects and minimizing type 1 and type 2 errors. Less attention has been devoted to the estimation of effects, perhaps because there were rather few convincingly significant effects. However, the relative dearth of estimates is changing. For example, in the field of obesity, in which phenotypes such as fatness are inherently quantitative, compelling linkages have begun to be found (e.g., see Comuzzie et al. 1997; Kissebah et al. 2000), and QTL-effect estimates are beginning to be provided in obesity, as well as in other areas (e.g., see Zhu et al. 1999; Walder et al. 2000). Estimates of effect sizes can be useful in the prioritization of linkages, to follow up replication studies or fine-mapping; in the conducting of power analyses for future studies; in the evaluation of the public health magnitude of genetic variation at the putative QTL; and in the evaluation of the potential predictive power of the gene, once identified, for the detection of people who are at risk. For all of these endeavors, the MOM estimator and, perhaps, other possible alternatives offer more-accurate estimates than estimates that do not take into account the bias imposed by the estimation of effect sizes only for significant linkages. As a progressively greater number of compelling QTL linkages are detected, QTL-effect estimation will become increasingly important. We hope that this article is a useful aid toward that end.