Abstract
Data-centric estimation methods such as Model-on-Demand and Direct Weight Optimization form attractive techniques for estimating unknown functions from noisy data. These methods rely on generating a local function approximation from a database of regressors at the current operating point with the process repeated at each new operating point. This paper examines the design of optimal input signals formulated to produce informative data to be used by local modeling procedures. The proposed method specifically addresses the distribution of the regressor vectors. The design is examined for a linear time-invariant system under amplitude constraints on the input. The resulting optimization problem is solved using semidefinite relaxation methods. Numerical examples show the benefits in comparison to a classical PRBS input design.
I. INTRODUCTION
Most real-world phenomena is nonlinear in nature. Towards this, there have been various approaches to nonlinear black-box system identification from experimental data such as neural networks, wavelets and Nonlinear AutoRegressive with eXogenous input model (NARX) [1]–[3]. The conventional modeling philosophy is to derive a ‘global’ mathematical representation using the input-output data and post validation, the dataset is discarded. In general, the associated optimization problem for these structures is nonconvex, thus resulting in computational issues. An alternative approach is to build a ‘local’ function approximation (which can be well approximated by linear models) on-line based on the current operating point. In the system identification literature, this technique is called Just-in-Time learning [4], Model-on-Demand (MoD) [5]–[7] and Direct Weight Optimization (DWO) [8]. Unlike global black-box approaches, these online local modeling methods are computationally tractable and well complemented by modern computing. In addition, on-line local methods can readily utilize any new data available. These local linear models can then be used by a model predictive controller, for example, for control of uncertain systems [6], [7] and nonlinear hybrid systems [9].
An area of recent interest for these methods is adaptive behavioral interventions, where intervention components are adjusted by a controller based on participant response over time [10]. These interventions are characterized by multiple participants with significant individual variability, with data being continuously collected during the process. The data-centric modeling approach is much more suitable for such complex scenarios where building a global model is difficult and inefficient. A Model-on-Demand model predictive controller (MoDMPC) for adaptive interventions has been proposed in [9].
Traditional experiment design for system identification considers some scalar measure of the parameter covariance matrix with specific requirements on the input signal spectrum [1], [11]. Although the field is quite vast, none of these methods, to the best of our knowledge, directly address design issues in the regressor space. In this paper, an input signal design methodology is presented to generate informative data for data-centric identification algorithms by specifically addressing the distribution of the regressor vectors. Prior work for data-centric estimation addressed distribution of only the outputs using Weyl’s criterion [12], [13]. Constraints on the input and output are incorporated in this approach to achieve plant-friendly operation [11], [13]–[15]. For the purposes of this paper, the focus is specifically on the requirements for Model-on-Demand by considering linear time-invariant models under amplitude constraints on the input. The subsequent optimization problem corresponds to a maximization of convex quadratic function which is NP-hard in general [16]. A semidefinite relaxation of the nonconvex quadratic problem is proposed to obtain an approximate solution in polynomial time. A case study is undertaken to examine the feasibility of this approach.
The paper is organized as follows: Section II briefly describes the MoD data-centric modeling methodology used in this paper. In Section III, the problem formulation is presented with discussion on its implications, with semidefinite relaxation discussed in Section IV. Numerical examples are shown in Section V and summary, conclusions and directions of future work are presented in Section VI.
II. MODEL-on-DEMAND ESTIMATION
The methodology of building local linear models on-line or Model-on-Demand [5] is now briefly described. Consider a SISO process for a given data set ( ) as
| (1) |
where y(k) ∈ ℝ, f(·) is an unknown (nonlinear) mapping, ϕ(k) ∈ ℝm is the regressor vector (generally composed of lagged output and input)
| (2) |
and e(k) ∈ ℝ is the noise. The MoD predictor attempts to estimate output predictions based on a local neighborhood of desired operating point (ϕ*) in the regressor space. The predictor function f̄ is obtained by a linear combination of observed outputs
| (3) |
where the weights are, in general, dependent on the distance of regressors from the current operating point (ϕ* − ϕ(k)), noise variance and properties of f. The weights emphasize the size of the neighborhood from the desired operating point, and this is referred to as ‘bandwidth’ of the estimator. Thus, it governs the tradeoff between bias and variance errors of the estimate. To select these weights, the following two methods can be used:
-
Kernel-based approach: The weights are assigned as per a kernel or window function (W(·)) according to the distance of given regressors from ϕ* to asymptotically minimize the mean square error of the estimate [1], [5], [17]
(4) where M ∈ ℝm×m is scaling matrix for the Euclidean distance and h is the bandwidth.
-
Optimization-based approach: The choice of weights using statistical measures is as per asymptotic arguments and in practice, the number of data points is finite. Another approach of selecting these weights is through explicit use of optimization by minimizing the exact mean square error (MSE) or worst case MSE
(5) where w = [w(1), …, w(N)]T and W(·) is some function of the MSE [6], [8]. Consequently, some of the resulting weights are zero and thus the ‘bandwidth’ of the estimator is automatically calculated.
The methods outlined so far have focused on obtaining the function approximation f̄(ϕ*). In the next step, a local linear estimate can be obtained by solving
| (6) |
where ℓ(·) is a quadratic norm function, W(·) assigns weight as per the estimator bandwidth and the local model structure can be:
| (7) |
which is linear in the unknown parameters and hence an estimate can be computed using least squares.
III. MoD INPUT SIGNAL DESIGN
The quality of the estimate from MoD depends primarily on the following factors:
-
Regressor vector:
The structure of the regressor vector, i.e., the number of lagged outputs and inputs. The regressor structure should correspond to what is suitable for a local linear model (e.g., from linearization of an a priori nonlinear model).
The distribution in the regressor space. From (4) and (5), it can be observed that the choice of the weights is a function of distance of ϕ* from the available regressor vectors ϕ(k).
N: number of data points. For high dimensional space and for finite N, the distance between two regressor can become very large. In practice, large number of systems can be well approximated by low order regressors.
Properties of f: smoothness in general and in particular, bounds on the Hessian matrix.
Noise in the experimental data.
From (3), it is clear that the estimate is formed by interpolation of available outputs. In other words, if the current operating point (ϕ*) lies beyond the convex hull of available regressor points, the estimator would have to extrapolate rather than interpolate. Thus, the aim of input signal is to excite the full span of output so to make sure that the estimator is always interpolating. These observations lead to the following problem statement:
Problem Statement: Given N regressor vectors of fixed finite dimension, distribute the regressor points as far apart from each other as possible in the regressor space under constraints on the input and output signals.
A. Regressor Structure
The regressor vector contains finite lagged data about the system. The AutoRegressive with eXogenous input (ARX) regressor structure is commonly used [2], [6]:
| (8) |
where na, nb and nk denote the number of previous output, input and the degree of delay in the model and ϕ(k) ∈ ℝm where m = na + nb. It is assumed that the dimension of the regressor vector is selected by the user. In general, it is useful to start with nk = 1 without a priori information.
B. Problem Formulation
Consider an input signal u ∈ ℝN = [u(1), …, u(N)]T and corresponding output signal y ∈ ℝN = [y(1), …, y(N)]T generated by a linear time-invariant system represented as:
| (9) |
where G ∈ ℝN×N is the Toeplitz matrix of system impulse responses. To be used by the optimization procedure, the regressor vector has to be parameterized. For the purpose of illustration, consider the ARX regressor vector as shown in (8). The regressor vector ϕ(k) can be written in terms of u as:
| (10) |
where Pk ∈ ℝna×N and Qk ∈ ℝnb×N. One can readily observe that these matrices are sparse and the rank of Pk, Qk = max{na, nb}. The case of Finite Impulse Response (FIR) regressor structure can be derived as a special case
| (11) |
For the FIR case, the dimension of the regressor m has to be generally large to capture all of the dynamics. In contrast, a relatively low dimension is often suitable in the case of ARX structure. Before presenting the problem objective, a distance pair of two regressors has to be defined. It can be readily seen that for given N regressor points there will be NC2 = N(N − 1)/2 unique distance pairs and hence the number of distance pairs scales polynomially in N i.e. number of distance pairs ≃ N2/2 ∀N ≫ 1.
The notion of distance in the Euclidean space ℝm can be defined using any p-norm distance. In this formulation, the Euclidean distance (2-norm distance) is used as the metric which is also used to calculate the bandwidth of the estimator as discussed in Section II. Based on the parametrization shown in (10), the square of the Euclidean distance between two regressor points dij can be defined as:
| (12) |
| (13) |
The problem statement defined previously states that the objective is to distribute the points as far apart as possible. This directly implies that the sum of all the distances will have to be maximized. This objective can be mathematically represented as:
| (14) |
For the problem to be bounded, it is necessary to assume amplitude constraints on the input
| (15) |
where, for the purpose of illustration, the bounds are symmetric (umin = −umax). Based on (13), (14) and (15), the formal optimization problem can be written as
| (16) |
where is defined by the sum of distance pairs as per (14). It can be noted that Qij is positive semidefinite (Qij ⪰ 0) as it represents the square of the distance. Hence, Q which is defined as the sum of positive semidefinite matrices is also positive semidefinite (Q ⪰ 0). This implies that the resulting quadratic maximization problem (or minimization of negative semidefinite problem) is NP-hard [16].
IV. CONVEX RELAXATION
Convex relaxation of nonconvex optimization problems has developed as a powerful approach to solve (approximately, and sometimes exactly) otherwise hard problems [18]–[20]. In a relaxation approach, the idea is to identify the main source of nonconvexity and then either drop it or replace it with a ‘relaxed’ version that is convex and hence more tractable. Clearly, there has be to a meaningful relationship between the original nonconvex problem and the relaxed convex problem. Semidefinite programming (SDP) relaxation (also dual of the Lagrangian dual) for the case of quadratic problems has been particularly successful with proven bounds on suboptimality for many scenarios [21].
A. Semidefinite Relaxation
Consider the problem in (16) which is restated here for completeness.
| (17) |
where νQP is the objective value of the original nonconvex problem. First, by change of variables
| (18) |
where Tr(·) is the trace operator and uuT = U ∈ ℝN×N. Similarly, (15) can be written in terms of variable U. Thus, the original problem can be written as
| (19) |
where diag(·) denotes vector formed from the matrix’s diagonal. This problem (19) is exactly equivalent to (17) and hence nonconvex. The key step in relaxing this problem is to first note that
| (20) |
Hence, the nonconvexity of the problem has been transformed into the rank constraint. Now problem (19) can be relaxed into a SDP problem by neglecting the (nonconvex) rank constraint on U
| (21) |
where νSDP gives an upper bound on the nonconvex maximization problem in (17) i.e. νQP ≤ νSDP.
B. Feasible Input and Bounds on Suboptimality
The solution of (21) would yield an objective value νSDP and the optimal matrix variable U*. Given that this was a relaxation and bounds are generally not exact, the rank of U* will not be unity and hence it is not possible to decompose as U* = u*u*T. Hence, the SDP only gives the bound on the problem and no direct feasible solution. The general process in such cases is to generate feasible inputs through a process of randomization. In this problem, a random feasible input is sampled from a Gaussian distribution with covariance matrix U* [21]. For the case of maximization, it can be observed that the maximum values will be obtained when the input is either umin or umax. In other words, a binary signal will attain the maximum value. When enough random samples are picked, a good suboptimal point can be obtained [19]. Generally for any given SDP relaxation, there is no bound on this suboptimality. For this maximization structure, it can be shown that there not only exists a hard finite upper bound (as with any feasible SDP relaxation), but also a hard lower bound on the solution.
Theorem 1 (Nesterov [22], Ye [23])
Given the quadratic optimization problem
| (22) |
where Q ⪰ 0, the approximation bounds can be given by
| (23) |
This result holds for both FIR and ARX type regressors. For the FIR case, Q has additional properties and a tighter bound holds true:
Theorem 2 (Goemans and Williamson [24])
Given the quadratic optimization problem
| (24) |
where Q ⪰ 0 and all off-diagonal elements are nonpositive (Q(c, d) ≤ 0, c ≠ d), the approximation bounds can be given by
| (25) |
C. Extensions
So far, only amplitude constraints on the input have been considered. Since the problem is formulated in the decision variable u, any time-domain constraints can be included. An important constraint, for example, is bound on the output based on a given model. More time-domain constraints are discussed in [13] which can be written as linear inequalities and hence can also be included. It should be noted that it is unlikely that bounds on suboptimality exist in those scenarios. However, in practice good objective values are found although generation of feasible inputs remains nontrivial and is not considered in this paper.
V. NUMERICAL EXAMPLE
Consider a continuous-time second order system with a zero
| (26) |
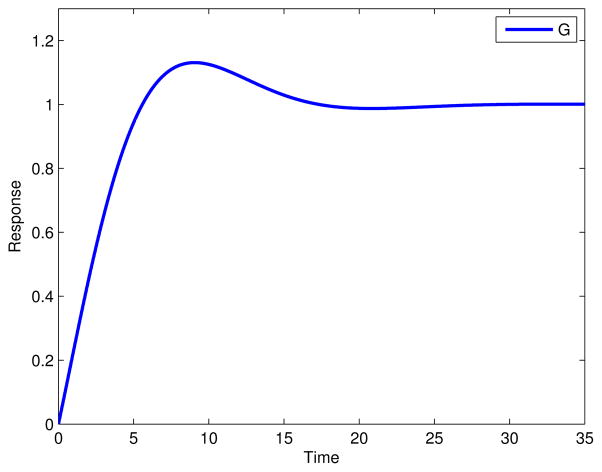
where Kp = 1, τa = 2, τ = 3 and ζ = 0.6. The system step response is shown in Figure 1. This model was discretized at unit sampling using zero-order hold. This system can be fully parameterized by an ARX regressor of order [2 2 1]
Fig. 1.
Step response of system as shown in (26).
| (27) |
The output prediction at time k can be written as
| (28) |
where θ = [1.58, −0.6703, 0.2282, −0.1375]T based on the discretization of (26).
The optimal input was generated by solving the semidefinite program shown in (21). For purposes of simulation, it was assumed umin = [−1, …, −1], umax = [1, …, 1]. The SDP was coded in MATLAB with YALMIP [25] interface using SeDuMi [26] as the SDP solver. Using the SDP results, a feasible input was generated using randomization. This binary (sub) optimal signal is compared with a classical Pseudo Random Binary Sequence (PRBS) [1]. A PRBS signal is uniquely defined by switching time Tsw and the number of shift registers nr to excite the system bandwidth:
| (29) |
where typically αs = 2 and βs = 3 [12]. Based on these specifications, the switching time can be calculated as:
| (30) |
and the length of signal (N) can be calculated as:
| (31) |
The time constant was found to be from (26) and consequently the length of the PRBS input for one period was found to be N = 62.
Table I compares the objective values for the two signals. For the optimal signal, νSDP is the maximum value that can be attained by the maximization problem shown in (16). Based on Theorem 1, a lower bound on the objective can be assigned as shown. The randomization procedure then produces an input whose objective value lies in this bound. In this case, it was found that the best objective value from 20000 candidates was 0.9 times of the SDP objective. It is worth noting that it is not known where the global optimal lies, but that it lies between the upper and lower bound calculated from the SDP problem. Further, the objective value for PRBS was lower than the guaranteed objective from the optimal input. In fact, the randomization procedure gave an objective value improvement of 44.2% over the PRBS objective.
TABLE I.
Tabulation of sum of unique distances between all regressors for the example problem (26).
| Upper bound (νSDP) | 16038 |
| Lower bound (0.63νSDP) | 10104 |
| Best objective from randomization | 14516 ≃ (0.9νSDP) |
| PRBS objective | 10065 |
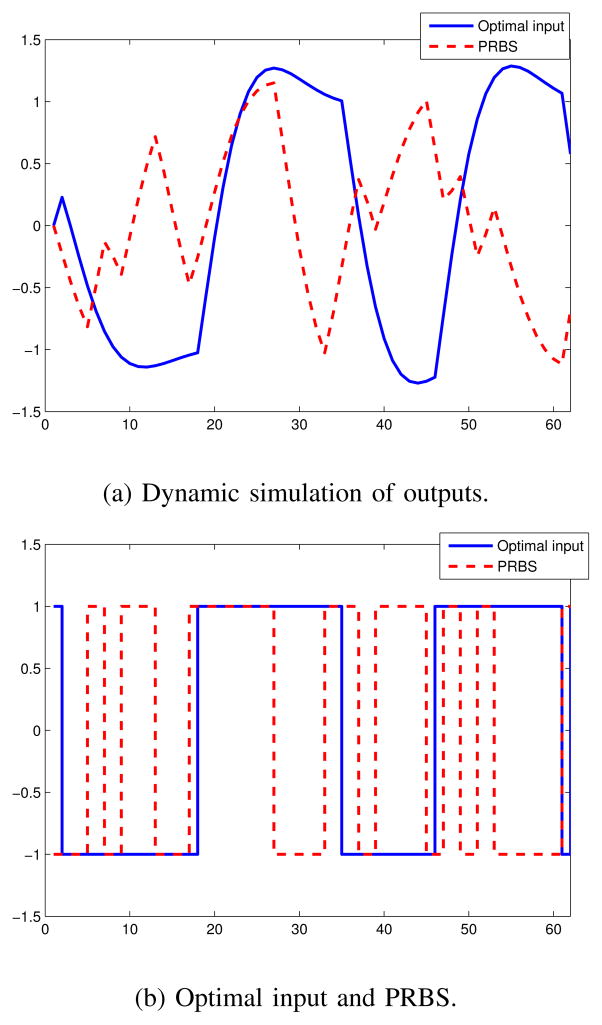
Figure 2 compares the optimal input and the PRBS input, as shown in Figure 2b, with the resulting output signal as shown in Figure 2a. An interesting observation is to note that the PRBS input switches more frequently to emphasize the frequency band where as the optimal signal switches relatively less frequently, and thereby covers more output span than the PRBS input as shown in Figure 2a.
Fig. 2.
Input-output simulation for example system shown in (26) under optimal input and PRBS input.
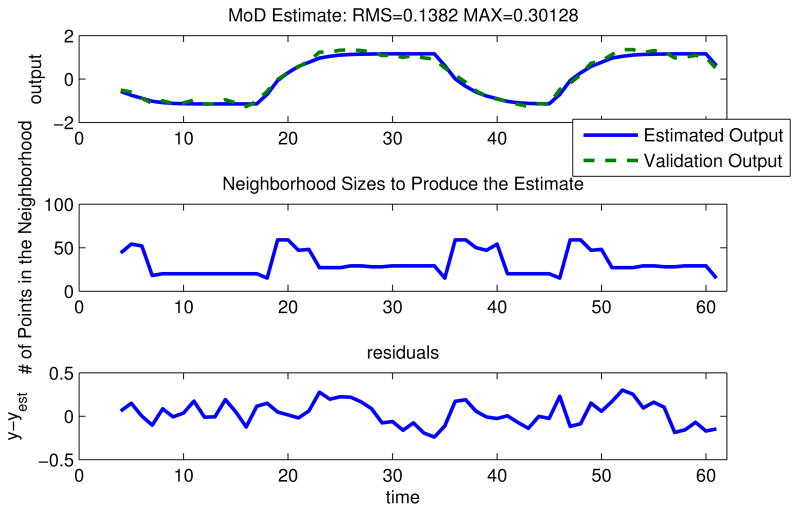
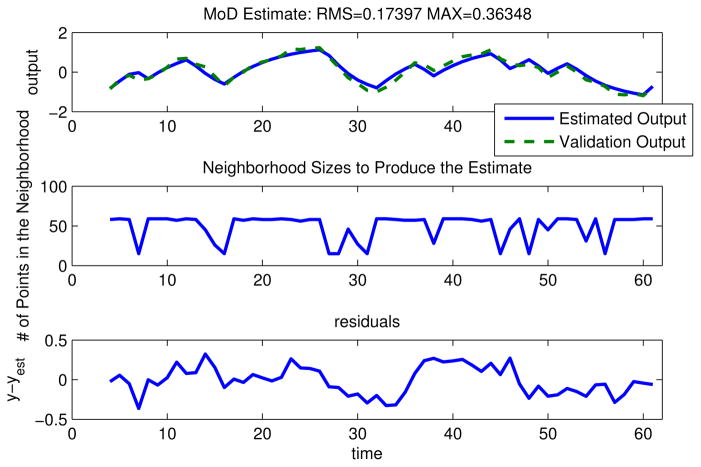
While the optimal input is not directly designed to minimize root mean square (rms) estimation error, it is interesting to note how it performs in comparison to PRBS input under noisy conditions. Towards this, a database of regressors from the two inputs and their corresponding outputs was created. In practice, the data is corrupted so a zero mean Gaussian noise with standard deviation σest = 0.1 was added to the estimation dataset. Next, sets of input-output validation dataset were created with output corrupted by zero mean Gaussian noise with standard deviation σval. The function values were estimated from the MoD estimator and compared with true predictions as per (28). Average rms values of error taken over 100 simulations for each σval are tabulated in Table II. It can be observed that, with increasing noise, the average estimation error from the optimal input dataset is consistently of a lower value than from the PRBS input dataset. The improvement in rms error is 26.4% for no noise in the validation set (σval = 0) and approximately 1% under very noisy conditions (σval = 1). One simulation case under noise with standard deviations σest = 0.1, σval = 0.1 is shown in Figure 3 for the optimal input, and in Figure 4 for the PRBS input. These figures plot the simulated output along with the number of data points required from the neighborhood and the estimation error. For this case, the rms error for the optimal input (0.1382) is lower than rms error for the PRBS input (0.17397) under similar noisy conditions.
TABLE II.
Tabulation of average rms errors over 100 simulations from the MoD estimator for two input signals.
| σval | Optimal input avg. rms | PRBS avg. rms |
|---|---|---|
| 0 | 0.10593 | 0.1441 |
| 0.1 | 0.14817 | 0.1723 |
| 0.2 | 0.22642 | 0.2362 |
| 0.5 | 0.50942 | 0.52259 |
| 1 | 1.0063 | 1.0171 |
Fig. 3.
MoD estimate for the dataset generated from the optimal input under noisy conditions (σest = 0.1, σval = 0.1).
Fig. 4.
MoD estimate for the dataset generated from the PRBS input under noisy conditions (σest = 0.1, σval = 0.1).
VI. SUMMARY, CONCLUSIONS AND FUTURE WORK
This paper introduces an approach for optimal input signals for data-centric estimation algorithms such as Model-on-Demand. The objective is to distribute the regressors in the given finite dimensional space, as measured by their Euclidean distances, so that they are as far apart as possible under dynamical constraints. To illustrate this proposition, a linear time-invariant system is considered subject to amplitude constraints on the input. The resulting nonconvex quadratic optimization problem was approximately solved through the method of semidefinite relaxation. When using the ARX regressor structure, generation of optimal input requires knowledge of the true system; this is a known issue in optimal experiment design [1]. However, for the FIR structure the regressor is only a function of the input and has tighter relaxation bounds. The total sum of all regressor distances was evaluated where the optimal input offers significant improvement over the PRBS input.
In future work, the formulation will be extended to account for distribution of regressors under stochastic and deterministic disturbances, knowledge of model uncertainty and additional time-domain constraints of practical importance. Further, this formulation can be extended to the case of MISO systems by stacking the individual SISO regressors to form a MISO regressor, and hence results from SISO systems naturally carry over to the MISO systems. It is expected that this design approach will provide significant improvements in models from data-centric methods for nonlinear systems and this is currently under investigation.
Acknowledgments
Support for this work has been provided by the Office of Behavioral and Social Sciences Research (OBSSR) of the National Institutes of Health (NIH) and the National Institute on Drug Abuse (NIDA) through grants R21 DA024266 and K25 DA021173. We also thank ASU Advanced Computing Center for providing the Saguaro cluster computing platform.
Contributor Information
Sunil Deshpande, Email: sdeshpa2@asu.edu, Control Systems Engineering Laboratory (CSEL), Arizona State University, Tempe, AZ, USA. Doctoral student in the electrical engineering program at Arizona State.
Daniel E. Rivera, Email: daniel.rivera@asu.edu, Control Systems Engineering Laboratory (CSEL), Arizona State University, Tempe, AZ, USA. School for Engineering of Matter, Transport, and Energy
References
- 1.Ljung L. System identification :theory for the user. Upper Saddle River, NJ: Prentice Hall PTR; 1999. [Google Scholar]
- 2.Sjöberg J, Zhang Q, Ljung L, Benveniste A, Delyon B, Glorennec PY, Hjalmarsson H, Juditsky A. Nonlinear black-box modeling in system identification: a unified overview. Automatica. 1995;31(12):1691–1724. [Google Scholar]
- 3.Ljung L. Perspectives on system identification. Annual Reviews in Control. 2010;34(1):1–12. [Google Scholar]
- 4.Cybenko G. Just-in-Time learning and estimation. In: Bittanti S, Picci G, editors. Identification, Adaptation, Learning. The Science of Learning Models from data, ser. NATO ASI Series. Springer; 1996. pp. 423–434. [Google Scholar]
- 5.Braun MW, Rivera DE, Stenman A. A ‘Model-on-Demand’ identification methodology for non-linear process systems. International Journal of Control. 2001;74(18):1708–1717. [Google Scholar]
- 6.Stenman A. PhD dissertation. Linköping University; Sweden: 1999. Model on Demand: Algorithms, analysis and applications. [Google Scholar]
- 7.Braun M. PhD dissertation. Arizona State University; USA: 2001. Model-on-Demand nonlinear estimation and model predictive control: Novel methodologies for process control and supply chain management. [Google Scholar]
- 8.Roll J, Nazin A, Ljung L. Nonlinear system identification via direct weight optimization. Automatica. 2005;41(3):475–490. [Google Scholar]
- 9.Nandola N, Rivera DE. Model-on-Demand predictive control for nonlinear hybrid systems with application to adaptive behavioral interventions. Proceedings of the 49th IEEE Conference on Decision and Control (CDC); Dec. 2010; pp. 6113–6118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Deshpande S, Nandola N, Rivera DE, Younger J. A control engineering approach for designing an optimized treatment plan for fibromyalgia. Proceedings of the 2011 American Control Conference (ACC); 2011. pp. 4798–4803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rivera DE, Lee H, Mittelmann H, Braun MW. Constrained multisine input signals for plant-friendly identification of chemical process systems. Journal of Process Control. 2009;19(4):623–635. [Google Scholar]
- 12.Rivera DE, Lee H, Mittelmann H, Braun MW. High-purity distillation. IEEE Control Systems Magazine. 2007 Oct;27(5):72–89. [Google Scholar]
- 13.Deshpande S, Rivera DE, Younger J. Towards patient-friendly input signal design for optimized pain treatment interventions. Proceedings of the 16th IFAC Symposium on System Identification; July 2012; pp. 1311–1316. [Google Scholar]
- 14.Manchester IR. Input design for system identification via convex relaxation. Proceedings of the 49th IEEE Conference on Decision and Control (CDC); Dec. 2010; pp. 2041–2046. [Google Scholar]
- 15.Narasimhan S, Rengaswamy R. Plant friendly input design: Convex relaxation and quality. IEEE Transactions on Automatic Control. 2011;56(6):1467–1472. [Google Scholar]
- 16.Pardalos P, Vavasis S. Quadratic programming with one negative eigenvalue is NP-hard. Journal of Global Optimization. 1991;1:15–22. [Google Scholar]
- 17.Fan J, Gijbels I. Local polynomial modeling and its applications. Chapman & Hall; 1996. [Google Scholar]
- 18.Boyd S, Vandenberghe L. Convex Optimization. Cambridge University Press; 2004. [Google Scholar]
- 19.Ben-Tal A, Nemirovski A. Lectures on Modern Convex Optimization. SIAM; 2001. [Google Scholar]
- 20.Laurent M. Sums of squares, moment matrices and optimization over polynomials. In: Putinar M, Sullivant S, editors. Emerging Applications of Algebraic Geometry, ser. The IMA Volumes in Mathematics and its Applications. Vol. 149. Springer; New York: 2009. pp. 157–270. [Google Scholar]
- 21.Luo ZQ, Ma WK, So A, Ye Y, Zhang S. Semidefinite relaxation of quadratic optimization problems. IEEE Signal Processing Magazine. 2010 May;27(3):20–34. [Google Scholar]
- 22.Nesterov Y. Semidefinite relaxation and nonconvex quadratic optimization. Optimization Methods and Software. 1998;9(1–3):141–160. [Google Scholar]
- 23.Ye Y. Approximating quadratic programming with bound and quadratic constraints. Mathematical Programming. 1999;84:219–226. [Google Scholar]
- 24.Goemans M, Williamson D. Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming. Journal of the ACM. 1995;42(6):1115–1145. [Google Scholar]
- 25.Löfberg J. YALMIP : a toolbox for modeling and optimization in matlab. 2004 IEEE International Symposium on Computer Aided Control Systems Design; 2004. pp. 284–289. [Google Scholar]
- 26.Sturm J. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optimization Methods and Software. 1999;11–12:625–653. [Google Scholar]