Rapid extraction of mean emotion and gender from sets of faces

We frequently encounter crowds of faces. Here we report that, when presented with a group of faces, observers quickly and automatically extract information about the mean emotion in the group. This occurs even when observers cannot report anything about the individual identities that comprise the group. The results reveal an efficient and powerful mechanism that allows the visual system to extract summary statistics from a broad range of visual stimuli, including faces.

The apparent effortlessness with which we see our world belies the extraordinary complexity of visual perception. The brain must reduce billions of bits of information on the retina to just a few manageable percepts. To this end, the visual system relies, not simply on filtering irrelevant information, but also on combining statistically related visual information. Texture perception, for example, occurs when the visual system groups a set of somewhat similar items to create a single percept; although the identities of many individual features may be lost, what is gained is a computationally efficient and elegant representation. This sort of statistical summary or ensemble coding has been found for low-level features such as orientated lines, gratings, and dots [1–3], and it makes intuitive sense. If we were not able to extract summary statistics from arrays of dots [1] or gratings [3], texture perception itself would be difficult or impossible.

Because statistical extraction may serve to promote texture perception [4], it may operate only at the level of surface perception or mid-level vision [5]. We show here that this is not the case. We found that subjects were able to extract and precisely report the mean emotion in briefly presented groups of faces, despite being unable to identify any of the individual faces. The following three experiments suggest that, as was seen for low-level features, observers summarize sets of complex objects statistically while losing the representation of the individual items comprising that set.

Three individuals (one woman, mean age 26.33 years) affiliated with the University of California, Davis participated in three experiments. Informed consent was obtained for all volunteers, who were compensated for their time and had normal or corrected-to-normal vision.

A series of ‘morphed’ faces were created from two emotionally extreme faces of the same person [6]. The morphs were 50 linear interpolations spanning happy to sad, with the happiest face labeled number 1 in the sequence and the saddest face labeled number 50 (Figure 1). Face 1 and face 2 were nominally separated by one emotional unit. In follow- up control experiments, faces were morphed from neutral to disgusted, or from male to female (see Figure S1 in the Supplemental data available on- line with this issue).

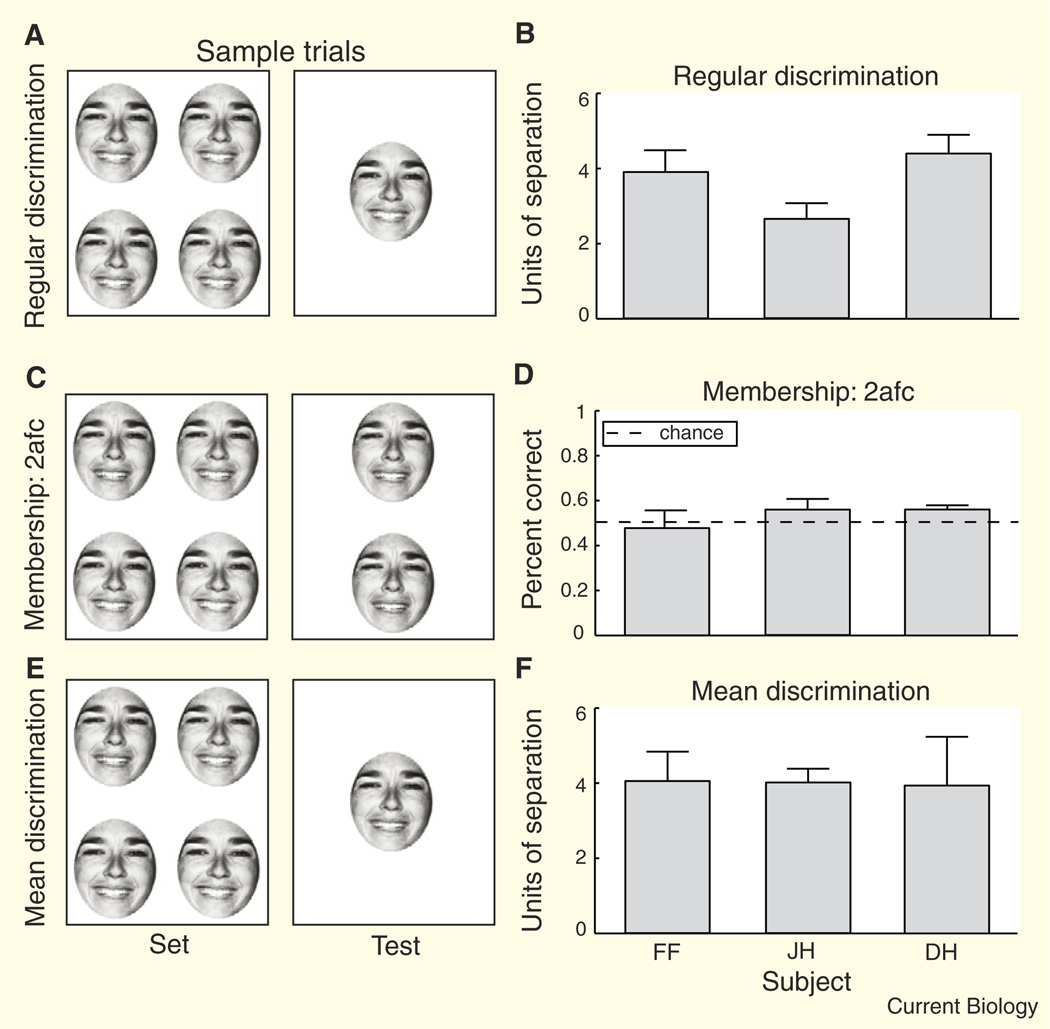
Figure 1. Sample trials and results for the three experiments.

(A,B) To discriminate whether a test face was happier or sadder than a previously viewed set of homogeneous faces with 75% accuracy, the test face had to be 3–4 units happier or sadder than the set (experiment 1). The test face in (A) is 6 units happier than the set. (C,D) Observers were at chance when indicating which of two test faces was a member of the preceding heterogeneous set (experiment 2), suggesting that they had not retained any information about the set’s individual identities. The target in (C) is the top face. (E,F) Observers indicated whether the test face was happier or sadder than the mean emotion of the preceding set (experiment 3). Despite lacking a representation of the individual set members (D), observers had a remarkably precise representation of the mean emotion of that set. Their 75% correct discrimination of the mean emotion of the set was almost as precise as their ability to discriminate two faces that displayed different emotions (compare B and F). The test face in (E) is 4 units sadder than the mean emotion of the set. Error bars in (B and F) indicate 95% confidence intervals based on 5000 Monte Carlo simulations [11], and error bars in (D) are ± 1 SEM.

In all experiments, each trial consisted of two intervals: the first interval contained a set of faces displayed for 2000 ms in a grid pattern, and the second interval contained one or two test faces displayed until a response was received (0 interstimulus interval; Figure 1A,C,E). In experiment 1, observers judged whether a single test face was happier or sadder than the preceding set of four identical faces (Figure 1A). For each observer, we derived a 75% discrimination threshold, defined by the number of emotional units separating the set and test (Figure 1B).

In experiments 2 and 3, every face set contained four emotions separated from one another in increments of six emotional units (a suprathreshold separation; Figure 1C,E). The faces were centered on the mean emotion of the set. In each trial, the mean emotion was randomly selected from among our gallery of morphed faces (the emotional mean could range from extremely happy to extremely sad). The emotionality of each face comprising the set was randomly assigned a position within the grid.

In experiment 2, we tested the extent to which observers represented the individual constituents of a set of emotionally varying faces using a two-alternative-forced-choice (2-AFC) paradigm (Figure 1C). Observers had to indicate which of two simultaneously presented test faces was a member of the preceding set of four faces. The target face was randomly selected from the set of four faces previously displayed. The distracter face was three emotional units happier or sadder than the target face. Observers also performed a control experiment in which the separation between the two test faces was increased to either 15 or 17 emotional units (Figure S2). Observers performed 480 trials over three runs.

In experiment 3, we tested whether observers had precise information about the mean emotion of a set of faces, even though the mean emotion was never presented in the set. Set size was either 4 or 16 faces, although only four distinct emotions were present on any given trial. Therefore, there were four incarnations of each of the four emotions in set size 16. Observers had to indicate whether a single test face was happier or sadder than the mean emotion of the preceding set. Test faces were 1, 2, 4, or 5 faces happier or sadder than the mean emotion of the set (Figure 1E). Observers performed 832 trials over four runs. In follow-up control experiments, observers performed a similar discrimination task on other emotions (neutral to disgusted) and on another face dimension (gender; Figure S1).

When asked to identify which of two test faces appeared in the preceding set (experiment 2), observers performed at chance levels (Figure 1D; 53% correct, averaged across the three subjects). Even when the separation between test faces was increased to 15 emotional units, observers were still unable to select the set member at above chance performance (Figure S2). They either lost or were unable to code information about individual face emotion. Despite this, Figure 1F demonstrates that they possessed a remarkably precise representation of the mean emotion of the set (experiment 3). In fact, for two of three subjects, discrimination of the mean emotion was as good as discrimination of the relative emotionality of two faces (measured by the number of units of emotional separation required for 75% correct performance; compare Figures 1B and 1F). Mean discrimination threshold was approximately equal between set sizes 4 and 16, indicating that mean emotion was extracted even for large sets of faces. Importantly, we found that mean extraction generalizes to other emotions (Figure S1A) and even other face dimensions, such as gender (Figure S1B). In these cases, mean discrimination performance was at least as good as regular discrimination. Further precise mean discrimination occurred for stimulus durations as brief as 500 ms (Figure S3).

It is unlikely that the mean extraction revealed here was driven by feature-based processing. Noise added to the faces to reduce low-level cues, such as brightness differences and facial marks, did not impair mean discrimination (Figure S1B). Moreover, when presented with sets of scrambled faces, stimuli thought to require a feature-based strategy [7], observers’ ability to discriminate the mean emotion significantly declined.

Our findings — the statistical extraction of mean emotion or gender — contrast with the prototype effect, in which individuals form an idealized representation of a face based on the frequent occurrence of various features over an extended time period, even though that ideal, or prototype, was never viewed [8,9]. Whereas the prototype and other statistical learning effects [10] take several minutes of exposure and cannot be quickly modified in sequential trials, mean extraction occurs rapidly and flexibly on a trial-bytrial basis and takes less than 500 ms — two sequential trials can have very different means, yet observers code each mean precisely. Naïve observers were even able to extract a mean from a novel set of faces that had never been seen before (Figure S4), providing further evidence against a prototype effect. More importantly, unlike the prototype effect, the rapid extraction of mean emotion may reflect an adaptive mechanism for coalescing information into computationally efficient chunks.

We have demonstrated that observers precisely and automatically extract the mean emotion or gender from a set of faces while lacking a representation of its constituents. This sort of statistical representation could serve two primary functions. First, a single mean can succinctly and efficiently represent copious amounts of information. Second, statistical representation may facilitate visual search, as detecting deviants becomes easier when summary statistics are available [4]. Our results suggest that the adaptive nature of ensemble coding or summary statistics is not restricted to the level of surface perception but extends to face recognition as well.