Abstract
Mapping by admixture linkage disequilibrium (MALD) is a potentially powerful technique for the mapping of complex genetic diseases. The practical requirements of this method include (a) a set of markers spanning the genome that have large allele-frequency differences between the parental ethnicities contributing to the admixed population and (b) an understanding of the extent of admixture in the study population. To this end, a DNA-pooling technique was used to screen microsatellite and diallelic insertion/deletion markers for allele-frequency differences between putative representatives of the parental populations of the admixed Mexican American (MA) and African American (AA) populations. Markers with promising pooled differences were then confirmed by individual genotyping in both the parental and admixed populations. For the MA population, screening of >600 markers identified 151 ethnic-difference markers (EDMs) with δ>0.30 (where δ is the absolute value of each allele-frequency difference between two populations, summed over all marker alleles and divided by two) that are likely to be useful for MALD analysis. For the AA population, analysis of >400 markers identified 97 EDMs. In addition, individual genotyping of these markers in Pima Amerindians, Yavapai Amerindians, European American (EA) individuals, Africans from Zimbabwe, MA individuals, and AA individuals, as well as comparison to the CEPH genotyping set, suggests that the differences between subpopulations of an ethnicity are small for many markers with large interethnic differences. Estimates of admixture that are based on individual genotyping of these markers are consistent with a 60% EA:40% Amerindian contribution to MA populations and with a 20% EA:80% African contribution to AA populations. Taken together, these data suggest that EDMs with large interpopulation and small intrapopulation differences can be readily identified for MALD studies in both AA and MA populations.
Introduction
Mapping by admixture linkage disequilibrium (MALD) is a developing tool for application to the field of human complex genetic disease. MALD is based on the concept that, when admixture occurs between two populations, linkage disequilibrium (LD) is initially created between all loci that have large allele-frequency differences between the two populations. With successive admixed generations, the LD between unlinked loci quickly decays, whereas the LD between linked markers persists for many more generations. Thus, a recently admixed population will have much larger regions of LD between loci than are seen in a standard population (Rife 1954; Chakraborty 1986; Briscoe et al. 1994; Stephens et al. 1994). If any disease-susceptibility alleles or disease-protective alleles are present in a sufficiently different frequency distribution in the parental populations, then MALD can be used to map the susceptibility gene or protective gene in the admixed population. The greater LD in the admixed population will thus theoretically translate into less demanding requirements for both marker saturation and sample size (Stephens et al. 1994; McKeigue 1998). Present-day Mexican American (MA) and African American (AA) populations are thought to be appropriate admixed populations for this type of analysis (Stephens et al. 1994; Zheng and Elston 1999). Indeed, LD has been shown to be detectable for ⩽30 cM in the AA population (Lautenberger et al. 2000).
The importance of MALD as a generally applicable tool for identification of genes contributing to complex genetic disease is currently unclear. MALD has been evaluated theoretically and has been suggested as being an approach potentially more powerful than a standard association study (Briscoe et al. 1994; Parra et al. 1998). Association-based genome scans are likely to require substantially more than 50,000 markers. Although screens of this magnitude are becoming more and more feasible, MALD presents an attractive alternative, since only 500–2,000 markers are believed to be required for sufficient power (Stephens et al. 1994; McKeigue 1998). However, MALD suffers from some disadvantages, compared with association studies in general populations. MALD can map only disease-associated alleles that are present in different frequencies in the two parental populations, and the increased regions of LD may hinder fine-scale mapping.
Compared with general association studies, MALD has the important advantage of not being deterred by multiple independent mutational events, since only an allele’s ethnic identity is used in computations. General association studies have been criticized because of their significantly decreased power in the presence of allelic heterogeneity, especially since allelic heterogeneity is likely to be very common in complex genetic diseases (Terwilliger and Weiss 1998). Furthermore, MALD has the potential to map genes that, within a nonadmixed population, are not sufficiently polymorphic to be detected by either association or linkage studies. In addition, modeling studies suggest that multiple waves of parental contribution to the admixed population, such as those suggested for the AA population, may enhance, rather than retard, the ability of MALD to identify chromosomal regions of interest with regard to a given complex disease (Pfaff et al. 2001). However, several assumptions inherent in the application of MALD have not been adequately addressed, and the validation of these assumptions will be a necessary prerequisite before the method can be used on a genomewide basis to map disease-susceptibility loci.
MALD requires a set of polymorphic markers covering the genome that have large frequency differences between parental ethnicities. A commonly used measure of this difference is δ—the absolute value of each allele-frequency difference between two populations, summed over all marker alleles and divided by two. Thus, markers with large δ's between the European American (EA) and the African (AF) populations will be required for use in MALD analysis of the AA population, and markers with large δ's between the EA and the Amerindian (AI) populations will be required for use in MALD analysis of the MA population. Several investigators have suggested that markers with δ>0.30 will be useful for MALD (Stephens et al. 1994; Shriver et al. 1997), although recent simulations suggest that genomewide studies of complex disease may require markers with even greater differences (McKeigue 1998; McKeigue et al. 2000). Thus, the first assumption of the MALD approach is that a set of such markers can be identified. Here we report a large-scale screen of microsatellite and diallelic short insertion/deletion polymorphism (SIDP) markers that uses a DNA-pooling method followed by individual genotyping for confirmation. We identified 97 markers with δ>0.30 between the EA and the AF populations and 151 markers with δ>0.30 between the EA and the AI populations. These markers (i.e., ethnic-difference markers [EDMs]) should be very useful in both further theoretical evaluation of the MALD method and actual application of MALD to genomewide studies.
The second requirement of the MALD method is that the putative EDMs can be used to determine the contribution of the parental populations to each chromosomal region of the admixed population. In practice, this means providing some evidence (a) that the set of EDM markers distinguish between the likely parental contributors (e.g., AF individuals from western Africa and EA individuals) to the admixed population (e.g., the AA population) and (b) that a mixture of the putative parental contributors can adequately describe the admixed population. For this to be true, there must not have been significant divergence in the EDM allele frequencies of each parental ethnicity since the time it contributed to the admixed ethnicity. In addition, there must be only small differences within any of the original parental populations that contributed to the admixed population. Here, by individually genotyping Pima AI individuals, Yavapai AI individuals, EA individuals, AF individuals from Zimbabwe, MA individuals, and AA individuals and comparing to the CEPH genotyping-set data, we are able to address both these assumptions. In addition, both microsatellite and SIDP EDMs are used to estimate the admixture proportions in present-day MA and AA populations.
Material and Methods
Collection of Samples
Blood- or buccal-cell samples were obtained from all individuals, according to protocols and informed-consent procedures approved by institutional review boards, and were labeled with an anonymous code number. None of the individuals were first-degree relatives of each other, and ethnicities were self-described. In the MA and AA samples, all individuals had no known parents or grandparents whom they would describe as being of direct European, AI, or AF heritage. The MA and EA individuals were random volunteers from northern California. For AA individuals, ∼75% of samples were volunteers from northern California, and ∼25% were from a wide distribution of other geographic locations in the United States. AI individuals used for individual genotyping were either Yavapai (a Yuman-speaking tribe of southwestern Arizona; samples were kindly donated by Dr. David Smith of the University of California, Davis), or Pima from Arizona (samples provided by R.L.H. and W.C.K.). AF samples were from Zimbabwe Shona (a Bantu-speaking group) and were supplied by R.C. according to National Institutes of Health guidelines. In addition, genotyping data from the CEPH sets of families from France and Utah were examined (see the Web site of the Fondation Jean Dausset CEPH).
DNA Isolation and Pooling
DNA was isolated from blood and serum samples by QIAamp DNA Blood Mini Kits (Qiagen); DNA was isolated from buccal swabs by a simple NaOH method, as described elsewhere (Bali et al. 1999). All markers were first examined for differences between DNA pools, and promising markers were then confirmed by individual genotyping. In previous studies, DNA pools have been shown to be accurate in estimating the allele-frequency differences between two sets of 50–200 individuals (Collins et al. 2000). DNA samples to be pooled were quantified in microtiter trays, by PicoGreen fluorescence assay (Molecular Probes) and the FMBIO II fluorescence reader (Hitachi). Pools were constructed by the BIOMEK 2000 (Beckman) robot and consisted of nanogram-equal aliquots from each sample. AA, MA, EA, and AF pools each contained 200 individuals, whereas the AI pool contained 48 Pima individuals (Yavapai AI samples were not used in DNA pools because their quantities were insufficient). The final concentration of each pool was then confirmed by PicoGreen fluorescence assay, and all pools were diluted to 1 ng/μl, by a solution of 10 mM Tris and 1 mM EDTA.
Marker Sets and PCR Conditions
Markers screened included subsets of the Marshfield screening set 8A, the ABI PRISM linkage-mapping set, unlabeled SIDPs supplied by Marshfield, and other microsatellite and SIDP markers available from other projects in our laboratories (see the Web site of the Center for Medical Genetics, Marshfield Medical Research Foundation). A small subset of SIDP markers was specifically included in this screen because of results of preliminary genotyping done by Marshfield on a small number of Amazonian AI and EA individuals. In addition, 50 microsatellites were included in the screen because a comparison between the CEPH data set and the results of the genotyping of AI individuals suggested a potential difference. A list of all markers screened that gave negative results is available on request. All markers were screened under the following conditions: extension for 3 min at 95°C; 32 cycles of 45 s at 95°C, 1 min 30 s at 58°C, and 45 s at 72°C; and, finally, extension for 6 min at 72°C. PCR was performed in 384-well plates (Phenix Research Products) and consisted of 0.5 μl of PCR buffer, 0.7 μl of 2.5 mM dNTP mix (Pharmacia & Upjohn), 0.05 μl cDNA polymerase (Clonetech Advantage), 0.1 μl of 10 μM primer mix, 2.65 μl of ddH20, and 1 μl of 1 ng of DNA/μl, for total reaction volume of 5 μl. For the majority of markers, fluorescently tagged primers were used, but, for the unlabeled set of SIDPs supplied by Marshfield, fluorescent dUTPs (ABI PRISM) were added as one-third of the dNTP mix. PCR was performed in a 9700 GeneAmp PCR System, and PCR products were electrophoresed on a 3700 DNA Analyzer (PE Applied Biosystems).
Data Analysis
The total allele-frequency difference between ethnic pools was estimated by calculation of a total allele content difference (ΔTAC) value (Collins et al. 2000). In brief, the peak height of each allele within a pooled electrophoretogram profile is calculated as a percentage of that total pool. The two pools are then compared, and, for each allele, the absolute value of the difference in peak-height percentages is calculated. These values are divided by two and are summed, to obtain the ΔTAC value, which has been shown to have a strong correlation (r=0.975) with the δ value, for comparisons between pools of 200 (Collins et al. 2000). A simple program (PoolTool) to perform this analysis was created. For the majority of markers, all ethnicities were examined, although, later in the screening process, markers were examined only for parental ethnicities, since preliminary data had confirmed the validity of the pooling method. If a marker did not amplify under the standard conditions, it was not further analyzed. If a marker had a ΔTAC value of <30%, it was not further examined by individual genotyping.
In the majority of cases, markers with ΔTAC values >30% were then examined by individual genotyping for the ethnic comparison in which they were promising. Minimum genotyping for EDMs included 50 individuals of each parental and admixed ethnicity, although the average was ∼85 for EA individuals and AF individuals, ∼150 for MA individuals and AA individuals, and ∼65 for AI individuals.
Genomic Positions
The approximate megabase position for each EDM was determined by use of the Human Genome Browser (J. Kent, University of California, Santa Cruz), based on the August 6, 2001 human-genome draft assembly (see the Web site of the UCSC Human Genome Project Working Draft). For many markers not found in initial search, GenBank accession numbers of sequences within short (i.e., <50-kb) contigs were used. For some markers, approximate positions were determined by analysis of alternate genetic markers closely linked on the Marshfield genetic maps. Genetic-map positions either were determined on the basis of the Marshfield maps or were placed on this map on the basis of sequence location; in the latter case, map positions were approximated by analysis of the genetic-map position of markers physically located within 1 Mb of the marker in question.
Statistical Analysis
In addition to examination of the δ values for microsatellite EDMs, also, for the specific analyses described below, the microsatellites were converted to diallelic markers and then were reexamined. This conversion was performed by grouping alleles on the basis of their frequencies in the parental ethnic groups, to maximize the ethnic difference. This is a modification of a collapsing method devised for analysis by the transmission/disequilibrium test (Kaplan et al. 1998), and it removes artificial differences due to small numbers of individuals typed for rare alleles. In addition, it greatly simplifies the data, making comparisons and statistical analysis much more straightforward. This transformation also allowed examination of whether, between subpopulations, there were frequency differences in ethnically informative alleles. In brief, a separate allele grouping was performed for each marker, for the EA:AF and EA:AI comparisons. An allele was included in the grouping (i.e., was considered ethnically informative) if (a) its highest frequency in either the admixed or either parental ethnicity was ⩾30% greater than its lowest allele frequency or (b) it had an individual δ of 0.075. The alleles were then grouped into two categories, according to which parental ethnicity possessed the higher frequency.
To estimate the admixture proportions of the AA and MA samples, the observed allele frequencies were compared with their expectations at various specified admixture proportions. The expected allele frequencies were calculated by averaging the parental frequencies, weighting each for the proportion of admixture being assumed. A weighted-least-squares method was used to determine whether there was a statistically significant difference between the predicted allele frequencies and the observed data (Long 1991). For the microsatellites, the statistical calculation was performed after the data had been transformed to diallelic form. In addition, the best estimate of admixture contributions was calculated by estimation of χ, the proportion contributed from non-European sources. This was accomplished by minimizing the equation
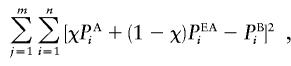 |
where PAi is the individual allele frequency in either the AF or the AI population, PEAi is the allele frequency in the EA population, PBi is the allele frequency in either the AA or the MA population, χ is the contribution from either the AF or the AI population, n is the number of alleles, and m is the number of markers.
Confidence intervals (CIs) around this best fit were determined by a bootstrapping method using 1,000 simulations in which data sets were randomly generated on the basis of our genotyping results.
Results
Identification of EDMs
For identification of EDMs, microsatellites and SIDPs were examined in DNA pools of EA, AI, AF, MA, and AA individuals. The screen of 603 markers in EA individuals and AI individuals identified 151 EDMs (δ>0.30), and a screen of 413 markers in EA and AF individuals identified 97 EDMs. These microsatellite and SIDP markers are positioned throughout the genome, as shown in table 1. All EDMs were either confirmed by individual genotyping in both parental and admixed ethnicities (136 of 151 in the EA:AI comparison, 68 of 97 in the EA:AF comparison) or by a second pooled PCR comparison. For all EDMs, the δ between the admixed population and either parental population was intermediate between that of the δ between the two parental populations (table 1 and data not shown).
Table 1.
Positions and δ Values of EDMs Discovered in Genome Screen
|
Position |
δ between Populations EA anda |
|||||
| Marker | Megabaseb | Centimorganc | AI | MA | AF | AA |
| Chromosome 1: | ||||||
| D1S468 | 4 | 4.0 | .48 | .19 | ND | ND |
| D1S552 | 21 | 45.3 | .32 | .13 | .43 | .22 |
| D1S1622 | 35 | 56.7 | .58† | .38 | ND | ND |
| D1S2134 | 55 | 75.6 | .61 | .29 | ND | ND |
| D1S1728 | 95 | 109.0 | .35 | .15 | .46 | .29 |
| D1S1595 | 184 | 161.1 | .35 | .11 | ND | ND |
| D1S2635 | 188 | 165.6 | .33 | .20 | .16† | ND |
| D1S2707 | 189 | 168.5 | .31 | .18 | ND | ND |
| D1S2844 | 192 | 175.0 | .53 | .30 | .23† | ND |
| D1S2878 | 195 | 177.9 | .39 | .20 | .58 | .55 |
| D1S194 | 195 | 178.4 | .32 | .17 | .15† | ND |
| D1S426 | 195 | 177.9 | .24† | .11† | .69 | .56 |
| D1S2681 | 197‡ | 179.1 | .50 | .18 | .39 | .28 |
| D1S518 | 220 | 202.2 | .46 | .32 | .32 | .29 |
| D1S1678 | 238 | 218.4 | ND | .10† | .35 | .25 |
| D1S2871 | 258 | 241.3 | .47 | .20 | .31 | .23 |
| D1S439 | 262 | 242.3 | .42 | .25 | .29† | ND |
| D1S1656 | 267 | 245.1 | .34 | ND | ND | ND |
| D1S251 | 269 | 245.1 | .35 | .17 | .51 | .42 |
| D2S1400 | 12 | 27.6 | ND | .07 | .61 | .36 |
| Chromosome 2: | ||||||
| D2S1360 | 18 | 38.3 | .57 | .29 | .21† | ND |
| MID-366 | 31 | 48§ | .41 | .12 | .71 | .54 |
| MID-426 | 39 | 56§ | .36 | .15 | .23† | ND |
| D2S441 | 72 | 86.8 | .33 | .17 | .15 | .07 |
| D2S2964 | 89 | 103.2 | .32 | ND | ND | ND |
| MID-55 | 117 | 123§ | .45 | .20 | .11 | .07 |
| D2S1399 | 153 | 152.0 | .73 | .40 | .29† | ND |
| D2S1776 | 175 | 173.0 | .44 | .25 | .19† | ND |
| D2S117 | 204 | 194.4 | ND | ND | .69† | .61† |
| MID-485 | 208.5 | 199§ | .25 | .21 | .68 | .51 |
| D2S126 | 227‡ | 221.1 | ND | .09 | .56 | .42† |
| D2S172 | 241 | 235.1 | ND | ND | .44† | .39 |
| D2S427 | 242 | 236.7 | ND | ND | .40† | .30 |
| D2S2193 | 242 | 236.7 | .42 | .19 | ND | ND |
| MID-185 | 245 | 250.0§ | .50 | .21 | .49 | .36 |
| Chromosome 3: | ||||||
| D3S2387 | 3 | 5.5 | .51† | .45 | .26† | ND |
| D3S1050 | 6‡ | 14.5 | .40 | ND | ND | ND |
| D3S1768 | 41 | 61.5 | .39 | .21 | .26† | ND |
| D3S1752 | 109 | 114.0 | .43 | ND | ND | ND |
| D3S3045 | 120 | 124.2 | .66 | .26 | ND | ND |
| Chromosome 4: | ||||||
| D4S391 | 30 | 43.6 | .46 | .31 | .40† | .33† |
| D4S1645 | 68 | 72.5 | .45 | ND | ND | ND |
| D4S398 | 68 | 72.5 | .27 | .23 | .47 | .28 |
| D4S3243 | 75 | 88.4 | ND | .08† | .51 | .37 |
| D4S2361 | 92 | 93.5 | .61† | .40† | .45† | .33 |
| D4S2634 | 109 | 104.8 | .32 | ND | ND | ND |
| MID-52 | 110 | 106§ | .57 | .32 | .23 | .12 |
| D4S3240 | 120 | 114.0 | .56 | ND | ND | ND |
| D4S2623 | 122 | 114§ | .43 | .14 | .37 | .32 |
| D4S408 | 202 | 195.1 | .36 | .19 | .25† | ND |
| Chromosome 5: | ||||||
| D5S392 | 1 | .0 | .49 | .27 | ND | ND |
| D5S1473 | 26 | 36.3 | .34 | ND | ND | ND |
| D5S426 | 39 | 52.0 | .24† | .11† | .45† | .39† |
| (continued) | ||||||
| D5S1721 | 114 | 112.5 | .50 | ND | ND | ND |
| D5S1453 | 118 | 114.8 | .57 | .32 | ND | ND |
| D5S2490 | 158‡ | 149.5 | .64 | ND | ND | ND |
| D5S820 | 173 | 159.8 | .39 | .25 | ND | ND |
| D5S1471 | 185 | 172.1 | .41 | .18 | ND | ND |
| D5S1478 | 130 | 129.8 | .34 | ND | ND | ND |
| Chromosome 6: | ||||||
| D6S344 | 2 | 1.0 | .34 | .17 | .37 | .27 |
| MID-206 | 3 | 9§ | .08† | .00† | .80† | ND |
| SE30 | 4 | 9.2 | .24† | .17† | .40 | .22 |
| MID-461 | 9 | 13.5§ | .05† | .06† | .43† | ND |
| D6S1006 | 15 | 26.7 | .52 | ND | ND | ND |
| MID-514 | 19 | 32.5§ | .33 | .16 | .26 | .16 |
| MID-533 | 21 | 34§ | .21† | .15† | .32† | ND |
| D6S285 | 22 | 34.0 | .16 | .11 | .31 | .23 |
| D6S461 | 27 | 40.1 | .31 | .21 | .39 | .34 |
| D6S299 | 27 | 42.3 | .20 | .15 | .39 | .27 |
| D6S276 | 28 | 44.4 | .27† | .14† | .67 | .62 |
| D6S464 | 31 | 44.4 | .20† | .15† | .47 | .46 |
| D6S306 | 32 | 44.4 | .10† | .09 | .55 | .42 |
| D6S2707 | 33 | 44.6§ | .53 | .18 | .45 | .35 |
| D6S510 | 34 | 44.6§ | .34 | .15 | ND | ND |
| M6S201 | 34 | 46§ | .31 | .22 | .29† | ND |
| D6S2705 | 34 | 44.7§ | .45 | .24 | .63 | .45 |
| M6S101 | 35 | 45§ | .56 | .27 | .49 | .38 |
| D6S273 | 35 | 45.0 | .28† | .19† | .32 | .24 |
| MID-108 | 36 | 45§ | .45 | .23 | .12 | .10 |
| MID-104 | 36 | 45§ | .42 | .14 | .15 | .12 |
| D6S1666 | 40 | 45.5 | .12 | .10 | .45 | .32 |
| MID-439 | 43‡ | 49§ | .30 | .10 | ND | ND |
| D6S291 | 43 | 49.5 | ND | .07† | .40 | .36 |
| D6S1019 | 46 | 53.8 | .33 | ND | ND | ND |
| D6S1641 | 47 | 53.8 | .10 | .06 | .37† | .30† |
| MID-248 | 54 | 66.4§ | .23 | .10† | .45 | .29 |
| MID-457 | 61 | 77§ | .39 | .20 | .30 | .29 |
| D6S1043 | 106 | 100.9 | .61 | .24 | .24† | ND |
| D6S1056 | 108 | 102.8 | .43 | .20 | .25† | ND |
| MID-417 | 112 | 104§ | .35 | .12 | .25 | .20 |
| MID-418 | 112 | 104§ | .30 | .08 | ND | ND |
| MID-196 | 114 | 106§ | .50 | .26 | .04 | .07 |
| D6S434 | 117 | 109.2 | .43 | .20 | .31 | .22 |
| D6S1021 | 120 | 112.2 | .48† | .19† | .40† | .35† |
| D6S287 | 136 | 122.0 | .48 | .34 | .29 | .27 |
| MID-202 | 160 | 141§ | .35 | .10 | .42 | .37 |
| D6S1003 | 163 | 144.5 | .44 | ND | ND | ND |
| MID-474 | 163 | 145§ | .32 | .11 | .32 | .21 |
| GATA184A08 | 167 | 146.1 | .36 | .25 | ND | ND |
| D6S2436 | 174 | 154.6 | .30† | .22† | .60† | ND |
| D6S1035 | 180 | 164.8 | .38 | ND | ND | ND |
| MID-460 | 189 | 165§ | .29 | .17 | .31 | .27 |
| MID-462 | 189 | 165§ | .29 | .17 | .31 | .26 |
| MID-398 | 183 | 167§ | .40 | .17 | .45 | .40 |
| D6S264 | 188 | 179.1 | .33 | .15 | .37 | .36 |
| D6S1027 | 190 | 187.2 | .61† | .34 | .61 | .45 |
| MID-237 | 191 | 188§ | .69 | .26 | .25 | .17 |
| MID-472 | 191 | 188§ | .48 | .16 | .04† | ND |
| (continued) | ||||||
| Chromosome 7: | ||||||
| MID-425 | 25 | 38§ | .44 | .22 | .09 | .12 |
| D7S657 | 98 | 104.9 | .40† | .20† | .58† | .53† |
| MID-271 | 109 | 112§ | .35 | ND | .09 | .02† |
| D7S1822 | 136 | 129.6 | .41 | ND | ND | ND |
| D7S530 | 140 | 134.6 | .33 | .18 | ND | ND |
| D7S1824 | 151 | 149.9 | .40 | .27 | ND | ND |
| D7S2195 | 156 | 155.1 | .49 | .25 | ND | ND |
| D7S3058 | 167 | 173.7 | .10† | .16† | .43† | .33† |
| D8S277 | 9 | 8.3 | .44 | .26 | .57 | .49 |
| Chromosome 8: | ||||||
| D8S1106 | 16 | 26.4 | .47 | .21 | .28† | ND |
| D8S1128 | 146 | 139.5 | .47 | .19 | ND | ND |
| D8S284 | 149 | 143.8 | ND | .12 | .48† | .31† |
| D8S272 | 156 | 154.0 | ND | ND | .42† | .38† |
| MID-476 | 22 | 34§ | .51 | .19 | .40 | .34 |
| Chromosome 9: | ||||||
| D9S741 | 27 | 42.7 | .35 | ND | ND | ND |
| D9S301 | 80 | 66.3 | .55† | .30† | .15† | ND |
| D9S175 | 84 | 70.3 | .25† | .13† | .54† | ND |
| D9S920 | 80 | 87.5 | .35 | ND | ND | ND |
| D9S922 | 89 | 80.3 | .65 | .28 | .20† | ND |
| D9S1120 | 95 | 88.9 | .31 | ND | ND | ND |
| Chromosome 10: | ||||||
| D10S466 | 21 | 46.2 | .59 | ND | ND | ND |
| D10S1221 | 60 | 75.6 | .44 | .21 | .49† | ND |
| MID-122 | 81 | 95§ | .38 | .19 | .12 | .02 |
| D10S677 | 104 | 117.4 | .44 | .19 | .25† | ND |
| MID-170 | 121 | 130§ | ND | .08 | .41 | .37 |
| D10S169 | 144 | 173.0 | .38 | ND | ND | ND |
| Chromosome 11: | ||||||
| D11S1984 | 1 | 2.1 | .66 | .24 | ND | ND |
| D11S1999 | 11 | 17.2 | .49 | .18 | ND | ND |
| D11S2365 | 62 | 58.4 | .39 | ND | ND | ND |
| D11S2000 | 121 | 100.6 | ND | .28 | ND | ND |
| D11S968 | 153 | 147.8 | .38 | ND | ND | ND |
| Chromosome 12: | ||||||
| D12S391 | 14 | 26.2 | .44 | .20 | ND | ND |
| D12S1042 | 30 | 48.7 | .41 | .15 | ND | ND |
| D12S351 | 106 | 95.6 | .15 | .07 | .42† | ND |
| D12S2070 | 133 | 125.3 | .73 | .31 | ND | ND |
| D12S2082 | 135 | 130.9 | .41 | ND | ND | ND |
| D12S1045 | 151 | 160.7 | .58 | .25 | ND | ND |
| Chromosome 13: | ||||||
| MID-280 | 18 | 27§ | .21 | .13 | .30 | .25 |
| D13S265 | 92 | 68.7 | ND | .16 | .51 | .42 |
| D13S779 | 104 | 82.9 | .39 | .24 | .08† | ND |
| D13S173 | 112 | 93.5 | .18† | .11† | .57† | .47† |
| Chromosome 14: | ||||||
| D14S587 | 50 | 55.8 | ND | .09 | .33 | .25 |
| D14S745 | 54 | 57.4 | .37 | ND | ND | ND |
| MID-257 | 70 | 80§ | .36 | .11 | .00 | .02 |
| Chromosome 15: | ||||||
| MID-132 | 21 | 6§ | .13 | .18 | .47 | .33 |
| D15S822 | 24 | 12.3 | .64 | .27 | ND | ND |
| D15S165 | 27 | 20.2 | ND | ND | .44 | .26 |
| D15S642 | 108 | 122.1 | .37† | .26 | .44† | .32† |
| (continued) | ||||||
| Chromosome 16: | ||||||
| D16S764 | 18 | 30.0 | .62 | .21 | .12† | ND |
| MID-225 | 21 | 35§ | .41 | .28 | .55 | .52 |
| D16S416 | 61 | 66§ | .09† | .07† | .61 | .52 |
| D16S2623 | 62 | 66.1 | .50 | ND | ND | ND |
| D16S3032 | 66 | 73.2 | ND | .08 | .51 | .49 |
| D16S3112 | 66 | 73.3§ | .36 | .20 | .22† | ND |
| D16S3071 | 67 | 75.3 | .29 | .22 | .38 | .31 |
| D16S422 | 99 | 111.1 | .67 | ND | ND | ND |
| D16S2621 | 102‡ | 130.4 | .42 | .22 | .11† | ND |
| Chromosome 17: | ||||||
| MID-278 | 69 | 84§ | .08 | .03 | .64 | .48 |
| MID-286 | 72 | 86§ | .52 | .20 | .12 | .09 |
| Chromosome 18: | ||||||
| D18S976 | 6 | 12.8 | ND | ND | .40† | .36† |
| MID-151 | 13 | 42.0 | .07 | ND | .39 | .33 |
| D18S1364 | 74 | 99.4 | ND | ND | .45 | .41 |
| D18S541 | 81 | 106.8 | .46 | ND | ND | ND |
| D18S70 | 90 | 126.0 | .46 | ND | ND | ND |
| Chromosome 19: | ||||||
| D19S221 | 16 | 36.2 | .56 | .25 | .25† | .16† |
| D19S222 | 36 | 49.8 | .35† | .16† | .42† | .39† |
| Chromosome 20: | ||||||
| D20S103 | 1 | 2.1 | .40 | .21 | ND | ND |
| D20S117 | 1 | 2.8 | .38† | .29† | .37† | ND |
| MID-152 | 2 | 8§ | .58 | .27 | .05 | .04 |
| D20S602 | 8‡ | 21.1 | .35 | ND | ND | ND |
| D20S186 | 12 | 32.3 | .28 | .16 | .64† | .67 |
| D20S477 | 22 | 47.5 | .43 | .21 | .16† | ND |
| MID-161 | 35 | 50.8§ | .52 | .22 | .07† | .06† |
| D20S119 | 45 | 61.8 | .48 | .27 | .29† | ND |
| D20S196 | 52 | 75.0 | .59 | ND | ND | ND |
| Chromosome 21: | ||||||
| D21S1440 | 36 | 36.8 | .33 | .11 | .32 | .18 |
| D21S266 | 40 | 45.9 | .33 | .23 | .26 | .23 |
| Chromosome 22: | ||||||
| D22S446 | 19 | 14.4 | .40 | .26 | .60 | .51 |
| MID-96 | 22 | 21.2§ | .30 | .13 | .25 | .17 |
| D22S1133 | 23 | 21.2§ | .25 | .11 | .42 | .37 |
| D22S419 | 23 | 21.5 | .30 | .14 | .15† | ND |
| D22S315 | 23 | 21.6 | .33† | .23 | ND | ND |
| D22S1154 | 23 | 23.4 | .15 | .09 | .38 | .20 |
| D22S1167 | 24 | 24.7 | .33† | .19† | .49 | .35 |
| MID-102 | 24 | 25.8§ | .37 | .17 | .01 | .00 |
| D22S1144 | 24 | 27.5 | .36 | .21 | .20† | .19† |
| MID-105 | 32 | 33.7§ | .16 | .03 | .49 | .33 |
| MID-106 | 32 | 33.7§ | .14 | .05 | .53 | .35 |
| D22S445 | 34 | 45.8 | .29† | .20† | .47† | ND |
| MID-107 | 36 | 46§ | .16 | .12 | .36 | .28 |
| D22S423 | 37 | 46.4 | .35 | .17 | .53 | .44 |
| MID-93 | 39 | 47.3§ | .46 | .33 | .54 | .40 |
| D22S1170 | 45 | 55.3 | .17 | .20 | .38† | ND |
| Chromosome X: | ||||||
| MID-218 | 13 | 20§ | .67 | .40 | .40 | .39 |
| MID-219 | 16 | 25§ | .17 | .10 | .63 | .53 |
| DXS9896 | 26‡ | 30.8 | ND | ND | .46† | ND |
| MID-220 | 76 | 57§ | .40 | .14 | .08 | .06 |
| DXS6800 | 77 | 57.4 | ND | ND | .40† | .31† |
| (continued) | ||||||
| MID-76 | 101 | 65§ | .33 | .17 | .03 | .05 |
| MID-193 | 144 | 97§ | .56 | .16 | .17 | .12 |
ND = not determined. A dagger (†) indicates that δ was estimated on the basis of the ΔTAC value between ethnic pools.
Approximate position determined by use of the Human Genome Browser based on the August 6, 2001, human genome draft assembly, with either the marker name or the sequence within marker amplimers, by the BLAT search function (see the Web site of the UCSC Human Genome Project Working Draft). A double dagger (‡) indicates that the approximate position was determined by analysis of alternate genetic markers closely linked on the Marshfield genetic maps (see the Web site of the Center for Medical Genetics, Marshfield Medical Research Foundation).
Sex-averaged genetic-map position, as determined either by Marshfield or, in the case of those positions designated by a section symbol (§), on the basis of the sequence location; in the latter case, map positions were approximated by analysis of the genetic-map position of markers physically located within 1 Mb of the marker in question.
The number of markers examined and their respective δ values are summarized in table 2. Some of these markers were preselected on the basis of earlier results (see the “Marker Sets and PCR Conditions” subsection of the “Material and Methods” section, above); therefore the screen was slightly biased, and the percentages of EDM markers identified may be an overestimate of what would be expected in a truly random screen. To determine the percentage of EDMs that could be expected in a random screen, we examined sets of randomly selected markers screened for each ethnic comparison. A subset of 96 SIDP markers located on chromosomes 6 and 22 provided an unbiased estimate of the percentage of SIDP EDMs. In this subset, 14.6% of the markers had δ>0.30, and 9.1% had δ>0.40, between the EA and AI populations. Similarly, 12.5% of markers had δ>0.30, and 8.2% had δ>0.40, between the EA and AF populations. For microsatellites, percentages expected in a random screen were calculated on the basis of data for all markers reported in table 2, excluding the 50 preselected markers (for a total of 479-50=429 markers in the EA:AI comparison and 311-32=279 markers in the EA:AF comparison, since only 32 of the 50 markers had been examined in that comparison). In this subset, 21.7% had a δ>0.30, and 13.9% had a δ>0.40, in the EA:AI comparison. Similarly, 22.4% had a δ>0.30, and 17.9% had a δ>0.40, in the EA:AF comparison. A Web site titled “Ethnic Difference Marker (EDM) Allele Frequencies,” displaying the allele frequencies of these markers, has been established and will be updated as further markers are identified.
Table 2.
Summary of Screen for EDMs
|
No. with δ |
|||||
| Marker Type | No. Screened | >.30 | >.40 | >.50 | >.60 |
| EA:AI comparison:a | |||||
| Microsatellite | 479 | 116 | 69 | 30 | 13 |
| Insertion/deletion | 124 |
35 |
21 |
10 |
2 |
| Total | 603 | 151 | 90 | 40 | 15 |
| EA:AF comparison:b | |||||
| Microsatellite | 311 | 71 | 52 | 22 | 10 |
| Insertion/deletion | 102 |
26 |
18 |
8 |
5 |
| Total | 413 | 97 | 70 | 30 | 15 |
AI samples are from Pima and Yavapai tribes.
AF samples are from Zimbabwe.
Characterization of EDMs
Individual allele frequencies were examined to further characterize the relationship between the putative parental and admixed populations. EDM alleles with large frequency differences between two parental populations demonstrated intermediate allele frequencies in the admixed population, as illustrated in table 3. For example, allele 158 of the microsatellite D4S3243 was present at a frequency of 45.4% in the EA population and at a frequency of 1.3% in the AF population, and its frequency in the AA population was intermediate, at 11.8%. This finding was also true for the MA population, as demonstrated by the SIDP MID-237, with allele 120 present at a frequency of 4.3% in the EA population, 73.6% in the AI population, and 30.9% in the MA population. Moreover, for microsatellite EDMs, the distribution of the allele frequencies in the admixed population is consistent with those expected on the basis of the putative parental contribution (e.g., for D4S3243, the frequency of alleles 158, 162, 166, and 170 in the AA population all suggest an ∼80% contribution by the AF population and an ∼20% contribution by the EA population). These consistent results were obtained despite the fact that AF samples were from Zimbabwe, rather than from a western-African location (see the “Discussion” section).
Table 3.
Examples of Microsatellite and Insertion/Deletion Allele Frequencies in Parental and Admixed Populations
| Allele | No. Observedin Population | ||
| EA:AA:AFa Comparison |
|||
| EA |
AA |
AF |
|
| D4S3243 (δ=51.1): | |||
| 146 | 0 | 0 | 1.3 |
| 150 | 0 | 0 | 2.5 |
| 154 | 0 | 1.3 | 0 |
| 158 | 45.4 | 11.8 | 1.3 |
| 162 | 5.6 | 2.6 | 2.5 |
| 166 | 17.6 | 35.5 | 37.5 |
| 170 | 24.1 | 39.5 | 48.8 |
| 174 | 6.5 | 7.9 | 2.5 |
| 178 | 0 | 1.3 | 2.5 |
| MID-106 (δ=52.5): | |||
| 114 | 39.0 | 74.5 | 92.2 |
| 119 | 61.0 |
25.5 |
7.8 |
| EA:MA:AIb Comparison |
|||
| EA |
MA |
AI |
|
| D10S677 (δ=44.1): | |||
| 195 | 7.8 | 4.1 | .6 |
| 199 | 29.0 | 17.5 | 3.4 |
| 203 | 6.6 | 10.1 | 16.0 |
| 207 | 11.8 | 9.0 | .9 |
| 211 | 23.6 | 23.5 | 24.8 |
| 215 | 12.9 | 24.6 | 44.5 |
| 219 | 6.0 | 7.4 | 7.3 |
| 223 | 1.1 | 2.5 | .7 |
| 227 | .3 | .3 | 1.7 |
| MID-237 (δ=69.3): | |||
| 120 | 4.3 | 30.9 | 73.6 |
| 131 | 95.7 | 69.1 | 26.4 |
AF samples are from Zimbabwe.
AI samples are from the Pima tribe (in the case of D10S677) and from the Yavapai tribe (in the case of MID-237).
To determine whether markers that are EDMs in one ethnic comparison are more likely to be EDMs in another ethnic comparison, we examined all markers that had been either individually typed or typed by repeated pools in both EA:AF and EA:AI comparisons. Of these 307 markers, 75 (24.4%) were EDMs in the EA:AF comparison, and 88 (28.7%) were EDMs in the EA:AI comparison; 39 (or 12.7%) were EDMs in both comparisons, significantly more than the 22 (307×0.244×0.287) that would be expected by chance (P<.0001; Z-score 3.8, binomial test).
Variation of EDM Frequencies within Populations
Ten microsatellite markers with large differences between the pooled EA DNA sample and the pooled AI (Pima) DNA sample were individually typed in EA individuals and both Pima and Yavapai AI individuals, to determine whether large differences between subpopulations of AI also existed for these EDMs. The sample sizes for these comparisons were small because of our limited supply of AI samples; however, 37–45 Pima and 33–37 Yavapai individuals were typed for each comparison. In the EA:AI comparison, the mean ± SD δ was 0.473 ± 0.114; in contrast, that in the Yavapai:Pima comparison was 0.184 ± 0.092. Much of this difference is likely due to the cumulative difference of allele-frequency variations in rare alleles, because of the small numbers. When these microsatellites were converted to diallelic markers, by grouping alleles according to their EA:Pima differences, the EA:AI δ remained large, at 0.54 ± 0.145, whereas that in the Yavapai:Pima comparison decreased to 0.062 ± 0.034. This suggests that intraethnic differences are small, at least within the ethnically informative alleles of these EDMs.
In addition, EDMs were examined for differences between EA individuals from northern California (see the “Collection of Samples” subsection, above) and the CEPH genotyping set (this set includes families predominantly from France and Utah). Ten microsatellite EDMs in the EA:AF comparison were examined. These markers had a mean ± SD δ of 0.55 ± 0.073 in the EA:AF comparison; in contrast, they had a mean ± SD δ of 0.131 ± 0.056 in the EA:CEPH comparison. When these markers were converted to diallelic markers, the mean ± SD δ in the EA:AF comparison remained high, at 0.559 ± 0.094, whereas that in the EA:CEPH comparison decreased to 0.03 ± 0.029. Ten microsatellite EDMs in the EA:AI comparison also were examined (the 50 microsatellites included in the initial screen, on the basis of a comparison of the CEPH genotyping set versus the AI genotyping set, were excluded from this analysis). For these EDMs, the mean ± SD δ in the EA:AI comparison was 0.493 ± 0.103, whereas that in the EA:CEPH comparison was 0.145 ± 0.046. When these markers were converted to diallelic markers, the mean ± SD δ in the EA:AI comparison remained high, at 0.554 ± 0.154, whereas that in the EA:CEPH comparison decreased to 0.049 ± 0.039.
Admixture Estimations by Use of EDMs
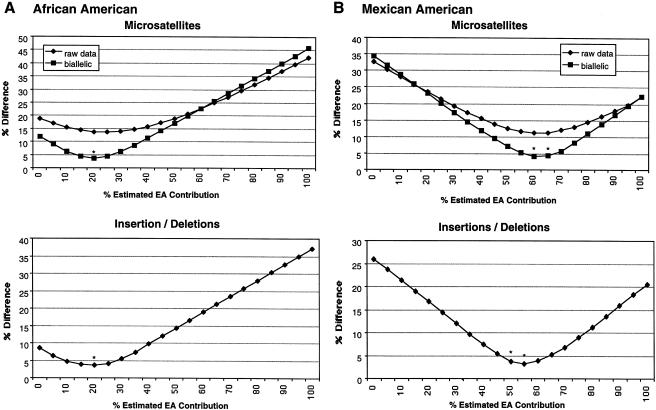
Admixture ratios in present-day AA and MA populations were examined by use of both microsatellite and SIDP EDMs with large δ values (fig. 1). For the estimation of admixture in the AA population, 20 microsatellites with an average EA:AF δ of 0.54 and 20 SIDPs with an average δ of 0.46 were typed in EA, AF, and AA samples. The predicted allele frequencies in the AA population were calculated at varying admixture ratios of the two putative parental-population allele frequencies, and the resulting allele frequencies were compared with the actual AA allele frequencies determined on the basis of individual genotyping. Figure 1A plots the difference between the predicted and actual AA allele frequencies. A 20% EA:80% AF mixture of the EA and AF allele frequencies predicted AA allele frequencies with the smallest difference from actual AA allele frequencies (nadir of curves in fig. 1A): for SIDPs, the predicted AA allele frequencies were not significantly different from actual AA allele frequencies (best fit for SIDPs is 19.3% [95% CI = 16.3%–22.5% for EA contribution to the AA population]); for microsatellites, this same nadir was also observed, both before and after these multiallelic markers had been transformed, on the basis of ethnic differences, into diallelic markers (see the “Statistical Analysis” subsection, above). For the transformed diallelic microsatellite markers, the predicted AA allele frequencies were not significantly different from actual AA allele frequencies (best fit for “ethnic diallelic microsatellites” is 22.7% [95% CI = 20.5%–28.5%]). These results suggest that, for these EDMs, the ethnic allele-frequency differences between the putative parental populations may be appropriate for characterization of the admixed population.
Figure 1.
Percent difference between predicted and actual admixed population allele frequencies, on the basis of microsatellite and insertion/deletion data from putative parental and admixed populations. Microsatellite data are plotted as both the total percent difference (raw data) and the percent difference after conversion of the microsatellite to a diallelic marker by grouping of alleles (see text). Asterisks (*) indicate that, for these percent contributions, the predicted admixed-population allele frequencies are not significantly different from the actual admixed-population allele frequencies, by least-squares analysis. A, Difference between predicted and actual AA allele frequencies, plotted at varying admixture ratios. Predicted frequencies are based on mixing of EA and AF allele frequencies in the indicated percentages. An average of 90 EA, 90 AF, and 270 AA individuals were typed for each marker. B, Difference between predicted and actual MA allele frequencies, plotted at varying admixture ratios. Predicted frequencies are based on mixing of EA and AI allele frequencies in the indicated percentages. An average of 90 EA, 80 AI, and 300 MA individuals were typed for each marker.
For the estimation of MA allele frequencies, 20 microsatellites with an average EA:AI δ of 0.49 and 20 SIDPs with an average δ of 0.47 were typed in EA, AI, and MA samples. For microsatellites, a 60% EA:40% AI and a 65% EA:35% AI mixture best predicted MA allele frequencies. After conversion of these microsatellites to diallelic markers, these ratios predicted MA allele frequencies that were not significantly different from actual MA allele frequencies (fig. 1B; best fit for the EA contribution to the MA sample is 61.9% [95% CI = 57.4%–65.3%]); in contrast, for SIDPs, both a 50% EA:50% AI mixture and a 55% EA:45% AI mixture predicted MA allele frequencies that were not significantly different from actual MA allele frequencies (best fit for the EA contribution to the MA sample is 55.1% [95% CI = 52.7–59.7%]).
Discussion
This large-scale screen has demonstrated that both microsatellite and SIDP markers with δ>0.30 can be readily identified in both the EA:AF and EA:AI comparisons. Although a variety of evidence suggests that the time since the separation of EA and AF is greater than that since the separation of EA and AI (Cavalli-Sforza et al. 1988; Bowcock et al. 1994), similar percentages of EA:AI and EA:AF EDMs were identified (table 2 and the “Identification of EDMs” subsection of the “Results” section). Much of the sequence variation between ethnicities has been suggested to be the result of major bottlenecks that have occurred since the separation of these populations (Dean et al. 1994). We speculate that the similar EDM characteristics seen in the EA:AF and EA:AI comparisons are likely the result of these putative bottlenecks and, hence, may not directly reflect the length of time since specific population-separation events. Recently, consistent with these speculations, Reich et al. (2001) have presented data suggesting that a very large bottleneck occurred in northern Europeans ∼27,000–53,000 years ago. This putative demographic event would have been subsequent to the separation of the European population from the Asian population that subsequently gave rise to the AI population.
In addition, we have observed that the percentage of EDMs common to both the EA:AF and the EA:AI comparisons is significantly greater than what would be expected on the basis of chance overlap. We hypothesize that this may be due, in part, to bottlenecks within the EA population (see the preceding paragraph). In addition, because of a combination of factors, such as repeat type and genomic location, markers may have varying levels of stability. Most EDM markers would be expected to have an intermediate or high level of stability, such that variations are neither rapidly created nor quickly dissolved because of a high mutation rate. Therefore, markers that have the correct inherent level of stability may be more likely to be ethnically informative in any comparison.
Previous investigators examining randomly selected markers have suggested that allele-frequency differences within populations are as large as or larger than differences between populations (Lewontin 1972; Nei and Roychoudhury 1974; Latter 1980; Barbujani et al. 1997). However, the MALD approach assumes that there are a subset of markers for which there are (a) a large allele-content difference between the ethnicities that have admixed and (b) only small differences within any of the original parental populations that contributed to the admixed population. For the MA population, the first requirement appears to be met by our identification of EDMs with large allele-frequency differences between the EA and AI populations that we examined. The second requirement is more difficult to assess, since the original parental populations are no longer available for direct examination. However, for informative EDM alleles, we observed only small differences between subpopulations that are likely descendents of parental contributors. This was true for the Yavapai:Pima comparison and for the EA:CEPH comparison (in which the EA samples are from northern California and the CEPH genotyping set includes families predominantly from France and Utah).
Although we did not assess subpopulation differences within the AF population, another suggestion of EDM stability may be inferred from analysis of the genotyping results for the AF population (Shona from Zimbabwe) in relation to those for the AA population. Zimbabwe, a country in southeastern Africa, is not thought to have contributed significantly to the slave trade, which took place mainly along the coast of western Africa (reviewed in Parra et al. 1998). However, the Shona are a Bantu-speaking group thought to have migrated to Zimbabwe ∼300 b.c. and therefore may be genetically related to western African groups (Iliffe 1995). The allele frequencies of EDMs in the AA population were consistently between those in the EA population and those in the AF population—with a 20% EA:80% AF contribution ratio (tables 1 and 3 and fig. 1A). This finding was supported by examination of individual alleles for microsatellite polymorphisms (table 3). These results therefore suggest that recent subpopulation differences (i.e., those since the separation of the major population groups of eastern and western Africa) are relatively small for these EDMs. Analysis of EDM allele frequencies in various AF subpopulations will be necessary to test this hypothesis.
Using a mixture of present-day EA and AF populations to estimate the allele frequencies in the AA population produces a best fit to actual AA genotyping data, with a 20% EA:80% AF ratio, in general agreement with the findings of previous, more limited studies (Parra 1998). Similarly, a mixture of present-day EA and AI populations best estimates present-day MA allele frequencies, with a 50%–60% EA:40%–50% AI ratio, which also is in agreement with the findings of previous studies (Chakraborty et al. 1986; Hanis et al. 1986). At these ratios of admixture, the allele frequencies estimated by a weighted mixture of parental-population genotyping results are not significantly different from the observed admixed-population allele frequencies for SIDPs and for ethnic diallelic microsatellites. Therefore, these results further support the hypothesis that, since the time when they contributed to the MA and AA populations, relatively little divergence in EDM allele frequencies has occurred in present-day EA, AF, and AI populations. Although definitive conclusions concerning multiple unknown factors are impossible, the results are consistent with the hypothesis that our chosen representatives of the parental-population contributors are appropriate for the AA and MA populations that we have studied.
For the AA population, both microsatellites and SIDPs produced identical estimates of admixture ratios (fig. 1A); in contrast, for the MA population, the best estimate of parental-population admixture ratios when microsatellites and SIDPs were used differed by ∼5%. This interesting observation needs to be confirmed by use of larger numbers of EDMs. However, it is a conceivable result if one assumes that microsatellites inherently have a slightly lower level of stability than do SIDPs and that the MA population was created by admixture between the EA population and two different AI subpopulations. These subpopulations would have to have diverged enough to allow small differences in microsatellite allele frequencies to be created, but, because of higher stability, their SIDP frequencies would remain identical in each subpopulation. These subpopulations would have to have diverged more than the Pima and Yavapai AI subpopulations, since we have found that microsatellite differences between the latter two groups are insignificant. Even if this hypothesis is true, the differences between the two AI subpopulations would be small, since the admixture-ratio difference predicted by SIDPs and EDMs is small. This effect is unlikely to change the outcome of MALD analysis using MA subjects.
The results of the present study provide researchers with a genomewide set of markers useful for MALD analysis. The average chromosomal interval between the EDMs presented herein is 31 cM for the AA sample and 20 cM for the MA sample. This set clearly needs to be further expanded, to allow the saturation required for MALD analysis, which is estimated to require a marker every 2–10 cM (McKeigue 1998; Lautenberger et al. 2000; Pfaff et al. 2001). For the AA population, additional markers have recently been identified by Smith et al. (2001). In addition, markers with larger δ values should be obtainable, on the basis of large-scale single-nucleotide polymorphism (SNP) genotyping, as has been suggested elsewhere (McKeigue 1998). In the present study, the frequency of SIDPs with δ>0.60 was ∼3% (table 2). This frequency should correspond roughly with the frequency of SNPs, suggesting that screening of ∼50,000 SNPs should provide the 1,500 markers genomewide that may be needed to optimize MALD’s potential. Although far from having reached this goal, the present study does greatly increase the number of identified EDMs and allows further theoretical testing of the extent and characteristics of admixture linkage disequilibrium. Moreover, the results of the present study provide additional support for the feasibility of the MALD approach in two admixed populations that form a substantial proportion of the American population.
Acknowledgments
Support for this research was provided by National Institutes of Health grants U01- DK57249 (to M.F.S.), N01-HV-48141 and R01-HV-62681 (both to J.L.W.), and HL45508 (to R.C.). We thank Dr. David Smith (Department of Anthropology, University of California, Davis) for generously providing Yavapai AI samples and useful discussions on this work. In addition, we thank Ripan Malhi (Department of Anthropology, University of California, Davis) for a critical reading of the manuscript.
Electronic-Database Information
Accession numbers and URLs for data in this article are as follows:
- Center for Medical Genetics, Marshfield Medical Research Foundation, http://research.marshfieldclinic.org/genetics/ (for screening set 8A, unlabeled SIDPs, and genetic maps)
- Ethnic Difference Marker (EDM) Allele Frequencies, http://roweprogram.ucdavis.edu/Ethnic_Difference_Markers.pdf (for allele frequencies of markers)
- Fondation Jean Dausset CEPH, http://www.cephb.fr/cephdb/ (for genotyping data sets)
- UCSC Human Genome Project Working Draft, http://genome.ucsc.edu/ (for megabase positions of EDMs)
References
- Bali D, Gourley IS, Kostyu DD, Goel N, Bruce I, Bell A, Walker DJ, Tran K, Zhu DK, Costello TJ, Amos CI, Seldin MF (1999) Genetic analysis of multiplex rheumatoid arthritis families. Genes Immun 1:28–36 [DOI] [PubMed] [Google Scholar]
- Barbujani G, Magagni A, Minch E, Cavalli-Sforza LL (1997) An apportionment of human DNA diversity. Proc Natl Acad Sci USA 94:4516–4519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowcock AM, Ruiz-Linares A, Tomfohrde J, Minch E, Kidd JR, Cavalli-Sforza LL (1994) High resolution of human evolutionary trees with polymorphic microsatellites. Nature 368:455–457 [DOI] [PubMed] [Google Scholar]
- Briscoe D, Stephens JC, O’Brien SJ (1994) Linkage disequilibrium in admixed populations: applications in gene mapping. J Hered 85:59–63 [PubMed] [Google Scholar]
- Cavalli-Sforza LL, Piazza A, Menozzi P, Mountain J (1988) Reconstruction of human evolution: bringing together genetic, archaeological and linguistic data. Proc Natl Acad Sci USA 85:6002–6006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakraborty R (1986) Gene admixture in human populations: models and predictions. Yearbook Phys Anthropol 29:1–43 [Google Scholar]
- Chakraborty R, Ferrell RE, Stern MP, Haffner SM, Hazuda HP, Rosenthal M (1986) Relationship of prevalence of non-insulin-dependent diabetes mellitus to Amerindian admixture in the Mexican Americans of San Antonio, Texas. Genet Epidemiol 3:435–454 [DOI] [PubMed] [Google Scholar]
- Collins HE, Li H, Inda SE, Anderson J, Laiho K, Tuomilehto J, Seldin MF (2000) A simple and accurate method for determination of microsatellite total allele content differences between DNA pools. Hum Genet 106:218–226 [DOI] [PubMed] [Google Scholar]
- Dean M, Stephens JC, Winkler C, Lomb DA, Ramsburg M, Boaze R, Stewart C, Charbonneau L, Goldman D, Albaugh BJ, Goedert JJ, Beasley RP, Hwang L, Buchbinder S, Weedon M, Johnson PA, Eichelberger M, O’Brien SJ (1994) Polymorphic admixture typing in human ethnic populations. Am J Hum Genet 55:788–808 [PMC free article] [PubMed] [Google Scholar]
- Hanis CL, Chakraborty R, Ferrell RE, Schull WJ (1986) Individual admixture estimates: disease associations and individual risk of diabetes and gallbladder disease among Mexican-Americans in Starr County, Texas. Am J Phys Anthropol 70:433–441 [DOI] [PubMed] [Google Scholar]
- Iliffe J (1995) Africans: the history of a continent. Cambridge University Press, Cambridge [Google Scholar]
- Kaplan NL, Martin ER, Morris RW, Weir BS (1998) Marker selection for the transmission/disequilibrium test, in recently admixed populations. Am J Hum Genet 62:703–712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latter BDH (1980) Genetic differences within and between populations of the major human subgroups. Am Nat 116:220–237 [Google Scholar]
- Lautenberger JA, Stephens JC, O’Brien SJ, Smith MW (2000) Significant admixture linkage disequilibrium across 30 cM around the FY locus in African Americans. Am J Hum Genet 66:969–978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewontin RC (1972) The apportionment of human diversity. Evol Biol 6:381–398 [Google Scholar]
- Long JC (1991) The genetic structure of admixed populations. Genetics 127:417–428 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKeigue PM (1998) Mapping genes that underlie ethnic differences in disease risk: methods for detecting linkage in admixed populations, by conditioning on parental admixture. Am J Hum Genet 63:241–251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKeigue PM, Carpenter JR, Parra EJ, Shriver MD (2000) Estimation of admixture and detection of linkage in admixed populations by a Bayesian approach: application to African-American populations. Ann Hum Genet 64:171–186 [DOI] [PubMed] [Google Scholar]
- Nei M, Roychoudhury AK (1974) Genetic variation within and between the three major races of man, Caucasoids, Negroids, and Mongoloids. Am J Hum Genet 26:421–443 [PMC free article] [PubMed] [Google Scholar]
- Parra EJ, Marcini A, Akey J, Martinson J, Batzer MA, Cooper R, Forrester T, Allison DB, Deka R, Ferrell RE, Shriver MD (1998) Estimating African American admixture proportions by use of population-specific alleles. Am J Hum Genet 63:1839–1851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfaff CL, Parra EJ, Bonilla C, Hiester K, McKeigue PM, Kamboh MI, Hutchinson RG, Ferrell RE, Boerwinkle E, Shriver MD (2001) Population structure in admixed populations: effect of admixture dynamics on the pattern of linkage disequilibrium. Am J Hum Genet 68:198–207 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich DE, Cargill M, Bolk S, Ireland J, Sabeti PC, Richter DJ, Lavery T, Kouyoumjian R, Farhadian SF, Ward R, Lander ES (2001) Linkage disequilibrium in the human genome. Nature 411:199–204 [DOI] [PubMed] [Google Scholar]
- Rife DC (1954) Population of hybrid origin as source material for the detection of linkage. Am J Hum Genet 6:26–32 [PMC free article] [PubMed] [Google Scholar]
- Shriver MD, Smith MW, Jin L, Marcini A, Akey JM, Deka R, Ferrell RE (1997) Ethnic-affiliation estimation by use of population-specific DNA markers. Am J Hum Genet 60:957–964 [PMC free article] [PubMed] [Google Scholar]
- Smith MW, Lautenberger JA, Doo Shin H, Chretien J, Shrestha S, Gilbert DA, O’Brien SJ (2001) Markers for mapping by admixture linkage disequilibrium in African American and Hispanic populations. Am J Hum Genet 69:1080–1094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens JC, Briscoe D, O’Brien SJ (1994) Mapping by admixture linkage disequilibrium in human populations: limits and guidelines. Am J Hum Genet 55:809–824 [PMC free article] [PubMed] [Google Scholar]
- Terwilliger JD, Weiss KM (1998) Linkage disequilibrium mapping of complex disease: fantasy or reality? Curr Opin Biotechnol 9:578–594 [DOI] [PubMed] [Google Scholar]
- Zheng C, Elston RC (1999) Multipoint linkage disequilibrium mapping with particular reference to the African-American population. Genet Epidemiol 17:79–101 [DOI] [PubMed] [Google Scholar]