Evidence of Genetic Interaction between the β-Globin Complex and Chromosome 8q in the Expression of Fetal Hemoglobin

Abstract

During human development, the switch from fetal to adult hemoglobin (Hb) is not complete with the residual γ-globin expression being restricted to a subset of erythrocytes termed “F cells” (FC). Statistical analyses have shown the FC trait to be influenced by a common sequence variant (C→T) at position −158 upstream of the Gγ-globin gene, termed the “XmnI-Gγ polymorphism.” The XmnI-Gγ site is believed to be involved in the expression of the Gγ-globin gene through interaction with transcription factors, and polymorphisms in the transcription factors could be influencing fetal Hb expression, conditional on the XmnI-Gγ site. Using a two-locus model, in which the second locus was the known quantitative-trait locus (QTL) at the XmnI-Gγ site, we showed suggestive linkage to chromosome 8q. A maximum single-point LOD score of 4.33 and a multipoint LOD score of 4.75 were found in a 15–20 cM region of chromosome 8q. A single-locus analysis failed to show linkage of FC to the region when the XmnI-Gγ site was accounted for by removing its effects from the data or including it as a covariate. Results of the single-locus analysis were significant when the effects of the XmnI-Gγ site were not accounted for in any way. The results of analysis in a large Indian kindred indicate that there is an interaction between the XmnI-Gγ site and a QTL on chromosome 8q that is influencing the production of fetal Hb.

The switch from fetal (α₂γ₂) to adult (α₂β₂) hemoglobin (Hb) synthesis is not complete, in that small amounts of fetal Hb (Hb F) continue to be synthesized throughout adult life. This residual γ-globin expression in adults is restricted to a minority of erythrocytes termed “F cells” (FC) (Boyer et al. 1975). Surveys of normal blood donors have shown that the levels of Hb F and FC vary considerably within populations (>20-fold) and that the distribution of the trait is substantially positively skewed (Zago et al. 1979; Miyoshi et al. 1988; Economou et al. 1991; Sampietro et al. 1992). Between 10% and 15% of normal adults have Hb F levels ⩾0.6% of the total Hb corresponding to ⩾4.0% FC.

As an initial step toward dissection of the genetic basis of the control of Hb F and FC production in adults, samples of MZ and DZ twins (in a healthy European population) were used to demonstrate that the trait is highly heritable (heritability = 0.89) (Garner et al. 2000b). Statistical analyses have shown the trait to be influenced by several factors, including age, sex, and a common sequence variant (C→T) at position −158 upstream of the Gγ-globin gene, a variant commonly referred to as the “XmnI-Gγ polymorphism” (Gilman and Huisman 1985; Garner et al. 2000a). The XmnI-Gγ site has been shown to be associated with high FC levels and to account for 13%–32% of the total phenotypic variance of the trait (Garner et al. 2000a). On the basis of the results of a combined linkage and association analysis, we conclude that the XmnI-Gγ site is influencing—either directly or in strong linkage disequilibrium with another locus—Gγ-globin gene expression on the β-globin complex (Garner et al. 2000a). Linkage to adult Hb F and FC levels has been identified in two other regions of the genome. One locus has been mapped to chromosome 6q23 in an extensive Asian Indian kindred (see below) with β-thalassemia and high FC levels (in the range defined as heterocellular hereditary persistence of fetal hemoglobin) (Craig et al. 1996); the other locus, which is associated with FC variation in sickle cell disease, has been mapped to chromosome Xp22.2-p22.3 (Dover et al. 1992).

In earlier studies, as part of a systematic search for loci that regulate γ-globin gene expression in β-thalassemia, a large, Asian Indian kindred was identified that included individuals with β-thalassemia and elevated FC levels (Thein and Weatherall 1989). The extended family included 210 individuals spanning seven generations. With the use of a genomewide quantitative-trait linkage–mapping strategy that accounted for the covariate effects of known genetic and nongenetic factors, a gene modifying Hb F and FC production was mapped to chromosome 6q23 in this kindred (Thein et al. 1994; Craig et al. 1996). A genomewide linkage analysis similar to the one performed by Craig et al. (1996), now accounting for the chromosome 6q23 locus and XmnI-Gγ site, as well as the other covariates, failed to identify additional loci influencing FC levels in the kindred; however, significant familial correlations of FC levels were observed.

Clinical and epidemiological studies suggest that the Gγ-158 C→T substitution predisposes toward increased Hb F production in adult life, particularly in conditions of erythroid stress, such as β-thalassemia (Labie et al. 1985; Thein et al. 1987; Ho et al. 1998) and sickle cell anemia (Labie et al. 1985). Although the sequence in this region of the Gγ promoter is not a recognized binding motif for any of the known transcription factors (Wood 2001), the mechanism of increased γ-globin expression is likely to involve a network of transcription factors and their coactivators, which function within multiprotein complexes (Kadonaga 1998). In such a scenario, altered expression of the Gγ-globin gene could arise from an alteration of the cis-binding site itself or from a change in one of the transcription factors in the multiprotein network. The latter could involve a protein-protein interaction or a DNA-protein interaction. Thus, the XmnI-Gγ site could be fine-tuning the expression of the Gγ-globin gene through its interactions with transcription factors, and polymorphisms in the transcription factors—or subunits thereof—could be influencing Hb F expression, conditional on the XmnI-Gγ site. To test this hypothesis, a reanalysis of genomewide marker data in the Indian kindred was performed, under a two-locus genetic model, with one of the loci being the XmnI-Gγ site. Given sufficient power, this model could detect linkage to loci that have an effect on FC levels that is conditional upon the presence of the XmnI-Gγ site. We have identified a locus on chromosome 8q that shows suggestive linkage to the FC trait, and the observed linkage is conditional upon the effects associated with the XmnI-Gγ site.

The kindred, which was described elsewhere in detail (Thein et al. 1994), was analyzed as six independent pedigrees, to break several inbreeding relationships, as described by Craig et al. (1996). FC assays and determination of the FC values were described elsewhere (Craig et al. 1996). DNA was extracted from peripheral blood leukocytes, using standard procedures. The T→C polymorphism at position −158 of the Gγ-globin gene and the β-thalassemia mutations were determined, as described by Craig et al. (1993). The marker data were the same as those used by Craig et al. (Craig et al. 1996) in the previous genome screen of the Indian kindred, with an additional 45 markers that were genotyped to follow up on results from the original study. Additional markers were typed using an automated DNA sequencer (ABI 377 or ABI 3100).

The effects of the covariates—age, sex, β-thalassemia, and the chromosome 6q23 locus—on the variance in FC levels were estimated by linear regression and removed from the data prior to the linkage analysis. The effect of the XmnI-Gγ polymorphism was similarly removed prior to analysis, where indicated. Allele frequencies of the 266 markers analyzed in the study were estimated by counting the alleles in the founders of the kindred. Genotype errors were identified using the program PedCheck (O'Connell and Weeks 1998) and were either reassigned on the basis of a reevaluation of the data or excluded from the data.

The two-locus probability models used are extensions of the single, major-locus model for quantitative-trait data in families. A statistical description of the models is given in the Appendix. Likelihoods were computed using the program VITESSE (O'Connell and Weeks 1995). The genomewide analysis was performed under the unrestricted two-locus model, in which the nine joint-genotype means are independent. The parameters of the unrestricted, two-locus model include the following: (1) allele frequencies of the two QTLs (QTL1 and QTL2), (2) allele frequencies of the XmnI-Gγ site and the test marker, (3) nine joint-genotype means, (4) a single within-genotype variance, and (5) the recombination rates between the XmnI-Gγ site and QTL1 and between the test marker and QTL2. Markers that were not linked to the XmnI-Gγ site were the only ones tested according to the assumption that the two QTLs segregate independently. Forty markers on chromosome 8q were tested using an additional two-locus model, termed the additive model. In the additive model, the nine joint-genotype means are represented by five parameters: a single mean for the low-trait joint-genotype mean of the two QTLs and four parameters measuring allelic and dominance effects that were constrained to have positive values (see Appendix).

For both the unrestricted and the additive models, the marker and XmnI-Gγ allele frequencies were fixed at the values estimated from the data, and the allele frequency of QTL1 was fixed to be the same as that for the XmnI-Gγ site. The polymorphism marked by the XmnI-Gγ site is common, having a frequency of ∼0.35 in the founders of the kindred. The allele frequencies of QTL1 and the XmnI-Gγ polymorphism were assumed to be equal. The recombination rate between the XmnI-Gγ site and QTL1 was fixed at 0.001. Likelihoods of the unrestricted model were maximized on 12 parameters: the allele frequency of QTL2, nine joint-genotype means, a single within-genotype variance, and the recombination fraction between QTL2 and the test marker. Likelihoods of the additive model were maximized on eight parameters, because the joint-genotype means were restricted to a five-parameter model, as described above and in the Appendix. LOD scores were calculated as the difference between the log₁₀ of the maximum likelihood and the log₁₀ of the likelihood of that model, with the recombination fraction between the test marker and QTL2 being fixed at 0.50.

Likelihoods were computed for 10 markers under the single-locus mixed model (Morton and MacLean 1974) using the program PAP (Hasstedt 1994). The effect from the XmnI-Gγ genotype was ignored, estimated, or removed from the data by linear-regression analysis prior to the linkage analysis or was included in the model as a covariate. The likelihoods were maximized on the basis of six or seven parameters, depending on whether the covariate effect of the XmnI-Gγ site was included in the model. The parameters included the allele frequency of the QTL, three genotype means, one within-genotype variance, the recombination fraction between the marker and the QTL, and the coefficient of covariance for the XmnI-Gγ site. LOD scores were calculated as described above.

LOD scores greater than an arbitrarily set threshold of 1.5 were observed for four microsatellites, namely, D2S2216, D6S283, D7S531, and D8S283; these markers and the linked flanking markers were genotyped in the full kindred of 210 individuals. The additional genotyping did not increase the evidence of linkage to chromosomes 2, 6, and 7; however, LOD scores of 3.14, 1.75, and 2.41 were observed at markers D8S1810, D8S283, and D8S1722, respectively. Thirty-seven additional markers across ∼15 cM of chromosome 8q were genotyped and analyzed for linkage under the unrestricted and additive two-locus models (results shown in table 1). The average heterozygosity of the markers was 0.66, ranging from 0.20 (for marker D8S517) to 0.89 (for marker D8S1828). The average LOD scores of the 40 markers were 1.50 and 1.30, under the unrestricted and additive models, respectively. The correlation between the LOD scores computed under the two models was 0.72 (P<.0001). There was a weak correlation between the LOD scores and heterozygosities of the markers under both models (unrestricted: r=.28, P=.08; additive: r=.30, P=.06). Six markers had LOD scores >3.0, with marker D8S1833 having the highest LOD score (4.33 under the unrestricted model). Two markers (D7S1758 and D8S538) showed LOD scores >3.0 under both the unrestricted and additive models. Two markers (D8S283 and D8S532) showed LOD scores >3.0 under the additive model only, and two markers (D8S1810 and D8S1833) did under the unrestricted model only.

Table 1.

Results of Two-Locus Linkage Analysis for 40 Markers on Chromosome 8q

			Unrestricted Model		Additive Model
Marker	Locationa	Heterozygosity	LOD Score	θ2	LOD Score	θ2
D8S540	60	.61	2.44	<.001	1.75	<.001
D8S1770	59.4	.41	.00	.49	.00	.49
D8S1810	59.4	.66	3.14	<.001	.29	.30
D8S278	60	.69	2.53	<.001	2.31	.05
D8S259	60	.79	1.26	.13	.67	.23
D8S1758	60	.66	3.70	<.001	3.39	.04
D8S513	60	.68	.45	.29	.50	.27
D8S1709	60	.70	1.48	.025	2.34	.06
D8S1845	60	.64	.64	.18	.25	.27
D8S283	60	.73	1.75	<.001	3.15	<.001
D8S535	60	.74	1.47	<.001	.67	<.001
D8S505	60	.64	.11	.29	.00	>.50
D8S1700	60.6	.66	1.22	.13	.85	.16
D8S1766	60.6	.49	.79	<.001	.40	>.50
D8S1750	60.6	.77	1.18	.13	2.12	.09
D8S1803	60.7	.75	2.95	<.001	2.91	<.001
D8S1722	60.7	.85	2.41	.08	2.63	.07
D8S536	61.5	.68	.23	.33	.27	.28
D8S1791	62.3	.79	.31	.23	.17	.25
D8S1821	62.3	.76	.86	.20	.83	.21
D8S255	64	.72	1.68	.11	1.64	.10
D8S515	64.6	.66	1.08	.10	1.10	.13
D8S532	64.6	.78	1.52	<.001	3.15	<.001
D8S1817	64.6	.72	.86	.12	.15	>.50
D8S268	64.6	.23	1.05	<.001	.29	.06
D8S531	65.7	.61	1.79	<.001	1.51	<.001
D8S1745	65.8	.80	1.52	<.001	1.99	<.001
D8S1831	66.9	.72	.54	.26	.15	.33
D8S538	66.9	.74	3.14	<.001	3.53	.03
D8S1773	66.9	.66	2.44	<.001	2.75	<.001
D8S517	66.9	.20	.01	>.50	.01	.42
D8S524	66.9	.66	1.89	<.001	1.93	.04
D8S1815	66.9	.67	1.05	<.001	.00	<.001
D8S1833	66.9	.66	4.33	<.001	2.53	<.001
D8S509	69.2	.61	.48	.17	.10	.33
D8S1816	70.6	.48	1.38	<.001	2.45	<.001
D8S1828	70.6	.89	2.06	<.001	1.14	.08
D8S285	70.6	.64	1.46	.003	.10	.33
D8S1723	74.9	.49	1.58	<.001	1.48	<.001
D8S507	75	.82	1.40	.076	.69	.16

^aThe locations of the markers were obtained from the published Whitehead YAC physical order (Hudson et al. 1995) and from the Généthon genetic map (Dib et al. 1996).

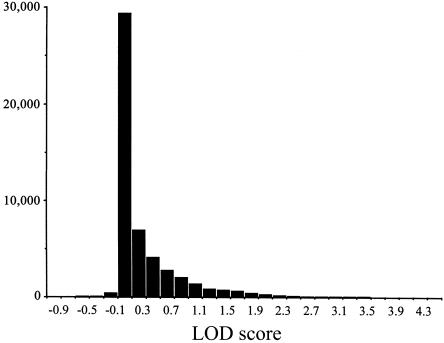
To assess the fit of the model to the data and the significance of the results, a sample from the null distribution of LOD scores was generated for the unrestricted model. Figure 1 shows the simulated distribution of LOD scores. The following probabilities were calculated from the distribution: Pr_{(LOD > 1.0)} = .095; Pr_{(LOD > 2.0)} = .018; Pr_{(LOD > 3.0)} = .0037; and Pr_{(LOD > 4.0)} = .0008.

Figure 1.

Null distribution of LOD scores computed under the unrestricted two-locus models. The distribution was generated from 50,000 replicates, in which a simulated marker was unlinked to QTL2. The pedigree structure, trait values, and XmnI-Gγ genotypes were identical to the analyzed data. A gene-dropping algorithm written by C.G. generated the replicate marker data.

On the basis of these results—and without consideration of multiple testing—the probability of observing the LOD score of 4.33 at marker D8S1833 is <.0008. A Bonferroni multiple-test correction of this P value for the 40 markers on chromosome 8q, tested under the unrestricted model gives an adjusted P value of .032; a genomewide correction for 305 tests gives a P value of .24. These adjusted significance levels are highly conservative, given that the analysis was of a single kindred and that linkage (nonindependence) extends over large genetic distances. The significance levels found from simulation are not consistent with the typical assumption that a LOD score >3.0 roughly corresponds to a P value <.0001 (Lander and Kruglyak 1995). The observed LOD score of 4.33 is a suggestive finding. Negative LOD scores were observed for a very small proportion of the simulated replicates (fig. 1), suggesting a problem with the maximum-likelihood computation in these tests. Maximum likelihoods of the data were computed twice, from different starting values, to confirm that the results were consistent. Figure 2 shows the results of the multipoint linkage analysis. The maximum multipoint LOD score was at the location of marker D8S538 for both orders; LOD = 4.75 for order 1 and LOD = 3.13 for order 2 (fig 2). A one-LOD-unit confidence interval around the peak of the multipoint LOD score under order 1 extends ∼4 cM from marker D8S1722 to D8S507.

Figure 2.

Multipoint LOD scores for two groups of four markers (orders 1 and 2) computed under the unrestricted two-locus model. The two marker orders were chosen so that when combined, multipoint LOD scores would be computed approximately every 2 cM across the chromosome 8q region. Marker names are shown above the line for order 1 and below the line for order 2. Locations are given in centimorgans, starting from the most centromeric location tested. The distances between the markers were estimated using the program CRIMAP (Green et al. 1990) and by comparison with the published Généthon map (Dib et al. 1996). Likelihoods were computed using the program VITESSE (O'Connell and Weeks 1995).

Table 2 shows the results from the single-locus analyses. When the XmnI-Gγ genotype is not accounted for in any way, 7 of the 10 markers showed LOD scores >1.0, with the markers D8S1722 and D8S538 having LOD scores of 2.49 and 3.52, respectively. When the data are preadjusted for the genotype, the LOD scores show a substantial reduction; markers D8S1833, D8S278, and D8S540 show LOD scores of 1.14, 1.17, and 1.37, respectively. A similar effect is observed when the genotype is modeled as a covariate; markers D8S1833 and D8S540 show LOD scores of 1.07 and 1.31, respectively. These results suggest that the linkage signal observed between chromosome 8q and FC levels is conditional on the XmnI-Gγ effect.

Table 2.

Results of Single-Locus Linkage Analysis for 10 Markers on Chromosome 8q

	Scores from Single-Locus Models with
	No Accounting for XmnI-Gγ		Preadjustment for XmnI-Gγ		XmnI-Gγ as a Covariate
Marker	LOD	θ	LOD	θ	LOD	θ
D8S540	1.32	.05	1.37	.06	1.31	.08
D8S1810	.00	>.50	.29	>.50	.00	>.50
D8S278	.78	.21	1.17	.24	.90	.24
D8S1758	1.09	.13	.68	.22	.44	.22
D8S1803	1.70	<.001	.17	.35	.11	.38
D8S1722	2.49	<.001	.25	.32	.20	.30
D8S538	3.52	<.001	.66	.27	.65	.24
D8S1773	1.32	<.001	.39	.18	.72	.11
D8S1833	1.68	<.001	1.14	.18	1.07	.17
D8S1828	.00	.48	.16	.37	.01	.47

The maximum-likelihood estimates of the unrestricted and additive model parameters does not reveal any consistent pattern that would allow one to speculate on the mechanism by which the putative QTL on chromosome 8q is interacting with the known QTL at the β-globin complex. The simplest mechanism would be a purely additive one, with no dependence between the two loci. Under a purely additive model, one would expect that accounting for the covariate effects of the XmnI-Gγ genotype would cause the single-locus LOD scores at chromosome 8q to increase, because taking those effects into account would reduce the variance within each of the chromosome 8q QTL genotypes. The opposite effect was observed. Accounting for the XmnI-Gγ genotype effect as a covariate or by removing its effect from the FC distribution gave substantially lower LOD scores than did the single-locus analysis of the data with the effects unaccounted for. The two-locus models tested here almost certainly do not represent the true mechanism by which the locus on chromosome 8q and the XmnI-Gγ site are influencing FC levels; rather, the two-locus models are simply more powerful than a single-locus model, given the underlying true mechanism. The results indicate that part of this complex mechanism involves a conditional interaction between the chromosome 8q locus and either the XmnI-Gγ site or another polymorphism nearby.

The 8q QTL could encode for a regulatory factor, or a subunit thereof, which could act either as a repressor or a transcriptional activator that binds directly to the XmnI-Gγ site or another binding site nearby. Alternatively, the 8q protein could act as a molecular bridge in a protein-protein interaction. In these situations, the effects of any changes in the trans-regulatory protein would be conditional on the presence of the cis-binding site. There is evidence that coinheritance of some of the genetic determinants of high levels of Hb F may play a significant role in modifying the phenotype of β-thalassemia and sickle cell anemia. Hence, knowledge of the different genetic factors that contribute to the levels of Hb F and FCs could lead to improved therapeutic strategies for Hb F augmentation that would benefit patients with severe hemoglobinopathies.

Appendix

The two-locus models are described in terms of the following components: P(g) = the probability distribution of genotypes in the population; P(g_O|g_F,g_M) = the probability that an offspring has genotype g_O, given that the father and mother have genotypes g_F and g_M, respectively; P(Y|g) = the probability that an individual has phenotype Y, given that he or she has genotype g (i.e., the penetrance probability); and θ = the recombination rate.

The two-locus model is an extension of the single-locus model for QTL genotype g to the joint-genotypes G of QTL1 and QTL2. QTL1 and QTL2 have two alleles, A,a and B,b, respectively. The frequencies of A and a in the population are p and (1−p), respectively, and of B and b are q and (1−q), respectively. The product of the Hardy-Weinberg equilibrium frequencies of the two loci gives the probability distribution of joint-genotypes, P(G). For example, the expected population frequency of the AA, Bb joint-genotype is 2p²q(1−q).

Let τ_g1 = P (a parent with genotype g at QTL1 transmits allele A to a child) and τ_g2 = P (a parent with genotype g at QTL2 transmits allele B to a child), then, with Mendelian inheritance, τ_AA=1, τ_Aa=0.5, and τ_aa=0, and τ_BB=1, τ_Bb=0.5, and τ_bb=0. The conditional probabilities that an offspring has joint genotypes G_O, given that the father and mother have joint genotypes G_F and G_M, respectively, for three offspring joint genotypes, are as follows:

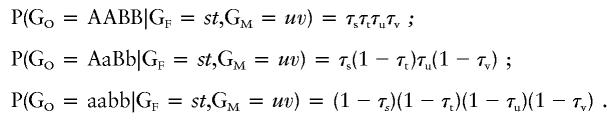The remaining six probabilities are found similarly. Given a normally distributed trait, with mean μ and variance σ², the phenotype Y at point X of the normal distribution is denoted by 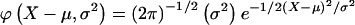, then the joint-genotype penetrance function for the quantitative trait is the probability-density function .

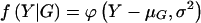The means of the joint-genotype (μ_G), under the unrestricted and additive models are shown in tables 3 and 4. Under the additive model, the heterozygote means were constrained to be between the homozygous means so that the model does not allow for overdominance. There is a single within-genotype standard deviation, σ².

Table 3.

Joint-Genotype Means for the Unrestricted Two-Locus Model

Genotype	BB	Bb	bb
AA	μ1	μ4	μ7
Aa	μ2	μ5	μ8
aa	μ3	μ6	μ9

Table 4.

Joint-Genotype Means for the Additive Two-Locus Model

Genotype	BB	Bb	bb
AA	μ1	μ1 + b1	μ1 + b1 + b2
Aa	μ1 + a1	μ1 + a1 + b1	μ1 + a1 + b1 + b2
aa	μ1 + a1 + a2	μ1 + a1 + a2 + b1	μ1 + a1 + a2 + b1 + b2

The probability of an offspring's marker (QTL2 and XmnI-Gγ—QTL1) oligogenotypes is expressed in terms of the product of the recombination fraction, θ, and the penetrance function. When the gametic phase of the parents is known, the probability of the offspring's phenotype, given their genotypes at the marker and the XmnI-Gγ polymorphism, is the sum of the probabilities of all of the offspring's possible oligogenotypes. When the parental phase is unknown, there is a sum over all possible parental phases that are informative for linkage. The likelihood of a family of arbitrary size is: