Individual-Specific Liability Groups in Genetic Linkage, with Applications to Kindreds with Li-Fraumeni Syndrome

Abstract

In this report, we present a simple and powerful way to incorporate individual-specific liability classes into linkage analysis. The proposed method is applicable to both quantitative and qualitative traits. In linkage studies, we may have information about different covariates. Incorporation of these covariates along with the estimates of residual familial effects, age-at-onset effects, and susceptibility in the definition of liability classes can increase the power to detect genetic linkage. In this study, we show how one can form individual-specific liability classes and use these classes in standard linkage-analysis programs, such as the widely used LINKAGE package, to perform more powerful genetic linkage analysis. Our simulation study shows that this approach yields higher LOD scores and more-accurate estimates of the recombination fraction in the families showing linkage. The proposed method is also applied to kindreds collected, at the M. D. Anderson Cancer Center, through probands with childhood soft-tissue sarcoma. Confirmed germ-line mutations in the p53 tumor-suppressor gene have been identified in these families. Application of our method to these families yielded significantly higher LOD scores and more-accurate recombination fractions than did analysis that did not account for individual-specific covariate information.

In linkage analysis, liability classes are used to define penetrance values for each of the possible genotypes of the trait loci. A diallelic locus with disease allele D and normal allele N has three possible genotypes—NN, ND, and DD—and one usually specifies a penetrance value for each of these three genotypes (Terwilliger and Ott 1994). For example, if the disease follows single dominant Mendelian inheritance, then one would specify penetrance values of 0, 1, and 1 for NN, ND, and DD, respectively. If the penetrance is reduced with possible phenocopies, then one might specify penetrance values of, say, 0.1, 0.8, and 0.8, respectively. Liability groups are useful for classification of individuals into different penetrance groups, on the basis of their age and sex. While performing linkage analysis, investigators typically use 10–20 liability groups based on the subjects’ age and sex. For the kth age group (which includes individuals of age x_k-1 to x_k), the penetrance may be defined for the ith genotype, as (1/2)[F_i(x_k-1)+F_i(x_k)] where, at the lower limit of the kth age group, penetrance is F_i(x_k-1), and, at the upper limit, it is F_i(x_k) (Ott 1999). In this report, we propose the use of individual-specific liability classes. This is a useful and powerful approach for modeling, because, even if two individuals are in the same age group and have the same sex, they may have different environmental exposures, smoking statuses, eating habits, and ethnicities, any of which might further modify their risk of developing a disease.

Incorporation of these environmental and behavioral risk factors to develop individual-specific penetrance classes should result in more-powerful tests of linkage. This approach would be useful for complex disorders such as cancer, in which many factors—such as smoking, disease status of first- and second-degree relatives, ethnic group, sex, eating habits, and socioeconomic status—play an important role in modifying one’s risk. The proposed approach can be easily adapted in the standard linkage-analysis programs—such as FASTLINK, LINKAGE, and VITTESE (Cottingham et al. 1993; Terwilliger and Ott 1994; O’Connell and Weeks 1995)—in a very simple manner, by modifying the parameter file and recompiling the program in order to allow enough liability classes to model each individual.

To evaluate the power gain due to this approach, we performed simulation studies. We generated phenotype value according to the model

where g_i is the major gene effect, G_i is the polygenic effect, X values are uncorrelated environmental effects, and e_i is the error. We assumed a polygenic variance of σ²_G=2, error variance σ²_e=1, and β₁=β₂=2. The X covariates were generated from a normal distribution with mean and variance equal to 1. We considered a dominant disease model with a disease-allele frequency of 0.1 (the results for other disease models were similar and are not presented). Because we are considering a dominant disease model, g_i takes two values: a for genotypes homozygous and heterozygous for the disease allele and −a for the genotypes homozygous for the normal allele. We chose values of a=1.5, 2.0, and 2.5; these choices resulted in heritabilities of 0.11, 0.18, and 0.26, respectively. Individuals were classified as affected if their phenotypic values exceeded a given threshold. These thresholds were chosen so that, conditional on covariate values, phenocopies are ∼12.4% and penetrances for the disease allele genotypes are 71%–95%. Prevalence of the disease can be calculated by the usual methods. Let p and q be the frequencies of the normal and the disease allele, respectively. Then, for a dominant model, prevalence is defined as p²* phenocopies + (2pq+q²)* penetrance. Here, one would use mean values of phenocopies and penetrances, of all individuals in the sample. For our simulated data, prevalence was 23%–28%. A four-allele equifrequent marker was simulated at a recombination fraction (θ) of 0.0, 0.05, and 0.1. We simulated 500 replicate samples. In each replicate, we simulated 100 sibships with five sibs per sibship. We performed linkage analysis in three ways: first, by assigning a single liability class for all individuals; second, by assigning 10 liability classes, by dividing groups into 10 classes based on their covariate values; and, finally, by assigning each individual to a separate class, conditional on the covariate values. The 10 classes were obtained by dividing the range of covariate values into 10 groups. From equation (1), conditional on g_i and on covariates X_1i and X_2i, the mean phenotype value of the ith individual is μ_ci=g_i+β₁X_1i+β₂X_2i, and the conditional variance σ²_c is equal to σ²_G+σ²_e. Then, the individual-specific penetrance for the ith individual is k∞φ(x,μ_ci,σ²_c)dx, where k is the given threshold and φ(x,μ_ci,σ²_c) is the normal density function with mean μ_ci and variance σ²_c. We use the μ_ci and σ²_c given above. In general, one would obtain these parameter estimates on the basis of regressive model-based segregation analysis (S.A.G.E. 1997).

The results of this analysis are reported in table 1: the true values of θ are given in the first column, and the means of estimated values of θ, as well as of the corresponding LOD scores, when individual-specific liabilities are used, are given in the second and the third columns, respectively; when a single liability class is used for all individuals, these parameter estimates are given in the fourth and the fifth columns, respectively; and, finally, when 10 liability classes are used, these estimates are given in the sixth and the seventh columns, respectively; all values in parentheses are median estimates of these two parameters. From table 1, it can be seen that the use of individual-specific liability groups significantly increased the power to detect linkage. The mean LOD scores were two to three times higher when our method was used. Also noteworthy is that the estimates of θ were more accurate when the proposed method was used. Also, the 95% confidence intervals based on the proposed method were significantly smaller (data not shown). Assigning, say, 20 classes would increase the LOD scores, compared with the results for 10 classes, but these LOD scores were still smaller than those resulting from our approach (data not shown).

Table 1.

Estimates of θ and of LOD Scores, for a Dichotomized Trait

	Mean (Median) Estimates
	Individual-Specific Liabilities		Common Liabilities		10 Liabilities
True θ	Estimated θ	LOD Score	Estimated θ	LOD Score	Estimated θ	LOD Score
Heritability .26:
.0	.015 (.0)	4.37 (4.24)	.047 (.0)	1.62 (1.44)	.0 (.0)	2.42 (2.34)
.05	.05 (.05)	3.12 (3.00)	.08 (.05)	1.22 (1.02)	.0 (.0)	1.91 (1.86)
.1	.1 (.1)	2.09 (1.82)	.13 (.1)	.90 (.73)	.02 (.0)	1.42 (1.37)
Heritability .18:
.0	.025 (.0)	2.23 (2.14)	.095 (.01)	.71 (.55)	.01 (.0)	1.02 (.98)
.05	.06 (.01)	1.63 (1.50)	.13 (.05)	.55 (.39)	.02 (.0)	.81 (.79)
.1	.11 (.1)	1.13 (.89)	.18 (.1)	.43 (.22)	.04 (.0)	.61 (.57)
Heritability .11:
.0	.07 (.0)	.78 (.61)	.16 (.01)	.26 (.16)	.05 (.0)	.30 (.27)
.05	.12 (.05)	.58 (.43)	.20 (.1)	.21 (.09)	.09 (.0)	.23 (.20)
.1	.16 (.1)	.43 (.25)	.22 (.1)	.18 (.05)	.13 (.0)	.19 (.14)

Usually in linkage analysis, underlying quantitative phenotype values are available, on the basis of which individuals are classified as either affected or unaffected, according to whether their phenotype exceeds a certain predetermined threshold (as we did in our simulation in the previous paragraph); but it is known that use of these quantitative-trait values instead of dichotomization of the trait can give much more power to detect linkage. Our method can easily be applied to quantitative traits. We used the individual-specific liability-classes method for the quantitative trait simulated earlier. In this case, we used a normal probability-density function for the penetrance classes. Conditional on covariates, for the ith individual with genotype g_i and phenotype Y_i, penetrance was defined as the probability-density function, φ(Y_i,μ_ci,σ²_c), where μ_ci and σ²_c are as defined above. The results of this analysis are reported in table 2. Once again, as expected, we observed a significant gain in power (i.e., a 5–10-fold increase) to detect linkage when we used these individual-specific liability classes. The estimates of θ were also more accurate, and the 95% confidence intervals (data not shown) were much smaller, in the data analysis that used the proposed method. Also, the LOD scores were higher when quantitative-trait values, rather than dichotomization of the trait, were used.

Table 2.

Mean (Median) Estimates of θ and of LOD Scores, for a Quantitative Trait

	Mean (Median) Estimates
	Individual-Specific Densities		Unconditional Densities		10 Groups of Densities
True θ	Estimated θ	LOD Score	Estimated θ	LOD Score	Estimated θ	LOD Score
Heritability .26:
.0	.0 (.0)	17.52 (17.36)	.021 (.0)	3.44 (3.25)	.0 (.0)	6.82 (6.82)
.05	.05 (.05)	11.91 (11.71)	.052 (.05)	2.50 (2.36)	.0 (.0)	5.42 (5.42)
.1	.1 (.1)	7.85 (7.62)	.1 (.1)	1.68 (1.46)	.0 (.0)	4.08 (3.96)
Heritability .18:
.0	.0 (0.0)	10.87 (10.88)	.05 (.0)	1.45 (1.37)	.0 (.0)	2.83 (2.80)
.05	.04 (.05)	7.62 (7.34)	.08 (.05)	1.08 (.90)	.0 (.0)	2.27 (2.24)
.1	.08 (.1)	5.12 (4.77)	.13 (.1)	.82 (.54)	.0 (.0)	1.74 (1.72)
Heritability .11:
.0	.01 (.0)	4.66 (4.60)	.12 (.01)	.49 (.35)	.0 (.0)	.81 (.79)
.05	.04 (.01)	3.31 (3.12)	.16 (.05)	.38 (.22)	.01 (.0)	.65 (.62)
.1	.08 (.05)	2.32 (2.07)	.18 (.1)	.31 (.14)	.01 (.0)	.51 (.47)

Next, linkage analysis using the proposed approach was performed on three large white families ascertained through childhood soft-tissue sarcoma and found to have Li-Fraumeni syndrome (LFS [MIM 151623]). LFS is characterized by increased incidence of soft-tissue sarcoma, osteosarcoma, breast cancer, adrenocortical carcinoma, leukemia, and brain tumors, at early ages and in multiple family members (Li and Fraumeni 1969, 1982). The families studied here are part of a study of patients with childhood sarcoma who were surveyed at The University of Texas M. D. Anderson Cancer Center. The details of the clinical data and of the method of data collection have been reported elsewhere (Strong et al. 1987). Confirmed germline mutations in the p53 tumor-suppressor gene have been identified in these families. Excess aggregation of cancer in relatives of patients with childhood sarcoma was found to be well described by segregation of a rare autosomal dominant locus with age-dependent penetrance (Bondy et al. 1992; Lustbader et al. 1992). Here we studied linkage in three families in which confirmed mutations in the p53 gene have been identified; these three families with LFS included 610, 32, and 31 individuals, with 51, 5, and 9 affected by cancer, respectively.

To elucidate genetic and other covariate effects, we performed regressive logistic model-based segregation analysis implemented by the REGTL program of S.A.G.E. (Bonney 1986; S.A.G.E. 1997). The best-fitting model was a rare dominant disorder, as expected. Various parameter estimates are reported in table 3. The mean ages at onset were 32.19 years for those carrying the disease allele and 104.6 years for subjects homozygous for the normal allele, for both males and females. The advanced estimated age at onset for normal-allele homozygotes indicates that these individuals would die from other competing risk factors before developing the disease—and, hence, would likely be censored before developing cancer. Susceptibility was found to be 100%. The individual-specific penetrance was calculated by use of the estimates of various parameters associated with the regressive model, as follows. Let y_i be the phenotype (0 or 1) of the ith individual. Here, phenotypic value 1 means that the individual was affected, and 0 means that the individual was unaffected. For an affected individual i with genotype u_i and age at onset a_i, we use the penetrance

where s_i is the sex of i; X_i is a vector of covariates; S_i, M_i, and F_i are the spouse, mother, and father of i; and γ_si is the susceptibility (i.e., the probability that a randomly selected individual from this population is affected).

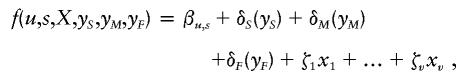where β_u,s is a baseline parameter that is the natural logarithm of the odds of being affected versus being unaffected (when other components are zero), α_u,s is the age coefficient, and δ's are regressive familial effects. We integrate equation (2) from zero, to the age at examination, a^′_i, both for unaffected individuals and for affected individuals for whom the age at onset, a_i, is unknown (Bonney 1986; Elston and George 1989). This gives the penetrance value

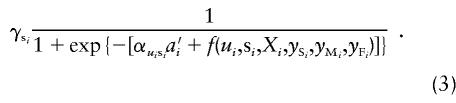Table 3.

Estimates of Various Parameters of the Segregation Analysis

Parameter	Estimate (SD)
Frequency of A	.01301 (.0072)
Baseline parameter βAA	−2.8061 (.5192)
Baseline parameter βBB	−7.4107 (1.3096)
Coefficient of smoking	−.0952 (.0619)
Age-adjusted coefficient of AA	.0872 (.0109)
Age-adjusted coefficient of BB	.0709 (.0149)
Mean age at onset for AA	32.19 (4.866)
Mean age at onset for BB	104.59 (18.482)
Susceptibility	1.000 (…)

Missing covariate information can be handled by using various techniques, such as imputation for missing data, which we will not discuss here because they are not the primary concern of this report. We performed linkage analysis by using the FASTLINK program with individual-specific penetrance classes, obtained by use of equations (2) and (3), for the p53 mutation–carrying families with LFS that have been described above. We found very strong evidence for linkage, with a LOD score of 8.27 at θ=0.01; at θ=0, the LOD score was 8.23. Linkage analysis with a single penetrance class gave a LOD score of 4.27 at θ=0.1 and of 1.56 at θ=0. We also analyzed these families by using 10 liability classes. An individual was assigned to one of the 10 classes based on affection status, and either age at onset or, for an unaffected individual, age at examination. Penetrance for each class was assigned as average risk, by genotype, for that group. This linkage analysis gave a LOD score of 6.68 at θ=0. Hence, when these mutation-carrier families were used, we obtained a higher LOD score and more-accurate estimates of θ by using individual-specific penetrances. This observation is consistent with our simulation results presented in tables 1 and 2.

In conclusion, for complex diseases involving multiple genetic and environmental determinants, it is extremely useful to employ techniques that are simple to implement and that result in higher power to detect true linkage. In this report, we have presented a simple yet very powerful way to incorporate individual-specific liability classes into linkage analysis of quantitative and qualitative traits. Compared with the use of just a single liability class, the use of 10–20 classes based on age and/or sex can increase a LOD score; nonetheless, individual-specific liability classes still yield higher LOD scores and more-accurate estimates of θ. In addition, our method of forming liability classes is more objective than arbitrarily establishing 10–20 classes based on age and/or sex only. This is particularly important in the study of complex disorders, which can be strongly dependent on, among other factors, environmental covariates and ethnic group. This approach can be implemented whenever one has estimates of various genetic and environmental covariate effects, which are usually obtained by segregation analysis.

Comparison of the proposed approach with other methods that jointly allow for adjustment of covariates would be interesting. Although the variance-components method can include covariates jointly in the modeling of linkage, that procedure treats allele effects as random, and so this method is distinct from what we propose here.