Abstract
To understand the strategies used by the brain to analyze complex environments, we must first characterize how the features of sensory stimuli are encoded in the spiking of neuronal populations. Characterizing a population code requires identifying the temporal precision of spiking and the extent to which spiking is correlated, both between cells and over time. In this study, we characterize the population code for speech in the gerbil inferior colliculus (IC), the hub of the auditory system where inputs from parallel brainstem pathways are integrated for transmission to the cortex. We find that IC spike trains can carry information about speech with sub-millisecond precision, and, consequently, that the temporal correlations imposed by refractoriness can play a significant role in shaping spike patterns. We also find that, in contrast to most other brain areas, the noise correlations between IC cells are extremely weak, indicating that spiking in the population is conditionally independent. These results demonstrate that the problem of understanding the population coding of speech can be reduced to the problem of understanding the stimulus-driven spiking of individual cells, suggesting that a comprehensive model of the subcortical processing of speech may be attainable in the near future.
Introduction
One of the primary goals of systems neuroscience is to understand how sensory information is represented in the spike trains of neuronal populations (Averbeck et al., 2006). A common approach to characterizing population coding is to use experimental data to describe the relationship between the sensory stimulus and neuronal responses. Such descriptions range from simple static functions that relate the value of a single stimulus parameter to the average spike rate of individual cells, i.e., tuning curves, to complex models that combine selectivity for multiple stimulus features with other dynamic properties to predict the joint spike times of a neuronal population (Pillow et al., 2008). Describing the relationship between stimulus and response often requires a trade-off between tractability and accuracy; tuning curves, while easily measured, may ignore important information in spike timing, but models that predict spike timing may be impossible to fit with limited experimental data. Thus, the first step in characterizing any population code is to assess which features of spike trains carry information about the stimulus (Strong et al., 1998; Brenner et al., 2000). With the results of this assessment, the simplest description required to capture the relevant features of the spike trains can be determined and, in the event that this minimal description is not tractable and a simpler one must be used, the cost associated with ignoring the features that cannot be captured can be quantified.
In recent years, much has been learned about the nature of the population code in many brain areas, but there have not yet been any comprehensive analyses of population spike trains in the subcortical auditory pathway. In this study, we characterize the neural code for speech in the inferior colliculus (IC), the central station of the auditory midbrain where inputs from parallel pathways in the brainstem are integrated for transmission to the cortex. The first step in determining the important features of a population code is to specify its temporal resolution, i.e., the critical level of spike time precision (Butts et al., 2007). IC cells are known to respond to tones and broadband sounds with time-locked spikes for carrier frequencies >1 kHz and modulation frequencies up to several hundred Hertz (Frisina, 2001; Joris et al., 2004; Liu et al., 2006; Horvath and Lesica, 2011; Chen et al., 2012), suggesting that they have the capacity to encode the acoustic features of speech with high temporal precision. Once the temporal precision of spiking has been determined, the nature of the correlations between successive spikes from individual cells as well as between spikes from neighboring cells must be assessed. The correlations between successive spikes imposed by refractoriness can shape spike patterns in the auditory nerve (Gaumond et al., 1982; Miller, 1985; Avissar et al., 2013), and it is likely that such correlations play a significant role in the IC as well. The noise correlations between spikes from neighboring cells have not been studied in detail in any subcortical auditory area, and, given the diversity of correlation structures observed in other brain areas, it is difficult to predict the impact that such correlations might have in the IC.
Materials and Methods
In vivo recordings.
Adult male gerbils (70–90 g, P60–P120) or mice (C57BL/6, 25–30 g, P60–P70) were anesthetized for surgery with an initial injection of a mix of ketamine, xylazine, and saline or a mix of fentanyl, medetomidine, and midazolam, and the same solution was infused continuously during recording. A small metal rod was mounted on the skull and used to secure the head of the animal in a stereotaxic device in a sound-attenuated chamber. A craniotomy was made over the inferior colliculus or the primary auditory cortex (A1), an incision was made in the dura mater, and a multi-tetrode array (Fig. 1A; Neuronexus) was inserted into the brain. Only recordings from the central nucleus of the IC and A1 were analyzed. Because the array covered a large area, recording sites in the central nucleus of the IC could be distinguished from those in other areas by comparison of their responses to tones (Aitkin et al., 1975; Syka et al., 2000), and A1 could be distinguished from other fields based on the direction of the tonotopic gradient (Thomas et al., 1993). A1 recordings were made in deeper layers, most likely layer V (between 1 and 1.5 mm from the cortical surface).
Figure 1.
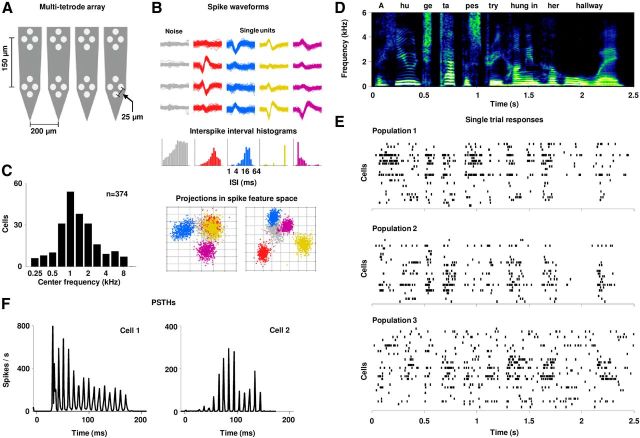
Multitetrode recordings of population responses to speech in the IC. A, A schematic diagram of the electrode arrangement on the array. Thirty-two electrodes were grouped into eight tetrodes. B, Example recordings from one tetrode in the IC. For each tetrode, spikes were grouped into clusters corresponding to nonisolated multiunit activity (noise) and single units. The waveforms and ISI histograms for each cluster are shown (note the logarithmic axis for the ISIs). Clusters were identified by projecting each spike into principal component space (12 dimensions corresponding to 3 principal components for each electrode). Two-dimensional projections that illustrate the isolation of the different single unit clusters are shown. C, The distribution of center frequencies in our sample of IC cells. D, A spectrogram of the one of the segments of speech used in this study, the sentence “A huge tapestry hung in her hallway.” E, Raster plots of spike trains recorded during a single presentation of speech for three example populations. F, Mean responses (PSTHs with 0.7 ms time bins) for two example cells for a 200 ms segment of speech.
Spike sorting.
The procedure for the isolation of single-unit spikes consisted of (1) bandpass filtering each channel between 500 and 5000 Hz; (2) whitening each tetrode, i.e., projecting the signals from the four channels into a space in which they are uncorrelated; (3) identifying potential spikes as snippets with energy (Choi et al., 2006) that exceeded a threshold (with a minimum of 0.7 ms between potential spikes); (4) projecting each of the snippets into the space defined by the first three principal components for each channel; (5) identifying clusters of snippets within this space using KlustaKwik (http://klustakwik.sourceforge.net) and Klusters (Hazan et al., 2006); and (6) quantifying the likelihood that each cluster represented a single unit using isolation distance (Schmitzer-Torbert et al., 2005). Isolation distance assumes that each cluster forms a multi-dimensional Gaussian cloud in feature space and measures, in terms of the SD of the original cluster, the increase in the size of the cluster required to double the number of snippets within it. The number of snippets in the “noise” cluster (non-isolated multiunit activity) for each tetrode was always at least as large as the number of spikes in any single-unit cluster. Only single-unit clusters with an isolation distance >20 were analyzed.
Sound delivery.
For gerbil experiments, sounds were generated with a 48 kHz sampling rate, attenuated, and delivered to speakers. In some experiments (2 animals; 4 of 20 IC populations), a free-field speaker (TDT MF1) was positioned 10 cm from the ear contralateral to the recording site. In these experiments, sounds were filtered such that the effective frequency response of the speaker measured at the location of the ear was flat (±5 dB SPL) between 0.5 and 20 kHz. In other experiments (9 animals; 16 of 20 IC populations and all 4 A1 populations), speakers (Etymotic ER2) coupled to tubes were inserted into both ear canals for diotic sound presentation along with microphones for calibration. The frequency response of these speakers measured at the entrance of the ear canal was flat (±5 dB SPL) between 0.2 and 5 kHz. For mouse experiments (2 animals; 4 populations), sounds were generated with a 192 kHz sampling rate, attenuated, and delivered to a free-field speaker (Avisoft Vifa) that was positioned 10 cm from the ear contralateral to the recording site. The effective frequency response of the speaker measured at the location of the ear was flat (±10 dB SPL) between 4 and 80 kHz. At each recording site, a sequence of tones with different frequencies and intensities with 5 ms cosine on and off ramps were presented to characterize basic response properties. For gerbil experiments, one of three 2–3 s segments of female speech from the UCL SCRIBE database (http://www.phon.ucl.ac.uk/resource/scribe) was presented either 512 or 1024 times. Of the 384 cells in the main analysis, 58% were presented with segment 1 (spectrogram shown in Fig. 1D), 22% with segment 2, and 20% with segment 3. All of the A1 data were with segment 1. An additional 6 min segment of speech was repeated twice for all populations. For mouse experiments, a 2.5 s segment of a dynamic random chord sound (5 ms tones, average density of 2 tones/octave) was presented 64 times.
Calculation of correlation functions.
Correlation functions were computed after converting spike trains to binary vectors with 0.7 ms time bins. For each cell or pair of cells, the total correlation function was obtained by computing the correlation coefficient between the actual spike trains. The signal correlation function was computed after shuffling the order of repeated trials for each time bin. The noise correlation function was obtained by subtracting the signal correlation function from the total correlation function. For cells recorded on the same tetrode, the value of the correlation functions at lags −1, 0, and 1 were influenced by the 0.7 ms lockout period used for spike detection during spike sorting. Thus, these values were ignored and the correlation functions were interpolated to fill in the gap. For a number of tetrodes, we split the four channels into two pairs for independent spike sorting and observed no qualitative difference in the results.
Calculation of mutual information.
The mutual information between two variables measures how much the uncertainty about the value of one variable is reduced by knowing the value of the other. The mutual information between a sensory stimulus and a neural response can be computed as the difference between the entropy of the response before and after conditioning on the stimulus, as follows:
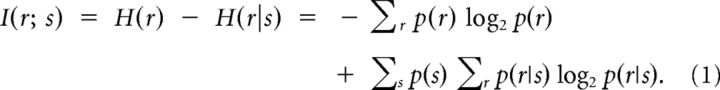 |
To measure the information that is carried by spike trains about speech without having to specify which features of the speech were relevant, we used the approach pioneered by Strong et al. (1998) of discretizing a continuous stimulus into separate “stimuli” in time. To measure information, the total entropy of the response is compared with the average entropy of the response in each time bin (the noise entropy):
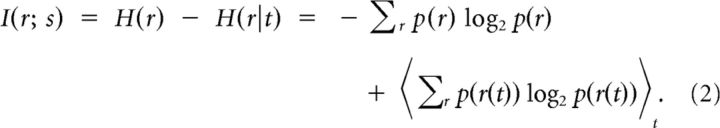 |
All information calculations were performed using the Direct Method via infoToolbox for Matlab (Magri et al., 2009) with bias correction via the shuffling method and quadratic extrapolation (Panzeri et al., 2007). Only cells with single spike information rates >0.5 bits/s were included in the analysis (368 of 374 cells). For all calculations, spike trains were represented as binary patterns.
Calculation of single spike information.
To determine the critical level of spike timing precision, it is important to represent spike trains with the highest possible temporal resolution; if the time bins used to represent the response are too large, the critical level of precision may be underestimated. For each cell, we first determined the smallest time bin that allowed for reliable information estimates by starting with 80 μs bins and increasing in increments of 40 μs until the information computed using all of the trials was within 5% of the mean information computed from 25 random subsets of half the trials, ensuring that the calculation was stable. For 80% of cells, the bin size used was smaller than 0.2 ms.
Calculation of information in temporal spike patterns.
For the calculation of information in temporal patterns, a bin size of 0.7 ms was used and we determined the longest pattern that allowed for reliable information estimates by starting with patterns of two time bins and increasing until the information computed using all of the trials was >5% different from the mean information computed from 25 random subsets of half the trials, which occurred for patterns longer than 16 bins (∼12 ms).
Calculation of information in population spike patterns.
For the calculation of information in population spike patterns, the response in each time bin was specified as a binary pattern with one element corresponding to each neuron. For all calculations (except as noted in Fig. 4C), a bin size of 0.7 ms was used and only a single time bin was considered (i.e., temporal correlations were ignored). We determined the largest population that allowed for reliable information estimates by starting with populations of two cells and increasing until the information computed using all of the trials was >5% different from the mean information computed from 25 random subsets of half the trials, which occurred for populations larger than 14 cells.
Figure 4.
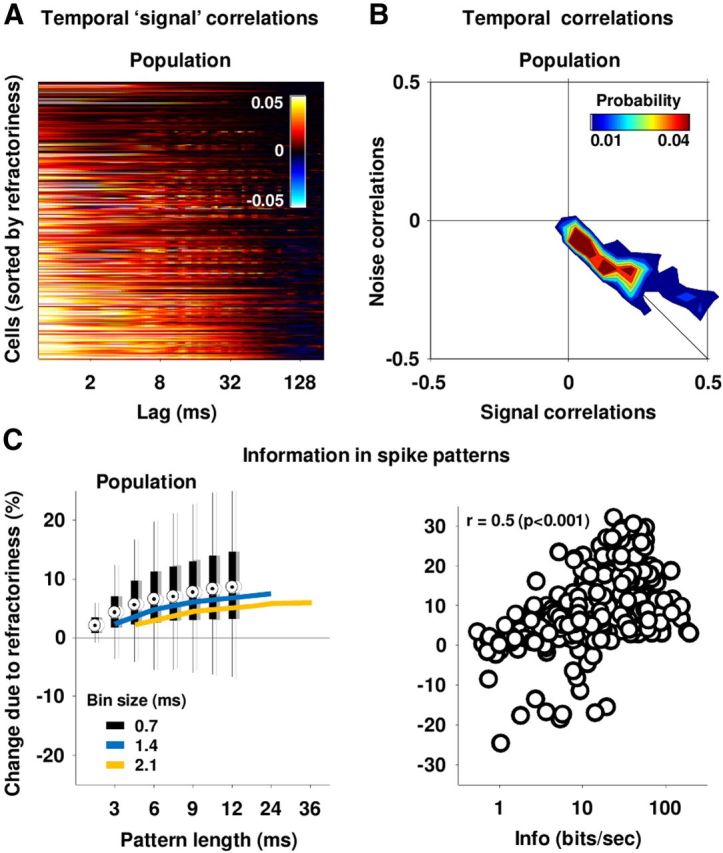
Refractoriness and information transmission. A, The temporal signal correlation functions for the IC cells in our sample. Cells were ordered for plotting as in 3A. B, The distribution of temporal signal and noise correlations for our sample of cells. To obtain these values, the temporal signal and noise correlation functions for each cell were summed over lags up to 12 ms. C, The black distributions in the left panel show the effects of temporal noise correlations on the information in spike patterns of different lengths with 0.7 ms time bins for our sample of cells. The percentage change in information due to temporal noise correlations was computed as 100 × Icor–ind/(I0 + Isig–sim) (see Materials and Methods for definitions of information theoretic quantities). The gray distributions are those obtained when only half of the trials were used indicating the stability of the result. The blue and orange lines show the median values for the same quantity computed with 1.4 and 2.1 ms bins, respectively. The right panel shows a scatter plot of the effects of temporal noise correlations on the information in spike patterns that were 16 bins long with 0.7 ms bins versus the single spike information for each cell in our sample.
Calculation of the effects of noise correlations on information.
For the calculation of the effects of noise correlations on information in spike patterns, we used an information breakdown approach (Pola et al., 2003) and computed the information breakdown quantity Icor-ind = − Σr pind(r)log2 pind(r) − Σr p(r)log2 pind(r), where pind(r) is an estimate of the probability of a spike pattern assuming there are no noise correlations between cells or time bins. Icor–ind captures only the average effect of noise correlations on information (Oram et al., 1998; Panzeri et al., 1999; Pola et al., 2003) and ignores any additional effects due to stimulus modulation of noise correlations (Nirenberg et al., 2001; Pola et al., 2003). The effects of these stimulus-independent noise correlations depend on their interaction with signal correlations. Signal correlations elongate the distributions of responses to different stimuli along a direction that increases their overlap and, thus, reduces stimulus discriminability. If noise correlations have the same sign as signal correlations, they will further elongate the response distributions in the same direction, further increasing overlap and reducing discriminability, but if noise correlations have the opposite sign from signal correlations, they will elongate the response distributions in a direction that is orthogonal to the direction of overlap and improve discriminability. Measurements of additional stimulus-dependent effects of noise correlations (information breakdown quantity Icor–dep) from our data with sufficiently small time bins did not satisfy the stability criterion defined above, even for relatively short patterns, so we did not include them. To express the effect of noise correlations on information as a percentage of the information without noise correlations, Icor–ind was compared with I0 + Isig–sim. I0 is the single spike information as described above and Isig–sim is the information loss due to signal correlations − Σr pind(r) − Σr plin(r)log2 plin(r), where plin(r) is an estimate of the probability of a spike pattern assuming there are no signal or noise correlations between cells or time bins. The effect of noise correlations on information was computed as 100 × Icor–ind/(I0 + Isig–sim).
Fitting a generalized linear model of IC spike trains.
We modeled IC spike trains using the generalized linear model (GLM) p(r[n]) = flink(gstim[n] + ghist[m] + c) where the probability of a spike occurring in time bin n on a given trial depends on a linear combination of a function gstim that describes the feed-forward influence of the stimulus and depends only on n, a function ghist that captures the effect of spike history based on the time since the last spike m, and a constant c (see schematic in Fig. 5A). The link function that converts this combination to a probability value between 0 and 1 is the logistic function flink(x) = ex/(ex + 1). For each cell, model parameters were fit using the Matlab function glmfit with half of the recorded response trials. The input matrix was binary with N × I rows and N × M columns, where N was the total number of time bins in a trial (N = 3571 for a 2.5 s segment of speech with 0.7 ms bins), I was the total number of trials used for training (I = 256 or 512), and M was longest interval for which the spike history was considered (M = 20 for 0.7 ms bins). In each row of the input matrix, only two elements corresponding to the index n of the relevant time bin and the interval n since the last spike were non-zero. The output vector was binary with N × I elements indicating whether or not a spike occurred in each time bin on each trial. The similarity of the model spike trains to the actual data was assessed on the half of the trials that were not used for model fitting.
Figure 5.
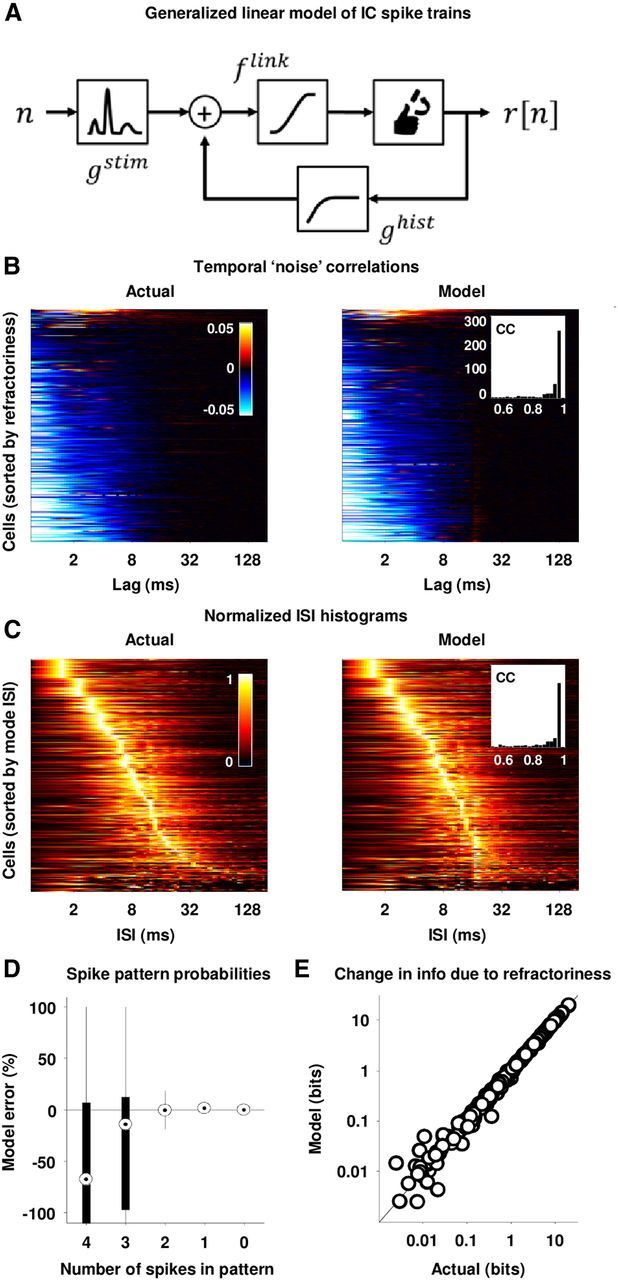
Modeling refractoriness in IC spike trains. A, A schematic diagram of a generalized linear model of IC spike trains. B, The temporal noise correlation functions for the actual and model generated spike trains for the IC cells in our sample. The left panel is the same as the right panel in Figure 3A. The right panel shows the correlation functions for the model generated spike trains, with cells ordered for plotting as in the left panel. The inset in the right panel shows the distribution of the correlation coefficients between the temporal noise correlation functions for the actual and model-generated spike trains for the cells in our sample. C, The ISI histograms for the actual and model generated spike trains for the IC cells in our sample. The left panel is the same as the left panel in Figure 3B. The right panel shows the ISI histograms for the model generated spike trains, with cells ordered for plotting as in the left panel. The inset in the right panel shows the distribution of the correlation coefficients between the ISI histograms for the actual and model generated spike trains for the cells in our sample. D, The difference between the probability of different spike patterns in the actual and model generated spike trains for our sample of cells. For each cell, probabilities were averaged across all possible spike patterns with a given number of spikes. For this analysis, spike patterns were represented as binary patterns that were 16 bins long with 0.7 ms bins. E, A scatter plot of the effects of temporal noise correlations on the information in actual and model generated spike trains for our sample of cells. For this analysis, spike patterns were represented as binary patterns that were 16 bins long with 0.7 ms bins.
Results
We made multitetrode recordings (Fig. 1A) from the central nucleus of the IC of anesthetized gerbils during the presentation of tones and speech. Recordings yielded between 14 and 29 single units recorded simultaneously across the set of 8 tetrodes (20 populations for a total of 374 cells). Example recordings from one tetrode are shown in Figure 1B. Recordings were targeted to areas with low preferred frequencies. In our sample of cells, 95% of all center frequencies (frequency at which a response was observed at the lowest intensity) were between 400 Hz and 5 kHz, as shown in Figure 1C.
Speech is encoded in spike timing with sub-millisecond precision
To assess the contribution of different features of spike trains to the neural code, we recorded responses to repeated presentations of one of several 2–3 s segments of speech. Figure 1, D and E, show the spectrogram of one of the speech segments along with the responses of three example populations to a single presentation. Our first step was to determine the critical timescale for the information carried by single spikes of individual neurons. The responses of two example cells to repeated presentations of a short segment of the speech are shown in Figure 1F. The responses are time-locked to the speech with high precision, indicating the capacity of the cells to transmit information on a fine timescale.
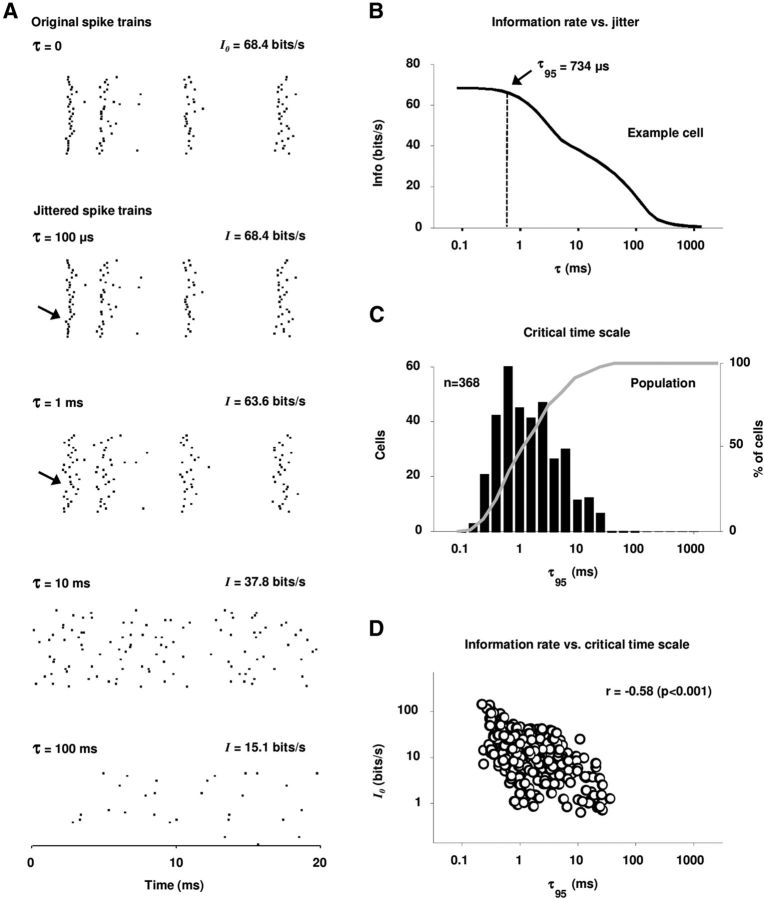
To measure the critical timescale for each cell, we converted the spike trains to binary vectors and computed the mutual information between the stimulus and response in single time bins using the smallest time bin that yielded an unbiased result for each cell (see Materials and Methods). This quantity is equivalent to the information carried by the PSTH on the same timescale (Brenner et al., 2000). We first computed the information in the actual responses (I0), and then measured the decrease in information that resulted from jittering the spike times with successively larger amounts of noise as illustrated in Figure 2A (Lu and Wang, 2004; Kayser et al., 2010). The top row shows a short segment of the actual responses for one example cell that had an information rate of 68.4 bits/s. The second row shows the responses after the addition of jitter drawn from a uniform distribution with a width of τ = 0.1 ms, which had no visible effect on the responses and no impact on the information. The third row shows the responses after the addition of noise with τ = 1 ms, which resulted in a clear decrease in the precision of some response events across repeats (see event marked by arrow) and a drop in information to 93% of I0. The fourth row shows the responses after the addition of noise with τ = 10 ms, which resulted in severe degradation of all response events and reduced the information to 55% of I0. Finally, the bottom row shows the responses after the addition of noise with τ = 100 ms, which left little observable structure or information in the responses.
Figure 2.
The temporal precision of IC spike trains. A, Raster plots of the responses of an example IC cell to a 20 ms segment of speech. The top row shows the actual responses and the bottom rows show the responses after the addition of different amounts of random jitter to the spike times. For each response, the single spike information is shown. B, The single spike information for the example cell as a function of the amount of added jitter. The critical timescale at which the information is decreased to 95% of its original value I0 is marked as τ95. C, The histogram (black) and cumulative distribution function (gray) of the critical timescale τ95 for our sample of IC cells. D, A scatter plot of the single spike information I0 versus the critical time scale τ95 for our sample of IC cells. The correlation coefficient between I0 and τ95 with logarithmic scaling is shown.
The single spike information for this example cell as function of the amount of added jitter is shown in Figure 2B. We defined τ95, the critical timescale at which information is encoded, as the value of τ for which the information dropped to 95% of I0, which, for this cell, was 0.7 ms. Figure 2C shows the distribution of τ95 for our sample of cells, which had a median value of 2 ms [only cells with information rates of at least 0.5 bits/s were analyzed (n = 368)]. To gain additional insight into how the critical timescale varied across the population, we examined the relationship between τ95 and the information in the responses (I0). As shown in Figure 2D, the critical timescale was finest for the most informative cells [the correlation coefficient between τ95 and I0 was −0.58 (p < 0.001) after logarithmic scaling], suggesting that when considering the total information transmitted by the population, an even finer timescale may be appropriate.
Refractoriness shapes spikes patterns and increases information transmission
The above analysis considered only the information in single spikes and, thus, ignored any correlations between spikes. As a first step toward assessing the impact of correlations in IC spike patterns, we considered the temporal correlations between spikes from the same cell. The total correlations in the actual spike trains can be decomposed into “signal” and noise components (Gawne and Richmond, 1993). For single cells, the signal correlations are the temporal correlations in the PSTH and the noise correlations are the temporal correlations in the deviation of the response in each time bin from the PSTH. We focused our analysis mainly on noise correlations (since the signal correlations are defined by the PSTH, any description of spike trains that captures the PSTH on the relevant timescale will also capture the effects of signal correlations on spike patterns). Figure 3A shows the temporal noise correlation functions are shown for three example cells (left) and for all cells in sample (right). Most cells had negative temporal noise correlations for short time lags, indicating a decreased probability of multiple spikes in short time windows that we will refer to as “refractoriness.” Because the timescale of the refractoriness is similar to the critical level of precision with which spikes are time-locked to speech, it can play a significant role in shaping spike patterns. To assess the impact of refractoriness, we compared spike patterns before and after shuffling the trial order for each time bin. This shuffling removed the temporal noise correlations, resulting in spike trains for which the probability of spiking in a given time bin on a single trial was independent of the spike history and could be described entirely by the PSTH.
Figure 3.
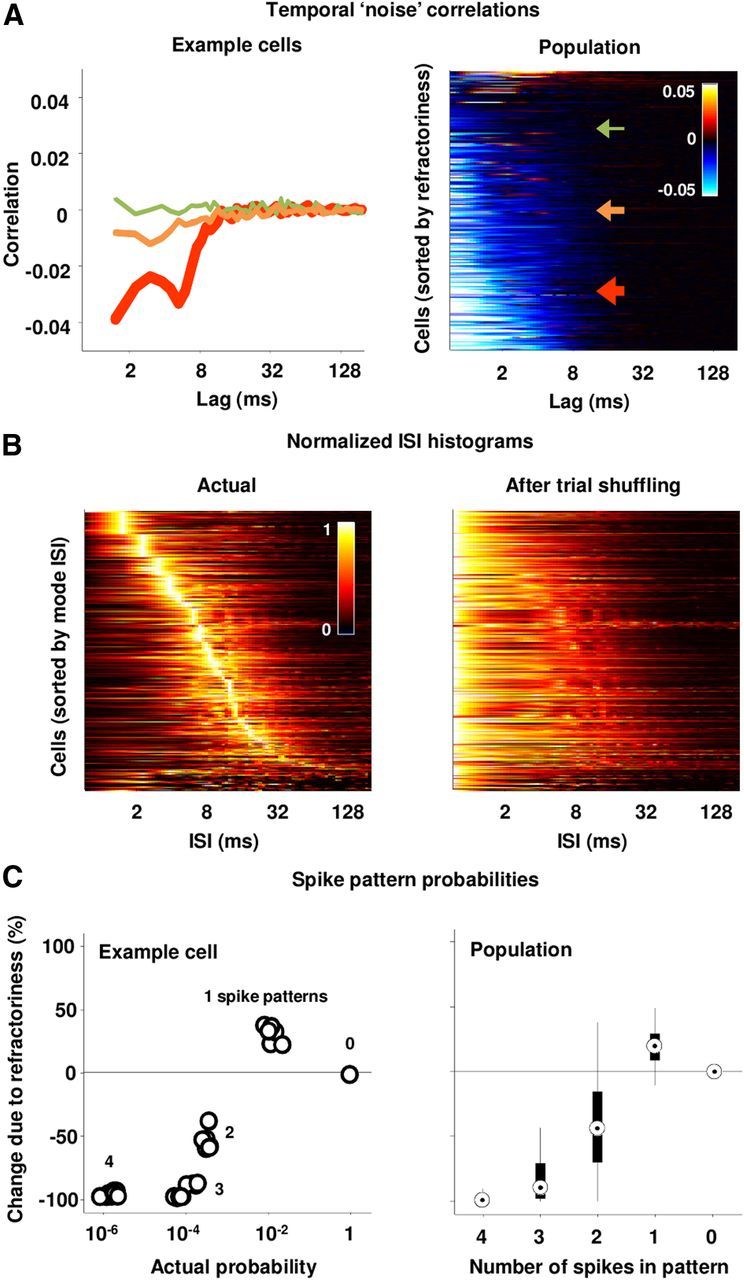
Refractoriness in IC spike trains. A, The temporal noise correlation functions for the IC cells in our sample. The left panel shows three example cells, and the right panel shows all cells, with the example cells marked by arrows. Colors in the right panel indicate the correlation. Cells were ordered for plotting according to the integral of their temporal noise correlation function. B, The ISI histograms for the IC cells in our sample before and after shuffling the trial order for each time bin. Histograms were computed using a bin size of 0.7 ms. The histogram for each cell was normalized to have a maximum value of 1. Cells were ordered for plotting according to their mode ISI. Colors indicate the normalized frequency of occurrence of each ISI. C, The left panel shows the effects of temporal noise correlations on the probability of spike patterns containing 0 to 4 spikes for an example cell. Each dot corresponds to a unique pattern. For this analysis, spike patterns were represented as binary patterns that were 16 bins long with 0.7 ms bins. The percentage change in probability due to temporal noise correlations was computed by comparing probabilities before and after shuffling the trial order for each time bin as 100 × (p(actual) − p(shuffled))/p(shuffled). The right panel shows the distributions of the effects of temporal noise correlations on the probability of spike patterns for our sample of cells. For each cell, probabilities were averaged across all possible spike patterns with a given number of spikes. The circles indicate the median, the thick lines span the 25th to 75th percentiles, and the thin lines span the fifth to 95th percentiles.
As a first step toward assessing the impact of refractoriness on spike patterns, we examined the distribution of interspike intervals (ISIs) before and after shuffling. Because refractoriness decreased the probability of short ISIs, the peak of the ISI histograms for IC cells were typically between 2 and 10 ms, as shown in Figure 3B. After removing the effects of refractoriness by shuffling, the maximum of all of the ISI histograms shifted to the smallest value, suggesting that refractoriness can change the distribution of spike patterns over short-time windows. To quantify this effect, we computed the probability of observing different binary spike patterns with a length of 12 ms before and after shuffling (for this and all further analyses, 0.7 ms time bins were used). As shown in Figure 3C, refractoriness resulted in an increase in the occurrence of patterns with a single spike, and a decrease in the occurrence of patterns with multiple spikes.
To gain further insight into the impact of refractoriness, we measured its effect on the information transmitted by spike patterns. The impact of noise correlations on information transmission depends on the sign and magnitude of the signal correlations (Oram et al., 1998; Panzeri et al., 1999). Generally, information transmission will be decreased if signal and noise correlations have the same sign, and increased if they have opposite signs. Signal correlations elongate the distributions of responses to different stimuli along a direction that increases their overlap and, thus, reduces stimulus discriminability. If noise correlations have the same sign as signal correlations, they will further elongate the response distributions in the same direction, further increasing overlap and reducing discriminability, but if noise correlations have the opposite sign from signal correlations, they will elongate the response distributions in a direction that is orthogonal to the direction of overlap and improve discriminability. Figure 4A shows the temporal signal correlation functions, i.e., the temporal correlations in the PSTH, for each cell in our sample. Most cells had positive temporal signal correlations for short time lags. The distribution of the temporal signal and noise correlations (summed over lags up to 12 ms, the longest spike patterns for which information could be reliably calculated) for each cell in our sample is shown in Figure 4B. Temporal signal and noise correlations were typically similar in magnitude and opposite in sign, suggesting that the negative temporal correlations imposed by refractoriness may increase information transmission by offsetting the positive temporal correlations in speech. To quantify the impact of refractoriness on information, we used an information breakdown approach to compute the impact of stimulus-independent noise correlations on the information in spike patterns (Pola et al., 2003). The black distributions in Figure 4C show the effects of refractoriness on the information in spike patterns of increasing length for our sample of cells with 0.7 ms time bins. The effects of refractoriness were generally positive, reaching a median value of approximately 10% of the total information in spike patterns that were 12 ms long, which was the maximum length for which we could reliably compute information. To provide an indication as to whether these effects were stable for longer spike patterns, we recomputed the information with larger time bins, allowing information to be measured over longer time scales at the cost of decreased temporal resolution. As shown in Figure 4C, using larger bins resulted in an overall decrease in information due to the loss of temporal resolution, but confirmed that the information reaches a steady value for patterns between 10 and 20 ms. This is consistent with the timescale of the relative refractory periods for these cells (i.e., the temporal noise correlation functions in Fig. 3A), which was typically <10 ms. Finally, we examined the extent to which the effects of refractoriness varied across the population. As shown in Figure 4D, the effects of refractoriness (measured for 12 ms spike patterns with 0.7 ms bins) tended to be stronger for the more informative cells.
The effects of refractoriness can be captured by a simple model
Given that refractoriness can play a significant role in shaping IC spike patterns, we sought to find the simplest modeling framework that could adequately capture its effects. We used the generalized linear model
where the probability of a spike occurring in time bin n on a given trial depends on a linear combination of a function gstim that describes the feed-forward influence of the stimulus and depends only on n, a function ghist that captures the effect of spike history based on the time since the last spike m, and a constant c (see schematic in Fig. 5A). The link function that converts this combination to a probability value between 0 and 1 is the logistic function flink(x) = ex/(ex + 1). This model is not designed to predict responses to novel stimuli, but simply to capture the effects of temporal noise correlations on responses to the same stimulus on which it is trained (with trials divided into two sets for training and testing). Thus, the feedforward influence is not estimated by passing the stimulus through a filter, but simply as a nonparametric function of the time since stimulus onset. For a cell without temporal noise correlations, since the probability of spiking in a given time bin is described completely by the PSTH and is independent of spike history, gstim matches exactly the PSTH and ghist is all zeros (given adequate training data). In the presence of temporal noise correlations such as refractoriness, gstim is a PSTH-like function that, when combined with the effects of spike history captured by ghist, best describes the probability of spiking on a trial-by-trial basis.
It is important to note that because of the linear form of the spike history dependence in this model, there is no guarantee that it will accurately capture the effects of refractoriness on spike patterns, as the interactions between successive spikes may be nonlinear. To assess the performance of the model, we used the model to generate spike trains and compared the patterns in the model spike trains to those in the actual data. As shown in Figure 5, B and C, both the temporal noise correlation functions and ISI histograms of the model spike trains closely matched those of the actual data (see insets). The model also accurately captured the probability of patterns with 0, 1, and 2 spikes within a 12 ms time window (Fig. 5D). While spike patterns with 3 and 4 spikes were reproduced less well, these patterns were extremely rare (average probabilities of 3.7 × 10−6 and 2.6 × 10−8, respectively, across our sample of cells), and thus, the failure of the model to match these patterns did not impair its ability to capture the effects of refractoriness on information transmission (Fig. 5E). These results demonstrate that the effects of the interactions between successive spikes on IC spike patterns can be accurately described by a simple model.
Noise correlations between IC cells are extremely weak
Thus far, we have considered only the temporal correlations between spikes from the same cell, but correlations between spikes from different cells can also play a significant role in shaping population spike patterns. As above, we focused our analysis on noise correlations, since any description that captures the PSTHs of the individual cells in a population on the relevant timescale will also capture the effects of their signal correlations on population spike patterns. As shown in Figure 6, A and B, the noise correlations in our sample of IC populations were extremely small. Figure 6A shows the noise correlation functions for all simultaneously recorded pairs of cells in our sample with the same color scale that was used for the temporal noise correlation functions in the previous figures, and Figure 6B shows the distribution of pairwise noise correlations (summed over lags between ±5 ms). The distributions are shown for pairs separated by different distances.
Figure 6.
Noise correlations between IC cells. A, The noise correlation functions for the pairs of simultaneously recorded IC cells in our sample. Color scale is the same as Figure 3A. B, The distributions of pairwise noise correlations for gerbil IC, gerbil A1, and mouse IC. To obtain these values, the noise correlation functions for each pair were summed over lags between ±5 ms. Distributions are shown for pairs recorded on tetrodes separated by different distances. C, The distributions of the effects of noise correlations on the information in spike patterns for populations of different size with 0.7 ms bins for our sample of cells. The percentage change in information due to noise correlations was computed as 100 × Icor–ind/(I0 + Isig–sim) (see Materials and Methods for definitions of information theoretic quantities).
To demonstrate that our experimental approach was capable of detecting noise correlations, we recorded responses to the same sounds with the same electrodes in the primary auditory cortex (A1), where strong noise correlations have been observed previously (Eggermont, 2006; Luczak et al., 2009). As shown in Figure 6B, the pairwise noise correlations in A1 populations were much larger. We also verified that the lack of noise correlations in IC was not species specific by recording in the IC of mice. Figure 6B shows the distribution of pairwise noise correlations in population spike trains in mouse IC recorded during the presentation of dynamic random chord sounds. As in the gerbil, the noise correlations in the mouse IC were extremely weak. Finally, to verify that noise correlations between cells did not have a significant impact on IC population spike patterns, we measured their effect on the information transmitted by the population using the same information breakdown approach as described above. For this analysis, the response in each 0.7 ms time bin was specified as a binary pattern with one element corresponding to each neuron and only a single time bin was considered (i.e., temporal correlations were ignored). As shown in Figure 6C, noise correlations between cells had no impact on the information transmitted by population spike patterns for the range of population sizes that could be accurately assessed from our data.
Discussion
Our results provide a characterization of the population code for speech in the IC, suggesting that any description of the processing of speech in the subcortical auditory pathway should consider spike times with sub-millisecond precision and include the effects of refractoriness, but can treat spike trains as conditionally independent (at least to second order) as noise correlations between pairs of cells were extremely weak. The observed temporal precision in the IC is much finer than that observed in other mammalian brain areas under natural stimulus conditions (Schnupp et al., 2006; Butts et al., 2007; Kayser et al., 2010; Shusterman et al., 2011; Roussin et al., 2012) and is consistent with the ability of IC cells to respond to tones and broadband sounds with time-locked spikes for carrier frequencies of >1 kHz and modulation frequencies up to several hundred Hertz (Frisina, 2001; Joris et al., 2004; Liu et al., 2006; Horvath and Lesica, 2011; Chen et al., 2012). The influence of refractoriness in shaping IC spike patterns is similar to its effects in the visual periphery and auditory nerve (Gaumond et al., 1982; Miller, 1985; Berry and Meister, 1998; Kara et al., 2000; Uzzell and Chichilnisky, 2004; Avissar et al., 2013). The increase in information that results from refractoriness is due to temporal decorrelation of the spike trains; the negative temporal correlations imposed by refractoriness offset the redundancy in the spike trains due to the positive temporal correlations in the speech (Dan et al., 1996; Brenner et al., 2000; Reinagel and Reid, 2000). Our observation that the noise correlations between IC cells are negligible is an important step forward in our understanding of population coding in the auditory system; while noise correlations in auditory cortex have been well documented (Eggermont, 2006; Luczak et al., 2009), our results provide the first comprehensive assessment of their effects on spike trains in a subcortical auditory area (Johnson and Kiang, 1976; Voigt and Young, 1988; Lesica et al., 2010). Noise correlations between cells can have a major impact on population coding (Shadlen and Newsome, 1998; Abbott and Dayan, 1999; Averbeck et al., 2006) and have been shown to play an important role in shaping spike trains in many brain areas. The fact that noise correlations between cells in the IC can be ignored greatly simplifies the problem of understanding its function (see below) and has important implications for speech processing in auditory cortex. Recent studies have reported weak noise correlations in some cortical populations (Ecker et al., 2010; Hansen et al., 2012; Smith et al., 2013), but whether these weak cortical correlations reflect weak correlations in subcortical inputs or active decorrelation due to recurrent connectivity in cortex (Renart et al., 2010) remains to be determined.
Our approach to characterizing the neural code for speech in the IC suggests a template for studying spike trains in any sensory brain area based on answering three questions: (1) What is the critical time scale for the information in single spikes? (2) Are there temporal noise correlations and, if so, do they have a significant impact on spike patterns? (3) Are there noise correlations between cells and, if so, do they have a significant impact on spike patterns? Answering the first question is equivalent to specifying the size of the time bin that should be used if spike trains are to be described only by their PSTHs, while answering the second and third questions requires assessing the extent to which PSTHs are a sufficient description for the spike trains of individual cells and the population. While the first question is easily answered given limited experimental data, the second and third may not be if, for example, the timescale of the noise correlations is large relative to the resolution of the single spike information; if small time bins must be used to capture the single spike information, but long time windows must be considered to capture the full impact of the correlations, it may be difficult to accurately measure the probabilities of different spike patterns. Furthermore, additional difficulties may arise if the timescale of the correlations is finer than that of the information in single spikes (Brenner et al., 2000), if correlations are of a high order (Ohiorhenuan et al., 2010), or if the recording technique is not able to sample the neuronal population at the appropriate spatial scale (Smith and Kohn, 2008). There are also many ways to measure the impact of noise correlations on spike patterns. We chose to look directly at the effect of noise correlations on pattern probabilities and mutual information in IC spike trains, which is reasonable for a subcortical area where spiking is predominantly driven by stimulus-driven input from sensory receptors, but may be less appropriate for the cortex where intrinsic dynamics play a larger role. Ultimately, the impact of noise correlations should be assessed by their impact on perception and behavior (Gutnisky and Dragoi, 2008; Cohen and Maunsell, 2009; Gu et al., 2011; Jeanne et al., 2013).
Our results suggest that the problem of understanding population coding in the IC can be reduced to the problem of understanding the stimulus-driven spiking of individual cells and their refractoriness. While this is still a difficult problem, it is simpler than the analogous problem in many other sensory areas, where spike trains are influenced not only by stimulus-driven input, but also by intrinsic influences from the surrounding neural network. The problem of understanding the stimulus-driven input to individual IC cells is made difficult by the many nonlinearities of the cochlea (Robles and Ruggero, 2001), which appear to play a significant role in the processing of speech (Young and Sachs, 1979; Sinex and Geisler, 1983; Delgutte and Kiang, 1984; Palmer et al., 1986). Fortunately, much progress has been made toward characterizing these nonlinearities (Brown et al., 2010; Hudspeth et al., 2010; Zilany and Carney, 2010), and the additional nonlinearities in the auditory brainstem appear to be relatively modest (Chen et al., 1996; Delgutte et al., 1998; Young, 2008). Thus, based on our results and other recent progress in the field, we are optimistic that a comprehensive model of the processing of speech in the IC may be attainable in the near future.
Footnotes
This work was supported by the German Research Foundation (DFG) and the Wellcome Trust. We thank P. Latham, M. Sahani, J. Linden, and T. Mrsic-Flogel for comments on the manuscript and K. Harris and P. Chadderton for advice on spike sorting.
The authors declare no competing financial interests.
References
- Abbott LF, Dayan P. The effect of correlated variability on the accuracy of a population code. Neural Comput. 1999;11:91–101. doi: 10.1162/089976699300016827. [DOI] [PubMed] [Google Scholar]
- Aitkin LM, Webster WR, Veale JL, Crosby DC. Inferior colliculus. I. Comparison of response properties of neurons in central, pericentral, and external nuclei of adult cat. J Neurophysiol. 1975;38:1196–1207. doi: 10.1152/jn.1975.38.5.1196. [DOI] [PubMed] [Google Scholar]
- Averbeck BB, Latham PE, Pouget A. Neural correlations, population coding and computation. Nat Rev Neurosci. 2006;7:358–366. doi: 10.1038/nrn1888. [DOI] [PubMed] [Google Scholar]
- Avissar M, Wittig JH, Jr, Saunders JC, Parsons TD. Refractoriness enhances temporal coding by auditory nerve fibers. J Neurosci. 2013;33:7681–7690. doi: 10.1523/JNEUROSCI.3405-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berry MJ, 2nd, Meister M. Refractoriness and neural precision. J Neurosci. 1998;18:2200–2211. doi: 10.1523/JNEUROSCI.18-06-02200.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner N, Strong SP, Koberle R, Bialek W, de Ruyter van Steveninck RR. Synergy in a neural code. Neural Comput. 2000;12:1531–1552. doi: 10.1162/089976600300015259. [DOI] [PubMed] [Google Scholar]
- Brown GJ, Ferry RT, Meddis R. A computer model of auditory efferent suppression: implications for the recognition of speech in noise. J Acoust Soc Am. 2010;127:943–954. doi: 10.1121/1.3273893. [DOI] [PubMed] [Google Scholar]
- Butts DA, Weng C, Jin J, Yeh CI, Lesica NA, Alonso JM, Stanley GB. Temporal precision in the neural code and the timescales of natural vision. Nature. 2007;449:92–95. doi: 10.1038/nature06105. [DOI] [PubMed] [Google Scholar]
- Chen C, Read HL, Escabí MA. Precise feature based time scales and frequency decorrelation lead to a sparse auditory code. J Neurosci. 2012;32:8454–8468. doi: 10.1523/JNEUROSCI.6506-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen GD, Nuding SC, Narayan SS, Sinex DG. Responses of single neurons in the chinchilla inferior colliculus to consonant-vowel syllables differing in voice onset time. Aud Neurosci. 1996;3:179–198. [Google Scholar]
- Choi JH, Jung HK, Kim T. A new action potential detector using the MTEO and its effects on spike sorting systems at low signal-to-noise ratios. IEEE Trans Biomed Eng. 2006;53:738–746. doi: 10.1109/TBME.2006.870239. [DOI] [PubMed] [Google Scholar]
- Cohen MR, Maunsell JHR. Attention improves performance primarily by reducing interneuronal correlations. Nat Neurosci. 2009;12:1594–1600. doi: 10.1038/nn.2439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dan Y, Atick JJ, Reid RC. Efficient coding of natural scenes in the lateral geniculate nucleus: experimental test of a computational theory. J Neurosci. 1996;16:3351–3362. doi: 10.1523/JNEUROSCI.16-10-03351.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delgutte B, Kiang NY. Speech coding in the auditory nerve: I. Vowel-like sounds. J Acoust Soc Am. 1984;75:866–878. doi: 10.1121/1.390596. [DOI] [PubMed] [Google Scholar]
- Delgutte B, Hammond BM, Cariani PA. Neural coding of the temporal envelope of speech: Relation to modulation transfer functions. In: Palmer AR, Reese A, Summerfield AQ, Meddis R, editors. Psychophysical and Physiological Advances in Hearing. London: Whurr; 1998. pp. 595–603. [Google Scholar]
- Ecker AS, Berens P, Keliris GA, Bethge M, Logothetis NK, Tolias AS. Decorrelated neuronal firing in cortical microcircuits. Science. 2010;327:584–587. doi: 10.1126/science.1179867. [DOI] [PubMed] [Google Scholar]
- Eggermont JJ. Properties of correlated neural activity clusters in cat auditory cortex resemble those of neural assemblies. J Neurophysiol. 2006;96:746–764. doi: 10.1152/jn.00059.2006. [DOI] [PubMed] [Google Scholar]
- Frisina RD. Subcortical neural coding mechanisms for auditory temporal processing. Hear Res. 2001;158:1–27. doi: 10.1016/s0378-5955(01)00296-9. [DOI] [PubMed] [Google Scholar]
- Gaumond RP, Molnar CE, Kim DO. Stimulus and recovery dependence of cat cochlear nerve fiber spike discharge probability. J Neurophysiol. 1982;48:856–873. doi: 10.1152/jn.1982.48.3.856. [DOI] [PubMed] [Google Scholar]
- Gawne TJ, Richmond BJ. How independent are the messages carried by adjacent inferior temporal cortical neurons? J Neurosci. 1993;13:2758–2771. doi: 10.1523/JNEUROSCI.13-07-02758.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu Y, Liu S, Fetsch CR, Yang Y, Fok S, Sunkara A, DeAngelis GC, Angelaki DE. Perceptual learning reduces interneuronal correlations in macaque visual cortex. Neuron. 2011;71:750–761. doi: 10.1016/j.neuron.2011.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutnisky DA, Dragoi V. Adaptive coding of visual information in neural populations. Nature. 2008;452:220–224. doi: 10.1038/nature06563. [DOI] [PubMed] [Google Scholar]
- Hansen BJ, Chelaru MI, Dragoi V. Correlated variability in laminar cortical circuits. Neuron. 2012;76:590–602. doi: 10.1016/j.neuron.2012.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hazan L, Zugaro M, Buzsáki G. Klusters, NeuroScope, NDManager: a free software suite for neurophysiological data processing and visualization. J Neurosci Methods. 2006;155:207–216. doi: 10.1016/j.jneumeth.2006.01.017. [DOI] [PubMed] [Google Scholar]
- Horvath D, Lesica NA. The effects of interaural time difference and intensity on the coding of low-frequency sounds in the mammalian midbrain. J Neurosci. 2011;31:3821–3827. doi: 10.1523/JNEUROSCI.4806-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudspeth AJ, Jülicher F, Martin P. A critique of the critical cochlea: Hopf—a bifurcation—is better than none. J Neurophysiol. 2010;104:1219–1229. doi: 10.1152/jn.00437.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeanne JM, Sharpee TO, Gentner TQ. Associative learning enhances population coding by inverting interneuronal correlation patterns. Neuron. 2013;78:352–363. doi: 10.1016/j.neuron.2013.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson DH, Kiang NY. Analysis of discharges recorded simultaneously from pairs of auditory nerve fibers. Biophysical J. 1976;16:719–734. doi: 10.1016/S0006-3495(76)85724-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joris PX, Schreiner CE, Rees A. Neural processing of amplitude-modulated sounds. Physiol Rev. 2004;84:541–577. doi: 10.1152/physrev.00029.2003. [DOI] [PubMed] [Google Scholar]
- Kara P, Reinagel P, Reid RC. Low response variability in simultaneously recorded retinal, thalamic, and cortical neurons. Neuron. 2000;27:635–646. doi: 10.1016/S0896-6273(00)00072-6. [DOI] [PubMed] [Google Scholar]
- Kayser C, Logothetis NK, Panzeri S. Millisecond encoding precision of auditory cortex neurons. Proc Natl Acad Sci U S A. 2010;107:16976–16981. doi: 10.1073/pnas.1012656107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lesica NA, Lingner A, Grothe B. Population coding of interaural time differences in gerbils and barn owls. J Neurosci. 2010;30:11696–11702. doi: 10.1523/JNEUROSCI.0846-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu LF, Palmer AR, Wallace MN. Phase-locked responses to pure tones in the inferior colliculus. J Neurophysiol. 2006;95:1926–1935. doi: 10.1152/jn.00497.2005. [DOI] [PubMed] [Google Scholar]
- Lu T, Wang X. Information content of auditory cortical responses to time-varying acoustic stimuli. J Neurophysiol. 2004;91:301–313. doi: 10.1152/jn.00022.2003. [DOI] [PubMed] [Google Scholar]
- Luczak A, Barthó P, Harris KD. Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron. 2009;62:413–425. doi: 10.1016/j.neuron.2009.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magri C, Whittingstall K, Singh V, Logothetis NK, Panzeri S. A toolbox for the fast information analysis of multiple-site LFP, EEG and spike train recordings. BMC Neurosci. 2009;10:81. doi: 10.1186/1471-2202-10-81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller MI. Algorithms for removing recovery-related distortion from auditory-nerve discharge patterns. J Acoust Soc Am. 1985;77:1452–1464. doi: 10.1121/1.392040. [DOI] [PubMed] [Google Scholar]
- Nirenberg S, Carcieri SM, Jacobs AL, Latham PE. Retinal ganglion cells act largely as independent encoders. Nature. 2001;411:698–701. doi: 10.1038/35079612. [DOI] [PubMed] [Google Scholar]
- Ohiorhenuan IE, Mechler F, Purpura KP, Schmid AM, Hu Q, Victor JD. Sparse coding and high-order correlations in fine-scale cortical networks. Nature. 2010;466:617–621. doi: 10.1038/nature09178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oram MW, Földiák P, Perrett DI, Sengpiel F. The “Ideal Homunculus”: decoding neural population signals. Trends Neurosci. 1998;21:259–265. doi: 10.1016/S0166-2236(97)01216-2. [DOI] [PubMed] [Google Scholar]
- Palmer AR, Winter IM, Darwin CJ. The representation of steady-state vowel sounds in the temporal discharge patterns of the guinea pig cochlear nerve and primarylike cochlear nucleus neurons. J Acoust Soc Am. 1986;79:100–113. doi: 10.1121/1.393633. [DOI] [PubMed] [Google Scholar]
- Panzeri S, Schultz SR, Treves A, Rolls ET. Correlations and the encoding of information in the nervous system. Proc Biol Sci. 1999;266:1001–1012. doi: 10.1098/rspb.1999.0736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panzeri S, Senatore R, Montemurro MA, Petersen RS. Correcting for the sampling bias problem in spike train information measures. J Neurophysiol. 2007;98:1064–1072. doi: 10.1152/jn.00559.2007. [DOI] [PubMed] [Google Scholar]
- Pillow JW, Shlens J, Paninski L, Sher A, Litke AM, Chichilnisky E, Simoncelli EP. Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature. 2008;454:995–999. doi: 10.1038/nature07140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pola G, Thiele A, Hoffmann KP, Panzeri S. An exact method to quantify the information transmitted by different mechanisms of correlational coding. Network. 2003;14:35–60. doi: 10.1088/0954-898X/14/1/303. [DOI] [PubMed] [Google Scholar]
- Reinagel P, Reid RC. Temporal coding of visual information in the thalamus. J Neurosci. 2000;20:5392–5400. doi: 10.1523/JNEUROSCI.20-14-05392.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renart A, de la Rocha J, Bartho P, Hollender L, Parga N, Reyes A, Harris KD. The asynchronous state in cortical circuits. Science. 2010;327:587–590. doi: 10.1126/science.1179850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robles L, Ruggero MA. Mechanics of the mammalian cochlea. Physiol Rev. 2001;81:1305–1352. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roussin AT, D'Agostino AE, Fooden AM, Victor JD, Di Lorenzo PM. Taste coding in the nucleus of the solitary tract of the awake, freely licking rat. J Neurosci. 2012;32:10494–10506. doi: 10.1523/JNEUROSCI.1856-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitzer-Torbert N, Jackson J, Henze D, Harris K, Redish AD. Quantitative measures of cluster quality for use in extracellular recordings. Neuroscience. 2005;131:1–11. doi: 10.1016/j.neuroscience.2004.09.066. [DOI] [PubMed] [Google Scholar]
- Schnupp JW, Hall TM, Kokelaar RF, Ahmed B. Plasticity of temporal pattern codes for vocalization stimuli in primary auditory cortex. J Neurosci. 2006;26:4785–4795. doi: 10.1523/JNEUROSCI.4330-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J Neurosci. 1998;18:3870–3896. doi: 10.1523/JNEUROSCI.18-10-03870.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shusterman R, Smear MC, Koulakov AA, Rinberg D. Precise olfactory responses tile the sniff cycle. Nat Neurosci. 2011;14:1039–1044. doi: 10.1038/nn.2877. [DOI] [PubMed] [Google Scholar]
- Sinex DG, Geisler CD. Responses of auditory-nerve fibers to consonant–vowel syllables. J Acoust Soc Am. 1983;73:602–615. doi: 10.1121/1.389007. [DOI] [PubMed] [Google Scholar]
- Smith MA, Kohn A. Spatial and temporal scales of neuronal correlation in primary visual cortex. J Neurosci. 2008;28:12591–12603. doi: 10.1523/JNEUROSCI.2929-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Jia X, Zandvakili A, Kohn A. Laminar dependence of neuronal correlations in visual cortex. J Neurophysiol. 2013;109:940–947. doi: 10.1152/jn.00846.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strong SP, Koberle R, de Ruyter van Steveninck RR, Bialek W. Entropy and information in neural spike trains. Phys Rev Lett. 1998;80:197–200. doi: 10.1103/PhysRevLett.80.197. [DOI] [Google Scholar]
- Syka J, Popelár J, Kvasnák E, Astl J. Response properties of neurons in the central nucleus and external and dorsal cortices of the inferior colliculus in guinea pig. Exp Brain Res. 2000;133:254–266. doi: 10.1007/s002210000426. [DOI] [PubMed] [Google Scholar]
- Thomas H, Tillein J, Heil P, Scheich H. Functional organization of auditory cortex in the mongolian gerbil (Meriones unguiculatus). I. Electrophysiological mapping of frequency representation and distinction of fields. Eur J Neurosci. 1993;5:882–897. doi: 10.1111/j.1460-9568.1993.tb00940.x. [DOI] [PubMed] [Google Scholar]
- Uzzell VJ, Chichilnisky EJ. Precision of spike trains in primate retinal ganglion cells. J Neurophysiol. 2004;92:780–789. doi: 10.1152/jn.01171.2003. [DOI] [PubMed] [Google Scholar]
- Voigt HF, Young ED. Neural correlations in the dorsal cochlear nucleus: pairs of units with similar response properties. J Neurophysiol. 1988;59:1014–1032. doi: 10.1152/jn.1988.59.3.1014. [DOI] [PubMed] [Google Scholar]
- Young ED. Neural representation of spectral and temporal information in speech. Philos Trans R Soc Lond B Biol Sci. 2008;363:923–945. doi: 10.1098/rstb.2007.2151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young ED, Sachs MB. Representation of steady-state vowels in the temporal aspects of the discharge patterns of populations of auditory-nerve fibers. J Acoust Soc Am. 1979;66:1381–1403. doi: 10.1121/1.383532. [DOI] [PubMed] [Google Scholar]
- Zilany MSA, Carney LH. Power-law dynamics in an auditory-nerve model can account for neural adaptation to sound-level statistics. J Neurosci. 2010;30:10380–10390. doi: 10.1523/JNEUROSCI.0647-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]