CLASSIFICATION OF TUMOR HISTOPATHOLOGY VIA SPARSE FEATURE LEARNING

Abstract

Our goal is to decompose whole slide images (WSI) of histology sections into distinct patches (e.g., viable tumor, necrosis) so that statistics of distinct histopathology can be linked with the outcome. Such an analysis requires a large cohort of histology sections that may originate from different laboratories, which may not use the same protocol in sample preparation. We have evaluated a method based on a variation of the restricted Boltzmann machine (RBM) that learns intrinsic features of the image signature in an unsupervised fashion. Computed code, from the learned representation, is then utilized to classify patches from a curated library of images. The system has been evaluated against a dataset of small image blocks of 1k-by-1k that have been extracted from glioblastoma multiforme (GBM) and clear cell kidney carcinoma (KIRC) from the cancer genome atlas (TCGA) archive. The learned model is then projected on each whole slide image (e.g., of size 20k-by-20k pixels or larger) for characterizing and visualizing tumor architecture. In the case of GBM, each WSI is decomposed into necrotic, transition into necrosis, and viable. In the case of the KIRC, each WSI is decomposed into tumor types, stroma, normal, and others. Evaluation of 1400 and 2500 samples of GBM and KIRC indicates a performance of 84% and 81%, respectively.

1. INTRODUCTION

Our goal is to evaluate tumor composition in terms of a multiparametric morphometric indices and link them to clinical data. If tissue histology can be characterized in terms of different components (e.g., stroma, tumor), then nuclear morphometric indices from each component can be tested against a specific outcome. However, such an analysis usually needs to be performed in the context of a cohort, where histology sections are generated at different labs, or at the same lab, but at different times with a significant amount of technical variations.

In this paper, we extend and evaluate automated feature learning from unlabeled datasets. Features are learned using a generative model, based on a variation of the restricted Boltzmann machine (RBM) [1], with added sparsity constraints. It operates in two stages of feedforward (e.g., encoding) and feedback (e.g., decoding). The decoding step reconstructs each original patch from an overcomplete set of basis functions called the dictionary through sparse association. A second layer of pooling is added to make the system robust to translation in the data. Learned features are then trained against an annotated dataset for classifying a collection of small patches in each image. This approach is orthogonal to manually designed feature descriptors, such as SIFT [2] and HOG [3] descriptors, which tend to be complex and time consuming. The tumor signatures are visualized from hematoxylin and eosin (H&E) stained histology sections. We suggest that automated feature learning from unlabeled data is more tolerant to batch effect (e.g., technical variations associated with sample preparation) and can learn pertinent features without user intervention. The RBM framework with limited connectivity between input and output is shown in Figure 1(a). Such a network structure can also be stacked for deep learning. Our overall recognition framework which includes the auto-encoder and a layer of max-pooling for feature generation is shown in Figure 1(b).

Fig. 1.

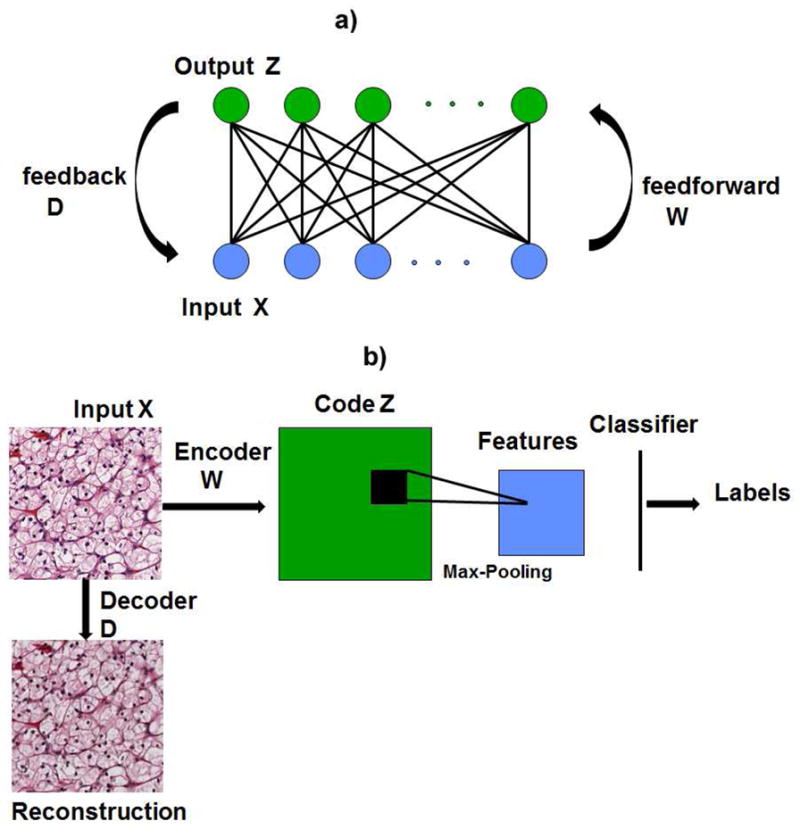
(a) Architecture for restricted Boltzmann machine (RBM), where connectivity is limited between the input and hidden layer. There is no connectivity between the nodes in the hidden layer. (b)Illustration of the 2-layer recognition framework including the encoder, decoder and pooling.

The organization of the paper is as follows. Section 2 reviews prior research. Section 3 outlines the proposed method. Section 4 provides a summary of the experiment data. Section 5 concludes the paper.

2. REVIEW OF PREVIOUS RESEARCH

Histology sections are typically visualized with H&E stains that label DNA and protein contents, respectively, in various shades of color. These sections are generally rich in content since various cell types, cellular organization, cell state and health, and cellular secretion can be characterized by a trained pathologist with the caveat of inter- and intra- observer variations [4]. Several reviews for the analysis and application of H&E sections can be found in [5, 6, 7, 8]. From our perspective, three key concepts have been introduced to establish the trend and direction of the research community.

The first group of researchers have focused on tumor grading through either accurate or rough nuclear segmentation [9] followed by computing cellular organization [10] and classification. In some cases, tumor grading has been associated with recurrence, progression, and invasion carcinoma (e.g., breast DCIS), but such associations is highly dependent on tumor heterogeneity and mixed grading (e.g., presence of more than one grade). This offers significant challenges to the pathologists, as mixed grading appears to be present in 50 percent of patients [11]. A recent study indicates that detailed segmentation and multivariate representation of nuclear features from H&E stained sections can predict DCIS recurrence [12] in patients with more than one nuclear grade. In this study, nuclei in the H&E stained samples were manually segmented and a multidimensional representation was computed for differential analysis between the cohorts. The significance of this particular study is that it has been repeated with the same quantitative outcome. In other related studies, image analysis of nuclear features has been found to provide quantitative information that can contribute to diagnosis and prognosis values for carcinoma of the breast [13], prostate [14], and colorectal mucosa [15].

The second group of researchers have focused on patch-based (e.g., region-based) analysis of tissue sections by engineering features and designing classifiers. In these systems, representation is often based on the distribution of color, texture, or a group of morphometric features while the classification is based on either kernel-based classifier, regression tree classifier, or sparse coding [16, 17, 18, 19]. More recently, some systems have initiated the use of automatic feature learning [20, 21]. In its simplest form, automated feature learning can be based on independent component analysis (ICA). However, learned kernels from ICA are not grouped and lack invariance properties. In contrast, independent subspace analysis (ISA) shows that invariant kernels can be learned from the data through non-linear mapping [20]. Yet, one of the shortcomings of ISA is that it is strictly feedforward, which means it lacks the ability to also reconstruct the original data. Reconstruction, through feedback is an important positive attributes that RBM can offer.

The third group of researchers have suggested utilizing the detection autoimmune system (e.g., lymphocytes) as a prognostic tool for breast cancer [22]. Lymphocytes are part of the adaptive immune response, and their presence has been correlated with nodal metastasis and HER2-positive breast cancer, ovarian cancer [23], and GBM.

3. APPROACH

In the next two sections, details of unsupervised feature learning and classification are presented. The feature learning code was implemented in MATLAB and the performance was evaluated using support vector classification implemented through LIBSVM [24].

3.1. Unsupervised Feature Learning

Given a set of histology images, the first step is to learn the dictionary from the unlabeled images. A sparse auto-encoder is used to learn these features in an unsupervised manner. The inputs for feature learning are a set of vectorized image patches, X, that are randomly selected from the input images. The objective of the auto-encoder is to arrive at a representation Z for each input X with a simple feedforward operation on the test sequence without having to solve the optimization function again, where the representation code Z is constrained to be sparse. The feedback mechanism computes the dictionary, D, which minimizes the reconstruction error of the original signal. Thus, for an input vector of size n forming the input X, the auto-encoder consists of three components: an encoder W, the dictionary D and a set of codes Z. The overall optimization function is expressed as:

$$F(X)={\Vert WX-Z\Vert }^2+\lambda {\Vert Z\Vert }_1+{\Vert DZ-X\Vert }^2,$$ (1)

where X ∈ ℝⁿ, Z ∈ ℝ^k, dictionary D ∈ ℝ^n×k and encoder W ∈ ℝ^k×n. The first term represents the feedforward or the encoding, the second term denotes the sparsity constraint and the last term denotes the feedback/decoding. λ is a parameter that controls the sparsity of the solution, i.e., sparsity is increased with higher value of λ. The parameter λ is varied between 0.05 and 1 in steps of 0.05 and the optimum value is selected through cross validation to minimizes F(X). Here, we used λ = 0.3.

The learning protocol involves computing the optimal D, W and Z that minimizes F(X). The process is iterative by fixing one set of parameters while optimizing others and vice versa, i.e., iterate over steps (2) and (3) below:

1. Randomly initialize D and W.

2. Fix D and W and minimize Equation 1 with respect to Z, where Z for each input vector is estimated via the gradient descent method.

3. Fix Z and estimate D and W, where D, W are approximated through stochastic gradient descent algorithm.

The stochastic gradient descent algorithm approximates the true gradient of the function by the gradient of a single example or the sum over a small number of randomly chosen training examples in each iteration. This approach is used because the size of the training set is large and a traditional gradient descent can be very computationally intensive. Examples of computed dictionary elements from the KIRC and GBM datasets are shown in Figure 2. It can be seen that the dictionary captures color and texture information in the data which are difficult to obtain using hand engineered features.

Fig. 2.

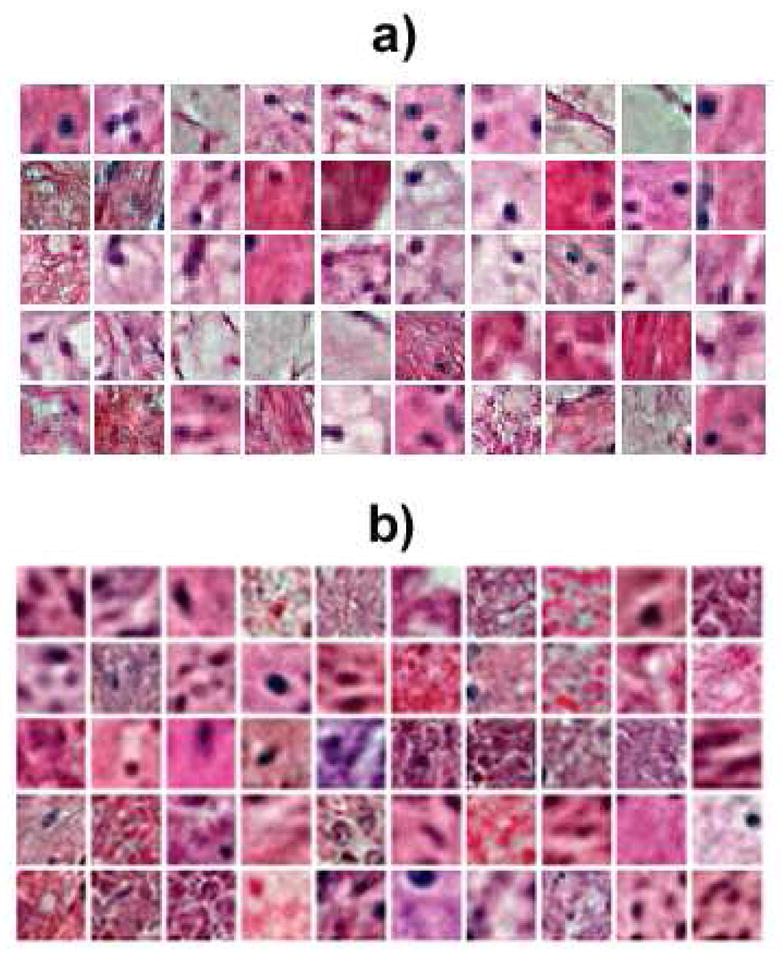
Representative set of computed basis function, D, for a) the KIRC dataset and b) the GBM dataset.

3.2. Classification

The computed encoder W is then used to train a classifier on components of the tissue architecture using a small set of labeled data. Every image, in the training dataset, is divided into non-overlapping image patches. The codes for these patches are computed by the feedforward operation Z = W X.

In order to account for the translational variation in the data, an additional pooling layer is added to the system. We perform a max-pooling of the sparse codes over a local neighborhood of adjacent codes. The pooled codes form the features for training. A support vector machine classifier is used to model the different tissue types. We use a multi-class regularized support vector classification with a regularization parameter 1 and a polynomial kernel of degree 3.

4. DISCUSSION

We have applied the proposed system to two datasets derived from (i) Glioblastoma Multiforme (GBM), and (ii) kidney clear cell renal carcinoma (KIRC) from The Cancer Genome Atlas (TCGA) at the National Institute of Health. Both datasets consist of images that capture diversities in the batch effect (e.g., technical variations in sample preparation). Each image is of 1K-by-1K pixels, which is cropped from a whole slide image (WSI). These whole slide images are publicly available from the NIH repository.

In GBM, necrosis has been shown to be predictive of outcome; however, necrosis is a dynamic process. Therefore, we opted to curate three classes that correspond to necrosis, “transition to necrosis” (an intermediate step), and tumor. Such a categorization should provide a better boundary between these classes. Purely necrotic regions are free of DNA contents, while transition to necrosis regions have diffused or punctate DNA contents. The dataset contained a total of 1, 400 images of samples that have been scanned with 20X objective. For feature learning, the system extracted 50 randomly selected patches of size 25 × 25 pixels from each image in the dataset. These patches were down sampled by a factor of 2 from each image and were normalized in the range of 0 – 1 in the color space. A set of 1, 000 bases were then computed for the entire dataset. The number of basis were chosen to minimize the reconstruction error using cross-validation, where reconstruction error is a measure of how well the computed bases represent the original images. From a total of 12, 000, 8, 000 and 16, 000 patches obtained for necrosis, transition to necrosis and tumor, we randomly selected 4, 000 patches from each class for training, and another 4000 patches were used for testing with cross-validation repeated 100 times. The max-pooling was performed on every patch of size 100 × 100 pixels, i.e., max-pooling operates on a 4-by-4 neighboring patches of the learning step. With this strategy, an overall classification accuracy of 84.3% has been obtained with the confusion matrix shown in Table 1. Example of reconstruction of a heterogeneous test image containing transition to necrosis on the left and tumor on the right using the dictionary derived from the auto-encoder is shown in Figure 3. From this example it is evident that necrosis transition is visually distinguishable from tumor in reconstruction.

Table 1.

Confusion matrix for classifying three different morphometric signatures in GBM.

Tissue Type	Necrosis	Tumor	Transition to necrosis
Necrosis	77.6	7.7	14.6
Tumor	0.5	93.3	6
Transition to necrosis	10.9	6.3	82.8

Fig. 3.

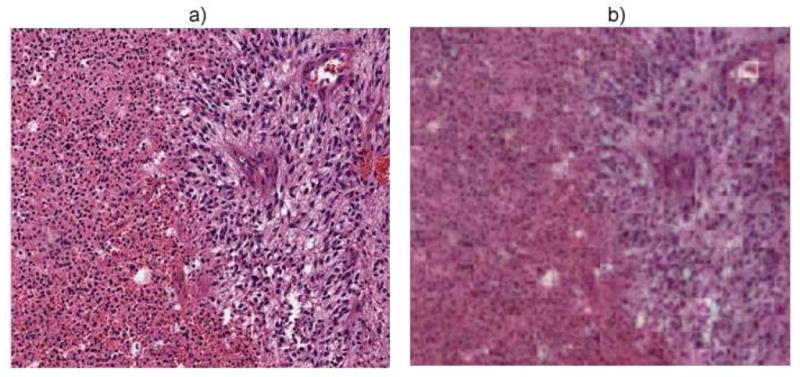
(a) A heterogeneous tissue section with transition to necrosis on the left and tumor on the right, and (b) its reconstruction after encoding and decoding

In KIRC, tumor type is the best prognosis of outcome, and in most sections, there is mix grading of clear cell carcinoma (CCC) and Granular tumors. In addition, the histology is typically complex since it contains components of stroma, blood, and cystic space. Some histology sections also have regions that correspond to the normal phenotype. In the case of KIRC, we opted the strategy to label each image patch as normal, granular tumor type, CCC, stroma, and others. The dataset contains 2, 500 images of samples that have been scanned with a 40X objective. Each image was down sampled by the factor of 4, and the same policy for feature learning and classification was followed as before. Here, from a total of 10, 000 patches for CCC, 16, 000 patches for normal and stromal tissues, and 6, 500 patches for tumor and others, we used 3, 250 patches for training from each class and the rest for testing. The overall classification accuracy was at 80.9% with the confusion matrix shown in Table 2.

Table 2.

Confusion matrix for classifying five different morphometric signatures in KIRC.

Tissue Type	CCC	Normal	Stromal	Granular	Others
CCC	89.8	3.6	4.1	1.2	0
Normal	7.5	75.9	7.4	8.5	0.2
Stromal	5.0	4.6	76.2	5.9	8.2
Granular	6.0	9.0	3.8	80.1	0
Others	0	0	0.2	0	99.8

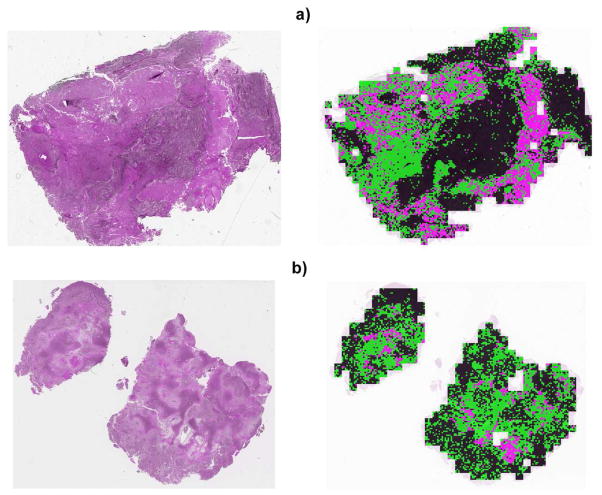
To test the preliminary efficacy of the system, several whole slide sections of the size 20, 000 × 20, 000 pixels were selected, and each 100-by-100 pixel patch were classified against the learned model with examples shown in Figure 4. Classification has been consistent with the pathologist evaluation and annotation.

Fig. 4.

Two examples of classification results of a heterogeneous GBM tissue sections. The left and right images correspond to the original and classification results, respectively. Color coding is black (tumor), pink (necrosis), and green (transition to necrosis).

5. CONCLUSION

In this paper, we presented a method for automated feature learning from unlabeled images for classifying distinct morphometric regions within a whole slide image (WSI). We suggest that automated feature learning provides a rich representation when a cohort of WSI has to be processed in the context of the batch effect. Automated feature learning is a generative model that reconstructs the original image from a sparse representation of an auto encoder. The system has been tested on two tumor types from TCGA archive. Proposed approach will enable identifying morphometric indices that are predictive of the outcome.