Classification of Tumor Histology via Morphometric Context

Abstract

Image-based classification of tissue histology, in terms of different components (e.g., normal signature, categories of aberrant signatures), provides a series of indices for tumor composition. Subsequently, aggregation of these indices in each whole slide image (WSI) from a large cohort can provide predictive models of clinical outcome. However, the performance of the existing techniques is hindered as a result of large technical and biological variations that are always present in a large cohort. In this paper, we propose two algorithms for classification of tissue histology based on robust representations of morphometric context, which are built upon nuclear level morphometric features at various locations and scales within the spatial pyramid matching (SPM) framework. These methods have been evaluated on two distinct datasets of different tumor types collected from The Cancer Genome Atlas (TCGA), and the experimental results indicate that our methods are (i) extensible to different tumor types; (ii) robust in the presence of wide technical and biological variations; (iii) invariant to different nuclear segmentation strategies; and (iv) scalable with varying training sample size. In addition, our experiments suggest that enforcing sparsity, during the construction of morphometric context, further improves the performance of the system.

1. Introduction

Histology sections provide a wealth of information about the tissue architecture that contains multiple cell types at different states of cell cycles. These sections are often stained with hematoxylin and eosin (H&E) stains, which label DNA (e.g., nuclei) and protein contents, respectively, in various shades of color. Abberations in the histology architecture often lead to disease progression. It is desirable to quantify indices associated with these abberations since they can be tested against the clinical outcome, e.g., survival, response to therapy. Even though there are inter- and intra- observer variations [7], a trained pathologist always uses rich content (e.g., various cell types, cellular organization, cell state and health), in context, to characterize tumor architecture.

In this paper, we propose two tissue classification methods based on representations of morphometric context, which are constructed from nuclear morphometric statistics of various locations and scales based on spatial pyramid matching (SPM) [18] and linear spatial pyramid matching (Linear SPM) [28]. Due to the effectiveness of our representations, our methods achieve excellent performance even with small number of training samples across different segmentation strategies and independent datasets of tumors. The performance is further complemented by the fact that one of the methods has a superior result with linear classifiers. These characteristics dramatically improve the (i) effectiveness of our techniques when applied to a large cohort, and (ii) extensibility to other cell-based assays.

Organization of this paper is as follows: Section 2 reviews related works. Sections 3 and 4 describes the details of our proposed mehods and experimental validation. Lastly, section 5 concludes the paper.

2. Related Work

For the analysis of the H&E stained sections, several excellent reviews can be found in [13, 8]. Fundamentally, the trend has been based either on nuclear segmentation and corresponding morphometric representaion, or patch-based representation of the histology sections that aids in clinical association. For example, a recent study indicates that detailed segmentation and multivariate representation of nuclear features from H&E stained sections can predict DCIS recurrence [1] in patients with more than one nuclear grade.

The major challenge for tissue classification is the large amounts of technical and biological variations in the data, which typically results in techniques that are tumor type specific. To overcome this problem, recent studies have focused on either fine tuning human engineered features [2, 16, 17], or applying automatic feature learning [19, 14], for robust representation.

In the context of image categorization research, the traditional bag of features (BoF) model has been widely studied and improved through different variations, e.g., modeling of co-occurrence of descriptors based on generative methods [4, 3, 20, 24], improving dictionary construction through discriminative learning [9, 22], modeling the spatial layout of local descriptors based on spatial pyramid matching kernel (SPM) [18]. It is clear that SPM has become the major component of the state-of-art systems [10] for its effectiveness in practice.

Pathologists often use “context” to assess the disease state. At the same time, SPM partially captures context because of its hierarchical nature. Motivated by the works of [18, 28], we encode morphometric signatures, at different locations and scales, within the SPM framework. The end results are highly robust and effective systems across multiple tumor types with limited number of training samples.

3. Approaches

The computational workflows for the proposed methods are shown in Figure 1, where the nuclear segmentation can be based on any of the existing methods for delineating nuclei from background. For some tissue images and their corresponding nuclear segmentation, let:

1. M be the total number of segmented nuclei;

2. N be the number of morphometric descriptors extracted from each segmented nucleus, e.g. nuclear size, and nuclear intensity;

3. X be the set of morphometric descriptors for all segmented nuclei, where X = [x₁, …, x_M]^⊤ ∈ ℝ^{M × N}.

Our proposed methods are described in detail as follows.

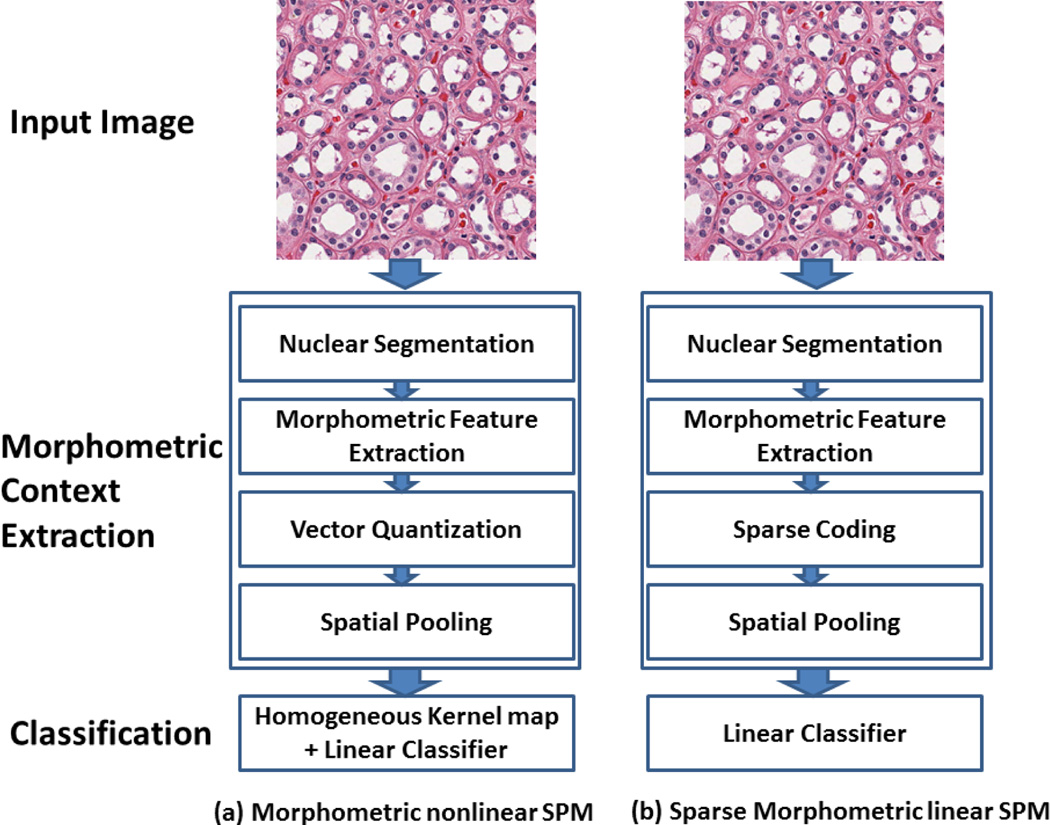
Figure 1.

Computational workflows: (a) Morphometric nonlinear kernel SPM; (b) Sparse Morphometric linear SPM. In both approaches, the nuclear segmentation could be based on any of the existing methods.

3.1. Morphometric nonlinear kernel SPM (MKSPM)

In this approach, we utilize the nuclear morphometric information within the SPM framework to construct the morphometric context at various locations and scales for tissue image representation and classification. It consists of the following steps:

1. Construct dictionary (D), where D = [d₁, …, d_K]^⊤ are the K nuclear morphometric types to be learned by the following optimization:

   $$\underset{\mathbf{D},\mathbf{Z}}{\text{min}}\sum _{m=1}^M\parallel {\mathbf{x}}_m-{\mathbf{z}}_m\mathbf{D}{\parallel }^2\text{subject to}card({\mathbf{z}}_m)=1,|{\mathbf{z}}_m|=1,{\mathbf{z}}_m⪰0,\forall m$$ (1)

   where Z = [z₁, …, z_M]^⊤ indicates the assignment of the nuclear morphometric type, card(z_m) is a cardinality constraint enforcing only one nonzero element of z_m, z_m ⪰ 0 is a non-negative constraint on the elements of z_m, and |z_m| is the L1-norm of z_m. During training, Equation 1 is optimized with respect to both Z and D; In the coding phase, for a new set of X, the learned D is applied, and Equation 1 is optimized with respect to Z only.
2. Construct spatial histogram as the descriptor for the morphometric context for SPM [18]. This is done by repeatedly subdividing an image and computing the histograms of different nuclear morphometric types over the resulting subregions. As a result, the spatial histogram, H, is formed by concatenating the appropriately weighted histograms of all nuclear morphometric types at all resolutions. The SPM kernel is then implemented as a single histogram intersection as follows,

   $$\kappa (H_i,H_j)=\sum _{q=1}^Q\text{min}(H_i(q),H_j(q))$$ (2)

   where H_i and H_j are the spatial histograms for image I_i and I_j, respectively, and Q is the length of the spatial histogram. For more details about SPM, please refer to [18, 12].

3. Transfer a χ² support vector machine (SVM) into a linear SVM based on a homogeneous kernel map [26]. In practice, the intersection kernel and χ² kernel have been found to be the most suitable for histogram representations [28]. In this step, a homogenous kernel map is applied to approximate the χ² kernels, which enables the efficiency by adopting learning methods for linear kernels, e.g., linear SVM. For more details about the homogeneous kernel map, please refer to [26].

4. Construct multi-class linear SVM for classification. In our implementation, the classifier is trained using the LIBLINEAR [11] package.

3.2. Sparse Morphometric Linear SPM (SMLSPM)

Inspired by the work in [28], which indicates that the sparse coding of the SIFT features may serve as a better local descriptor in general image processing tasks, we propose to utilize the sparse coding of the nuclear morphometric information within a linear SPM framework to construct the morphometric context at various locations and scales for tissue image representation and classification. It consists of the following steps:

1. Construct dictionary (D), where D = [d₁, …, d_K]^⊤ are the K nuclear morphmetric types to be learned by the following sparse coding optimization:

   $$\underset{\mathbf{D},\mathbf{Z}}{\text{min}}\sum _{m=1}^M\parallel {\mathbf{x}}_m-{\mathbf{z}}_m\mathbf{D}{\parallel }^2+\lambda |{\mathbf{z}}_m|\text{subject to}\parallel {\mathbf{d}}_k\parallel \le 1,\forall k$$ (3)

   where ∥d_k∥ is a unit L2-norm constraint for avoiding trivial solutions, and |z_m| is the L1-norm enforcing the sparsity of z_m. During training, Equation 3 is optimized with respect to both Z and D; In the coding phase, the learned D will be applied to a new set of X, with Equation 3 optimized with respect to Z only.
2. Construct spatial pyramid representation as the descriptor of morphometric context for the linear SPM [28]. Let Z be the sparse codes calculated through Equation 3 for a descriptor set X. Based on pre-learned and fixed dictionary D, the image descriptor is computed based on a pre-determined pooling function as follows,

   $$\mathbf{f}=\mathbb{P}(\mathbf{Z})$$ (4)

   In our implementation, ℙ is selected to be the max pooling function on the absolute sparse codes

   $$f_j=\text{max}\{|z_{1j}|,|z_{2j}|,\dots ,|z_{Mj}|\}$$ (5)

   where f_j is the j-th element of f, z_ij is the matrix element at i-th row and j-th column of Z, and M is the number of nuclei in the region. The choice of max pooling procedure is justified by biophysical evidence in the visual cortex [25], algorithms in image categorization [28], and our experimental comparison with other common pooling strategies (see Table 7). Similar to the construction of SPM, the pooled features from various locations and scales are then concatenated to form a spatial pyramid representation of the image, and a linear SPM kernel is applied as follows,

   $$\kappa ({\mathbf{f}}_i,{\mathbf{f}}_j)={{\mathbf{f}}_i}^{\top }{\mathbf{f}}_j=\sum _{l=0}^2\sum _{s=1}^{2^l}\sum _{t=1}^{2^l}\langle {\mathbf{f}}_i^l(s,t),{\mathbf{f}}_j^l(s,t)\rangle$$ (6)

   where f_i and f_j are spatial pyramid representations for image I_i and I_j, respectively, 〈f_i, f_j〉 = f_i^⊤ f_j, and ${\mathbf{f}}_i^l(s,t)\text{and}{\mathbf{f}}_j^l(s,t)$ are the max pooling statistics of the sparse codes in the (s, t)-th segment of image I_i and I_j in the scale level l, respectively.

3. Construct multi-class linear SVM for classification. In our implementation, the classifier is trained using the LIBLINEAR [11] package.

Table 7.

Comparison of performance for SMLSPM using different pooling strategies on the GBM and KIRC datasets. For GBM, the number of training images per category was fixed to be 160, and the dictionary size was fixed to be 1024; for KIRC, the number of training images per category was fixed to be 280, and the dictionary size was fixed to be 512.

	Sqrt	Abs	Max
GBM	92.85 ± 0.94	90.90 ± 1.11	92.91 ± 0.84
KIRC	97.60 ± 0.49	97.49 ± 0.38	98.50 ± 0.42

4. Experiments And Results

We have evaluated five classification methods on two distinct datasets, curated from (i) Glioblastoma Multiforme (GBM) and (ii) Kidney Renal Clear Cell Carcinoma (KIRC) from The Cancer Genome Atlas (TCGA), which are publicly available from the NIH (National Institute of Health) repository. The five methods are:

1. SMLSPM: the linear SPM that uses linear kernel on spatial-pyramid pooling of morphometric sparse codes;

2. MKSPM: the nonlinear kernel SPM that uses spatial-pyramid histograms of morphometric features and χ² kernels;

3. ScSPM [28]: the linear SPM that uses linear kernel on spatial-pyramid pooling of SIFT sparse codes;

4. KSPM [18]: the nonlinear kernel SPM that uses spatial-pyramid histograms of SIFT features and χ² kernels;

5. CTSPM: the nonlinear kernel SPM that uses spatial-pyramid histograms of color and texture features and χ² kernels;

In the implementations of SMLSPM and MKSPM, morphometric features were extracted and normalized independently with zero mean and unit variance based on three different segmentation strategies:

1. MRGC [6]: A multi-reference graph cut approach for nuclear segmentation in histology tissue sections;

2. SRCD [5]: A single-reference color decomposition approach for nuclear segmentation in histology tissue sections;

3. OTGR: A simple Otsu thresholding [23] approach for nuclear segmentation in histology tissue sections. In our implementation, nuclear mask was generated by applying Otsu thresholding on gray-scale image, and refined by geometric reasoning [27]. The same refinement was also used in the MRGC and SRCD approaches.

A comparison of the segmentation performance, for the above methods, is quoted from [6], and listed in Table 1, and the computed morphometric features are listed in Table 2.

Table 1.

Comparison of average segmentation performance among MRGC [6], SRCD [5], and OTGR.

Approach	Precision	Recall	F-Measure
MRGC	0.75	0.85	0.797
SRCD	0.63	0.75	0.685
OTGR	NA	NA	NA

Note: 1) the information above is quoted from [6]; 2) the OTGR performance is not listed due to the unavailability of the data used in [6], however, based on our experience with histological sections, simple thresholding methods typically generate less favorable results than sophisticated ones.

Table 2.

Morphometric features used in SMLSPM and MKSPM, where the curvature values were computed with σ = 2.0, and the nuclear background is defined to be outside the nuclear region, but inside the bounding box of nuclear boundary.

Feature	Description
Nuclear Size	#pixels of a segmented nucleus
Nuclear Voronoi Size	#pixels of the voronoi region, where the segmented nucleus resides
Aspect Ratio	Aspect ratio of the segmented nucleus
Major Axis	Length of Major axis of the segmented nucleus
Minor Axis	Length of Minor axis of the segmented nucleus
Rotation	Angle between major axis and×axis of the segmented nucleus
Bending Energy	Mean squared curvature values along nuclear contour
STD Curvature	Standard deviation of absolute curvature values along nuclear contour
Abs Max Curvature	Maximum absolute curvature values along nuclear contour
Mean Nuclear Intensity	Mean intensity in nuclear region measured in gray scale
STD Nuclear Intensity	Standard deviation of intensity in nuclear region measured in gray scale
Mean Background Intensity	Mean intensity of nuclear background measured in gray scale
STD Background Intensity	Standard deviation of intensity of nuclear background measured in gray scale
Mean Nuclear Gradient	Mean gradient within nuclear region measured in gray scale
STD Nuclear Gradient	Standard deviation of gradient within nuclear region measured in gray scale

In the implementation of ScSPM and KSPM, the dense SIFT features were extracted on 16 × 16 patches sampled from each image on a grid with stepsize 8 pixels. In the implementation of CTSPM, color features were extracted in the RGB color space; texture features were extracted via steerable filters [29] with 4 directions and 5 scales (σ ∈ {1, 2, 3, 4, 5}) on the grayscale image; and the feature vector was a concatenation of texture and mean color on 20 × 20 patches.

For both SMLSPM and ScSPM, we fixed the sparse constraint parameter γ to be 0.15, empirically, to achieve the best performance. For MKSPM, KSPM and CTSPM, we used standard K-means clustering for the construction of dictionaries. Additionally, for all five methods, we fixed the level of pyramid to be 3, and used linear SVM for classification. All experimental processes were repeated 10 times with randomly selected training and testing images. The final results were reported as the mean and standard deviation of the classification rates.

4.1. GBM Dataset

The GBM dataset contains 3 classes: Tumor, Necrosis, and Transition to Necrosis, which were curated from whole slide images (WSI) scanned with a 20X objective (0.502 micron/pixel). Examples can be found in Figure 2. The number of images per category are 628, 428 and 324, respectively. Most images are 1000 × 1000 pixels. In this experiment, we trained on 40, 80 and 160 images per category and tested on the rest, with three different dictionary sizes: 256, 512 and 1024. Detailed comparisons are shown in Table 3. For SMLSPM and MKSPM, we also evaluated the performance based on three different segmentation strategies: MRGC, SRCD and OTGR. Detailed comparisons are shown in Table 4.

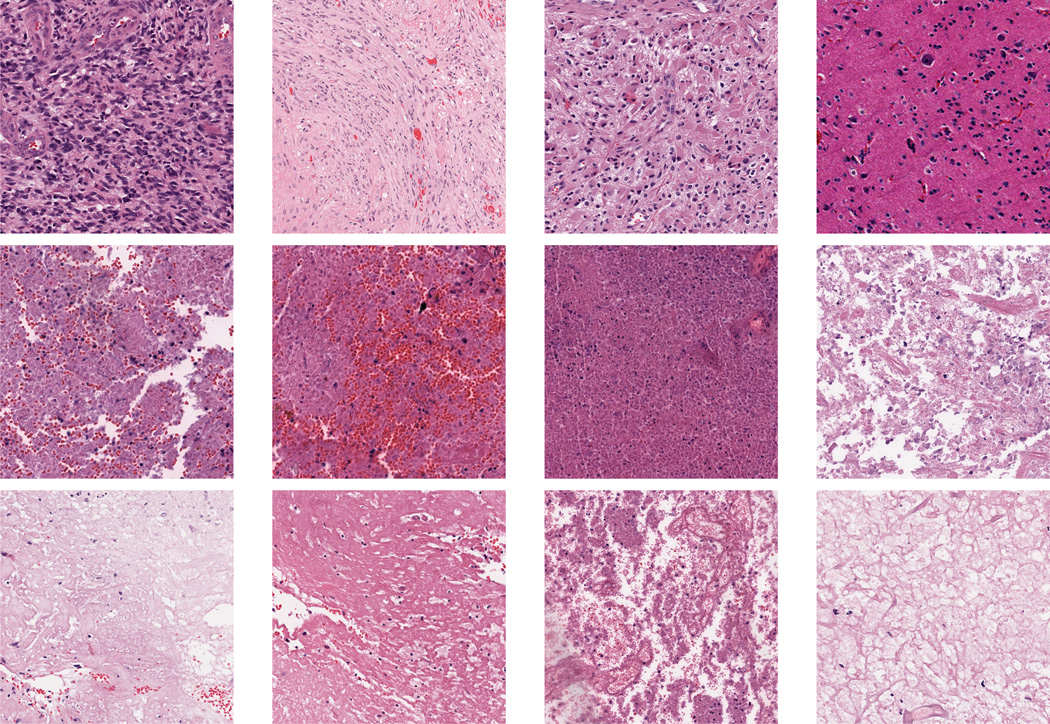
Figure 2.

GBM Examples. First row: Tumor; Second row: Transition to necrosis; Third row: Necrosis.

Table 3.

Performance of different methods on the GBM dataset, where SMLSPM and MKSPM were evaluated based on the segmentation method: MRGC [6].

	Method	DictionarySize=256	DictionarySize=512	DictionarySize=1024
160 training	SMLSPM	92.35 ± 0.83	92.57 ± 0.91	92.91 ± 0.84
	MKSPM	91.85 ± 0.98	91.95 ± 0.83	91.76 ± 0.97
	ScSPM [28]	79.58 ± 0.61	81.29 ± 0.86	82.36 ± 1.10
	KSPM [18]	85.00 ± 0.79	86.47 ± 0.55	86.81 ± 0.45
	CTSPM	78.61 ± 1.33	78.71 ± 1.18	78.69 ± 0.81
80 training	SMLSPM	90.82 ± 1.28	90.29 ± 0.68	91.08 ± 0.69
	MKSPM	89.83 ± 1.15	89.78 ± 1.09	89.44 ± 1.20
	ScSPM [28]	77.65 ± 1.43	78.31 ± 1.13	81.00 ± 0.98
	KSPM [18]	83.81 ± 1.22	84.32 ± 0.67	84.49 ± 0.34
	CTSPM	75.93 ± 1.18	76.06 ± 1.52	76.19 ± 1.33
40 training	SMLSPM	88.05 ± 1.38	87.88 ± 1.04	88.54 ± 1.42
	MKSPM	87.38 ± 1.38	87.06 ± 1.52	86.37 ± 1.73
	ScSPM [28]	73.60 ± 1.68	75.58 ± 1.29	76.24 ± 3.05
	KSPM [18]	80.54 ± 1.21	80.56 ± 1.24	80.46 ± 0.56
	CTSPM	73.10 ± 1.51	72.90 ± 1.09	72.65 ± 1.41

Table 4.

Performance of SMLSPM and MKSPM on the GBM dataset based on three different segmentation approaches, where the number of training images per category was fixed to be 160, and the dictionary sizes for SMLSPM and MKSPM were fixed to be 1024 and 512, respectively, to achieve optimal performance.

	MRGC	SRCD	OTGR
SMLSPM	92.91 ± 0.84	93.56 ± 0.91	91.03 ± 1.15
MKSPM	91.95 ± 0.83	93.33 ± 0.90	90.94 ± 0.87

4.2. KIRC Dataset

The KIRC dataset contains 3 classes: Tumor, Normal, and Stromal, which were curated from whole slide images (WSI) scanned with a 40X objective (0.252 micron/pixel). Examples can be found in Figure 3. The number of images per category are 568, 796 and 784, respectively. Most images are 1000 × 1000 pixels. In this experiment, we trained on 70, 140 and 280 images per category and tested on the rest, with three different dictionary sizes: 256, 512 and 1024. Detailed comparisons are shown in Table 5. For SMLSPM and MKSPM, we also evaluated the performance based on three different segmentation strategies: MRGC, SRCD and OTGR. Detailed comparisons are shown in Table 6

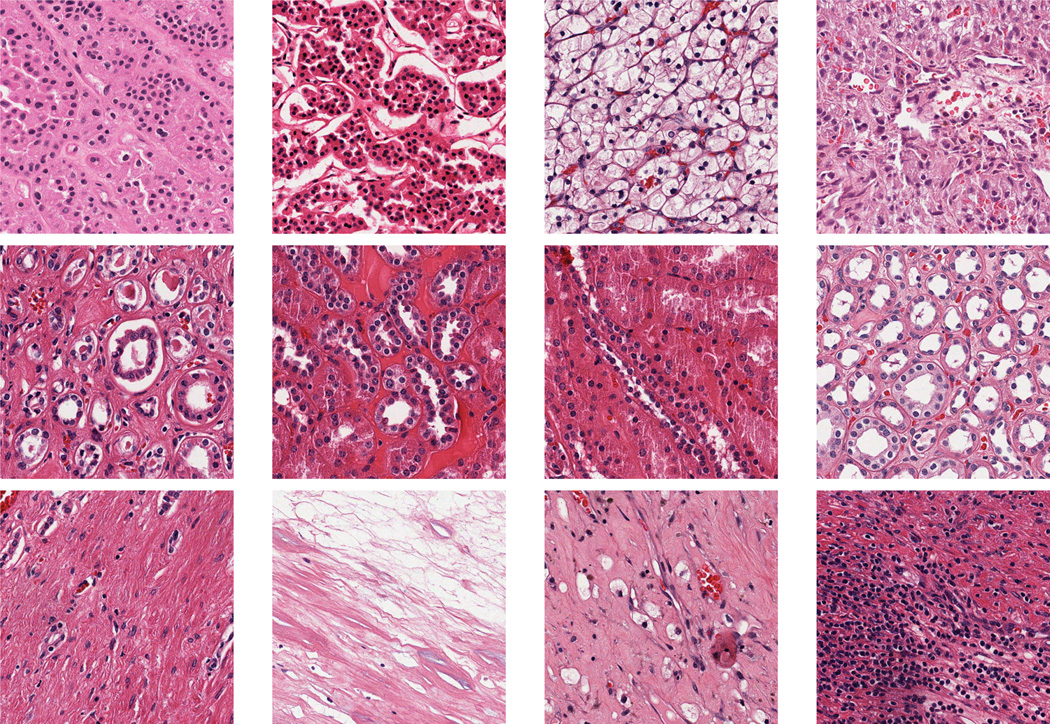
Figure 3.

KIRC Examples. First row: Tumor; Second row: Normal; Third row: Stromal.

Table 5.

Performance of different methods on the KIRC dataset, where SMLSPM and MKSPM were evaluated based on the segmentation mehtod: MRGC [6].

	Method	DictionarySize=256	DictionarySize=512	DictionarySize=1024
280 training	SMLSPM	98.15 ± 0.46	98.50 ± 0.42	98.21 ± 0.44
	MKSPM	97.37 ± 0.49	97.34 ± 0.48	97.22 ± 0.50
	ScSPM [28]	94.52 ± 0.44	96.37 ± 0.45	96.81 ± 0.50
	KSPM [18]	93.55 ± 0.31	93.76 ± 0.27	93.90 ± 0.19
	CTSPM	87.45 ± 0.59	87.95 ± 0.49	88.53 ± 0.49
140 training	SMLSPM	97.40 ± 0.50	97.98 ± 0.35	97.35 ± 0.48
	MKSPM	96.56 ± 0.53	96.54 ± 0.50	96.41 ± 0.56
	ScSPM [28]	93.46 ± 0.55	95.68 ± 0.36	96.76 ± 0.63
	KSPM [18]	92.50 ± 1.12	93.06 ± 0.82	93.26 ± 0.68
	CTSPM	86.55 ± 0.99	86.40 ± 0.54	86.49 ± 0.58
70 training	SMLSPM	96.20 ± 0.85	96.37 ± 0.85	96.19 ± 0.62
	MKSPM	95.62 ± 0.62	95.47 ± 0.71	95.27 ± 0.72
	ScSPM [28]	91.93 ± 1.00	93.67 ± 0.72	94.86 ± 0.86
	KSPM [18]	90.78 ± 0.98	91.34 ± 1.13	91.59 ± 0.97
	CTSPM	84.76 ± 1.32	84.29 ± 1.53	83.71 ± 1.42

Table 6.

Performance of SMLSPM and MKSPM on the KIRC dataset based on three different segmentation approaches, where the number of training images per category was fixed to be 280, and the dictionary sizes for both SMLSPM and MKSPM were fixed to be 512, to achieve the optimal performance.

	MRGC	SRCD	OTGR
SMLSPM	98.50 ± 0.42	98.30 ± 0.34	97.66 ± 0.49
MKSPM	97.34 ± 0.48	97.66 ± 0.45	95.90 ± 0.54

The experiments, conducted on two distinct datasets, demonstrate the following merits of our approach,

1. Extensibility to different tumor types. Tables 3 and 5 indicate that, with the exception of (KIRC; 140 training; Dictionary size 1024), our methods consistently outperform ScSPM, KSPM and CTSPM with different combinations of experimental factors (e.g., training sample size, dictionary size). However, KSPM and ScSPM appear to be tumor-type dependent, as KSPM outperforms ScSPM on GBM while ScSPM outperforms KSPM on KIRC. Since GBM and KIRC are two vastly different tumor types with significantly different signatures, we suggest that the consistency in performance assures extensibility to different tumor types.

2. Robustness in the presence of large amounts of technical and biological variations. With respect to the GBM dataset, shown in Table 3, the performance of our methods, based on 40 training samples per category, is better than the performance of ScSPM, KSPM and CTSPM based on 160 training samples per category. With respect to the KIRC dataset, shown in Table 5, the performance of our methods, based on 70 training samples per category, is comparable to the performance of ScSPM, KSPM and CTSPM based on 280 training samples per category. Given the fact that TCGA datasets contain large amount of technical and biological variations [17, 19], these results clearly indicate the robustness of our morphometric context representation, which dramatically improved the reliability of our approaches.

3. Invariance to different segmentation algorithms. Tables 4 and 6 indicate that the performance of our approaches are almost invariant to different segmentation algorithms, given the fact that the segmentation performance itself varies a lot, as shown in Table 1. More importantly, even with the simplest segmentation strategy OTGR, SMLSPM outperforms the methods in [28, 18] on both datasets, and MRSPM outperforms the methods in [28, 18] on the GBM dataset, while generating comparable results on the KIRC dataset. Given the fact that, in a lot of studies, both nuclear segmentation and tissue classification are necessary components, the use of pre-computed morphometric features dramatically improve the efficiency by avoiding extra feature extraction steps. For example, in our implementation, SIFT costs 1.5 sec/block ( a block is a 1000 × 1000 image decomposed from a whole slide tissue section). For the whole GBM dataset (~600,000 blocks), by avoiding SIFT operation, it saves ~10 days for processing.

4. Scalability of training and high speed testing for SMLSPM. Our experiments show that the morphometric context representation in SMLSPM works well with linear SVMs, which dramatically improves the scalability of training and the speed of testing. This is very important for the analyzing large cohort of whole slide images.

To study the impact of pooling strategies on the SMLSPM method, we also provide an experimental comparison among max pooling and two other common pooling methods, which are defined as follows,

$$\mathit{\text{Sqrt}}:f_j=\sqrt{\frac{1}{M}\sum _{i=1}^M{z}_{ij}^2}\mathit{\text{Abs}}:f_j=\frac{1}{M}\sum _{i=1}^M|z_{ij}|$$ (7)

where the meaning of the notations are the same as in Equation 5. As shown in Table 7, the max pooling strategy outperforms the other two, which is probably due to its robustness to local translations.

The experiments above also indicate a slightly improved performance of SMLSPM over MKSPM; this is probably due to the following factors: i) sparse coding has much less quantization errors than vector quantization; ii) the statistics derived by max pooling are more robust to local translations compared with the average pooling in the histogram representation.

5. Conclusion and Future Work

In this paper, we proposed two spatial pyramid matching approaches based on morphometric features and morphometric sparse code, respectively, for tissue image classification. By modeling the context of the morphometric information, these methods outperform traditional ones which were typically based on pixel- or patch-level features. The most encouraging results of this paper are that, our methods are highly i) extensible to different tumor types; ii) robust in the presence of large amounts of technical and biological variations; iii) invariant to different segmentation algorithms; and iv) scalable to extremely large training and testing sample sizes. Due to i) the effectiveness of our morphometric context representations; and ii) the important role of cellular context for the study of different cell assays, proposed methods are suggested to be extendable to image classification tasks for different cell assays. Future work will be focused on accelerating the sparse coding through the sparse auto encoder [15], utilizing supervised dictionary learning [21] for possible improvement, and further validating our methods on other tissue types and other cell assays.