Haplotype Inference in Random Population Samples

Abstract

Contemporary genotyping and sequencing methods do not provide information on linkage phase in diploid organisms. The application of statistical methods to infer and reconstruct linkage phase in samples of diploid sequences is a potentially time- and labor-saving method. The Stephens-Smith-Donnelly (SSD) algorithm is one such method, which incorporates concepts from population genetics theory in a Markov chain–Monte Carlo technique. We applied a modified SSD method, as well as the expectation-maximization and partition-ligation algorithms, to sequence data from eight loci spanning >1 Mb on the human X chromosome. We demonstrate that the accuracy of the modified SSD method is better than that of the other algorithms and is superior in terms of the number of sites that may be processed. Also, we find phase reconstructions by the modified SSD method to be highly accurate over regions with high linkage disequilibrium (LD). If only polymorphisms with a minor allele frequency >0.2 are analyzed and scored according to the fraction of neighbor relations correctly called, reconstructions are 95.2% accurate over entire 100-kb stretches and are 98.6% accurate within blocks of high LD.

Introduction

Haplotypes are closely linked alleles—for our purposes, SNPs—inherited as a unit. Linkage phase is the relationship between different nucleotides at heterozygous sites in diploid sequences; it determines the two haplotypes from the set possible from various permutations of the heterozygous sites. Phase information can be critical to the mapping of a disease gene, by allowing a more precise localization of it within a target area initially found significant by linkage analysis. Thus far, it has been successfully employed for a plethora of monogenic disorders, including cystic fibrosis, Huntington disease, Friedreich ataxia, and others (Lazzeroni 2001). Its application has also been extended to complex disease genetics; haplotypes have proved valuable in locating susceptibility genes for Hirschsprung disease (Puffenberger et al. 1994) and Crohn disease (Hugot et al. 2001; Rioux et al. 2001). Recently, linkage phase information has gained greater utility in the mapping of complex diseases by comprehensive whole-genome association studies (Risch and Merikangas 1996). To date, these studies have been technologically infeasible because of the number of genotyping assays required. As a means of overcoming this obstacle, haplotype information might be exploited to reduce the number of assays necessary to genotype a subject’s genome (Patil et al. 2001).

Contemporary sequencing and genotyping methods currently do not provide phase information in diploids, such as humans. Empirical methods for ascertaining phase involve conversion of diploid to haploid cells, by the creation of somatic cell hybrids (Papadopoulos et al. 1995). Recently, Patil et al. (2001) arrived at the haplotypes of the entire chromosome 21 by this manner. However, phase information from somatic cell hybrids are also subject to experimental error; Douglas et al. (2001) reported that, in testing 90 hybrids for the retention of a particular chromosome, 4 gave ambiguous results that could have arisen from insertions and deletions. Moreover, this extra step before genotyping is lengthy and expensive. Alternatively, phase is usually inferred from the genotypes of a subject’s parents. Notwithstanding the fact that some loci in any family (trio) may not be informative for determining haplotypes, this method has the drawback of potentially tripling the genotyping burden.

Ideally, one would like to obtain linkage phase information solely from genotypes of the subjects directly relevant to a study, via a quick and inexpensive methodology. The inference of haplotypes from samples of diploid individuals by application of statistical methods implemented in a computer program is a methodology that holds these attributes. To date, there are three main methods that are widely used. First, Clark’s method (Clark 1990) lists known haplotypes from unambiguous genotypes (i.e., genotypes with one or no heterozygous sites) and then attempts to resolve ambiguous genotypes into one of the known haplotypes and its complement, which is added to the list of knowns. Second, one may use the EM algorithm to maximize the likelihood of finding the sample of genotypes by calculating the frequency of possible haplotypes (Excoffier and Slatkin 1995; Fallin and Schork 2000). A derivative method, the partition-ligation (PL) algorithm, incorporates Bayesian Monte Carlo statistics into the basic expectation-maximization (EM) model to increase input capacity (Niu et al. 2002). Third, the method devised by Stephens et al. (2001a) is based in a Bayesian framework calculated via the Markov chain–Monte Carlo (MCMC) technique; unknown haplotypes are regarded as unobserved random quantities and are sampled from a conditional distribution that considers how randomly sampled individuals are related genealogically, as described by the neutral coalescent (Stephens and Donnelly 2000). In the study introducing the Stephens-Smith-Donnelly (SSD) method, Stephens et al. (2001a) demonstrated that their algorithm reduced mean error rates by >50% when applied to simulated sequences generated according to a neutral mutation-drift model. Further, the superiority of SSD over EM was reaffirmed on empirically derived phase data from population samples in Stephens and colleagues’ reply (Stephens et al. 2001b) to a letter to the editor by Zhang et al. (2001). It should be noted that the coalescent model upon which the SSD algorithm is based does not take recombination into consideration.

In the present study, we made several modifications to the SSD program, the two most important being to account for missing data and to recover a portion of phase calls indiscernible in the original implementation. We then applied this SSD-based computer program to empirically derived, phase-known sequences. The sequences comprise eight X-linked regions from a sampling of 40 male subjects (Cutler et al. 2001) and range from 87 to 327 kb in length, with 45–165 segregating sites per locus. We applied the modified SSD algorithm, as well as the EM and PL algorithms, to random pairings of the male sequences to simulate diploid data. Until now, the metric used to assess the accuracy of haplotype reconstruction on individuals, namely, the mean standard error (SE), has involved the whole haplotype—either all heterozygous sites are called correctly for the phase reconstruction of a given diploid sequence or the reconstruction is summarily considered wrong. Given the sheer length of the input sequences in our study, it was found that, although the heterozygous sites in a given diploid sequence were rarely called completely accurately, a large number were, in fact, correct. Hence, we scored the accuracy by the fraction of neighboring relations between heterozygous sites correctly called. By both this measure and the mean SE, the accuracy of the modified SSD method was found to be better than the other algorithms examined. Given the new metric, we were able to examine the neighboring relations that were being incorrectly called. We found that the majority straddled sites at which recombinations had occurred. These results have major implications for complex disease genetic studies.

Material and Methods

Data Analyzed

We acquired sequence data on eight X-linked genomic regions derived from 40 male subjects (Cutler et al. 2001): three loci from the p arm and five from the q arm, all regularly spaced (table 1). The 40 samples came from the National Institutes of Health Polymorphism Discovery Resource at the Coriell Institute for Medical Research (Collins et al. 1998). The Polymorphism Discovery Resource consists of anonymous DNA samples from individuals who, in aggregate, have equally represented ancestry from Africa, America, Asia, and Europe. The loci were sequenced with Affymetrix Resequencing arrays, and genotyping calls were made with ABACUS (Cutler et al. 2001) at a quality threshold of 30 (at this value, replicate experiments called all 841,236 paired genotypes identically). The sequences of these loci were 87–327 kb in length, with 45–165 segregating sites. The loci are listed in table 1.

Table 1.

Comparison of Switch Accuracy and Mean SE between the SSD-Based and PL Programs, for All Sites

			Switch Accuracy		Mean SE
Locus (Length)	Physical Location	Name (No.of SNPs Used)	SSD	PL	SSD	PL
Glycine receptor, α2 (89 kb)	Xp22.1-p21.2	GLRA2 (102)	.863	.835	.787	.892
Monoamine oxidase A (102 kb)	Xp11.4-p11.3	MAOA (97)	.904	.875	.614	.761
Potassium voltage-gated channel, Shal-related family, member 1 (122 kb)	Xp11.23	KCND1 (60)	.781	.727	.535	.719
α Thalassemia/mental retardation syndrome X-linked (RAD54 [S. cerevisiae] homolog) (151 kb)	Xq13	ATR (45)	.713	.683	.615	.718
α-Galactosidase (102 kb)	Xq21.3-q22	GLA (116)	.781	.838	.885	.790
Transient receptor potential channel 5 (327 kb)	Xq23	TRPC5 (165)	.872	.799	.578	.724
Bombesin-like receptor 3 (87 kb)	Xq25-27	BRS3 (66)	.860	.845	.720	.793
Methyl CpG binding protein 2 (106 kb)	Xq28	MECP2 (103)	.773	.813	.846	.637
Average			.832	.824	.704	.757

SSD Method

The SSD method begins by making a guess of the haplotypes of each individual. An individual is then randomly chosen and, with a probability derived from a neutral coalescent model, has his/her haplotypes reconstructed to resemble the others, on the assumption that the rest are correctly phased. Iterations of this process give an approximation of the posterior distribution of haplotypes, given the sample of genotypes.

Our program is based on algorithm 2 of Stephens et al. (2001a), with several modifications. First, whole haplotypes are not taken into account for the generation of various lists and vectors. Rather, an individual’s ambiguous sites are updated by considering in the other individuals only positions corresponding to those ambiguous sites. Second, the algorithm was modified to allow missing sites. Two other changes were made to the final haplotype reconstruction. First, uncertainty estimates of the phase calls are neither computed nor reported, because such values were not used for any subsequent analysis. Second, for a given individual, phase calls are made conditional on calls of neighboring heterozygous phase relations. A more complete description of our program can be found in appendix A.

Measures of Accuracy

For each genomic region, the sequences were randomly paired to create 20 genotypes in which phase information was ignored. It should be noted that such sampling makes the expected frequency of genotypes observed conform to Hardy-Weinberg expectations. These data were subjected to three methods: (1) our SSD-based computer program, which was run for 10,000 iterations, the first 5,000 of which were discarded as “burn-in” and the remainder of which were thinned by storing every 20th iteration; (2) an implementation of the PL algorithm, HTYPER (kindly provided by J. S. Liu), which was run at 20 rounds; and (3) an implementation of the EM algorithm, SNPEM2001 (kindly provided by D. Fallin), which was run with 15 restarts and 150 maximum iterations.

The program output was then compared with the original haploid sequences, and, for genotypes with more than one heterozygous site, the accuracy was scored in two ways: the error rate—that is, the proportion of individuals whose haplotypes are incorrectly inferred (Clark 1990; Stephens et al. 2001a)—and switch accuracies. The latter is applied to each individual reconstruction and is formally defined as (n-1-sw)/(n-1), where n denotes the number of heterozygous sites and sw is the number of switches between neighboring heterozygous sites needed in the computer-phased haplotype to recover the original haploid sequence (see fig. 4 for an example). For each X-linked region, 100 such simulations were run, with resultant accuracy scores averaged.

Figure 4.

Illustration of how the SSD-based program and LD block information can be used. Genotype i is one member of the sample of genotypes to be input into the SSD-based program. Of course, in a genotyping experiment, the haplotypes of which it is composed will not be known a priori. Nucleotide positions that, when paired, give segregating sites, are marked with colors for each haplotype. The SSD-based program yields phase reconstructions, the one corresponding to individual i labeled as i′. Boundaries between blocks of high LD indicate phase relationships that are less likely to be correct. In this example, we see that, indeed, misphasing occurred between segregating sites 8 and 9 (demarcated by an asterisk [*]), which happen to straddle the boundary between blocks 3 and 4. The switch accuracy for this reconstruction is 13/14. This example was culled from a simulation on the X-linked GLRA2 locus in 40 male subjects, performed with q>0.2. Single-letter representations of heterozygous sites are as follows: Y = C/T, S = G/C, and R = G/A.

Linkage Disequilibrium (LD) Blocks

LD is the association between alleles at different loci. Studies suggest that patterns of LD in the genome are highly structured, with blocks of sequences characterized by little recombination and low haplotype diversity (Daly et al. 2001; Jeffreys et al. 2001). In our study, two operational definitions of LD blocks were examined, to capture this concept of often co-inherited, linked alleles. The first type, |D′| blocks, are constructed such that all relative coefficients of disequilibrium, as measured by pairwise |D′| values (Lewontin 1988) within a block, are above a set threshold. The two-locus haplotype frequencies required for these calculations were estimated by a Weir-Cockerham EM algorithm (Weir and Cockerham 1989). The second definition involves delimiting regions of low haplotype diversity, as in the study by Daly et al. (2001). In brief, these blocks represent local minima of the quotient observed haplotypic heterozygosity over expected haplotypic heterozygosity.

To measure the performance of the SSD-based program on LD blocks, we used two procedures; both involved initially determining the block structure. In the first procedure, genotype sequences were phased, broken into blocks (however defined), and then scored by switch accuracies within blocks. The other procedure involved randomly permuting the order of sites before proceeding with phasing and other steps of the process as before. For comparison of different types of runs, the accuracies were treated as independent samples, arcsine transformed, and subjected to t tests (Sokal and Rohlf 1981).

Results

The performance of the SSD-based computer program on the eight X-linked genomic regions, compared with that of implementations of the PL and EM algorithms, is shown in tables 1 and 2. Table 2 was generated in the same way as table 1, except that only segregating sites with a minor allele frequency >0.2 were analyzed. Application of the EM algorithm was restricted, because the implementation used in this study could handle no more than 10 sites in a single locus. By both mean SE and switch accuracy, the SSD-based program was shown to be superior in correctly reconstructing phase (P<.001). In aggregate, the percent frequency at which the SSD-based method correctly reconstructed neighboring phase relations in samples of 20 individuals, for all sites, was 83.2%.

Table 2.

Comparison of Switch Accuracy and Mean SE among the SSD-Based, PL, and EM Methods for Common (q>0.2) Allelic Variants

	Switch Accuracy			Mean SE
Locus (Length, No. of SNPs Used)	SSD	PL	EM	SSD	PL	EM
GLRA2 (89 kb, 34)	.960	.919	…	.398	.578	…
MAOA (89 kb, 19)	.952	.917	…	.397	.452	…
KCND1 (118 kb, 7)	.983	.903	.841	.0504	.211	.325
ATR (97 kb, 6)	.998	.938	.958	.0142	.124	.0818
GLA (98 kb, 26)	.949	.901	…	.365	.389	…
TRPC5 (78 kb, 7)	.960	.952	.926	.0955	.144	.199
BRS3 (35 kb, 6)	.966	.872	.807	.0685	.253	.381
MECP2 (106 kb, 19)	.922	.877	…	.311	.465	…
Average (all loci)	.952	.908	…	.254	.368	…
Average (KCND1, ATR, TRPC5, and BRS3)	.973	.918	.884	.0550	.185	.254

Comparison of tables 1 and 2 reveals that samples of sequences with only common allelic variants are phased more accurately, regardless of method. As pointed out by Stephens et al. (2001a), lower-frequency variants are less easily estimated statistically; indeed, there is less contextual information about phase for singletons (i.e., variants that occur once in the sample) versus nonsingletons. The generally lower-accuracy values from scoring only the phase relations between singleton sites and flanking heterozygous sites corroborates this notion (table 3). In any case, on average, the SSD method correctly reconstructed phase 95.2% of the time, as measured by switch accuracy for sites with a minor allele frequency >0.2.

Table 3.

Accuracy of Haplotype Inference using the SSD-Based Method in Relation to SNP Frequencies

	Switch Accuracy (No. of SNPs Used)
Locus	All Sitesa	Singleton	q>.20 Sitesa
GLRA2	.863 (102)	.577 (28)	.960 (34)
MAOA	.904 (97)	.728 (26)	.952 (19)
KCND1	.781 (60)	.792 (33)	.983 (7)
ATR	.713 (45)	.677 (21)	.998 (6)
GLA	.781 (116)	.594 (54)	.949 (26)
TRPC5	.872 (165)	.866 (102)	.960 (7)
BRS3	.860 (66)	.699 (28)	.966 (6)
MECP2	.773 (103)	.603 (40)	.922 (19)
Average	.832	.692	.952

^aFrom table 1.

Because the coalescent model on which the SSD algorithm is based does not incorporate recombinations, we suspected that the algorithm was likely to be highly accurate within—but less so between—stretches in which few recombinations occurred (i.e., LD blocks). To test this hypothesis, we phased the sequences as before but scored within blocks, two definitions of which were tried as described in the “Material and Methods” section (table 4). Clearly, the definition involving |D′| yielded the higher-accuracy scores (P<.00001).

Table 4.

Accuracy of Haplotype Reconstruction in Relation to Blocks of LD

	Fraction Correct
		SNPs in LD Blocksb
Name	All SNPsa	|D′| > .8c	Low Haplotype Diversity
GLRA2	.863 (102)	.938 (4)	.915 (6)
MAOA	.904 (97)	.966 (6)	.924 (7)
KCND1	.781 (60)	.834 (5)	.813 (10)
ATR	.713 (45)	.766 (4)	.696 (4)
GLA	.781 (116)	.810 (5)	.786 (5)
TRPC5	.872 (165)	.968 (4)	.925 (8)
BRS3	.860 (66)	.942 (5)	.917 (5)
MECP2	.773 (103)	.813 (4)	.774 (9)
Average	.832	.902	.868

^aFrom table 1. Values in parentheses are the number of SNPs in the locus.

^bValues in parentheses are the average number of SNPs in blocks.

^cBlocks were defined as SNPs with interpair LD |D′| > .8.

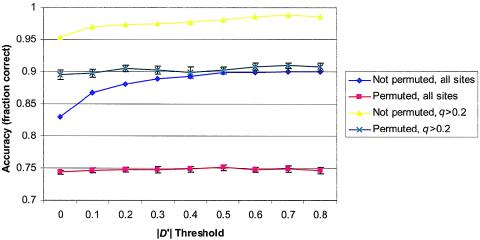
However, regardless of the block definition, accuracy scores were improved over those from phasing whole genotypes. To evaluate whether the improvement in accuracy was due to LD and not merely an artifact of block size or some other property, we performed further simulations. The boundaries of the |D′| blocks were found as in the original data. However, to eliminate the effects of LD, the order of the sequence sites was randomly permuted before phasing and scoring within blocks. Plots of accuracy scores from runs with and without permutations for various thresholds of |D′| are shown in figure 1. The lower switch accuracies for the permuted sequences imply that the improvement of scoring within blocks is due to properties of LD.

Figure 1.

Accuracy within |D′| blocks versus |D′| threshold. Accuracy averages of single runs over the eight X-linked loci were treated as independent samples. The means and standard error of the means of 100 such samples are plotted against the |D′| threshold.

To test the capacity of our SSD-based program to handle larger data sets, the eight X-linked loci of each individual were concatenated in their sequential order as found in the X chromosomes. When all sites were considered, resultant sequences were 754 segregating sites long and covered 1.09 Mb; for sites with a minor allele frequency >0.2, sequences were 124 segregating sites long and covered 709 kb. Accuracy scores were generated as before (table 5). Of note, HTYPER can accommodate only 256 sites.

Table 5.

Accuracy of Haplotype Reconstruction on Concatenated Loci

	Fraction Correct
SNPFrequency	All SNPsa	SNPs in LDBlocks (|D′| > .8 )b
All SNPs	.797 (754)	.891 (5)
q>.2	.882 (124)	.966 (3)

^aValues in parentheses are the number of SNPs in the sequence.

^bValues in parentheses are the average number of SNPs in blocks; blocks were defined as SNPs with interpair LD |D′| > .8.

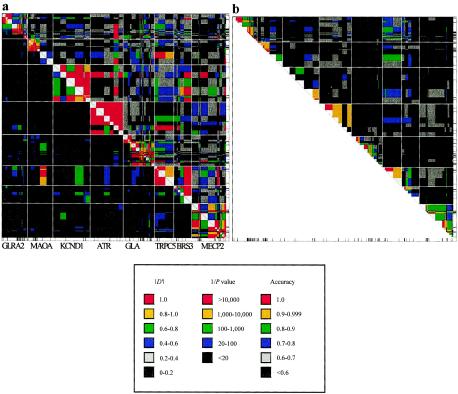
To examine visually the mistakes incurred by our SSD-based program in relation to LD, we constructed plots of LD and two-site accuracies (fig. 2). The regions depicted are the eight concatenated X-linked loci, for which only sites with frequency >0.2 are considered. Two-site accuracies are derived from the same types of phase reconstruction runs used to generate table 5. The plots show that LD for the various loci vary widely; however, there is virtually no LD between the different loci. Also, areas of high LD correlate with those of high accuracy.

Figure 2.

Patterns of LD (a) and pairwise accuracies (b) across eight concatenated X-linked loci. a, Plot of LD, constructed in a fashion similar to that of Jeffreys et al. (2001). |D′|, represented in the upper right of the plot, and inverse of the P value, on the lower left, were calculated from 40 haploid sequences in which the minor allele frequency of the sites was >0.20. The P value is from a Fisher’s exact test (Sokal and Rohlf 1981). Each region, colored according to the legend, is plotted as a rectangle centered on each SNP (represented below and to the right of the plots) and extends halfway to each adjacent marker. The region displayed represents the eight X-linked loci, concatenated in the order that they appear on the X chromosome, with white lines demarcating the interloci. b, Corresponding plot of pairwise accuracies, derived from application of the SSD-based method on 100 random pairings of the 40 concatenated X-linked sequences.

It should be emphasized how quickly our SSD-based program ran on standard 800-MHz personal computers. For the locus with the most segregating sites (i.e., TRPC5, which has 165 segregating sites), 10,000 iterations of the SSD-based method took no more than 10 s. Ten thousand iterations of the concatenated loci with 754 segregating sites took no more than 6 min.

Discussion

Comparisons of the SSD, PL, and EM algorithms on our simulated data created from empirically derived sequences show that the SSD method reconstructs phase most accurately. Clark’s method was not included in these comparisons, since, on average, 10% of simulated samples for the loci did not include an individual whose haplotypes were unambiguous, a requirement necessary to commence Clark’s inferential cascade. That SSD performs best—albeit only slightly better than PL, when all sites are considered—may be attributed to the fact that the neutral coalescent model, which the SSD algorithm incorporates, is a reasonable approximation of the random collection of human sequences used as test data. This finding is, in fact, consistent with Niu et al.’s (2002) results from application of the SSD, PL, EM, and Clark’s methods to coalescent-based, simulated data. Trends in how the various methods compared with each other were maintained regardless of the metric used to gauge accuracy of phase reconstructions.

In examinations of statistical methods of reconstructing haplotypes, several measures of accuracy have been employed thus far in the literature. Measures of how close estimated haplotype frequencies are to actual population frequencies have been applied in a number of studies (Excoffier and Slatkin 1995; Fallin and Schork 2000; Stephens et al. 2001a). Other metrics involve finding the frequency of incorrectly reconstructed haplotypes (Clark 1990; Stephens et al. 2001a). Both aforementioned measures give whole-haplotype assessments of accuracy.

Switch accuracies are measures only of neighboring phase relations. However, other metrics, such as the mean number of contiguous sites phased correctly, are for all intents and purposes equivalent, since both decrease monotonically as more neighboring phase relations are incorrectly called.

A weightier issue is whether phase relations beyond neighboring ones need to be taken into account in a valid metric. Such a consideration demands attention only if there exist heterozygous sites that have no phasing information with immediate neighbors but have some phasing information with more distal sites. In these cases, the former phase relations will be phased randomly, whereas the latter will be phased correctly more often. Figure 2 suggests that this occurrence is extremely unlikely.

Scoring by switch accuracy can give a finer picture of the performance of a phase reconstruction method. One can directly examine which phased relationships were incorrectly called, which, in our study, was done for the SSD method. However, application of switch accuracy yields qualitative results comparable to mean SE; that is, comparison of phase reconstruction methods in tables 1 and 2 shows that, if one method scored higher than another by switch accuracy for a particular locus, then it concomitantly incurred a lower mean SE, and vice versa.

The underlying principle of the SSD method is that, with a probability proportional to the neutral expectation, haplotypes are updated to be exactly the same as or similar to haplotypes already observed. In haplotyping long stretches of sequences, the pattern of one local region may prevent the SSD method from correctly predicting phase relationships in another, if a recombination event has occurred in between (fig. 3). The modification of the way in which final haplotypes are determined from periodic saves of the MCMC-generated haplotype distribution, as described in appendix A, reduces this problem, with switch accuracy scores increasing, on average, by 4% (data not shown).

Figure 3.

Illustration of the rationale behind breaking sequences into blocks to allow for more accurate phase reconstruction. Suppose a list of haplotypes is known from, say, homozygotes. In reconstruction of the haplotypes of the ambiguous individual shown, phasing the whole sequence with the original SSD program will give uncertain calls for the third and fourth positions. However, the phase relationship between the third and fourth positions is clear. By implementation of the method by which final phase relations are called as described in appendix A, the aforementioned phase relationship can be recovered. Incidentally, multiple recombination events presumably occurred between the second and third positions, and the corresponding phase relationship is likely to be impossible to ascertain by statistical methods.

Although the aforementioned modification allows recovery of relationships within blocks in which few recombinations occurred, as figure 3 also illustrates, some phase relationships across regions with many recombinations may be impossible to infer by statistical methods. After sufficient generations, even linked loci appear to be randomly associated when examined at the population level, because of meiotic crossing-over. Therefore, reconstruction of phase relations spanning multiple recombinations will prove as elusive as doing so over loci on different chromosomes. In any case, the implication is that accuracy will improve if phase relations across recombinations are eliminated. Operationally, this task can be accomplished by scoring within LD blocks. Indeed, scoring within |D′| blocks improved switch accuracy scores by 7% when all sites were considered (table 4). Further simulations in which sequence positions were randomly permuted suggested that this improvement is not an artifact of the small block sizes but is instead due to intrinsic properties of the LD blocks (fig. 1).

In running various types of simulations, we attempted breaking sequences into LD blocks first and then phasing them separately (data not shown). When all sites were considered, this method yielded switch accuracy scores 1.5% higher than did phasing unbroken sequences and then scoring within blocks. When only common alleles were considered, switch accuracy for the latter method was already remarkably high (98.6%; see fig. 1), and the improvement in phasing only blocks was 0.9%. These findings suggest that, for common alleles, the length of sequences to be phased should have little influence on accuracy within |D′| blocks. This notion is further buttressed by the accuracy scores for the concatenated loci (table 5). For the handling of vast data sets, computer memory and iteration number sufficiency may be weightier considerations. It should be noted that increasing iteration, burn-in, and thinning parameters by an order of magnitude for runs on the concatenated loci did not significantly change accuracy scores (data not shown).

That SSD reconstructs accurately only in regions of high LD can also be appreciated visually on plots of LD and accuracy for the eight X-linked loci (fig. 2). Comparison of the plots reveals that areas of high LD and high accuracy are correlated. It should be noted that the correlation between high LD and high accuracy are maintained even in regions of comparable size—for example, the subplots for loci ATR (97 kb) and GLA (98 kb). This observation is consistent with the notion that SSD reconstructs phase more accurately, not simply when heterozygous sites are close together but rather when LD exists between them.

Although in the present study the accuracy scores resulted from simulations on empirically derived, phase-known sequences, differences between X-linked and autosomal regions must be kept in mind when generalizing the results of this study to the rest of the genome. X-linked sequences are known to be less variable (International SNP Map Working Group 2001) and theoretically have lower recombination rates, since the vast majority of the X chromosome does not undergo homologous recombination in males. Nevertheless, LD patterns between X-linked and autosomal regions are not vastly different (data not shown).

The results of the present study demonstrate that phase reconstruction by a modified SSD method within regions of high |D′| for common alleles is remarkably accurate. Thus, in laying the groundwork for conducting future gene-mapping studies, it can be argued that simply genotyping individuals and subjecting sequences to the SSD method is the most efficient manner by which to arrive at haplotypes. Once sequences are phased, boundaries between blocks of high LD can be used to indicate phase relations that are less likely to be correct (fig. 4). Finally, our inability to accurately phase interblock regions may not be particularly important for disease-marker association studies, since association may be sought to blocks rather than to markers.

Appendix A

The algorithm implemented in our modified SSD program is as follows. Let H=(H₁,…,H_n) denote the (unknown) haplotype pairs. Given the diploid sequences of n individuals, make a random guess of H.

• 1. Randomly pick an individual i and remove his or her two current haplotypes from H (so that the list now contains the haplotypes in H_−i). Let Y constitute the positions where the diploid sequence in individual i is heterozygous or unknown, and let h_j(Y) denote the nucleotides in haplotype j for the positions in Y. From H_−i, make a list of the partial haplotypes h(Y)=[h₁(Y),…,h_m(Y)], with corresponding counts r=(r₁,…,r_m) of the number of times that each partial haplotype appears.
• 2. Calculate a vector p=(p₁,…,p_m) as follows: Let S constitute the positions where the diploid sequence in individual i is heterozygous. For j=1,…,m, check whether the diploid sequence in individual i could be made up of h(S) plus a complementary haplotype h′(S). If not, then set p_j=0; if so, then search for h′(S) in the list h(Y). With all h_k(S) in the list h(Y) in which h^′(S)=h_k(S), set p_j=Σ_k[r_jr_k+θ/M(r_j+r_k)], where 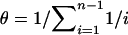, n is the number of alleles in the sample, M=2^d, and d is the number of segregating sites. If no h_k(S) can be found, set p_j=r_j(θ/M).
• 3. With probability 2^k(θ/M)²/[Σ_jp_j+2^k(θ/M)²], reconstruct all heterozygous and unknown sites randomly. (Phase at each heterozygous site is assigned with probability one-half. Missing data are assigned according to multinomial sampling probabilities proportional to site-specific frequencies.) Otherwise, with probability p_j/Σ_j^′p_j^′, h_j(Y) is assigned to individual i. This step automatically determines the complement h′(S) but not h′(Y), which includes unknown sites. If there exist h_k(S) in list h(Y) such that h^′(S)=h_k(S), then h′(Y) is set to h_k(Y) with probability r_k/Σ_k^′r_k^′. If no such h_k(S) exist, then unknown sites are reconstructed randomly for both h_j and h′.
• 4. Add the reconstructed haplotypes back to H_−i.

The output in the original implementation of the SSD method included estimates of uncertainty for each phase call. Since our study did not utilize such values, code for their calculation was excluded from the program.

For the reconstruction of final haplotypes of individual i, sites with missing data were filled in with the most common nucleotide found at corresponding sites among the haplotypes stored periodically during the iterative process. The same was done to make the call on the first heterozygous position. For the second heterozygous position, the most common nucleotide was chosen from those haplotypes with the specific nucleotide of the first call. Likewise, for all subsequent positions, the most common nucleotide was chosen conditional on the specific call made at the immediately prior heterozygous site.