The Fingerprint of Phantom Mutations in Mitochondrial DNA Data

Abstract

Phantom mutations are systematic artifacts generated in the course of the sequencing process itself. In sequenced mitochondrial DNA (mtDNA), they generate a hotspot pattern quite different from that of natural mutations in the cell. To identify the telltale patterns of a particular phantom mutation process, one first filters out the well-established frequent mutations (inferred from various data sets with additional coding region information). The filtered data are represented by their full (quasi-)median network, to visualize the character conflicts, which can be expressed numerically by the cube spectrum. Permutation tests are used to evaluate the overall phylogenetic content of the filtered data. Comparison with benchmark data sets helps to sort out suspicious data and to infer features and potential causes for the phantom mutation process. This approach, performed either in the lab or at the desk of a reviewer, will help to avoid errors that otherwise would go into print and could lead to erroneous evolutionary interpretations. The filtering procedure is illustrated with two mtDNA data sets that were severely affected by phantom mutations.

Introduction

The assessment of intraspecific mtDNA variation (Avise 2000) through sequencing of the hypervariable segments (HVS-I and HVS-II) of the mtDNA control region has become a routine matter in the past decade (and large sets of sequences of the whole molecule promise to become routine in this decade). This, however, does not automatically imply that the results of the sequencing efforts in print or in the databank are free of serious artifacts (see the articles by Bandelt et al. [2001] and Röhl et al. [2001], for an investigation of several pertinent cases). One kind of error is the occurrence of phantom mutations—that is, mutations that are generated in the sequencing process itself; systematic misreading of sequencing outputs may, of course, generate seeming phantom mutations. No matter what the reason is for such artifacts, one would expect that the pattern of phantom mutations differs significantly from that of natural mutations. It is known that the vast majority of transitions in human HVS-I sequences occur at a minority of sites (Hasegawa et al. 1993), with other types of mutations (outside C runs) being considerably less frequent anyway. In a recent count (V. Macaulay, unpublished data), 90% of transitions, within the scoring frame 16051–16365, occurred at only 27% of sites (458 reconstructed transitions in a total of 508 occurred at 84 of the 315 sites) and, hence, a randomly generated artificial transition has a 7.5-fold higher chance of showing up among the infrequent mutations, compared with a real transition. Moreover, if an artificial mutation hits the same site more than once in the sample, then incompatibilities with several other sites are to be expected. We can thus increase the focus on such events by filtering out the frequent mutations. Although the incompatibilities in the filtered data could be demonstrated with the compatibility matrix (Jakobsen and Easteal 1996), the visualization through the (quasi-)median network is preferable in this context, since it provides a more detailed view of the structure of character incompatibilities and at the same time represents the (filtered) data.

Methods

Weighty HVS-I Filter

Since reliable trees for evaluating site mutational variability cannot be reconstructed from HVS-I data alone (Bandelt et al. 2000), we have employed previously published as well as new data, from Eurasia and Africa, that combine HVS-I with RFLP information (amounting to 873 combined sequences), for which trees have then been reconstructed at the haplogroup level (giving more weight to mutations in the coding region and using the parsimony criterion; V. Macaulay, unpublished data). We distinguish between transitions, transversions, and indels affecting a particular site (but we do not, e.g., discriminate between different transitions at the same site); a complete table of inferred mutational hits is available from the authors' Web site. The list of all sites within nucleotide positions (nps) 16051–16365 for which transitions are estimated to occur at a rate at least as high as the average transitional rate, as inferred from the estimated trees for our data is as follows (numbers represent nps minus 16000): 051, 078, 086, 092, 093, 111, 114, 124, 126, 129, 140, 145, 147, 148, 150, 163, 172, 173, 176, 186, 187, 189, 192, 193, 209, 212, 213, 214, 216, 217, 223, 227, 231, 232, 234, 235, 239, 240, 241, 242, 245, 249, 255, 256, 257, 258, 260, 261, 263, 264, 265, 266, 270, 274, 278, 284, 287, 288, 290, 291, 292, 293, 294, 295, 296, 298, 300, 301, 304, 309, 311, 316, 319, 320, 325, 327, 335, 352, 354, 355, 356, 357, 360, and 362. These we dub the “speedy transitions,” and the remaining ones are then called the “weighty transitions.” Transversions and indels are regarded as weighty mutations, since their rates typically do not exceed the average transitional rate, the only exceptions being the length polymorphisms and flanking transversions to C in and around C runs, which we disregard altogether, since they are extremely frequent. Otherwise, all transversions and indels were unique in our data set of 873 sequences, except for 16111C→A, 16188C→A, and 16265A→C (which each occurred twice), as well as 16166del (which occurred three times). Heteroplasmy and ambiguous nucleotides at a site are ignored, and the scored nucleotide is most parsimoniously reconstructed. The ratio between the numbers of speedy and weighty transitions is 9.2 in our data, and, hence, the ratio between the speedy and weighty transition rates equals 25.2. The ratio of the number of weighty transitions to the number of transversions plus indels, here called the “WTTI ratio,” is estimated as 2.3. In cases where phantom mutations abound, the WTTI ratio may strongly deviate from the corresponding ratio in comparable data sets and, thus, hint at potential anomalies.

To probe for potential major artifacts in particular data sets, we filter out all speedy transitions and thus score only weighty mutations in a given mtDNA data set. The rationale is that speedy transitions, although hitting only a minority of sites, are expected to be responsible for the bulk of homoplasy in the data. When character incompatibilities caused by the genuine speedy transitions are weeded away, the patterns of incompatibilities generated by the phantom mutations will become more pronounced. We can realize the filtering by recoding the input sequences. First, the largest common scoring frame within nps 16051–16365 needs to be specified, for which all samples under consideration have been analyzed. The general alphabet for the aligned sequences of each sample is formed by A, G, C, T, and d (missing nucleotide). Whenever a scored site is listed among those with speedy transitions (see the above list), then we let the alphabet at this site consist of R (purine), Y (pyrimidine), and d (missing nucleotide). Programs for converting sequences and realizing the weighty filter are available from the authors' Web site.

Quasi-Median Portrait

Every data table of DNA sequences can be turned into a (full) median network, provided that each character (which represents sites with identical distribution patterns of nucleotides) is binary. When all characters are pairwise compatible, then the corresponding network is a tree; at the opposite extreme, when the characters are pairwise incompatible, then the network is a hypercube (see Bandelt et al. [2000] for more details). Normally, with HVS-I data sets of reasonable size, full median networks are gigantic and, thus, useless, without hypothesizing some recurrent mutations prior to network construction. When the levels of homoplasy and resolution are low, however, as is the case with the weighty mutations in HVS-I, full median networks become feasible for display, even with sample sizes well above 100. The network construction can then be executed either by hand, following the guidelines of Bandelt et al. (2000), or by computer, with Network 2.1 or 3.1 (Shareware Phylogenetic Network Software Web site). Since the data are binary, one can employ the reduced-median algorithm (Bandelt et al. 1995) with the reduction threshold r set to infinity (which, for most practical applications, may be realized as 99).

When, however, the data are nonbinary (in that there is more than one kind of weighty mutation at a particular site), the more general quasi-median networks come into play. They can be constructed with the above-mentioned network programs, by applying the median-joining algorithm (Bandelt et al. 1999) with the tolerance threshold ε set to infinity (alias 99). For mitochondrial data with low levels of homoplasy, one triangle here or a prism there will show up in the quasi-median network, so that one is not too far from a genuine median network (which has no odd cycles). In such cases, the (weighty) data can be coerced into binary form by suppressing the few nonbinary sites first and constructing a median network, before finally reintroducing the suppressed characters by hand to achieve the quasi-median network.

From the Incompatibility Spectrum to the Cube Spectrum

Incompatibilities between characters in a binary data set are manifest in squares and higher-dimensional cubes in the associated median network. More specifically, any set of k pairwise incompatible characters gives rise to a multitude of k-dimensional cubes in the median network, which are connected by the median subnetwork associated with those other characters that are incompatible with all of the k (Bandelt et al. 2000). According to a result of Dress et al. (1997), the total number of sets of (pairwise) incompatible characters (thereby counting the empty set and all singletons, by convention) equals the number of nodes in the full median network. To establish this one-to-one correspondence, assume that one node of the network is distinguished, say, as the root. Then, for each node x of the network, consider all the links that are incident with x and that are on some shortest paths between x and the root; the characters corresponding to these links are then pairwise incompatible and constitute the set associated with x. Conversely, for k pairwise incompatible characters, there is a unique corresponding k-dimensional cube (representing this k-set) closest to the root; its node furthest from the root is then the desired node x. To prove uniqueness, apply the speedy construction process of Bandelt et al. (2000) with a shelling order in which the k characters in question come last; a straightforward induction on the total number of characters then proves the claim.

The preceding one-to-one correspondence actually conveys more information: to count all j-dimensional cubes in the network (for j=0, these are just the nodes), we need to count only the pairs w, x of nodes where w is on a shortest path between x and the root at distance j from x. This translates, via the correspondence, into the count of the (k-j)-subsets of the k-sets (k⩾j⩾0) of pairwise incompatible characters. When we denote the number of k-sets of pairwise incompatible characters in the (weighty) data set by s_k and the number of j-dimensional cubes in the (weighty) median network by f_j, we have just established the formula

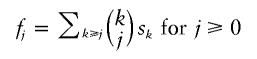(see the Remark in Dress et al. [1997]). Binomial inversion then turns this into the converse relationship

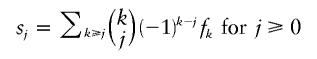(see Graham et al. 1990, p. 192, “Trick 3”). The equation for s₀, in particular, yields an Euler formula for median networks, found by Soltan and Chepoi (1987) and rediscovered by Škrekovski (2001), who also found the formula for s₁: 1=f₀-f₁+f₂-f₃±… . These two equations can also be seen as particular instances (q=1 and q=0, respectively) of the general equation 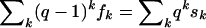, for q real, which follows from the binomial theorem. For q>0, we could view this sum as a kind of complexity measure of the median network; the larger the value of q, the more one penalizes the occurrence of clustered incompatibilities and, thus, high-dimensional cubes in the network. In particular, when q=3, the complexity measure sums up (over all vertices u) the number of k-dimensional cubes (k⩾0) in which each vertex u is contained. The entire sequences (s_k) and (f_k), however, provide us with more structural information than a single number. We call the sequences (or their finite truncations comprising all nonzero entries) s=(s_k) the “incompatibility spectrum” of the data set, and we call f=(f_k) the “cube spectrum” of the associated median network. The latter spectrum has been introduced by Brešar et al. under the name “cube polynomial” (article available online from the CiteSeer Web site).

The cube spectrum (as well as the intimately related incompatibility spectrum) for some binary data set thus permits us to describe certain properties of the corresponding median network without actually generating it. In simulation studies, for example, numerous spectra can easily be computed, stored, and compared. For the purpose of illustration, let us assume that an HVS-I sample of size 100 has been randomly hit by artificial transitions at eight sites independently, with probability 4% per site. Typically, we might observe two sites each at which three, four, or five sequences bear the variant nucleotide, and a single site with two or six sequences bearing the variant nucleotide. The expected incompatibility spectrum (obtained by randomizing the associated data matrix 1,000 times and then rounding to integers) equals (1, 8, 4, 1), which, in turn, yields the cube spectrum (14, 19, 7, 1). Now assume instead that the total of 32 mutations affected only a minor part (25%) of the sample randomly, so that the other 75 sequences remain unvaried from the outset. When the same number of variant nucleotides at eight sites is randomly distributed over 25 sequences, then the expected incompatibility spectrum is (1, 8, 14, 8, 2), with associated cube spectrum (33, 68, 50, 16, 2). Not unexpectedly, the tighter clustering of the artificial mutations creates more incompatibilities, which are manifest in higher-dimensional cubes. Thus, whenever several sites in a subsample have been affected by artifacts more than once, then there is a good chance of seeing a strong signal in the median network representing the variation at those sites. Since artificial mutations do not respect the phylogenetic hierarchy of the data set, we may expect further incompatibilities with naturally mutated sites.

Results

Brazilian Benchmark

For a weighty view of continental mtDNA variation, we have chosen the Brazilian HVS-I data set of Alves-Silva et al. (2000), which had been carefully examined for potential reading or sequencing artifacts (this did not, however, prevent a shift of the last 11 haplotype numbers by one in the printed HVS-II table, thereafter corrected in an erratum). Specifically, both strands had been sequenced, and each sequencing output had been read at least twice. Then, following the guidelines of Bandelt et al. (2001), potentially doubtful sites in individual sequences were read again, and suspicious sequences were resequenced. These Brazilian data represent a sample of 247 mtDNAs of Native American, sub-Saharan African, or western Eurasian (mainly European, including Near Eastern or North African) ancestry, which had been assayed in a random order and subjected to the same posterior quality control. Haplotype numbers 1–53 belong to haplogroup M (all of Native American ancestry, except for one haplotype of Asian ancestry); haplotype numbers 54–109 constitute haplotypes of sub-Saharan African haplogroups; and haplotype numbers 110–170 belong to haplogroup N (mainly from Europe, with a few from North Africa and possibly the Near East). Each of the three fractions of the Brazilian data set captures a good deal of the basal mtDNA variation of the respective (sub)continent.

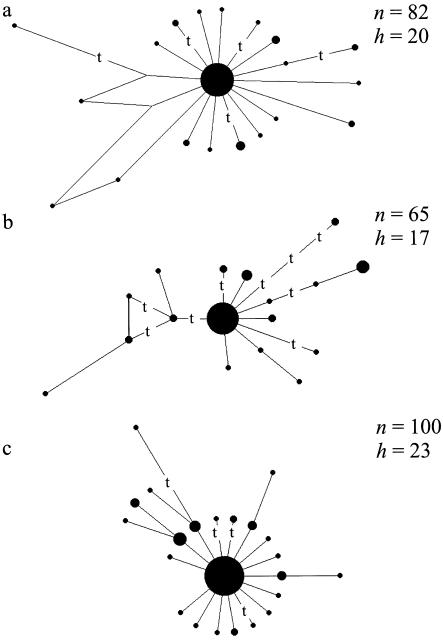
Each of the three subsets (referred to here as “American,” “African,” and “European”) then had its speedy mutations filtered out, to condense the data to the weighty variation only. Figure 1 displays the resulting weighty networks, in each of which the most frequent haplotype corresponds to the Cambridge reference sequence (CRS): the European network is a perfect tree (i.e., no homoplasy is manifest in the weighty data), whereas the African network displays a single triangle (indicating the ambiguity as to whether two transversions or one transversion and one weighty transition have affected site 16286), and the American network contains two 4-cycles. This is the result of two mutations at site 16142: one on a haplogroup A and the other on a haplogroup D background. The latter haplotype is well documented in northern Brazil (Santos et al. 1996). The low WTTI ratio of 1.5 may seem to be a puzzling feature of the African weighty network; however, comparison with the worldwide human mtDNA database reveals that this observed transversion pattern in Africa is real. On the other hand, the corresponding high ratios (3.8 and 4.8) for the American and European weighty networks might be seen as more puzzling. Although the deviation from the estimated worldwide ratio of 2.3 is not significant here, one should be prepared to model the mutational process of HVS-I in a more complex way than merely by a gamma distribution of site rates (e.g., Yang and Kumar 1996).

Figure 1.

The full quasi-median networks representing the weighty variation within 16051–16365 (i.e., not scoring the speedy transitions listed in the “Weighty HVS-I Filter” subsection of the “Methods” section) for the following three subsets of the Brazilian mtDNA data (Alves-Silva et al. 2000): American (a), African (b), and European (c). Every unit-length link signifies one weighty transition, except where “t” indicates a transversion. The size of the nodes is proportional to the number of sampled mtDNAs of this haplotype; n is the sample size and h the number of sampled haplotypes (relative to the weighty mutations).

Transversion and Indel Havoc

The early mtDNA data of the Yanomami, as reported by Easton et al. (1996), are known to suffer from an excess of transversions (as explained by Merriwether et al. 2000). The weighty network reflects this very well (not shown), although it displays little reticulation (i.e., only one prism). The WTTI ratio is (most parsimoniously) estimated as 0.5 or 0.7, which is significantly smaller (at the 5% level of a one-tailed Fisher's exact test) than the estimated “American” ratio of 3.8. The new Yanomami data (table 7.3 of Merriwether et al. [2000], corrected for the obvious downward shift by one row in the frequency information), though much more numerous (129 mtDNAs sampled from various villages), are weightily represented by a small network (not shown) that no longer displays any excess of transversions. The long branches have disappeared, but some reticulation still remains (i.e., a triangle for site 16104 and a square involving the transitions at sites 16110 and 16259).

The Volga-Finnic mtDNA sample of Sajantila et al. (1995) is notable for its tremendous excess of deletions (Bandelt et al. 2001). The weighty network, though a perfect tree, highlights this (not shown). The six scored deletions are indeed record-breaking, given that true (scored) indels are very rare. Beyond the scoring frame, one sequence has a doublet deletion (at nps 16047–16048) and another one has a deletion at site 16381. It is plausible that these artificial deletions (seeming phantom mutations) were not produced by the sequencing process itself but rather through the sequencing outputs, which were not critically read; it is conspicuous that in four of the six deletion instances, a probable A was deleted after a T.

Heavy Strand Din

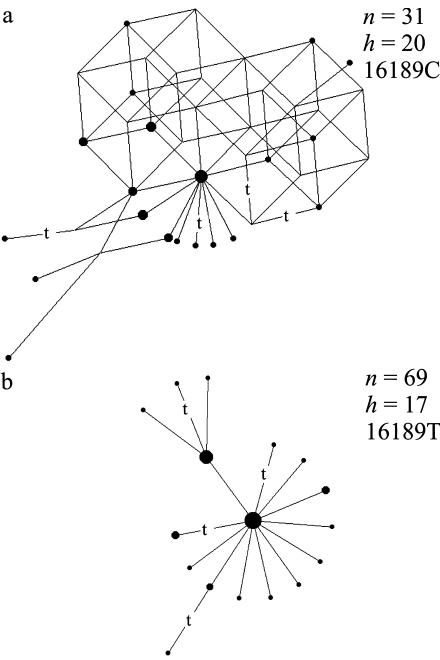
The 100 Japanese mtDNAs of Seo et al. (1998), percolated through the weighty HVS-I filter, end up in a bulky network (not shown). All the reticulation is actually contained in the weighty network of those 31 mtDNAs that harbor C at 16189; its cube spectrum f=(40,74,49,16,2), and especially the two overlapping four-dimensional cubes, bear witness to the noise in the data (fig. 2a). In sharp contrast, the 69 remaining mtDNAs (with T at site 16189, as in the CRS) that do not have the long C run respond harmoniously to the weighty filter, yielding a perfect tree (fig. 2b). This suggests that the long C run inhibited the further reading of the light strand, so that beyond the C run, only the heavy strand was available for evidence on the variation, which may have been difficult to decipher in some stretches. The C run slippage constitutes a well-known obstacle for standard sequencing methods, so that effectively only sesquisequencing of the mtDNA is guaranteed. This problem can be overcome by using two primer pairs (i.e., with an additional forward primer at the end of the C run), as executed, for example, by Imaizumi et al. (2002). The 162 Japanese mtDNAs they analyzed partition into 60 mtDNAs bearing 16189C and 102 mtDNAs with 16189T. The corresponding weighty networks do not display the contrast seen with the Seo et al. (1998) data; for the 102 sequences, the network departs from a perfect tree only by a triangle that results from the three bases present at site 16293, and, for the 60 sequences with a long C run, a double-prism and a triangle constitute the only reticulation, incurred by a transition and a transversion at sites 16194 and 16318.

Figure 2.

The full median networks representing the weighty variation in the Japanese mtDNA data (Seo et al. 1998) for the mtDNAs with 16189C (yielding a long C run) (a) and 16189T (b). Symbols are as in figure 1.

For the potential identification of the phantom mutations in the Seo et al. (1998) data, we first search for the smallest set(s) of mutations that could be responsible for the reticulation in the network. The minimum number here is four, realized by precisely two sets, which comprise the transitions at 16248 and 16321 and the C→G transversion at 16239, plus either the transition at 16344 or the transversion at 16232. The latter, however, is a real mutation characterizing a clade in haplogroup F, whereas the former characterizes a subclade of the latter (found in Japan, Korea, and China [Horai and Hayasaka 1990; Horai et al. 1996; Lee et al. 1997; Yao et al. 2002]). This incompatibility analysis would thus suggest that the mutations at sites 16239, 16248, and 16321 could be artificial. Suppressing these mutations in the weighty data leaves us with a single incompatibility, the one between the mutations at sites 16232 and 16344, which—judging from the original sequences—could be explained by assuming that in one haplotype the transversion at site 16232 was simply overlooked. This transversion (which seems unlikely to have back-mutated) appears to have also been misscored in earlier studies (Horai et al. 1996; Lee et al. 1997). Among the speedy transitions, the odds would lead us to expect about one phantom mutation; indeed, the speedy transition at site 16242 appears to be coupled with the weighty transition at site 16248. The perfect correlation is disrupted only in those cases in which there are (real) transitions at site 16243 (inhibiting the 16242 transition) or at site 16249 (inhibiting the 16248 transition).

In a second approach, we focus on the private weighty mutations, by comparing both the Seo et al. (1998) and Imaizumi et al. (2002) data with the general Asian database. To this end, we allocate each sequence to its putative haplogroup, following the phylogenetic scheme of Yao et al. (2002). Any mutation that is not supported by sequences from the same (sub-)haplogroup obtained by another lab is then regarded as a private mutation. In the Imaizumi et al. (2002) data, we find four private weighty types each in the 16189T and 16189C subsamples, each occurring in exactly one individual. In the Seo et al. (1998) data, we find six private weighty types in the 16189T subsample and eight in the 16189C subsample, all of which occur once, except for the private weighty type 16248. All but one of the private weighty types in the latter subsample are affected by (five different) combinations of 16239C→G, 16248, and 16321; removing those mutations would leave only three private weighty types. The former transversion has otherwise been observed worldwide only in a single one-step descendant of the CRS (sampled in Iceland and the British Isles). In this data set, however, this transversion, together with the transition at 16321 (never observed elsewhere in conjunction with one another) has hit sequences in haplogroup M7b2 and two sister clades of haplogroup F1; the otherwise never recorded transitional pair 16242-16248 occurs in sequences from haplogroups D5 and M7b2 and in two sister clades of B4b. This tandem pattern leads us to expect that nearly all instances of those four mutations are phantom mutations.

High Alpine Variation

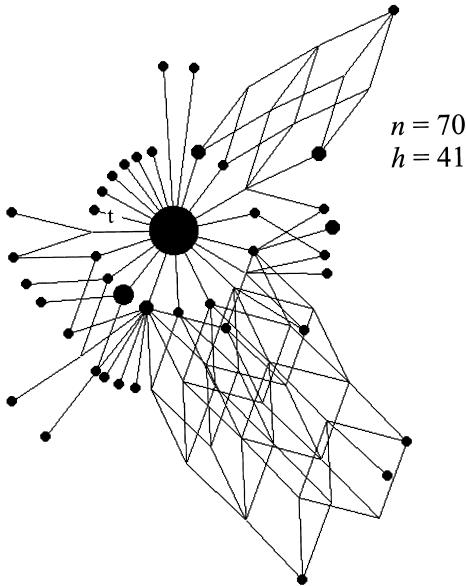
The 70 Ladin mtDNAs, praised for their high variation in the Alps (Stenico et al. 1996), yield a very weighty network—full of cubes—a pattern of homoplasy hardly ever observed in any mtDNA phylogeny (fig. 3). A whole array of unexplainable mutations springs to the eye: transitions at sites 16106, 16221 (as detected by Bandelt et al. 2001), and many more. The WTTI ratio (49.0) is highly significantly greater than the ratio of 4.8 estimated from the European fraction of the Brazilian mtDNA sample. The total number of sites with phantom mutations is difficult to estimate, since the artificial mutations overwhelm the real mutations in the weighty data and, moreover, on top of the disaster with the phantom mutations, the data seem to suffer from poor reading as well. For example, the two mtDNAs with transitions scored at 16126-16163-16260-16315 and 16163-16186-16211, respectively, may be corrupted T1 sequences, which should bear the motif 16126-16163-16186-16189-16294 (Richards et al. 2000). We would then predict that about half an artificial mutation, on average, has been added to every real HVS-I sequence from the sample, except for the 10 Mocheni mtDNAs in this data set, which are almost exempt from artifacts. It therefore seems that the excess of mtDNA variation in the Ladins compared with other European populations is essentially due to these sequencing artifacts, leaving aside potential drift effects. This is dramatically illustrated in table 1, where the hefty cube spectrum of the Ladins dwarfs the rather puny spectra generated from proximate samples in Europe as well as the pooled sample (more than an order of magnitude larger than the Ladin sample). The very impoverishment of these spectra reassures us that our present choice of weighty mutations is not too suboptimal.

Figure 3.

The full median network representing the weighty variation in the Ladin mtDNA data (Stenico et al. 1996). Symbols are as in figure 1.

Table 1.

Cube Spectra for Samples Proximate to the Ladins

				Cube Spectrum
Population	Reference(s)	n	h	0	1	2	3	4
Ladins	Stenico et al. 1996	70	41	73	124	69	19	2
Switzerland	Dimo-Simonin et al. 2000	154	31	34	37	4	0	0
Austria	Parson et al. 1998	101	25	25	24	0	0	0
Ireland	Richards et al. 2000	101	16	17	17	1	0	0
Bulgaria	Richards et al. 2000	111	23	23	22	0	0	0
Basque	Bertranpetit et al. 1995; Richards et al. 2000	156	21	22	21	0	0	0
Greece	Richards et al. 2000	125	25	25	24	0	0	0
Sicily	Richards et al. 2000	90	17	17	16	0	0	0
Pooled (without Ladins)	…	838	88	94	114	22	1	0

A new study of 20 mtDNAs from Ladin speakers of Colle Santa Lucia (Vernesi et al., in press) revealed an HVS-I data set with absolutely no sign of the aforementioned artifacts. Six of the 10 distinct haplotypes match with haplotypes sampled in Germany, Austria, or Switzerland, whereas four haplotypes are apparently novel in the worldwide HVS-I database but at a single mutational step (each involving a speedy transition) from haplotypes sampled in those neighboring countries. To better understand the structure of the phantom mutations in the first Ladin data set, we have performed a permutation test on the (binary) haplotype table with regard to the weighty variation. That is, we assume that mtDNAs that are not distinguished by weighty mutations have identical weighty types, because of descent, and therefore should not be disrupted. For each run, the nucleotides in each column (representing a single site) of the weighty haplotype table are permuted. Permuted columns yielding the same partition of the rows (the new types) are merged into one character; then, the incompatibility spectrum is determined and converted into the cube spectrum. This randomization is repeated 1,000 times, and the average cube spectra along with the SD sequences are calculated (see table 2, where the first 10 permutations are listed as well). The results show that there is quite a bit of variation in the cube spectra, but, in any case, the spectrum of the original Ladin sample falls well within the distribution of the spectra of the permuted data. For example, the Ladin cube spectrum dominates 5 of the first 10 spectra of the permuted data, and its complexity (with respect to q=3) exceeds that of the permuted ones in 7 of the 10. We conclude that the phylogenetic content in the weighty data is invisible and that the nature of the process that created the phantom mutations could have been essentially random.

Table 2.

Cube Spectra for the Raw and Permuted Weighty Ladin Data

	Cube Spectrum
Ladin Data Type	0	1	2	3	4	5	6	Complexity (q=3)
Raw	73	124	69	19	2	0	0	781
Permutation:
1	118	280	284	171	61	12	1	4,606
2	82	151	95	28	3	0	0	1,036
3	65	102	46	8	0	0	0	517
4	64	103	51	12	1	0	0	586
5	76	124	61	13	1	0	0	688
6	75	129	70	16	1	0	0	757
7	79	146	92	27	3	0	0	1,003
8	62	97	46	11	1	0	0	544
9	62	96	44	10	1	0	0	526
10	65	98	40	6	0	0	0	469
Mean (SD)	70 (11)	116 (34)	61 (40)	16 (25)	2 (10)	0 (3)	0 (0)

Pitfall with the Kit

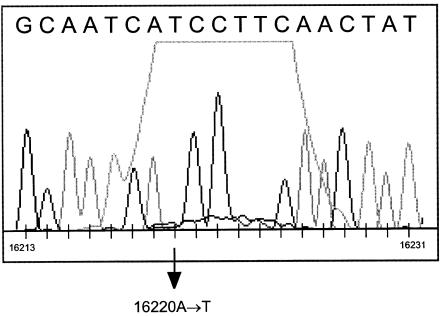
In a large population sample of ∼300 mtDNAs, we observed in the sequencing output an otherwise rare A→T transversion at site 16220 in eight mtDNAs, which belong to at least six different haplogroups. In the weighty network, this mutation would be responsible for a new one-step descendant (occupied by five mtDNAs) of the central node, with three subsequent offshoots, one of which would create a square. In all those mtDNAs showing the A→T transversion at site 16220, this polymorphism disappeared when they were resequenced. It turned out that this transversion occurred only in a particular batch of samples that were sent out to a sequencing service. The sequences presenting this mutation were not consecutive in the gel, since this set was processed in a capillary sequencer machine. There is no obvious relation between the general quality of the sequence output and the presence of this phantom “T,” but inspection of the chromatogram reveals that the stretch between sites 16218 and 16227 has been affected by an overdominant peak that has altered the automatic interpretation of the chromatogram at the positions presenting a weak (true) signal (here, site 16220; see fig. 4). It is possible that there was an excess of dye (from the kit used to perform the sequence reaction) and that this kit was polluted by a nonsoluble contaminant that usually gives this kind of artifact. This example clearly indicates that it is indispensable to inspect the whole chromatogram, even when the sequence output does not exhibit any ambiguity (nondetermined bases).

Figure 4.

Portion of the chromatogram of a mtDNA sequence exhibiting the A→T 16220 artifact.

This pitfall also provoked us to question some earlier sequencing results reported by two of us (H.-J.B. and L.Q.-M.). The data published by Quintana-Murci et al. (1999; their table 1) are suspicious in two respects: first, the WTTI ratio (0.88) is rather low, and second, a readability problem toward the end of the sequences was manifest in four instances (see the footnote to their table). We have therefore resequenced three available samples—O32, O38, and I872—and found that the reported variants 16360, 16363, 16363A, and 16364A were artificial. Consequently, we should regard the variants 16360, 16363A, and 16366+C in AP62 and I906 as artifacts as well. This cleansing has the effect that the weighty network, which originally had one prism, now becomes a perfect tree.

Discussion

Rate Estimation on a Site-by-Site Basis

At a relatively early stage of the worldwide HVS-I screening of human mtDNA, the mutational pattern in HVS-I became apparent: a high transition/transversion ratio and a quite uneven distribution of mutations across sites (Hasegawa et al. 1993). In that study, <400 HVS-I sequences (sampled from Africa, Eurasia, and America, and sequenced in several laboratories) were available, and the estimation of a phylogenetic tree (using maximum parsimony) could not profit from any additional coding-region information at the time. Nevertheless, their top 29 sites (Hasegawa et al. 1993; their table 3) are all found in our list (see the “Weighty HVS-I Filter” subsection of the “Methods” section) of speedy transitions. When we take their list of sites (with at least two hits) as a proxy for sites with frequent transitions (since transversions are generally much rarer), we still see the contrast between the Brazilian data subsets and the Japanese and Ladin data sets, although it is slightly less pronounced. A similar comment applies to the reconstructed HVS-I mutational spectrum of Malyarchuk et al. (2002; their fig. 2), based on 4,072 West Eurasian sequences. In the latter case, however, only lower bounds on the number of mutational hits per site were inferred from the data, by counting for each HVS-I site only the number of haplogroups (out of a total of 34 distinguished haplogroups or subgroups) in which the site appears polymorphic. The advantage of distinguishing transitions from transversions and of using more solid and detailed phylogenetic information is that more major African and Eurasian haplogroups can be recognized by at least one mutation in the filtered data, so that we have a better chance of seeing phantom mutations in character conflict with real mutations.

Enigma of Phantom Mutations

Our analysis of published mtDNA data and our own lab experience indicate that phantom mutations do occur but that the constraints under which they operate remain enigmatic. In any case, the phantom mutation process is anomalous in comparison with the real mutation process and seems to depend on the specific biochemical conditions set up and maintained in a lab, and so it is impossible to predict a universal hotspot spectrum. Our chances to discover phantom mutations by posterior data analysis are enhanced by the happy circumstance that, under identical sequencing conditions, a relatively small ensemble of sites is revisited by phantom mutations. Thus, in extreme cases, phantom mutations will show up in the weighty network as extensive reticulation. The mtDNAs responsible for the commotion in the network are then the first candidates for checking and, potentially, for resequencing. If, instead, numerous sites are hit by phantom mutations only once, then the weighty network will have longer branches, which typically carry private mutations relative to the global mtDNA phylogeny.

Quality Check

In a first go at judging a new data set, it is advisable to compare it with any (reliable) data set (to serve as a standard) of similar size and phylogenetic composition. A site-by-site comparison with the worldwide database of published sequences (≫10,000) may give an idea about the frequency of a transversion or transition at a particular site. For example, the transversion at site 16037 observed by Lee et al. (1997) has never been observed elsewhere, and yet it occurs in two different haplogroups (alongside a transition at site 16037 in a third haplogroup). Similarly, transversions at 16042 had been observed worldwide in only two sequences (one Estonian and one French mtDNA); until recently, they appeared in three Syrian sequences from Vernesi et al. (2001) belonging to three different haplogroups (U3, K, and another one, most likely H).

The case of the 16220 transversion warns us that the weighty network need not necessarily be hypertrophic when some minor systematic artifacts occur, unless a real disaster happens, as in the above cases of the Japanese and Ladin samples. Nevertheless, the weighty network may still let us quickly pinpoint the artifacts; one may wish to reread or resequence all those sites in the aberrant mtDNAs that label links of the weighty network, provided that the unfiltered HVS-I sequences of those aberrant types are not matched by other sequences reported in the published database. In this spirit, a partial rereading of the Galician data of Salas et al. (1998) identified problems with a (rare) transition at 16094, which, however, did not generate any reticulation in the weighty network. In fact, 16093C had been misscored as 16094C in the samples SEQ45 and SEQ52, and the sequence trace for the third instance (SEQ15) was ambiguous there; resequencing confirmed that this mutation is in fact absent. Since another instance of 16094C (Rando et al. 1998) has been identified as an artifact (Bandelt et al. 2000), one may wonder whether some conservative HVS-I sites might be hotspots for phantom mutations and other artifacts.

Since for population studies in forensics, both hypervariable segments (HVS-I and HVS-II) are routinely sequenced but rarely subjected to effective a posteriori control (Bandelt et al. 2001), it is desirable to include HVS-II in the quality check. Unfortunately, a list of potentially speedy transitions in HVS-II analogous to our list of speedy HVS-I transitions is not yet available—the attempt by Meyer et al. (1999) biased sites that were hit by ancient mutations, as is seen, for example, with the transition at the site 247 (an excellent marker for the superhaplogroup L2’3 [Alves-Silva et al. 2000; Ingman et al. 2000]), which, in that study, came out as hypervariable. The list provided by Malyarchuk et al. (2002), highlighting sites 146, 150, 151, 152, 185, 189, 195, 199, 204, 207, 217, and 227 as mutational hotspots, may be taken as a proxy for the speedy HVS-II transitions. In a more conservative strategy, one could at least add all transversions and indels (disregarding C runs) in HVS-II to the weighty mutations of HVS-I. Applied to the recently published mtDNA data from Taiwan (Tsai et al. 2001), we see that the C→G transversion at site 162 is responsible for one square in the (extended) weighty network (not shown); in fact, we would reconstruct four independent events for this otherwise never-observed transversion.

The application of a systematic quality check, through the weighty filter, will be very useful not only in forensic science but also in human evolutionary studies, where population history inferred from mtDNA data may be distorted by the presence of these artifacts. Although our examples have focused on the mtDNA control region, there is no reason to assume that the coding region will be immune to phantom mutations. Since there are also a few mutational hotspots in the coding region, phantom mutations acting on the sequenced fragments of the coding region could be mistaken as evidence for new hotspots, quite as in the case of the control region. As the database of reliable coding-region sequence increases (e.g., Herrnstadt et al. 2002), we will build up a picture of the weighty mutations there and so be able to apply an analogous filtering process to the one we have applied to HVS-I here. Phantom mutations are, alas, too widespread to be blindly ignored.