Upward Bias in Estimation of Genetic Effects

Abstract

Because of the large number of tests for linkage that are performed in genome scans, the naive estimator of the size of a genetic effect in cases of borderline significance can be inflated and lead to unrealistic expectations for successful replication. As a remedy, this report proposes lower confidence limits that account for the multiple comparisons of the genome scan.

Genetic mapping is often discussed in the statistical language of hypothesis testing, with primary interest focused on detecting markers linked to the trait. It is of secondary interest to estimate the genomic location of trait loci and of tertiary interest to estimate the sizes of the genetic effects of detected or perhaps only suggested loci. This third issue is particularly important in cases of borderline detection, for which precise estimation of genomic location is problematic. Natural questions about future research involve (i) the sample size that would be reasonable for a replication experiment and (ii) the fraction of the total heritability of the trait explained by the detected locus.

Göring et al. (2001) have described the upward bias that occurs if one uses the naive estimator for the genetic effect when a genome-scanning statistic barely exceeds the threshold for significance. They report that the bias is particularly severe when the true genetic effect is small and vanishes asymptotically when the genetic effect is large. They briefly consider bias correction on the basis of an analysis of the conditional expected value of the locus-specific log likelihood–ratio statistic given that it exceeds the significance threshold, but they conclude that “attempts at bias correction give unsatisfactory results.”

Allison et al. (2002) suggest a more robust but otherwise similar approach to bias reduction and “demonstrate its validity via Monte Carlo simulation” (p. 575). An unsatisfactory feature of this approach is that the bias-corrected estimate depends on the threshold selected, and it typically decreases as the threshold increases. Thus Allison et al. (2002), who choose to illustrate their method with the relatively small threshold of 1.2 (LOD scale) in order “to minimize the simulation time” (p. 578), obtain larger estimates of genetic effects than they would if they used the LOD 3 threshold of Göring et al. (2001). (A numerical example is given below.)

A different approach is to estimate the genetic effects by means of a confidence interval that accounts for multiple testing of many markers throughout the genome (which the estimators of the cited articles do not) and avoids the problem of selecting a somewhat arbitrary threshold with its resulting effect on the estimate. More to the point, in view of the concern that the naive point estimators are biased upward, one might give lower confidence limits. A conceptual distinction between hypothesis testing and confidence limits is that, whereas a test of hypothesis attempts to determine whether the data are reasonably consistent with the hypothesis of no genetic effect, a lower confidence limit seeks to determine the range of genetic parameters that are consistent with the data. Suppose the genetic effect on a trait is measured by a parameter ξ⩾0, with the value ξ=0 indicative of no genetic effect. The hypothesis ξ=0 is rejected if the data are found to be inconsistent with this hypothesized value. To find a lower confidence limit for ξ, we ask for every ξ₀⩾0 if the data are consistent (at a significance level γ) with the hypothesis ξ⩽ξ₀. The set of values ξ₀ that are not rejected by such hypothesis tests has a smallest value, say ξ_*, which gives a (1-γ)100% lower confidence limit (Lehmann 1986, p. 90). It is important when considering this approach to note that although confidence limits are often, in fact, computed only in cases when the hypothesis of no genetic effect is rejected, in principle they are calculated in all cases. Accepting or rejecting the value ξ=0 is equivalent to saying that this null value is or is not as large as the confidence limit. As a practical matter, it may be easier to perform the test of ξ=0 first, since failure to reject the hypothesis of no genetic effect at the significance level γ is equivalent to saying that the (1-γ)100% lower confidence limit is 0.

The method described below applies to both qualitative and quantitative traits in human and experimental genetics. The case of a qualitative trait is illustrated by a discussion of affected sib pairs. To allow for numerical comparisons with the article by Göring et al. (2001), the discussion of quantitative traits follows the hypothetical example studied in detail in that article. The method can be adapted to larger sibships and more-distant relatives, but the details given below would change.

For both cases, we assume that data for N sib pairs are obtained from fully informative markers spaced at 2 cM along an autosomal genome of 22 chromosomes of average length 150 cM. (Göring et al. [2001] assume that one also includes the parents of the sibs, but ignoring the parents simplifies and unifies what follows without changing the basic picture.) All trait loci are assumed to lie on different chromosomes and to act additively without interaction, so the power to detect a given trait locus depends primarily on the ratio σ²_A/K² of the additive variance associated with that locus to the squared trait frequency, in the case of a qualitative trait, and on the ratio h²=σ²_A/σ²_Y of the additive variance to the overall phenotypic variance, for a quantitative trait.

For their numerical examples Göring et al. (2001) also assume that H², the overall heritability of the trait, is 0.5 and that N=1,000. This corresponds to N=302 for a qualitative trait in the sense that the factors multiplying α in equation (1) given below and h² in equation (3) would then be equal.

Let ν_n,t denote the number of alleles shared identical by descent by the nth sib pair at the marker locus t. For a sample of N affected sib pairs, the mean sharing statistic (which is also the score statistic under the assumptions given above) standardized to have mean 0 and variance 1 under the hypothesis that the marker t is unlinked to the trait is

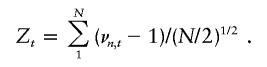By the central limit theorem, it is approximately normally distributed when N is large. Its expectation at a trait locus τ is given by

where the parameter α can be expressed in terms of the trait frequency and variance components or, alternatively, in terms of the “apparent” risk ratios (Risch 1990) (i.e., the risk ratios for a monogenic trait that would yield the given value of α). The appropriate relation is α=(2λ_S-λ_O-1)/λ_S, where λ_S is the apparent risk ratio for siblings and λ_O is for offspring. Under our assumption of additive penetrances, λ_S=λ_O.

In the case of a quantitative trait, using the standard normality assumption of variance components analysis, one can derive the score statistic or likelihood ratio statistic to test the hypothesis that the marker t is unlinked. A robust version of the score statistic, suggested by Tang and Siegmund (2001), is of the form

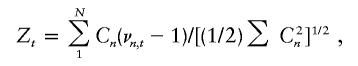where the C_n are functions of the quantitative phenotypes only. By the central limit theorem, this statistic is approximately normally distributed for large N whether or not the phenotypes satisfy the standard normality assumption. The robust Haseman-Elston (1972) statistic studied by Allison et al. (2002) is of the same form but with different and simpler C_n because of the Haseman-Elston starting point of reducing the two-dimensional phenotypic values to one-dimensional squared phenotypic differences.

The expected value of Z_τ at a QTL τ is approximately

where h²=σ²_A/σ²_Y is the locus-specific heritability, ρ is the phenotypic correlation between sibs, and c²=EC²_n (Tang and Siegmund 2001). When the normality assumption of variance component analysis is true, c²=(1+ρ²)/(1-ρ²)², and equation (2) simplifies to

In what follows, we directly estimate the noncentrality parameter ξ. Equations (1) or (2)-(3) allow us to convert an estimate of ξ into an estimate of λ_S or h². Under the assumed model described above, ρ=H²/2. For simplicity, I assume that ρ and c² are known, say from previous segregation analyses. Otherwise they can be estimated from the data. Alternatively, one can draw limited conclusions directly from the estimate of ξ. Since estimates of ρ and c² are based only on phenotype data, there is no particular concern that they have been biased by the genome scan. Some numerical experimentation with equation (3) shows reasonable robustness against misspecification of ρ, at least in the case of greatest interest, that neither h² nor ρ is large and N is large.

Since the locus τ is unknown, detection of linkage in a genome scan is determined by a threshold z, such that if Z_t⩾z, one concludes that there is a gene linked to t contributing to the trait. The P value, taking multiple comparisons into account, is 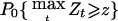, where the maximum is taken over all marker loci t and the subscript 0 denotes the null hypothesis that there are no trait loci linked to the genomic region studied. (An approximation is given below.) For a scan based on our assumptions of marker density and genome length, for either of the statistics 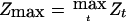defined above, the detection threshold z to guarantee a genomewide false-positive error rate of 0.05 is z=3.85, or equivalently on the LOD scale, LOD=z²/4.6=3.22. This is slightly higher than the conventional level of LOD=3 used by Göring et al. (2001).

A naive estimate for the genetic effect in a particular genomic region is obtained by solving the equation 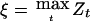, where now the maximum is taken over all markers linked to the genomic region under consideration. In the principal example of Göring et al. (2001), the genomewide maximum is assumed to be roughly equal to the detection threshold, say z=3.85, so by equation (3), the estimated value of h² when N=1,000 and ρ=H²/2=0.25, would be 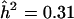, which suggests a substantial genetic effect. This is roughly the same value obtained by Göring et al. (2001) for a slightly different value of z by a slightly different argument. This argument applied to the case of a qualitative trait with N=302 leads to the same value of 0.31 for the naive estimate of α, which converts to 1.45 for the apparent λ_S.

To get some understanding of the bias-corrected estimates of Allison et al. (2002) with a minimum of technical fuss, suppose that at a given trait locus τ the probability distribution of the score statistic, Z_τ, or of the square root of twice the log–likelihood ratio statistic is exactly normal with mean value ξ proportional to h² (α for a qualitative trait) and variance equal to 1. This is approximately true in large samples for both of the slightly different cases discussed in Allison et al. (2002) and Göring et al. (2001). Given a threshold T and that Z_τ⩾T, the suggested estimator for ξ would be the maximum of 0 and the solution ξ to the equation obtained by setting the observed value of Z_τ equal to its conditional expectation given that it exceeds the threshold, namely Z_τ=ξ+ϕ(T-ξ)/[1-Φ(T-ξ)], where ϕ and Φ are the standard normal probability density function and cumulative distribution function, respectively. For Z_τ=3.85, which is substantially above the threshold T=2.35 (LOD=1.2) of Allison et al. (2002), the estimate of h² (and of α) would be 0.30, which involves hardly any bias correction compared with the naive estimator; the more stringent threshold, T=3.71 (LOD=3) of Göring et al. (2001) would lead by the same method to estimate h² or α to be 0 (hence λ_S=1).

To obtain a lower confidence limit for ξ and hence for the genetic effects, assume following Göring et al. (2001) that there are k mutually unlinked genes contributing equally to the trait and a perhaps much larger number of polygenes whose minor contributions are at the level of noise for the sample size N. For the observed value of 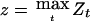, from the relation between tests and confidence limits described above, we can find a lower 1-γ level confidence limit for ξ by solving for ξ the equation

See below for a simple approximation to the required probability in the (conservative) case that the trait loci are assumed to coincide with marker loci. A lower confidence limit for α, hence for λ_S, or for h² can be obtained from the lower confidence limit for ξ via equations (1) or (2), respectively.

The 95% lower confidence limit for α and for h² is 0 when Z_max=maxZ_t equals the .05 significance threshold, 3.85. If a 95% lower confidence limit is regarded as an unnecessarily pessimistic assessment of the locus-specific heritability, one could use a different confidence coefficient. For example, a 50% lower confidence limit gives a median unbiased point estimator (Lehmann 1986), which has the property that if the same experiment could be repeated a large number of times, the estimate, which would vary from one experiment to another, would be below the true parameter value approximately as often as it would be above. (This interpretation follows from putting γ=0.5 in equation (4).) For the QTL case, table 1 gives 95%, 80%, and 50% lower confidence limits for k=1 and different hypothetical values for Z_max. For comparison, the naive estimator 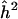suggested above is also given. One sees that the naive estimator increases linearly with the observed value of Z_max, and over the given range it always suggests a substantial genetic effect. The confidence limits at first equal 0, indicating the reasonable possibility of no genetic effect whatever, then increase rapidly, and finally increase roughly parallel to 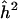. In the range of rapid increase there is substantial bias correction; the confidence limit is a warning against the “irrational exuberance” of an uncritical acceptance of the naive estimator. To suggest a sample size that might suffice for replication, the 80% lower confidence limit provides a (perhaps) reasonable compromise between the conservative 95% limit and the median unbiased estimator. In the case of a qualitative trait with N=302, the lower confidence limits in table 1 apply directly to α and can then be converted into limits for λ_S.

Table 1.

Lower Confidence Limits for h^2[Note]

			Lower Limit for Confidence Interval
Zmax	(LOD)		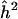95%	80%	50%
3.00	(2.0)	.24	.00	.00	.00
3.10	(2.1)	.25	.00	.00	.08
3.25	(2.3)	.26	.00	.00	.18
3.50	(2.7)	.28	.00	.12	.24
3.85	(3.2)	.31	.00	.21	.29
4.05	(3.6)	.33	.15	.24	.31
4.25	(3.9)	.35	.18	.26	.33
4.60	(4.6)	.37	.22	.29	.36
5.25	(6.0)	.43	.28	.35	.42

Note.— The sample size is N=1,000 and the sib correlation is ρ=0.25. The maximum value of the Z-statistics is Z_max. (The equivalent LOD score is given in parentheses.) The naive estimator of locus specific heritability is .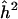

(Table 1 focuses on the estimated genetic effect, described by h² or by α in the two cases under consideration. It may be worth noting that the bias correction, defined to be the difference between the naive estimate and the confidence limit, decreases with increasing values of Z_max, once this latter value is large enough that the confidence limit is positive, and—by equations (1) and (2)—it decreases with increasing values of N.)

If there are more contributing loci, there are more opportunities for a weak locus to lead to a deceptively large maximum, so the lower confidence limit would decrease. The magnitude of the change is surprisingly small (e.g., for Z_max=4.25 the 95% lower confidence limit of 0.18 for h² in table 1 when k=1 becomes 0.16 or 0.14 for k=2 or 3, respectively.) The change would be substantially smaller if the second and/or third trait loci have smaller locus-specific heritability. Since we cannot expect to know the true number of trait loci, it is reassuring that the confidence limit is relatively insensitive to the assumed number.

It is apparent that there is useful information in other properties of the process Z_t besides its maximum. For example, suppose we let 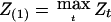, where the maximum is taken over all chromosomes, Z₍₂₎ the maximum value over the other chromosomes that did not give the value Z₍₁₎, and so on. Large values for both Z₍₁₎ and Z₍₂₎ would suggest that there are two important genes contributing to the trait. If z₁⩾z₂ denotes the observed values of these two statistics, then we could find joint lower confidence limits for ξ₁⩾ξ₂ by solving the equation

for which a more elaborate application of the approximations given below could be used. This would be a substantially more complex undertaking than what we have described above, both technically and in its interpretation, since it would lead to additional statistical issues of multiple comparisons. Hence we do not pursue it here.

One can obtain upper confidence limits by similar reasoning, although these seem less relevant to the current concerns. In the case of QTLs, they will often provide about the same information as the obvious inequality h²⩽H²=2ρ. For example, for Z_max=3.85 and k=1, the upper 95% confidence limit for h² is 0.43. For the qualitative trait mentioned above, the upper confidence limit for the apparent λ_S would be 1.75.

In applications there will be numerous complicating features to the simple model discussed above. Those that make the true distribution of maxZ_t stochastically smaller than the nominal distribution will make the lower confidence limit conservative (i.e., smaller). The most important of these are incompletely informative markers that are analyzed by multipoint analysis with parents also genotyped. The analysis of Teng and Siegmund (1999) suggests that the effect is not large if markers are reasonably informative and closely spaced. In the QTL case, major genes also tend to make the distribution of maxZ_t stochastically smaller than nominal. As shown by Tang and Siegmund (2001), the effect is small unless there are rare additively acting alleles of large effect or a substantial level of dominance. More bothersome is that under a variety of conditions the true distribution of maxZ_t can be stochastically larger, so the lower confidence limits would be anticonservative. If a relatively small number of large pedigrees are used, the central limit theorem will not apply, and the statistics Z_t may not be approximately normally distributed. Tang and Siegmund (2001) give a correction for the probability approximations described below that account for the dependencies of identity-by-descent counts within families. Features that would be more difficult to account for analytically are missing genotype information for substantial numbers of founders and radically nonnormal distributions for phenotypes in the QTL case.

To account for these and perhaps other complications, one may substitute simulations for the analytic approximations given below. This is a relatively simple matter for unlinked chromosomes, since then phenotypes and genotypes are unrelated, so the simulation requires only that the identity-by-descent counts be simulated under a suitable model of recombination for the marker informativeness actually obtained and (in the QTL case) associated at random to the phenotypes. The problem of simulation for linked chromosomes is more complicated in at least two respects: (i) one must choose a locus τ and a trial value of ξ (i.e., of underlying genetic parameters) and must iterate the simulation to obtain an approximate solution of equation (4); and (ii) in the QTL case, one must also choose a phenotype distribution. To minimize the number of iterations required, one can use the approximations given below to obtain a reasonable starting value for ξ. A flexible class of tractable phenotype distributions can be obtained from multivariate t distributions (Lange et al. 1989) with varying numbers of df (which include the normal distribution if one allows an infinite number of df) combined with the possibility of diallelic major genes. If the simulated probabilities are critically dependent on the distribution chosen for the phenotypes or on the specific location chosen for the gene (which might occur if marker information varies widely from one location to another), it is probably a danger signal, and the results should be interpreted with considerable caution.

Although it is the point of view of this report that confidence regions are generally more informative than hypothesis tests, there are legitimate reasons that hypothesis tests and the associated P values remain a primary mode of analysis. To obtain a locus-specific P value or a conservative approximation for a genomewide P value as a summary of the evidence against the hypothesis of no linkage, one need only assume the legitimacy of Mendel’s laws. Although the confidence limits given above are reasonably robust with regard to estimation of the noncentrality parameter ξ, conversion of bounds on ξ to bounds on genetically interpretable parameters (locus-specific heritability, risk ratios, etc.) requires a relatively specific model of the relation of genotype to phenotype and can be misleading if the underlying model is not at least approximately correct.

Appendix A

The following approximations are adapted from Feingold et al. (1993). Assume that markers are equally spaced at intermarker distance Δ on a genomic region consisting of C chromosomes of total genetic length L. Under the null hypothesis of no linkage

where Φ(x) and φ(x) are the standard normal cumulative and density function, respectively. The function ν is a discreteness correction for the distance Δ between markers. The defining expression can be found in Siegmund (1985, p. 82). For the purposes of this report, it is adequate to approximate ν(x) by exp(-0.583x).

For one linked chromosome, where the trait locus is assumed for simplicity to coincide with a marker locus and not to lie near the end of the chromosome, and the noncentrality at the trait locus equals ξ, we have

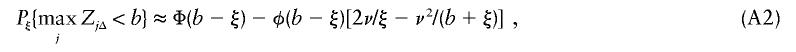where ν=ν(b{2βΔ}^1/2), as above and the maximum is taken over linked markers.

Given b, let Q₁(b,C,L) denote the probability in equation (A1) and Q₂(b,ξ) denote the probability in equation (A2). Then for equation (4) we use the approximation

One can also deal with the case when the trait locus is between marker loci. The result is more complicated and the consequence insignificant unless marker loci are widely spaced. For example, for Z_max=3.85 and an intermarker distance of Δ=10 cM, the 80% lower confidence limit for h² would be 0.23 if the trait locus is assumed to coincide with a marker locus and 0.26 if it lies midway between marker loci. The most conservative case is to assume that the trait locus coincides with a marker locus.