Skip to main content
PMC home page
Acta Orthopaedica logoLink to Acta Orthopaedica
. 2013 Dec 2;84(6):571–578. doi: 10.3109/17453674.2013.865097

Eliciting health state utilities for Dupuytren’s contracture using a discrete choice experiment

Ning Yan Gu 1,2,✉, Marc F Botteman 1, Robert A Gerber 3, Xiang Ji 1, Roelien Postema 4,5, Yin Wan 1, Grzegorz Sianos 6, Iain Anthony 6, Joseph C Cappelleri 3, Piotr Szczypa 7, Ben van Hout 8,9
PMCID: PMC3851672  PMID: 24286567

Abstract

Background and purpose

An internet-based discrete choice experiment (DCE) was conducted to elicit preferences for a wide range of Dupuytren’s contracture (DC)-related health states. An algorithm was subsequently developed to convert these preferences into health state utilities that can be used to assess DC’s impact on quality of life and the value of its treatments.

Methods

Health state preferences for varying levels of DC hand severity were elicited via an internet survey from a sample of the UK adult population. Severity levels were defined using a combination of contractures (0, 45, or 90 degrees) in 8 proximal interphalangeal and metacarpophalangeal joints of the index, middle, ring, and little fingers. Right-handed, left-handed, and ambidextrous respondents indicated which hand was preferable in each of the 10 randomly-selected hand-pairings comparing different DC severity levels. For consistency across comparisons, anatomically precise digital hand drawings were used. To anchor preferences onto the traditional 0–1 utility scale used in health economic evaluations, unaffected hands were assigned a utility of 1.0 whereas the utility for a maximally affected hand (i.e., all 8 joints set at 90 degrees of contracture) was derived by asking respondents to indicate what combination of attributes and levels of the EQ-5D-5L profile most accurately reflects the impact of living with such hand. Conditional logistic models were used to estimate indirect utilities, then rescaled to the anchor points on the EQ-5D-5L.

Results

Estimated utilities based on the responses of 1,745 qualified respondents were 0.49, 0.57, and 0.63 for completely affected dominant hands, non-dominant hands, or ambidextrous hands, respectively. Utility for a dominant hand with 90-degree contracture in t h e metacarpophalangeal joints of the ring and little fingers was estimated to be 0.89. Separately, reducing the contracture of metacarpophalangeal joint for a little finger from 50 to 12 degrees would improve utility by 0.02.

Interpretation

DC is associated with substantial utility decre- ments. The algorithms presented herein provide a robust and flexible framework to assess utility for varying degrees of DC severity.

Dupuytren‘s contracture (DC) is a fibroproliferative disorder whereby the disease progression leads to flexion contrac- tures (Dupuytren 1834, Bainbridge et al. 2012a, b, Dahlin et al. 2012). DC is more commonly observed in white, older, northern European men. However, higher risk of DC has been reported to be associated with comorbid conditions and life- styles (Loos et al. 2007). The flexion deformity of DC mainly affects the metacarpophalangeal (MCP) and/or the proximal interphalangeal (PIP) joints of the ring and little fingers (Dupuytren 1834, Loos et al. 2007). Clinically, the degrees of contractures of the MCP and PIP joints may be combined into Tubiana stages to define varying DC severity levels (Tubiana 1999).

Previous studies have assessed the burden of DC in terms of impaired health-related quality of life (HRQoL) and direct and indirect costs (Desai and Hentz 2010, Macaulay et al. 2012). Evaluation of different treatments for DC requires information on their relative HRQoL and eco- nomic benefits. In particular, cost-effectiveness evaluations of DC treatments require the use of preference-based health state utilities to compute quality-adjusted life years (QALYs) to capture the effect of treatments on the quality and the length of life simultaneously (Gold et al. 1996, Neumann et al. 2000, Brazier et al. 2009).

Although there is no cure for DC, several surgical or non- surgical (e.g., Clostridium histolyticum collagenase) treat- ments are available. Estimates of DC utilities and the extent to which treatments improve them can allow for more compre- hensive assessments of disease burden and treatment effect. However, directly measuring DC utilities is challenging, in part because DC severity depends on complex and varying associations of affected joints, fingers and hands. The impact of DC may vary according to age, sex, comorbidity, or lifestyle (e.g. the extent to which one‘s life or work environment requires hand functionality). If one were to actually measure the DC-related HRQoL and degrees of contracture among patients, prohibitively large sample sizes would be needed to control for heterogeneity.

A number of alternative preference assessment methods may be considered. Traditional health-state elicitation meth- ods such as standard gamble (SG) and time trade-off (TTO)– which require one to trade life-expectancy to avoid unfavor- able health states (Johnson et al. 2009)–may not be appropri- ate for the valuation of a disease that does not affect survival, such as DC. The discrete choice experiment (DCE) methodol- ogy is an ordinal measurement technique that does not suffer from this limitation. DCEs can be used in surveys to elicit healthcare consumer preferences by describing a health state using discrete combinations of attributes and levels (McFadden 1974, Louviere et al. 2000, Amaya-Amaya et al. 2008, Batley 2008). DCE has its theoretical basis in random utility theory and draws upon Lancaster‘s economic theory of value (Lancaster 1966, Burgess et al. 2006, Ryan et al. 2006). In economic research, the DCE approach was first used in the area of transportation and has been increasingly used in health economics research (Ryan et al. 2008, Street et al. 2008).

The advantage of DCE is that it requires less abstract reasoning from respondents as compared with direct elicitation techniques such as SG or TTO (Louviere et al. 2000, Ratcliffe et al. 2009). On the other hand, one ultimately needs to make assumptions about the distribution of the estimates from DCEs to be able to derive a scale. Additionally, DCE only derives indirect utility weights that are not readily comparable to traditional health state utilities. For instance, a value of 0.5 for a given health state on a TTO scale can be interpreted as one valuing 2 years in this health state equally as 1 year in perfect health. However, no such meaning can be directly given to the values on a DCE scale. We report herein a method to translate via an anchoring approach, indirectly elicited utility weights from a DCE into traditional health state utilities. Specifically, the state without any problems (i.e. the best health state) can be ascribed a value of 1 as a natural anchor at the top of the scale. The value at the bottom of the scale (i.e. the worst health state) can be obtained by describing this state based on respondents’ valuations on a generic measure of utility. One such measure is the EQ-5D-5L (van Hout et al. 2012), which assesses utility across 5 dimensions (mobility, self-care, usual activities, pain/ discomfort, anxiety/depression) using 5 response levels (no problems, slight problems, moderate problems, severe problems, and extreme problems). Respondents can then be asked to imagine themselves in the worst health state, and then indicate which combination of EQ-5D-5L domains and levels most accurately reflects this imagined health state. This information can subsequently be converted into a utility score using an EQ-5D-5L valuation algorithm proposed by van Hout et al. (2012). We emphasize that this is consistent with studies in which a crossover is established between disease- specific instruments and the EQ-5D-3L or SF-6D (Brazier et al. 2004, Gu et al. 2011, 2012, Gillard et al. 2012, Badia et al. 2013, Roset et al. 2013).

Methods

DCE design

To identify a set of attributes and levels that can adequately describe and delineate DC hand severities, a focus group (con- sisting of DC patients and their treating surgeons) was held at the Glasgow Royal Infirmary (Glasgow, UK; IRB approval: 10/S0704/27). The resulting set of attributes included the 8 PIP and MCP joints from the index, middle, ring, and little fingers (Table 1). The 8 joints were each characterized by 3 degrees of contracture: 0, 45, and 90 degrees (Table 1). These degrees of contracture were selected because they correspond to the pivotal contracture points used to define the Tubiana stages (Table 2). Distal interphalangeal (DIP) and thumb joints were excluded from the design because they are less- commonly affected by DC.

Table 1.

Attributes (8 joints) and levels (3 degrees of contracture) used in the DCE design

Attributes Levels
Joint #1: index finger, PIP joint 0, 45, 90 Inline graphic
Joint #2: index finger, MCP joint 0, 45, 90
Joint #3: middle finger, PIP joint 0, 45, 90
Joint #4: middle finger, MCP joint 0, 45, 90
Joint #5: ring finger, PIP joint 0, 45, 90
Joint #6: ring finger, MCP joint 0, 45, 90
Joint #7: little finger, PIP joint 0, 45, 90
Joint #8: little finger, MCP joint 0, 45, 90
Open in a new tab

Table 2.

Tubiana stages

Stage Description
0 (PIP+MCP) = 0
1 0 < (PIP+MCP) ≤ 45
2 45 < (PIP+MCP) ≤ 90
3 90 < (PIP+MCP) ≤ 135
4 135 < (PIP+MCP) ≤ 180
Open in a new tab

With 3 degrees of contracture and 8 joints, there were 6,561 (= 38) possible DC hand profiles considered. It was impractical to include all these hand profiles in the survey. Thus, we extracted a subset of 54 defined hand profiles (see Appendix A, supplementary data) using the orthogonal DCE fractional factorial design (Huber and Zwerina 1996, Kuhfeld 2005, Street et al. 2005, Johnson et al. 2006).

It was determined that respondents would need visual rep- resentations of the hand severity profiles because it would be cognitively demanding to compare textual descriptions of joints and degrees of contracture. Hence, hand profiles were described by anatomically consistent images rendered by a medical artist using a 3-dimensional hand model allowing for precise control of joint contracture for each finger.

Survey design

The survey was designed to elicit respondents‘ preferences for various levels of DC-associated hand impairments based on their stated preferences in a series of hypothetical choices between 2 hand profiles differing in degrees of contractures at the 8 PIP and MCP joints.

There were 54 DC hand profiles populating 27 choice sets. The choice set depicting profiles A and B was only used as a test to identify irrational respondents. Specifically, profile A had at least 1 “better” level on at least 1 attribute and no “worse” level on any of the other attributes compared to profile B. Hence, respondents who indicated a preference for profile B were considered “irrational” and thus excluded from the analysis.

The remaining 52 hand profiles were ranked by their sum of degrees of contracture to create 26 adjacent hand pairings with similar DC severity within each pairing. This step eliminated situations whereby an extremely affected hand might have otherwise been paired with a mildly affected hand. In addition, except for the choice set including profiles A and B used to test respondent rationality, none of the remaining sets contained unequivocally preferable (i.e. dominant) hands. This was to ensure that the necessary DCE design criteria would be satisfied (Huber and Zwerina 1996).

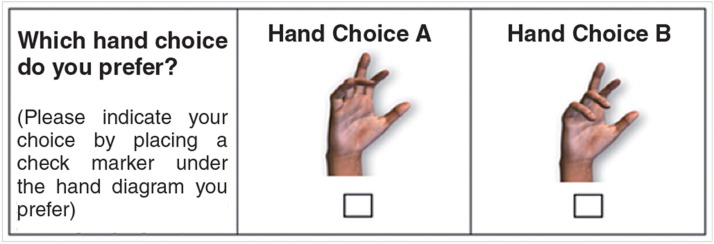
Each participant was required to indicate his/her preference in 10 choice sets (9 random choice sets plus the rationality test using profiles A and B). Therefore, after excluding the rationality test pair and using a sample of 2,000 respondents, each pair was expected be used 692 (= 2,000*9/26) times and a 35% (= 692/2,000 or = 9/26) chance to be drawn. An example survey question using profiles A and B is presented in Figure 1.

Figure 1.

Figure 1.

Open in a new tab

Sample DCE question for pairwise hand comparisons.

Sampling design

A cross-sectional, web-based survey was carried out in the UK by Survey Sampling International (SSI) (Rotterdam, the Netherlands). The sample was stratified by age and sex to be representative of the general adult population in the UK. Respondents were identified on the basis of their willingness to participate in previous SSI surveys and screened to verify eligibility for study participation.

Respondents first answered 11 background and eligibility screening questions, including: (1) country of residence, (2) country of citizenship, (3) gender, (4) age, (5) education level, (6) employment status / occupation, (7) handedness (right, left, or ambidextrous), (8) general health status, (9) whether the respondent had been diagnosed with DC or any other hand impairments, (10) whether the respondent knew or had known someone who had been diagnosed with DC, and if yes, (11) what was their relationship with that person.

Qualified respondents were adults (≥ 18 years old) who resided in England, Scotland, Wales, or Northern Ireland and who had passed the aforementioned rationality test. To minimize heterogeneity, we excluded respondents who had been previously diagnosed with DC or any other hand impair- ments. Additionally, we also excluded respondents who took an unreasonable amount of time to complete the survey (e.g. < 1 min or > 60 min).

Data analysis

Following data inspection, respondents meeting inclusion and exclusion criteria were identified. Descriptive analyses were conducted to examine sample characteristics. Each respondent provided responses for 10 pairs of discrete choice options. The dependent choice variable was binary-coded as 0 or 1 (1 = chosen; 0 = not chosen). Thus, we collected 20 responses from each respondent (10 chosen hands and 10 not chosen hands). Given the panel data structure, conditional logistic models (CLMs) were used to quantify the preferences, also called the indirect utility weights, for each joint‘s degree of contracture. This models the probability of an individual making the choice between 2 alternatives (McFadden 1974, Louviere et al. 2000, 2010). The explanatory variables were the attributes of modeled joints. Respondents‘ characteristics were not taken into account, as there were no plans to control for these to correct for a potential lack of representativeness for the whole population.

The joint model served as the primary model, which esti- mated the hand preferences on the basis of degrees of contracture of the 8 joints (i.e. 8 attributes). From this primary model, other hand impairment models can be developed. For instance, the Tubiana stage model is presented herein as an extension of the joint model. The Tubiana staging is presented in Table 2. In the Tubiana stage model, DCE preference estimates were made based on each of the 4 fingers instead of 8 joints. Thus, the impairments were the summed degrees of MCP and PIP joint contracture for each finger.

SAS 9.2 (SAS Institute Inc., Cary, NC. U.S.A.) was used for DCE design and data preparation. STATA 11 (StataCorp L P, College Station, TX, U.S.A.) was used for CLM estimation. Microsoft Excel was used for programming the mathematical link between the EQ-5D-5L health state utilities and DC severities, which were represented by varying joint or finger contractures.

Utility rescaling

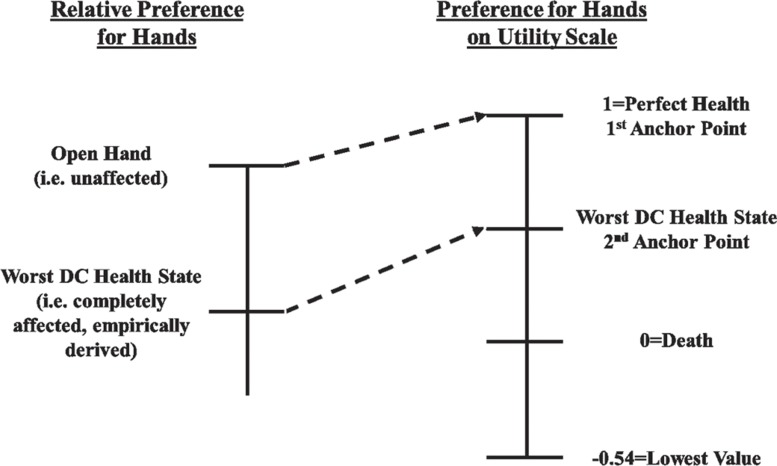
The analysis provided CLM regression estimates of preferences for modeled joints (using the joint model) or fingers (using the Tubiana stage model). However, this produced the indirect utility weights with no meaning on the utility scale needed for QALY computations. For this, at least 2 anchors were needed. No problems (i.e. a hand with no affected joints) were assigned the natural value of 1. A second anchor was obtained by asking respondents to imagine themselves living with a “DC hand” characterized by all modeled joints bent at 90 degrees (i.e. the worst state possible by design as shown in Figure 2) and subsequently indicate how living with this hand would affect their health status as described by the EQ- 5D-5L profile.

Figure 2.

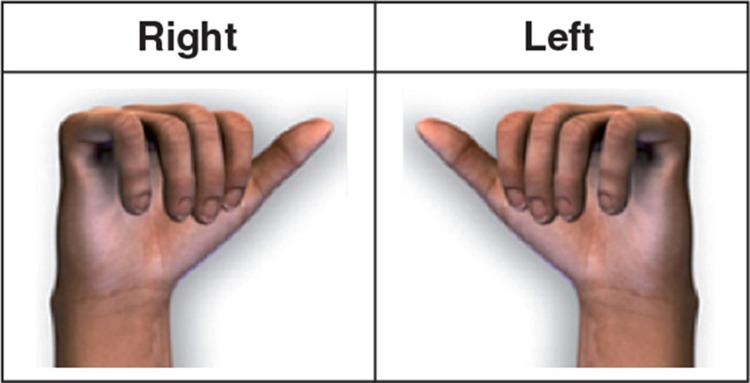
Figure 2.

Open in a new tab

The “worst” hands (right and left) used for anchoring.

Thus, to establish the worst health state anchor, respon- dents were first presented with the following prompt: “Imagine for a moment that you are currently in perfect health except that your RIGHT hand is affected by Dupuytren‘s contracture as shown in the diagram. Under each heading below, please select the option that best describes how your health would be with the affected hand.” The same question was repeated for the left hand. Respondents were also asked whether they were right- handed, left-handed, or ambidextrous. It was hypothe- sized that, all things being equal, health state utility values for DC-affected dominant hands would be worse than those for non-dominant and/or ambidextrous hands.

The 2-anchor rescaling approach is illustrated in Figure 3. The first anchor point was what was thought to be the best possible hand (with zero degrees of contracture in all joints, i.e. a normal hand). This best hand was assumed to be associated with a utility of 1.0 (holding other things constant). The second anchor point is the worst health-state anchor. Its utility was derived empirically on the basis of respondents' classifications of the worst possible hand (i.e. 90 degree contracture of all joints, Figure 2) on the EQ-5D- 5L profile (as described previously). Specifically, each respondent's assessment was converted into a utility using the algorithm reported by van Hout et al. (2012). The mean of these utilities was the utility for the second anchor point.

Figure 3.

Figure 3.

Open in a new tab

Utility rescaling method.

The estimated utility weights were subsequently rescaled to the 0–1 (“death–full health”) EQ-5D-5L utility values using equation (1).

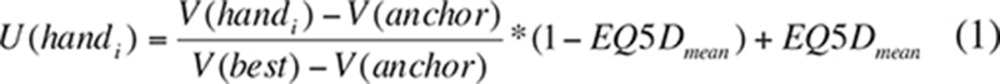graphic file with name ORT-84-571-e001.jpg

where U(hand i) = computed health utility value associated with hand i; V(hand i) = indirect utility weight for hand i from the CLM model estimate; V(best) = indirect utility weight for a hand without being affected by DC; V(anchor) = indirect utility weight associated with the worst (anchor) hand; EQ5D mean = the mean value of EQ-5D-5L utilities in referencing of the worst right/left hands.

Results

Of the 2,282 respondents, 1,745 (77%) satisfied inclusion/ exclusion criteria and were retained in the final analyses. Of the 537 excluded respondents (representing 24% of all respondents), 461 demonstrated "irrational" preferences (i.e., they chose the dominated profile B over profile A). The rest of excluded respondents used < 1 min or > 60 min to complete the survey.

Compared to excluded respondents, included respondents were older (48 vs. 44 years), were more likely to be female (53% vs. 47%), were more likely to be not working or to have unknown working status (57% vs. 49%), and approximately 60% in both groups had a college education or a higher degree.

The majority of the included sample was right-handed (87%) and had rated their health as being good or better (79%). Overall, 6.5% of the included sample indicated they knew or had known someone with DC. After excluding outliers for the time spent on the survey (< 1 min or > 60 min), the average time to complete the survey was approximately 3 min (Table 3, see supplementary data).

The CLM model estimates from the joint and the Tubiana stage models suggested that the increasing degrees of joint contracture were associated with decreasing preferences. In the joint model, respondents generally expressed greater preferences for the MCP joints than the PIP joints. In the Tubiana stage model, greater preference was placed on the ring finger. All estimated beta coefficients were significant (p < 0.001) (Table 4, see supplementary data).

The rescaled utilities using the EQ-5D-5L varied according to hand dominance (i.e. handedness). Specifically, when a hand had all 4 fingers (and 8 modeled joints) bent at 90 degrees, the utility value was 0.49 if the affected hand was dominant, 0.57 if the hand was non-dominant, and 0.634 if the person was ambidextrous. The results suggest that losing hand function in a dominant hand would have a greater effect on one‘s HRQoL than losing hand function in a non-dominant hand, or if the person was ambidextrous. The findings also suggest that right-handed respondents and left-handed respondents valued their dominant hands almost equally (0.51 vs. 0.47). Likewise, they also valued their non-dominant hand almost equally (0.58 vs. 0.56). Ambidextrous respondents showed almost equal preference regarding which hand would be affected (right hand: 0.63; left hand: 0.64). In addition, ambidextrous respondents indicated less disutility than non- ambidextrous respondents for more severe hand states. This was in line with the hypothesis that ambidextrous respondents would be able to replace the loss of functionality in one hand with functionality from the other (non-affected) hand (Table 5, see supplementary data).

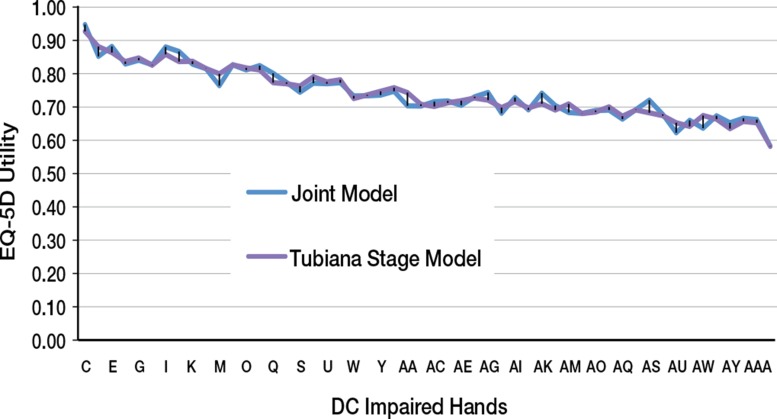
Figure 4 presents a comparison of dominant-hand utilities (y-axis) as estimated by the joint and Tubiana stage models for each of the 52 hands used in the survey (x-axis, hands C- AAB), ranked by summed degrees of contracture at all 8 joints. The y-axis represents the EQ-5D utility values with 1.00 = full health and 0 = death. Overall, the two models gave consistent results. Patterns of decreasing hand utility were observed as DC hand severity increased. Similar patterns were observed with the non-dominant and ambidextrous hand estimations (results not shown).

Figure 4.

Figure 4.

Open in a new tab

Rescaled EQ-5D-5L utilities for 52 DCE survey hands.

Using the algorithm developed herein, one can compute hypothetical marginal utility gains that would result from specific reductions in joint contracture of DC-impaired hands. For example, let us assume that an MCP joint of the little finger has 50 degrees of contracture (while the degrees of contracture in all other joints are zero) and that a treatment can reduce the contracture to 12 degrees. In this scenario, the estimated utility improvements associated with reducing the MCP's degree of contracture from 50 to 12 degrees with the joint and Tubiana models were + 0.022 and + 0.027, respectively, for a dominant hand; +0.019 and +0.023 for a non-dominant hand; and +0.016 and +0.019 for an ambidextrous person. As these results indicate, the marginal utility gains estimated via the Tubiana stage model were greater than those estimated with the joint model. This was not particularly surprising, as the Tubiana stage model is a simplification of the joint model. In the Tubiana stage model, reducing the degree of contracture of the MCP joint of a little finger from 89 degrees to 12 degrees would be associated with the same utility gain as reducing the contractures from 50 degrees to 12 degrees. In both scenarios, the improvement in the little finger‘s MCP joint is from Tubiana stage 2 to Tubiana stage 1, whereas when the joint model is used, every degree of contracture between 89 and 50 degrees and 50 and 12 degrees counts in the model estimation.

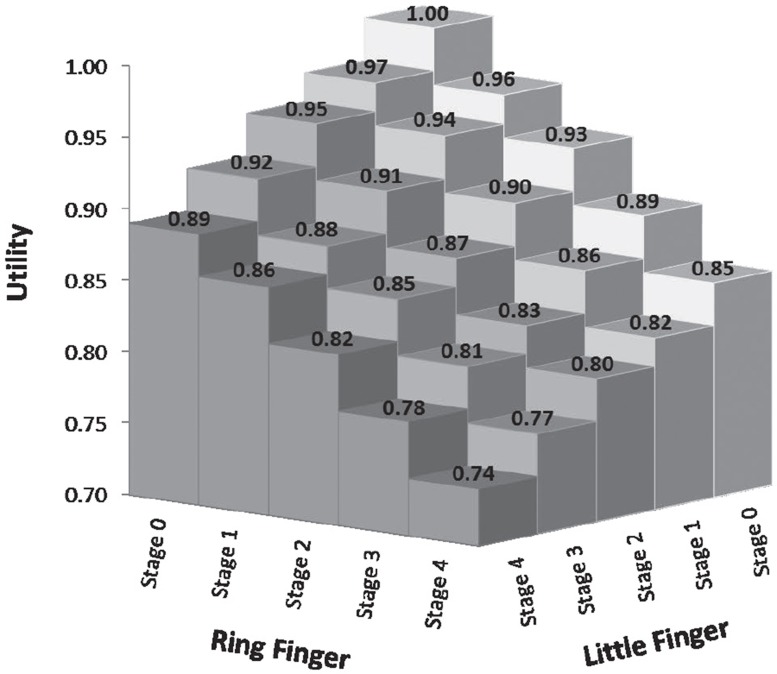
The present algorithm developed can estimate utility values for various DC hands severities based on different combinations of finger and/or joint contractures. Using the Tubiana stage model, for instance, the average EQ-5D-5L utility values for a dominant hand with different combinations of DC impairments in the little ring fingers (the 2 fingers most commonly affected by DC) showed that decreasing EQ-5D-5L utilities were associated with increase in Tubiana stage (i.e. increasing DC impairment), holding other joints constant at 0 degrees (Figure 5). For example, when both the little finger and the ring finger were at stage 4, the average utility was 0.74. When both fingers were at Tubiana stage 0, the average utility was 1.0 (i.e. full health) (Figure 5).

Figure 5.

Figure 5.

Open in a new tab

Average utilities for Tubiana stage combinations of the little and ring finger.

Discussion

In recent years, there has been increasing interest in the development and application of various quantitative methods to study individual choices and/or preferences to not only understand how choices are made but also to estimate the outcomes of these choices (Hensher et al. 2005). In health outcomes research, the DCE technique has been increasingly applied to assess individuals‘ preferences. One advantage of DCE in cases where the health states are mild and non-lethal is that this technique imposes no a priori assumptions compared to traditional elicitation techniques (Mentzakis et al. 2011), and therefore captures more reliable underlying health preference weights.

There is ongoing debate about how to rescale the DCE preference estimates into cardinal health utility values for computation of QALYs (Brazier et al. 2009, Ratcliffe et al. 2009). The technique used in this analysis is an innovative approach to directly rescale DCE estimates into health utility values using the EQ-5D-5L as an anchor. To the best of our knowledge, this is the first time such approach is used to develop an algorithm to estimate utilities for DC. There have been few publications reporting utilities related to DC-related impairments. Chen et al. (2011) conducted a comparative effectiveness study of 3 alternative methods for treatment of DC; they used the SG technique to elicit DC-procedure- related preferences for a dominant hand with only the little and ring only the little and ring fingers affected. Their SG questionnaire asked the respondents to choose between varying chances of cure (with or without complications) and varying chances of death. The resulting utilities had a minimum value of 0.971 for successful treatment with complications and 0.994 for successful treatment without any complications. When no treatment was given, the preference measure was 0.987. The major difference between our study and Chen et al. (2011) is the choice of elicitation technique (i.e. DCE combined with anchoring on the EQ-5D-5L vs. SG). The use of SG is perhaps a less appropriate elicitation technique in the case of a non-lethal condition such as DC. In addition, in the present approach, a multi-attribute framework is used whereby DC severity can be defined according to any degree of contracture in up to 8 joints from 4 fingers for dominant, non-dominant, or ambidextrous hands. This allows for the assessment of utilities for a wide range of DC severities, which would be more difficult to accomplish using a traditional SG approach.

Our DCE results demonstrated that the respondents could distinguish between--and state--preferences for DC-affected pairs of hands that differed in severities. The elicitation tech- nique we adopted was intended to impose minimum cogni- tive burden on respondents. All DCE properties were satisfied in our study. We had balanced and sufficient responses on all profiles (Appendix C) and choice sets (Appendix D). The esti- mated results were statistically significant and consistent for computation of health state utilities that vary by DC severity. Moreover, our findings suggest that the health state utilities associated with the impairment of a DC hand could be estimated flexibly with the algorithms presented herein.

Appendix B-1 illustrates how to calculate health state utili- ties for two different dominant hands (i.e., hands #1 and #2). Both the joint and Tubiana stage models are used for illus- tration. For hand #1, DC impairments are located in the PIP joint of the index finger, the PIP and MCP joints of the middle finger, and the MCP joint of the little finger. Referencing Table 2 for Tubiana stages, these impairments correspond to Tubiana stages 2, 3, 0, and 1 for the index, middle, ring, and little fingers, respectively. The estimated and rescaled utility for hand #1 is 0.82 using the joint model, and 0.83 using the Tubiana stage model. Hand #2 has MCP joints contracted to 90 degrees for the ring and the little fingers. Again, referencing Table 2, the corresponding Tubiana stages for the index, middle, ring, and littler fingers are 0, 0, 2, and 2, respectively. The estimated utility is 0.89 in both models. Using Appendix B-2, equation (1), and coefficient estimates from CLM (Table 4), one may follow how a utility value of 0.82 was derived.

It is important to note that the 54 hand profiles selected for the survey were designed to capture as wide a range of DC severity as possible while satisfying the DCE design criteria. Thus, in the models, each joint or finger is subject to approximately equal chance of being affected by the disease. While this approach may satisfy the methodological requirements of the present DCE, it produced representations of DC hands that may sometimes be considered clinically uncommon or unrealistic. However, as demonstrated in Appendices B-1 and B-2, any degree of DC impairments associated with PIP or MCP joints of the index, middle, ring, or little fingers can be calculated using the algo- rithms presented here. Such calculations can be performed separately for a dominant hand, a non-dominant hand, or an ambidextrous hand. Considering the diversity and number of attributes (i.e., contracture degree, joints, fingers, and hands) included in our analysis, our algorithm provides a flexible and robust framework to estimate utilities for DC hands in future studies. For instance, in Appendix B-1, hand #1 was a modeled hand of our design (hand “P”, see Appendix A). The DC impairment for this hand could be viewed as a rare case empirically. However, hand #2 might represent a more realistic case because the ring and the little fingers are the fingers most commonly affected by DC.

It is also important to note that the method used to link DC hand severity to the EQ-5D-5L utilities did not require respondents to provide answers regarding their own current state of health but rather to imagine how a DC-affected hand would affect one's health status as described by the EQ-5D-5L profile. Our study had some limitations. First, to minimize redundancy and respondent burden, the graphical hands used were based on a right hand and no separate elicitations were done using a left hand. It is possible that preferences elicited with right-handed illustrations represent a different burden of illness for right-handed respondents compared to left-handed respondents. Nevertheless, the potential bias may be mitigated by the subsequent EQ-5D-5L exercise, where both a right hand and a left hand was used for the rescaling purpose.

Secondly, we used a standard CLM model rather than a more general model with possibly varying parameters because the need to specify parameter distributions for the more gen- eral approach may give rise to model mis-specification. Given that our interest laid primarily in the mean values, the ben- efit of using a more complex modeling approach is therefore questionable. Furthermore, using the standard CLM assumes that modeled joints and fingers were relatively independent and that there was no correlation between the joints and degrees of contractures and other factors not included in the model. For instance, we explored incorporating interactions between joints and fingers in the model, but the results were not superior to those from the main effects model that we used in the study, whereas the use of interactions introduced a great amount of complexity to the algorithms.

We also did not investigate the 461 respondents (20%) who were excluded from the study (20%) on the grounds of irrationality. It is important to note that this test was also designed to determine whether respondents were paying attention to the hand comparisons. Although this proportion of respondents would be able to serve as a comparison group for the respondents who did not fail the test and who were included in the final analysis, a number of reasons justify the decision not to pursue these comparisons: (1) choice behavior analysis and comparison was not our primary study objective; rather, we needed a set of quality- controlled data to develop the working algorithms to derive hand utilities; (2) we had a sufficient sample size (n =1,745) to perform the main analysis after excluding the disqualified respondents, and (3) the exclusion rate reported from the existing literature after performing a similar rationality test ranged from 27% (Richardson et al. 2009) to as high as 44% (San Miguel et al. 2005). We therefore did not consider the exclusion rate (on the basis of rationality) to have been abnormal.

Finally, although the models developed herein are innovative, the rescaling algorithm is sample-dependent by design. To overcome this limitation, we collected data using a sufficiently large sample size across the UK, but it is possible that different results could have been obtained with another sample. Testing and validation of our algorithms and models in other studies is strongly encouraged.

To conclude, our study has provided innovative research methods and the best available evidence to date on how to estimate values linking severity of DC with average popula- tion values. While findings suggest that DC may have a large impact on HRQoL, the magnitude of the effect will depend on the number of joints affected, the degree(s) of contracture, and the hand affected. Based on this study, successful treatment of DC may result in substantial gains in HRQoL. The algorithms developed from this study can assist clinicians in evaluating the burden of disease by looking at the effects of DC on HRQoL, but most importantly can also provide a reliable method of assessing the effectiveness (i.e. utility improvement) of DC therapies based on simple clinical measures such as affected hands, fingers, joints, degrees of contracture, and/ or Tubiana scores.

Acknowledgments

NYG, MFB, RAG, JCC, and BvH initiated and designed the study. RP and IA worked on organizing the focus group meeting and obtaining the IRB approval. NYG, RP, GS, IA, PS, and BvH conducted the focus group meet- ing. NYG, MFB, and XJ carried out the pilot testing and analyzed the data. NYG planned the manuscript. MFB, RAG, JCC, and BvH made significant contributions to the manuscript. All the authors critically reviewed it.

This study was sponsored by Pfizer Inc. NYG, MFB, XJ, YW, and BvH are employees of Pharmerit International, which was paid a consulting fee by Pfizer Inc. for this study and in relation to the development of the manuscript. NYG was the Senior Scientist at Pharmeit International when this project was conducted; she is currently assistant professor at University of New Mexico. RP was a Research Consultant at Pharmerit International when this project was conducted; she is currently at Eli Lilly and Company in the Netherlands. GS and IA are researchers from Glasgow Royal Infirmary Hospital, which was contracted by Pharmerit International to conduct the focus group meet- ing in that hospital. RAG, JCC, and PS are employed by and have shares in Pfizer Inc. FD Sante, Ltd provided medical art for a fee. The authors thank Akshay Kharat of University of New Mexico and John Carter of Pharmerit International for editorial assistance in preparation of the manuscript. No remuneration was provided for AK’s assistance.

Supplementary data

Tables 3–5 and Appendices A, B-1, B-2, C, and D are available at Acta’s website (www.actaorthop.org), identification number 6066.

Click here for additional data file. (972.8KB, pdf)

References

  1. Amaya-Amaya M, Gerard K, Ryan M. Discrete choice experiments in a nut- shell. In: Using discrete choice experiments to value health and health care: The economics of non-market goods and resources (eds Ryan M, Gerard K, Amaya-Amaya M) . Springer, The Netherlands. 2008;1:13–46. [Google Scholar]
  2. Badia X, Roset M, Valassi E, Franz H, Forsythe A, Webb SM. Mapping CushingQOL scores to EQ-5D utilityvalues using data from the European Registry on Cushing‘s syndrome (ERCUSYN) . Qual Life Res. 2013 doi: 10.1007/s11136-013-0396-7. Epub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bainbridge C, Dahlin LB, Szczypa PP, Cappelleri JC, Guerin D, Gerber RA. Current trends in the surgical management of Dupuytren‘s disease in Europe: an analysis of patient charts . Eur Orthop Traumatol. 2012a;3:31–41. doi: 10.1007/s12570-012-0092-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bainbridge C, Gerber RA, Szczypa PP, Smith T, Kushner H, Cohen B, Grav- erand-Gastineau M. Efficacy of collagenase in patients who did and did not have previous hand surgery for Dupuytren‘s contracture . J Plast Surg Hand Surg. 2012b;46(3-4):177–83. doi: 10.3109/2000656X.2012.683795. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Batley R. On ordinal utility, cardinal utility and random utility . Theory and Decision. 2008;64:37–63. [Google Scholar]
  6. Brazier JE, Kolotkin RL, Crosby RD, Williams GR. Estimating a pref- erence-based single index for the impact of weight on quality of life-lite (IWQOL-Lite) instrument from the SF-6D . Value Health. 2004;7(4):490–8. doi: 10.1111/j.1524-4733.2004.74012.x. [DOI] [PubMed] [Google Scholar]
  7. Brazier J, Rowen D, Yang Y, Tsuchiya A. Using rank and discrete choice data to estimate health state utility values on the QALY scale . MPRA Paper 29891, University Library of Munich, Germany. 2009.
  8. Burgess L, Street DJ, Viney R, Louviere J. Design of choice experiments in health economics. In: The Elgar Companion to Health Economics (Ed. Jones A) . Edward Elgar Publishing, Inc: Gheltenham, UK, Massachusetts, USA. 2006. pp. 415–26.
  9. Chen NC, Shauver MJ, Chung KC. Cost-effectiveness of open partial fas- ciectomy, needle aponeurotomy and collagenase injection for dupuytren contracture . J Hand Surg Am. 2011;36(11):1826–34. doi: 10.1016/j.jhsa.2011.08.004. [DOI] [PubMed] [Google Scholar]
  10. Dahlin LB, Bainbridge C, Szczypa PP, Cappelleri JC, Guerin D, Gerber RA. Current trends in the surgicalmanagement of Dupuytren‘s disease in Europe: the surgeon‘s perspective . Eur Orthop Trauma. 2012;3:25–30. doi: 10.1007/s12570-012-0091-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Desai SS, Hentz VR. Collagenase clostridium histolyticum for Dupuytren‘s contracture . Expert Opin Biol Ther. 2010;10(9):1395–404. doi: 10.1517/14712598.2010.510509. [DOI] [PubMed] [Google Scholar]
  12. Dupuytren B. Permanent retraction of the fingers, produced by an affection of the palmar fascia . Lancet. 1834;2:222–5. [Google Scholar]
  13. Gillard PJ, Devine B, Varon SF, Liu L, Sullivan SD. Mapping from disease- specific measures to health-state utility values in individuals with migraine . Value Health. 2012;15(3):485–94. doi: 10.1016/j.jval.2011.12.007. [DOI] [PubMed] [Google Scholar]
  14. Gold MR, Siegel JE, Russell LB, Weinstein MC. Cost-effectiveness in health and medicine . New York: Oxford University Press. 1996.
  15. Gu NY, Botteman MF, Ji X, Bell C, Carter JA, van Hout B. Mapping of the insomnia severity index and other sleep measures to EuroQol EQ-5D health state utilities . Health Qual Life Outcomes. 2011;9(1):119. doi: 10.1186/1477-7525-9-119. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gu NY, Bell C, Botteman MF, Ji X, Carter JA, van Hout B. Estimating preference-based EQ-5D health state utilities or item responses from neu- ropathic pain scores . Patient. 2012;5(3):185–97. doi: 10.1007/BF03262491. [DOI] [PubMed] [Google Scholar]
  17. Hayton MJ, Gray I CM. Dupuytren‘s contracture: a review . Curr Orthop. 2003;17(1):1–7. [Google Scholar]
  18. Hensher DA, Rose JM, Greene WH. Applied choice analysis: A primer. Cambridge, UK: Cambridge, University Press . 2005.
  19. Huber J, Zwerina K. The importance of utility balance in efficient choice designs . J Marketing Resh. 1996;33:307–17. [Google Scholar]
  20. Johnson FR, Kanninen B, Bingham M, Ozdemir S. Experimental design for stated choice studies. In: Valuing environmental amenities using stated choice studies (ed Kanninen B J) . Springer. 2006. pp. 159–202.
  21. Johnson FR, Hauber AB, Ozdemir S. Using conjoint analysis to estimate healthy-year equivalents for acute condition: an application to vasomotor symptoms . Value Health. 2009;12(1):146–52. doi: 10.1111/j.1524-4733.2008.00391.x. [DOI] [PubMed] [Google Scholar]
  22. Kuhfeld WF. Marketing research methods in SAS: TS-722. SAS Institute Inc.: Cary, NC, USA . 2005.
  23. Lancaster KJ. A new approach to consumer theory . J Polit Econ. 1966;74(2):132–57. [Google Scholar]
  24. Loos B, Puschkin V, Horch RE. 50 years‘ experience with Dupuytren‘s con- tracture in the Erlangen University Hospital – A retrospective analysis of 2919 operated hands from 1956 . BMC Musculoskeletal Disorders. 2007;8(60) doi: 10.1186/1471-2474-8-60. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Louviere JJ, Hensher DA, Swait JD. Stated choice methods: Analysis and application . Cambridge, UK, Cambridge University Press. 2000.
  26. Louviere JJ, Pihlens D, Carson R. Design of discrete choice experiments: a discussion of issues that matter in future applied research . J Choice Model- ling. 2010;4(1):1–8. [Google Scholar]
  27. Macaulay D, Ivanova J, Birnbaum H, Sorg R, Skodny P. Direct and indirect costs associated with Duypuytren‘s contracture . J Med Econ. 2012;15(4):664–71. doi: 10.3111/13696998.2012.670678. [DOI] [PubMed] [Google Scholar]
  28. McFadden D. Conditional logit analysis of qualitative choice behavior . Aca- demic Press. 1974.
  29. Mentzakis E, Ryan M, McNamee P. Using discrete choice experiments to value informal care tasks: exploring preference heterogeneity . Health Econ. 2011;20(8):930–44. doi: 10.1002/hec.1656. [DOI] [PubMed] [Google Scholar]
  30. Neumann PJ, Goldie SJ, Weinstein MC. Preference-based measures in eco- nomic evaluation in health care . Annu Rev Public Health. 2000;21:587–611. doi: 10.1146/annurev.publhealth.21.1.587. [DOI] [PubMed] [Google Scholar]
  31. Ratcliffe J, Brazier J, Tsuchiya A, Symonds T, Brown M. Using DCE and ranking data to estimate cardinal values for health states for deriving a preference-based single index from the sexual quality of life questionnaire . Health Econ. 2009;18(11):1261–76. doi: 10.1002/hec.1426. [DOI] [PubMed] [Google Scholar]
  32. Richardson G, Bojke C, Kennedy A, Reeves D, Bower P, Lee V, Middleton E, Gardner C, Gately C, Rogers A. What Outcomes are important to patients with long term conditions? A discrete choice experiment . Value in Health. 2009;12(2):331–9. doi: 10.1111/j.1524-4733.2008.00419.x. [DOI] [PubMed] [Google Scholar]
  33. Roset M, Badia X, Forsythe A, Webb SM. Mapping CushingQoL scores onto SF-6D utility values in patients with Cushing‘s syndrome . Patient. 2013 doi: 10.1007/s40271-013-0010-7. Epub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Ryan M, Gerard K, Currie G. Using discrete choice experiments in health economics. In: The Elgar companion to health economics (Ed Jones A) . Edward Elgar Publishing, Inc: Gheltenham, UK; Massachusetts, USA. 2006. pp. 405–13.
  35. Ryan M, Watson V, Gerard K. Practical issues in conducting a discrete choice experiment. In: Using discrete choice experiments to value health and health care: The economics of non-market goods and resources (Eds Ryan M, Gerard K, Amaya-Amaya M) . Springer, The Netherlands. 2008. pp. 73–97.
  36. San Miguel F, Ryan M. Amaya-Amaya M. ‘Irrational‘ stated preferences: a quantitative and qualitative investigation . Health Economics. 2005;14:307–22. doi: 10.1002/hec.912. [DOI] [PubMed] [Google Scholar]
  37. Street DJ, Burgess L, Louviere JJ. Quick and easy choice sets: Constructing optimal and nearly optimal stated choice experiments . Intern J of Research in Marketing. 2005;22:459–70. [Google Scholar]
  38. Street DJ, Burgess L, Viney R, Louviere JJ. Designing discrete choice experiments for health care. In: Using discrete choice experiments to value health and health care: The economics of non-market goods and resources. (Eds Ryan M, Gerard K, Amaya-Amaya M) . Springer, The Netherlands. 2008. pp. 47–72.
  39. Tubiana R. Dupuytren‘s disease of the radial side of the hand . Hand Clin. 1999;15(1):149–59. [PubMed] [Google Scholar]
  40. van Hout B, Janssen MF, Feng YS, Kohlmann T, Busschbach J, Golicki D, Lloyd A, Scalone L, Kind P, Pickard AS, Interim scoring for the EQ- 5D-5L: mapping the EQ-5D-5L to EQ-5D-3L value sets . Value Health. 2012;15(5):708–15. doi: 10.1016/j.jval.2012.02.008. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (972.8KB, pdf)

Articles from Acta Orthopaedica are provided here courtesy of Nordic Orthopaedic Federation

RESOURCES