Thermodynamic contribution and nearest-neighbor parameters of pseudouridine-adenosine base pairs in oligoribonucleotides

Pseudouridine (Ψ) is the most common noncanonical nucleotide in naturally occurring RNA. This study examines the thermal stability of Ψ-A base pairs and A-U base pairs and demonstrates that Ψ-A base pairs are more stable. These findings will enable improved secondary structure prediction for A-form RNAs containing Ψ-A base pairs.

Abstract

Pseudouridine (Ψ) is the most common noncanonical nucleotide present in naturally occurring RNA and serves a variety of roles in the cell, typically appearing where structural stability is crucial to function. Ψ residues are isomerized from native uridine residues by a class of highly conserved enzymes known as pseudouridine synthases. In order to quantify the thermodynamic impact of pseudouridylation on U-A base pairs, 24 oligoribonucleotides, 16 internal and eight terminal Ψ-A oligoribonucleotides, were thermodynamically characterized via optical melting experiments. The thermodynamic parameters derived from two-state fits were used to generate linearly independent parameters for use in secondary structure prediction algorithms using the nearest-neighbor model. On average, internally pseudouridylated duplexes were 1.7 kcal/mol more stable than their U-A counterparts, and terminally pseudouridylated duplexes were 1.0 kcal/mol more stable than their U-A equivalents. Due to the fact that Ψ-A pairs maintain the same Watson-Crick hydrogen bonding capabilities as the parent U-A pair in A-form RNA, the difference in stability due to pseudouridylation was attributed to two possible sources: the novel hydrogen bonding capabilities of the newly relocated imino group as well as the novel stacking interactions afforded by the electronic configuration of the Ψ residue. The newly derived nearest-neighbor parameters for Ψ-A base pairs may be used in conjunction with other nearest-neighbor parameters for accurately predicting the most likely secondary structure of A-form RNA containing Ψ-A base pairs.

INTRODUCTION

RNA is an important class of biomolecules ubiquitous to all forms of life. RNA plays crucial roles in virtually all steps of protein synthesis, including, but not limited to, acting as the transcript of DNA (mRNA), gene regulation (siRNAs and snRNA), the recognition and delivery of amino acids to the ribosome (tRNA), and the creation of peptide bonds in nascent proteins (rRNA). RNA also may act as the genetic material for viruses that utilize reverse transcription to create complementary DNA copies that can subsequently commandeer cellular machinery for viral synthesis and propagation. Like its more stable, genomic counterpart, DNA, RNA is typically composed of four canonical nucleotides that pair via hydrogen bonding: guanosine, cytidine, adenosine, and uridine. However, unlike DNA, RNA may contain a wide variety of modified, noncanonical bases that may contribute special structural or catalytic properties, allowing RNA to serve in the variety of aforementioned processes. These modified nucleotides are the product of RNA-editing enzymes that chemically modify specific bases as part of the process of producing mature RNA (Grosjean et al. 1998). Of the many modified nucleotides found in nucleic acids, pseudouridine (Ψ) is the most common and serves a variety of roles within the cell (Grosjean et al. 1998; Charette and Gray 2000; Ofengand et al. 2001; Del Campo et al. 2007).

Pseudouridine, as the name suggests, is a modification of the canonical uridine residue that is formed by a class of enzymes collectively known as Ψ synthases (Del Campo et al. 2007; Vaidyanathan et al. 2007). These highly conserved enzymes often modify a single specific uridine residue and function by detaching the residue's base from its sugar and “rotating” it 180° along the N3-C6 axis followed by reattachment of the base's 5-carbon to the 1′-carbon of the sugar (Fig. 1; Charette and Gray 2000).

FIGURE 1.

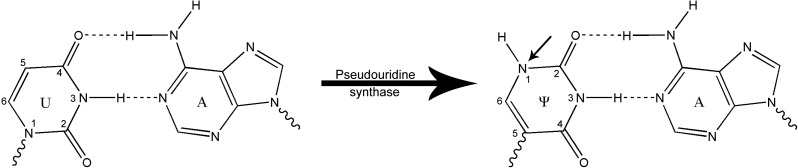
Pseudouridine (Ψ) synthases isomerize uridine residues, resulting in the creation of a new hydrogen bond donor (N1H) in the major groove of the Ψ-A pair (indicated by arrow).

The resultant Ψ residue features the same Watson-Crick hydrogen bonding capabilities as the parent uridine residue; however, an imino group (N1H) now resides at the position that C5 previously occupied, resulting in a new hydrogen donor that is situated in the major groove when in the preferred anti conformation (Charette and Gray 2000). This modification results in increased stability, attributed to the enhanced stacking between adjacent RNA bases (Davis 1995; Charette and Gray 2000), as well as the novel hydrogen bonding capabilities afforded by the N1H imino proton (Charette and Gray 2000; Ofengand et al. 2001). Although the N1 imino proton does not directly interact with Ψ’s pairing partner, it has been shown to coordinate a water molecule to the phosphodiester backbone of the RNA. The rigidity imparted by this novel interaction acts as an additional support to the backbone of the RNA, giving rise to a stabilizing effect that is propagated throughout the entire molecule (Hall and McLaughlin 1992; Charette and Gray 2000; Schroeder et al. 2005). Due to Ψ’s highly stabilizing nature, it is not surprising that this modified nucleotide very commonly appears in biochemical roles where structure is vital to function.

Ψ is found in virtually all organisms spanning all kingdoms of life, with a strong correlation between Ψ frequency and organism complexity (Ofengand et al. 2001). For example, prokaryotic Escherichia coli large subunit (LSU) rRNA contains 10 Ψ residues, whereas eukaryotic Homo sapiens LSU rRNA has 55 Ψ residues (Ofengand et al. 2001). In LSU rRNA, these residues have been shown to cluster at catalytically important sites such as the peptidyltransferase center, where nascent peptides are elongated (Bakin and Ofengand 1993; Bakin et al. 1994; Ofengand et al. 2001). In stark contrast, Ψ has not been found to cluster in functionally important domains in small subunit (SSU) rRNA and instead may act in the capacity of quality control factors (Ofengand et al. 2001; Vaidyanathan et al. 2007). For example, previous studies have shown that Ψ may be used to mark correctly folded precursory SSU rRNA as it proceeds through the stages of synthesis and assembly (Vaidyanathan et al. 2007). This suggests that Ψ may only act in structural or quality control roles in SSU rRNA, while LSU rRNA may employ Ψ for both structural and catalytic purposes. Irrespective of purpose or point of modification, deletion of certain Ψ residues on the ribosome has been shown to produce dominantly lethal mutants, likely due to improper manufacture or assembly of ribosomal subunits (Vaidyanathan et al. 2007). It is therefore vital to understand how pseudouridylation is able to impart stability and viability on a ribosome simply by isomerizing a native uridine residue.

Ψ is also thought to play an integral part in the stabilization of tRNA structure due to its ubiquitous presence in the TΨC loop of tRNAs, as well as its frequent presence in the anticodon-stem–loop (ASL) (Charette and Gray 2000). Experiments have shown that while E. coli lacking Ψ in the ASL are viable and therefore are able to maintain a functional structure, deletion results in retarded organism growth, increased translation errors, and lowered rates of polypeptide elongation (Davis and Poulter 1991). This is thought to be due to stabilization imparted by Ψ’s novel hydrogen bonding capabilities, resulting in more accurate and stable recognition interactions between tRNA and the ribosome (Davis and Poulter 1991). Notably, this property is exploited by the HIV genome, which relies on the stabilization afforded by the pseudouridylation of tRNA^Lys3 to act as a reverse transcriptase primer (Bilbille et al. 2009). Ψ may also play a prominent role in spliceosomal RNA responsible for gene regulation. Oftentimes, Ψ is present in regions involved in RNA–RNA or RNA–protein interactions that promote the assembly and reaction of a spliceosome to yield viable mRNA such as in AU/AC intron splicing. For example, Ψ has been shown to assist in the stabilization of snRNA/intron transition states during splicing, which allows a nucleophilic residue to assume a less-transient near-attack conformation (Charette and Gray 2000). Such splice site–specific Ψ residues are highly conserved in related species but vary between genera within a family (Charette and Gray 2000; Ofengand et al. 2001).

Given that structure–function relationships form the basis for current biochemical schools of thought, it is necessary to understand how base modifications affect RNA structure, stability, and function. Free energy minimization using the nearest-neighbor model is a common method of predicting RNA thermodynamics and the most likely secondary structure adopted by an RNA sequence (Xia et al. 1998; Wright et al. 2007). The nearest-neighbor model uses linearly independent thermodynamic parameters for consecutive base pairs in an RNA duplex to predict the change in enthalpy, entropy, and Gibbs’ free energy parameters. These nearest-neighbor parameters have been generated for each set of adjacent canonical RNA base pairs (Xia et al. 1998; Chen et al. 2012); however, parameters for adjacent base pairs containing modified bases are lacking. Recent efforts have yielded novel parameters for inosine (RNA nucleotide with hypoxanthine as the base) paired with uridine, which suggested that significant changes in thermodynamic stability are imparted by conversion of an A-U pair to an I-U pair (Wright et al. 2007). While previous studies have thermodynamically characterized molecules containing Ψ residues (Hall and McLaughlin 1991; Davis 1995; Sipa et al. 2007), linearly independent parameters for use in nearest-neighbor predictions have yet to be experimentally derived.

The availability of Ψ nearest-neighbor parameters would aid in the prediction of stability and structure for RNA containing Ψ residues. In particular, the availability of parameters characterizing Ψ-A base pairs would be of value because many uridine residues are paired with adenosine prior to pseudouridylation. Predictive Ψ-A nearest-neighbor parameters would also assist in the investigation of their suspected role in tRNA stabilization and recognition as well as the catalysis of spliceosomal RNA; the prediction of how secondary structure is dependent on pseudouridylation may elucidate Ψ’s role in these critical biological reactions and whether its role is catalytic, structural, or perhaps both. Additionally, comparison of Ψ-A to U-A base pairs could reveal how the isomerization of a uridine residue imparts enhanced hydrogen bonding, stacking, and major groove interactions, thus increasing our understanding of nucleic acid structure and stability as a whole.

This study reports linearly independent nearest-neighbor parameters for adjacent base pairs containing a Ψ-adenosine (Ψ-A) base pair. Oligoribonucleotides comprised of all possible Ψ-A nearest-neighbor pairs have been chemically synthesized, purified, and thermodynamically characterized by optical melting. The derived thermodynamic parameters were analyzed using linear regression to generate nearest-neighbor parameters for Ψ-A base pairs. These parameters aim to improve the efficacy of secondary structure prediction for RNA containing Ψ-A pairs and thus aid in elucidating the thermodynamic implications of adding Ψ-A base pairs to natural or synthetic RNA.

RESULTS

Thermodynamic parameters of duplexes containing Ψ-A pairs

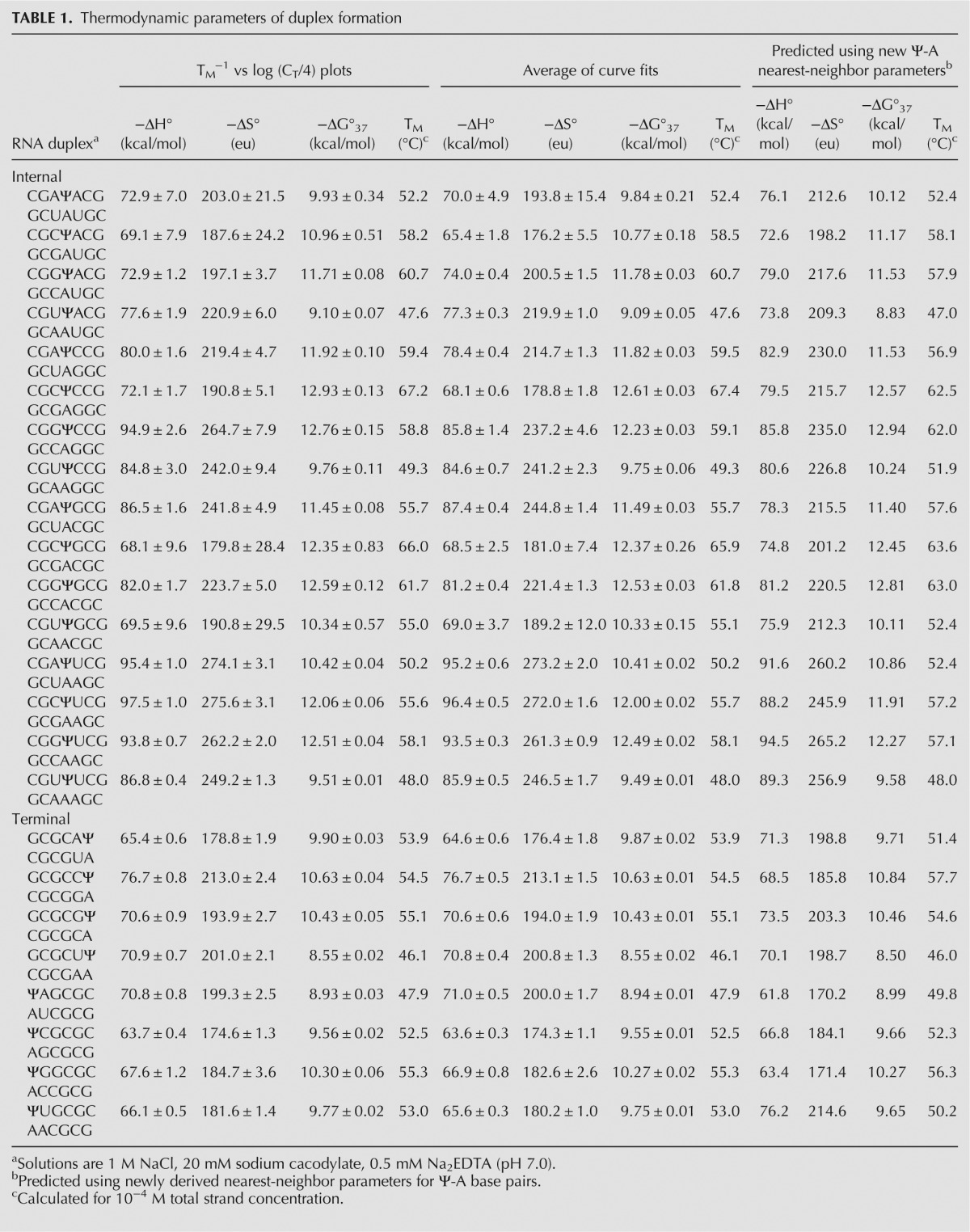
The thermodynamic parameters of duplex formation derived by fitting observed optical melting curves to a two-state model as well as from their corresponding van't Hoff (T_M vs. log(C_T/4)) plots are shown in Table 1. All van't Hoff plots exhibited a positive correlation coefficient of at least 0.95, with most being greater than 0.99, and all enthalpy values derived from the average of curve fits were within 15% of the enthalpy values derived from the van't Hoff plot, suggesting that all duplexes melted in a two-state manner (Schroeder and Turner 2009).

TABLE 1.

Thermodynamic parameters of duplex formation

Comparison of Ψ-A experimental free energies to U-A predicted free energies

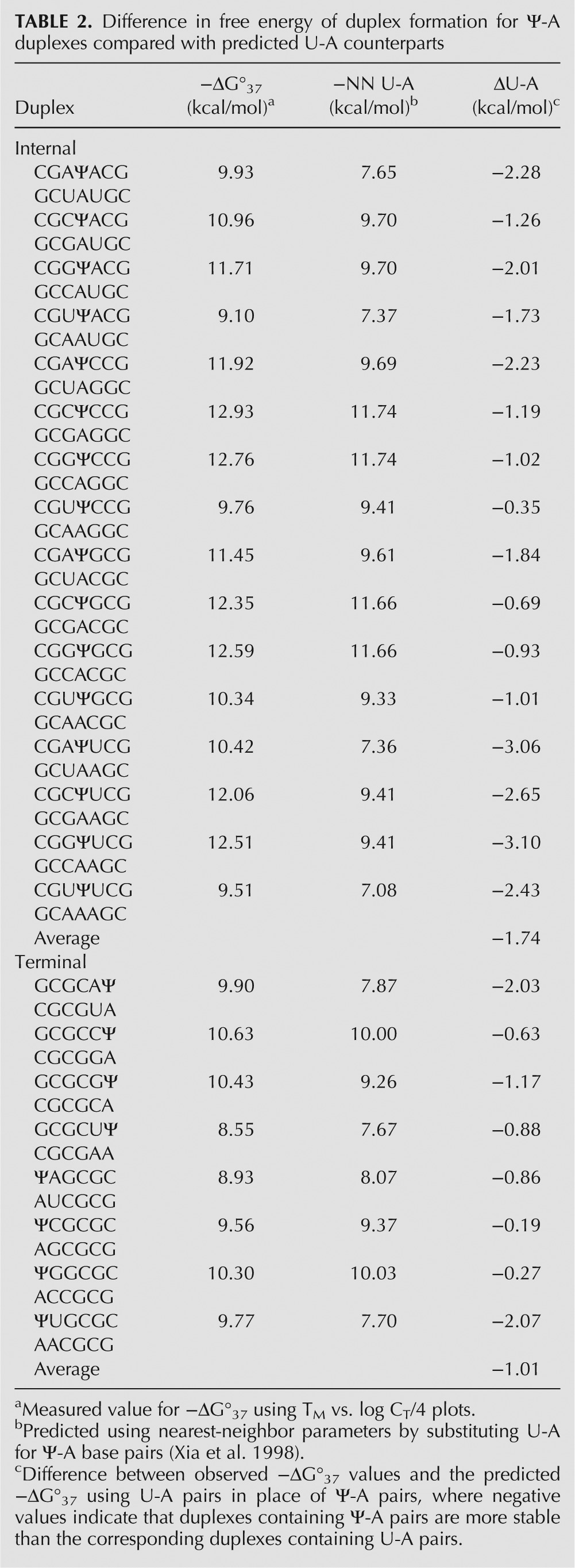
All of the duplexes containing Ψ-A pairs were more stable than what is predicted for the same duplexes containing U-A pairs (Table 2). Specifically, duplexes containing Ψ-A pairs are on average 1.7 and 1.0 kcal/mol more stable than what is predicted for the same duplexes containing internal and terminal U-A pairs, respectively. Similar calculations and comparisons for enthalpy and entropy are shown in Supplemental Tables S1 and S2.

TABLE 2.

Difference in free energy of duplex formation for Ψ-A duplexes compared with predicted U-A counterparts

Thermodynamic contribution of Ψ-A base pairs and derivation of nearest-neighbor parameters

The thermodynamic contribution of Ψ-A base pairs to duplex thermodynamics, calculated by subtracting Watson-Crick nearest-neighbor contributions from the measured duplex thermodynamics (as shown in Equation 4), is shown in Supplemental Table S3. As described in Materials and Methods, these values were used to generate linearly independent nearest-neighbor parameters for Ψ-A pairs (Table 3). All of the generated Ψ-A nearest-neighbor free energy contributions are more stabilizing than their canonical U-A equivalents (Table 3), with a general trend of increased stability afforded by 3′-stacked Ψ-A pairs compared with 5′-stacked Ψ-A pairs, as evidenced by the ranking order of 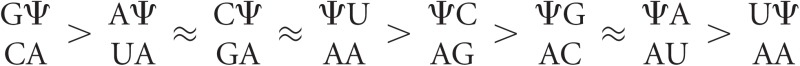(Supplemental Table S4). Specifically, the average value of 3′-stacked Ψ-A parameters was −2.62 kcal/mol, and the average for 5′-stacked Ψ-A parameters was −2.38 kcal/mol. This is in contrast with canonical U-A doublets where 3′-stacked U-A pairs contribute on average −1.59 kcal/mol and 5′-stacked U-A pairs contribute on average −1.68 kcal/mol (Xia et al. 1998). Additionally, the terminal Ψ-A penalty of 0.31 kcal/mol is less destabilizing than the 0.45 kcal/mol penalty assigned to terminal U-A pairs (Xia et al. 1998).

TABLE 3.

Experimentally derived nearest-neighbor parameters for Ψ-A pairs

The newly generated nearest-neighbor parameters for Ψ-A, in conjunction with previously generated parameters for canonical base pairs, can be used to predict thermodynamic parameters for any RNA duplex containing nonadjacent Ψ-A pairs using the nearest-neighbor model as described in Materials and Methods. These new parameters were used to predict the experimental thermodynamics of the duplexes studied here (Table 1), and average deviations between the experimental and predicted thermodynamics were 1.7% (0.15 kcal/mol), 6.7% (4.00 kcal/mol), and 8.0% (13.06 entropy units [eu]) for ΔG°₃₇, ΔH°, and ΔS° respectively. These deviations are comparable to previous models reported for canonical base pairs (3.2%, 6.0%, and 6.8%) (Xia et al. 1998), and inosine–uridine base pairs (5.1%, 4.6%, and 5.1%) (Wright et al. 2007).

DISCUSSION

Helix to coil transition of Ψ-A oligoribonucleotides

As stated in the Results, a positive correlation was observed between melting temperature and RNA concentration, suggesting duplex formation occurred instead of unimolecular folding. Additionally, all melt curves exhibited sharp first derivative plots with a single maximum, indicative of a single helix-to-coil transition. Lastly, all of the enthalpy values derived via van't Hoff analyses were within 15% of the enthalpy values derived from individual melt curve fits, also suggesting that the duplexes melted in a two-state manner (Schroeder and Turner 2009).

Comparison of Ψ-A stability to predicted U-A counterparts

Ubiquitously, duplexes containing Ψ-A base pairs were more stable than predicted for their canonical counterparts containing U-A pairs (Table 2). This is in agreement with previous studies that have shown that pseudouridylation almost always results in imparting stability that is not present with canonical U-A base pairs (with notable exception being pseudouridylation of nonclosing base pairs on some hairpins) (Meroueh et al. 2000; Ofengand et al. 2001). The source of this increased stability has been attributed to several different sources (Davis 1995; Charette and Gray 2000). Perhaps the most obvious source of stability is the creation of the new hydrogen bond donor at the relocated N1H imino group. Several studies have confirmed via temperature-dependent NMR studies that the N1H imino group coordinates a water molecule to the phosphodiester backbone of RNA. Furthermore, the structure of A-form RNA appears to be ideally suited to protect this coordinated water molecule from exchanging with bulk solvent by limiting access to the major groove, thus conferring exceptional stability due to this hydrogen bond (Hall and McLaughlin 1992; Schroeder et al. 2005).

Since the novel hydrogen bonding capabilities are unlikely to be the only contributor of stabilization in duplexes containing Ψ, an additional and likely source is enhanced stacking interactions. Previous studies involving NMR spectra of RNAs containing Ψ suggest that pseudouridylation causes the residue's sugar to favor the C3′-endo conformation by constraining the conformational freedom of the RNA (Davis 1998; Charette and Gray 2000), resulting in negentropy, which is consistent with our data (Supplemental Table S2). This entropic tradeoff is countered by the fact that the C3′-endo conformation is strongly correlated to enhanced stacking between the attached nucleotide and neighboring bases, with literature reporting a more pronounced enhancement on preceding, i.e., 5′, nucleotides (Davis 1995). This is mostly consistent with the derived Ψ-A nearest-neighbor parameters, which demonstrate stronger stabilization afforded by 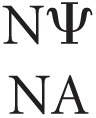(3′-stacking Ψ-A) parameters compared with the stability imparted by 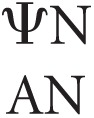(5′-stacking Ψ-A) parameters (Supplemental Table S4). This effect seems exclusive to Ψ-A stacking; when base pair order (and thus stacking) is reversed (i.e., going from the 5′ 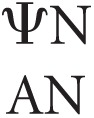doublet to the 3′ 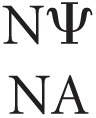doublet), there is a significant difference in stabilities of up to 1.1 kcal/mol (Equation 1):

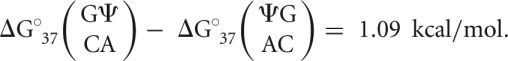(1)

This is strikingly different from canonical doublets containing U-A, which only display increased stability with more hydrogen bonding (i.e., a G-C base pair) and do not differ significantly (<0.30 kcal/mol) when the same stacking reversal is performed (Equation 2):

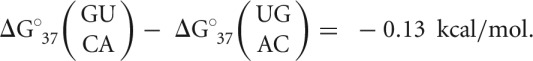(2)

Nearest-neighbor parameters for Ψ-A doublets

As can be seen in Table 3, the linearly independent nearest-neighbor parameters for internal Ψ-A base pairs contribute anywhere from −1.62 to −3.29 kcal/mol to duplex stability. This is in stark contrast to the analogous canonical U-A doublets, which only contribute −0.93 to −2.35 kcal/mol to duplex stability (Xia et al. 1998). Unexpectedly, Ψ-A doublets containing G-C pairs were not always more stable than those containing A-U pairs (as is the case with canonical bases) (Table 3; Supplemental Table S4), indicating that the stability pseudouridylation imparts is highly dependent on sequence and cannot simply be attributed to water coordination. This observation also suggests that pseudouridylation significantly alters Ψ’s stacking interactions. The penalty added for terminal Ψ-A pairs, 0.31 kcal/mol, is slightly less destabilizing than U-A pairs, suggesting that Ψ is not as susceptible to terminus-based destabilization (fraying) as U-A pairs are.

As stated previously, an unexpected feature of the derived Ψ-A parameters is that there is a significant difference between 5′- and 3′-stacked Ψ-A doublets (e.g., comparing vs. ) in stability contributed to duplex formation. This feature is not present in canonical doublets, which differ by <0.30 kcal/mol when the nucleotide order is reversed. Since a water-mediated hydrogen bond is likely to be constant and unaffected by neighboring intrastrand nucleotides, such a difference in energetics is likely due to novel stacking interactions as a result of the relocation of the N1 during pseudouridylation. Nucleotide stacking can be thought to be composed of multiple components, including electrostatics (dipole–dipole interactions) and electrodynamics (induced dipoles, van der Waals interactions, etc.) (Hill et al. 2003). It is particularly revealing to compare the electrostatic maps of uridine and Ψ, which were generated using atomic substitution in conjunction with previously optimized geometries for U (Johnson et al. 2011), operating under the assumption that Ψ assumes the same geometry as the parent U residue (Fig. 2). The relocation of the imino group during pseudouridylation likely leads to different stacking interactions between the resultant Ψ residue and neighboring bases due to the change in dipole and charge localization. For instance, the new electron-deficient imino group becomes situated exactly above the C5-C6 double bond of pyrimidines and directly above the electron rich ring system of purines when Ψ is 3′-stacked on these bases (Fig. 3A,B), possibly resulting in dipole interactions or increased polarizability and thus stronger van der Waals interactions, which are not present in uridine. Such an interaction would not be possible for 5′-stacked Ψ as the N1 is located in “dead space” and cannot directly stack with the neighboring nucleotide (Fig. 3C,D); this offers a convenient explanation for why 3′-stacked Ψ-A parameters tend to offer additional stability to duplex formation compared to their 5′-stacked counterparts. Another plausible mechanism of stabilization is that the relocated imino group is able to pull electron density away from the O4 of Ψ and thus reduce clashing with the O6 of a guanosine or O4 of a uridine in either direction. It should be noted that these preliminary electronic arguments are based on an assumption that Ψ adopts a similar geometry to U in an A-form duplex. It is unknown how correct this assumption is due to the fact that no structures in the Protein Data Bank contain Ψ without nearby motifs, ligands, etc., which may significantly perturb standard A-form geometry. Due to the unknown validity of this assumption and the fact that a thorough survey of Ψ electronic properties is beyond the scope of this investigation, such explanations for Ψ’s stability must be taken as purely hypothetical; however, electronic arguments offer a convenient starting point in justifying the large range of differences in stability observed for Ψ-A compared with U-A.

FIGURE 2.

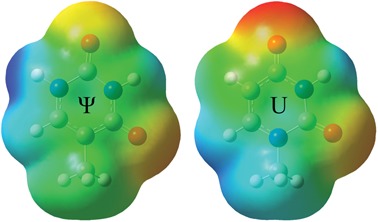
Electrostatic maps for Ψ and uridine using a methyl group to simulate the electronic contribution of the ribose ring. These maps were generated in Gaussian 09 (Frisch et al. 2009) using previously computed geometries for uridine (Johnson et al. 2011) with the corresponding atoms being substituted to produce Ψ.

FIGURE 3.

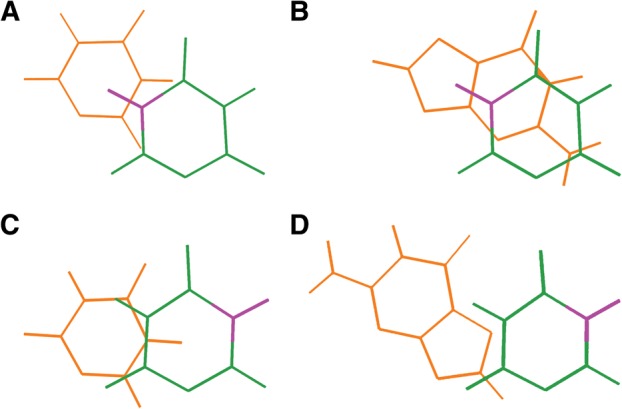
The ability of the relocated imino group (purple) on Ψ (green) to impact stacking interactions is likely decided by the positioning (5′ or 3′) of Ψ relative to the adjacent base (orange). Stacks shown are as follows: (A) 5′-UΨ; (B) 5′-GΨ; (C) 5′-ΨU; and (D) 5′-ΨG. These stacks were generated using InsightII (Accelrys) for geometries and PyMOL (Schrodinger 2010) for visualization.

Biochemical impact of Ψ-A nearest-neighbor parameters

Given the pervasiveness of Ψ residues in biological systems, the ability to predict the stability of pseudouridylated RNA may aid in both modeling RNA folding as well the design of synthetic RNA for use in laboratory or clinical settings. The newly derived parameters for Ψ-A pairs may be used to determine the stability of any RNA molecule containing nonconsecutive Ψ-A base pairs; specifically, free energy minimization can be used to predict how base modification affects RNA secondary structure, the strength of siRNA's base-pairing, or the stability of tRNA recognition interactions.

MATERIALS AND METHODS

Sequence selection, synthesis, and purification

Oligoribonucleotides containing Ψ-A pairs were designed to encompass all possible combinations of surrounding canonical base pairs, 16 internal Ψ-A duplexes, and eight terminal Ψ-A duplexes, including both 5′ and 3′ terminal Ψ-A pairs. The Ψ-A pair and adjacent base pairs were placed within a stem sequence that consists of G-C pairs. The G-C rich stem was chosen to ensure that the melting temperature would exceed 50°C to avoid issues with misalignment and nonduplex motif formation and to avoid fraying of duplexes during optical melting experiments. Predictive melting temperatures were calculated using nearest-neighbor values by substituting a U-A pair in place of the intended Ψ-A pair. Oligonucleotides containing Ψ were purchased from the Keck Lab at Yale University (New Haven, CT), and complementary strands containing standard nucleotides were ordered from Integrated DNA Technologies. Deprotection and purification of the oligoribonucleotides were performed using previously described, standard procedures (Wright et al. 2007).

Duplex formation, lyophilization, and reconstitution

Single-strand concentrations of the RNA were calculated according to the method previously described (Richards 1975) using the application RNACalc, except that the extinction coefficient for uridine (1.0 × 10⁴ M⁻¹ • cm⁻¹) was used instead of Ψ (8.1 × 10³ M⁻¹ • cm⁻¹) (Hall 1971). Absorbance readings were performed at 85°C in order to disrupt any undesired single-strand folding. Equimolar amounts of complementary single-stranded RNA were mixed to form double-stranded RNA (dsRNA). The total concentration of RNA was then assayed again at 85°C using the average of the single-strand extinction coefficients to calculate the total concentration of RNA. An appropriate volume was dried and reconstituted in 100 μL melt buffer (1 M NaCl, 20 mM sodium cacodylate, 0.5 mM disodium EDTA at pH 7.0); the volume of the aliquot was chosen to ensure that maximum absorbance would be ∼2 absorbance units during melting experiments.

Optical melting experiments

An optical melting scheme was devised that featured three melting experiments using three different concentrations for each melting experiment; successive experiments used the previous experiment's solutions mixed with more buffer to modify the concentration of dsRNA while keeping the salt concentration constant. This scheme resulted in nine different dsRNA concentrations that spanned an approximately 50-fold gamut. Each optical melting experiment was performed by monitoring the absorbance at 280 nm using a Beckman-Coulter DU800 spectrometer equipped with a Beckman-Coulter high performance temperature controller using a heating rate of 1°C/min from 10°C to 90°C.

Thermodynamic analysis of optical melting experiments

The optical melting curves obtained for each duplex were analyzed using MeltWin (McDowell and Turner 1996), which fits the sigmoidal melt curves to a two-state model by assuming linear sloping baselines, as well as temperature independent values for the standard entropy and enthalpy (Petersheim and Turner 1983; McDowell and Turner 1996). Thermodynamic parameters for the melt curves were calculated using the melting temperature (T_M) values at various concentrations according to the method described by Borer et al. (1974):

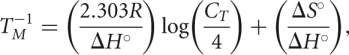(3)

where R is the gas constant 1.987 cal/mol*K. The change in Gibbs’ free energy at 37°C was calculated using the following equation:

(4)

Values calculated using the melt curve fits were found to be in excellent agreement with the T_M versus log C_T (van't Hoff) plots; however, only the thermodynamic parameters derived from the van't Hoff plots were used for later analyses.

Isolation of thermodynamic contribution of Ψ-A pairs

The observed thermodynamic parameters derived from the optical melting experiments were subjected to analysis using the nearest-neighbor model. Each duplex's thermodynamic contribution can be written in the following form, which sums the contributions of all nearest-neighbor interactions in the RNA duplex:

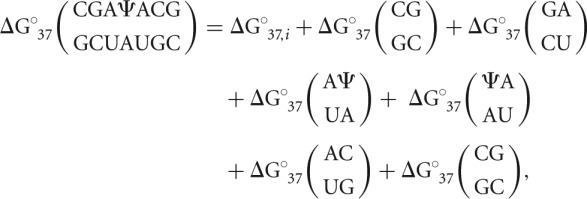(5)

where 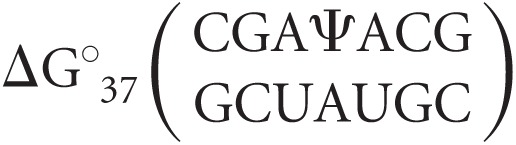is the observed Gibbs free energy change associated with the duplex (determined via optical melting), ΔG°_37,i is the free energy change penalty for duplex initiation (4.09 kcal/mol) (Xia et al. 1998), and all other parameters are individual nearest-neighbor contributions to the free energy change (Xia et al. 1998). The thermodynamic contribution of Ψ-A nearest-neighbor interactions were isolated for each duplex by subtracting off nearest-neighbor parameters for all canonical base pair doublets:

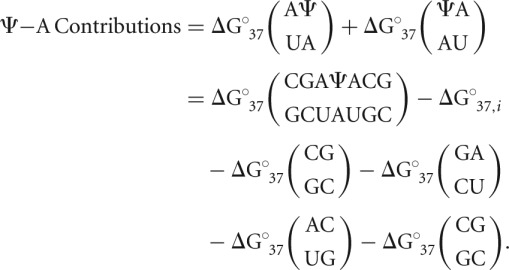(6)

For the duplexes with internal Ψ-A pairs, the value for Ψ-A contribution yielded by this operation contains two nearest-neighbor parameters, in this example, both 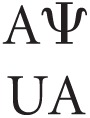and . The same operation performed on duplexes containing terminal Ψ-A pairs resulted in only one Ψ-A nearest neighbor. All of these Ψ-A nearest-neighbor values were then subjected to linear regression in order to determine linearly independent nearest-neighbor parameters. Similar analyses were performed for all duplexes to isolate the entropic and enthalpic contribution of the Ψ-A nearest-neighbor pairs.

Linear regression and derivation of linearly independent Ψ-A nearest-neighbor parameters

The isolated Ψ-A contributions for each duplex were assembled into a matrix in Microsoft Excel and subjected to linear regression using the LINEST function. The variables used in this analysis were all possible Ψ-A nearest-neighbor combinations and an additional terminal parameter if the thermodynamic value was contributed by a terminal Ψ-A pair. For instance, the Ψ-A contributions for the previously used example of would be as follows:

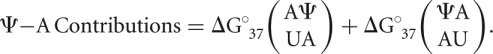(7)

These same analyses were performed for values for ΔH° and ΔS°. Linear regression of the entire data set yielded linearly independent nearest-neighbor parameters for all eight possible Ψ-A nearest-neighbor combinations as well as a penalty for a terminal Ψ-A pair.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article. Tables showing enthalpy and entropy comparisons, the isolated Ψ-A contribution to thermodynamics, and the rank order of canonical U-A nearest-neighbor pairs and newly derived Ψ-A nearest-neighbor pairs are available as supporting information in Microsoft Word format.