Mathematics is differentially related to reading comprehension and word decoding: Evidence from a genetically-sensitive design

Abstract

Although evidence suggests that individual differences in reading and mathematics skills are correlated, this relationship has typically only been studied in relation to word decoding or global measures of reading. It is unclear whether mathematics is differentially related to word decoding and reading comprehension. The current study examined these relationships at both a phenotypic and etiological level in a population-based cohort of 5162 twin pairs at age 12. Multivariate genetic analyses of latent phenotypic factors of mathematics, word decoding and reading comprehension revealed substantial genetic and shared environmental correlations among all three domains. However, the phenotypic and genetic correlations between mathematics and reading comprehension were significantly greater than between mathematics and word decoding. Independent of mathematics, there was also evidence for genetic and nonshared environmental links between word decoding and reading comprehension. These findings indicate that word decoding and reading comprehension have partly distinct relationships with mathematics in the middle school years.

There has been growing interest in the links between reading and mathematics, both to determine the factors contributing to individual differences in these domains and to better understand why children with reading difficulties often have co-occurring difficulties with mathematics. Much of this research has been hampered, however, by assessment issues. In particular, studies of reading and mathematics have typically used only a single measure of word decoding or a global measure, such as overall reading achievement. This is problematic because word decoding skills (word recognition) are demonstrably distinct from reading comprehension (e.g., Nation & Angell, 2006), and thus may have different relationships with mathematics. Clarifying the nature of the relationships among word decoding, reading comprehension and mathematics may provide a more solid understanding of reading and mathematics development. In the present study, we sought to examine the relationships among word decoding, reading comprehension and mathematics skill from both phenotypic and genetic perspectives. We focus specifically on the middle school years.

Word decoding, reading comprehension, and mathematics

Word decoding and reading comprehension are robustly correlated during middle childhood (e.g., Catts, Hogan, & Adlof, 2005; Betjemann, Willcutt, Olson, Keenan, DeFries & Wadsworth, 2008). This makes intuitive sense: when word decoding skills are weak, words are likely to be misidentified and fewer cognitive resources can be devoted to the processing of meaning. Moreover, word decoding and reading comprehension draw on many of the same skills, such as word knowledge, syntactic competence and verbal working memory. Nonetheless, word decoding and reading comprehension are also dissociable. Word decoding does not account for all of the variance in reading comprehension, indicating that the ability to recognize words does not guarantee comprehension (e.g., Catts et al., 2005; Cutting & Scarborough, 2006). In addition, the trajectories of word decoding and reading comprehension differ, with word decoding being the focus of early reading, and reading comprehension becoming more important once children have become relatively proficient at word decoding (Verhoeven & van der Leeuwe, 2008).

The high but imperfect association between word decoding and reading comprehension has led to growing recognition that the skills required for comprehending texts are partly distinct from those required for word decoding (Oakhill, Cain, & Bryant, 2003). According to the triangle model (Bishop & Snowling, 2004), word decoding depends on the ability to recognize the systematic correspondences between letters and phonemes (phonological processing), as well as exceptions to these regularities (orthographic knowledge). In learning to read, children gradually apply these skills with greater speed and accuracy so that words are recognized fluently and automatically. Reading comprehension, on the other hand, depends substantially on listening comprehension skills that enable the reader to form a coherent representation of the content of text (Rapp & van den Broek, 2005). For example, the reader must be able to derive the meanings of individual words and sentences, determine the key ideas or themes and make inferences to fill information that is implicit in text..

Against this background, the relationship of word decoding and reading comprehension to mathematics is intriguing. There is robust evidence for a phenotypic relationship between mathematics and reading, with studies reporting moderate to high correlations (~.24 to .62) (e.g., Durand, Hulme, Larking, & Snowling, 2005; Hart, Petrill, Thompson, & Plomin, 2009; Hecht, Torgesen, Wagner, & Rashotte, 2001). In most cases, these studies have focused on word decoding or global measures of reading, in conjunction with global measures of mathematics or arithmetic. Similarly, there is substantial comorbidity between difficulties in word reading and mathematics (e.g., Dirks, Spyer, van Lieshout, & de Sonneville, 2008; Landerl & Moll, 2011). The overlap between reading and mathematics has typically been attributed to language and working memory processes that are required for both, such as phonological processing skills (e.g., de Smedt et al., 2010; Hecht et al., 2001),

We argue that it is equally important to determine the relation of reading comprehension to mathematics. Recent evidence for a connection comes from Pimperton and Nation (2010), who examined the mathematical profiles of poor comprehenders aged 7-8 years. These children did not differ significantly from controls (matched for word decoding and nonverbal ability) on a numerical operations task, but they performed at a significantly lower level on a mathematical reasoning task. The authors argue that results from this study demonstrate that oral language may act as limiting factor on aspects of math that test children’s abilities through verbally-presented items, irrespective of basic arithmetic skills.

The importance of language for mathematics is particularly relevant in the middle school years. During this time, mathematical learning is principally concerned with developing mathematical reasoning skills and mastering complex mathematical procedures (e.g., multi-digit arithmetic) (Geary, 1994). These skills are typically taught and assessed using mathematical texts, which pose several challenges (Freitag, 1997). First, they tend to be very concise: each word and symbol must be read and understood with precision. Second, they use a high density of information-bearing words, including ‘everyday’ words with new meanings in mathematical contexts (e.g., product, odd, per). Third, mathematical texts often contain more concepts per sentence than other content areas, and complex grammatical processes are often used to compress complex ideas into just a few words (e.g., in “There is an even number between 200 and 300 that is divisible by 5 and 9; what is that number?”, divisible is shorthand for can be divided by). These characteristics place an onus on good reading skills. They also directly raise the question of whether word decoding and reading comprehension differ in their links with mathematics. To date, few studies have explicitly examined this issue. In the present study, we examine the links among mathematics, word decoding, and reading comprehension from a multivariate behavioral genetic perspective.

Behavioral genetic research on reading and mathematics

Multivariate behavioral genetic analysis decomposes the covariance among two or more phenotypic (observed) traits into genetic and environmental effects. In the case of word decoding and reading comprehension, we may expect that some of the genetic and environmental factors that contribute to individual differences in one domain also overlap with the other. Simultaneously, there may be sources of genetic and environmental variance specific to each. Multivariate genetic research does not identify the specific genetic and environmental factors involved, but it provides a window on the extent to which the relationships among two or more variables are due to common genetic or common environmental influences or both, which in turn may lead to new questions about the processes by which reading and mathematics are associated.

Most quantitative genetic studies of reading and mathematics have used the twin design, which takes advantage of the difference in genetic relatedness between monozygotic (MZ) and dizygotic (DZ). Specifically, this design yields estimates of the proportion of variance in the study population that is due to genetic and environmental influences. In general, twin studies of word decoding and reading comprehension show substantial genetic effects that are somewhat higher for word decoding (e.g., .68-.84) than for reading comprehension (e.g., .51-.67) (e.g., Betjemann, Keenan, Olson, & DeFries, 2011; Betjemann et al., 2008; Byrne et al., 2009; Byrne et al., 2007; Keenan, Betjemann, Wadsworth, DeFries, & Olson, 2006). For mathematical skills, genetic effects have varied widely, ranging from .20 to .90 (e.g., Hart, Petrill, & Thompson, 2010; Hart, Petrill, Thompson, & Plomin, 2009; Kovas, Haworth, Petrill & Plomin, 2007; Polderman, Huizink, Verhulst, van Beijsterveldt, Boomsma, & Bartels, 2011; Thompson, Detterman, & Plomin, 1991). Across both reading and mathematics studies, shared (between-family) environmental effects have tended to be small to moderate. All studies show nonshared (individual-specific) environmental effects and measurement error.

Several studies have examined the etiological relationships among various reading or mathematics ability tests. Typically these studies report genetic and environmental correlations, which index the extent to which the genetic or environmental influences on one trait correlate with those on a second trait. Genetic and environmental correlations can range from 1 (complete overlap) to 0 (no overlap). For reading, there is substantial genetic overlap between word decoding and reading comprehension (e.g., Betjemann et al., 2011, 2008; Byrne et al., 2007, 2009; Keenan et al., 2006). Furthermore, the magnitude of genetic overlap decreases over time, consistent with evidence that word decoding and reading comprehension correlate less highly as children move from an emphasis on word decoding to reading comprehension (e.g., Byrne et al., 2007; Betjemann et al., 2008, 2011; Keenan et al., 2006). The extent of environmental overlap is more difficult to determine: shared and nonshared environmental correlations, as well as their confidence intervals, have varied widely across studies. However, a majority of studies have reported substantial shared environmental overlap (Betjemann et al., 2008, 2011; Keenan et al., 2006), and significant nonshared environmental overlap between word decoding and reading comprehension (Betjemann et al., 2008, 2011; Byrne et al., 2007, 2009). For mathematics, we are aware of only one multivariate genetic study of different mathematical skills. In a sample of 10-year-old twins (n = 1,250 pairs) from the Twins Early Development Study (TEDS), Kovas and colleagues (2007) examined relationships among five mathematical tests: mathematical application, numerical knowledge, computation skill, mathematical interpretation, and non-numerical mathematical processes. These measures were almost perfectly correlated at a genetic level (mean r_A = .91). The substantial genetic correlation indicates that despite the putative differences among mathematical tests used in this study, the same genes largely affected individual differences in all five aspects of mathematics. Shared environmental correlations were generally high (mean r_C = .86; range = .61 - .99), but associated with substantial confidence intervals; nonshared environmental correlations were generally moderate (mean r_E = .24; range = .13 - .35).

A few multivariate studies have examined reading and mathematics simultaneously. Typically these have used general reading achievement test scores or composite scores, rather than separate measures of word decoding and reading comprehension. In the TEDS sample, genetic correlations between mathematics and reading were .75 at age 7 (Kovas, Harlaar, Petrill, & Plomin, 2005), .57 at age 10 (Davis et al., 2008) and .75 at age 12 (Davis, Haworth, & Plomin, 2009). Across these studies, shared environmental correlations were substantial (close to 1.00), while nonshared environmental correlations ranged from .15 to .59. An independent study of 6 to 12 year-old twins (n = 278 pairs) revealed a genetic correlation of .98, shared environmental correlation of .92 and nonshared environmental correlation of .28 between general measures of mathematics and reading achievement (Thompson et al., 1991). Using a sample of 15 to 18-year-old Australian twins (n = 400 pairs), Wainwright et al. (2004) examined the relationships among arithmetic and two tests of word decoding. The word decoding measures showed moderate genetic correlations with arithmetic (mean r_A = .56). No reading comprehension measures were available in this study, however.

To our knowledge, only one study has considered the relationship among mathematics and separate indicators of word decoding and reading comprehension. Hart et al. (2010) examined word decoding accuracy, word decoding fluency, reading comprehension, and mathematics in 9-year-old twins (n = 228 pairs). A single genetic latent factor was sufficient to account for the genetic covariance among these four domains. The three reading factors had high and similar loadings on the common genetic factor (above .80 for each), while the loading for mathematics on the common genetic factor was smaller but significantly different from zero (.45). Word decoding fluency and mathematics also showed factor-specific genetic variance, independent of the common genetic factor. All four factors loaded on a single common shared environmental factor, where loadings were moderate for word decoding accuracy (.29), word decoding fluency (.29), and reading comprehension (.39), and substantial for mathematics (.74). In contrast, there was little evidence for overlap at the level of nonshared environmental factors.

These findings present an intriguing picture. Word decoding and reading comprehension are substantially correlated at a phenotypic level, yet are also clearly distinct. Etiologically, they show substantial genetic correlations and moderate or substantial environmental correlations. The overlap between genetic and environmental factors across word decoding and reading comprehension is not perfect, however, indicating that there are genetic and environmental factors unique to both aspects of reading. It remains unclear whether word decoding and reading comprehension are differentially related to mathematics. The results of Hart et al. (2010) suggest that word decoding (whether assessed as accuracy or fluency) and reading comprehension show similar etiological relationships with mathematics; however, this is a single study.

The goal of the present study was to examine the etiology of the relationships among mathematics, word decoding, and reading comprehension at age 12. Do genetic and environmental associations between mathematics and reading vary depending on which aspect of reading is being assessed – word decoding or reading comprehension? Because multiple measures of reading and mathematics were available, we examined this question at the level of latent factors. The use of latent variables in a genetically-sensitive design is highly informative, because it enables us to focus on genetic and environmental influences that contribute to variance in the target ability (as indexed by the common variance among measures), independent of measure-specific variance and uncorrelated measurement error. In addition, estimates of relationships involving latent variables are more reliable (Loehlin, 2004).

METHODS

Participants

Twins in our sample were participating in TEDS, a longitudinal study of twins ascertained from population records of live twin births in England and Wales (Oliver & Plomin, 2007). Our study included 5162 twin pairs (794 male MZ pairs, 750 male DZ pairs, 1050 female MZ pairs, 914 female DZ pairs, and 1654 opposite-sex DZ pairs) who took part in assessments of reading and mathematics ability in TEDS between 11 and 12 years of age (M = 11.87 years; SD = .60 of testing). Zygosity of same-sex twin pairs was verified using DNA obtained from buccal swabs. For the purpose of this study, we excluded pairs in which one or both twins had a neurological condition or specific medical syndrome (e.g., cystic fibrosis, cerebral palsy, organic brain damage). We also excluded children whose first language in the home was not English.

Measures

Participants completed an online battery of cognitive, reading and mathematics ability tests (Haworth et al., 2007). All of the measures included in the current analyses come from this battery with the exception of the Test of Word Reading Efficiency (TOWRE), which was administered by telephone. Families who consented to participate in the web-based testing received a secure username and password for access to the test pages. Participants could attempt each test only once. Parents were asked to supervise the testing by ensuring that each twin completed the test alone and without knowledge of their co-twin’s responses. Telephone assessment of the TOWRE took place at approximately the same time as the web-based testing. Families who consented to participate in the telephone testing were mailed the test stimuli (one sealed envelope for each twin), which twins opened at the time of testing. Both twins in a pair were assessed by the same tester, who was blind to zygosity. Further details on the tests, including validity and reliability, is provided in Haworth et al. (2007).

Mathematics

Mathematics was assessed using three tests from the National Foundation for Educational Research 5-14 Mathematics Series (NferNelson, 2001). Understanding Number (33 items) requires an understanding of the numerical and algebraic process to be applied when solving problems. Computation and Knowledge (37 items) assesses the ability to recall mathematical facts and to perform straightforward computations. Non-Numerical Processes (25 items) requires understanding of non-numerical mathematical processes and concepts, such as rotational vs. reflective symmetry.

Word decoding

Word decoding was assessed using the Woodcock-Johnson III (WJ-III) Reading Fluency Test (Woodcock et al., 2001) and the Test of Word Reading Efficiency (TOWRE, Torgesen, Wagner, & Rashotte, 1999). The WJ-III Reading fluency test (98 items) requires participants to read and comprehend simple sentences quickly. The TOWRE assesses fluency and accuracy in word reading and phonemic decoding (167 items). Both the WJ-III Reading fluency test and the TOWRE have a 3 minute time limit.

Reading comprehension

Reading comprehension was assessed using the reading comprehension subtest of the Peabody Individual Achievement Test (PIAT_rc; Markwardt, 1997) and the GOAL Formative Assessment in Literacy for Key Stage 3 (Global Online Assessment for Learning, 2002). The PIAT_rc uses a multiple-choice picture format to test literal comprehension of sentences (82 items). The GOAL assesses both literal and inferential reading comprehension. Questions about words, sentences, and short paragraphs are asked (40 items in each category).

Analysis

The mathematics, word decoding and reading comprehension tests were used as indicators of latent phenotypic factors in structural equation models (SEM). Models were estimated from the raw data using full-information maximum likelihood (FIML), which yields maximum-likelihood estimates for the effects of interest while taking missing data into account. All analyses were undertaken in Mx (Neale, Boker, Xie & Maes, 2006). Two statistics were used to ascertain model fit: the Bayesian Information Criterion (BIC; Raftery, 1995) and the Deviance Information Criterion (DIC; Spiegelhalter, Best, Carlin, & van der Linde, 2002). These are indices of relative fit, where smaller values indicate better model fit (i.e., the model that reproduces the observed variances and covariances with as few unknown estimated parameters as possible). We designated model parameters as significant if their 95% confidence intervals (CI) did not include zero. For the purpose of analyses, scores were standardized on the whole sample to a mean of zero and a SD of 1. For the genetic analyses, scores were adjusted for age and sex (McGue & Bouchard, Jr., 1984).

RESULTS

Descriptive statistics and correlation analyses

Table 1 shows means and standard deviations for each measure by zygosity and sex. DZ twins scored higher on all measures, while boys scored higher on the mathematics measures and on PIAT_rc. However, all zygosity and sex differences were of small effect size (Cohen, 1992).

Table 1. Means and standard deviations by zygosity and sex.

	MZ		DZ		Cohen’s	Females		Males		Cohen’s
	M (SD)	N	M (SD)	N	D	M (SD)	N	M (SD)	N	D
Math1	−.03 (1.00)	3254	.02 (1.00)	5804	−.05	−.08 (.99)	4979	.10 (1.00)	4079	−.18
Math2	−.04 (.99)	3254	.02 (1.00)	5804	−.06	−.04 (.99)	4979	.05 (1.01)	4079	−.09
Math3	−.03 (.99)	3254	.01 (1.00)	5804	−.04	−.05 (.99)	4979	.06 (1.01)	4079	−.11
WD1	−.04 (.99)	3022	.02 (1.00)	5206	−.06	.05 (.99)	4527	−.07 (1.00)	3701	.12
WD2	−.03 (1.01)	3404	.02 (.99)	5956	−.05	.02 (.99)	5121	−.02 (1.01)	4239	.04
RC1	−.06 (1.01)	3430	.03 (.99)	6114	−.09	−.03 (.98)	5210	.03 (1.02)	4334	−.06
RC2	−.04 (1.00)	3496	.02 (1.00)	6234	−.06	.03 (.94)	5284	−.04 (1.06)	4446	.06

Note: Mathl = Understanding Number; Math2 = Non-Numerical Processes; Math3 = Computation and Knowledge; WD1 = TOWRE; WD2 = WJ-III Reading Fluency; RC1 = PIAT_rc; RC2 = GOAL.

Phenotypic analyses

Table 2 shows the correlations among the individual measures. The word decoding measures correlated moderately (.36 - .42) with the reading comprehension subtests. Correlations between the word decoding and mathematics subtests were also moderate (.27 - .35), and significantly lower than the correlations between reading comprehension and the mathematics subtests (.46 – .51). There was little differentiation in the correlations between the reading and mathematics subtests, with one exception: the two word decoding measures showed significantly lower correlations with Non-Numerical processes than with Understanding Number and Computation and Knowledge, whereas the two reading comprehension measures showed similar correlations with the three mathematics subtests.

Table 2. Phenotypic correlations among mathematics and reading measures (95% CI in parentheses).

	Math 1	Math 2	Math 3	WD 1	WD 2	RC 1
Math2	.66 (.65, .67)
Math3	.72 (.71, .73)	.60 (.59, .61)
WD1	.35 (.33, .36)	.28 (.26, .30)	.34 (.32, .35)
WD2	.35 (.33, .36)	.27 (.25, .28)	.32 (.30, .33)	.60 (.58, .61)
RC1	.51 (.50, .52)	.48 (.47, .49)	.48 (.46, .49)	.36 (.34, .37)	.36 (.35, .38)
RC2	.51 (.49, .52)	.49 (.48, .51)	.46 (.45, .47)	.40 (.38, .42)	.42 (.40, .43)	.57 (.55, .58)

Note: Mathl = Understanding Number; Math2 = Non-Numerical Processes; Math3 = Computation and Knowledge; WD1 = TOWRE; WD2 = WJ-III Reading Fluency; RC1 = PIAT_rc; RC2 = GOAL.

The next step was to examine the relationships among mathematics, word decoding, and reading comprehension at the level of latent factors that represent the variance common to the measures used to assess each skill domain. We applied a Cholesky decomposition model (Neale & Cardon, 2002), analogous to a hierarchical regression model within an SEM framework (see Figure 1). To ensure model identification, the variance of each latent factor was constrained to unity and residual influences on the measures were not estimated. In addition, because we only had two measures per factor for word decoding and reading comprehension, we imposed equality constraints on the factor loadings for these factors. No constraints were placed on the factor loadings for the mathematics factor, which was indexed by three measures.

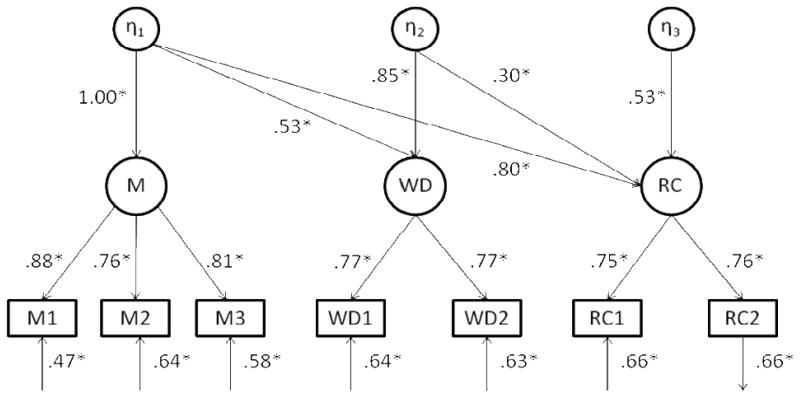
Figure 1.

Phenotypic Cholesky decomposition model. Measured variables are: Math1 = Understanding Number; Math2 = Non-Numerical Processes; Math3 = Computation and Knowledge; WD1 = TOWRE; WD2 = WJ-III Reading Fluency; RC1 = PIAT_rc; RC2 = GOAL. Asterisk indicates estimate is significantly greater than zero (p < .05).

The predictor factors were entered in the following order: mathematics, word decoding, and reading comprehension. This order was chosen in order to focus the analysis on: (1) the overall associations among mathematics, word decoding, and reading comprehension; and (2) the relationship between word decoding and reading comprehension independent of mathematics. Squaring the factor loadings indicates that the mathematics tests accounted for between 58% and 78% of the variance in the mathematics factor, the word decoding tests each accounted for about 60% of the variance in the word decoding factor, and the reading comprehension tests accounted for about 57% of the reading comprehension factor.

The first second-order factor (n₁), indexed by mathematics, accounted for 28% (CI: .27, .31) of the variance in word decoding and 64% (CI: .61, .68) of the variance in reading comprehension. Independent of mathematics, there was a second factor (n₂) that accounted for 72% (CI: .69, .74) of the variance in word decoding and 9% (CI: .07, .16) of the variance in reading comprehension. The third factor (n₃) accounted for the remaining variance in reading comprehension (27%; CI: .20, .30), representing the variance in reading comprehension independent of both word decoding and mathematics. Overall, these results indicate that mathematics, word decoding, and reading comprehension are separable factors.

Phenotypic correlations among the latent factors were substantial. Mirroring the pattern of correlations among the measured variables (Table 2), the association between mathematics and reading comprehension (.79, CI: .77, .80) was significantly greater than the association between mathematics and word decoding (.51; CI: .49, .53). Word decoding and reading comprehension were substantially correlated (.66; CI: .64, .68).

Genetic analyses

The next stage of our analyses was quantitative genetic modeling (description and assumptions are provided in Plomin, DeFries, McClearn, & McGuffin, 2008). Table 3 shows the MZ and DZ correlations for each measure. The MZ correlations were uniformly higher than the DZ correlations, whereas the DZ correlations were greater than half the MZ correlations. These findings implicate both genetic and shared environmental contributions to the variance of each measure. Additionally, MZ correlations are less than unity, the expected value if these measures were entirely determined by genetic and shared environmental influences, thus suggesting non-shared environmental influences and measurement error. Inspection of MZ and DZ correlations by gender and twin type (male MZ pairs, female MZ pairs, male DZ pairs, female DZ pairs, and opposite-sex DZ pairs) revealed no evidence for either quantitative or qualitative sex differences in genetic and environmental influences on any measure (details available from the first author).

Table 3. Intraclass twin correlations and proportion of variance due to A, C, E (95% CI in parentheses).

	Mathl	Math2	Math3	WD1	WD2	RC1	RC2
			Twin correlations
MZ	.62 (.59, .65)	.55 (.52, .59)	.57 (.53, .60)	.77 (.74, .79)	.72 (.70, .74)	.46 (.42, .50)	.56 (.52, .59)
n pairs	1627	1627	1627	1511	1702	1715	1748
DZ	.39 (.36, .42)	.35 (.32, .38)	.32 (.29, .36)	.39 (.36, .42)	.41 (.38, .44)	.30 (.27, .33)	.37 (.33, .40)
n pairs	2902	2902	2902	2603	2978	3057	3117
		Proportion of variance due to A, C, E
a2	.47 (.38, .53)	.42 (.34, .49)	.50 (.42, .56)	.74 (.68, .76)	.64 (.59, .70)	.34 (.27, .42)	.37 (.30, .44)
c2	.16 (.10, .23)	.15 (.08, .21)	.08 (.03, .14)	.02 (.01, .08)	.08 (.03, .13)	.13 (.04, .19)	.18 (.13, .24)
e2	.37 (.35,.40)	.44 (.41, .47)	.42 (.40, .45)	.24 (.22, .25)	.28 (.26, .30)	.53 (.50, .56)	.45 (.42, .47)

Note: Mathl = Understanding Number; Math2 = Non-Numerical Processes; Math3 = Computation and Knowledge; WD1 = TOWRE; WD2 = WJ-III Reading Fluency; RC1 = PIAT_rc; RC2 = GOAL.

Estimates for the proportion of variance in each measure due to A, C, and E (also shown in Table 3) confirm the pattern suggested by the twin correlations. All measures showed significant genetic influences, which accounted for around 46% of the variance in the mathematics tests, 36% of the variance in the reading comprehension tests, and around 69% of the variance in the word decoding tests. The genetic effects on word decoding were significantly greater than those on mathematics and reading comprehension. Shared environmental influences had small effects (c² = .02 - .18), whereas the effects of nonshared environmental influences (which include measurement error) were moderate (.27 - .49).

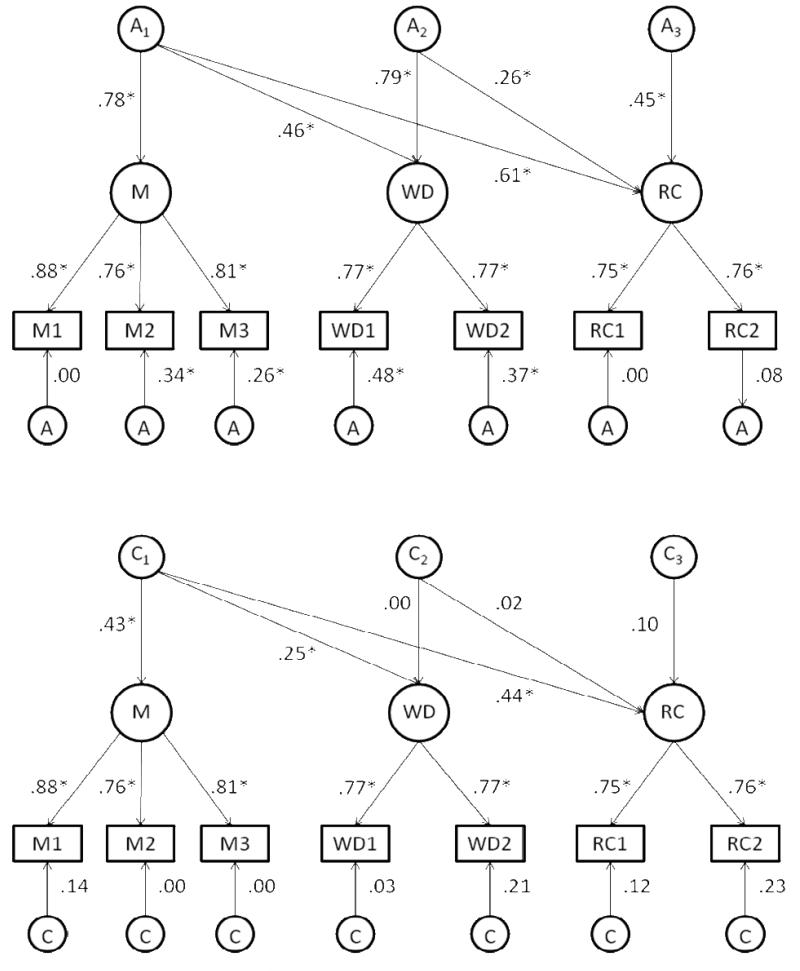
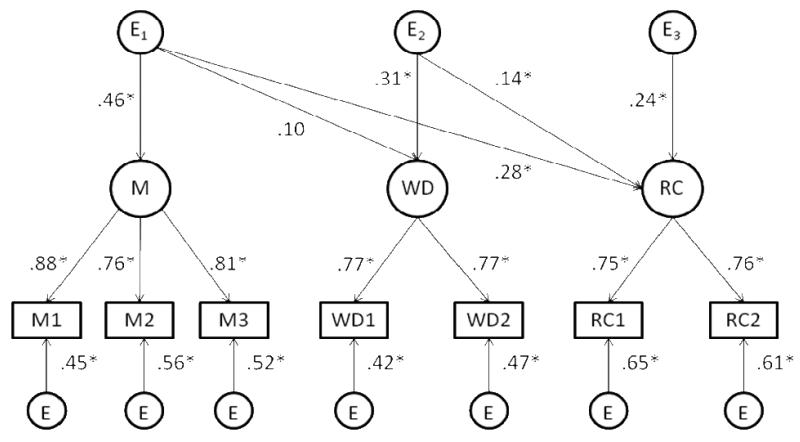
We next used multivariate genetic model-fitting to examine the relationships among mathematics, word decoding, and reading comprehension. Our baseline model (shown in Figure 2), is an extension of the phenotypic Cholesky decomposition model. Within this model, the variance and covariance among the three phenotypic factors is decomposed into A, C, and E effects (for clarity, these are shown in the top, middle, and lower panels, respectively). Because A, C, and E are not measured directly, but inferred from pattern of twin similarity, they do not have a natural scale; consequently, we fixed the total variance (i.e., the sum of A, C, and E) within each measure to equal unity.

Figure 2.

Standardized path coefficients from genetic Cholesky decomposition model of mathematics (M), word decoding (WD), and reading comprehension (RC) (shown for one member of a twin pair). Measured variables are: Math1 = Understanding Number; Math2 = Non-Numerical Processes; Math3 = Computation and Knowledge; WD1 = TOWRE; WD2 = WJ-III Reading Fluency; RC1 = PIAT_rc; RC2 = GOAL. Asterisk indicates estimate is significantly greater than zero (p < .05).

From our baseline model, we estimated the proportion of the total variance in each phenotypic factor due to A, C, and E (shown in Table 4). These estimates can be obtained from the standardized path coefficients in Figure 2. The total genetic variance in each factor is equal to the sum of the squared standardized path coefficients associated with that factor. For mathematics, this is simply the square of A₁ (i.e., .776² = .60). For word decoding, the total genetic variance is the sum of the squared estimates for A₁ and A₂ (i.e., .457² + .791² = .83). For reading comprehension, the total genetic variance is the sum of the squared estimates for A₁, A₂, and A₃ (.603² + .259² + .454² = .64). Analogous calculations were used to derive estimates of the proportion of variance in each latent factor due to shared environmental and nonshared environmental factors. These estimates are shown in boldface in the lefthand column of Table 4. Mathematics, word decoding, and reading comprehension each showed substantial genetic effects that accounted for most of the variance in the measures. Both shared and nonshared environmental effects were small but significant. There were few differences across measures, although word decoding showed significantly higher heritability (.84) compared with mathematics (.60) and reading comprehension (.64).

Table 4. Proportion of variance in latent mathematics (Math), word decoding (WD) and reading comprehension (RC) factors due to A, C, E, and squared estimates from Cholesky decomposition analysis for A, C, E (95% CI in parentheses).

	Proportion of variance due to  A, C, E	Squared estimates from Cholesky decomposition analysis   (breakdown of a2, c2, e2 for each factor)
Effects of A	a2	A1	A2	A3
Math	.60 (.53, .67)	.60 (.53, .67)
WD	.83 (.78, .88)	.20 (.16, .27)	.63 (.54, .66)
RC	.64 (.53, .73)	.36 (.29, .45)	.07 (.04, .09)	.21 (.12, .25)
Effects of C	c2	C1	C2	C3
Math	.18 (.12, .24)	.18 (.12, .25)
WD	.07 (.02, .14)	.07 (.02, .12)	.00 (.00, .07)
RC	.20 (.13, .28)	.20 (.11, .28)	.00 (.00, .09)	.00 (.00, .08)
Effects of E	e2	E1	E2	E3
Math	.22 (.19, .24)	.22 (.19, .24)
WD	.10 (.08, .12)	.01 (.00, .02)	.09 (.07, .11)
RC	.16 (.12, .19)	.08 (.06, .10)	.02 (.01, .04)	.06 (.03, .09)

Note: A₁, C₁, E₁ represent common ACE effects on Math, WD, and RC; A₂, C₂, E₂ represent ACE effects on WD and RC that are independent of Math; A₃, C₃, E₃ represent ACE effects on RC that are independent of both Math and WD. The proportion of variance due to A, C, E (in boldface) can be obtained by summing the squared estimates from the Cholesky decomposition analysis.

As well as estimating the total proportion of genetic and environmental variance in each latent phenotypic factor, it is of interest to examine the extent to which the variance in each factor can be subdivided into (1) genetic and environmental effects that are common to mathematics, word decoding, and reading comprehension (i.e., the effects of A₁, C₁, and E₁), (2) genetic and environmental effects linking word decoding and reading comprehension independent of mathematics (A₂, C₂, and E₂), and (3) genetic and environmental effects on reading comprehension independent of both mathematics and word decoding (A₃, C₃, and E₃). These estimates are shown in the righthand columns of Table 4, and are obtained from the squared standardized path coefficients associated with each factor. For example, the proportion of variance in reading comprehension that is due to genetic factors shared with mathematics and word decoding is the square of the loading of reading comprehension on A₁ (i.e., .61² = .37). Summing across each row gives the total proportion of genetic, shared environmental, and nonshared environmental variance within each factor.

Genetic factors common to all three factors (represented by A₁) accounted for all of the genetic variance in mathematics (.60), 25% of the genetic variance in word decoding (.21/.83 = .25, where .83 is the total genetic variance in word decoding), and 56% of the genetic variance in reading comprehension (.36/.64 =.56, where .64 is the total genetic variance in reading comprehension). Genetic factors specific to word decoding and reading comprehension (represented by A₂) accounted for 75% of the genetic variance in word decoding (.63/.83 = .75) and 11% of the genetic variance in reading comprehension. Finally, 33% of the genetic variance in reading comprehension reflected genetic influences independent of mathematics and word decoding (represented by A₃). Thus, there was substantial genetic overlap among all three factors, but word decoding and reading comprehension were differentially related to mathematics: genetic variance in word decoding primarily reflected genetic influences independent of mathematics, whereas genetic variance in reading comprehension substantially reflected genetic influences shared with both mathematics and word decoding.

A somewhat different picture emerged for shared environmental influences. The first shared environmental factor, C₁, accounted for all of the shared environmental variance in mathematics (.18), as well as all of the shared environmental variance in word decoding (.06) and reading comprehension (.20). Thus, shared environmental factors account for a relatively small proportion of the variance in mathematics, word decoding, and reading comprehension, and these factors are essentially the same across all three factors.

Nonshared environmental factors largely mirrored the pattern of genetic effects, although their influence was relatively small for each domain (10% - 22%). Nonshared environmental effects common to all three factors (E₁) accounted for all of the nonshared environmental variance in mathematics (.22), and 50% of the nonshared environmental variance in reading comprehension (.08/.16 = .50). It did not account for significant nonshared environmental variance in word decoding. Nonshared environmental factors specific to word decoding and reading comprehension (represented by E₂) accounted for 90% of the nonshared environmental variance in word decoding (.09/.10 = .90) and 13% of the nonshared environmental variance in reading comprehension (.02/.16 = .13). Finally, 38% of the nonshared environmental variance in reading comprehension reflected nonshared environmental influences independent of mathematics and word decoding (.06/.16 = .38) (represented by A₃).

Model-fit comparisons confirmed the general pattern of results: compared with the baseline model reported above −2LL: 150245.77, df = 64021, DIC: −139706.06, sample size adjusted BIC: −96818.731), a better fit (-2LL: 150245.85, df =64024, DIC: −139716.08, sample-size adjusted BIC: −96826.745) was obtained for a reduced model that included three genetic factors and three nonshared environmental factors (A₁, A₂, A₃, and E₁, E₂, E₃), but only one shared environmental factor that influenced all three factors (C₁). Both models provided a better fit to the data than a saturated model that represented all possible genetic and environmental covariances among the factors (-2LL: 149789.425, df = 63831, DIC: −139296.66, sample size adjusted BIC: −96536.617).

An alternative way to express genetic and environmental overlap among mathematics, word decoding, and reading comprehension is in terms of the genetic and environmental correlations (Table 5). As described in the Introduction, genetic and environmental correlations index the extent to which genetic or environmental factors on one trait correlate with another trait. Reading comprehension showed high genetic correlations with both mathematics (.76) and word decoding (.66). The genetic correlation between word decoding and mathematics was .50, significantly lower than the genetic correlation between reading comprehension and mathematics. The shared environmental correlations, in contrast, were uniformly high and not significantly different from unity. Finally, mirroring the genetic correlations, reading comprehension showed high nonshared environmental correlations with mathematics (.71) and word decoding (.54), whereas the nonshared environmental correlation between word decoding and mathematics was moderate but significant (.30).

Table 5. Genetic (r_A), shared environmental (r_C) and nonshared environmental (r_E) correlations between mathematics (Math), word decoding (WD), and reading comprehension (RC) (95% CI in parentheses).

	Math-WD	Math-RC	WD-RC
rA	.50 (.45, .57)	.76 (.71, .80)	.66 (.60, .73)
rc	1.00 (1.00, 1.00)	0.97 (.79, 1.00)	.97 (.81, 1.00)
rE	.30 (.21, .39)	.71 (.61, .80)	.54 (.42, .67)

Are different aspects of mathematics differentially related to word decoding and reading comprehension?

In a supplementary analysis, we sought to determine whether word decoding and reading comprehension are differentially related to the different skills assessed by our mathematics tests. We applied a Cholesky decomposition model to the individual measures of mathematics, word decoding, and reading comprehension. The genetic, shared environmental, and nonshared environmental correlations from this analysis are shown in Table 6. The genetic correlations between mathematics and word decoding did not vary significantly as a function of the specific mathematics test. The genetic correlations between the mathematics and reading comprehension tests were significantly greater than those between mathematics and the word decoding tests, mirroring the results from our analysis of the latent phenotypic factors, but these genetic correlations also did not vary significantly as a function of the mathematics tests. The same pattern emerged at the level of the shared and nonshared environmental influences for both word decoding and reading comprehension. We return to the question of components of mathematics ability below.

Table 6. Genetic, shared environmental, and nonshared environmental correlations among mathematics and reading measures (95% CI in parentheses).

	Math 1	Math 2	Math 3	WD 1	WD 2	RC 1
			Genetic correlations
Math2	.84 (.79, .92)
Math3	.92 (.88, .97)	.83 (.77, .92)
WD1	.42 (.36, .49)	.37 (.31, .45)	.42 (.37, .48)
WD2	.49 (.43, .56)	.41 (.36, .49)	.45 (.40, .52)	.75 (.70, .79)
RC1	.77 (.67, .87)	.75 (.65, .55)	.73 (.65, .84)	.52 (.44, .60)	.59 (.49, .70)
RC2	.70 (.61, .80)	.65 (.55, .76)	.66 (.57, .75)	.56 (.49, .65)	.62 (.54, .72)	.99 (.87, 1.00)
		Shared environmental correlations
Math2	.98 (.84, 1.00)
Math3	.98 (.77, 1.00)	.96 (.75, .44)
WD1	.94 (.34, 1.00)	.99 (.21, .77)	.92 (.33, 1.00)
WD2	.49 (.16, .78)	.48 (.21, .77)	.49 (.15, .83)	.50 (.14, .96)
RC1	.80 (.59, 1.00)	.84 (.66, 1.00)	.89 (.59, 1.00)	.84 (.33, 1.00)	.50 (.19, .89)
RC2	.81 (.63, .99)	.89 (.73, 1.00)	.79 (.57, 1.00)	.93 (.44, 1.00)	.70 (.40, .97)	.81 .70, 1.00)
		Nonshared environmental correlations
Math2	.36 (.33, .40)
Math3	.42 (.38, .45)	.31 (.27, .34)
WD1	.14 (.09, 18)	.06 (.03, .11)	.13 (.09, .17)
WD2	.06 (.02, 10)	.02 (.01, .06)	.07 (.03, .11)	.23 (.19, .28)
RC1	.20 (.16, .24)	.17 (.13, .21)	.19 (.14, .22)	.14 (.10, .19)	.09 (.05, .14)
RC2	.18 (.14, .22)	.20 (.17, .24)	.19 (.15, .23)	.13 (.09, .17)	.09 (.04, .13)	.19 (.15, .23)

Note: Mathl = Understanding Number; Math2 = Non-Numerical Processes; Math3 = Computation and Knowledge; WD1 = TOWRE; WD2 = WJ-III Reading Fluency; RC1 = PIAT_rc; RC2 = GOAL.

Discussion

This study provides support at an etiological level for differentiating word decoding and reading comprehension when considering the relationship between reading and mathematics. These components of reading have typically been treated interchangeably. Indeed, our study found substantial overlap between word decoding and reading comprehension, as well as among mathematics, word decoding, and reading. However, we also show that the etiological relationships between reading and mathematics varies as a function of reading skill, with mathematics being more closely linked with reading comprehension than with word decoding. These findings are discussed in turn, and is followed by a synopsis of what is needed next in research on the links between reading and mathematics.

Overlap among mathematics, word decoding and reading comprehension

Genetic overlap among mathematics, word decoding, and reading comprehension was indicated in three ways: by the Cholesky decomposition analysis, which provided evidence for a common genetic factor influencing all three latent factors; by the genetic correlations, which ranged from .50 to .76; and by the evidence that the phenotypic correlations among the measures were primarily due to genetic factors. There was also shared environmental overlap among all three domains. Even though shared environmental influences accounted for a relatively small proportion of the variance in mathematics, word decoding, and reading comprehension, the very high shared environmental correlations (close to unity) imply that the shared environmental influences on each of the traits are almost entirely identical.

A possible explanation for this overlap is that it reflects genetic and environmental effects on oral language skills such as word knowledge and syntactic competence. These skills have been directly implicated in word decoding and reading comprehension, and are also important for reading mathematical texts. In addition, mathematics may overlap with word decoding and reading comprehension due to general cognitive or information-processing abilities. For example, it has been shown that aspects of working memory (e.g., phonological loop and verbal working memory) are associated with learning new mathematical skills among children and adolescents (e.g., Raghubar, Barnes, & Hecht, 2010).

We also found close links between word decoding and reading comprehension independent of mathematics. At an etiological level, genetic factors specific to word decoding and reading comprehension accounted for 75% of the genetic variance in word decoding and 11% of the genetic variance in reading comprehension. Similarly, nonshared environmental influences independent of mathematics accounted for 90% of the nonshared environmental variance in word decoding and 13% of the nonshared environmental variance in reading comprehension. The reading-specific links between word decoding and reading comprehension could be described as marking the intuitive boundary between literacy and numeracy. Although reading and mathematics draw on some common language skills, the form and function of language involved in each domain differ in important ways. Mathematics is written in a highly decontextualized, universal, and semantically precise symbolic system, whereas many of the texts that school-age children are expected to read are based on natural language forms which are culturally specific, relatively more contextualized, and semantically fuzzy.

Overall, our results are consistent with previous behavioral genetic studies (e.g., Hart et al., 2010; Betjemann et al., 2008; Betjemann et al., 2011; Byrne et al., 2009; Byrne et al., 2007; Keenan et al., 2006). However, the genetic overlap between word decoding and reading comprehension obtained here is somewhat lower than that reported in studies of similar-age twins that used untimed measures of word decoding (Betjemann et al., 2008; Keenan et al., 2006). This difference in results suggests the intriguing possibility that the magnitude of genetic overlap depends on whether word decoding fluency or accuracy is assessed, the latter showing stronger genetic (and phenotypic) associations with reading comprehension by the middle school years when variance in word decoding is more likely to be driven by fluency rather than accuracy (Torgesen et al., 1999).

It is noteworthy that we found residual genetic and nonshared environmental influences on reading comprehension independent of word decoding, as did Keenan et al. (2006) and Betjemann et al. (2008, 2011). The evidence that reading comprehension is not completely accounted for by word decoding is consistent with the triangle model (Harm & Seidenberg, 2004; Bishop & Snowling, 2004). As described in the Introduction, this suggests that distinct factors are important for word decoding and reading comprehension, with listening comprehension being more central for reading comprehension. A similar point is emphasized in other cognitive models of reading, such as the Simple View of Reading (Hoover & Gough, 1990). Consistent with these models, Keenan et al. (2006) and Betjemann et al. (2008, 2011) have demonstrated that genetic variance in reading comprehension that is independent of word decoding can be accounted for almost completely by genetic influences on listening comprehension.

Overlap between mathematics and reading comprehension

The most important new finding from the current study is that word decoding and reading comprehension were also differentially related to mathematics. This was indicated by the phenotypic and genetic correlations with mathematics, which were significantly higher for reading comprehension than for word decoding. In addition, we found evidence for a nonshared environmental link between reading comprehension and mathematics, independent of word decoding.

We suggest that the specific link between mathematics and reading comprehension likely reflects the importance of executive function skills such as working memory, inhibition, strategic planning, and goal-directed preparedness to act. Executive function is vital for developing skills that require focused attention and practice to acquire competence (Best & Miller, 2010). Planning and organization skills would appear especially important for reading comprehension, and in fact they have been shown to be more strongly associated with reading comprehension than with word decoding (e.g., Locascio, Mahone, Eason, & Cutting, 2010; Sesma, Mahone, Levine, Eason & Cutting, 2009). Similarly, in the mathematics domain, complex executive function skills are more closely related to mathematical reasoning tasks compared with other tasks (e.g., calculation) (Best, Miller, & Naglieri, 2011). Individual differences in executive function skills are highly heritable (e.g., Friedman, Miyake, Young, DeFries, Corley, & Hewitt, 2008); thus the genetic overlap between reading comprehension and mathematics may reflect genetic influences on common executive function processes.

Our finding of partly differential genetic overlap for word decoding and reading comprehension with mathematics is inconsistent with that of Hart et al. (2010). Our Cholesky decomposition analysis indicated that the genetic loadings from the first genetic factor were significantly higher for mathematics and reading comprehension than for word decoding, whereas Hart et al. (2010) found that word decoding accuracy, word decoding fluency, and reading comprehension had high and very similar loadings on a general genetic factor that also influenced mathematics. Several factors may account for this discrepancy. For example, twins in Hart et al. (2010) were approximately two years younger than twins in the current study. Reading comprehension may have stronger links with mathematics in early adolescence than earlier, reflecting developmental and education-based changes that increasingly emphasize higher-level comprehension in both domains. There are also noteworthy differences in the reading comprehension measures in the two studies. Our measures, the PIAT_rc and GOAL, tapped both literal and inferential reading comprehension skills, whereas the measures used by Hart et al. (2010), the PIAT_rc and the Passage Comprehension Subtest of the Woodcock-Johnson Reading Mastery Test (Woodcock, 1987), primarily reflect literal comprehension. Inferential comprehension draws on higher-level verbal reasoning processes, some of which are likely to also be important for mathematics.

Limitations

Along with a number of important strengths, including the large, population-based sample and the latent factor design, our study had several limitations. First, many commonly used measures of reading comprehension, including the PIAT_rc, are heavily influenced by both decoding skill and specific content knowledge (e.g., Cutting & Scarborough, 2006; Keenan, Betjemann & Olson, 2008). This is less problematic for our second reading comprehension measure, the GOAL, which places greater demands on domain-general language and cognitive processes. However, the selection of reading comprehension measures requires careful consideration in future studies, as different tests of putatively the same construct (i.e., reading comprehension) may manifest very different patterns of genetic covariation (Betjemann et al., 2011).

Second, all three factors examined in the current study were assessed with limited test batteries. This is of particular concern in relation to mathematics. Our measures of mathematics were highly correlated (r_p ~ .66), and thus our analyses used a global indicator of mathematics. A supplementary Cholesky model of the individual mathematics and reading measures confirmed that there were no significant differences between word decoding and reading comprehension in terms of their etiological links to the specific mathematics tests. Nonetheless, it seems likely that mathematics tests that emphasize reasoning and application of mathematical knowledge may be more strongly related to reading comprehension, whereas simple computational procedures that draw on verbal working memory may be more strongly related to word decoding.

Implications for educational assessment and molecular genetic research

To date, most studies of the relationship between reading and mathematics have focused on word decoding, or have used global measures of reading. The present results suggest that the relationship between reading comprehension and mathematics in the middle school years also requires detailed examination. In particular, our results lead to the prediction that children with reading difficulties are at elevated risk for co-occurring difficulties in mathematics, and this risk is highest for children with deficits in reading comprehension. Although schools in the U.S. and other countries typically assess children across all academic domains every three to four years, the results imply that mathematics should be specifically considered in educational assessments of children who present with reading difficulties at any time in elementary and middle school, especially among children with reading comprehension difficulties. The relationship between reading and mathematics should also be specifically considered within progress monitoring (e.g., response to intervention) initiatives (Justice, 2006) in order to reduce the risk for comorbid difficulties in reading and mathematics.

The current study also has implications for molecular genetic studies. The evidence for genetic overlap among mathematics, word decoding, and reading comprehension is consistent with the effects of multiple pleiotropic or ‘generalist’ genes (Plomin & Kovas, 2005).To our knowledge, there have been no systematic multivariate efforts to identify genetic variants for word decoding and reading comprehension separately, although there have been efforts to identify genes associated with components of word decoding, such as phonological decoding, phoneme awareness, and orthographic coding (Skiba et al., 2011). Molecular genetic research on mathematics abilities and disabilities is also sparse (Docherty et al., 2010a); however, two studies have provided suggestive evidence that some genetic variants may influence both reading and mathematics abilities (Docherty et al., 2010b; Marino et al. (2011). We predict that a network of highly pleiotropic genes contributes to the overlap between mathematics and reading comprehension, and to a lesser extent word decoding. In addition, some genetic networks may have narrower pleiotropic effects, influencing word decoding and reading comprehension only.

An agenda for future research

Continued progress in developing a full understanding of the relationships between reading and mathematics will require a clear research agenda. A substantial body of behavioral genetic studies of reading, as well as the wealth of evidence supporting the generalist genes hypothesis (Plomin & Kovas, 2005) strongly implies that both overlap and independence will be found among all aspects of reading and mathematics. Clarifying the extent and nature of these associations is an important first goal, but this needs to be followed by systematic study of the processes that underlie genetic and environmental sources of variation in reading and mathematical abilities.

We suggest that future work on the relationship between reading and mathematics should include the following three themes. Of foremost importance is the need to root any study within a developmental framework. Different aspects of mathematics and reading develop at different times through the school years, with later-emerging abilities, such as reading comprehension and advanced arithmetic competences, building on early-emerging skills. Thus the conclusions of the present study may or may not be applicable to younger and older students. Given the results of Hart et al. (2010) and those of Byrne et al. 2007, 2009), we suspect that stronger phenotypic and genetic links between mathematics, word decoding and reading comprehension may be observed at earlier ages. Middle school curricula typically emphasize reading comprehension, complex arithmetic operations, and mathematical reasoning, leading to the hypothesis that reading comprehension will show stronger phenotypic and genetic links with mathematics – particularly mathematical reasoning – than word decoding. It is also important to consider development within each domain. For example, as suggested earlier, development of word decoding accuracy precedes fluency. Thus, there may continue to be strong overlap among mathematics, word decoding and reading comprehension in middle childhood when assessments emphasize word decoding accuracy, but weaker overlap when fluency in word decoding is assessed. A number of behavioral genetic studies of reading and mathematics are prospectively following children across the school years, which should enable systematic analyses of developmental sequences underlying the relationship between reading and mathematics.

Second, almost all behavioral genetic studies to date have used measures of outcomes; for example, how well children can understand texts, how accurately and fluently children can read words, and how accurately children can complete multi-digit arithmetic. There is a need for measures that focus on the processes that occur during reading and mathematics task.. For example, improvements in basic arithmetical competencies reflect changes in the strategies used in problem solving, as well as advances in conceptual understanding of arithmetic and related domains, such as counting (Geary, 1994). Similarly, more fine-grained, developmentally-appropriate assessments of reading comprehension processes are needed, including language comprehension, inference generation, and anaphoric processing (Oakhill & Cain, 2003; Verhoeven & Perfetti, 2008). For word decoding, specific measures of both fluency and accuracy in word decoding would be helpful, as well as measures of the cognitive skills that underlie word decoding, such as phonological processing and orthographic knowledge. Finally, it will be essential to consider more general processes and skills that contribute to all three domains, such as executive function and general cognitive ability, in the design of behavioral genetic studies of reading and mathematics.

Third, there is a need to consider more precisely which environmental factors are involved in the relationships among word decoding, reading comprehension, and mathematics. We have identified three environmental links: (1) a shared environmental link among mathematics, word decoding, and reading comprehension, (2) a nonshared environmental link between mathematics and reading comprehension, and (3) a separate nonshared environmental link between word decoding and reading comprehension. The current study does not reveal which specific shared and nonshared environmental factors are important. However, there are numerous candidates, ranging from distal influences such as family socioeconomic status and the classroom environment, to more proximal influences such as parental involvement in education and student classroom engagement. From a behavioral genetic perspective, there are numerous challenges in examining the effects of specific environmental factors. For example, putative ‘environmental’ influences are often partly genetic due to gene-environment correlations (Plomin, 1994). Ultimately, however, identifying the specific environmental influences involved, determining the precise nature of each influence, and determining the mechanisms by which they interact with specific genetic factors, will enable us to gain greater purchase on the relationships among mathematics, word decoding, and reading comprehension.