A Hidden Markov Model method, capable of predicting and discriminating β-barrel outer membrane proteins

Abstract

Background

Integral membrane proteins constitute about 20–30% of all proteins in the fully sequenced genomes. They come in two structural classes, the α-helical and the β-barrel membrane proteins, demonstrating different physicochemical characteristics, structure and localization. While transmembrane segment prediction for the α-helical integral membrane proteins appears to be an easy task nowadays, the same is much more difficult for the β-barrel membrane proteins. We developed a method, based on a Hidden Markov Model, capable of predicting the transmembrane β-strands of the outer membrane proteins of gram-negative bacteria, and discriminating those from water-soluble proteins in large datasets. The model is trained in a discriminative manner, aiming at maximizing the probability of correct predictions rather than the likelihood of the sequences.

Results

The training has been performed on a non-redundant database of 14 outer membrane proteins with structures known at atomic resolution; it has been tested with a jacknife procedure, yielding a per residue accuracy of 84.2% and a correlation coefficient of 0.72, whereas for the self-consistency test the per residue accuracy was 88.1% and the correlation coefficient 0.824. The total number of correctly predicted topologies is 10 out of 14 in the self-consistency test, and 9 out of 14 in the jacknife. Furthermore, the model is capable of discriminating outer membrane from water-soluble proteins in large-scale applications, with a success rate of 88.8% and 89.2% for the correct classification of outer membrane and water-soluble proteins respectively, the highest rates obtained in the literature. That test has been performed independently on a set of known outer membrane proteins with low sequence identity with each other and also with the proteins of the training set.

Conclusion

Based on the above, we developed a strategy, that enabled us to screen the entire proteome of E. coli for outer membrane proteins. The results were satisfactory, thus the method presented here appears to be suitable for screening entire proteomes for the discovery of novel outer membrane proteins. A web interface available for non-commercial users is located at: http://bioinformatics.biol.uoa.gr/PRED-TMBB, and it is the only freely available HMM-based predictor for β-barrel outer membrane protein topology.

Background

Integral membrane proteins are divided into two distinct structural classes, the α-helical membrane proteins and the β-barrel membrane proteins. The former class is the more abundant and well studied, since proteins of that type are located mostly in the cell membranes of both prokaryotic and eukaryotic organisms, performing a variety of biologically important functions. Proteins of that class have their membrane spanning regions forming α-helices, which consist mainly of hydrophobic residues [1]. A variety of algorithms and computational techniques have been proposed for the prediction of the transmembrane segments of α-helical membrane proteins, with high accuracy and precision. The members of the latter class (β-barrel membrane proteins) are located in the outer membrane of gram-negative bacteria, and presumably in the outer membrane of chloroplasts and mitochondria. The members of that class are having their membrane spanning segments formed by antiparallel β-strands, creating a channel in a form of a barrel that spans the outer membrane [2]. The first known members of that class were found to be the bacterial trimeric porins, forming water-filled channels that mediate the passive transport of ions and small molecules through the outer membrane [2]. During the last few years, more β-barrel proteins were found in the bacterial outer membrane, and a number of structures have been solved in atomic resolution [2]. These proteins perform a wide variety of functions such as active ion transport, passive nutrient uptake, membrane anchoring, adhesion, and catalytic activity. A large number of pathogens are actually bacteria belonging to the gram negative bacteria class. Considering additionally the important biological functions in which outer membrane proteins are involved in, it is not a surprise that those proteins attract an increased medical interest. This is confirmed by the continuously increasing number of completely sequenced genomes of gram-negative bacteria deposited in the public databases. On the other hand, the extensive study of the structure of transmembrane β-barrel proteins, could reveal special aspects of the process of protein folding, and give us useful insights on protein structure and function. For the reasons mentioned above, there is clearly a need to develop computational tools for predicting the membrane spanning strands of those proteins, and also discriminating them from water-soluble proteins when searching entire genomes.

In contrast to the α-helical membrane proteins, whose membrane spanning segments can be identified by statistical methods, neural networks, or Hidden Markov Models with high accuracy, this task is more difficult in the case of the β-barrel membrane proteins of the outer membrane. This is due to the lack of a clear pattern in their membrane spanning strands, such as the stretch of 15–30 consecutive hydrophobic residues or the Positive Inside rule, which occur in the α-helical proteins. Furthermore, discrimination of transmembrane strands from other β-strands, forming β-barrel structures in water-soluble proteins, is even more difficult. The reason for that is the fact that water-soluble proteins that form β-barrel structures, share (up to a certain degree) common features with the transmembrane strands of the bacterial outer membrane proteins, such as amphipathicity.

A few approaches have been made, in the direction of predicting the transmembrane strands of outer membrane proteins and/or identifying those proteins when searching large data sets; they are based on study of the physicochemical properties of the β-strands, such as hydrophobicity and amphipathicity [3], statistical analyses based on the amino acid composition of the known structures [4], or machine learning techniques like neural network predictors [5,6], and Hidden Markov Models [4,7,8]. Recently, a method based on a sequence profile-based HMM [8], requiring as input evolutionary information derived from multiple alignments, achieved the highest accuracy.

In this work we developed a Hidden Markov Model method based solely on the amino acid sequence, without the requirement of evolutionary information. The model is cyclic, and captures the structural characteristics of the transmembrane β-strands of the outer membrane proteins. For training and evaluating the model, we compiled a non-redundant dataset of 14 outer membrane proteins with structure known at atomic resolution (Table 1, see Materials and methods section), and tested it with a jacknife procedure. The model is also used for discriminating outer membrane proteins, in large-scale genome analyses.

Table 1.

The non-redundant data set of outer membrane proteins used in this study.

Protein name	Number of β-strands	PDB code[29]	Organism
OmpA	8	1QJP	Escherichia coli
OmpX	8	1QJ8	Escherichia coli
OmpT	10	1I78	Escherichia coli
OpcA	10	1K24	Neisseria Meningitidis
OmpLA	12	1QD5	Escherichia coli
Omp32	16	1E54	Comamonas Acidovorans
OmpF	16	2OMF	Escherichia coli
Porin	16	2POR	Rhodobacter capsulatus
Porin	16	1PRN	Rhodobacter blasticus
Sucrose porin	18	1A0S	Salmonella typhimurium
Maltoporin	18	2MPR	Salmonella typhimurium
FepA	22	1FEP	Escherichia coli
FhuA	22	2FCP	Escherichia coli
FecA	22	1KMO	Escherichia coli

Results and discussion

The results obtained from the model are presented in additional file 1 and Table 2 (for a definition of the transmembrane, TM, segments, see the Materials and methods section). Table 2 shows the results obtained comparing the predicted strands and topologies with the PDB annotation and also those comparing with the manual annotation used for training (see Materials and methods). The model correctly predicts the location of 96.3% of the transmembrane strands (206 out of 214). Two (2) additional strands were predicted correctly but slightly misplaced from their observed positions. These misplaced strands, which belong to the proteins with PDB codes 1PRN and 2POR, were the only strands that have been falsely predicted (false positives). The total number of correctly predicted topologies (correct prediction of β-strands and orientation of the loops) is 10 and, when counting the misplaced strands, 11 out of 14 proteins in the training set. When the comparison against the manual annotation used for training was performed, it was noted that there is one additional strand (the second TM strand of 1I78), which is predicted slightly misplaced. The model has also been tested with the well-known jacknife procedure. The jacknife procedure consists of removing a protein from the training set, training the model with the remaining proteins and performing the test on the protein removed. This process is tandemly repeated for all proteins in the training set, and the final prediction accuracy summarizes the outcome of all independent tests. Thus, this procedure is regarded as most appropriate for the assessment of a prediction method based on independent training and test data.

Table 2.

Overall measures of accuracy, obtained in the Self-consistency and in the Jacknife testing.

	Type of test	TP	FP	FN	TOP1	TOP2	Qβ	Cβ
(A)	Self-consistency	205	3	9	9	11	88.1%	0.824
	Jacknife	203	13	11	8	10	84.2%	0.720
(B)	Self-consistency	206	2	8	10	11	66.9%	0.604
	Jacknife	204	12	10	9	10	65.7%	0.532

(A): Comparison against the manual annotation of the TM-segments. (B): comparison against the observed strands of PDB [29]. TP: True Positives. FP: False Positives. FN: False Negatives. TOP1: Proteins with correctly predicted topologies (strand localization and orientation of the loops). TOP2: Proteins with correctly predicted topologies, with the inclusion of shifted strand predictions. Q_β: Percentage of correctly predicted residues [36]. C_β: Matthews Correlation Coefficient [36].

The result of the jacknife test concerning the correctly predicted TM strands was 204 out of 214 (95.3%), with 12 over-predicted strands. The overall number of correctly predicted topologies was 9 out of 14. When counting the predicted misplaced strands, the number of correctly predicted topologies raises to 10 out of 14. Once again when comparing against the manual annotation, the second TM strand of 1I78, is predicted slightly misplaced.

The per-residue accuracies and correlation coefficients (see Materials and methods) for both the self-consistency and jacknife tests are listed also in Table 2, with respect to either the PDB annotation or the manual annotation used for training. Apparently, the significantly lower percentages reported in the case of comparison with the PDB annotation, is a clear consequence of the fact that the strands extend in some cases far beyond the lipid bilayer. These strands could not have been predicted as transmembrane along their entire length, and our model predicts only the part of the strand that it is inserted into the membrane. 1I78 is a perfect example of such a case since all of its strands are clearly extending far beyond the membrane by 8 or more residues. In addition to the self-consistency and jacknife test, we performed another independent test. We divided the training set in two datasets of seven proteins each and used the one for training and the other for testing. This procedure was repeated 5 times, choosing randomly 7 different proteins each time, and the results concerning the per-residue accuracy and the correlation coefficient were in the range 0.78 – 0.80 and 0.57 – 0.71 respectively. We also tested the performance of the model on the Neisserial Surface Protein A (Nspa) [9], the Outer Membrane Enzyme Pagp from E. coli [10], and the Outer Membrane Cobalamin Transporter (Btub) from E. coli [11] The structures of these proteins have been very recently solved, they have not been included in the training set, and they do not show any significant homology with any protein of the training set. For NspA, and BtuB the model correctly locates all the transmembrane strands and the proteins' full topologies, whereas for Pagp we get two over-predicted strands. For the three proteins the per-residue accuracy is 90.9% and the correlation coefficient is 0.78.

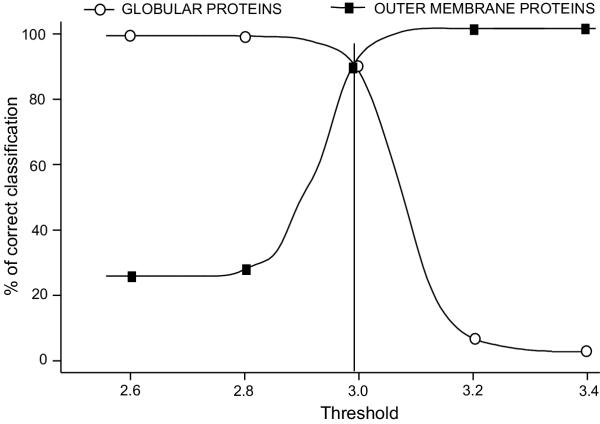
When we tested the ability of the model to discriminate between outer membrane and globular proteins, the percentage of the correctly classified outer membrane proteins (at a fixed threshold) was 88.8% whereas the percentage of correctly classified globular proteins was 89.2%, (Figure 1). The absolute value of the score threshold obtained this way was 2.995, with values lower than that indicating the possibility of the protein being an outer membrane protein.

Figure 1.

Evaluation of the discrimination score. The percentage of correctly predicted outer membrane proteins (filled boxes) and globular ones (open circles) as a function of different score thresholds in the validation of the discrimination procedure. The optimal proportion of correctly classified proteins was obtained using the value of 2.995 as a threshold (determined from, approximately, the intersection of the two curves).

Furthermore, we developed a protocol that allowed us to apply the newly developed method to search the complete proteome of E. coli [12] for β-barrel membrane proteins. The protocol consists of three steps: In the first step we perform a search using the PRED-CLASS algorithm [13], with the aim of identifying and removing α-helical membrane proteins. According to the PRED-CLASS prediction, 1157 proteins out of 5361 were classified as transmembrane and hence they were removed. In the second step, the remaining proteins were filtered with the SignalP program, for finding the secreted proteins, since it is apparent that the majority, if not all, of the outer membrane proteins posses a signal peptide sequence necessary for the translocation to the outer membrane. In order not to discard potential candidates for being identified as outer membrane proteins, we applied both versions of SignalP, the Neural Network [14] and the Hidden Markov Model [15], and if at least one of them indicated the presence of a signal peptide, the protein was not discarded. Then, the signal peptide predicted by the Neural Network algorithm of SignalP was removed, since this algorithm is more accurate than the Hidden Markov algorithm in locating the correct splicing site from all the candidate proteins. This procedure resulted to 978 proteins. In the third and final step, the remaining 978 protein sequences were submitted to our HMM predictor having set the discrimination score at the pre-specified threshold mentioned above. In total, 236 proteins scored below the threshold for the outer membrane proteins (after excluding fragments and sequences shorter than 60 residues) accounting for 4.4% of the complete proteome. Among the top scoring proteins, 42 are well known outer membrane proteins according to the existing annotation, including many fimbrial proteins, usher proteins and transporters, and 87 were proteins whose annotation was "putative" but suggested that their localization was to the outer membrane. The number of proteins whose annotation suggested that they were misclassified, including a lot of periplasmic proteins and enzymes, was 34, whereas the "putative" misclassified proteins were 23. Finally, the remaining 50 proteins were hypothetical proteins or proteins with completely unknown function. Apparently, the 57 over-predictions probably are resulting from the fact that outer membrane proteins are only a small fraction compared to the whole proteome. Since it is believed that outer membrane proteins constitute around 2–4% of the complete proteomes, it is natural that even a method with 99% of correct predictions, will result in a large number of false positives. Nevertheless, given the constrains mentioned above, this method clearly offers a useful tool for the automatic annotation of entire proteomes, since the false positives could be easily removed considering other sequence characteristics.

Comparing our method with the best method proposed so far for the prediction of transmembrane β-barrel proteins by Martelli et al. [8], as well as with the HMM method proposed by Liu et al. [7], the following points should be mentioned. The HMM-profile based method by Martelli et al. [8], uses as input the evolutionary information included in multiple alignments. The method proposed here, uses as input only the amino acid sequence of the protein, hence it is computationally simpler. Even though our method does not outperform the profile based HMM method by Martelli et al. [8] in the per residue accuracy, when it comes to the number of correctly predicted transmembrane strands and overall topologies, the two methods are practically equivalent. The same argument holds for the case of the discriminative power of the two methods, since the percentage of correctly classified β-barrel proteins was 84%, and percentage of correctly classified water soluble proteins was 90% as reported in [8], showing that better results can be obtained even without the use of evolutionary information. Concerning the method proposed by Liu et al, which uses as input single sequences, the results about strand localization and overall topology assignment are also comparable with our method, but no discrimination could be performed between outer membrane proteins and soluble ones in their method, thus requiring a separate method for the discrimination purposes. Furthermore in Liu et al [7], no overall measures of accuracy were reported.

Both methods mentioned above use HMMs with architectures quite similar to the model shown here, with minor differences, and this is not a surprise. For the sake of argument, the two most successful methods for the prediction of transmembrane segments of α-helical membrane proteins use a similar architecture; that architecture reflects the most obvious way to map the biological features of transmembrane proteins to the mathematical formalism of the Hidden Markov Model. Finally, the methodology that we used for the training and the decoding is completely different from those used by Martelli et al. [8], and Liu et al. [7]. Our model was trained according to the Conditional Maximum Likelihood criterion, which differs significantly from the Maximum Likelihood training scheme, performed with the Baum-Welch algorithm, by the two methods mentioned. For the decoding, Martelli et al use the so-called posterior decoding method, with the aid of a dynamic programming algorithm, whereas Liu et al, rely on the traditional Viterbi algorithm. Even when in our tests the N-best decoding does not outperform significantly the Viterbi decoding (data not shown), when it comes to newly discovered proteins, the option to perform decoding with the best method available is a clear advantage.

When our method is compared against the methods developed by Zhai and Saier [3] and Wimley [4], we observe that none of the above methods controlled for the number of false positives and false negatives, since they were not validated statistically. They both report the finding of a number of predicted outer membrane proteins, for which the genome annotation suggested localization to the outer membrane. The fact that we report 236 predicted outer membrane proteins in E. coli proteome, compared to 118 in [3] and 200 in [4], reflects the fact that we chose to retain the threshold obtained from cross-validation. Clearly, in real life applications using our method we could lower the threshold and obtain fewer predictions (<200), with the cost of loosing 5–10 outer membrane proteins.

Conclusions

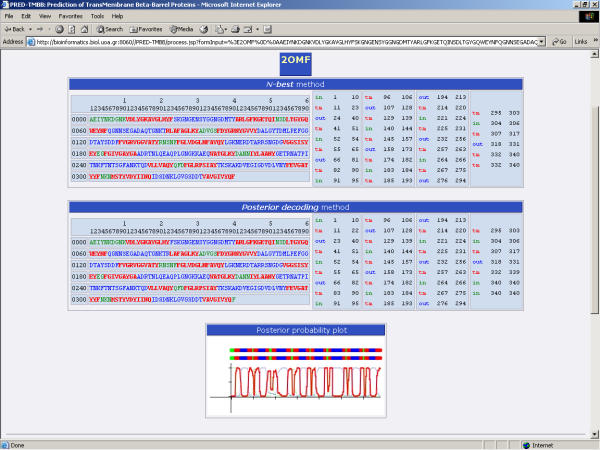
We present here a novel method, based on a Hidden Markov Model, for the prediction of the transmembrane β-strands of the outer membrane proteins of Gram-negative bacteria, and for the discrimination of these proteins from globular proteins. To our knowledge, a Hidden Markov Model trained with a discriminative method is applied for the first time in molecular biology for such a task. We show here that we can achieve predictions at least equally successful to other existing methods, without the use of evolutionary information. We also showed that the method is powerful when used for discrimination purposes, as it can discriminate outer membrane proteins from water soluble proteins in large datasets with a high accuracy, suggesting that it is a very reliable solution for screening entire genomes of Gram negative bacteria, for the discovery of novel β-barrel proteins as possible drug targets. Compared to other single sequence methods (for both discrimination and strand prediction) our method is unambiguously the best currently available. Compared to multiple sequence methods (requiring evolutionary information) our method achieves comparable results. Clearly, our method combines equally, higher rates for both strand localization and sequence discrimination, from any existing method. A web server running the application is located in our laboratory and it is the only HMM-based application currently freely available, making our method accessible to scientists around the world. The user may submit a sequence in FASTA format, and has the option to choose between decoding by either the N-best algorithm, the standard Viterbi algorithm or posterior decoding with a dynamic programming algorithm (Figure 2). The output consists of the prediction for the transmembrane strands (Figure 3). Optionally the user may obtain a graphical plot showing the posterior probabilities in a 3-state mode (extracellular, periplasmic and transmembrane), which may be useful in the case of ambiguously defined topologies. The application also returns the score used for discrimination purposes thus, helping the user to identify possible β-barrel outer membrane proteins.

Figure 2.

The submission form of the web-based application.

Figure 3.

Output of the prediction obtained from the web predictor for the OmpF of E. coli (PDB code: 2OMF [29]).

Materials and methods

The Hidden Markov Model

Hidden Markov Models have been extensively used for pattern recognition problems, with the most known example found in the speech recognition methodology [16]. Hidden Markov Models have been used in bioinformatics during the last few years for generating probabilistic profiles for protein families [17], the prediction of transmembrane helices in proteins [18,19], the prediction of signal peptides and their cleavage sites [15], the prediction of genes [20] and recently for the prediction of the transmembrane β-strands [7,8]. An excellent introduction of those applications in molecular biology is the book of Durbin et al [21] whose notation will follow hereafter.

The Hidden Markov Model is a probabilistic model consisting of several states, connected by means of the transition probabilities, thus forming a markov process. If we consider an aminoacid sequence of a protein with length L, denoted by:

x = x₁, x₂,..., x_L,

with a labeling (corresponding to transmembrane, intracellular and extracellular regions):

y = y₁, y₂,..., y_L

then, the transition probability for jumping from a state k to a state l is defined as:

α_kl = P(π_i = l|π_i-1 = k)

Where π is the "path" in the particular position of the amino acid sequence (i.e. the sequence of states, as opposed to the sequence of symbols). Each state k is associated with a distribution of emission probabilities, meaning the probabilities that any particular symbol could be emitted by the current state. Assuming an alphabet Σ, consisting of the symbols corresponding to the 20 amino acids, the probability that a particular amino-acid b is emitted from state k is defined as:

e_k(b) = P(x_i = b|π_i = k)

The term 'hidden' is justified by the fact that when one observes the emitted symbols he cannot see the underlying states, thus the true state process is hidden from the observer. The total probability of the observation sequence given the model, P(x|θ), is computed using the efficient Forward algorithm [16], whereas the joint probability of the sequence and the labeling denoted by P(x,y|θ), by its trivial modification proposed by Krogh [22].

Training and decoding algorithms

Traditionally, the parameters of a Hidden Markov Model are optimized according to the Maximum Likelihood criterion [16],

A widely used algorithm for this task is the efficient Baum-Welch algorithm (also known as Forward-Backward) [16,23], which is a special case of the Expectation-Maximization (EM) algorithm, proposed for Maximum Likelihood (ML) estimation for incomplete data [24]. The algorithm, updates iteratively the model parameters (emission and transition probabilities), with the use of their expectations, computed with the use of the Forward and Backward algorithms. Convergence to at least a local maximum of the likelihood is guaranteed. The main disadvantage of ML training is that it is not discriminative. In this work, we used Conditional Maximum Likelihood (CML) training for labeled data, as proposed by Krogh [25]. The Conditional Maximum Likelihood criterion is:

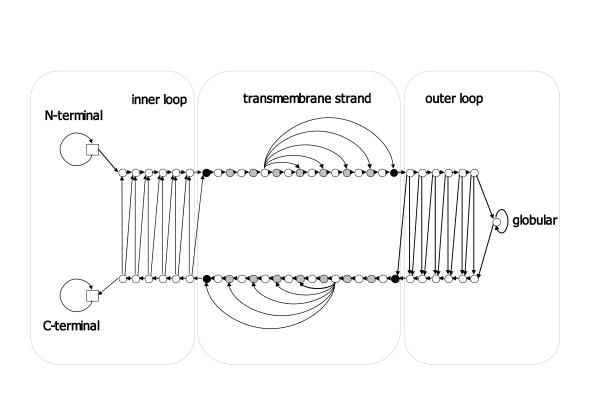
This kind of training, often referred to as discriminating training, seeks to maximize the probability of the correct prediction, i.e. the probability of the labeling y for a given sequence x and a model θ. The parameters of the model (transition and emission probabilities) are updated simultaneously, using the gradients of the likelihood function as described in [26], and the training process terminates when the likelihood does not increase beyond a pre-specified threshold. To reduce the number of the free parameters of the model, and thus improve the generalization capability, states expecting to have the same emission probabilities, were tied together (Figure 4). Furthermore, to avoid overfitting, the iterations started from emission probabilities corresponding to the initial amino-acid frequencies observed in the known protein structures and small pseudocounts were added in each step.

Figure 4.

The architecture of the model used in this work. The 3 "sub-models" corresponding to the 3 labels are shown separately. In the transmembrane sub-model different colors correspond to the tied states. Black circles correspond to the aromatic belt, gray to exterior of the strand's core, and white to the interior side. In the inner and outer loop sub-models, the states forming the ladder are tied together respectively, whereas the N-terminal tail is tied with the C-terminal and the globular outer loop state is not tied with another state. The allowed transitions are shown with arrows.

The decoding was performed using the N-best algorithm [27] (Figure 5), as formulated in [25]. This algorithm is a heuristic that attempts to find the most probable labeling of a given sequence, as opposed to the well-known Viterbi algorithm [16], which guarantees to find the most probable path of states. Since there are several states contributing to the same labeling of a given sequence (as in our case), the N-best algorithm will always produce a labeling with a probability at least as high as that computed by the Viterbi algorithm, in other words it always returns equal if not better results. Its main drawback is the memory requirements and computational complexity, resulting in a slowdown of the decoding process. For the purpose of discrimination, the information included in the prediction of the putative TM segments is not sufficient, since a prediction for a transmembrane strand could occur even in globular proteins. Thus, there is need for a global predictor reflecting the overall fit of the query sequence to the model. This predictor is the negative log-likelihood of the sequence given the model, as computed by the Forward algorithm and normalized for the length of the sequence. Thus, the statistical score used for discrimination is:

Figure 5.

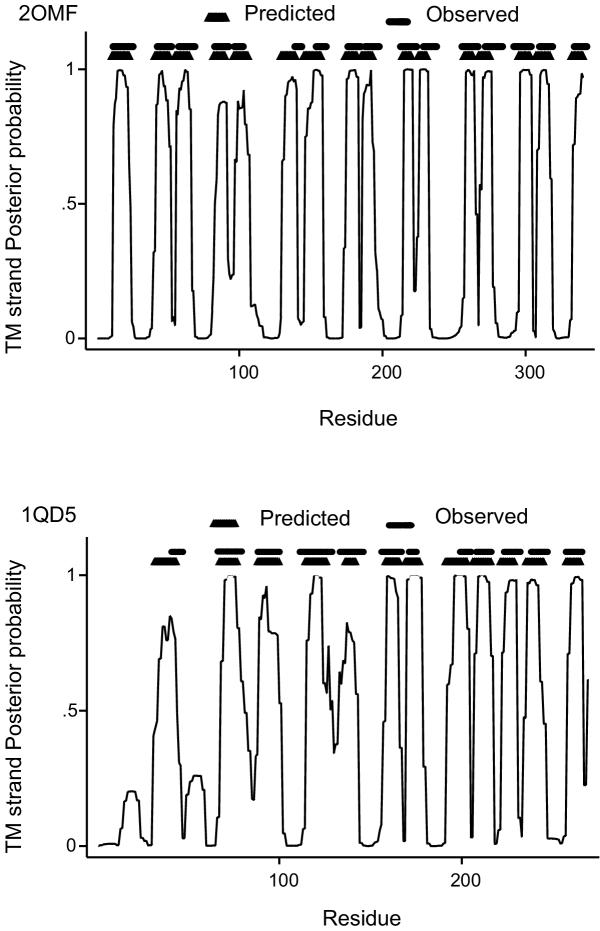
Posterior probabilities plot. Graphs showing posterior probabilities along the sequence, for residues to be in a transmembrane β-strand, for the proteins with PDB codes 2OMF and 1QD5 [29]. The observed strands taken from PDB [29] and the predicted transmembrane strands obtained by the N-best algorithm are also plotted.

where L is the length of the sequence. We studied the proportion of correctly classified proteins as a function of the discrimination score used as the threshold. We defined the optimal threshold as the value that maximizes that function. Proteins with score values below the threshold should be declared as beta-barrel membrane proteins. All algorithms and tools used throughout this work have been implemented by the authors, using the Java programming language by Sun Microsystems.

The model architecture

The model that we used is cyclic, consisting of 61 states, (Figure 4). The architecture has been chosen so that it could fit as much as possible to the limitations imposed by the known structures. The model consists of three "sub-models" corresponding to the three desired labels to predict, the TM (transmembrane) strand sub-model and the inner and outer loops sub-models respectively. The TM strand model incorporates states to model the special architecture of the transmembrane strands. Thus, there are states that correspond to the core of the strand and the aromatic belt located at the lipid bilayer interface. Furthermore, other states correspond to the amino acid residues facing the bilayer (the external side of the barrel) and the residues facing the barrel interior. All states are connected with the appropriate transition probabilities in order to be consistent with the known structures (i.e. to ensure appropriate length distributions and to model the alternating pattern of hydrophobic-non hydrophobic residues, corresponding to the external-internal residues of the barrel). The minimum allowed length for a transmembrane strand is 7 residues, whereas the maximum is 17.

The inner and outer loops are modeled with a "ladder" architecture, whereas at the top of the outer loop there is a self transitioning state corresponding to residues too distant from the membrane; these cannot be modeled as loops, hence that state is named "globular". The "inner" loop sub-model has no corresponding "globular" state, reflecting the fact that inner loops are significantly shorter than the outer ones, since none of the known structures possesses an inner loop longer than twelve residues. In order to capture the fact that all known structures are having their N-terminal tail falling into the periplasmic space (the "inside" with respect to the outer membrane) we allowed the begin state of the model to be followed only by states belonging to the inner loop or to TM strands directing to the external side of the outer membrane. Finally, we allowed a self-transitioning absorbing state to follow the inner loop states, in order to correctly model sequences that have a long C-terminus falling in the periplasmic space. States expected to have the same emission probabilities are tied together.

Training and testing sets

The training set that we used has been compiled with consideration of the SCOP classification [28]. In particular, we selected all PDB codes from SCOP that belong to the fold "Transmembrane beta-barrels", and obtained the corresponding structures from the Protein Data Bank (PDB) [29]. For variants of the same protein, we kept the structure solved at the highest resolution, and we removed multiple chains, keeping only one chain for each structure. The sequences of the remaining structures have been submitted to a redundancy check, removing chains with a sequence identity above some threshold. We considered two sequences as being homologues, if they demonstrated an identity above 30% in a pairwise alignment, in a length longer than 80 residues. For the pairwise local alignment we used BlastP [30] with default parameters, and the homologous sequences were removed implementing Algorithm 2 from Hobom et al [31]. The remaining 14 outer membrane proteins constitute our training set (Table 1). The structures of TolC [32] and alpha-hemolysin [33], were not included in the training set for the following reasons: TolC is a mixed beta-barrel and alpha-helical protein which spans both the outer membrane and the periplasmic space of gram negative bacteria. Three TolC protomers assemble to form a continuous, solvent accessible conduit, a "channel-tunnel" over 140 Å long. Each monomer of the trimer contributes 4 β-strands to the 12 strand β-barrel. Alpha-hemolysin secreted from S. aureus is active as a transmembrane heptamer, where the transmembrane domain is a 14-strand antiparallel β-barrel, in which two strands are contributed by each monomer. Both structures are not included in the fold "transmembrane beta-barrel" of the SCOP database. In summary, the set includes proteins being monomeric, dimeric or trimeric, with a number of TM β-strands ranging from 8 to 22, and is representative of the known functions of outer membrane proteins. As an independent test set of outer membrane proteins, we chose the dataset used in the validation of the PSORT-B algorithm [34], consisting of 377 proteins. This set was also checked for redundancy with the same criteria mentioned above, and the closest homologues were removed along with the proteins showing similarity to at least one protein from the training set, leaving us with 119 outer membrane proteins. To test the discriminative power of the model we used an additional dataset of globular proteins, with 3-dimensional structures deposited in PDB [29]. This set was compiled using the PAPIA [35] server, with the sequence similarity threshold set to 25%, and excluding membrane proteins, proteins with a length lower than 80 residues, and proteins with at least one unidentifiable residue in the sequence; finally we came up with 1100 sequences of such globular proteins.

It is noteworthy that even in structures known at atomic resolution, the exact boundaries of the TM strands are not obvious, and in some situations the PDB annotations for the strands are clearly extending far beyond the membrane. Since our primary objective was to predict the TM segments of the strands rather than the entire β-strands, the model was trained to identify these particular segments. It is well known that discriminative training algorithms are very sensitive to data mislabeling, thus the training could not have been performed with labels based on the PDB annotation for the TM-strands. In [18], an automated method for re-labeling the data was proposed, but in our case since the training data set was limited we chose a manual approach. For the training purposes, the labels for the TM segments were set manually, by identifying the aromatic belts of the barrel [2] after inspection of the 3-dimensional structures of the proteins of the training set using molecular graphics. All residues contained between the two aromatic belts of each β-strand of the β-barrel were set to define a TM segment, including the residues of the belts. In cases where the aromatic belt residues of a β-strand are not clearly defined, neighbouring β-strands of the β-barrel helped in the "belt" identification. The resulting dataset used for training is shown in additional file 1 (second column, TM).

Measures of accuracy

To assess the accuracy of the predictions, we used several measures. For the transmembrane strand predictions we calculated the number of correctly predicted strands (True Positives, TP), the number of missed strands (False Negatives, FN) and the number of the over-predicted strands (False Positives, FP). We also calculated the total number of correctly predicted topologies, i.e. when both the strand localization and the loops topology have been predicted correctly. As measures of the accuracy per residue, we report here both the total fraction of the correctly predicted residues (Q_β) in a two-state model (transmembrane versus non-transmembrane), and the well known Matthews Correlation Coefficient (C_β) [36]. The comparisons have been performed against our manual annotation of the TM segments to show the efficiency of the model as well as against the PDB annotation for the transmembrane strands, for demonstration purposes. We feel that this had to be done in order to allow a fair comparison with other published methods [6-8], since in each one of the published methods the comparisons were performed against the PDB annotation.

Authors' contributions

PB carried out the design of the algorithms and the model, the data collection, the training and testing procedures, and also participated in the implementation. TL implemented most of the algorithms, and also participated in the model design. IS created the web interface. SH coordinated the whole project, suggesting the general directions and innovating features of the method. All authors have read and accepted the final manuscript.

Supplementary Material

Additional File 1

5.63 kb, a list of the observed β-strands taken from PDB [29], the manually annotated transmembrane segments (TM), and the predicted transmembrane segments of the 14 proteins of the training set.