Excited State Dynamics Can Be Used to Probe Donor-Acceptor Distances for H-Tunneling Reactions Catalyzed by Flavoproteins

Abstract

In enzyme systems where fast motions are thought to contribute to H-transfer efficiency, the distance between hydrogen donor and acceptor is a very important factor. Sub-ångstrom changes in donor-acceptor distance can have a large effect on the rate of reaction, so a sensitive probe of these changes is a vital tool in our understanding of enzyme function. In this study we use ultrafast transient absorption spectroscopy to investigate the photoinduced electron transfer rates, which are also very sensitive to small changes in distance, between coenzyme analog, NAD(P)H₄, and the isoalloxazine center in the model flavoenzymes morphinone reductase (wild-type and selected variants) and pentaerythritol tetranitrate reductase (wild-type). It is shown that upon addition of coenzyme to the protein the rate of photoinduced electron transfer is increased. By comparing the magnitude of this increase with existing values for NAD(P)H₄-FMN distances, based on charge-transfer complex absorbance and experimental kinetic isotope effect reaction data, we show that this method can be used as a sensitive probe of donor-acceptor distance in a range of enzyme systems.

Introduction

A major contributor to the efficiency of enzyme-catalyzed reactions is the kinetic and thermodynamic “cost” of forming precise reactive geometries between the enzyme, substrate, and reactive groups. There is evidence that even sub-ångstrom changes to the reactive complex can have major effects on enzyme efficiency and mechanism (1). Experimentally it is challenging to monitor the precise geometry of the enzyme reactive complex; even high-resolution x-ray crystal structures cannot generally resolve sub-Å changes. Understanding the importance of subtle changes to reactive geometries is particularly important for promiscuous enzymes, and this has implications for the rational (re)design of enzyme catalysts for applications in biotechnology. We have previously developed specialized experimental probes of the reactive complex geometry of flavoproteins based on system-specific absorbance and kinetic features (2,3). However, a more general probe would be useful that can be applied to a broad range of enzyme systems. In principle, the excited state lifetimes of enzyme cofactors can be used as a sensitive probe of reactive complex environment (4,5). In the present article, we test this concept using two well-characterized enzyme systems as benchmarks of the utility of excited state dynamics in probing reactive geometries in relation to donor-acceptor distances associated with the enzymatic reaction coordinate.

Enzymes commonly utilize (in)organic cofactors to assist chemical conversion in the enzyme catalytic cycle. These cofactors are bound to the protein via covalent or noncovalent bonds, can mediate a broad range of chemical reactions, and are central to most cellular processes. Flavoenzymes contain either the cofactor flavin mononucleotide (FMN) or flavin adenine dinucleotide (FAD) and are able to catalyze redox reactions with a wide range of substrates and in different cellular contexts. Two such flavoenzymes are morphinone reductase (MR) and pentaerythritol tetranitrate reductase (PETNR), both are members of the old yellow enzyme family and catalyze ene-reduction reactions, not only for specific reactions such as the reduction of codeinone to hydrocodone, but also stereoselectively for a wide range of activated alkenes (6–8). The catalytic cycle can be separated into reductive and oxidative half-reactions. The reductive half-reaction (RHR) of the flavoenzymes MR and PETNR have been used as model systems to investigate a range of fundamental principles in enzyme catalysis, including the importance of nuclear tunneling, protein and solvent dynamics, driving force, and active site architecture (3,9–12). The RHR involves hydride transfer from nicotinamide adenine dinucleotide (NADH) coenzyme (nicotinamide C4) to the cofactor FMN (isoalloxazine N5). The reactive FMN-NAD(P)H complex is characterized by a coplanar, π-stacked configuration of the nicotinamide (phosphate) (NAD(P)H) and isoalloxazine (FMN) moieties (Fig. 1). Hydrogen-transfer (H-transfer) reactions maintain a precise reactive complex geometry, which is critical to H-transfer that occurs by quantum mechanical tunneling (10,13–16). The distance between the donor and acceptor atom is important in optimizing wavefunction overlap (i.e., the donor-acceptor distance) for the H-nucleus in donor-acceptor wells, thereby ensuring a high probability of transfer (17,18). Further, there is mounting evidence that fast motions can contribute to enzyme H-transfer reactions (12,19–22). The majority of experimental evidence indicates that these motions come into play at increased donor-acceptor distances and are a less important for shorter donor-acceptor distance reactive geometries (23). Thus, apparently counterintuitively, longer donor-acceptor distances can result in increased rates of H-transfer because of the increased contribution of the fast motions outweighing the loss of wavefunction overlap (9).

Figure 1.

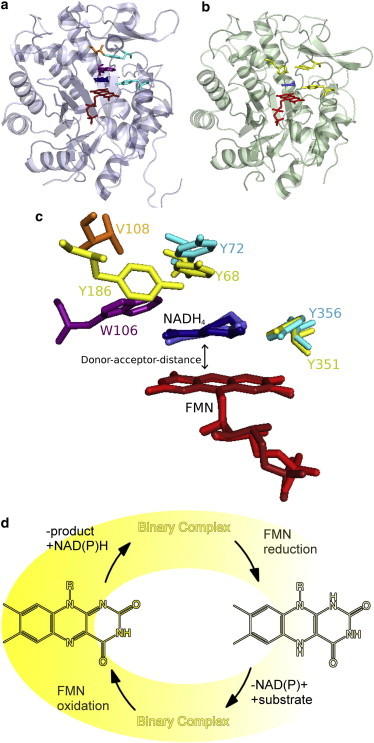
X-ray crystal structures of (a) wild-type MR (2R14.pdb) (11) and (b) wild-type PETNR (3KFT.pdb) (9) bound to nonreactive NADH analog; (c) an overlay of the key residues (MR: cyan, orange, purple, PETNR: yellow) in the coenzyme binding site and nicotinamide ring of the coenzyme (MR: dark blue, PETNR: light blue), aligned on the isoalloxazine ring of the FMN (MR: dark red, PETNR: light red); and (d) catalytic cycle of MR and PETNR, adapted from (12). To see this figure in color, go online.

In MR and PETNR, spectroscopic and kinetic “rulers” have previously been developed based on the intensity of an absorption feature attributed to π-stacking of the isoalloxazine and the nicotinamide moieties (Fig. 2 a), and the magnitude of the secondary kinetic isotope effect (2° KIE), respectively (2,3). These studies have suggested that mutating selected residues in the active site of MR allows the donor-acceptor distance to be finely manipulated on sub-Å scales (2). Reducing (MR variants V108A and W106A) and increasing (MR variant V108L) side chain bulk in the enzyme active site were suggested to shorten and lengthen donor-acceptor distances, respectively. These charge-transfer spectroscopic rulers have been used further to probe reactive geometries in the related enzyme PETNR in complex with the coenzyme analogs NADH₄ and NADPH₄. In this case, the findings suggest that the donor-acceptor distance is similar with both coenzymes (9).

Figure 2.

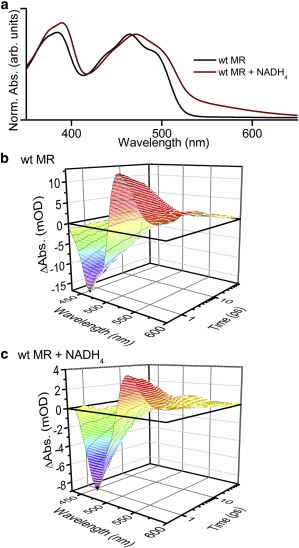
(a) Ground state absorption spectra of wild-type MR with and without NADH₄ coenzyme, the features at ∼375 nm, 470 nm, and 550 nm (in the coenzyme bound spectrum) are due to the S₀ → S₂ and S₀ → S₁ transitions, and a charge-transfer band respectively. Example transient absorption difference three-dimensional spectra are shown, after excitation at 375 nm, of wild-type MR (b) without and (c) with NADH₄ coenzyme, the negative absorption feature at ∼470 nm, results from a bleach of the ground state (S₀ → S₁), whereas a positive absorption feature at ∼530 nm originates from excited state absorption (S₁ → S_n). To see this figure in color, go online.

The photochemistry of flavins has been widely investigated (24,25). Multiple studies, using ultrafast transient absorption (26–28) and time-resolved fluorescence (29,30) spectroscopy, have been carried out on flavin-containing protein systems. In solution, the photoexcitation of FMN is characterized by one comparatively long (ca. 3 ns) excited state lifetime (31). In contrast, the excited state dynamics of FAD are more complex, comprising both ps and ns components attributed to π-stacking of the isoalloxazine and adenine moieties (26,32). Intramolecular charge transfer on timescales of 5 to 9 ps, followed by charge recombination in 30 to 40 ps, can occur between the adenine and the isoalloxazine moieties (27,33), which greatly reduces the excited state lifetime. This effect has also been seen where the isoalloxazine ring is in close proximity to other aromatic groups such as the side chains of tyrosine and tryptophan (5,34,35). Electron transfer in protein systems is a well-studied phenomena (36–38), and the average distance between the two moieties is critical in controlling the excited state dynamics, with negligible quenching of the excited state seen at distances further than 5 to 6 Å (39). From the decay kinetics of excited state flavin the electron transfer rates, and thus average donor-acceptor distance, can be calculated (40). Previous studies have used the rate of decay of the excited state (S₁, S₂, etc.) population to calculate these rates of electron transfer. In this study we monitored the recovery of the ground state (S₀) population to the same effect. As shown in Fig. 3 the kinetic pathway we monitored has both a common product (S₀) and common reactant (S₁). So, assuming the rate of internal conversion, k_IC, from S₂ to S₁ is very fast, the reactions occurring will be as follows:

$$\begin{array}{l}{\text{S}}_1\stackrel{k_{\text{NR}}}{\to }{\text{S}}_0\\ {\text{S}}_1\stackrel{k_{\text{F}}}{\to }{\text{S}}_0\\ {\text{S}}_1\stackrel{k_{\text{CT}}}{\to }{\text{S}}_{CT}\stackrel{k_{\text{CR}}}{\to }{\text{S}}_0\\ {\text{S}}_1\stackrel{k_{\text{ISC}}}{\to }{\text{T}}_1\stackrel{k_{\text{P}}}{\to }{\text{S}}_0\end{array}$$

where k_NR is the rate of nonradiative decay; k_F is the rate of fluorescence decay; k_CT and k_CR are the rate of charge transfer and charge recombination, respectively; and k_ISC and k_P are the rates of intersystem crossing and phosphorescence, respectively. The rate of loss of S₁ (i.e., fluorescence decay) can be written as follows:

$$-\frac{d\left[{\text{S}}_1\right]}{dt}\approx (k_{\text{NR}}+k_{\text{F}}+k_{\text{CT}}+k_{\text{ISC}})\left[{\text{S}}_1\right]$$

As k_ISC from S₁ to T₁ is likely to be much greater than the rate of phosphorescence from T₁ to S₀, and as, from our global analysis of the transient absorption data described in the results section, we see evidence for an “inverse kinetic” scheme where the rate of charge recombination exceeds the rate of charge transfer (41), the rate of recovery of S₀ (i.e., ground state bleach recovery) can be written as follows:

$$\frac{d\left[{\text{S}}_0\right]}{dt}\approx (k_{\text{NR}}+k_{\text{F}}+k_{\text{CT}}+k_{\text{P}})\left[{\text{S}}_1\right]$$

As a result the only difference between monitoring fluorescence and change in absorbance should be the k_ISC and k_P terms, both of which are so slow as to be negligible over the time frames in this study. Monitoring changes in absorbance has the additional benefit that strong quenching of emissive states does not significantly affect the magnitude of the signal, whereas fluorescence measurements on similar systems will suffer from very low signal strength in strongly quenched systems. In the case of MR, crystal structures of both the coenzyme bound and unbound states have been solved at resolutions of 1.3 and 2.2 Å, respectively (11,42) and the structures were found to be virtually identical. This being the case we can assume that the only rate affected by coenzyme binding is that of charge transfer and recombination, then by taking the difference in rates of repopulation of S₀ between the coenzyme bound and unbound systems the rate of photoinduced charge transfer from the coenzyme can be found. It has been shown that the rate of excited state quenching of flavins by neighboring aromatic groups displays a correlation with average distance, rather than the edge-to-edge (shortest) distance or angle between the two moieties (4,40). Consequently, this method provides a more sensitive probe of the active site, without the need to make complex isotope measurements, or rely on a unique absorbance feature as with the spectroscopic and kinetic “rulers” described above. In this work we expand on previous donor-acceptor distance investigations in MR and PETNR, using the ultrafast excited state properties of the flavin, as described above, to probe both the active site environment fluctuations in flavoproteins (when no coenzyme is bound and only nearby electron-donating residues affect the excited state lifetime) and donor-acceptor distance (when the bound coenzyme acts as an efficient electron-donor and reduces the excited state lifetime compared with the coenzyme unbound system).

Figure 3.

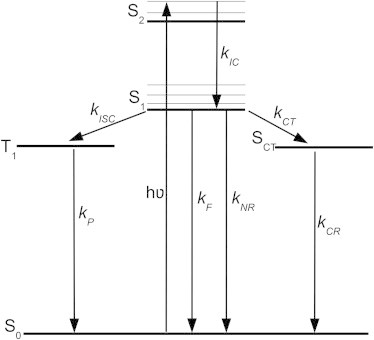
Diagram illustrating relaxation pathways after excitation to the S₂ state: internal conversion from S₂ to S₁ (k_IC), intersystem crossing from S₁ to T₁ (k_ISC), phosphorescence from T₁ to S₀ (k_P), fluorescence (k_F) and nonradiative decay (k_NR) from S₁ to S₀, and charge transfer (k_CT) and charge recombination (k_CR) from S₁ to S₀. The rate of photoinduced electron transfer, k_ET, is the sum of the rates of charge transfer and charge recombination.

Materials and Methods

Expression and purification of the wild-type and the W106A, V108L, and V108A variant MR and PETNR enzymes was carried out as described previously (2,3). We prepared 1,4,5,6 tetrahydroNADH (NADH₄) and 1,4,5,6 tetrahydroNADPH (NADPH₄) using NADH and NADPH, respectively, from Melford laboratories, as described previously (14). Concentrations of solutions were determined by absorbance measurements at 464 nm for MR and PETNR enzymes (ε = 11.3 mM^-1cm⁻¹) and at 288 nm for NAD(P)H₄ (ε = 16.8 mM^-1cm⁻¹). The concentration of NAD(P)H₄ was kept at least 10 times the dissociation constant of the enzyme-substrate complex (2) to ensure saturation of the enzyme active site.

The laser system used for the transient absorption experiments comprises a Ti:sapphire amplifier (a hybrid Legend Elite-F-HE, Coherent, Santa Clara, CA) pumped by a Q-switched Nd:YLF laser (Evolution-30, Positive Light, Santa Clara, CA) and seeded by a Ti:sapphire laser (Mai Tai, Spectra Physics, Santa Clara, CA). The amplifier output, which has a wavelength of 800 nm, a 1 kHz repetition rate, and ∼120 fs pulse duration is split, and part of the output is used to generate the 375 nm pump beam using a noncollinear optical parametric amplifier (TOPAS-White, Light Conversion, Vilnius, Lithuania). The transient absorption experiments used a Helios (Ultrafast Systems) spectrometer with an instrument response function of around 0.2 ps. Samples were contained within 2 mm pathlength quartz cuvettes and stirred to prevent photodegradation. Data were corrected for spectral chirp using SurfaceXplorer (Ultrafast Systems, Sarasota, FL) and were fitted over a time period of 85 ps from 0.4 ps after T0 (where pump and probe first overlap) to ensure any coherent artifacts were avoided (43). Data were globally analyzed using the open-source software Glotaran (44). The global analysis procedure reduces the three-dimensional data matrix of wavelength, time, and change in absorbance, to one or more exponentially decaying time components, each of which has a corresponding difference spectrum. The resulting difference spectra and time constants can be used to gain insight into the processes occurring after photoexcitation. A parallel model of independently decaying components yielded decay associated difference spectra (DADS), which represent the loss or gain of emission or absorption with a certain lifetime. The number of components fitted to each data set was determined by increasing the number of components until the residuals were effectively zero. The photoinduced electron transfer rate, k_ET, from the coenzyme analogs to the isoalloxazine moiety was calculated as the difference between the rate of ground state recovery, k_S0, for the bound and unbound systems, based on the assumption that upon coenzyme binding the only rate to change is k_ET. The feature we monitor in the transient absorption experiments originates solely from the S₁ → S₀ transition (which is reasonable to assume, given the S₂ → S₀ transition is centered at ca. 375 nm, instead of the ca. 465 nm for the S₁ → S₀ transition – see Fig. 2 a). Data averaged over the wavelength region 430 to 465 nm, where only ground state bleaching features contributed to the difference spectra (Fig. S1 in the Supporting Material), were fitted to multiexponential function with the formula $y=y_0+{\sum }_i{A}_i{e}^{\raisebox{1ex}{$-x$}\!\left/ \!\raisebox{-1ex}{${\tau }_i$}\right.}$, where y₀ is a constant, A_i is the proportional amplitude, and τ_i is the corresponding lifetime of each component. The rate of ground state recovery was calculated as: $k_{S0}=1/{\sum }_i{A}_i{\tau }_i$.

Results and Discussion

Decay associated difference spectra

We monitored the time-resolved difference spectra for each of the MR variants (wild-type MR, V108A, V108L, and W106A MR) with NADH₄, and PETNR with NADPH₄ and NADH₄. NADPH₄ and NADH₄ are excellent mimics of NADPH and NADH, respectively, in that they bind to the protein and form similar charge-transfer complexes, but they cannot then reduce the flavin (11). In all cases, a negative absorption feature arises at ∼470 nm, resulting from a bleach of the ground state (S₀ → S₁), whereas a positive absorption feature at ∼530 nm originates from excited state absorption (S₁ → S_n) (Fig. 2). To gain insight into photochemistry occurring after excitation, the data recorded for wild-type MR with and without bound coenzyme were globally analyzed to produce the DADS shown in Fig. 4. Although not necessary for the calculation of photoinduced electron transfer rates, this analysis provides extra information on the processes occurring. The data could be fitted by four components (see Figs. S2 and S3 in the Supporting Material), each sample consisting of a combination of; τ₁ ≈ 0.6 ps, τ₂ ≈ 4 ps, τ₃ ≈ 18 ps, and τ₄ ≈ 500 ps. The spectra are broadly similar to those reported for FAD (41), where no spectral signatures of photoinduced electron transfer were observed, but a strong argument was proposed for an “inverse kinetic” scheme where the rate of charge recombination exceeds the rate of charge separation, so no spectral features deriving from the charge separated state could be observed. The three shortest-lived components will all have spectral contributions from the photoinduced electron transfer processes in addition to the excited state relaxation. DADS1, corresponding to the fastest decay time, is red-shifted compared with the longer lifetime components. It has been suggested in other flavin systems that this component may originate from the hot singlet excited state (28), or structural and solvent relaxation after the initial excitation pulse (41). The “middle” components, DADS2, and DADS3 all have similar spectral shapes and are likely to originate from the radiative relaxation of the singlet excited states of different structural conformations (28,29). The long lifetime component DADS4 will also contain elements from this process, but a broad positive feature at long wavelengths becomes more evident, which is likely to originate from formation of the excited triplet state (45).

Figure 4.

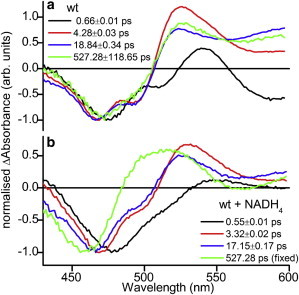
Normalized decay associated difference spectra from global analysis of transient absorption data of MR: (a) wild-type, (b) wild-type with NADH₄. Change in absorbance values for the ground state bleach minima varied from 0.008 to 0.016 OD. The negative absorption feature at ∼470 nm, results from a bleach of the ground state (S₀ → S₁), whereas a positive absorption feature at ∼530 nm originates from excited state absorption (S₁ → S_n). The black, red, blue, and green difference spectra represent the spectral components that decay in parallel with the associated increasing time constants shown, which if added together would represent the original dataset. To see this figure in color, go online.

Excited state kinetics in coenzyme-free enzymes

The rate constants and corresponding relative amplitudes, along with calculated rates of ground state recovery, k_S0, and photoinduced electron transfer from the coenzyme to the flavin, k_ET, derived from analysis of the data are shown in Table 1; the fitted data and residuals from the fits are shown in Figs. 5 and 6. The calculated k_S0 can be used as a convenient metric to observe trends in average changes in the local environment as it combines the fitted lifetime values and relative amplitudes, providing one easily comparable value, and discounts any contribution from free, unstacked flavin. There are significant observed differences between the k_S0 values for each of the MR variants (Table 1). Both the V108 variants have significantly smaller k_S0 than the wild-type enzyme. Based on the x-ray crystal structure (Fig. 1), V108 and W106 are in van der Waals contact and it seems likely that changes in side chain bulk of V108 will affect on the equilibrium position of W106. We suggest that replacement of V108 residue with the smaller alanine and larger leucine residues perturbs the equilibrium of conformational states of W106 so that it is located further from the isoalloxazine of FMN in both cases, leading to the observed changes in recovery of the ground state after photoexcitation. The W106A variant gives a small increase in k_ET. The physical basis of this change is not immediately obvious as replacement of a strongly electron-donating tryptophan side chain with a far less electron-donating alanine might be expected to reduce the magnitude of excited state quenching, leading to a decrease in the value of k_S0. However, replacement of such a large residue may also confer subtle conformational changes to the MR active site that may act to increase k_S0 e.g., by bringing electron donating residues (such as Y72, which is essentially within van der Waals contact with W106) into closer proximity to the FMN isoalloxazine. Finally, the k_S0 value for PETNR is significantly smaller than for the homologous wild-type MR, although similar to the V108L mutant. This likely reflects differences between the PETNR and MR active sites, despite the overall structural similarity as inferred from the x-ray structures of both enzymes (9).

Table 1.

Kinetic fit parameters and calculated rates of ground state recovery and photoinduced electron transfer rates for data averaged over the range 430 to 465 nm, after excitation at 375 nm, of wild-type, V108L, V108A, W106A MR, and wild-type PETNR with and without the addition of NAD(P)H₄ coenzyme

	τ1 (ps) relative amplitude	τ2 (ps) relative amplitude	τ3 (ps) relative amplitude	kS0 (ps−1)	kET (ps−1)
wt MR	0.26 ± 0.05 47 ± 12%	3.3 ± 0.2 33 ± 1%	16.6 ± 0.7 19 ± 1%	0.23 ± 0.01	0.10 ± 0.03
wt MR -NADH4	0.26 ± 0.03 63 ± 11%	3.2 ± 0.2 27 ± 1%	19.9 ± 1.3 10 ± 1%	0.33 ± 0.02
V108L	-	3.9 ± 0.1 58 ± 1%	22.3 ± 0.8 42 ± 1%	0.09 ± 0.01	0.07 ± 0.01
V108L-NADH4	0.24 ± 0.03 48 ± 10%	4.5 ± 0.1 33 ± 1%	26.2 ± 0.9 19 ± 1%	0.15 ± 0.01
V108A	-	3.0 ± 0.1 70 ± 2%	17.0 ± 1.0 30 ± 2%	0.14 ± 0.01	0.11 ± 0.05
V108A-NADH4	0.47 ± 0.08 53 ± 8%	4.4 ± 0.4 40 ± 2%	27.3 ± 8.5 8 ± 2%	0.25 ± 0.05
W106A	-	2.5 ± 0.3 81 ± 8%	8.1 ± 1.9 19 ± 9%	0.28 ± 0.06	0.25 ± 0.08
W106A - NADH4	0.34 ± 0.05 59 ± 9%	4.0 ± 0.4 43 ± 1%	-	0.53 ± 0.04
PETNR	-	1.8 ± 0.4 40 ± 4%	22.4 ± 1.9 60 ± 2%	0.07 ± 0.01
PETNR - NADH4	0.77 ± 0.11 79 ± 8%	-	8.5 ± 1.2 21 ± 2%	0.41 ± 0.06	0.34 ± 0.07
PETNR - NADPH4	0.63 ± 0.08 84 ± 8%	-	7.8 ± 1.1 16 ± 2%	0.56 ± 0.09	0.49 ± 0.09

Errors quoted on the lifetimes and relative amplitudes are those from the fitting procedure, it should be noted that the time resolution of the system is on the order of 200 fs, and this is the value used for error propagation to the rate values if the error on the fit is smaller than this.

Figure 5.

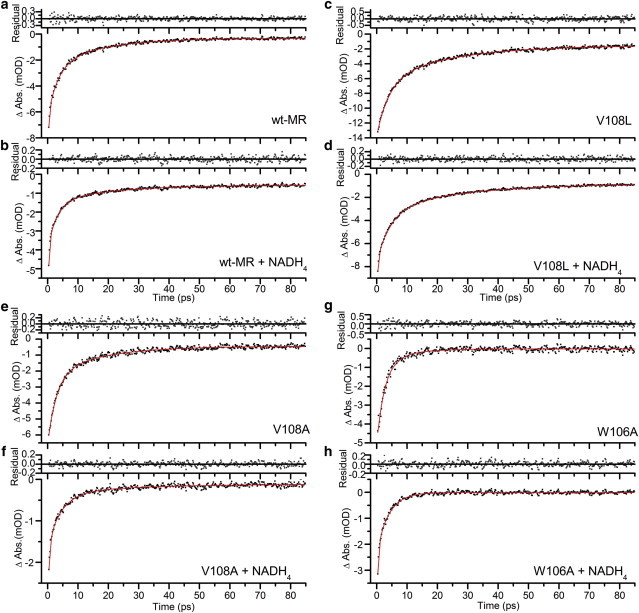
Exponential fits, and corresponding residuals, of ground state recovery for transient absorption data averaged over the range 430 to 465 nm, where only ground state bleaching features contributed to the difference spectra, after excitation at 375 nm, of MR: (a) wild-type, (b) wild-type with NADH₄, (c) V108L, (d) V108L with NADH₄, (e) V108A, (f) V108A with NADH₄, (g) W106A, and (h) W106A with NADH₄. To see this figure in color, go online.

Figure 6.

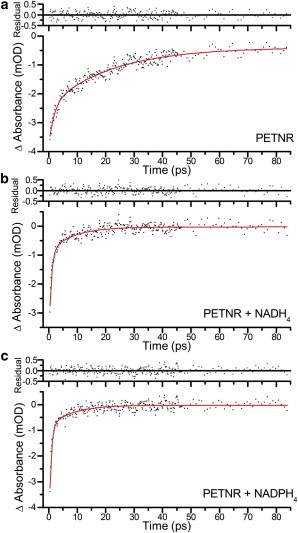
Exponential fits, and corresponding residuals, of ground state recovery for transient absorption data averaged over the range 430 to 465 nm, where only ground state bleaching features contributed to the difference spectra, after excitation at 375 nm, of (a) PETNR, (b) PETNR with NADH₄, (c) PETNR with NADPH₄ To see this figure in color, go online.

Excited state kinetics of coenzyme-bound enzymes

Previous x-ray crystallographic studies have shown that the structures of wild-type MR in the unbound and NADH₄-bound states, within the resolution of the method, are virtually identical (11). Thus we assume that any changes in k_S0 on coenzyme binding are purely because of the coenzyme rather than other changes in the local environment of the FMN isoalloxazine. If the addition of coenzyme affected the protein structure around the isoalloxazine then nearby residues that previously quenched the excited state of the flavin, may be moved further away, artificially reducing the rate of photoinduced electron transfer when the coenzyme was bound. In all the enzyme systems studied, the addition of NADH₄ affects the rate of ground state recovery, which consistently become faster (Table 1) as a result of increasing the rate of electron transfer. The absolute changes in k_S0 upon coenzyme binding, i.e., Δk_S0 or k_ET, should therefore be equal to the rate of electron transfer from the nicotinamide to the isoalloxazine. Analysis of fluorescence data collected over the same timescale for wild-type MR and PETNR with and without cofactors, analyzed using the same method described here yielded comparable rates (see Fig. S4 and Table S1 in the Supporting Material). If k_ET is directly proportional to donor-acceptor distance (smaller k_ET corresponds to a larger donor-acceptor distance) then the k_ET values give the following trend in donor-acceptor distance: V108L (0.07 ± 0.01 ps⁻¹) > wild-type (0.10 ± 0.04 ps⁻¹) > V108A (0.11 ± 0.06 ps⁻¹) > W106A (0.25 ± 0.10 ps⁻¹). These values imply that mutations at the V108 position do not significantly affect the donor-acceptor distance, within the detection limits of the experimental method, despite perturbing the structure of the free enzyme. However, the W106A mutation does seem to significantly shorten the donor-acceptor distance. Previous work with these variant enzymes estimated the donor-acceptor distance trend based on charge-transfer complex absorbance and experimental kinetic isotope effect reaction data as follows: V108L > wild-type > V108A > W106A (2), which are in agreement with the trends reported here using excited state dynamics as a probe of donor-acceptor distance. This is shown in Fig. 7 where good correlation is observed between the data we present in this study and previously reported data (2). It should be noted that even if k_S0, rather than k_ET is plotted the correlation remains significant, implying that the electron transfer term is a major component of the overall rate observed.

Figure 7.

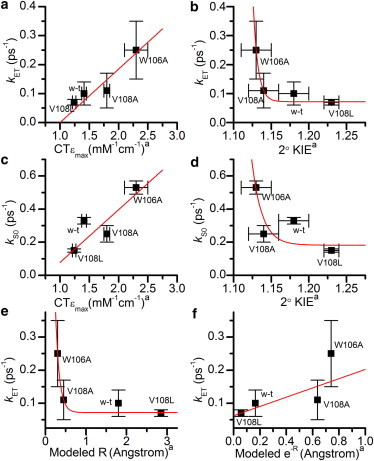
Correlation of the rates of photoinduced electron transfer (k_ET) and ground state recovery (k_S0) with previously recorded values for charge-transfer absorbance magnitude (a and c, respectively) and secondary kinetic isotope effect (b and d, respectively). Calculated photoinduced electron transfer rates from this work plotted against (e) numerically modeled donor-acceptor distances (R), and (f) ${\text{exp}}^{-R}$. Previously recorded values for charge-transfer absorbance magnitude, secondary kinetic isotope effect, and numerically modeled donor-acceptor distance data taken from (2). Red lines are exponential (log k_ET ∝ R ∝ 2° KIE (2,46)) or linear (k_ET ∝ CTε_max as both are electron transfer processes with rates related to R) fits to the data to aid the eye. To see this figure in color, go online.

In the case of PETNR, larger changes are seen upon addition of coenzyme than are observed for MR (Table 1). The unbound value of k_S0 for PETNR is substantially smaller than that of wild-type MR, but upon addition of the coenzyme the k_S0 value increases to a greater extent than observed with the MR enzymes. Clearly, there are subtle differences between the active sites of these two enzymes making direct comparison across the two enzyme types difficult. However, a comparison of the excited state dynamics of PETNR with NADH₄ and NADPH₄ bound is informative. Unlike MR, PETNR is able to reduce the FMN with both of these coenzymes, but the rate of hydride transfer is significantly (∼15 times) larger with NADPH compared with NADH. We have previously provided evidence that this difference is in large part because of the presence of fast dynamics coupled to the reaction coordinate with NADPH, but not NADH (9). Previous studies have suggested that, within the resolution of the techniques used, the donor-acceptor distance is similar for NADH and NADPH despite significant differences in the mechanism of H-transfer (9). However, the calculated k_ET value for NADPH₄ is larger than that for NADH₄, suggesting that NADPH binds closer to the isoalloxazine than NADH, probably contributing to the faster observed hydride transfer rate.

Estimate of donor-acceptor-distance from photoinduced electron transfer rates

Using a basic model for electron transfer, we calculated the donor-acceptor distances for the enzyme systems from the electron transfer rates. If, for simplicity, we assume the reaction occurring is a pure electron transfer process, with no proton-coupled contribution, we can make an estimate of the changes in donor-acceptor distance in the variant enzymes by using the approximate empirical formula:

$$\text{log}{k}_{ET}=15-0.6R-3.4{(\Delta G_0-\lambda )}^2/\lambda$$ (1)

where R is the donor-acceptor distance, ΔG₀ is the free energy, driving force, and λ is the reorganization energy (46). The free energy can be approximated as follows: $\Delta G_0=\Delta E-E_{0,0}$, where ΔE is the difference in redox potentials of the donor and acceptor, and E_0,0 is the energy of the excited state (47). The energy of the excited state can be estimated from an average of the absorption and emission bands, 2.45 eV in all cases. The measured redox potential values for flavin in coenzyme unbound MR and for NADH are -237 mV and -320 mV, respectively (48). However redox potential values for flavin in the coenzyme bound systems vary with reported values of -258, -264, and -218 mV for NADH₄ bound wild-type MR, V108L, and V108A, respectively (2), and values of -135 and 185 mV for PETNR bound to NADH₄ and NADPH₄, respectively (9). The redox potential for the coenzyme bound W106A variant has not been measured. Calculations are further complicated by the unknown redox potential for the NAD(P)H₄ coenzymes, which will be significantly higher than the NAD(P)H value (49). Fig. 8 shows plots of donor-acceptor distance, calculated using Eq. 1, for each of the enzyme systems for a range of reorganization energies and coenzyme redox potentials. The chosen reorganization energy range covers the most relevant values for intraprotein electron transfer, 0.7 eV is considered typical for these processes (46). If it is assumed that the coenzyme analogs are redox inactive in all cases in this study, we can estimate that the redox potential for NAD(P)H₄ is substantially more positive than -135 mV (the redox potential of the flavin in PETNR bound to NADH₄), and we have plotted a range of 1 V above this value to cover all reasonable options.

Figure 8.

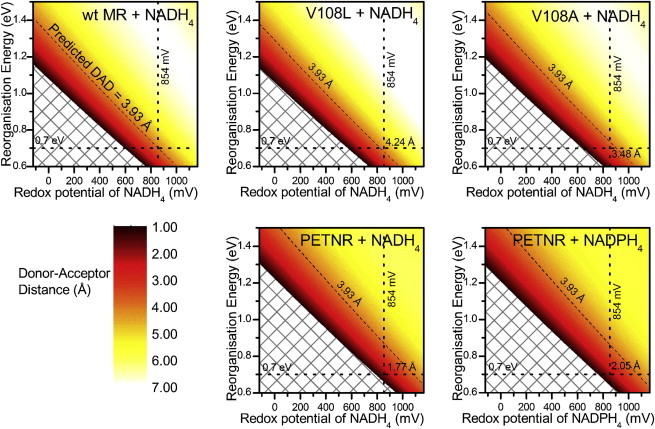
Donor-acceptor distances for the enzyme systems studied here, calculated using Eq. 1, plotted as a function of reorganization energy and coenzyme redox potential. Dashed lines show “typical” reorganization energy of 0.7 eV, assumed redox potential of coenzyme of +854 mV, and theoretically calculated donor-acceptor distance of wild-type MR of 3.93 Å (16). To see this figure in color, go online.

Using the value derived from molecular dynamics simulations for the donor-acceptor distance in wild-type MR, 3.93 Å (16) as a starting point it is possible, assuming the reorganization energy is a “typical” 0.7 eV, to solve equation 1 for R, which gives the redox potential of NAD(P)H₄ as +854 mV. Using these values we can then calculate the donor-acceptor distances for the enzyme systems in this study as follows: V108L(4.24 Å) > wild-type (3.93 Å) > V108A(3.48 Å). If the same values of reorganization energy and coenzyme redox potential are used for the PETNR data, the resulting donor-acceptor distances are calculated as 1.77 and 2.05 Å for NADH₄ and NADPH₄ bound enzymes, respectively. These values are significantly smaller than previous distances reported from molecular dynamics simulations of 3.73 and 3.63 Å respectively (9) highlighting the very qualitative nature of these values.

Conclusions

In this study we present a method of probing the active site of flavoproteins that can not only show trends in donor-acceptor distance, but also probe the local protein structure around the central chromophore, a useful tool for systems where stable enzyme-substrate analog complexes cannot be formed. Previous studies using excited state lifetimes to probe local geometry in flavoproteins have focused on the photochemistry (e.g., studies of BLUF domains (28,45)) rather than using the technique to rationalize enzyme mechanism and kinetics. Analysis of the ultrafast transient absorption data offers insight into the structural changes induced by selective mutations of MR, as well as informing on the donor-acceptor distances. By measuring the photoinduced electron transfer rate in a variety of MR variants, perturbations in active site geometry are inferred which were not observed by previously used methods, such as absorption features due to donor-acceptor interaction or magnitude of the secondary kinetic isotope effect. This comparatively quick and simple method could be used for screening in targeted mutagenesis before large quantities of enzyme, and time, is spent on exhaustive kinetic studies.