Optimization and evaluation of a proportional derivative controller for planar arm movement

Abstract

In most clinical applications of functional electrical stimulation (FES), the timing and amplitude of electrical stimuli have been controlled by open-loop pattern generators. The control of upper extremity reaching movements, however, will require feedback control to achieve the required precision. Here we present three controllers using proportional derivative (PD) feedback to stimulate six arm muscles, using two joint angle sensors. Controllers were first optimized and then evaluated on a computational arm model that includes musculoskeletal dynamics. Feedback gains were optimized by minimizing a weighted sum of position errors and muscle forces. Generalizability of the controllers was evaluated by performing movements for which the controller was not optimized, and robustness was tested via model simulations with randomly weakened muscles. Robustness was further evaluated by adding joint friction and doubling the arm mass. After optimization with a properly weighted cost function, all PD controllers performed fast, accurate, and robust reaching movements in simulation. Oscillatory behavior was seen after improper tuning. Performance improved slightly as the complexity of the feedback gain matrix increased.

1. Introduction

High-level (cervical C1–C4 level) spinal cord injury (SCI) involves the loss of most or all voluntary muscular function below the neck. In this type of injury, communication between the brain and skeletal muscles is impaired, while the peripheral neuromuscular system remains intact. Functional electrical stimulation (FES) can restore voluntary movement, but is particularly challenging in the proximal upper extremity (UE) (i.e. shoulder and elbow joints), because arm reaching movements tend to be goal-oriented and unique, requiring a novel muscle stimulation specification for each reaching task.

To date, FES systems used in humans have most commonly employed feedforward, or open-loop, control (Blana et al., 2009; Abbas and Triolo, 1997; Kilgore et al., 1989). Stimulation parameters are calculated by the controller to generate a desired movement. Feedforward control has been used for upper extremity movement including hand grasp (Keith et al., 1989; Mauritz and Peckham, 1987), single-joint arm movements (Lan and Crago, 1994), and elbow extension (Crago et al., 1998). Feedforward control has the advantage that no sensors are required, which facilitates rapid movements and greatly simplifies controller implementation in humans. However, drawbacks include the inability to make corrections if the actual movement deviates from the desired one due to muscle fatigue or change in environment, and the requirement to have detailed system behavior in order to produce an accurate movement (Crago et al., 1996).

Feedback control uses sensors to monitor output and to make corrections when the output does not behave as desired (Crago et al., 1996). Feedback has been used for a variety of UE FES applications, including hand grasp (Crago et al., 1991), wrist stabilization (Lemay and Crago, 1997) and elbow extension (Giuffrida and Crago, 2001). Feedback control has been investigated for numerous FES applications, as it addresses many of the shortcomings of feedforward control (Crago et al., 1996; Abbas and Triolo, 1997). However, because body-mounted sensors are required, the use of feedback control in clinical applications has been limited (Chizeck et al., 1988). Challenges to the success of feedback control include limitations in sensor signal quality, the relatively slow response properties of muscles (Abbas and Triolo, 1997), and inherent delays in system response, which are of particular concern for fast movements (Stroeve, 1996).

Beyond basic feedback controllers, advanced UE FES controllers have also been developed. Such controllers have used a variety of techniques, including combined feedforward and feedback control (Blana et al., 2009; Kurosawa et al., 2005; Abbas and Chizeck, 1995), reinforcement learning (Thomas et al., 2009; Izawa et al., 2004), and artificial neural networks (Iftime et al., 2005; Giuffrida and Crago, 2005; Winslow et al., 2003). To demonstrate the superiority of these advanced controllers, these highly tuned controllers are often compared to linear proportional-derivative (PD) and proportional-integral-derivative (PID) controllers (e.g. Dou et al., 1999; Reiss and Abbas, 2000) that may have been suboptimal. Although tuning algorithms such as the Ziegler–Nichols (Astrom and Hagglund, 2004; Blana et al., 2009) and Chien, Hrones and Reswick (Chien et al., 1952; Kurosawa et al., 2005) methods are often used for these linear controllers, such controllers cannot be considered optimized; in fact, the Ziegler–Nichols tuning often gives very poor results (Astrom and Hagglund, 2001), including excessively large overshoots for nonlinear processes (Dey and Mudi, 2009). Therefore, simple feedback controllers may have been dismissed as inferior, without having been tuned or optimized to the same degree as the more complex controllers. In this paper, we propose to optimize and evaluate a basic PD controller in order to determine the best possible performance that this simple controller is capable of, for a range of conditions that approximate the physical challenges faced by FES subjects. The PD controller architecture is particularly of interest because it recruits muscles according to the Equilibrium Point hypothesis, which has been successful in explaining basic features of motor control in the intact nervous system (Feldman et al., 1998).

This work, therefore, had two purposes: (1) to optimize a proportional derivative controller for a planar, 2-segment arm model and (2) to evaluate this optimized controller to determine whether it performed well for a range of challenging conditions that approximate a real-world set of FES reaching tasks.

2. Methods

2.1. Biomechanical model

The system used for all experiments described in this paper was a computational musculoskeletal model that approximated a human arm constrained to move in a single horizontal plane, as sliding along a tabletop (Fig. 1). Such planar movement is typical of FES arm movements that utilize mobile planar arm supports (Rahman et al., 2006) and is often used in basic research on arm control (e.g. Blana et al., 2009; Lan, 1997; Freeman et al., 2009; Dou et al., 1999). The model has two joints (shoulder, elbow) and six muscles. The equations of motion are described by

$$\mathbf{M}\mathbf{\phi ̈}=\mathbf{R}(\mathbf{\phi })\mathbf{F}+\mathbf{C}(\mathbf{\phi },\mathbf{\phi ̇})$$ (1)

where M is the mass matrix; φ is the vector of shoulder and elbow joint angles; R is the 2 × 6 matrix of muscle moment arms; F is the vector of 6 muscle forces; and C is the vector of gravitational, centrifugal and Coriolis effects, and friction. Equations of motion were generated by SD/Fast (PTC, Needham, MA). Mass properties of both arm segments were taken from (Winter, 2005) and listed in Table 1.

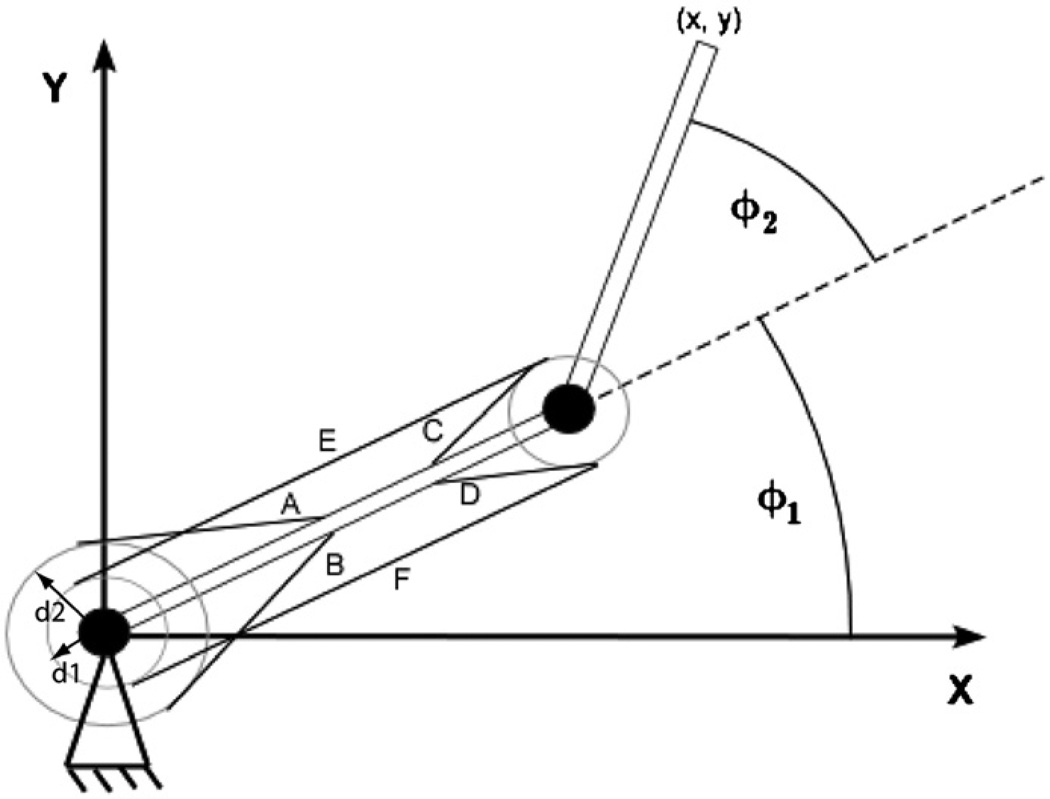
Fig. 1.

Top view of the 2-joint, 6-muscle biomechanical arm model. Y-axis is anterior. Movements occur in the sagittal plane with no gravity, as sliding across a frictionless tabletop. Antagonistic muscle pairs are as follows, listed as (flexor, extensor): monoarticular shoulder muscles: (A: anterior deltoid, B: posterior deltoid); monoarticular elbow muscles: (C: brachialis, D: triceps brachii (short head)); biarticular muscles: (E: biceps brachii, F: triceps brachii (long head)). φ₁ and φ₂ are shoulder and elbow joint angles, respectively.

Adapted from (Lan, 1997). Moment arm values: d₁ = 30 cm, d₂ = 50 cm.

Table 1.

Mass properties of arm segments.

	Upper arm	Forearm
Mass (kg)	2.24	1.76
Length (m)	0.33	0.32
CoM (m)1	0.1439	0.2182
I0 (kg m2)	0.0253	0.0395

CoM is distance between center of mass and prescribed joint; I₀ is moment of inertia with respect to the center of mass. With reference to (Winter, 2005).

The connection between each muscle and the skeleton was modeled by assuming constant moment arms (listed in Table 2), which implies a linear relationship between muscle–tendon length L_m and joint angles:

$$L_m=a_0-d_1{\phi }_1-d_2{\phi }_2$$ (2)

Table 2.

Muscles used in the model and their properties.

MUSCLE	Fmax (N)	LCEopt (m)	Lslack (m)	d1 (m)	d2 (m)	a0
Anterior Deltoid	800	0.1280	0.0538	0.05	0	0.1840
Posterior Deltoid	800	0.1280	0.0538	−0.05	0	0.1055
Biceps Brachii	1000	0.1422	0.2298	0.03	0.03	0.4283
Triceps Brachii (long head)	1000	0.0877	0.1905	−0.03	−0.03	0.1916
Triceps Brachii (short head)	700	0.0877	0.1905	0	−0.03	0.2387
Brachialis	700	0.1028	0.0175	0	0.03	0.1681

F_max is the maximum force that the muscle is able to generate. L_CEopt is the optimal length of the contractile element, and L_slack is slack length of the muscle; both values were taken from Garner and Pandy (2003). d₁ and d₂ are moment arms for the shoulder and elbow joints, respectively (Bhushan and Shadmehr, 1999). a₀ is the muscle length when both joint angles are 0; this anatomical parameter was chosen such that maximum isometric force is generated at similar joint angles as in human subjects (Kulig et al., 1984).

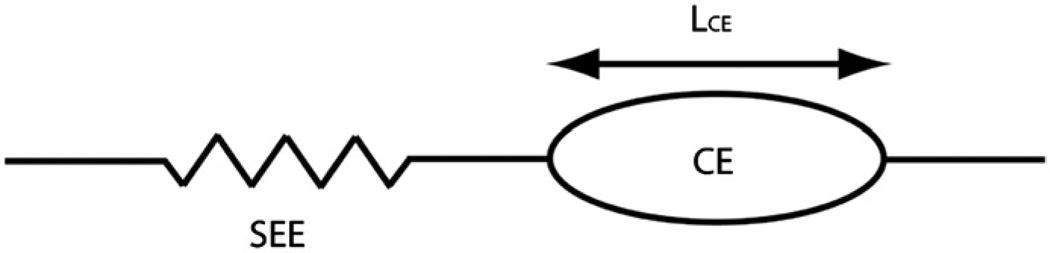
The four one-joint muscles have only one moment arm, while the biceps and long head of the triceps have moment arms at both joints. Each muscle was modeled using a standard Hill-based approach (Zajac, 1989), in which the contractile element (CE) had force–length and force–velocity properties as well as activation dynamics, and a nonlinear series elastic element (SEE) transmitted muscle force to the skeleton (Fig. 2). Passive muscle force was not modeled because it does not play a major role in the range of motion that was studied. This muscle model is standard in musculoskeletal simulation (Zajac, 1989) and represents each muscle by two first-order ordinary differential equations (McLean et al., 2003), which were simulated together with the mechanical state Eq. (1). The complete set of muscle properties is listed in Table 2.

Fig. 2.

Hill muscle model. CE is contractile element; SEE is series elastic element. L_CE is length of the contractile element.

2.2. Controller and controller optimization

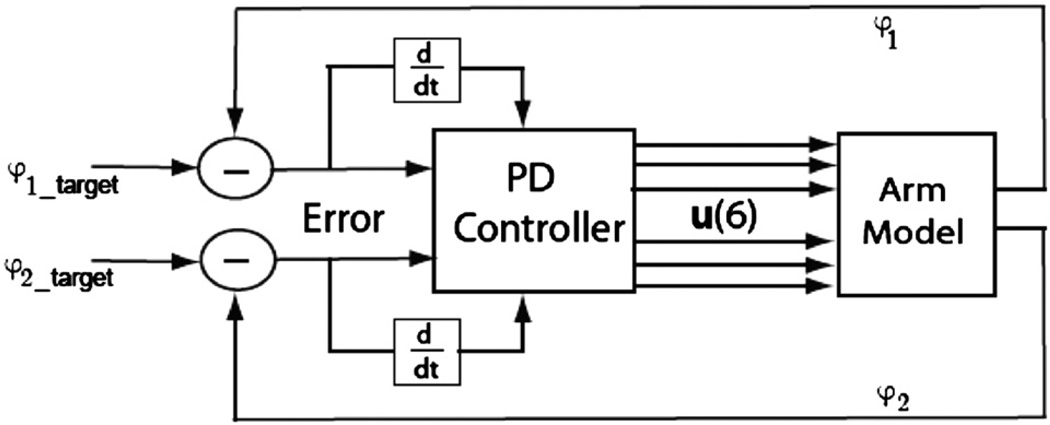
The proportional derivative (PD) controller generates muscle stimulations that are proportional to the errors in joint angles and their time-derivatives (Fig. 3).

Fig. 3.

PD controller architecture. φ₁ and φ_{1_target} are actual and target shoulder angles, respectively. φ₂ and φ_{2_target} are actual and target elbow angles, respectively. u(6) are muscle stimulation values.

The PD controller generates a vector u of six muscle stimulation levels according to

$$\mathbf{u}=\mathbf{G}(\mathbf{s}-{\mathbf{s}}_0)$$ (3)

where G is the 6 [muscles] × 4 [sensors] gain matrix, and s are sensor values. The four sensors were the joint angles and angular velocities for shoulder and elbow, expressed in radians and radians per second, respectively. The vector s₀ is a matrix of sensor targets, with joint angle targets for a specified reaching task and joint angular velocity targets equal to 0. Controllers with three types of gain matrix G were considered. A 24-parameter controller had the full 6 × 4 gain matrix, allowing one gain per muscle for each of the four sensors to be specified. The 16-parameter controller removed 8 parameters from the 24-parameter controller: for monoarticular muscles, gains corresponding to errors in the joint not directly controlled by that muscle were set to zero. The 2-parameter controller was similar to the 16-parameter version, except that all angle gains and all angular velocity gains had the same value.

Optimal controller gains G were found by minimizing a cost function consisting of an error term representing cumulative distance to the reaching target and an effort term derived from the amount of muscle force used. These costs were summed across a number of reaching movements. Specifically, the cost function is given by

$$f(\mathbf{G})=f_{\mathit{\text{error}}}+W{f}_{\mathit{\text{effort}}}$$ (4)

where f_error and f_effort are

$$f_{\mathit{\text{error}}}=\sqrt{\frac{1}{2T{N}_m}\sum _{i=1}^{N_m}\sum _{j=1}^2{\int }_0^T{({\phi }_{ij}(t)-{\phi }_{ij}^{\mathit{\text{target}}})}^{2}dt}$$ (5)

$$f_{\mathit{\text{effort}}}=\sqrt{\frac{1}{6T{N}_m}\sum _{i=1}^{N_m}\sum _{j=1}^6{\int }_0^T{(F_{ij}(t))}^{2}dt}$$ (6)

where φ_ij is the angle of joint j for movement i in degrees, ${\phi }_{ij}^{\mathit{\text{target}}}$ are the target joint angles, F_ij is the muscle force of muscle j for movement i in Newtons, and T is duration of the simulated movement. T was arbitrarily chosen to be 2 s, which allowed sufficient time for the completion of both normal human reaching movements (approx. 0.5 s) (Gottlieb et al., 1997), as well as potentially slower movements resulting from weakening of muscles. The cost functions were calculated over a set of N_m = 12 reaching tasks, representing all possible movements with each joint angle starting or ending at 20° or 80°. The weight W was set to 0.05° N⁻¹, based on preliminary work that showed that this caused neither term to be dominant in the cost function during optimization. If the weight was set too low, controller optimization produced higher gains, causing faster arm movements but oscillatory muscle activity rather than a relaxed steady state after reaching the target.

Optimizations were performed using the simulated annealing algorithm (Goffe et al., 1994). The temperature reduction factor of the simulated annealing algorithm set to reduce the temperature by 10% each time after 100 random variations in all parameters. If the “temperature” (and consequently, cost function fluctuations) fell below 10⁻⁶, the optimization was terminated and considered complete. All controller gains were constrained between a lower bound of −2 and an upper bound of 2. These gains are equivalent to producing full muscle stimulation at a position error of 0.5 radians or a velocity error of 0.5 radians per second.

2.3. Simulation experiments

2.3.1. Effect of controller architecture

In this investigation, the type of gain matrix used in the PD controller was varied, from 2 independent parameters, to 16, to 24. Gain parameters for each of the three controllers were optimized as described above. To determine whether a global optimum was found, we performed two optimizations of each controller, differing only by the random number seed used by the simulated annealing algorithm.

2.3.2. Generality test

To test the ability of the controllers to perform tasks for which they had not been optimized, each of the three optimized controllers was applied to a set of 1000 randomly generated reaching tasks that had not been included in the 12-task set. Each task specified an initial and target joint angle between 20° and 80° for both shoulder and elbow.

2.3.3. Robustness test

To investigate the robustness of the controllers, each of the six muscles included in our model was randomly weakened (maximal force was allowed to range between 0% and 100% of nominal muscle strength) to simulate muscle fatigue or atrophy, and the three already optimized controllers were applied to the 1000 randomly generated tasks as described above.

2.3.4. Added-friction test

To investigate controller performance in the presence of friction, as in an arm brace or when an arm slides along a tabletop, a frictional moment of 1.0 N m was applied to both joints in the arm, and the set of 1000 reaching tasks used above was performed. This friction value is within the range found in assistive devices (Tickel et al., 2002).

2.3.5. Doubled-mass test

To test the viability of the controller should mass properties of an actual subject substantially differ from the modeled values, the mass of the arm was doubled, and the same 1000 reaching tasks test were again performed.

In all of the above tests, we defined a failed trial as a movement in which one or both joints were not within 5° of their target angle after 2 s. For trials that did not fail, steady-state (SS) error was defined using (5), with the integration starting when both joint angles are within 5° of their target angles. Furthermore, error and effort were quantified using Eqs. (5) and (6).

3. Results

3.1. Effect of controller architecture

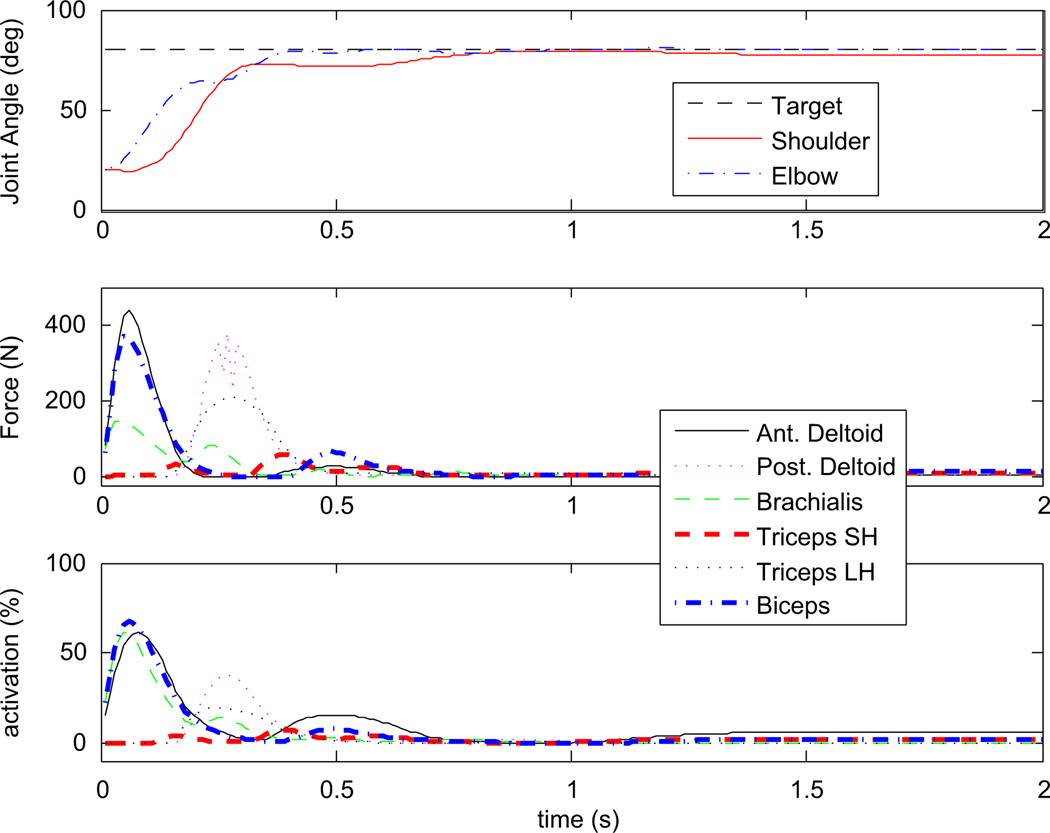
Optimized cost function values were lower with increasing number of controller parameters (Table 3). Fig. 4 shows joint angles and muscle forces and activations for a single reaching task performed by the optimized 24-parameter controller. Animations of the optimized 24- and 2-parameter controllers performing the set of 12 reaching tasks are included as Electronic Supplementary Material. Optimized gains were similar for repeated optimizations with a different random number seed. The largest differences between corresponding gains for different optimizations of the same controller were 9.27%, 12.01% and 0.12% for 24-, 16- and 2-parameter controllers, respectively. Optimized gain values for all 3 controllers are provided in the supplementary appendix.

Table 3.

Performance of the 3 optimized PD controllers (W=0.05) on the 12 reaching task set.

Controller (# parameters)	Cost function	Error (deg.)	Effort (N)
24	13.69	11.54	42.99
16	13.94	11.57	47.38
2	14.51	11.93	51.66

Values are averaged over 12 movements. Error and Effort values are calculated from (5) and (6), respectively.

Fig. 4.

Optimized (W = 0.05) 24-parameter controller outputs for the (20° shoulder, 20° elbow) to (80°, 80°) reaching task: (a) shoulder and elbow joint angles; (b) muscle forces and (c) muscle activations.

3.2. Generality test

Results of the generality test, in which the optimized controllers were applied to a set of 1000 randomly generated reaching tasks, are shown in Table 4. Error values were slightly lower for the more complex controllers, indicating better generalization to new movement tasks. There were no failed trials for any of the controllers (Table 4).

Table 4.

Tests of the 3 PD controllers.

PD controller (# of parameters)	Test	Error (deg.)	SS Error (deg.)	Effort (N)	# of Failed Trials (out of 1000)
24	Generality	5.29	1.03	22.18	0
	Robustness	7.28	3.95	15.69	107
	Added friction	5.62	2.97	22.29	2
	Doubled mass	5.98	1.23	30.91	0
16	Generality	5.32	1.09	23.26	0
	Robustness	7.41	4.41	15.99	117
	Added friction	5.70	3.00	23.61	6
	Doubled mass	6.02	1.40	31.88	0
2	Generality	5.50	1.17	25.10	0
	Robustness	7.51	4.59	17.31	122
	Added friction	6.08	4.06	26.83	14
	Doubled mass	6.18	1.55	34.50	0

Values are averaged over 1000 movements. Error (f_error) and Effort (f_effort) values are calculated from (5) and (6), respectively. Precision of movement is quantified by the steady-state (SS) error values, which are an average of shoulder and elbow. The steady-state phase is defined as beginning when both joints reach within 5° of their target angles, and remain within 5° of the target for the remainder of the movement. SS error values are calculated only from successful trials. Failed trials are defined as those in which either joint angle fails to attain a position within 5° of its target within the two second duration of the trial. Added friction was 1.0 N m.

3.3. Robustness test

Table 4 also presents results from the robustness test, in which muscles were randomly weakened. Similar to the results of the generality test, the controllers with more independent parameters performed better on all performance measures.

3.4. Added-friction test

When friction was added, error for each controller increased slightly, compared to corresponding values for the generality test on the unaltered model, while effort values were similar (Table 4). However, steady-state error increased to around three times its value for the generality test. The number of failed trials was relatively small, and decreased as number of controller parameters increased (Table 4).

3.5. Doubled-mass test

Error values for the doubled-mass condition were slightly but consistently larger than error values for the analogous generality and added-friction tests (Table 4). Steady-state error was slightly but consistently larger than values for the generality test. Effort values were approximately 37–39% larger than generality test values. All trials in the doubled-mass condition were successful (Table 4).

4. Discussion

We designed a PD controller for a 2-segment, 6-muscle UE model with Hill-type muscle properties. After optimization of feedback gains to minimize a combination of error and effort, arm movement generated by this controller in simulations (Fig. 4) was similar to typical human performances: smooth and sigmoid-shaped joint angle curves (Gottlieb et al., 1997), and the completion of movements was on a similar time scale as in humans (Wadman et al., 1980). Joint moments showed acceleration followed by deceleration, corresponding to alternating agonist and antagonist muscle activities.

In practical applications, angular velocity information may be noisy due to differentiation of angle sensor signals. We therefore also tested a proportional-only (P)-controller and found that it produced slower movements with overshoot of the target position. While muscle fibers (the contractile element in the model) provide damping, the series elastic coupling to the skeleton makes this less effective to stabilize arm movement. We conclude that derivative information is necessary to damp movements, but care must be taken to filter sensor signals to prevent noise from affecting performance. A PID controller was also investigated because of its potential to reduce steady-state error. We found that a PID controller could leave muscles activated when the reaching target has been achieved, which is a consequence of having more actuators than degrees of freedom.

While the more complex 24-parameter controller performed best for all controller tests performed, the differences were small (Table 4), and the 2-parameter controller with identical gains for all muscle–joint combinations may be preferred in clinical applications because of simpler tuning.

As expected, muscle weakness in the robustness test decreased the speed and accuracy of movements compared to generality test results (Table 4), as shown by larger error values. In contrast, average effort decreased for the robustness test, due to the lower muscle forces generated by the weakened muscles. Movements were still generally accurate but approximately 10% of the simulated movements failed to reach within 5° of the target angles (Table 4). From inspection of these failed trials, we found that most occurred when the difference between the initial joint angle and the target joint angle was very small for one or both joints; the set of 12 reaching tasks on which the PD controllers had been optimized had not included any small-angle reaching tasks. Had a wider diversity of reaching tasks been included in the optimization, these failures may have been avoided.

Friction caused an increase in steady-state error because the arm tends to “stick” when close to the target, because the PD controller generates insufficient muscle activity to overcome friction. This would affect precision of movements. Increased mass mainly caused slower movements, but no loss of precision. The results of the muscle weakening, friction and doubled-mass experiments (Table 4) demonstrate that performance of the optimized PD controller may be satisfactory, even when applied to a system that is very different from the model for which it was optimized.

The model on which experiments were performed is a simplification of human arm dynamics. While the muscle model is standard (Zajac, 1989), it does not represent certain known properties of muscle, such as history-dependent effects (Herzog, 2004). Such effects would be somewhat similar to muscle weakness and friction, so we expect the controller to be robust with respect to these muscle properties, but further research is needed to confirm this.

5. Conclusion and future directions

By optimization on a biomechanical arm model, a PD controller was designed that produced accurate and efficient arm movements. It was found to be important that the optimality criterion consist of appropriately weighted contributions of position error and muscular effort. Without much loss of performance, the feedback gain matrix could be simplified by having only two independent gain parameters, one for angle error and one for its derivative, and by eliminating feedback from joints not directly controlled by a muscle. The optimized controllers performed well for all reaching movements within the range of motion, even in the presence of muscle weakness, friction, and added mass.