Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 2013 Sep 30;591(Pt 22):5491–5508. doi: 10.1113/jphysiol.2013.261115

Modelling genetic reorganization in the mouse spinal cord affecting left–right coordination during locomotion

Ilya A Rybak 1, Natalia A Shevtsova 1, Ole Kiehn 2
PMCID: PMC3853491  PMID: 24081162

Abstract

The spinal neural circuit contains inhibitory (CINi) and excitatory (CINe) commissural interneurons with axons crossing the mid-line. Direction of these axons to the other side of the cord is controlled by axon guidance molecules, such as Netrin-1 and DCC. The cord also contains glutamatergic interneurons, whose axon guidance involves the EphA4 receptor. In EphA4 knockout (KO) and Netrin-1 KO mice, the normal left–right alternating pattern is replaced with a synchronized hopping gait, and the cord of DCC KO mice exhibits uncoordinated left and right oscillations. To investigate the effects of these genetic transformations, we used a computational model of the spinal circuits containing left and right rhythm-generating neuron populations (RGs), each with a subpopulation of EphA4-positive neurons, and CINi and CINe populations mediating mutual inhibition and excitation between the left and right RGs. In the EphA4 KO circuits, half of the EphA4-positive axons crossed the mid-line and excited the contralateral RG neurons. In the Netrin-1 KO model, the number of contralateral CINi projections was significantly reduced, while in the DCC KO model, the numbers of both CINi and CINe connections were reduced. In our simulations, the EphA4 and Netrin-1 KO circuits switched from the left–right alternating pattern to a synchronized hopping pattern, and the DCC KO network exhibited uncoordinated left–right activity. The amplification of inhibitory interactions re-established an alternating pattern in the EphA4 and DCC KO circuits, but not in the Netrin-1 KO network. The model reproduces the genetic transformations and provides insights into the organization of the spinal locomotor network.

Key points

  • EphA4, Netrin-1 and DCC are axon guidance molecules involved in mid-line crossing of axons of commissural and other spinal interneurons. Absence of these molecules in mice lead to specific locomotor pattern transformations.

  • We use a computational model of the bilateral spinal neural networks to simulate the genetically induced transformations in EphA4, Netrin-1 and DCC mutant mice.

  • The model closely reproduces the changes in the locomotor patterns in these mutants, including transformations from the normal left–right alternating pattern to a synchronized hopping pattern in EphA4 and Netrin-1 mutants, uncoordinated left–right activity in the DCC mutant, and re-establishment of the alternating patterns in EphA4 and DCC mutant cords by augmentation of inhibitory interactions.

  • The model suggests mechanistic explanations for the locomotor transformations and provides insights into the organization of the locomotor network in the spinal cord.

Introduction

It is currently well established that the basic rhythmic neuronal activities controlling vertebrate locomotion are generated within the spinal cord by neural circuits called central pattern generators (CPGs; Graham-Brown, 1911; Shik et al. 1966; Jankowska et al. 1967a,b; Grillner & Zangger, 1979; Grillner, 1981, 2006; Lundberg, 1981; Orlovsky et al. 1999; Kiehn, 2006; Jankowska, 2008; McCrea & Rybak, 2008; Stuart & Hultborn, 2008; Harris-Warrick, 2010; Whelan, 2010). These rhythmic activities can be evoked in multiple ways, including electrical stimulation of several brainstem and spinal cord areas (Guertin et al. 1995; Rossignol, 1996; Lafreniere-Roula & McCrea, 2005) and pharmacological interventions applied in vivo (Jankowska et al. 1967a,b) or in vitro (Kudo & Yamada, 1987; Smith & Feldman, 1987; Cazaletz et al. 1992; Kiehn & Kjaerulff, 1996b; Cowley & Schmidt, 1995; Bonnot & Morin, 1998; Jiang et al. 1999; Whelan et al. 2003). The ‘fictive’ locomotor pattern evoked in these conditions is characterized by alternating flexor–extensor and left–right activities, similar to the patterns of electromyographic activities of muscles controlling limb movements during real walking (Kiehn & Kjaerulff, 1996b; Lafreniere-Roula & McCrea, 2005; Markin et al. 2012).

An important aspect of locomotor gaits such as walking, trotting, hopping or galloping is the coordination between the left and the right side of the body. This coordination is maintained by commissural interneurons (CINs) that project to the contralateral side of the cord and innervate interneurons and motoneurons located there (Bannatyne et al. 2003; Butt & Kiehn, 2003; Kiehn & Butt, 2003; Lanuza et al. 2004; Hammar et al. 2004; Jankowska et al. 2005; Kiehn, 2006; Quinlan & Kiehn, 2007; Jankowska, 2008; Talpalar et al. 2013).

Both excitatory and inhibitory CINs are present in the mammalian spinal cord (Bannatyne et al. 2003; Butt & Kiehn, 2003; Kiehn & Butt, 2003; Hammar et al. 2004; Jankowska et al. 2005; Kiehn, 2006; Quinlan & Kiehn, 2007; Restrepo et al. 2009; Talpalar et al. 2013). The inhibitory CINs mediate mutual inhibition and promote the alternating activity. Excitatory CINs may provide direct excitation of contralateral neurons, promoting synchronized activity such as that seen in hopping or galloping, or contribute to mutual inhibition and left–right alternation by acting via inhibitory interneurons located on each side of the cord (Butt & Kiehn, 2003; Quinlan & Kiehn, 2007; Talpalar et al. 2013).

Significant progress in understanding the functional and structural organization of spinal motor circuits has been made using combinations of genetic, molecular and developmental approaches. Several classes of spinal interneurons have been defined in the embryonic and early postnatal spinal cord based on the dynamic expression pattern of transcription factors (Jessell, 2000; Kiehn, 2006, 2011; Goulding, 2009; Whelan, 2010; Gosgnach, 2011). In the ventral cord, where the CPG is localized (Kiehn & Kjaerulff, 1996a), these interneurons include V0 and V3 types representing CINs (Pierani et al. 2001; Lanuza et al. 2004; Zhang et al. 2008; Talpalar et al. 2013). The V0 neurons are composed of both excitatory and inhibitory CINs (Lanuza et al. 2004; Talpalar et al. 2013), while V3 CINs are excitatory (Zhang et al. 2008). Significant progress in the understanding of interactions between the ipsi- and contralateral spinal circuits and the role of CINs in locomotion has been based on the development of transgenic mice with mutations in, or knockout (KO) of, specific genes that result in abnormal locomotor phenotypes (Kullander et al. 2003; Lanuza et al. 2004; Akay et al. 2006; Lundfald et al. 2007; Crone et al. 2008, 2009; Zhang et al. 2008; Rabe et al. 2009; Zagoraiou et al. 2009; Restrepo et al. 2011; Talpalar et al. 2013).

A representative example of how genetic manipulations can reconfigure interactions between the ipsi- and contralateral neurons involved in control of locomotion in mice is based on the targeted deletion of the EphA4 receptor that is involved in axon guidance. In normal mice, EphA4-positive neurons are repelled by ephrin-B3 expressed at the mid-line of the cord. In EphA4 KO mice, the regular left–right alternating walking pattern is replaced with a rabbit-like, left–right synchronized hopping gait (Dottori et al. 1998; Kullander et al. 2003; Akay et al. 2006). It has been suggested that in the EphA4 KO mice, the normal left–right alternating activity, which usually results from crossed net inhibition, is overridden by the abnormal crossed excitatory interactions (Butt et al. 2005; Kiehn, 2006). Studies in the isolated spinal cord from EphA4 KO mice have confirmed that switching to the synchronized hopping pattern is accompanied by, and supposedly results from, an abnormal mid-line crossing of axons of some excitatory neurons that normally stay ipsilaterally (Restrepo et al. 2011).

During spinal cord development, differentiating CINs send their axons across the mid-line to the contralateral side of the cord. This process is guided by other axon guidance molecules, such as Netrin-1, which bind to and activate the axonal receptor DCC (Kennedy et al. 1994; Kaprielan et al. 2001; Tessier-Lavigne, 2002; Rabe et al. 2009; Rabe Bernhardt et al. 2012; Vallstedt & Kullander, 2013). In Netrin-1 KO mice, the number of inhibitory CINs whose axons cross the mid-line is significantly reduced, resulting in synchronization of left and right cord activities during fictive locomotion (Rabe et al. 2009; Vallstedt & Kullander, 2013). In DCC KO mice, the number of mid-line-crossing axons becomes reduced for both inhibitory and excitatory CINs, which leads to a collapse of left–right coordination (Rabe Bernhardt et al. 2012; Vallstedt & Kullander, 2013).

The main objective of the present study was to construct and investigate a minimal computational model of the bilaterally connected spinal circuits that would allow us to simulate and test the possible genetically induced reorganizations of spinal circuits within a functional framework of locomotor gait control. The proposed model represented a reduced and modified version of the previously published model of bilateral spinal circuits (Zhong et al. 2012). Despite its relative simplicity, the model was able to replicate the major locomotor gait transformations, such as switching from the alternating walking gait to the bilaterally synchronized hopping pattern, resulting from the different genetic manipulations described in the literature. The model may serve as a basis for developing more comprehensive models of the mammalian locomotor circuits and provide important insights into their organization.

Methods

The model was constructed as a bilaterally symmetric network of interacting neural populations (Fig. 1A). The model contains two intrinsically rhythmic neural populations representing left (l-RG-F) and right (r-RG-F) rhythm-generating flexor centres. The rhythmic activity in these centres is provided by the persistent (slowly inactivating) sodium current (INaP) in each neuron (known to be present in the rodent spinal neurons; see Zhong et al. 2007; Tazerart et al. 2008; Ziskind-Conhaim et al. 2008; Brocard et al. 2010, 2013) and the excitatory synaptic interactions within each population (for details see previous models by Rybak et al. 2006a,b; McCrea & Rybak, 2007; Zhong et al. 2012; Brocard et al. 2013; Jasinski et al. 2013). Similar to the model of Zhong et al. (2012), the excitability of RG-F neurons defined by the leak reversal potential was adjusted so that the frequency of population oscillations was within the range of oscillation frequencies observed in the isolated neonatal mouse spinal cord during NMDA/5-HT-evoked locomotor-like activity. While constructing the model, we assumed that half of the neurons in each RG-F centre are EphA4 positive, which means that the projection of their axons and their targets depend on the presence of the EphA4 receptors. Therefore, each RG-F population consists of two subpopulations containing EphA4-negative (RG-F0) and EphA4-positive (RG-FEphA4) neurons, respectively (Fig. 1A). The neurons in these subpopulations have the same set of ionic channels and biophysical properties and randomly distributed excitatory synaptic connections within the RG-F centre (i.e. within and between the RG-F0 and RG-FEphA4 subpopulations).

Figure 1. Model schematics.

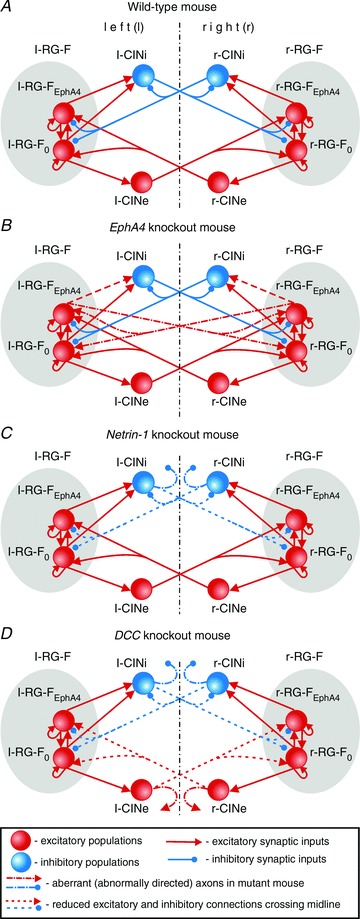
Figure 1

Open in a new tab

A, model of circuits in intact (wild-type) mouse. B, model of circuits in EphA4 KO mouse; half of the axons from each RG-FEphA4 population instead of projecting to the ipsilateral CINi cross the mid-line and activate the contralateral RG-F population. C, model of circuits in Netrin-1 KO mouse; most of the axons from the CINi populations do not cross the mid-line. D, model of circuits in DCC KO mouse; most of the axons from CINi and CINe populations do not cross the mid-line. See main text for details. Abbreviations: RG-F, left (l-) and right (r-) rhythm-generator flexor centre; RG-FEphA4 and RG-F0, EphA4-positive and EphA4-negative RG-F subpopulations, respectively; left (l-) and right (r-) populations of excitatory (CINe) and inhibitory (CINi) neurons.

Also, the model contains populations of left (l) and right (r) inhibitory (l-CINi and r-CINi) and excitatory (l-CINe and r-CINe) commissural interneurons projecting to the opposite side of the cord (see Fig. 1A). In the proposed model, these CIN populations receive direct excitation from the ipsilateral RG-F population and project to the contralateral RG-F population, hence mediating mutual inhibition (via l-CINi and r-CINi) and mutual excitation (via l-CINe and r-CINe) between the left and right RG-F centres (Fig. 1A).

All neurons were simulated in the Hodgkin–Huxley style as single-compartment models. Each RG-F subpopulation in the model contained 100 neurons; each CIN population had 50 neurons. Heterogeneity of neurons within each population was set by a random distribution of neuronal parameters and initial conditions to produce physiologically realistic variations of baseline membrane potential levels and spike frequencies. The formal description of neuron models and all parameters can be found in the Appendix with parameters for ionic channel kinetics specified in Table 1.

Table 1.

Steady-state activation and inactivation variables and time constants for voltage-dependent ionic channels

Ionic channels m∞(V) (V in millivolts) h∞(V) (V in millivolts) τm(V) (in milliseconds) τh(V) (in milliseconds)
Fast sodium Na 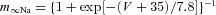Inline graphic τmNa= 0
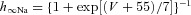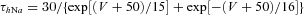Inline graphic Inline graphic
Persistent sodium NaP 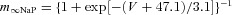Inline graphic τmNaP= 0
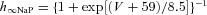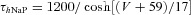Inline graphic Inline graphic
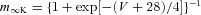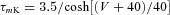Potassium rectifier K Inline graphic Inline graphic
hK= 1
Open in a new tab

All simulations were performed using the custom neural simulation package NSM 4.0 (Neural SiMulation 4.0) developed at Drexel University by S. N. Markin, I. A. Rybak and N. A. Shevtsova. Differential equations were solved using the exponential Euler integration method with a step size of 0.1 ms. This simulation package was previously used for development of other spinal cord models (Rybak et al. 2006a,b; McCrea & Rybak, 2007; Zhong et al. 2012; Brocard et al. 2013; Jasinski et al. 2013).

This package allows the simulation of interacting populations of neurons with a priori assigned probability of connection between the individual neurons so that, if a population B is assigned to receive an excitatory (or inhibitory) input from a population A with a probability P{A, B}, then each neuron of population B gets the excitatory (or inhibitory) synaptic input from each neuron of population A with the probability P{A, B}, and a random generator is used to define the existence of each connection. The weights of these individual synaptic connections are also defined by the random generator using the values of average synaptic weights and variances assigned in advance. All parameters of connections in the model, including the assigned probabilities of connections in each case, are specified in Table 2 in the Appendix.

Table 2.

Average weight of synaptic connections (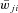Inline graphic) to one neuron of target population and probability of connection (P=P{A, B})

Target populations (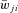Inline graphic, probability of connection P)
Source population Intact (‘wild-type’) Epha4 KO Netrin-1 KO DCC KO
i-RG-F0 i-RG-F0 (0.003, P= 0.1) i-RG-F0 (0.003, P= 0.1) i-RG-F0 (0.003, P= 0.1) i-RG-F0 (0.003, P= 0.1)
i-RG-FEphA4 (0.003, P= 0.1) i-RG-FEphA4 (0.003, P= 0.1) i-RG-FEphA4 (0.003, P= 0.1) i-RG-FEphA4 (0.003, P= 0.1)
i-CINi (0.015, P= 0.2) i-CINi (0.015, P= 0.2) i-CINi (0.015, P= 0.2) i-CINi (0.015, P= 0.2)
i-CINe (0.04, P= 0.2) i-CINe (0.004, P= 0.2) i-CINe (0.004, P= 0.2) i-CINe (0.004, P= 0.2)
i-RG-FEphA4 i-RG-F0 (0.003, P= 0.1) i-RG-F0 (0.003, P= 0.1) i-RG-F0 (0.003, P= 0.1) i-RG-F0 (0.003, P= 0.1)
i-RG-FEphA4 (0.003, P= 0.1) i-RG-FEphA4 (0.003, P= 0.1) i-RG-FEphA4 (0.003, P= 0.1) i-RG-FEphA4 (0.003, P= 0.1)
i-CINi (0.03, P= 0.2) i-CINi (0.03, P*= 0.1) i-CINi (0.03, P= 0.2) i-CINi (0.03, P= 0.2)
c-RG-F0 (0.0012*, P*= 0.1)
c-RG-FEphA4 (0.0012*, P*= 0.1)
i-CINi c-RG-F0 (−0.02, P= 0.2) c-RG-F0 (−0.02, P= 0.2) c-RG-F0 (−0.02, P*= 0.04) c-RG-F0 (−0.02, P*= 0.04)
c-RG-FEphA4 (−0.02, P= 0.2) c-RG-FEphA4 (−0.02, P= 0.2) c-RG-FEphA4 (−0.02, P*= 0.04) c-RG-FEphA4 (−0.02, P*= 0.04)
c-CINi (−0.02, P= 0.2) c-CINi (−0.02, P= 0.2) c-CINi (−0.02, P*= 0.04) c-CINi (−0.02, P*= 0.04)
i-CINe c-RG-F0 (0.007, P= 0.2) c-RG-F0 (0.007, P= 0.2) c-RG-F0 (0.007, P= 0.2) c-RG-F0 (0.007, P*= 0.06)
c-RG-FEphA4 (0.007, P= 0.2) c-RG-FEphA4 (0.007, P= 0.2) c-RG-FEphA4 (0.007, P= 0.2) c-RG-FEphA4 (0.007, P*= 0.06)
Open in a new tab

Prefixes i and c indicate ipsi- and contralateral populations; *indicate change in average synaptic weights (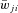Inline graphic) or probability of connections (P) in the KO mouse models relative to the intact model.

The probabilities of connections assigned prior to the simulations allowed us to perform multiple simulations in each case, which were run with the same assigned probabilities of connections. Circular diagrams were used to analyse the phase relationships between averaged activities of left and right RG-F populations, each representing an average activity in two corresponding subpopulations, RG-F0 and RG-FEphA4. The relative phase values were plotted on a unitary circle. These circular diagrams were used either for the representation of phase difference values averaged during each simulation (small filled squares) or for the representation of phase difference values during the first 25 step cycles within a particular simulation (indicated by small open circles). In the latter case, a vector and single filled square at the end of the vector represented the average phase in each simulation; the length of the vector was inversely proportional to the distribution of phase values around the mean (Kjaerulff & Kiehn, 19961996a; Berens, 2009).

Results

Modelling circuit operation in the intact (‘wild-type’) mouse

The model schematic for the ‘intact’ (‘wild-type mouse’) neural circuits is shown in Fig. 1A. The model includes two rhythm-generating neural populations, l-RG-F and r-RG-F, representing left and right flexor centres, respectively. The rhythmic activity in these centres is supported by the persistent sodium current in each neuron and excitatory synaptic interactions between neurons in each population. Each RG-F centre is split into two equal subpopulations, EphA4-negative (RG-F0) and EphA4-positive (RG-FEphA4). Neurons in these subpopulations have the same ionic channels, biophysical properties and probability of excitatory synaptic connections within RG-F centres (P{RG-F, RG-F} = 0.1).

The model also includes left (l) and right (r) populations of inhibitory (l-CINi and r-CINi) and excitatory commissural interneurons (l-CINe and r-CINe; Fig. 1A). Based on our suggestion, each inhibitory CIN population receives excitatory inputs from the ipsilateral rhythmogenic RG-F centre (both RG-F0 and RG-FEphA4 subpopulations) and provides direct inhibition of the contralateral rhythmogenic RG-F centre (both subpopulations) and contralateral CINi population. In turn, each excitatory CIN population receives excitatory inputs from the ipsilateral rhythmogenic RG-F0 population and provides direct excitation of the contralateral rhythmogenic RG-F centre (both subpopulations). Hence, the inhibitory CIN populations (l-CINi and r-CINi) mediate mutual inhibition between the left and right rhythmogenic centres and the excitatory CIN populations (l-CINe and r-CINe) mediate mutual excitation between these centres. As a result, the balance between these interactions defines the gait.

In the intact circuits (Fig. 1A), the EphA4-positive subpopulations (l-RG-FEphA4 and r-RG-FEphA4) send their axons to the ipsilateral population of inhibitory commissural interneurons (l-CINi and r-CINi, respectively; Fig. 1A), making synaptic connections with a probability P{RG-FEphA4, CINi} = 0.2. The default probabilities of connections from neurons of each ipsilateral CIN population (l-CINi, l-CINe and r-CINi, r-CINe) to the neurons of both contralateral RG-F subpopulations (r-RG-F0, r-RG-FEphA4 and l-RG-F0, r-RG-FEphA4) are equal to P{CINi, RG-F} =P{CINe, RG-F} = 0.2. However, the weights of mutual inhibitory interactions in the intact circuits have been set stronger than the weights of excitatory interactions (see Table 2). Therefore, the mutual inhibition between the RG-F centres mediated by the inhibitory CIN populations (CINi) is substantially stronger than the mutual excitation between them mediated by the excitatory CIN populations (CINe). This dominance of inhibitory interactions over excitatory ones determines the ‘default’ alternating out-of-phase activity between the left RG-F (l-RG-F0 and l-RG-FEphA4) and CIN populations (l-CINi and l-CINe) and the right RG-F (r-RG-F0 and r-RG-FEphA4) and CIN populations (r-CINi and r-CINe). This alternating pattern is shown in Figs 2A and 3A. Figure 2A shows both the integrated histograms of activity of each population and the corresponding raster plots of neuronal spiking within each population. Figure 3B shows a simulation of network activity with full suppression of inhibitory interaction obtained by setting all weights of inhibitory connections to zero. Suppression of inhibition in the model led to the synchronization of activity in all left and right neural populations.

Figure 2. Activity of neural populations in the models for intact (A) and EphA4 knockout (KO) mice (B).

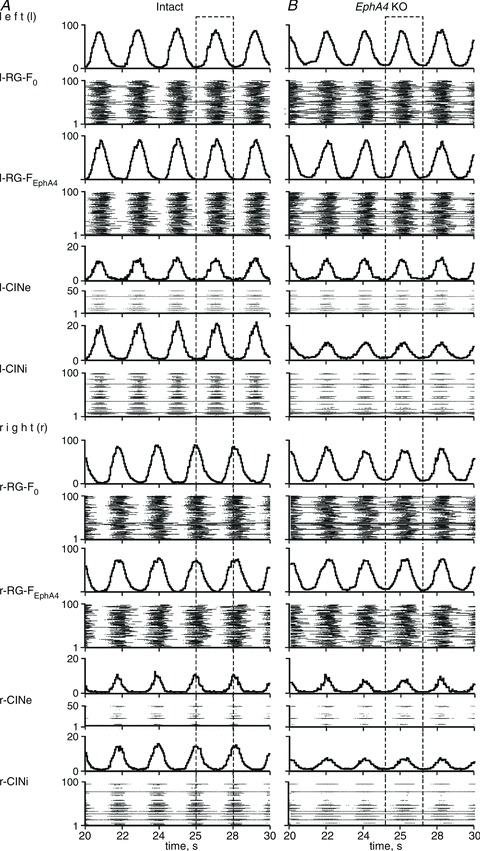
Figure 2

Open in a new tab

Activity of each population is shown in two forms, i.e. as an average population histogram (spikes per second per number of neurons; bin is 50 ms; top trace), and as a raster plot (the number of a neuron is shown on the vertical axis, each horizontal line represents a single neuron and each dot in the raster represents a spike). Dashed rectangles indicate switching from left–right alternation in A to hopping-like synchronized activity in B.

Figure 3. Activity of neural populations in the models for intact and EphA4 KO mice and effects of manipulating the inhibitory interactions.

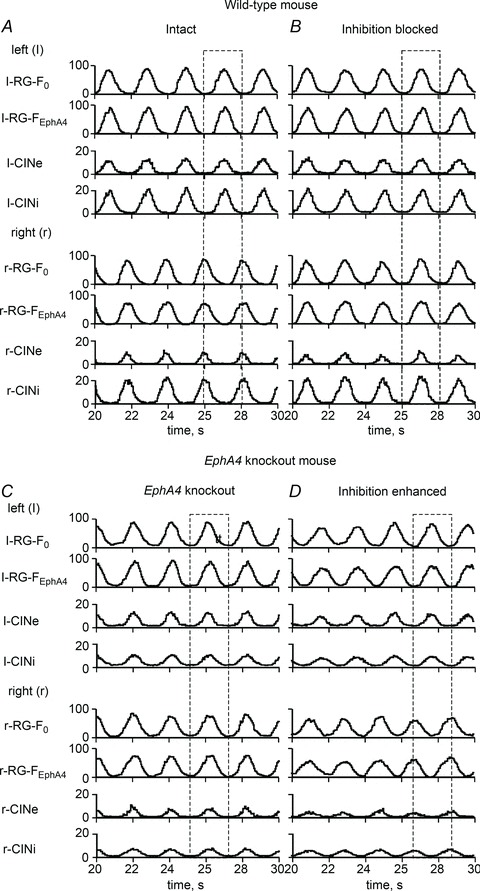
Figure 3

Open in a new tab

A, activity of all neural populations in the intact network, showing left–right alternation. B, switching to synchronized activity after a simulated blockade of inhibition (all inhibitory synaptic weights set to zero). C, synchronized activity of all neural populations in the EphA4 KO network. D, re-establishment of the left–right alternating pattern in the EphA4 KO network by the enhancement of inhibition (all inhibitory synaptic weights were multiplied by 2.5). Dashed rectangles indicate left–right alternation or synchrony.

Simulation of spinal circuit reorganization in the EphA4 KO mouse

To simulate the genetically reorganized network of the EphA4 KO mouse, we suggest that with the loss of EphA4 receptor, about half of the axons of RG-FEphA4 neurons on each side do not project to the ipsilateral CINi population. Therefore, the probability of these connections P{RGFEphA4, CINi} was reduced from 0.2 to 0.1. Moreover, the axons now cross the mid-line, making excitatory synaptic contacts with neurons of the contralateral RG-F populations (r-RG-F0 and r-RG-FEphA4 subpopulations or l-RG-F0 and l-RG-FEphA4 subpopulations, respectively) with the probability P{RG-FEphA4, RG-F} = 0.1 (see Fig. 1B). This reorganization changed the balance in the mutual inhibitory and excitatory interactions between the left and right RG-F centres, so that the mutual excitatory interaction became dominant, overcoming the mutually inhibitory interactions. As a result, the activities of these rhythm-generating centres and the activities of other left and right neural populations (CINi and CINe) became synchronized (see Figs 2B and 3C).

Figure 4Ab, Bb and Cb shows examples of activity of r-RG-F and l-RG-F centres (averaged over both subpopulations in each centre) together with circular diagrams representing several simulations in the intact (Fig. 4Ab; see schematic in Fig. 1A) and EphA4 KO circuits (Fig. 4Bb and Cb; see schematic in Fig. 1B). These simulations are qualitatively consistent with the corresponding examples of recordings from right and left L2 ventral roots and circular diagrams from the experimental studies in the intact and EphA4 KO mice shown in Fig. 4Aa Ba and Ca (Kullander et al. 2003). Hence, the simulations suggest that the switch to a hopping gate in the EphA4 KO mice may result from the aberrant redirection of axons of some rhythmically active excitatory neurons belonging to, or receiving input from, the ipsilateral RG.

Figure 4. Locomotor pattern transformation in EphA4 KO mice: data and simulations.

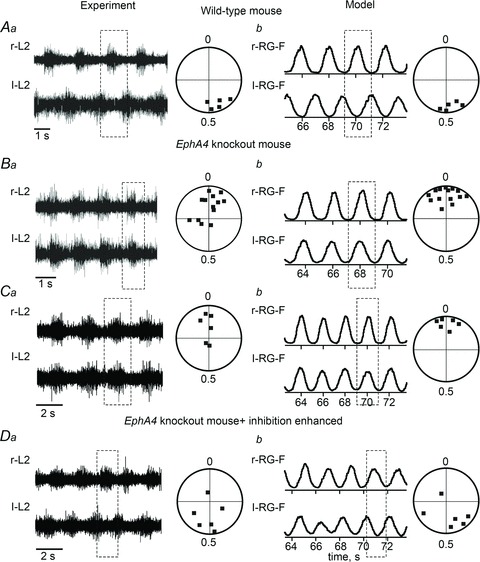
Figure 4

Open in a new tab

Aa, locomotor-like activity in the isolated spinal cord of a wild-type mouse evoked by the application of NMDA and 5-HT. Only records from the right (r-L2) and left ventral roots (l-L2) are shown. Circular phase diagram to the right shows average phase differences between r-L2 and l-L2 activities in 5 preparations (filled squares). Phase differences around 0.5 indicate left–right alternation (adapted from Kullander et al. 2003, Fig. 1D and J, with permission). Ab, integrated activities of r-RG-F and l-RG-F populations (each trace represents the average of activity in the two corresponding subpopulations) produced by the model of the intact mouse circuits (Fig. 1A). Circular phase diagram to the right shows average phase differences between activities of r-RG-F and l-RG-F populations in 5 simulations (filled squares), each run with a re-initialization of model parameters using a random generator. Similar to Aa, all simulations demonstrate left–right alternation. Ba, an example of r-L2 and l-L2 recordings from the isolated spinal cord of an EphA4 KO mouse and circular phase diagrams. Phase values around 0 indicate left–right synchrony between r-L2 and l-L2 activities (homozygote KO mice; adapted from Kullander et al. 2003, Fig. 1E and K, with permission). Bb, integrated activities of r-RG-F and l-RG-F populations produced by the model of EphA4 KO mouse circuits (Fig. 1B). Circular phase diagram to the right shows average phase differences between activities of r-RG-F and l-RG-F populations in 14 simulations (all around zero). Similar to panel Ba, all simulations demonstrate patterns with left–right synchrony. Ca and Da, recordings and circular diagrams from isolated spinal cord preparations of EphA4 KO mice before (Ca) and after application of sarcosine (Da), which augments inhibitory interactions. The administration of sarcosine leads to re-establishment of the left–right alternation in EphA4 KO mouse spinal cord (adapted from Kullander et al. 2003, Fig. 3A, B, E and F, with permission). Cb and Db, simulated activities of r-RG-F and l-RG-F populations produced by the EphA4 KO mouse circuit (Fig. 1B) with default parameters (Cb) and after a 2.5-fold increase of all inhibitory synaptic weights in the network (Db). The applied augmentation of inhibition re-established the left–right alternating pattern in the EphA4 KO circuit. Dashed rectangles indicate left–right alternation or synchrony.

Strengthening inhibition in EphA4 mutant cords by the administration of sarcosine (a glycine uptake blocker) or nipecotic acid (a GABA uptake blocker) results in reversal of synchronous locomotor activity to normal alternation (Fig. 4Ca and Da; adapted from Kullander et al. 2003). The model reproduced similar reversal of synchronous locomotor activity when the weights of all inhibitory synapses were increased 2.5-fold (see Figs 3D and 4Cb and Db).

We have also studied regimens of partial reversal using progressive amplification of inhibition. Figure 5 presents the results of single simulations in the intact (Fig. 5Aa–c) and the EphA4 KO circuits before (Fig. 5Ba–c) and after different increases of inhibition (Fig. 5Ca–c, Da–c and Ea–c). The corresponding Cartesian (Fig. 5Ab, Bb, Cb, Db and Eb) and circular diagrams (Fig. 5Ac, Bc, Cc, Dc and Ec) demonstrate that phase differences between left and right RG-F oscillations concentrate around 0.5 in the intact circuits (Fig. 5Ab and Ac) and around 0 or 1 in the EphA4 KO circuits (Fig. 5Bb and Bc). Figure 5 shows the sequential transition from the left–right synchronization (Fig. 5Ba–c) to the left–right alternation (Fig. 5Ea–c) via several intermediate stages obtained with 1.75-, 2.2- and 2.5-fold increase of inhibitory weights, respectively. Figure 5Ca–c and Da–c illustrates a non-stationary switching between alternation and synchronization regimens, which could be produced by variations of other parameters defining neuronal excitability and interactions and may reflect experimentally observed spontaneous returns to an alternation regimen in EphA4 KO mice.

Figure 5. Simulation of locomotor activity in EphA4 KO mice.

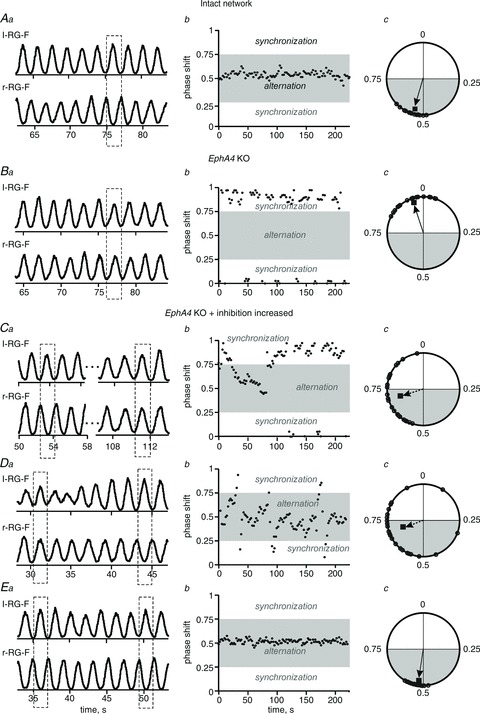
Figure 5

Open in a new tab

Aa, integrated activities of r-RG-F and l-RG-F populations (each trace represents the average of activity in the two corresponding subpopulations) produced by the model of intact mouse circuits (Fig. 1A). Ab, Cartesian representation of the phase differences between the activities of r-RG-F and l-RG-F populations in a single simulation (concentrated around 0.5, indicating alternating activities). Ac, circular phase diagram built for the first 25 steps cycles of activity (indicated by small open circles and the vector; see Methods). Ba–c, the same representations produced by the EphA4 KO circuits (Fig. 1B). The dashed rectangle in Ba and phase difference values around zero (in Bb and Bc) indicate left–right synchrony typical for EphA4 KO circuits. Ca–c, Da–c and Ea–c, re-establishing the left–right alternation in the EphA4 KO circuits by an increase in the weights of all inhibitory synapses in the network. These weights were multiplied by 1.75 in Ca–c (resulting in a mostly synchronized pattern with spontaneous switching to alternation), by 2.2 in Da–c (producing a mostly alternating pattern with spontaneous switching to synchronous activity) and by 2.5 in Ea–c (resulting in a full re-establishment of the alternating activity pattern). See dashed rectangles in Ca, Da and Ea, and areas highlighted by grey in Cb, Db and Eb and Cc, Dc and Ec.

Simulation of circuit reorganization in the Netrin-1 KO mouse

The axon guidance molecule Netrin-1 is involved in the attraction of commissural axons to the mid-line. Although the genetic knockout of this molecule affects both inhibitory and excitatory CINs, the effect on inhibitory CINs is much stronger. In the Netrin-1 KO mice, the majority of axons of inhibitory CIN do not cross the mid-line, whereas the most ventral population of excitatory CINs (V3 type) remains unaffected (Rabe et al. 2009; Vallstedt & Kullander, 2013). To simulate the modified network of the Netrin-1 KO mouse (Fig. 1C), the probabilities of connections from l-CINi and r-CINi populations to the contralateral RG-F (r-RG-F0, r-RG-FEphA4 and l-RG-F0, l-RG-FEphA4, respectively), P{CINi, RG-F}, and CINi populations, P{CINi, CINi}, were reduced from 0.2 to 0.04 (Fig. 1C).

Figure 6Ab and Bb shows an example of average activity of r-RG-F and l-RG-F centres and circular diagrams representing several simulations generated by the model of intact mouse circuits (Fig. 1A) and Netrin-1 KO circuits (Fig. 1C). Similar to the experimental data shown in Fig. 6Aa and Ba (Rabe et al. 2009), the simulations produced switching from phase-alternating to synchronized bursting in the average activities of left and right RG-F centres (Fig. 6Ab and Bb). Interestingly, in contrast to the EphA4 KO circuits (Figs 3D, 4Da–c and 5Ea–c), even a 4-fold increase in the weights of all inhibitory synapses in the model for Netrin-1 KO circuits could not re-establish an alternating pattern similar to what was seen experimentally when sarcosine/nipecotic acid was applied to the cord (Rabe et al. 2009).

Figure 6. Locomotor pattern transformation in Netrin-1 KO mice: data and simulations.

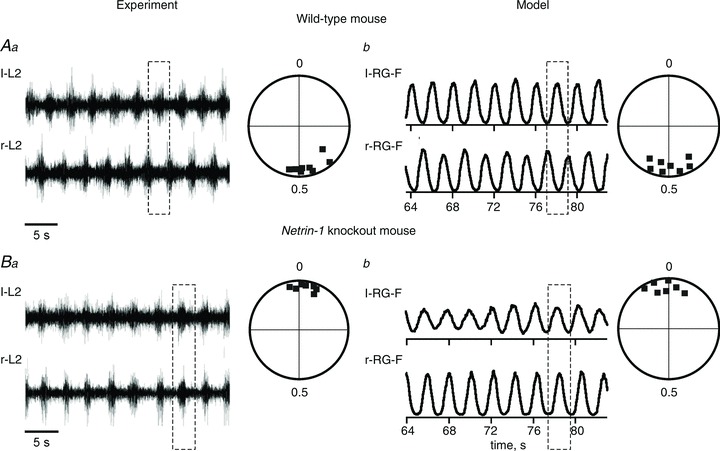
Figure 6

Open in a new tab

Aa, locomotor-like activity in the isolated spinal cord of a wild-type mouse evoked by the application of NMDA, 5-HT and dopamine. Only records from the left (l-L2) and right ventral roots (r-L2) are shown. Circular phase diagram to the right shows average phase differences between l-L2 and r-L2 activities (filled squares; adapted from Rabe et al. 2009, Fig. 3A, with permission). Ab, integrated activities of l-RG-F and r-RG-F populations produced by the model of intact mouse circuits (Fig. 1A). Circular phase diagram to the right shows average phase differences between activities of r-RG-F and l-RG-F populations in 7 simulations. Similar to Aa, all simulations demonstrate left–right alternation. Ba, an example of l-L2 and r-L2 recording from the isolated spinal cord from a Netrin-1 KO mouse and the corresponding circular phase diagram showing left–right synchrony and the average phase differences (concentrated around 0) between l-L2 and r-L2 activities (adapted from Rabe et al. 2009, Fig. 3B, with permission). Bb, integrated activities of l-RG-F and r-RG-F populations produced by the Netrin-1 KO circuit (Fig. 1C). Circular phase diagram to the right shows average phase differences between activities of r-RG-F and l-RG-F populations in 7 simulations. Similar to Ba, all simulations demonstrate patterns with left–right synchrony. Dashed rectangles indicate left–right alternating or synchronized activities.

These simulations confirm that the switch to a hopping gate in the Netrin-1 KO mice may occur because the majority of axons of inhibitory CINs that receive input from the ipsilateral RG stop projecting contralaterally to inhibit the contralateral RG neurons involved in rhythm generation.

Simulation of spinal circuit reorganization in the DCC KO mouse

Mice that carry a null mutation of DCC are characterized by the significant loss of both excitatory and inhibitory commissural projections to the opposite side of the cord (Rabe Bernhardt et al. 2012; Vallstedt & Kullander, 2013). The loss of the majority of CIN axons crossing the mid-line leads to uncoupling of left and right coordination (see Fig. 7Aa, Ba, Ca and Da). This experimental condition was modelled by reducing the probability of connection from both inhibitory (l-CINi and r-CINi) and excitatory CINs (l-CINe and r-CINe) to the contralateral RG-F populations, (P{CINi, RG-F} and P{CINe, RG-F}), from 0.2 to 0.04 and 0.06, respectively (Fig. 1D). Figure 7Bb, Cb and Db shows the results of our simulation of DCC KO circuits. Similar to the experimental data (Fig. 7Ca and Da), the model exhibited a variable frequency of oscillations on both sides and a lack of left–right coordination (Fig. 7Cb and Db). Our simulation of the augmentation of inhibitory interactions by sarcosine showed that a 2.5-fold increase of all inhibitory weights in DCC KO circuits led to the re-establishment of alternating activity between left and right RG-F centres (Fig. 8Ab and Bb), which is consistent with the experimentally demonstrated effect of sarcosine on the locomotor rhythm in DCC KO mice (Fig. 8Aa and Ba). Thus, our simulation supports the suggestion that the loss of DCC strongly reduces mid-line crossing by axons of CINs involved in both mutual inhibition and excitation between left and right rhythm-generating circuits.

Figure 7. Locomotor pattern transformation in DCC KO mice: data and simulations.

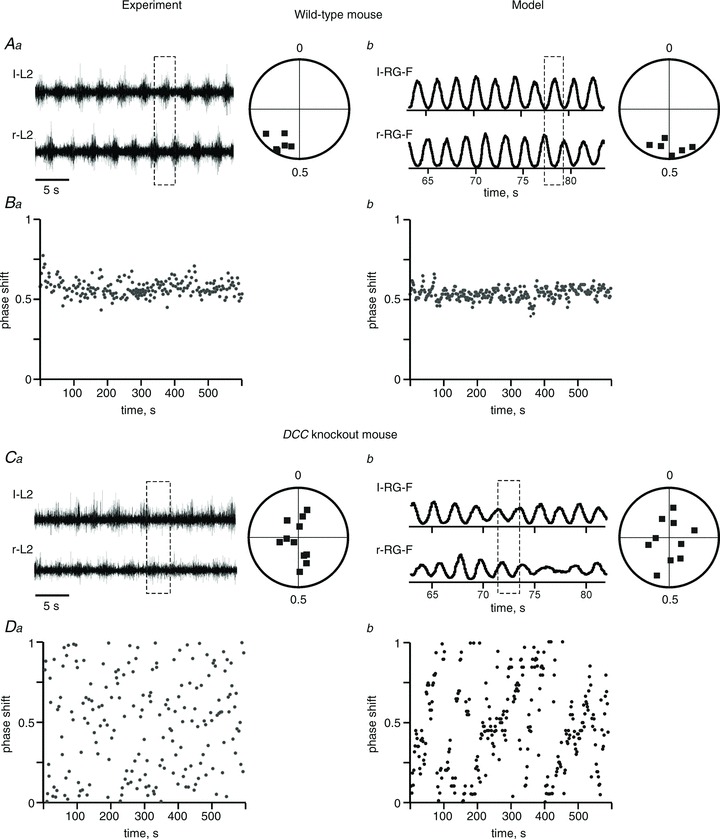
Figure 7

Open in a new tab

Aa, locomotor-like activity in the isolated spinal cord of a wild-type mouse evoked by the application of NMDA, 5-HT and dopamine. Only records from the left (l-L2) and right ventral roots (r-L2) are shown. Circular phase diagram to the right shows average phase differences between l-L2 and r-L2 activities. Ba, Cartesian representation of the phase differences between l-L2 and r-L2 during 600 s of recording (Aa and Ba are adapted from Rabe Bernhardt et al. 2012, Fig. 1A, B and I, with permission). Ab, integrated activities of l-RG-F and r-RG-F populations produced by the model of intact mouse circuits (Fig. 1A). Circular phase diagram to the right shows average phase differences between activities of r-RG-F and l-RG-F populations in 6 simulations. Similar to Aa, all simulations demonstrate left–right alternation. Bb, Cartesian representation of the phase differences between the activities of r-RG-F and l-RG-F populations during 600 s in a single simulation. Ca and Da, an example of l-L2 and r-L2 recording from the isolated spinal cord of a DCC KO mouse and the corresponding circular and Cartesian phase diagrams showing uncoordinated left and right activities (adapted from Rabe Bernhardt et al. 2012, Fig. 1E, F and L, with permission). Cb and Db, integrated activities of l-RG-F and r-RG-F populations produced by the DCC KO circuit (Fig. 1D). Circular phase diagram to the right (n= 10 simulations) and Cartesian phase diagram (for 600 s of one simulation) show uncoordinated left and right activities similar to Ca and Da. Dashed rectangles indicate left–right alternation or uncoordinated activities.

Figure 8. Partial re-establishment of left–right alternating pattern in DCC KO mice by enhancement of inhibition.

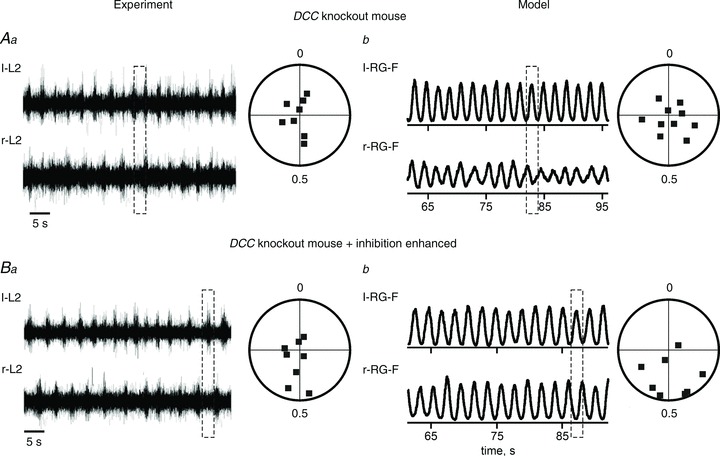
Figure 8

Open in a new tab

Aa and Ba, shift toward left–right alternation of activity in DCC KO mouse preparations after application of sarcosine (adapted from Rabe Bernhardt et al. 2012, Fig. 3L and M, with permission). Ab and Bb, simulated activities of l-RG-F and r-RG-F populations produced by the model before (Ab) and after 2.5-fold increase of all weights of inhibitory synaptic connections in the network (Bb). Similar to Aa and Ba, the applied augmentation of inhibition shows a tendency to re-establishment of left–right alternation in the DCC KO network. Dashed rectangles indicate uncoordinated or left–right alternating activities.

Discussion

Replication of locomotor pattern changes in genetically transformed spinal circuits with a simplified computational model

Recent advances suggest that both excitatory and inhibitory commissural neurons may be involved in left–right coordination (Butt & Kiehn, 2003; Jankowska et al. 2005; Kiehn, 2006; Quinlan & Kiehn, 2007; Jankowska, 2008; Talpalar et al. 2013). However, the exact inputs to these neurons on the ipsilateral side and their targets on the contralateral side remain mostly unknown. In this computational study, we used a relatively simple computational model to reproduce the experimentally demonstrated transformations of the locomotor-like activity observed in the isolated spinal cord of genetically transformed mice. The major point for model validation was the transformation of a normal walking pattern characterized by alternating left and right activities to a left–right synchronized hopping-like pattern. Our basic suggestion was that the normal alternating pattern of walking may result from the ‘default’ domination of inhibitory interactions between the left and right rhythm-generating circuits mediated by one group of CINs that overcome excitatory interactions between these circuits mediated by other groups of CINs. The specific suggestion of the present model is that the EphA4-positive neurons represent part of the RG circuits and are involved in the activation of the inhibitory CINs. The synchronized hopping-like pattern should then result from the domination of the mutual excitatory interactions between the left and right RG circuits.

The conversion of the left–right alternating walking pattern to a synchronized hopping activity in EphA4 KO mice was based on the idea that, with a lack of EphA4 molecules, axons from EphA4-postive neurons in the RG circuits, instead of contributing to mutual inhibition between left and right RGs via the ipsilateral CINi, project directly to the contralateral RG, hence shifting left–right interactions between the RGs from the domination of mutual inhibition to the domination of mutual excitation (also see Kullander et al. 2003; Butt et al. 2005; Restrepo et al. 2011).

We show that switching from the default alternating activity to a synchronized hopping pattern in Netrin-1 KO mice (Rabe et al. 2009) may result from a reduction in the number the axons of mostly inhibitory CINs projecting to the contralateral side, while keeping excitatory interactions unchanged.

The model of DCC KO circuits emulated a strong reduction in the number of mid-line-crossing axons from both inhibitory and excitatory CINs affecting the contralateral RG circuits that led to the misbalance of mutual interactions between the RGs and a collapse of left–right coordination, consistent with the experimental studies (Rabe Bernhardt et al. 2012).

By changing the ‘default’ probabilities of connections, the model could reproduce and suggest explanation for multiple experimental results obtained in three genetic knockout studies.

Re-establishment of the alternating activity pattern in KO mice by augmentation of inhibition

Our simulations confirmed the possibility of re-establishing the alternating activity pattern by sarcosine/nipecotic acid (Kullander et al. 2003; Rabe Bernhardt et al. 2012) in EphA4 KO and DCC KO circuits by augmentation of inhibition in the model. In both cases, an increase in the weights of inhibitory interactions could compensate for a reduction of mutual inhibitory pathways between the left and right RGs relative to the mutual excitatory pathways and return the balance back to a dominance of mutual inhibition. A switch from synchrony to alternation was not seen in the Netrin-1 KO circuit, in which the inhibitory interactions were strongly reduced in combination with the almost unchanged excitatory interactions. This result accords with the experimental data where application of sarcosine did not re-established the alternating pattern in the Netrin-1 KO mouse spinal cord (see Rabe et al. 2009).

The model also reproduced partial recovery of the alternating pattern by the progressively increasing inhibition and exhibited a series of intermediate regimens in which a generally synchronized pattern exhibited spontaneous switching to alternations and vice versa. Such switching between the locomotor activity patterns could be obtained by manipulations of many model parameters, especially when mutual inhibition and excitation between the RGs were close to each other. The EphA4 KO mice are sometimes able to move the hindlimbs in alternation, e.g. during a change in movement direction at very slow speeds of locomotion (O. Kiehn, unpublished observations). Moreover, the synchronous pattern in EphA4 KO mice can be shifted to alternating activity during recovery from isoflurane anaesthesia (Akay et al. 2006). Together with the finding that sarcosine can switch the synchronous pattern into alternation, these findings indicate that the inhibitory connections responsible for the normal left–right alternation still exist in EphA4-null mice.

The role of molecularly identified spinal neurons in locomotor pattern transformations

Genetic removal of excitatory ipsilaterally projecting V2a interneurons led to disruption of left–right coordination (Crone et al. 2008, 2009). Anatomical studies revealed a direct excitatory input of V2a-derived interneurons onto commissural interneurons, including a subset of molecularly defined V0-derived commissural interneurons (Crone et al. 2008). V2a interneurons express EphA4 (Lundfald et al. 2007). However, although many V2a interneurons express EphA4, no evidence has been found so far to support aberrant mid-line crossing by axons of these neurons in the EphA4 KO mice (Lundfald et al. 2007). In addition, the V2a neurons may not be involved implicitly in rhythm generation (Crone et al. 2008). Moreover, the V2a population is not homogeneous and may include neurons receiving direct inputs from the RG circuit and neurons not directly driven by the RG circuits (Zhong et al. 2012).

The function of inhibitory CINs (CINi) in our model could generally be performed by inhibitory interneurons derived from the molecularly identified V0 population (Pierani et al. 2001; Lanuza et al. 2004). Although other types of genetically identified interneurons (e.g. dI6) were suggested to be involved in left–right alternation (Rabe et al. 2009; Vallstedt & Kullander, 2013), recent studies have shown that that in the absence of V0 neurons, the normal alternating gait is not maintained by other commissural pathways (Talpalar et al. 2013). The V0 population is composed of inhibitory dorsal V0D (about two-thirds of all V0 neurons) and excitatory ventral V0V subpopulations (about one-third of all V0 neurons; Talpalar et al. 2013). The excitatory V0V CINs contribute to mutual inhibition between left and right RG populations, acting via inhibitory interneurons on each cord side, hence providing additional mutual inhibitory pathways (Quinlan & Kiehn, 2007; Kiehn, 2011). Thus, genetic ablation of the entire V0 population leads to hopping activity at all locomotor frequencies (reproduced by our model), whereas the selective ablation of inhibitory V0D neurons leads to lack of a left–right synchronized pattern at low locomotor frequencies, with mixed coordination at medium locomotor frequencies and alternation at high locomotor frequencies. In turn, when ablation is targeted to excitatory V0V neurons, left–right alternation is present at low frequencies and hopping is now restricted to medium and high locomotor frequencies (Talpalar et al. 2013). The present model has not considered these frequency-dependent changes and focused entirely on the direct inhibitory CIN pathways, such as those mediated by the inhibitory V0D type of CINs operating during slow locomotion. The contribution of V0V-mediated alternation recruited at higher locomotor frequencies has not been included in the model.

The excitatory commissural neurons (CINe) in this model may represent a subset of the excitatory V3-derived interneurons. It has been shown that V3-derived neurons are involved in the establishment of a robust, coherent and balanced motor rhythm during walking (Zhang et al. 2008). The excitatory CINs may also be involved in more complex interactions between the left and right RGs. For example, they may mediate excitatory inputs from the ipsilateral extensor centre to the contralateral flexor centres that in turn inhibit the ipsilateral flexor centres (Zhong et al. 2012). In our simplified model, removing V3-related CINe neurons did not disturb the alternating locomotor pattern generated by the intact network. Therefore, even if we focus only on the potential involvement of V3 neurons in interactions between left and right RGs, it is possible that these neurons play multiple roles in the CPG networks, which have not been fully considered in this simplified model.

Model limitations

Several important issues concerning the CPG organization per se and the left–right interactions involved in the locomotor pattern coordination have not been considered in the present study. First, we have not simulated the dual inhibitory pathways and have not investigated the possible gait transformations dependent on the locomotor speed (Crone et al. 2009; Talpalar et al. 2013). The two other critical simplifications of the present model are the lack of left and right extensor centres and circuits mediating flexor–extensor interactions on each side of the cord. Therefore, an important direction for future computational studies is the consideration of a more complete model that includes these elements in both rhythm generation (RG) and pattern formation (PF) networks (see Rybak et al. 2006a,b; McCrea & Rybak, 2007, 2008; Zhong et al. 2012).

Model validation and predictions

Despite relative simplicity, the model closely reproduces most of the changes in the locomotor pattern generated in several mouse mutants exhibiting transformation from the normal left–right alternating pattern to a synchronized hopping pattern. In addition, the model generates predictions about the structure of spinal locomotor network that are prone to experimental testing and validation. Specifically, removal of the commissural CINi populations in the model, which supposedly represent the V0-derived commissural neurons in the spinal cord, should convert the generated locomotor pattern from left–right alternating to synchronized hopping (similar to that seen in Netrin-1 KO mice). This modelling prediction has recently been confirmed by Talpalar et al. (2013), which provided additional validation to our model.

The CINi populations in our model (representing V0 populations in the spinal cord) receive synaptic excitation from the EphA4-positive neurons. Therefore, another prediction from the model is that genetic removal of EphA4-positive neurons should reduce the synaptic drive to V0 neurons. Moreover, since EphA4-positive V2a neurons (Lundfald et al. 2007; Crone et al. 2009) and the excitatory V0V CINs (Talpalar et al. 2013) are both involved in providing left–right alternation at high locomotor frequencies, we predict that the EphA4-positive neurons activate mostly the V0V subpopulation of V0 CINs and that a genetic removal of these EphA4-positive neurons should greatly reduce the activity specifically of V0V neurons and may potentially lead to synchronized hopping activity at high locomotor frequencies.

In conclusion, we believe that this study will provide important insights into the organization of the central pattern generator in the spinal cord and that the present model will serve as a basis for the development of more comprehensive models of mammalian spinal circuits.

Acknowledgments

None declared.

Glossary

CIN

commissural interneuron

CINe

excitatory commissural interneuron

CINi

inhibitory commissural interneuron

CPG

central pattern generator

KO

knockout

PF

pattern formation

RG

rhythm generator

Appendix

Model description

All neurons were modelled in the Hodgkin–Huxley style. The neuronal membrane potential (V) is described by the following differential equation:

graphic file with name tjp0591-5491-m1.jpg (A1)

where C is the membrane capacitance and t is time.

The following ionic currents (with the corresponding channel conductances) have been considered: fast sodium (INa, with maximal conductance 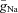Inline graphic); persistent (slowly inactivating) sodium current (INaP, with maximal conductance 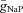Inline graphic); delayed-rectifier potassium (IK, with maximal conductance 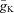Inline graphic); and leakage (IL, with constant conductance gL). The currents are described as follows:

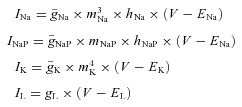graphic file with name tjp0591-5491-m2.jpg (A2)

where ENa, EK and EL are the reversal potentials for sodium, potassium and leakage currents, respectively; variables m and h with indexes indicating ionic currents represent, respectively, the activation and inactivation variables of the corresponding ionic channels. Bursting properties of RG-F0 and RG-FEphA4 interneurons were provided by INaP. This current was not included in CIN interneurons.

Activation m and inactivation h of voltage-dependent ionic channels (e.g. Na, NaP and K) in eqn (A1) are described by the following differential equations:

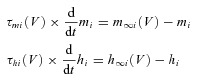graphic file with name tjp0591-5491-m3.jpg (A3)

where i identifies the name of the channel, m∞i(V) and h∞i(V) define the voltage-dependent steady-state activation and inactivation, respectively, and τmi(V) and τhi(V) define the corresponding time constants. Activation of the sodium channels is considered to be instantaneous (τmNa=τmNaP= 0). The parameters and expression for all channel kinetics are summarized in Table 1.

The synaptic excitatory (ISynE, with conductance gSynE and reversal potential ESynE) and inhibitory currents (ISynI, with conductance gSynI and reversal potential ESynI) are described as follows:

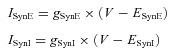graphic file with name tjp0591-5491-m4.jpg (A4)

The excitatory (gSynE) and inhibitory synaptic conductances (gSynI) are equal to zero at rest and may be activated (opened) by the excitatory or inhibitory inputs, respectively:

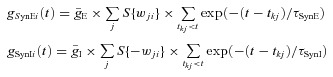graphic file with name tjp0591-5491-m5.jpg (A5)

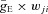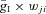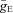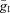where the function S{x} =x if x≥ 0 and S{x} = 0 if x < 0. Each spike arriving at neuron i from neuron j at time tkj increases the excitatory synaptic conductance by Inline graphic if the synaptic weight wji > 0, or increases the inhibitory synaptic conductance by Inline graphic if the synaptic weight wji < 0. The parameters Inline graphic and Inline graphic define an increase in the excitatory or inhibitory synaptic conductance, respectively, produced by one arriving spike at |wji|= 1. The parameters τSynE and τSynI are the decay time constants for the excitatory and inhibitory conductances, respectively. Values of synaptic weights (wji) were set using a random generator and were based on average values of these weights (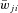Inline graphic; see Table 2) and variance, which were define as 5% of 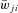Inline graphic for excitatory connections (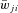Inline graphic > 0) and 10% of 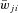Inline graphic for inhibitory connections (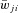Inline graphic < 0).

The neuronal heterogeneity of neurons within each population was set by a random distribution of EL (see mean values ± SD in next section) and initial conditions for values of membrane potential and channel conductances. In all simulations, initial conditions were chosen randomly from a uniform distribution for each variable, and a settling period of 50 s was allowed in each simulation before data were collected. Each simulation was repeated 15–20 times, and demonstrated qualitatively similar behaviour for particular values of the standard deviation of EL and initial conditions.

Model parameters

General parameters are as follows: C = 1 μF cm−2; ENa= 55 mV; EK=−80 mV; ESynE=−10 mV; ESynI=−70 mV; 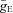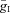Inline graphic=Inline graphic= 0.05 mS cm−2; and τSynE=τSynI= 5 ms.

Parameters for RG-F0 and RG-FEphA4 interneurons are as follows: 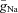Inline graphic= 30 mS cm−2; 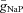Inline graphic= 0.35 mS cm−2; 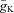Inline graphic= 1 mS cm−2; gL= 0.1 mS cm−2; and EL=−64 ± 0.64 mV.

For all CINs parameters are as follows: 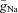Inline graphic= 120 mS cm−2; 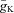Inline graphic= 100 mS cm−2; gL= 0.5 mS cm−2; and EL=−64 ± 3.2 mV.

Additional Information

Competing interests

None declared.

Author contributions

All modelling and simulations were performed in the Department of Neurobiology and Anatomy, Drexel University College of Medicine. I.A.R. and N.A.S. developed the model and conducted all simulations. I.A.R., N.A.S. and O.K. discussed the results and wrote the paper. All authors approved the final version for publication.

Funding

I.A.R. and N.A.S. were supported by the National Institutes of Health grant R01 NS081713. O.K. was supported by the Swedish Research Council, the European Research Council (advanced grant) and the Söderberg Foundation.

References

  1. Akay T, Acharya HJ, Fouad K, Pearson KG. Behavioral and electromyographic characterization of mice lacking EphA4 receptors. J Neurophysiol. 2006;96:642–651. doi: 10.1152/jn.00174.2006. [DOI] [PubMed] [Google Scholar]
  2. Bannatyne BA, Edgley SA, Hammar I, Jankowska E, Maxwell DJ. Networks of inhibitory and excitatory commissural interneurons mediating crossed reticulospinal actions. Eur J Neurosci. 2003;18:2273–2284. doi: 10.1046/j.l460-9568.2003.02973.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Berens P. CircStat: a MATLAB toolbox for circular statistics. J Stat Software. 2009;31:1–21. [Google Scholar]
  4. Bonnot A, Morin D. Hemisegmental localisation of rhythmic networks in the lumbosacral spinal cord of neonate mouse. Brain Res. 1998;793:136–148. doi: 10.1016/s0006-8993(98)00153-x. [DOI] [PubMed] [Google Scholar]
  5. Brocard F, Shevtsova NA, Bouhadfane M, Tazerart S, Heinemann U, Rybak IA, Vinay L. Activity-dependent changes in extracellular Ca2+ and K+ reveal pacemakers in the spinal locomotor-related network. Neuron. 2013;77:1047–1054. doi: 10.1016/j.neuron.2013.01.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Brocard F, Tazerart S, Vinay L. Do pacemakers drive the central pattern generator for locomotion in mammals. Neuroscientist. 2010;16:139–155. doi: 10.1177/1073858409346339. [DOI] [PubMed] [Google Scholar]
  7. Butt SJ, Kiehn O. Functional identification of interneurons responsible for left–right coordination of hindlimbs in mammals. Neuron. 2003;38:953–963. doi: 10.1016/s0896-6273(03)00353-2. [DOI] [PubMed] [Google Scholar]
  8. Butt SJ, Lundfald L, Kiehn O. EphA4 defines a class of excitatory locomotor-related interneurons. Proc Natl Acad Sci USA. 2005;102:14098–14103. doi: 10.1073/pnas.0503317102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cazalets JR, Sqalli-Houssaini Y, Clarac F. Activation of the central pattern generators for locomotion by serotonin and excitatory amino acids in neonatal rat. J Physiol. 1992;455:187–204. doi: 10.1113/jphysiol.1992.sp019296. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cowley KC, Schmidt BJ. Effects of inhibitory amino acid antagonists on reciprocal inhibitory interactions during rhythmic motor activity in the in vitro neonatal rat spinal cord. J Neurophysiol. 1995;74:1109–1117. doi: 10.1152/jn.1995.74.3.1109. [DOI] [PubMed] [Google Scholar]
  11. Crone SA, Quinlan KA, Zagoraiou L, Droho S, Restrepo CE, Lundfald L, Endo T, Setlak J, Jessell TM, Kiehn O, Sharma K. Genetic ablation of V2a ipsilateral interneurons disrupts left–right locomotor coordination in mammalian spinal cord. Neuron. 2008;60:70–83. doi: 10.1016/j.neuron.2008.08.009. [DOI] [PubMed] [Google Scholar]
  12. Crone SA, Zhong G, Harris-Warrick R, Sharma K. In mice lacking V2a interneurons, gait depends on speed of locomotion. J Neurosci. 2009;29:7098–7109. doi: 10.1523/JNEUROSCI.1206-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dottori M, Hartley L, Galea M, Paxinos G, Polizzotto M, Kilpatrick T, Bartlett PF, Murphy M, Köntgen F, Boyd AW. EphA4 (Sek1) receptor tyrosine kinase is required for the development of the corticospinal tract. Proc Natl Acad Sci U S A. 1998;95:13248–13253. doi: 10.1073/pnas.95.22.13248. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gosgnach S. The role of genetically-defined interneurons in generating the mammalian locomotor rhythm. Integr Comp Biol. 2011;51:903–912. doi: 10.1093/icb/icr022. [DOI] [PubMed] [Google Scholar]
  15. Goulding M. Circuits controlling vertebrate locomotion: moving in a new direction. Nat Rev Neurosci. 2009;10:507–518. doi: 10.1038/nrn2608. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Graham-Brown T. The intrinsic factors in the act of progression in mammals. Proc R Soc B. 1911;84:308–319. [Google Scholar]
  17. Grillner S. Control of locomotion in bipeds, tetrapods, and fish. In: Brooks VB, editor. Handbook of Physiology, section 1, The Nervous System, vol. II, Motor Control. Bethesda: American Physiology Society; 1981. pp. 1179–1236. [Google Scholar]
  18. Grillner S. Biological pattern generation: the cellular and computational logic of networks in motion. Neuron. 2006;52:751–766. doi: 10.1016/j.neuron.2006.11.008. [DOI] [PubMed] [Google Scholar]
  19. Grillner S, Zangger P. On the central generation of locomotion in the low spinal cat. Exp Brain Res. 1979;34:241–261. doi: 10.1007/BF00235671. [DOI] [PubMed] [Google Scholar]
  20. Guertin P, Angel MJ, Perreault MC, McCrea DA. Ankle extensor group I afferents excite extensors throughout the hindlimb during fictive locomotion in the cat. J Physiol. 1995;487:197–209. doi: 10.1113/jphysiol.1995.sp020871. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hammar I, Bannatyne BA, Maxwell DJ, Edgley SA, Jankowska E. The actions of monoamines and distribution of noradrenergic and serotoninergic contacts on different subpopulations of commissural interneurons in the cat spinal cord. Eur J Neurosci. 2004;19:1305–1316. doi: 10.1111/j.l460-9568.2004.03239.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Harris-Warrick RM. General principles of rhythmogenesis in central pattern generator networks. Prog Brain Res. 2010;187:213–222. doi: 10.1016/B978-0-444-53613-6.00014-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Jankowska E. Spinal interneuronal networks in the cat: elementary components. Brain Res Rev. 2008;57:46–55. doi: 10.1016/j.brainresrev.2007.06.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Jankowska E, Edgley SA, Krutki P, Hammar I. Functional differentiation and organization of feline midlumbar commissural interneurones. J Physiol. 2005;565:645–658. doi: 10.1113/jphysiol.2005.083014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Jankowska E, Jukes MGM, Lund S, Lundberg A. The effect of DOPA on the spinal cord. V. Reciprocal organization of pathways transmitting excitatory action to alpha motoneurones of flexors and extensors. Acta Physiol Scand. 1967a;70:369–388. doi: 10.1111/j.1748-1716.1967.tb03636.x. [DOI] [PubMed] [Google Scholar]
  26. Jankowska E, Jukes MGM, Lund S, Lundberg A. The effect of DOPA on the spinal cord. VI. Half-centre organization of interneurones transmitting effects from the flexor reflex afferents. Acta Physiol Scand. 1967b;70:389–402. doi: 10.1111/j.1748-1716.1967.tb03637.x. [DOI] [PubMed] [Google Scholar]
  27. Jasinski PE, Molkov YI, Shevtsova NA, Smith JC, Rybak IA. Sodium and calcium mechanisms of rhythmic bursting in excitatory neural networks of the pre-Bötzinger complex: a computational modelling study. Eur J Neurosci. 2013;37:212–230. doi: 10.1111/ejn.12042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Jessell TM. Neuronal specification in the spinal cord: inductive signals and transcriptional codes. Nat Rev Genet. 2000;1:20–29. doi: 10.1038/35049541. [DOI] [PubMed] [Google Scholar]
  29. Jiang Z, Carlin KP, Brownstone RM. An in vitro functionally mature mouse spinal cord preparation for the study of spinal motor networks. Brain Res. 1999;816:493–499. doi: 10.1016/s0006-8993(98)01199-8. [DOI] [PubMed] [Google Scholar]
  30. Kaprielian Z, Runko E, Imondi R. Axon guidance at the midline choice point. Dev Dyn. 2001;221:154–181. doi: 10.1002/dvdy.1143. [DOI] [PubMed] [Google Scholar]
  31. Kennedy TE, Serafini T, de la Torre JR, Tessier-Lavigne M. Netrins are diffusible chemotropic factors for commissural axons in the embryonic spinal cord. Cell. 1994;78:425–435. doi: 10.1016/0092-8674(94)90421-9. [DOI] [PubMed] [Google Scholar]
  32. Kiehn O. Locomotor circuits in the mammalian spinal cord. Annu Rev Neurosci. 2006;29:279–306. doi: 10.1146/annurev.neuro.29.051605.112910. [DOI] [PubMed] [Google Scholar]
  33. Kiehn O. Development and functional organization of spinal locomotor circuits. Curr Opin Neurobiol. 2011;21:100–109. doi: 10.1016/j.conb.2010.09.004. [DOI] [PubMed] [Google Scholar]
  34. Kiehn O, Butt SJ. Physiological, anatomical and genetic identification of CPG neurons in the developing mammalian spinal cord. Prog Neurobiol. 2003;70:347–361. doi: 10.1016/s0301-0082(03)00091-1. [DOI] [PubMed] [Google Scholar]
  35. Kjaerulff O, Kiehn O. Distribution of networks generating and coordinating locomotor activity in the neonatal rat spinal cord in vitro: a lesion study. J Neurosci. 1996a;16:5777–5794. doi: 10.1523/JNEUROSCI.16-18-05777.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Kiehn O, Kjaerulff O. Spatiotemporal characteristics of 5-HT and dopamine-induced rhythmic hindlimb activity in the in vitro neonatal rat. J Neurophysiol. 1996b;75:1472–1482. doi: 10.1152/jn.1996.75.4.1472. [DOI] [PubMed] [Google Scholar]
  37. Kudo N, Yamada T. N-methyl-D,L-aspartate-induced locomotor activity in a spinal cord-hindlimb muscles preparation of the newborn rat studied in vitro. Neurosci Lett. 1987;75:43–48. doi: 10.1016/0304-3940(87)90072-3. [DOI] [PubMed] [Google Scholar]
  38. Kullander K, Butt SJ, Lebret JM, Lundfald L, Restrepo CE, Rydstrom A, Klein R, Kiehn O. Role of EphA4 and EphrinB3 in local neuronal circuits that control walking. Science. 2003;299:1889–1892. doi: 10.1126/science.1079641. [DOI] [PubMed] [Google Scholar]
  39. Lafreniere-Roula M, McCrea DA. Deletions of rhythmic motoneuron activity during fictive locomotion and scratch provide clues to the organization of the mammalian central pattern generator. J Neurophysiol. 2005;94:1120–1132. doi: 10.1152/jn.00216.2005. [DOI] [PubMed] [Google Scholar]
  40. Lanuza GM, Gosgnach S, Pierani A, Jessell TM, Goulding M. Genetic identification of spinal interneurons that coordinate left-right locomotor activity necessary for walking movements. Neuron. 2004;42:375–386. doi: 10.1016/s0896-6273(04)00249-1. [DOI] [PubMed] [Google Scholar]
  41. Lundberg A. Half-centres revisited. In: Szentagothai J, Palkovits M, Hamori J, editors. Regulatory Functions of the CNS. Motion and Organization Principles. Budapest: Pergamon Akadem Kiado; 1981. pp. 155–167. [Google Scholar]
  42. Lundfald L, Restrepo CE, Butt SJ, Peng CY, Droho S, Endo T, Zeilhofer HU, Sharma K, Kiehn O. Phenotype of V2-derived interneurons and their relationship to the axon guidance molecule EphA4 in the developing mouse spinal cord. Eur J Neurosci. 2007;26:2989–3002. doi: 10.1111/j.1460-9568.2007.05906.x. [DOI] [PubMed] [Google Scholar]
  43. McCrea DA, Rybak IA. Modeling the mammalian locomotor CPG: insights from mistakes and perturbations. Prog Brain Res. 2007;165:235–253. doi: 10.1016/S0079-6123(06)65015-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. McCrea DA, Rybak IA. Organization of mammalian locomotor rhythm and pattern generation. Brain Res Rev. 2008;57:134–146. doi: 10.1016/j.brainresrev.2007.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Markin SN, Lemay MA, Prilutsky BI, Rybak IA. Motoneuronal and muscle synergies involved in cat hindlimb control during fictive and real locomotion: a comparison study. J Neurophysiol. 2012;107:2057–2071. doi: 10.1152/jn.00865.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Orlovsky GN, Deliagina TG, Grillner S. Neuronal Control of Locomotion. Oxford University Press, New York; 1999. [Google Scholar]
  47. Pierani A, Moran-Rivard L, Sunshine MJ, Littman DR, Goulding M, Jessell TM. Control of interneuron fate in the developing spinal cord by the progenitor homeodomain protein Dbx1. Neuron. 2001;29:367–384. doi: 10.1016/s0896-6273(01)00212-4. [DOI] [PubMed] [Google Scholar]
  48. Quinlan KA, Kiehn O. Segmental, synaptic actions of commissural interneurons in the mouse spinal cord. J Neurosci. 2007;27:6521–6530. doi: 10.1523/JNEUROSCI.1618-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Rabe N, Gezelius H, Vallstedt A, Memic F, Kullander K. Netrin-1-dependent spinal interneuron subtypes are required for the formation of left-right alternating locomotor circuitry. J Neurosci. 2009;29:15642–15649. doi: 10.1523/JNEUROSCI.5096-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Rabe Bernhardt N, Memic F, Gezelius H, Thiebes AL, Vallstedt A, Kullander K. DCC mediated axon guidance of spinal interneurons is essential for normal locomotor central pattern generator function. Dev Biol. 2012;366:279–289. doi: 10.1016/j.ydbio.2012.03.017. [DOI] [PubMed] [Google Scholar]
  51. Restrepo CE, Lundfald L, Szabó G, Erdélyi F, Zeilhofer HU, Glover JC, Kiehn O. Transmitter-phenotypes of commissural interneurons in the lumbar spinal cord of newborn mice. J Comp Neurol. 2009;517:177–192. doi: 10.1002/cne.22144. [DOI] [PubMed] [Google Scholar]
  52. Restrepo CE, Margaryan G, Borgius L, Lundfald L, Sargsyan D, Kiehn O. Change in the balance of excitatory and inhibitory midline fibre crossing as an explanation for the hopping phenotype in EphA4 knockout mice. Eur J Neurosci. 2011;34:1102–1112. doi: 10.1111/j.1460-9568.2011.07838.x. [DOI] [PubMed] [Google Scholar]
  53. Rossignol S. Neural control of stereotypic limb movements. In: Rowell LB, Shepherd J, editors. Handbook of Physiology, section 12, Exercise: Regulation and Integration of Multiple Systems. Bethesda: American Physiological Society; 1996. pp. 173–216. chapter 12. [Google Scholar]
  54. Rybak IA, Shevtsova NA, Lafreniere-Roula M, McCrea DA. Modelling spinal circuitry involved in locomotor pattern generation: insights from deletions during fictive locomotion. J Physiol. 2006a;577:617–639. doi: 10.1113/jphysiol.2006.118703. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Rybak IA, Stecina K, Shevtsova NA, McCrea DA. Modelling spinal circuitry involved in locomotor pattern generation: insights from the effects of afferent stimulation. J Physiol. 2006b;577:641–658. doi: 10.1113/jphysiol.2006.118711. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Shik ML, Severin FV, Orlovsky GN. Control of walking and running by means of electrical stimulation of the midbrain (in Russian) Biophysics. 1966;11:756–765. [Google Scholar]
  57. Smith JC, Feldman JL. In vitro brainstem-spinal cord preparations for study of motor systems for mammalian respiration and locomotion. J Neurosci Methods. 1987;21:321–333. doi: 10.1016/0165-0270(87)90126-9. [DOI] [PubMed] [Google Scholar]
  58. Stuart DG, Hultborn H. Thomas Graham Brown (1882–1965), Anders Lundberg (1920–), and the neural control of stepping. Brain Res Rev. 2008;59:74–95. doi: 10.1016/j.brainresrev.2008.06.001. [DOI] [PubMed] [Google Scholar]
  59. Tessier-Lavigne M. Wiring the brain: the logic and molecular mechanisms of axon guidance and regeneration. Harvey Lect. 2002;98:103–143. [PubMed] [Google Scholar]
  60. Talpalar AE, Bouvier J, Borgius L, Fortin G, Pierani A, Kiehn O. Dual mode operation of neuronal networks involved in left-right alternation. Nature. 2013;500:85–88. doi: 10.1038/nature12286. [DOI] [PubMed] [Google Scholar]
  61. Tazerart S, Vinay L, Brocard F. The persistent sodium current generates pacemaker activities in the central pattern generator for locomotion and regulates the locomotor rhythm. J Neurosci. 2008;28:8577–8589. doi: 10.1523/JNEUROSCI.1437-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Vallstedt A, Kullander K. Dorsally derived spinal interneurons in locomotor circuits. Ann N Y Acad Sci. 2013;1279:32–42. doi: 10.1111/j.1749-6632.2012.06801.x. [DOI] [PubMed] [Google Scholar]
  63. Whelan PJ. Developmental aspects of spinal locomotor function: insights from using the in vitro mouse spinal cord preparation. J Physiol. 2003;553:695–706. doi: 10.1113/jphysiol.2003.046219. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Whelan PJ. Shining light into the black box of spinal locomotor networks. Philos Trans R Soc Lond B Biol Sci. 2010;365:2383–2395. doi: 10.1098/rstb.2009.0322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Zagoraiou L, Akay T, Martin JF, Brownstone RM, Jessell TM, Miles GB. A cluster of cholinergic premotor interneurons modulates mouse locomotor activity. Neuron. 2009;64:645–662. doi: 10.1016/j.neuron.2009.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Zhang Y, Narayan S, Geiman E, Lanuza GM, Velasquez T, Shanks B, Akay T, Dyck J, Pearson K, Gosgnach S, Fan CM, Goulding M. V3 spinal neurons establish a robust and balanced locomotor rhythm during walking. Neuron. 2008;60:84–96. doi: 10.1016/j.neuron.2008.09.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Zhong G, Masino MA, Harris-Warrick RM. Persistent sodium currents participate in fictive locomotion generation in neonatal mouse spinal cord. J Neurosci. 2007;27:4507–4518. doi: 10.1523/JNEUROSCI.0124-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Zhong G, Shevtsova NA, Rybak IA, Harris-Warrick RM. Neuronal activity in the isolated mouse spinal cord during spontaneous deletions in fictive locomotion: insights into locomotor central pattern generator organization. J Physiol. 2012;590:4735–4759. doi: 10.1113/jphysiol.2012.240895. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Ziskind-Conhaim L, Wu L, Wiesner EP. Persistent sodium current contributes to induced voltage oscillations in locomotor-related Hb9 interneurons in the mouse spinal cord. J Neurophysiol. 2008;100:2254–2264. doi: 10.1152/jn.90437.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES