Influence of electron dose rate on electron counting images recorded with the K2 camera

Abstract

A recent technological breakthrough in electron cryomicroscopy (cryoEM) is the development of direct electron detection cameras for data acquisition. By bypassing the traditional phosphor scintillator and fiber optic coupling, these cameras have greatly enhanced sensitivity and detective quantum efficiency (DQE). Of the three currently available commercial cameras, the Gatan K2 Summit was designed specifically for counting individual electron events. Counting further enhances the DQE, allows for practical doubling of detector resolution and eliminates noise arising from the variable deposition of energy by each primary electron. While counting has many advantages, undercounting of electrons happens when more than one electron strikes the same area of the detector within the analog readout period (coincidence loss), which influences image quality. In this work, we characterized the K2 Summit in electron counting mode, and studied the relationship of dose rate and coincidence loss and its influence on the quality of counted images. We found that coincidence loss reduces low frequency amplitudes but has no significant influence on the signal-to-noise ratio of the recorded image. It also has little influence on high frequency signals. Images of frozen hydrated archaeal 20S proteasome (~700 kDa, D7 symmetry) recorded at the optimal dose rate retained both high-resolution signal and low-resolution contrast and enabled calculating a 3.6 Å three-dimensional reconstruction from only 10,000 particles.

1. Introduction

Thanks to improvements in microscopes and software, single particle electron cryomicroscopy (cryoEM) has recently reached milestones of being able to determine near atomic resolution three-dimensional (3D) structures of large macromolecular assemblies with high symmetry (Chen et al., 2009; Wolf et al., 2010; Zhang et al., 2008, 2011, 2010). The next challenge is to apply this technology routinely to a broad range of biological samples that are in general much smaller and of lower symmetry than large icosahedral viruses. From the experimental side, one of the challenges is to efficiently collect large datasets of high-resolution images. A major bottleneck has been the image-recording medium. Until now, the most commonly used media were either photographic film or scintillator based digital cameras (either charge-coupled device (CCD) or complementary metal–oxide-semiconductor (CMOS) cameras) that detect the emitted photons. The digital cameras offer many practical advantages over film, including immediate access to the acquired digital images, enabling on-the-fly image analysis and automated data acquisition (Carragher et al., 2000; Lyumkis et al., 2010; Zheng et al., 2010). More importantly, these cameras offer higher detective quantum efficiency (DQE) at low spatial frequency, giving good image contrast of frozen hydrated protein samples recorded with very limited electron doses, typically around 20–25 e⁻/Ų at the specimen (Booth et al., 2006; Sander et al., 2005). Unfortunately, the DQE of scintillator based digital cameras at high spatial frequency is significantly weaker than that of photographic film (McMullan et al., 2009a). Thus the data for most near atomic resolution 3D reconstructions have been recorded on photographic film (Chen et al., 2009; Cong et al., 2010; Wolf et al., 2010; Zhang et al., 2008, 2010), except for a few very recent cases (Cheng et al., 2011; Zhang et al., 2011). While the performance limitations of the scintillator based camera can be overcome by increasing the magnification and pixel binning, i.e. over-sampling, this comes at the expense of reducing image size, decreasing not only the total number of particles that can be recorded on each image but also the quality of Thon rings calculated from the image, which makes it harder to accurately determine the microscope contrast transfer function (CTF). Thus, in practice, a camera that could work at a relative low magnification while retain information with a sufficient signal-to-noise ratio (SNR) at better than 4 Å resolution will make the overall process more efficient.

The recent development of a new generation of CMOS based direct electron detection cameras offer clear advantages over both traditional photographic film and scintillator based digital cameras. These new direct detection cameras deliver the convenience and advantages of a traditional scintillator based digital camera plus improved DQE at high frequency, comparable to photographic films (McMullan et al., 2009a,b,c). The first commercially available direct detection camera characterized for its application in single particle cryoEM was the DE-12 camera from Direct Electron, LP (San Diego, CA) (Bammes et al., 2012; Milazzo et al., 2011). The 3D reconstructions calculated from data recorded by this camera have reached a level that is closer to its Nyquist limit than any scintillator based camera (Bammes et al., 2012).

Another commercially available direct electron detection camera is the K2 Summit™ from Gatan, Inc. (Pleasanton, CA), which we recently implemented into our data acquisition procedures for single particle cryoEM (UCSFImage (Avila-Sakar et al., 2013)) and cryoTomography (UCSFTomo (Zheng et al., 2007)). Different from the DE-12, the K2 Summit has two distinct operating modes, a “linear” mode and an electron counting mode. In the linear mode, there is an accumulation of charge generated from electrons striking the detector that are integrated over a fixed internal frame rate (of 400 frames/s, corresponding to 2.5 ms per frame) and then digitally summed for the full exposure. (The K2 Base model, which operates only in a linear mode, has a lower internal frame rate of 40 frames/s to reduce the readout noise.) By contrast, in the counting mode individual electron events are identified and only the digital events are accumulated over time. Counting the primary electrons can effectively reject camera readout noise and, more importantly, noise arising from the statistical deposition of energy by the primary electron (Landau noise), as well as dramatically improve the DQE (Li et al., 2013). By contrast any charge integration camera, including the K2’s linear mode, suffers from these noise sources and will have a decreased DQE. The K2 counting mode can further analyze the signal cluster created by each primary electron event and centroid the entry point with sub-pixel precision, similar to super-resolution methods in light microscopy (Shroff et al., 2007). In this super-resolution mode, the effective pixel size is half of the physical pixel size, quadrupling the total effective number of pixels. Using images collected from the K2 Summit, we have determined a 3D reconstruction of the 700 kDa archaeal 20S proteasome at a resolution of 3.3 Å (Li et al., 2013).

While many detectors can, in principle, do electron counting, operation at practical dose rates requires very high-speed readout capability so that only a single electron event occurs within each local detection area per frame. Even though the K2 uses a high internal frame rate (400 frames/s), multiple electron events in the 2.5 ms integration time will happen and begin to become noticeable at dose rates above ~4 electrons/pixel/s resulting in a non-linear relationship between the input electron dose rate (electrons/pixel/s) and the output signal (counts/pixel/s) (Li et al., 2013). As discussed below, minimizing this problem places practical limits on the maximal electron dose rate and can lead to very prolonged exposures.

Because the counting and centroiding approach used in the K2 Summit is so different from traditional linear imaging cameras, a counted image could have unique characteristics induced by coincidence loss. Thus, the conditions under which a counting camera delivers its best performance could also be different from a linear camera. To identify an optimal condition as well as to understand the influence of coincidence loss on image quality, we characterized the camera’s imaging performance as a function of dose rate. We found that the power spectrum of a counting image has slightly lower amplitudes at low resolution but a significantly better SNR at high resolution when compared to a linear recorded image under the same conditions. Data collected using the archaeal 20S proteasome as a test specimen demonstrate that the overall performance of the K2 Summit is superior to both photographic film and scintillator based CCD cameras for high-resolution single particle cryo-EM. As a more stringent test of camera performance, we sought to determine the maximum resolution that could be obtained from this sample using counting mode and many fewer particles than used previously (10,000 vs. 130,000).

2. Results

2.1. Comparison of counting and linear images

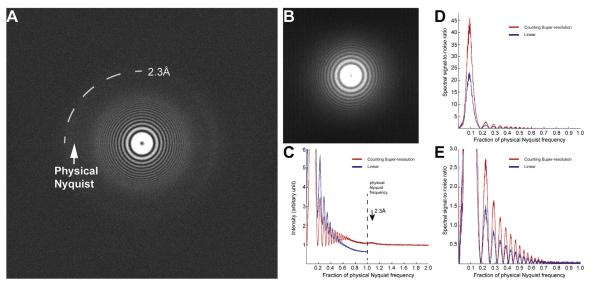
To quantitatively compare counting and linear modes of the K2 Summit camera, we recorded images of thin Pt/Ir films under the same conditions, including specimen area, magnification, defocus, total electron dose and dose rate (~10 counts/pixel/s) (Fig. 1A and B). Because super-resolution can only be obtained in counting mode, the Nyquist limits of these two images are different. The high-resolution information, both the Thon rings and the 2.3 Å platinum reflection ring, is clearer in the Fourier transform of the super-resolution image than that of the linear one. A rotational average of the Fourier power spectra clearly shows the difference between linear mode and counting mode. The power spectrum from the linear image has a smooth fall-off towards high resolution similar to what has been observed in scintillator based cameras (blue curve in Fig. 1C), but for the counted super-resolution image it increases slightly towards high resolution and plateaus at a nonzero value (red curve in Fig. 1C). We used the spectral signal-to-noise ration (SSNR), which is calculated by dividing background subtracted Thon ring intensity by the background intensity (Booth et al., 2006), to quantify the performance of the two modes. It is very clear that the SSNR of the counting image is nearly two times higher than that of the linear image (Fig. 1D and E) throughout the entire range where Thon rings are visible. This result is essentially the same as the nearly two times higher DQE of the counting mode than the linear mode (Li et al., 2013) and suggests that the counting image is significantly better than the linear image in all resolution ranges, making it particularly useful for high-resolution structure determination, consistent with early findings (Faruqi and McMullan, 2011).

Fig.1.

Comparison of images recorded with K2 counting and linear modes. Images of thin Pt/Ir film were recorded by the K2 Summit in both counting and linear modes. The imaging conditions were kept the same, i.e. magnification, defocus and total dose. The counting image was recorded in super-resolution mode, thus its image pixel size is only half of the linear image. (A) The Fourier transform of the counting image. (B) The Fourier transform of the linear image. (C) Rotational averages of power spectra from both linear (blue) and counting (red) images are plotted together for comparison. Both spectra are normalized by the total counts in the corresponding images. (D and E) Spectral signal-to-noise ratios (SSNRs) were calculated from linear (blue curve) and counting (red curve) images shown in Fig. 1C. 1.0 in horizontal axis is the physical Nyquist limit. (D) is shown as full scale in vertical axis and (E) is the enlarged view with vertical scale limited to 3.0.

2.2. Influence of dose rate on images recorded by K2 Summit

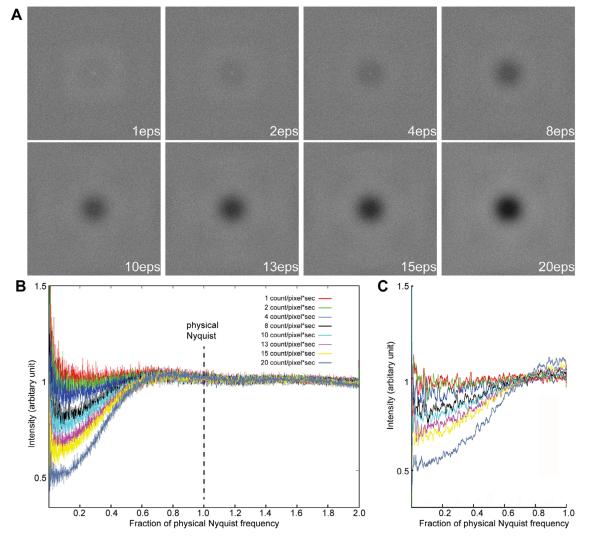
We noticed that the shape of the power spectrum baseline from the counting image is very different from that of a linear image and this shape is dependent on the electron dose rate on the camera, but not on the total electron dose used for imaging. In contrast, for linear images, the baseline is independent of both. We thus explored the influence of dose rate by a series of experiments. First, a set of 8 images was recorded with different electron dose rates in counting mode using a uniform electron beam illumination without a specimen (termed here “empty” images), ranging from 1–20 counts/pixel/s on the camera corresponding to 1–32 primary e⁻/pixel/s. Different dose rates were achieved by adjusting the electron beam intensity, without changing other microscope parameters. Different exposure times were used so that the total electron dose for each image was kept constant. Power spectra of these empty images give the noise power spectrum (NPS). An ideal empty counting image should contain only white noise and have a nearly flat power spectrum without falloff caused by the camera point spread function. However, the Fourier transforms of these experimental empty counting images showed a significant influence of dose rate. Below a dose rate of ~4 counts/pixel/s, the power spectrum is close to an ideal flat one. As the dose rate increased, the center of the Fourier transform became darker, with very obvious effects at dose rates above 10 counts/pixel/s (Fig. 2A). Similarly, in rotational averages, at a dose rate of 4 counts/pixel/s or less the noise power spectra are close to ideal (red, green and blue curves, Fig. 2B). Higher than that, the power spectrum starts to show a dip at low resolution but it recovers at near half of physical Nyquist, resulting in the dark center portion (Fig. 2A). These images suggest that coincidence losses at high dose rates introduce image defects resulting in an amplitude decrease at resolutions lower than half of the physical Nyquist limit.

Fig.2.

Influence of dose rate on counting images (A) Fourier transforms of empty super-resolution counting images recorded with different dose rates. Exposure time was adjusted so that the total dose used in each image is the same. The edge of the transform corresponds to twice the physical Nyquist limit. (B) Rotational averages of power spectra from empty counting images, i.e. noise power spectra, were plotted in different colors. (C) Simulated noise power spectra at different dose rates.

2.3. Coincidence loss at high dose rate

The finite frame rate of the K2 Summit inevitably leads to undercounting of primary electron events, termed coincidence loss. Hypothesizing that coincidence loss is the source of the power spectrum decrease at low resolution, we carried out a series of Monte Carlo calculations to simulate the behavior of counting images. Empty images at different dose rates were simulated by assuming an ideal pixel camera with an MTF of 1. If two or more events overlap (at the same or immediately adjacent pixels), only one was counted. The Fourier transform of a series of simulated empty images at different dose rates showed a decrease in the NPS at low resolution (Fig. 2C). In all simulated images, even with an incident dose rate as high as 32 e⁻/pixel/s (corresponding to 20 counts/pixel/s), the NPSs showed similar behaviors as the experimental data: a dip at low resolution but close to an ideal value of 1 from near half physical Nyquist to higher resolution. These simulations nicely and qualitatively describe the behavior of the experimental images shown in Fig. 2B and confirm that the NPS decrease at low frequency is due to coincidence loss.

2.4. Quantitative estimations of coincidence loss

The profile of the NPS at different dose rates can be fit nicely using a normalized sinc function:

$$\text{Intensity}=a-b\times {\mathit{sinc}}^2(k\times d)$$ (1)

where the intensity is normalized by the total counts on the image, and k is the resolution in units of 1/pixel. The numeric values of a, b and d were determined by least square fitting of the NPS curve at different dose rates (Fig. 3A and Table 1). These fittings suggest a simple model for explaining the shapes of the NPS with coincidence losses at different dose rates: for every counted primary electron, any other primary electron event occurring within a circular area of diameter d is not counted. This is equivalent to every counted primary electron carrying a circular mask with diameter d and any other primary electron event within this mask being lost. Thus, the Fourier transform of an empty image without specimen is the Fourier transform of the ideal image of white noise without any coincidence loss, which is a flat power spectrum of amplitude 1.0, minus the Fourier transform of the mask multiplied by a scaling factor, as formulated in (1). Indeed, Table 1 shows that a and d do not change with dose rate, where a = 1.005 ± 0.005 is very close to the flat power spectrum at 1.0 from an ideal empty counting image with pure white noise and d represents the diameter of the circular mask as 2.584 ± 0.044 pixel. As expected, the value of b increases with the dose rate, corresponding to the coincidence loss. This fitting provides a nice quantitative description of the contribution of coincidence loss to the power spectrum.

Fig.3.

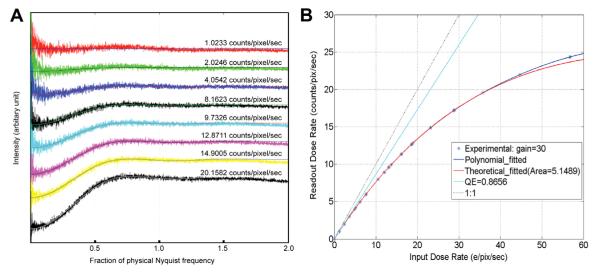
Fitting of experimental NPS and DCE curves. (A) Experimental NPS curves were fit by least square fitting using the formula (1). Parameters determined from the fittings are listed in Table 1. The dose rate of each curve is marked. (B) While the DQE curve can be fit by a polynomial function (blue curve) as previously described (Li et al., 2013), it can also be fit by the formula (4) derived from a binomial distribution model (red curve).

Table 1.

Least square fitting of NPS curve at different dose rate by the formula: Intensity = a − b × sinc² (k × d).

Dose rate	a	b	d	Average
1.0233	1.0097	0.0048	2.6788
2.0246	1.0037	0.0432	2.5812
4.0542	1.0015	0.0991	2.5397	a = 1.005 ± 0.005
8.1623	1.0001	0.2223	2.5900
9.7326	1.0003	0.2714	2.6056	d = 2.584 ± 0.044
12.8711	1.0035	0.3631	2.5680
14.9005	1.0079	0.4226	2.5715
20.1582	1.0168	0.5701	2.5398

We also estimated the probability of coincidence loss at different dose rates from the experimentally determined non-linear DCE curve (Li et al., 2013). Using a binomial distribution model, the probability of a number of primary electron events k overlapping with another event in a fixed area s (pixel²) during one internal accumulation period (see Method section for details) is:

$$P\left(k\right)=\frac{{\lambda }^k{e}^{-\lambda }}{k!}\text{and}\lambda =\frac{D\cdot s}{F}$$ (2)

where D is dose rate (e⁻/pixel/s), F is the frame rate. The probability of k = 0, which is the probability that an incoming electron does not overlap with any other primary event, at different dose rates is

$$P\left(0\right)=e^{-\frac{D\cdot s}{F}}$$ (3)

In addition to coincidence loss, there is also a linear count loss caused by the imperfect quantum efficiency (QE) of the detector, which is the ratio of output and input signals assuming no coincidence loss. Thus, the total count at a different dose rate is

$$P\left(0\right)\cdot \mathit{QE}=e^{-\frac{D\cdot s}{F}}\mathit{QE}$$ (4)

A least square fitting of the experimental DCE curve by formula (4) (Fig. 3B) gives QE = 86.56% and s = 5.1459 pixel², or a circle with diameter of 2.57 pixels, which is essentially identical to the value determined by fitting the NPS curves. Table 2 listed the probability of different overlapping events at different dose rate. At a dose rate of ~8e⁻/pixel/s, the total coincidence loss is ~10%.

Table 2.

Probability (%) of number of electrons overlaps (k) at different dose rates.

Dose rate	k = 0	1	2	3	4	5	6	7
1 eps	98.7208	1.2710	0.0082	0.0000	0.0000	0.0000	0.0000	0.0000
2 eps	97.4579	2.5095	0.0323	0.0003	0.0000	0.0000	0.0000	0.0000
4 eps	94.9804	4.8915	0.1260	0.0022	0.0000	0.0000	0.0000	0.0000
8 eps	90.2127	9.2919	0.4785	0.0164	0.0004	0.0000	0.0000	0.0000
16 eps	81.3833	16.7650	1.7268	0.1186	0.0061	0.0003	0.0000	0.0000
32 eps	62.9078	29.1578	6.7573	1.0440	0.1210	0.0112	0.0009	0.0001

2.4.1. Characterization of a counting camera

DQE has been an important method to characterize the performance of EM cameras. The definition of DQE is (Mooney, 2007):

$$\mathit{DQE}=\frac{{\mathit{SSNR}}_{\mathit{out}}}{{\mathit{SSNR}}_{\mathit{in}}}$$ (5)

and in practical terms, it can be calculated as (McMullan et al., 2009a):

$$\mathit{DQE}=\mathit{DQE}\left(0\right)\frac{{\mathit{MTF}}^2\left(k\right)}{\mathit{NPS}\left(k\right)}$$ (6)

where MTF(k) is the modulation transfer function, which can be determined from the image of a knife-edge. However, for a counting camera, such as the K2 Summit, in which the counting process removes all read-out noise, the DQE defined by formula (5) and determined by formula (6) may not be an appropriate parameter to characterize camera performance. At a high dose rate, the very different coincidence loss at different sides of the knife-edge enhances the contrast of the knife-edge (Fig. S1) and the low NPS value (<1) at the low frequency caused by coincidence loss increases the calculated DQE at low frequency. Thus, practically, obtaining an accurate DQE curve requires that the data be measured at a very low dose rate, such as 1–2 e⁻/pixel/s. At a higher dose rate, such as the one used for routine imaging, the DQE determined using formula (6) and a knife-edge is no longer accurate. Thus, instead of using DQE, we suggest using three different parameters to characterize the performance of a counting camera. They are the QE value, DCE and MTF curves. The QE measures the percentage of incident electrons counted by the camera assuming no coincidence loss. A better camera would have a QE closer to 1. The DCE describes the coincidence loss and non-linearity of the camera at different dose rates. It reflects the capability in separating adjacent electron events during counting and can be quantified by readout rate and the diameter of the counting mask, which is related to the counting algorithm used by the camera. Better counting with less coincidence loss makes the DCE curve closer to a straight line with a slope equaling QE (Fig. S2). The MTF curve measures mostly the effects of any mislocation of counted primary electron events due to major deposition of energy being offset from the site of initial entry.

2.5. Influence of coincidence loss on image amplitude and SSNR

To further evaluate the practical influence of coincidence losses on counting images, we compared 3 super-resolution images of a thin Pt/Ir film recorded with different electron dose rates, i.e. 1, 10 and 20 counts/pixel/s (Fig. 4). Again, the dose rate differences were compensated by exposure time so that the total electron doses used for each image were equivalent but the image counts are different due to the different coincidence losses. For ease of comparison, Thon ring intensities were calculated by normalization with total image counts and subtraction of the backgrounds of the rotational averages of the power spectra (Fig. 4B). The SSNRs (Fig. 4C) were calculated as described above (Fig. 1D). An obvious difference is that the Thon ring intensity at low resolution is reduced in images recorded with a higher dose rate, while there is almost no change at high resolution (Fig. 4B). This corresponds to the low-resolution dip in the power spectra of the empty images. Related, we also noticed a decrease in image contrast with increased dose rate and the contrast loss became severe at dose rates higher than 20 counts/pixel/s (data not shown). However, the high dose rate has only a minor influence on the SSNR at both low and high resolution (Fig. 4C), because the signal (Thon ring intensity) reduction is partially compensated by the similar reduction of background noise. This suggests that it is possible to correct the amplitude loss at low resolution (see below).

Fig.4.

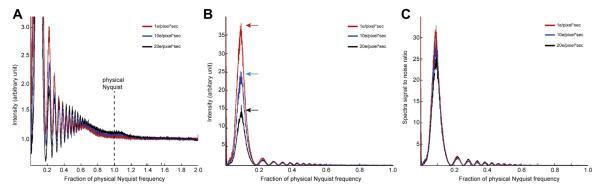
Comparison of super-resolution counting images recorded with different dose rates. (A) Rotational averages of power spectra without background subtraction from super-resolution counting images of thin Pt/Ir film recorded with different dose rate. The exposure time used for each image was adjusted so that the total doses used for all images were the same, allowing the power spectra to be compared directly without additional scaling. (B) Rotational averages of power spectra after background subtraction. Arrows indicate that the amplitude of first Thon ring is reduced significantly by increasing the dose rate. (C) SSNR calculated from (A).

Together, these data suggest that a dose rate between 8 and 10 counts/pixel/s on the camera seems to be the threshold for recording images that are close to ideal. At this dose rate, images should have an excellent low-resolution signal, good image contrast and good linearity. Also, the exposure time needed to achieve a certain amount of accumulative total dose on specimen is within an acceptable range in which any influence of sample/stage drift on image quality due to prolonged exposure times can be effectively eliminated by motion correction (Li et al., 2013). Above this dose rate, low frequency signal starts to degrade and image contrast becomes weaker, ultimately compromising the ability to detect and align particles. Importantly, the high-resolution information seemed not to be influenced by the dose rate, even at a level of ~20 counts/pixel/s. As shown next, this conclusion holds for real cryo images.

2.6. Imaging a frozen hydrated protein sample using K2 Counting mode

As a test specimen, we recorded images of frozen hydrated Thermoplasma acidophilum 20S proteasomes on the K2 Summit operated in the counting mode. It has D7 symmetry and a molecular weight of approximately 700 kDa. Its crystal structure has been determined by X-ray crystallography to a resolution of 3.4 Å (Lowe et al., 1995). The best 3D reconstruction of the same protein from images recorded on photographic films was at a resolution of ~5.6 Å (Rabl et al., 2008). Images were recorded at 300 kV and a magnification of 31kX, which gave a physical pixel size of 1.22 Å and a Nyquist limit of 2.44 Å. The beam intensity was set to produce a dose rate of ~10 counts/pixel/s on camera. We chose such a dose rate to balance the total electron dose used on the specimen and the total exposure time used to record the image. All images were recorded with an exposure time of 3.5 s, resulting in a total dose of ~33 e⁻/Ų at the specimen level. According to the data presented above, this dose rate would be expected to cause a roughly ~14% coincidence loss, as well as some low-resolution amplitude loss.

Defocus values ranged between −0.8 μm and −2 μm, and representative images at different defocuses are shown in Fig. 5A–C. Even with a defocus of −0.8 μm, the particles are clearly visible. This defocus range was significantly lower than the images of the same sample we previously collected on photographic films (Rabl et al., 2008), which was −1.5 μm to −3.5 μm at 200 kV, equivalent to −1.9 μm to −4.5 μm at −300 kV. The Fourier transform calculated from one of the best images (shown in Fig. 5D) shows visible Thon rings out to 3.2 Å, well beyond the half Nyquist of 4.8 Å. Recording images of such quality would be impossible with a scintillator based CCD camera or even from the K2 Base operated in the linear mode. Thus, at a dose rate of ~10 counts/pixel/s, images of frozen hydrated 20S proteasomes have good signal at low resolution (in terms of good image contrast) and excellent signal at high resolution (in terms of visible Thon ring at close to 3 Å resolution). Note that there is a dark ring in the background of the Fourier transform within the half Nyquist circle (Fig. 5D) caused by coincidence loss as shown above (Fig. 2A and B). This dark ring is seen in all images we recorded under these conditions, indicating that our dose rate was higher than ideal. Nevertheless, even with such a loss of low-resolution amplitude, images still have excellent contrast as well as high-resolution information.

Fig.5.

Images of frozen hydrated archaeal 20S proteasome recorded with the K2 camera in counting mode. The image pixel size is 1.2 Å, corresponding to a Nyquist of 2.4 Å. Image defocuses are approximately (A) −0.9 μm, (B) −1.1 μm, and (C) −1.5 μm. (D) A Fourier transform calculated from image (B). At a defocus of −1.1 μm, the visible Thon ring extends to 3.2 Å.

2.7. 3D reconstruction of archaeal 20S proteasome with amplitude correction

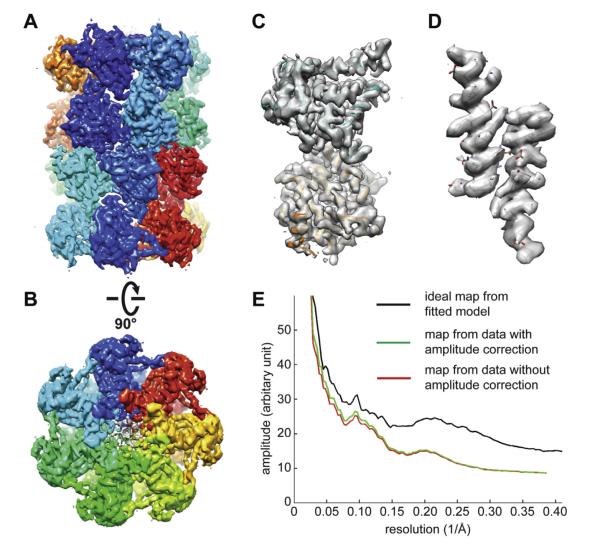
Because the SSNR is almost independent of the dose rate (Fig. 4C), it is possible to recover the low-frequency amplitude computationally by dividing the image amplitude by the square root of formula (1). We tested applying such amplitude correction to the image shown in Fig. 5B and observed a slight contrast improvement (data not shown). We further tested if such amplitude correction has any influence on the quality of the resultant 3D reconstruction, perhaps due to improved alignment accuracy. Previously, we collected a dataset of ~130,000 particles using K2 counting mode and determined a 3D reconstruction of archaeal 20S proteasome at a resolution of 3.3 Å (Li et al., 2013). We took the first 10,000 particles from this motion corrected dataset and determined two independent 3D reconstructions with and without the amplitude correction (Fig. 6A–D). Refinements of these two 3D reconstructions were independent from each other as well as independent from the published 3.3 Å 3D reconstruction determined from the entire 130,000 particles. The final 3D reconstructions reached almost the same resolution of ~3.6 Å (Fig. S3). The 3D reconstruction using the amplitude-corrected dataset had slightly higher amplitude at low resolution, corresponding to a slightly better B factor (Fig. 6E). The final 3D reconstructions after scaling their amplitudes to the ideal map showed very similar map quality. More importantly, the map qualities are comparable with the published density map at 3.3 Å resolution determined from ~130,000 particles. However, it is not clear if such a correction scheme would be even more helpful if the data were collected with a much higher dose rate, such as at ~20 e⁻/pixel/s.

Fig.6.

3D reconstruction of archaeal 20S proteasome with amplitude correction. 10,000 particles were taken from previously published dataset (Li et al., 2013) and corrected for coincidence loss induced low frequency amplitude loss. (A and B) Two different views of the 3D reconstruction after amplitude correction filtered to a resolution of 3.6 Å. (C) A single α- and β-subunits segmented from the 3D density map in A. (D) Two α-helices segmented from the α- and β-subunits showing clear side chain density. The quality of side chain density is similar to the published 3.3 Å map (Li et al., 2013). (E) Comparison of rotational averages of Fourier power spectra of the 3D reconstructions with (red) and without (green) amplitude correction.

3. Discussion

The K2 Summit is the first commercially available direct electron detection camera optimized for counting primary electron events combined with centroiding to double the effective detector resolution. The basic principle of counting is similar to that used in super-resolution light microscopy methods such as PALM (as photo-activated localization microscopy) (Shroff et al., 2007) or STORM (Stochastic Reconstruction Microscopy) (Rust et al., 2006). While any camera with sufficient sensitivity can be used to count primary electrons, doing so in a practical manner requires both very high internal frame rates and very high-speed on-the-fly image analysis to process the large number of electron events in each image frame. The K2 Summit achieves this performance using a 50 MHz readout rate and a high degree of parallelism to achieve a frame rate of 400 frames/s, which is about the practical limit of the current technology. (In comparison, currently the DE-12 has a readout rate of 40 frames/s and the Falcon camera (FEI Company) has a 17 frames/s readout.) However even at the 400 frames/s rate, coincidence losses become non-trivial, resulting in a compromises between the competing demands of dose rate and exposure time.

In this study, we addressed practical questions of imaging tradeoffs by quantitatively evaluating camera performance as a function of dose rate without a specimen as well as using thin Pt/Ir films. Coincidence losses at different dose rates and their influence on images were characterized and theoretical models developed. Our data showed that the main effect of undercounting is a reduction in both noise and signal at low spatial frequency, which compensate each other and yield only modest reductions in SSNR and preservation of the otherwise high DQE of the camera at low spatial frequencies.

When we used this camera to image a ~700 kDa frozen hydrated protein complex, images showed sufficient contrast at 300 kV even when recorded at defocus values less than −1 μm. Furthermore, undercounting had little effect on signal beyond half of the physical Nyquist limit. The visible Thon rings calculated from our best images extend to nearly 3 Å (Fig. 5D), which is comparable to or better than the best images of icosahedral virus samples recorded on photographic film (Zhang et al., 2010). The good contrast also enabled us to record images at relatively low defocus values, which also helped to extend the Thon rings to high resolution. Together, our data suggest that the electron counting and centroiding is suitable for all high-resolution single particle cryoEM.

In a separate study, we determined a 3.3 Å resolution 3D reconstruction of archaeal 20S proteasome using the K2 counting mode and correction of beam-induced image blurring (Li et al., 2013). This result validated the use of a counting camera for high-resolution cryoEM reconstructions, effectively obviating the need to use film for near atomic resolution single particle cryoEM. Resolution of this 3D reconstruction was well beyond the half physical Nyquist limit of the camera. This is superior to any other scintillator based CCD camera and photographic film. Our previous best efforts at determining 3D reconstructions for this same protein sample had only achieved a resolution of ~5.6 Å by using photographic film (Rabl et al., 2008). Together with our established semi-automated data acquisition and GPU cluster (Li et al., 2010), we determined a ~4 Å 3D reconstruction of archaeal 20S proteasome in only 5 days (data not shown), demonstrating the rapidity at determining a near atomic resolution single particle cryoEM structure for a well behaved sample.

The electron dose rate limitation in counting mode impacts the way low-dose cryoEM images need to be collected. A low dose rate requires a weak electron beam, which can be achieved by reducing both the C2 aperture size and C1 spot size, as well as spreading the beam. Such a setting has the benefit of improving the spatial coherence of the beam, which is critical for achieving high-resolution (Glaeser et al., 2011). However, with a fixed total dose at the specimen, such as ~25 e⁻/Ų, and a preferred dose rate on camera of <10 e⁻/pixel/s, images recorded at a lower magnification require a much longer exposure time. In our tests, the lowest magnification we used was 20kX, corresponding to a physical pixel size 1.96 Å / pixel on camera, and an exposure time of 10 s. With a 0.2 s subframe accumulation time, each image stack contains 50 subframes. Even with such prolonged exposures, any potential influence of image blurring caused either by beam-induced motion or sample/stage instability can be eliminated by motion corrections, as has been demonstrated (Campbell et al., 2012; Li et al., 2013).

It was a surprise that coincidence loss has minimal influence on the SSNR (Fig. 4C). Thus, it is possible to fully recover the lost low-frequency amplitude and image contrast caused by coincidence loss. Because the dataset was collected at a relative low dose rate (~10 e⁻/pixel/s), which minimized influence of coincidence loss, low-frequency amplitude correction did not make a significant difference. However, it is likely that such a correction could improve the contrast significantly of images recorded with much higher dose rates, such as 20–30 e⁻/pixel/s, where the contrast loss is more significant and noticeable. The rational of using a higher dose rate, such as 30 e⁻/pixel/s, to record an image is to reduce the total exposure time and thus to reduce the total number of subframes within an image stack, improving resistance to mechanical drift and data collection throughput. Low frequency renormalization could thus be especially useful to minimize exposure times for data collected at lower magnifications. More thorough tests are necessary.

4. Materials and methods

4.1. Instrumentation and data acquisition

The Gatan K2 Summit™ camera (Gatan Inc., Pleasanton, CA) was installed on a FEI TF30 Polara electron microscope (FEI Company, Hillsborough, OR) equipped with a field emission electron source and operated at an accelerating voltage of 300 kV. The K2 camera has a size of 3840 × 3840 physical pixels. In super-resolution mode, the centroiding process divides 1 physical pixel into 4 super pixels. Newly acquired hardware and software gain and dark references were carefully prepared using Gatan Microscopy Suite (GMS) for each dose rate immediately before data acquisition. The pixel sizes at different magnifications were calibrated by using a contaminating hexagonal ice crystal, using the known hexagonal ice lattice at −185 °C. The measured image physical pixel sizes are 0.97 Å at 39kX, 1.22 Å at 31kX and 1.96 Å at 20kX. We used UCSFImage4 to control all data acquisition.

4.2. Imaging Pt/Ir film

A series of linear and super-resolution empty images and Pt/Ir images were acquired at 31kX nominal magnification with the same total dose of 30 e⁻/Ų at dose rates of 1, 2, 4, 8, 10, 13, 15 and 20 counts/pixel/s. The exposure times are calculated according to the coincident loss curve measured in a separate study (Li et al., 2013) to maintain the same total input number of electrons, which were varied from ~42 s at 1 counts/pixel/s to ~1.5 sec at 20 counts/pixel/s. Each pair of linear and super resolution Pt/Ir film images was taken from adjacent areas in order to avoid any potential difference in sample caused by radiation damage. All images were recorded with the same defocus of −0.92 μm. To compare the linear image with the corresponding counting image, the intensity of linear images was scaled to number of electrons by a calibrated factor of 30 counts/electron (Li et al., 2013). The power spectra and their rotational averages were normalized by dividing the total pixel value of the image. Linear image pixel counts were converted to number of electrons by the gain factors obtained above.

4.3. Cryo-specimen imaging

The T. acidophilum 20S proteasome was expressed and purified from Escherichia coli according to established protocols (Yu et al., 2010). A drop of 2 μL of purified 20S proteasome at a concentration of ~0.9 μM was applied to glow-discharged Quantifoil holey carbon grids (Quantifoil, Micro Tools GmbH, Germany), and plunge-frozen using a Vitrobot Mark III (FEI company, USA). Grids of frozen hydrated samples were imaged at dose rate of ~10 counts/pixel/s with total dose ~33 e⁻/Ų. Frozen hydrated 20S proteasomes were imaged at nominal magnifications of 31kX with an exposure time of 3.5 s. The defocus was in the range of 0.8–1.9 μm. CTFFIND3 (Mindell and Grigorieff, 2003) was used to determine the defocus values. The 3D reconstruction was calculated using the first 10,000 particles from a dataset of ~130,000 particles collected with the K2 Summit in counting mode and corrected for motion induced image blurring (Li et al., 2013). Calculation and refinement of the 3D reconstruction follows the same procedure (Li et al., 2013).

4.4. Simulation of counting images

A simple simulation of the counting processing of an ideal pixel camera was performed to reproduce and better understand the phenomenon observed in the experimental images. The centroid processing after counting was not considered in this simulation, whose influence is mostly outside of the physical Nyquist frequency. We used a Monte Carlo approach to simulate the formation of empty images (no specimen) under a uniform beam. The simulated camera has the size of 1024 × 1024 pixels, and processes 400 frames per “second” as the real K2 camera. The counting was done on each frame: (1) find the local maximum and set its adjacent pixels to 0; (2) set all these local maxima to 1 as one electron count. The number of “electrons” recorded in a frame is calculated by dividing the total dose on the 1024 × 1024 camera area at a given dose rate by 400 frames. The final image is the sum of all frames after counting processing. Then, the simulated input image and output images were subsequently processed as the experimental images mentioned above.

4.5. Using a binomial distribution model to describe coincidence loss

Assuming a simple model of throwing n independent electrons one by one into a camera with a total of m × m pixels, the probability of an electron falling into a small subarea s is p. The binomial distribution can be used to describe the probability mass function of k electrons falling into s as:

$$P_n\left(k\right)=C_n^k{p}^k{(1-p)}^{n-k}=\frac{n!}{(n-k)!k!}{p}^k{(1-p)}^{n-k}$$ (7)

Under the condition where n is sufficiently large and p sufficiently small, Eq. (7) is approximated by Poisson function:

$$\underset{n\to \infty ,p\to 0}{\lim }{P}_n\left(k\right)=\underset{n\to \infty ,p\to 0}{\lim }{C}_n^k{p}^k{(1-p)}^{n-k}=\frac{{\lambda }^k{e}^{-\lambda }}{k!},\text{where}\lambda =\mathit{np}$$ (8)

For an electron beam as a plane wave, an electron has equal probability of hitting any position in the illuminated area, or the entire camera. Therefore, the probability of an electron falling into a small area s of a total of m × m pixels is $p=\frac{s}{m\cdot m}$. For K2 Summit with ~4,000 × 4,000 pixels, p → 0. with a dose rate of D (e⁻/pixel/s) and a frame rate of F, which is 400 frames/s for the K2 Summit, the total number of electron is $n=\frac{(m\cdot m)}{F}\to \infty$, the probability of k electrons falling into an area of s is

$$p_n\left(k\right)=\frac{n!}{(n-k)!k!}{p}^k{(1-p)}^{n-k}=\frac{{\lambda }^k{e}^{-\lambda }}{k!}\text{and}\lambda =\mathit{np}=\frac{D\cdot s}{F}$$ (9)

The value of k indicates the number of electrons overlapping with an electron already inside the small area s. Therefore, k = 0 means no overlap and no coincident loss, where k > 0 means coincidence loss of k electrons.