Measuring the Orientation of Taurine in the Active Site of the Non-Heme Fe (II)/α-Ketoglutarate Dependent Taurine Hydroxylase (TauD) using Electron Spin Echo Envelope Modulation (ESEEM) Spectroscopy

Abstract

The position and orientation of taurine near the non-heme Fe(II) center of the α-ketoglutarate (α-KG) dependent taurine hydroxylase (TauD) was measured using Electron Spin Echo Envelope Modulation (ESEEM) spectroscopy. TauD solutions containing Fe(II), α-KG, and natural abundance taurine or specifically deuterated taurine were prepared anaerobically and treated with nitric oxide (NO) to make an S=3/2 {FeNO}⁷ complex that is suitable for robust analysis with EPR spectroscopy. Using ratios of ESEEM spectra collected for TauD samples having natural abundance taurine or deuterated taurine, ¹H and ¹⁴N modulations were filtered out of the spectra and interactions with specific deuterons on taurine could be studied separately. The Hamiltonian parameters used to calculate the amplitudes and line shapes of frequency spectra containing isolated deuterium ESEEM were obtained with global optimization algorithms. Additional statistical analysis was performed to validate the interpretation of the optimized parameters. The strongest ²H hyperfine coupling was to a deuteron on the C₁ position of taurine and was characterized by an effective dipolar distance of 3.90 ± 0.25 Å from the {FeNO}⁷ paramagnetic center. The principal axes of this C₁-²H hyperfine coupling and nuclear quadrupole interaction tensors were found to make angles of 26 ± 5° and 52 ± 17°, respectively, with the principal axis of the {FeNO}⁷ zero-field splitting tensor. These results are discussed within the context of the orientation of substrate taurine prior to the initiation of hydrogen abstraction.

1. INTRODUCTION

Taurine hydroxylase (TauD) catalyzes the conversion of taurine and α-ketoglutarate (α-KG) to aminoacetaldehyde, carbon dioxide, and succinate while liberating sulfite to be used as a sulfur source in Escherichia coli.¹ TauD is considered the archetype enzyme for the class of non-heme Fe(II)/α-KG-dependent dioxygenases. Enzymes in this group rely on the proper coordination of α-KG and positioning of their primary substrate near a non-heme mononuclear Fe(II) center for reaction with molecular oxygen.^2–4 Members of this enzyme class catalyze a diverse set of reactions involved in antibiotic and small molecule synthesis, biodegradation, oxygen sensing, DNA repair, and epigenetic regulation. However, key steps in each mechanism are believed to be generally conserved.^{2, 5–6} A comprehensive review of TauD emphasizes its significant contributions to understanding the structure-function relationships for this class of enzyme.⁷

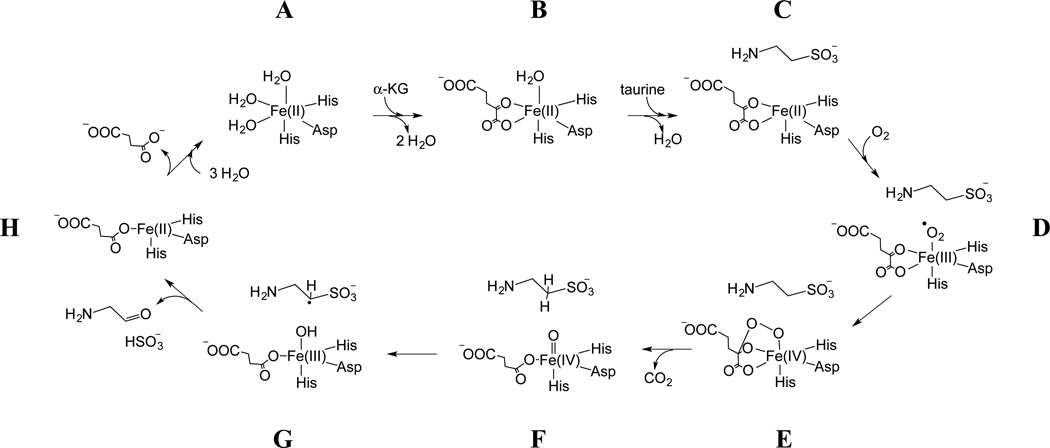
This mechanism involves the bi-dentate coordination of α-KG to Fe(II) displacing two water ligands (A–B). Taurine then binds to the active site resulting in the displacement of the apical H₂O and formation of a 5-coordinate Fe(II) center (B–C). O₂ binds to the open coordination site on Fe(II) yielding an Fe(III)-superoxo species (D). Subsequent oxidative decarboxylation of α-KG leads to formation of a Fe(IV)=O intermediate (D–F) that triggers hydroxylation of the C₁ carbon of taurine via hydrogen atom abstraction and radical rebound chemistry (F–H). The hydroxylated taurine spontaneously decomposes to sulfite and aminoacetaldehyde.

Mechanistic studies of TauD that address the energetics of the widely accepted hydrogen abstraction reaction pathway are supported by limited structural information. While detailed electronic structure analyses,^8–15 both theoretical (DFT) and experimental (EXAFS, Mössbauer, CD/MCD), have supplied a wealth of justification for the hydrogen abstraction, these studies predominately focus on the Fe center and directly coordinated ligands. One theoretical study addressed the importance of the orientation of the C-H bond of the “target” substrate with respect to the reactive Fe(IV)=O intermediate prior to hydrogen abstraction by including an analysis of frontier molecular orbital interactions.¹⁶ A clear energetic preference for an “optimal” orientation of the substrate was identified. To date, the cited structural support for these studies consists primarily of crystal structures for anaerobic TauD holoprotein in the presence of α-KG and taurine.^17–18 These structures only reveal the five coordinate geometry expected for species C in Scheme 1. With the highest resolution of these structures being 2.5 Å, the placement of a small molecule such as taurine, especially in the proper orientation, is subject to considerable error.¹⁹ Being that the structures are void of O₂ or a suitable surrogate, a relevant picture for visualizing species D or F in Scheme 1 is not available.

Scheme 1.

illustrates a widely cited catalytic mechanism for the enzyme.

To support further analyses of the mechanism, structural studies should address these intermediates whose structures are pivotal in dictating the type of reaction that would be energetically favorable. In an attempt to address this need, we have used an approach pioneered by Lipscomb and coworkers for EPR studies of non-heme Fe enzymes where NO is used as an O₂ surrogate to transform the integer-spin Fe(II) at the active site into an S=3/2, {FeNO}⁷ species that is amenable to EPR spectroscopy.^20–21 In addition to making the paramagnetic center half-integer spin, the Fe-N(O) bond also defines the principal axis of the zero-field splitting tensor allowing ligand hyperfine couplings gained from ESEEM and/or ENDOR experiments to be related to the molecular axes and by translation, the axis along which the Fe(IV)=O intermediate forms.^22–23 In an initial study, we used orientation-selective ²H-electron spin echo envelope modulation (ESEEM) spectroscopy to measure weak hyperfine couplings between the {FeNO}⁷ center and taurine, isotopically-substituted with deuterium at the C₁ and C₂ positions.²⁴ The data were analyzed by manual simulation of ²H-ESEEM spectra collected at four magnetic field positions, two in the g = 4 region of the spectrum and two at higher field near g = 2. Simulations that accounted for the general trends observed in deuterium modulation amplitudes and lineshapes were reported and structural parameters were extracted from the resulting spin Hamiltonian parameters. Briefly, the ²H-ESEEM was found to originate from one deuteron bound to each taurine carbon with the stronger coupling originating from the C₁ deuteron and characterized by an effective dipole-dipole distance of 3.4 Å and an orientation of the principal axis of the hyperfine tensor with respect to the principal axis of the zero field splitting (ZFS) tensor of 20°. A weaker coupling was detected for a deuteron bound to C₂ showing a dipolar distance of 4.5 Å and a tensor orientation angle of 63°. Manual positioning of the NO within the open coordination position of Fe(II), as it was reported in the PDB:1OS7 crystal structure,¹⁷ allowed us to account for both the effective dipole-dipole distances and the tensor orientations.²⁴

There are several problems with a manual analysis of ESEEM data such as the one described above. For the specific case at hand, each ²H-coupling is described minimally by five spin Hamiltonian parameters. A manual analysis of the data provides no information regarding the quality of a fit that can be used to determine the parameter set that best accounts for the data. Also, for an orientation selective study, the data collected at different field positions across the EPR spectrum are not treated in parallel with a quantifiable weighting. Over the past few years, Warncke and coworkers have implemented a global optimization strategy for the analysis of ESEEM data and have reported on several benefits of this approach: (1) it provides the most efficient way to find the best solution when fitting data sets with a spin Hamiltonian model that can have up to eleven adjustable parameters; (2) because the χ² surfaces for these calculations are fraught with false minima, it provides a means to identify them and ultimately find the best solution; (3) it provides for a statistical analysis of the measured parameters which helps to determine their significance when interpreted in the context of molecular structure.²⁵ Taken together, these characteristics should allow one to utilize the structural data available from magnetic coupling parameters to their full extent. For the task at hand, determination of ²H-hyperfine and nuclear quadrupole couplings and their orientations relative the magnetic axis system defined by the Fe-N(O) bond will allow us to infer the geometry of the intermediate depicted as “F” in Scheme 1. In principle, the precision with which structural information can be derived from magnetic resonance experiments exceeds that of X-ray crystallography, but the analysis must begin with an optimized set of spin Hamiltonian parameters and an evaluation of their standard deviations.

The work presented here is the application of a further developed method for directly measuring the position and orientation of taurine in the TauD active site using EPR that includes full analysis of ²H-ESEEM amplitudes and line shapes, statistical support for the numerical conclusions made from the data, and comparison of the conclusions with cited quantum mechanical treatments of the {FeNO}⁷ complex for placement of the NO ligand.^{22–23, 26} With this, structure-function relationships can now be addressed in more detail and the results can lend experimental support to theoretical descriptions of the mechanism. A model of the crystal structure PDB: 1GY9¹⁷ for TauD in which NO was positioned based on the previously reported quantum mechanical optimizations of the {FeNO}⁷ complex of TauD is used for comparison with the spectroscopic measurements. Agreement between the data presented here and the widely accepted structural aspects of the TauD active site suggests the potential of these electron paramagnetic resonance (EPR) techniques for characterization of other less well understood enzymes in this family.

2. EXPERIMENTAL METHODS

Sample preparation

The chemicals used in sample preparation were purchased from Sigma-Aldrich. The taurine deuterated at both the C₁ and C₂ positions was purchased from C/D/N Isotopes. The C₁ deuterated taurine was provided by J.C. Price and J. M. Bollinger and prepared as previously described.²⁷ TauD protein was expressed and purified as previously described.²⁸ Anaerobic preparation of the EPR samples was accomplished by suspending TauD apoprotein in degassed 20 mM Tris buffer at pH 8.0 that was treated with degassed solutions of Fe(II), taurine, and α-KG such that the final concentrations were: 1.5 mM TauD, 1.5 mM Fe(II), 6.0 mM taurine and 6.0 mM α-KG. The solutions were then treated with NO by filling the headspace of the sealed sample vial with NO gas and lightly swirling the solution. When the sample changed to a yellow color, the solution was quickly transferred anaerobically to an EPR tube with a syringe and frozen in liquid nitrogen. Additional samples were prepared in an identical fashion but were either treated with C₁-deuterated or perdeuterated taurine in place of natural abundance taurine.

CW EPR experiments

Continuous wave (CW) EPR spectra were collected on a Bruker ESP300E X-Band EPR spectrometer operating at 9.47 GHz. A model 4102ST probe was used and the sample temperature was maintained at 4 K using an Oxford Instruments ESR-900 liquid helium flow system. Helium flow was adjusted manually to maintain constant temperature. All EPR spectra were collected over a 300 mT range centered at 250 mT, with a modulation amplitude of 1 mT, a modulation frequency of 100 KHz, and a microwave power of ~1 mW. Spectra were averaged as necessary and fit using the “esfit” function in the EasySpin software package^29–30 to determine the spin Hamiltonian parameters.

ESEEM experiments

ESEEM spectra were collected using a Bruker E680 X-band spectrometer with a model ER4118-MD-X-5-W1 probe and a 5 mm dielectric resonator. An Oxford instruments model ITC-503 temperature controller and CF-935 liquid helium flow system was used to maintain a constant temperature of 4 K during ESEEM measurements. Data were collected using a three pulse stimulated echo sequence that consisted of three 16 ns (full width half-maximum) π/2 microwave pulses as follows (π/2 − τ − π/2 − T − π/2). The echo amplitude was recorded as a function of T while τ was held to values <200 ns because of short phase memory times. Data sets consisted of 512 points and were collected with a four step phase cycling procedure: (+,+,+), (−,+,+), (+,−,+), and (−,−,+) to remove unwanted echoes and baseline offsets.^31–32 Time-domain ESEEM data were baseline corrected, treated with a Hamming window, zero filled to 1024 points, and cosine Fourier transformed to observe the frequency spectrum. Data sets were collected every 20 mT starting with 170 mT and ending at 330 mT.

Deuterium ESEEM

Identical ESEEM experiments were carried out on samples made with natural abundance taurine, C₁-deuterated taurine, and taurine deuterated at the C₁ and C₂ positions (perdeuterated). A ratio procedure³³ was used to filter out unwanted ¹H and ¹⁴N modulations. To isolate the ²H ESEEM of the C₁-deuteron, time domain ESEEM data collected for the TauD sample treated with C₁-²H-taurine were normalized and divided by corresponding data collected for the sample treated with ¹H-taurine. To isolate the ²H ESEEM of the C₂ deuteron, time domain ESEEM data collected for the TauD sample treated with taurine deuterated at the C₁ and C₂ positions were divided by corresponding data collected for the samples treated with C₁-²H-taurine. To isolate the ²H-ESEEM of the C₁ and C₂ deuterons together, time domain ESEEM data collected for the TauD sample treated with taurine deuterated at the C₁ and C₂ positions were divided by corresponding data collected for the sample treated with natural abundance taurine. The ratio ESEEM data were baseline corrected, treated with a Hamming window, zero filled to 1024 points, and cosine Fourier transformed to observe the frequencies arising from the ²H couplings. Because the 3-pulse ESEEM function is the sum of product terms for the two coherence transfer pathways that lead to formation of the stimulated echo,³⁴ this procedure is approximate and can give rise to cross-terms that appear as peaks in the FFT if the modulations are deep.³⁵ For the studies presented here, we found that the quotient deuterium spectra in the g = 2 region were free from such distortions, but that spectra in the g = 4 region, where deeper, overlapping modulations from coupled ¹⁴N and ¹H were observed, often contained spurious peaks. To alleviate problems with these spurious peaks, τ-values corresponding to the period of the first or second harmonic of the proton Larmor frequency were used for data acquisition. The resulting uncertainty in ²H-ESEEM amplitudes was considered in our analysis and will be discussed below.

Fitting ESEEM data

The ESEEM spectra obtained from the ratios were dominated by a peak centered at the deuterium Larmor frequency. The data points that made up the peak were isolated and compared to their corresponding points in simulated spectra. The simulated spectra were calculated with the EasySpin software package^29–30 running in MATLAB. The Hamiltonian model used to simulate the spectra has the form,

$$Ĥ=D({Ŝ}_z^2+S(S+1)/3)+E({Ŝ}_x^2-{Ŝ}_y^2)+g\beta \mathrm{H̅}•Ŝ+Ŝ•A\text{'}•Î+ΕQ"•Î$$ (1)

where the spin system was modeled as an S=3/2 system with large ZFS (D=10 cm⁻¹) that is axially symmetric. The parameter “E” in Eqn 1 is used to describe the deviation of the ZFS from axial symmetry; in this case set to zero. The tensors describing the hyperfine (A) and nuclear quadrupole (Q) interactions were defined in their principal axis systems as,

$$A=\left(\begin{array}{ccc}\hfill a_{\mathit{\text{iso}}}-T(1-\rho )\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill a_{\mathit{\text{iso}}}-T(1+\rho )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill a_{\mathit{\text{iso}}}+2T\hfill \end{array}\right)$$ (2)

and,

$$Q=\frac{e^{2}qQ}{4h}\left(\begin{array}{ccc}\hfill -(1-\eta )\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -(1+\eta )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 2\hfill \end{array}\right)$$ (3)

Because taurine is not directly bound to the {FeNO}⁷ complex, the isotropic hyperfine coupling (a_iso in Eqn. 2) was set to zero and the hyperfine coupling tensor was assumed axial. The parameter “ρ” in Eqn 2. describes the deviation of the dipolar coupling from axial symmetry; in this case set to zero. The electrons that cause the electric field gradient at the ²H nucleus are shared in a single bond with carbon meaning the quadrupole tensor could also be considered axial. The parameter “η” in Eqn 3 describes the deviation of the quadrupole interaction from axial symmetry and was set to zero. The hyperfine and quadrupole tensors were related to the principal axes of the ZFS using ‘zyz’ Eulerian rotation matrices dependent on three angles (α, β, and γ). The five parameters that were considered variable when simulating the spectra were the effective dipolar distance to a single deuteron bound to taurine (r_eff) calculated from T using the point dipole-dipole approximation where,

$$T=\frac{g_e{\beta }_e{g}_n{\beta }_n}{h{r}_{\mathit{\text{eff}}}^3}$$ (4)

the β Euler angle that relates the principal axis of the hyperfine tensor to the principal axis of the ZFS (βHF), the quadrupole coupling constant (e²qQ/h), the β angle that relates the principal axis of the quadrupole tensor to the principal axis of the ZFS (βNQI), and the γ angle that orients the principal axis of the quadrupole tensor relative to an axis defined by the plane containing the Fe, N, and ²H (γNQI). Because the ZFS, hyperfine coupling, and nuclear quadrupole tensors are axial, the simulations were not sensitive to the αHF and αNQI Euler angles or the γHF angle that would orient the hyperfine tensor in the xy plane.

The time domain data and simulated time domain ESEEM traces were processed in an identical fashion using native MATLAB routines. The differences between the experimentally obtained ²H-ESEEM line shapes and the simulated line shapes were analyzed for quality of fit by calculating a χ² value for each sample where,

$${\chi }^2=\sum _{i=1}^N\sum _{j=f\text{min}}^{f\text{max}}\frac{{(y_{ij}^{\mathit{\text{calc}}}-y_{ij}^{\text{exp}})}^2}{{\sigma }_i^2}.$$ (5)

The sums of eqn. 5 are taken over “i” spectra collected at “N” different magnetic field positions and across the ²H-ESEEM lineshape at each field position for “j” frequency “bins” indexed from “fmin” to “fmax.” Typically, our analysis considered 4 – 6 ESEEM spectra collected at different field positions across the EPR spectrum. The indices for lineshape comparisons were determined from the individual spectra by selecting a span of 8 – 12 points that encompassed the ²H-ESEEM response. During the optimizations, the data points considered for each spectrum were weighted uniformly with a standard deviation, σ_i, that was estimated from the noise level observed in the 5–10 MHz range. Quotient spectra plagued by spurious peaks were either eliminated from consideration or weighted with larger standard deviations. Optimization of the simulated spectra was achieved with routines native to MATLAB that used fitting algorithms to iteratively vary specific Hamiltonian parameters while calculating the spectra and a χ² for comparison to the data until χ² was at a minimum. Various algorithms were used including Nelder/Mead simplex³⁶, genetic algorithm³⁷, and simulated annealing³⁸ to fit up to six spectra in parallel. In many cases, calculating χ² while varying multiple parameters allows for more than one local minimum to exist. The global minimum can be most successfully found with a global optimization algorithm that uses a heuristic search method. In this study simulated annealing was used. This algorithm allows for the successive polling of new parameter sets that may more closely resemble previous parameter sets that were less successful as opposed to rejection of any less successful parameter set. The probability (P_i) that any parameter set (i) is accepted as the starting parameter set in successive generations of the optimization is given by:

$$P_i=\frac{1}{1+\text{exp}\left(\frac{\mathrm{\Delta }}{T_i}\right)}$$ (6)

The current temperature parameter (T_i) is calculated using:

$$T_i=\frac{T_0}{\text{log}(K_i)}$$ (7)

Where T₀ is the temperature parameter from the previous iteration, K_i is the annealing parameter (usually the iteration number) and Δ is:

$$\mathrm{\Delta }={\chi }_i^2-{\chi }_{\mathit{\text{Best}}}^2$$ (8)

This means that even a “less fit” parameter set has a non-zero probability of being accepted for the basis of the next generation of test parameter sets. As the iteration number increases and the temperature parameter decreases the probability of accepting a “less fit” parameter set decreases. In this way simulated annealing can avoid being stuck in a potentially false local minimum at the beginning of the optimization and explore different minima that may include the global minimum. As the optimization proceeds, it is less likely that the algorithm will leave the current minimum.

Due to orientation selection in the individual ESEEM spectra³⁹ the fits that resulted in the best reproduction of the entire data set were obtained by fitting multiple spectra in parallel that spanned the EPR spectrum. Further statistical analysis was performed once the “best” set of parameters was obtained from the optimizations in order to estimate the standard deviation (σ) in each parameter. Because the parameters are covariant, σ was calculated from a covariance matrix. First, a Jacobian matrix (J_{m x n}) can be constructed consisting of m rows corresponding to the number of data points being compared in the calculation of χ² and n columns corresponding to the number of parameters being varied:

$$J_{m\times n}=\left(\begin{array}{ccc}\hfill \frac{\partial f(y_1)}{\partial p_1}\hfill & \hfill \dots \hfill & \hfill \frac{\partial f(y_1)}{\partial p_n}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \frac{\partial f(y_m)}{\partial p_1}\hfill & \hfill \dots \hfill & \hfill \frac{\partial f(y_m)}{\partial p_n}\hfill \end{array}\right)$$ (9)

where f is the function used to calculate χ² and p_n are the individual parameters that were varied in the optimization. Each y_m is a point in the data set that is being compared to the corresponding point in the simulation. Each term in the Jacobian matrix is defined as,

$$\frac{\partial f(y_m)}{\partial p_n}=\frac{{(f(p_n+d{x}_n)-f_{\mathit{\text{best}}})}_m+{(f(p_n-d{x}_n)-f_{\mathit{\text{best}}})}_m}{2d{x}_n}$$ (10)

The covariance matrix can be calculated from the Jacobian matrix by taking the inverse of the product of the Jacobian (J_{m x n}) with its transpose (J^T_{m x n}) and multiplying by the χ² for the parameter set being evaluated (χ²_best) divided by the difference between the number of data points (m) and the number of variable parameters (n):

$$\mathit{\text{Cov}}=\frac{{\chi }_{\mathit{\text{best}}}^2}{m-n}{(J_{m\times n}^T*J_{m\times n})}^{-1}$$ (11)

After solving for the eigenvalues of the covariance matrix, the standard deviations (σ_n) in each Hamiltonian parameter are the square roots of the corresponding diagonal terms. The 95% confidence interval for each Hamiltonian parameter p_n is defined as the range from 2σ_n below to 2σ_n above the “best” value.

Modeling the TauD {FeNO}⁷ complex with Avogadro

The crystal structure used for comparison was the 2.5 Å resolution 1GY9 structure.¹⁷ The 1GY9 structure was modified to include a bound NO using the Avogadro software package.⁴⁰ A visual model of the NO and taurine positions was generated by adding a bound NO to the Fe(II) center of the 1GY9 crystal structure and, while holding the position of the surrounding protein and Fe(II) center constant, the positions of taurine and NO were geometry optimized using the Unified Force Field option in the “Auto Optimize” tool. The optimization is an approximation meant to provide a visual aid for comparison with ESEEM data. The model is dependent on the assumption that the crystal structure was more accurate in modeling the protein side chains and Fe(II) center than it was in defining the position of taurine. This assumption was made on the grounds of similarity between multiple crystal structures for TauD and with other high resolution crystal structures for members of this enzyme family.^{17–18, 41} The validity of the model is based on agreement with previously reported quantum mechanical optimizations of identical non-heme Fe(II) centers that included a bound NO molecule.^{22–23, 26}

3. RESULTS

CW EPR

The CW EPR spectra for TauD samples are characteristic of the S=3/2 {FeNO}⁷ complex^{22, 24, 42} having large axially symmetric ZFS (E/D=0) that shows peaks at principal effective g values (g_eff) of g┴ =4 and g‖=2. The spectra were identical for each of the three TauD samples. Each spectrum overlaid with its simulation is provided in the supporting information (Figure S1). Previous studies have described the electron spin coupling between the Fe and NO as antiferromagnetic coupling of a S=5/2 Fe³⁺ to a S=1 NO⁻.²² The unpaired spin is contained in Fe d orbitals (d_xy, d_x²–y², and d_z²) and exchange interactions between the NO π* orbitals and the Fe d_xz and d_yz orbitals constitutes a bond between Fe and NO that has partial covalent nature.²⁶ The magnitude of the ZFS in {FeNO}⁷ model complexes and TauD has been estimated at ~10–20 cm⁻¹ in multiple studies.^{22–23, 26} Because this magnitude is much larger than the energy of the X-band CW EPR experiment (~0.3 cm⁻¹), the ZFS defines the principal magnetic axes of the spin system and other terms in the spin Hamiltonian are referenced to it.

Deuterium ESEEM

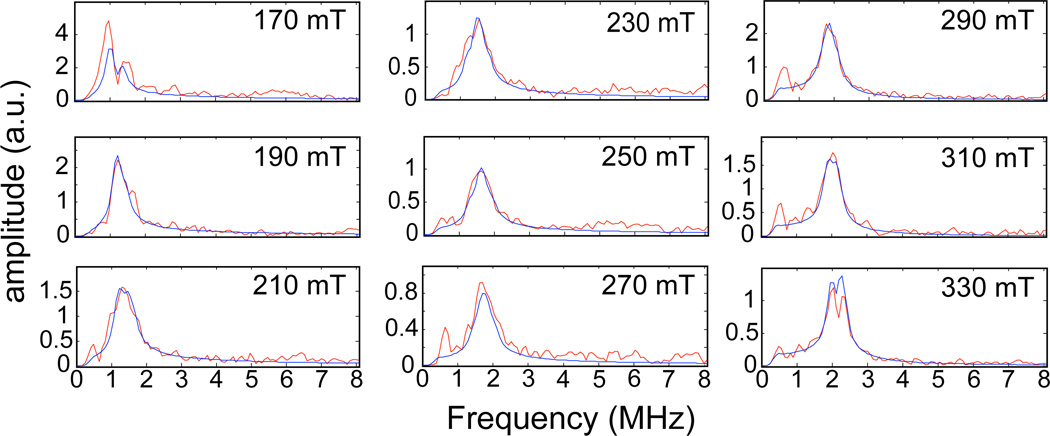
Three pulse ESEEM spectra were collected at 20 mT intervals across the EPR spectrum ranging from 170 mT to 330 mT. The spectra contained ¹⁴N and ¹H modulations from through-bond or through-space couplings to magnetic nuclei on coordinated ligands, substrate taurine, and any moieties in the distance range accessible by the ESEEM experiment; less than ~6–8 Å from the {FeNO}⁷ center.⁴³ The Fourier transform (FT) spectra contained broad overlapping lines that complicated analysis of any single coupling. These spectra were not analyzed, but examples are provided in the supporting information (Figure S2). Figure 1 shows the ²H ESEEM spectra that result from dividing the 3 pulse ESEEM data collected for TauD samples treated with α-KG and C₁-²H-taurine by corresponding data derived from TauD samples prepared with α-KG and ¹H-taurine. Peaks from the ²H at the C₁ carbon of taurine are clearly resolved at each of the 9 field positions (red traces) displayed in the figure. The data are overlaid with simulated spectra (blue).

Figure 1.

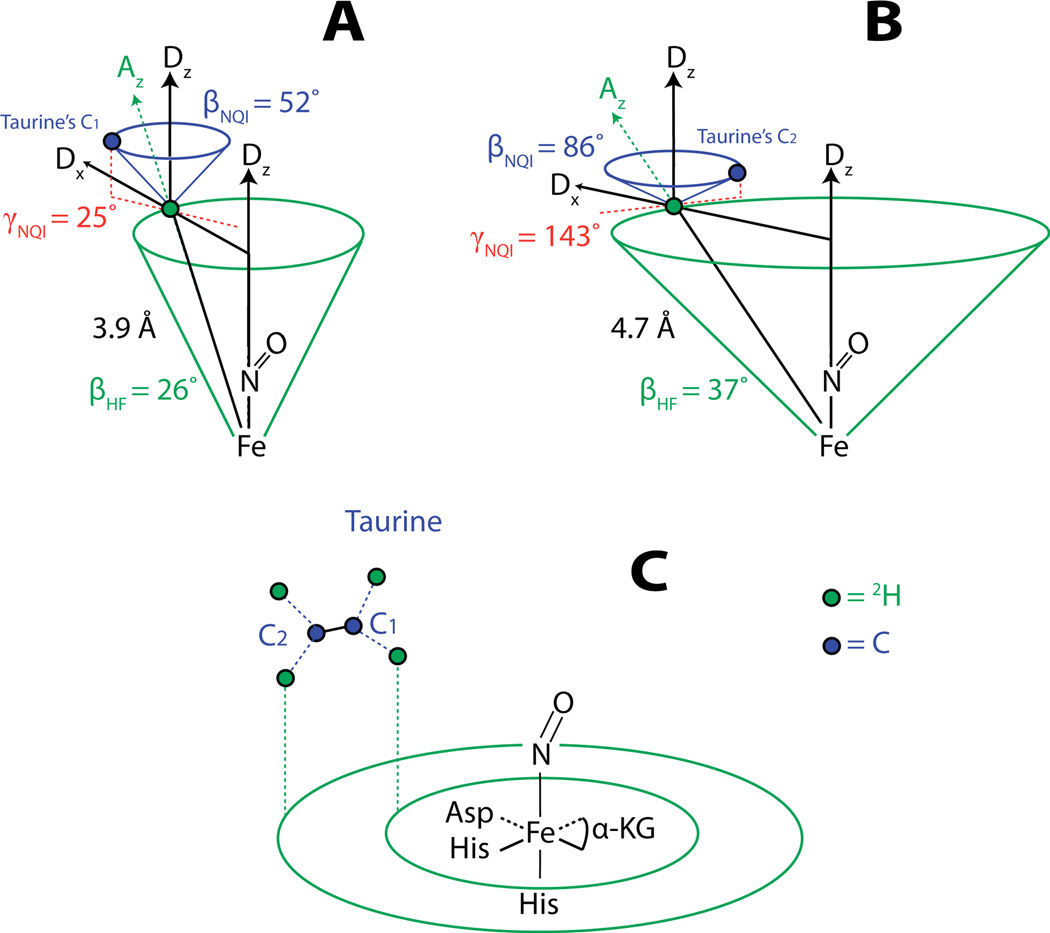
The magnetic field dependence of the FT ESEEM spectra obtained by dividing time domain ESEEM collected for the TauD samples treated with α-KG and C₁-²H-taurine by identical data for the TauD samples treated with α-KG and ¹H-taurine. Each plot is labeled with the field position at which the data were collected. The Hamiltonian parameters used to calculate the (blue) lines were: hyperfine coupling values of −0.21, −0.21, and 0.42 MHz; Euler angles for the hyperfine tensor of 0°, 26°, and 0°; e²qQ/h = 0.22 MHz and η=0; Euler angles for the nuclear quadrupole tensor of 0°, 52°, and 25°.

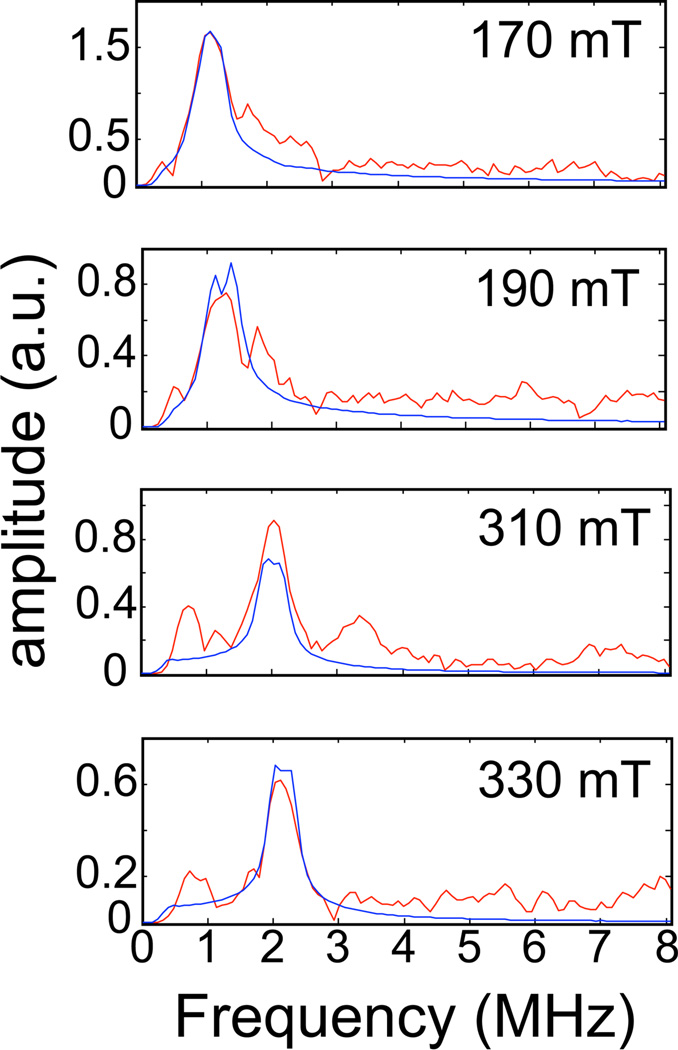
In Figure 1, the spectrum at 170 mT (near g┴) showed splitting of the ²H feature that was not observed again until 330 mT (near g‖). The remaining spectra are broadened, but not split. Additional low frequency (< 1 MHz) peaks are observed, particularly in the spectra collected at 210, 270, 290 and 310 mT, and are presumed to be artifacts of the ratio procedure that were not removed with the baseline correction. These artifacts are owed to incomplete suppression of ¹⁴N modulations by the ratio procedure. The undivided data show significant overlap of multiple, broadened, frequency lines in this spectral region. Examples of these spectra can be viewed in the supporting information (Figure S2). Figure 2 shows the ²H ESEEM spectra that result from dividing the 3 pulse ESEEM data collected for TauD samples treated with α-KG and perdeuterated taurine by corresponding data derived from TauD samples prepared with α-KG and C₁-²H-taurine. Peaks from the ²H at the C₂ carbon of taurine (red traces in the figure) are clearly resolved at only 4 of the 9 field positions studied.

Figure 2.

The magnetic field dependence of the ESEEM spectra obtained by dividing time domain ESEEM collected for the TauD samples treated with α-KG and perdeuterated taurine by identical data for the TauD samples treated with α-KG and C₁-²H-taurine. Each plot is labeled with the field position at which the data were collected. The Hamiltonian parameters used to calculate the (blue) lines were: hyperfine coupling values of −0.12, −0.12, and 0.24 MHz; Euler angles for the hyperfine tensor of 0°, 37°, and 0°; e²qQ/h = 0.22 MHz and η=0; Euler angles for the nuclear quadrupole tensor of 0°, 86°, and 143°.

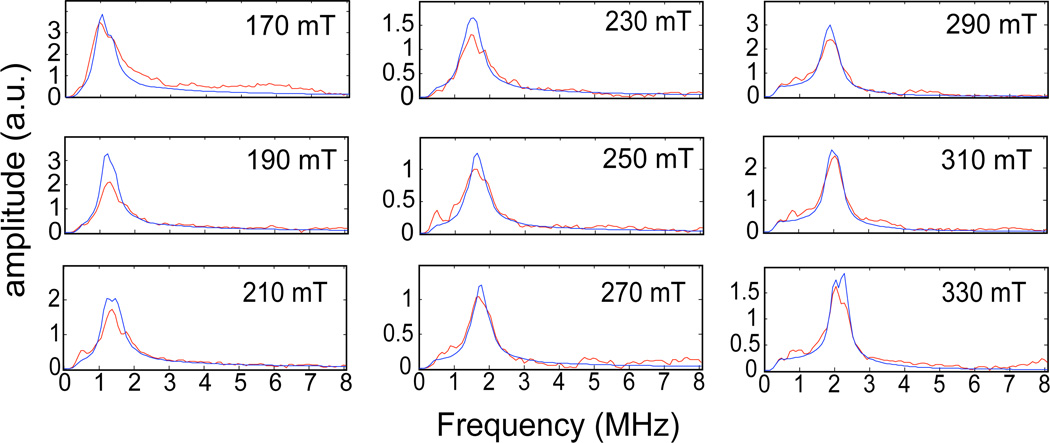
These spectra showed a considerably smaller signal to noise ratio. The spurious peaks in the low frequency region (< 1 MHz) are subject to the same interpretation as above. They appear more prominent in these spectra because the peaks due to the ²H-ESEEM are lower in amplitude, presumably due to weaker dipolar coupling to the closest C₂-²H. Regardless, the spectra collected at 170, 190, 310, and 330 mT showed resolved peaks centered at the ²H Larmor frequency that could be analyzed. Peaks at the deuterium Larmor frequency in the omitted spectra were matched or exceeded by the spurious peaks and were assumed to be unreliable as additions to the data set. The amplitude profile as a function of field position observed for both data sets shows reduced amplitudes for the deuterium peaks in the spectra collected in the intermediate field region (210–270 mT). These amplitude reductions are a consequence of orientation selection due, in part, to the nature (distance and orientation) of the coupling to the ²H nucleus, and the use of shorter τ-values for the purpose of maintaining matrix proton suppression at the first harmonic of the proton Larmor frequency as the field strength is increased. The enhancement of amplitude observed at 290 mT stems from switching the τ-value needed for proton suppression from the first to the second harmonic of the proton Larmor frequency. Figure 3 shows the ²H ESEEM spectra that result from dividing the 3-pulse ESEEM data collected for TauD samples treated with α-KG and perdeuterated taurine by corresponding data derived from TauD samples prepared with α-KG and natural abundance taurine. Peaks from the deuterons at the C₁ and C₂ carbons of taurine are clearly resolved at each of the 9 field positions (red traces) displayed in the figure.

Figure 3.

The magnetic field dependence of the ESEEM spectra obtained by dividing time domain ESEEM collected for the TauD samples treated with α-KG and perdeuterated taurine by identical data for the TauD samples treated with α-KG and natural abundance taurine. Each plot is labeled with the field position at which the data were collected. The Hamiltonian model used to calculate the simulated spectra (blue) included coupling with two deuterons. The Hamiltonian parameters used in the simulation are provided in the captions for Figures 1 and 2.

These spectra were similar to the spectra obtained for the C₁-²H alone but lacked any line splitting. The amplitudes and widths of the lines at the ²H Larmor frequency were generally enhanced by the additional coupling to the C₂ ²H, but were dominated by the coupling with the C₁ ²H. The spurious peaks in the low frequency region (< 1 MHz) are subject to the same interpretation given above.

Analysis

Five parameters were considered variable in the ESEEM simulations: r_eff, the effective dipole-dipole distance used to calculate the dipolar coupling; βHF, the Euler angle describing the orientation of the r_eff vector with respect to the z-axis of the ZFS tensor (the g_eff = 2.0 axis); e²qQ/h, the nuclear quadrupole coupling constant; βNQI and γNQI, the Eulerian angles discussed above. These five Hamiltonian parameters were varied by a global optimization routine in MATLAB with the goal of minimizing the χ² value calculated from parallel consideration of ²H ESEEM spectra collected at six field positions across the EPR spectrum. Table 1 lists the “best” set of Hamiltonian parameters for describing the ²H ESEEM spectra in Figure 1 where the modulations from the coupling with the proximal ²H at the C₁ position on taurine were isolated. The simulations that resulted from these parameters are shown as blue traces in Figure 1 along with the data (red traces).

Table 1.

Spin Hamiltonian Parameters for the C₁-²H Coupling

Hamiltonian parameters	“best” value	95% Conf. Interval
r (Å)	3.86	3.65–4.14
βHF (°)	26.4	21.3–31.4
e2qQ/h (MHz)	0.22	0.09–0.35
βNQI (°)	51.6	34.6–68.6
γNQI (°)	25.4	−26.3–77.1

The amplitudes and line shapes of the ²H-ESEEM spectra arising from C₁ deuterated taurine were best modeled considering a single ²H at an effective dipolar distance (r_eff) of 3.9 Å from the spin center and oriented at a βHF angle of 26° with respect to the principal axis of the ZFS. The quadrupole coupling strength (e²qQ/h) of 0.22 MHz was consistent with previously reported values^{42, 46} and the principal axis of the NQI tensor was oriented at a βNQI angle of 52° with respect to the principal axis of the ZFS and displaced by a γNQI angle of 25° from a plane defined by the z-axes of the ZFS and hyperfine tensors (depicted in Figure 5A & B). The simulations were least sensitive to the ²H nuclear quadrupole interaction parameters. These parameters mostly affect the shapes of the ²H-ESEEM peaks as a function of magnetic field strength and are more prone to distortions resulting from the ratio procedure than the peak amplitudes. The large confidence intervals for the Euler angles that describe the orientation of the nuclear quadrupole interaction principal axes reflect this uncertainty. The deuterium hyperfine parameters, r_eff and βHF, showed more modest confidence intervals of ± 0.2 Å and ± 5°, respectively, as they are largely determined by the amplitudes of the ESEEM peaks as a function of magnetic field strength.

Figure 5.

A) An illustration of the cones containing the C₁ carbon of taurine and its bound ²H that is observed with ESEEM. B) An illustration of the cones containing the C₂ carbon of taurine and its bound ²H that is observed with ESEEM. C) A drawing of the proposed orientation of the C₁–C₂ unit of taurine near the {FeNO}⁷ complex based on the ESEEM results.

Table 2 lists the “best” set of parameters for describing the ²H ESEEM spectra in Figure 2 where coupling with a ²H at the C₂ position on taurine was isolated. This set was also chosen from a list of parameter sets generated by the simulated annealing algorithm that gave similar χ² values. The parameters in Table 2 were used to simulate the spectra that are shown as the blue traces in Figure 2.

Table 2.

Spin Hamiltonian Parameters for the C₂-²H Coupling

Hamiltonian parameters	“best” value	95% Conf. Interval
r (Å)	4.66	4.4–4.99
βHF (°)	37.2	24.8–49.7
e2qQ/h (MHz)	0.22	−0.11–0.56
βNQI (°)	85.9	43.4–168.5
γNQI (°)	143.2	48.7–235.0

The amplitudes of the ESEEM frequencies in the 4 spectra were best modeled as arising from dipolar coupling with a single ²H at an effective dipolar distance of 4.7 Å and oriented at a βHF angle of 37° with respect to the principal axis of the ZFS. The quadrupole coupling strength (e²qQ/h) of 0.22 MHz was again consistent with previously reported values. The quadrupole tensor was oriented at a βNQI angle of 86° with respect to the principal axis of the ZFS and displaced from the ‘xz’ plane of the hyperfine tensor by a γNQI angle of 143°. Confidence intervals for the five variables used in the fitting procedure follow the same trend as discussed above for the coupled C₁ deuteron.

The spectra in Figure 3 were simulated using a Hamiltonian model that accounts for couplings with two deuterons: a single ²H on the C₁ carbon of taurine with the effective dipolar distance and Euler angles described in Table 1, and a single ²H on the C₂ carbon of taurine with the effective distance and Euler angles described in Table 2. While the simulations indicated that the spectra were dominated by the coupling with the C₁ ²H, the amplitudes of the ESEEM frequencies were most closely reproduced by accounting for the additional coupling with the C₂ ²H. Calculating confidence intervals for the parameters using this data set returned similar intervals for the parameters describing the C₁ ²H coupling that were obtained using the data set in Figure 1. Reasonable confidence intervals for the parameters describing the C₂ ²H coupling could not be obtained from this data set. Considering the minimal contribution to the spectra from the C₂ ²H, the change in χ² for calculation of the terms in the Jacobian matrix was unaffected by changing the C₂ ²H parameters.

Modeling the TauD {FeNO}⁷ complex with Avogadro

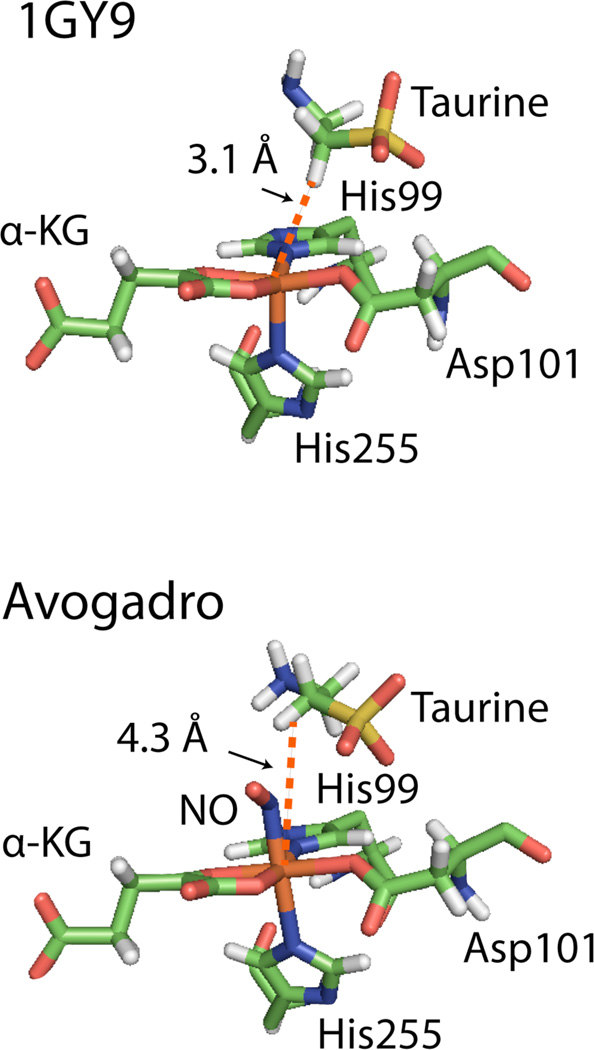
Figure 4 shows the model of the 1GY9 crystal structure¹⁷ generated using Avogadro.⁴⁰

Figure 4.

A rendition of the TauD active site predicted by the 1GY9 crystal structure¹⁷ compared with the modeled version. The 1GY9 crystal structure was loaded into Avogadro, the surrounding protein and Fe center were fixed, a NO molecule was placed into the open coordination site, and the orientations of taurine and NO were determined with the “Auto Optimize” tool using the Unified Force Field approximation.⁴⁰

The 1GY9 crystal structure predicted a distance of 3.1 Å from the Fe center to the C₁ ¹H on taurine. Using Avogadro, an NO molecule was modeled into the 1GY9 structure in the open coordination site and, with the protein and Fe center fixed, the positions and orientations of taurine and NO were geometry optimized using the Unified Force Field approximation. While the orientation of taurine was not significantly modified the distance between the Fe center and the closest C₁ ¹H on taurine was increased to 4.3 Å. The predicted bond lengths for the Fe-N bond, N=O bond and the Fe-N(O) bond angle were 1.98 Å, 1.19 Å, and a 122° respectively. These values compare well with previously reported values for TauD Fe-NO complexes²⁶ as well as FeEDTA-NO complexes²² such that the model can be considered an acceptable representation of the direction of the Fe-N(O) bond in the complex.

4. DISCUSSION

The CW EPR spectra for the TauD samples were consistent with previous descriptions of the spin center²⁴ and the theoretical model of the electronic structure.^{22, 26} The characteristic spectrum having effective principal g values of g‖= 2 and g┴ = 4 can be shown to arise from the M_S=±1/2 Kramers doublet of the S=3/2 {FeNO}⁷ complex by using an axial ZFS model with an isotropic electronic Zeeman term in a quantum mechanical description. The currently accepted electronic structure model of this {FeNO}⁷ complex in TauD was derived from studies by the Solomon group²² and has since been corroborated by additional theoretical and experimental investigations of TauD and other {FeNO}⁷ model complexes.^{23, 26} The electronic structure pictures the Fe d_xy, d_x²–y², and d_z² orbitals as containing the unpaired spins that give rise to the S=3/2 spin state. This localizes the unpaired spin density near the Fe center. Although a small degree of delocalization over the Fe-N(O) bond is suggested, assuming a point dipole at the Fe center greatly simplifies the analysis and may introduce only minor errors in the effective distances derived from our ESEEM results. The generally accepted view for the binding of NO to Fe is that antiferromagnetic exchange interactions between the unpaired electrons of NO π* orbitals with those of the d_yz, d_xz orbitals on the Fe orient the principal axis of the ZFS such that it is nearly coincident with the Fe-N(O) bond.^{22–23, 26} With the ESEEM measurements being in reference to the principal axis of the ZFS, the orientation of the taurine predicted by the ESEEM results can be put directly into the context of the structural model for TauD using the Fe-N(O) bond. The axial CW EPR spectra (E/D=0) support the placement of NO in the open coordination site trans to His255, as previously predicted in theoretical descriptions of the {FeNO}⁷ complex²⁶ and suggested by structural studies that place the open coordination site of the 5 coordinate Fe(II) in the same position.^17–18

This structural context can be used to relate the ESEEM measurements to the {FeNO}⁷ complex via the Fe-N(O) bond. Because the hyperfine coupling is also axial, our data are not sensitive to γHF and as such, the coupled ²H nuclei can only be constrained to the base of cones that make an angle (βHF) with the Fe-N(O) bond and have a side length of r_eff, the effective dipolar distance determined from the hyperfine coupling strength (T). The principal axis of the nuclear quadrupole interaction is coincident with the C-²H bond axis for the coupled ²H. The Euler angles βNQI and γNQI orient the bond relative to an ‘xz’ plane of the hyperfine tensor as defined by the positions of the Fe-N-²H atoms. Constructing a second cone about a z’ axis parallel to the principal axis of the ZFS with an apical angle of βNQI and then defining γNQI relative to the ‘xz’ plane of the hyperfine interaction, a direction for the ²H-C bond can be located. The ESEEM results for the C₁ ²H of taurine are best described by a cone with side length 3.9 Å that makes an angle of 26° with respect to the Fe-N(O) bond (Figure 5A).

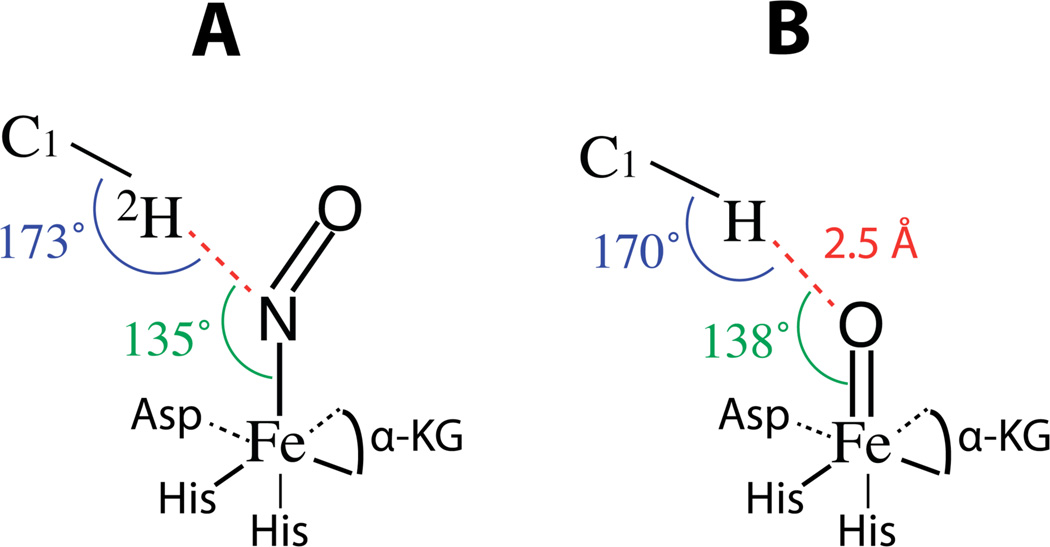
The ²H-C₁ bond makes an angle of 52° with respect to the Fe-N(O) bond and is oriented 25° from the ‘xz’ plane, similar to what was predicted in the crystal structure.¹⁷ The ESEEM results for the C₂ ²H predict a cone containing the C₂ ²H having a side length of 4.7 Å and making an angle of 37° to the Fe-N(O) bond. From this information alone and the assumption of a staggered geometry of the taurine molecule with bond angles between the distal and proximal deuterons consistent with sp³ hybridized carbon (109.5°), the orientation of the C₁–C₂ bond of the taurine molecule in the active site can be inferred (Figure 5C). The Euler angles βNQI=86° and γNQI=143° from the ESEEM results for the ²H-C₂ bond are consistent with this picture. Not only is this orientation of taurine consistent with the 1GY9 crystal structure as well as the Avogadro derived model of 1GY9 (Figure 4), but it is also intuitive in the context of the mechanism. To translate the ESEEM measurements made in reference to the Fe-N(O) bond of the {FeNO}⁷ complex to mechanistic arguments in the functioning enzyme it must first be assumed that Fe-N(O) is, in fact, a proper mimic of Fe-O(O) in species D in Scheme 1 or Fe=O in species F. In a study by Ye et al., the lowest energy position of NO binding in the TauD {FeNO}⁷ complex was derived from DFT calculations.²⁶ Their conclusion was that the placement of NO directly opposite His255, the same position represented in our model generated with Avogadro, was the minimum energy position. Because multiple detailed studies involving the reactive Fe(IV)=O complex place the Fe=O bond in the same position,^8–16 our measurements made with ESEEM on {FeNO}⁷ complexes can be translated to the analysis of Fe(IV)=O reactivity with C-H bonds. Importantly, the structural support we contribute is derived from experimentally determined magnetic couplings between the paramagnetic {FeNO}⁷ center and the hydrogen atom involved in the reaction as opposed to being inferred from crystallographic models. Theoretical descriptions of the hydrogen abstraction reaction suggest an optimal angle of ~120° between the Fe(IV)=O bond and the substrate hydrogen to be abstracted and a linear arrangement of (taurine)C₁ - H - O(Fe) to promote the chemistry.¹⁶ Figure 6 illustrates these two angles (A) derived from our ESEEM results for the Fe-N(O) bond related to the C₁-²H bond and (B) when translated into a picture of the Fe(IV)=O species related to the C₁-H bond.

Figure 6.

A) The geometric relationship between the C₁-²H bond of substrate taurine and the {FeNO}⁷ paramagnetic center at the active site of TauD as derived from the magnetic couplings presented in Table 1. Angles of 135° for the relationship of the N-²H vector to the Fe-N(O) bond and 173° for C₁ - ²H - N are in close agreement with optimal angles proposed for hydrogen abstraction of ~120° and ~180° respectively. For B, the Fe-N bond is considered a suitable mimic of the Fe(IV)=O bond in the functioning enzyme and the Fe-N bond distance of 1.76 Å is replaced with a Fe=O bond distance of 1.64 Å. The H-O-Fe and C-H-O angles are shifted to 138° and 170° respectively, as a result of the shorter Fe-O bond length. An O-H distance of 2.5 Å would be consistent with an early stage resting state of species F in Scheme 1 preceding the approach by the substrate.

If one uses the Fe-²H dipolar distance of 3.9 Å and βHF of 26° from the ESEEM results and a typical Fe-N bond distance of ~1.76 Å,¹⁶ the N-²H vector makes an angle of ~135° with respect to the Fe-N bond. When translated to the Fe(IV)=O species, assuming that the Fe-N bond is a good mimic of the orientation of the Fe=O bond, and using an Fe=O bond length of 1.64 Å,⁴⁵ the same angle is ~138°. The C₁-²H bond makes an angle of ~173° with the N-²H vector and, when translated, the C₁-H-O angle would be 170°. These angles are in close agreement with the optimal angles of ~120° and ~180° predicted in theoretical evaluations of the hydrogen abstraction reaction. With regards to the predicted O-H distance of ~2.5 Å in Figure 6 B, this represents an early stage resting state of species F in Scheme 1. Theoretical studies that address the transition from species F to the Fe-OH complex (transition from F to G in Scheme 1) propose that, as the substrate approaches, the Fe(IV)=O and C-H bonds are elongated bringing the O-H distance within range for the hydrogen atom abstraction to be energetically allowed.^{13, 16} While our measurements can not provide experimental evidence for transition states, an O-H distance of 2.5 Å places the C₁-H bond of taurine within range for unhindered approach and initiation of this proposed reaction pathway. These results not only support the theoretical predictions,^{13, 16} but lend support to the assumption that Fe-NO is a close mimic of Fe-O₂ or Fe=O for spectroscopic studies.

With the staggered geometry of the C₁–C₂ unit of taurine, it is not surprising that interaction with only a single deuteron at the C₁ and C₂ carbons on taurine is observed in the ESEEM. Based on generally accepted C-H bond distances of ~ 1 Å and H-C-H angles consistent with sp³ hybridized carbon, the distal deuterons at the C₁ and C₂ carbons would be ~1.6 Å further from the Fe-NO than the proximal deuterons. ESEEM amplitudes decay as a function of ~1/r⁶ for dipolar-coupled nuclei⁴⁶ meaning that the weak interaction arising from distal deuterons would give rise to negligible amplitude contributions to the ESEEM. The greater distance to the C₂ ²H supports the staggered geometry about the C₁–C₂ bond of taurine and the obvious notion that the C₂-²H bond is not in proximity or the proper orientation for reaction with the Fe(IV)=O intermediate. These conclusions are intuitive in the context of the mechanism considering that stereospecificity and position selectivity are key aspects of reactions catalyzed by this class of enzymes^2–6 and that only the target ¹H should be in proximity to the Fe(IV)=O intermediate in the functioning enzyme.

5. CONCLUSIONS

The results presented here represent a more detailed use of ESEEM for measuring the position of small molecules in the active site of non-heme Fe enzymes. The statistical fitting procedure was able to consistently select parameter sets in the same general range. The grouping of similar parameter sets with similar χ² values suggest the values are reasonably close to a global minimum. Although the weak dependence of the ESEEM simulations on the Euler angles that provide information on the orientations of the C-²H bonds lessened statistical support for these parameters, the optimization algorithm was able to find a mutual set of angles that predicted taurine’s orientation in general agreement with the Avogadro-derived model from the 1GY9 crystal structure¹⁷ as well as with structural models derived from detailed quantum mechanical treatments of Fe(IV)=O complexes and their chemistry.^{13, 16} This highlights the strength of the global optimization analysis used in this work over the manual fitting approach used previously. In the previous work, the effective dipolar distance reported for the C₁-²H of taurine was 0.5 Å shorter than that derived from the present work and 0.9 Å less than the distance predicted by the Avogadro-derived model. Furthermore, the orientation determined for the principal axis of the hyperfine coupling tensor for the C₂-²H with respect to the Fe-N(O) bond was almost 30° larger than that determined in the present work.²⁴ These findings are well outside experimental error and when taken together, they would predict a different orientation for the taurine molecule with respect to the magnetic axes.