Multiscale multiphysics and multidomain models—Flexibility and rigidity

Abstract

The emerging complexity of large macromolecules has led to challenges in their full scale theoretical description and computer simulation. Multiscale multiphysics and multidomain models have been introduced to reduce the number of degrees of freedom while maintaining modeling accuracy and achieving computational efficiency. A total energy functional is constructed to put energies for polar and nonpolar solvation, chemical potential, fluid flow, molecular mechanics, and elastic dynamics on an equal footing. The variational principle is utilized to derive coupled governing equations for the above mentioned multiphysical descriptions. Among these governing equations is the Poisson-Boltzmann equation which describes continuum electrostatics with atomic charges. The present work introduces the theory of continuum elasticity with atomic rigidity (CEWAR). The essence of CEWAR is to formulate the shear modulus as a continuous function of atomic rigidity. As a result, the dynamics complexity of a macromolecular system is separated from its static complexity so that the more time-consuming dynamics is handled with continuum elasticity theory, while the less time-consuming static analysis is pursued with atomic approaches. We propose a simple method, flexibility-rigidity index (FRI), to analyze macromolecular flexibility and rigidity in atomic detail. The construction of FRI relies on the fundamental assumption that protein functions, such as flexibility, rigidity, and energy, are entirely determined by the structure of the protein and its environment, although the structure is in turn determined by all the interactions. As such, the FRI measures the topological connectivity of protein atoms or residues and characterizes the geometric compactness of the protein structure. As a consequence, the FRI does not resort to the interaction Hamiltonian and bypasses matrix diagonalization, which underpins most other flexibility analysis methods. FRI's computational complexity is of $\mathcal{O}\left(N^2\right)$ at most, where N is the number of atoms or residues, in contrast to $\mathcal{O}\left(N^3\right)$ for Hamiltonian based methods. We demonstrate that the proposed FRI gives rise to accurate prediction of protein B-Factor for a set of 263 proteins. We show that a parameter free FRI is able to achieve about 95% accuracy of the parameter optimized FRI. An interpolation algorithm is developed to construct continuous atomic flexibility functions for visualization and use with CEWAR.

INTRODUCTION

Proteins have a diverse range of structures and functions. The understanding of protein structure, function, and dynamics has grown rapidly in the past few decades. The conventional dogma of sequence-structure-function² has been seriously challenged by the discovery that many intrinsically disordered proteins can also be functional.^{18, 41, 50, 65} The study of disordered proteins is of essential importance due to their connections to sporadic neurodegenerative diseases, such as mad cow disease, Alzheimer's disease, and Parkinson's disease.^{18, 59} Disordered proteins are traditionally assumed to be highly flexible. However, a frequently neglected fact is that well-folded proteins are flexible as well. Folded proteins experience everlasting intrinsic motions due to possible Brownian dynamics, rapid local motions of amino acid side chains, and spontaneous collective fluctuations. Therefore, flexibility, i.e., the ability to deform from the current conformation under external forces, is an intrinsic property of all proteins.

One of the major challenges in the biological sciences is the prediction of protein functions from protein structures. One key to protein function prediction is the protein flexibility which strongly correlates with enzymatic activity in proteins, such as allosteric transition, ligand binding and catalysis, as well as the stiffness and rigidity which is crucial to structural proteins. For instance, in enzymatic processes, protein flexibility enhances protein-protein interactions, which in turn reduce the activation energy barrier. Additionally, protein flexibility and motion amplify the probability of barrier crossing in enzymatic reactions. Therefore, the investigation of protein flexibility at a variety of energy spectra and time scales is vital to the understanding and prediction of protein functions. Currently, the most important technique for protein flexibility analysis is X-ray crystallography. Among the almost 100 000 structures in the protein data bank (PDB), more than 80% are collected by X-ray crystallography. The Debye-Waller factor, or B-factor, can be directly computed from X-ray diffraction or other diffraction data. Although atomic B-factors are directly associated with atomic flexibility, they can be influenced by the variations in atomic diffractive cross sections and chemical stability during the diffraction data collection. Therefore, only the B-factors for specific types of atoms, say C_α, can be directly interpreted as their relative flexibility without corrections. Another important method for accessing protein flexibility is nuclear magnetic resonance (NMR) which often provides structural flexibility information under physiological conditions. NMR spectroscopy allows the characterization of protein flexibility in diverse spatial dimensions and a large range of time scales. About 6% of structures in the PDB are determined by electron microscopy (EM) which does not directly offer the flexibility information at present.

In addition to experimental technologies, theoretical approaches play essential roles in biomolecular flexibility analysis and prediction. For example, molecular dynamics (MD) simulations have dramatically expanded our understanding of the conformational landscapes of proteins, particularly conformations that are not directly accessible via other techniques, i.e., protofibrils, amyloid-like fibrils, amyloids, intrinsically disordered proteins, and partially disordered proteins. However, the dynamics of large proteins typically occurs at time scales that are intractable to MD simulations. Alternative approaches have also been developed in the past few decades, including normal mode analysis (NMA),^{8, 25, 36, 55} elastic network model (ENM),⁵⁸ Gaussian network model (GNM),^{5, 6, 22} and anisotropic network model (ANM).⁴ In fact, these methods can be regarded as time-independent molecular mechanics (MM) and are connected to MD methods via the time-harmonic approximation.⁴⁴ Protein flexibility and B-factors can be approximated respectively from the first few eigenvectors and eigenvalues of the connection matrix. Such low-energy eigenvalues reflect the long-time behavior of the protein dynamics beyond the reach of MD simulations.^{6, 8, 36, 55, 58} These approaches have been improved in many aspects including crystal periodicity corrections^{28, 34, 35, 54} and density-cluster rotational-translational blocking.²⁰ These methods are relatively inexpensive particularly in their coarse-grained settings. Their computational complexity is typically dominated by that of the diagonalization of the Hamiltonian matrix, i.e., $\mathcal{O}\left(N^k\right)$, where N is the matrix dimension and k ≈ 3. These approaches give rise to quantitative predictions of biomolecular flexibility and their applications are discussed in many review papers.^{19, 38, 53, 68} However, for the structures of excessively large protein complexes which are typically obtained via cryo-EM, more efficient methods are required to analyze their flexibility. Although often called elastic models or elasticity analysis in the literature, the aforementioned methods are still microscopic in origin, and are fundamentally different from the stress and strain analysis of a truly continuum elasticity theory.

Recently, knowledge based methods, such as neural networks,⁴⁷ support vector regression,⁶⁹ and two-stage support vector regression,⁴³ have also been developed for flexibility analysis. These approaches typically utilize large protein data sets as input training data. Computational accuracy, reliability, and complexity of these methods depend on the training data set. Jacobs et al.³¹ have utilized techniques from graph theory to analyze the bond networks in proteins. Their approach employs both geometric and energetic criteria to identify the flexible and rigid regions.

Another class of approaches for biomolecular flexibility analysis utilizes phenomenological theories and/or continuum mechanics. Linear and nonlinear elasticity models have been proposed for excessively large biomolecules, such as membranes, molecular motors, microtubules, and protein complexes.^{32, 51} One of phenomenological approaches is the Willmore flow energy functional⁶⁶ which is in terms of the square of the difference between two principle curvatures. This model intends to minimize the deviation of a membrane surface from the local sphericity. As a generalization of the Willmore energy functional, Canham¹⁰ and independently, Helfrich,²⁷ proposed an elasticity model for cellular membranes. The free energy functional of membrane bending consists of the Gaussian curvature of the membrane surface and the square of the difference between the mean curvature and the spontaneous curvature of the membrane. The minimization of the Helfrich energy functional leads to the equilibrium shape of the membrane.⁴² According to the Gauss-Bonnet theorem, the Gaussian curvature in the free energy functional will contribute to an unphysical jump in the free energy whenever there is a topology change in the membrane morphology. Computationally, phase field models can be used to simulate membrane curvature formation and evolution.²¹ In the past decade, membrane curvature has been a popular research topic partially due to the fact that except for the curvature, there is very little other quantitative information associated with membranes and membrane protein/DNA interactions. Indeed, protein membrane interaction³⁹ and membrane curvature sensing have received much attention.^{3, 26, 45} So far, both theoretical modeling and numerical simulation in the field have been mostly phenomenological and qualitative,⁹ partially due to the lack of more quantitative experimental data. Another class of models directly utilizes continuum elasticity for biomolecular flexibility analysis. Recently, Zhou et al.⁷³ have proposed an elasticity model which allows the electrostatic force of biomolecules to influence membrane stress.

The other class of theoretical methods for flexibility analysis has been developed via multiscale formulations. These methods combine elastic mechanics and molecular mechanics to significantly reduce the number of degrees of freedom of large biomolecular systems.⁹ For example, the classical theory of elasticity for DNA loops is combined with the MD description of protein for protein-DNA interaction complexes.⁶⁰ Recently, the continuum elastic modeling of the Canham-Helfrich type of energy functional has been coupled with MD simulations to investigate the complex elastic behavior of Hepatitis B virus capsids.⁴⁹ Multiscale based flexibility analysis has a wide range of technical variability. In the best scenario, multiscale methods can take the advantage of each scale to achieve excellent modeling accuracy and computational efficiency. However, multiscale methods are typically technically demanding and computationally complex. A major issue in the field is how to go beyond the phenomenological domain and make these approaches quantitative and predictive. Consistency analysis and validation with experimental data are indispensable procedures. There is a need to further develop and validate innovative approaches for the flexibility analysis of biomolecular systems.

Recently, we have introduced a new class of multiscale models, differential geometry based multiscale approaches, for biological and chemical systems.^{62, 63, 64} The essential idea is to use the differential geometry theory of surfaces and the geometric measure theory as a natural means to separate the solvent domain from the macromolecular domains. A number of physical phenomena, including polar and nonpolar solvation, molecular dynamics, quantum mechanics, fluid dynamics, electrokinetics, electrohydrodynamics, electrophoresis, and elastic dynamics are considered in our multiscale models via a total energy functional and a variational strategy. By using the Euler-Lagrange variation, the self-consistently coupled Laplace-Beltrami equation and Poisson-Boltzmann equation is obtained for solvation analysis. For charge and mass transport, additional generalized Poisson-Nernst-Planck equations and/or Navier-Stokes equations are incorporated. Multiscale (implicit solvent) MM is utilized to allow local conformational changes and elastic dynamics is considered for excessively large chemical and biological systems. Step by step, our differential geometry based multiscale models have been carefully validated in the past few years.^{11, 12, 14, 15, 16, 17, 64} The first series of validations was done for multiscale solvation models.^{14, 15, 16, 17, 29, 57, 72} The Eulerian formulation,¹⁴ Lagrangian formulation,¹⁵ and quantum formulation are constructed¹⁶ for the solvation analysis of hundreds of small and large molecules, including nonpolar ones.¹⁷ The quantum formulation is able to considerably improve model accuracy. The robustness of our differential geometry based solvation approaches comes from a significant reduction in the number of free parameters that users must “fit” or adjust in applications to real-world systems.^{57, 70} In fact, our differential geometry based nonpolar model offers some of the best predictions of nonpolar solvation energies for a large number of compounds.¹⁷

Another series of validations was done on charge transport in realistic ion channels.^{64, 71} Continuum descriptions are applied to the solvent domain while channel proteins are treated in molecular detail. In our energy functional, nonpolar energy, polar (electrostatic) energy, chemical potential, and possibly fluid energy are considered on an equal footing. Non-electrostatic van der Waals (VDW) interactions among all the ions, and between ions and proteins, including size (steric) effects are accounted for in our treatment.⁶⁴ In this multiscale paradigm, the non-equilibrium multiscale transport theory reduces to the multiscale solvation model at equilibrium. Very good agreements between our model predictions and experimental measurements have been attained.⁶⁴

The other series of validations of our multiscale models was on the proton transport through membrane proteins.^{11, 12} Proton transport plays an important role in the molecular mechanism of biological energy transduction, sensory systems, and reproduction of influenza A viruses.¹³ Due to the small mass and size of protons, proton permeation across membrane proteins involves significant quantum effects.^{40, 46} However, the quantum mechanical treatment of all individual protons can be computationally expensive. A new density functional theory based on the Boltzmann statistics rather than the Fermi-Dirac statistics has been developed to describe proton dynamics quantum mechanically while implicitly treating numerous solvent molecules as a dielectric continuum. To account for the gating effect, membrane proteins are described in atomistic detail. Densities of all other ions in the solvent are approximated by using the Boltzmann distributions, which were introduced in our earlier work⁷¹ and have been independently confirmed by using Monte Carlo simulations.³³ Excellent predictions of experimental current-voltage curves have been observed.^{11, 12} Currently, the Poisson-Boltzmann model, or the Poisson model when there is no salt, has been proved to be a successful continuum model for biomolecular electrostatics at the quantitative level.^{1, 7, 24, 52} One of main reasons for its success is the continuum modeling which avoids the time consuming molecular dynamics description. While another reason for its success is the atomic detailed static charge description—the atomic point charges or charge distributions. In contrast, elasticity models are qualitative and phenomenological at moment. It is believed that elasticity analysis would play a much more important role in quantitative modeling and computation of biomolecular flexibility had atomic rigidity information been appropriately incorporated.

The objective of the present work is to develop differential geometry based multiscale, multiphysics, and multidomain models for biomolecular flexibility analysis. A major focus is to develop the theoretical model of continuum elasticity with atomic rigidity (CEWAR). Indeed, in our previous formulations, flexibility, rigidity, and elasticity have not been analyzed in detail, partially because of the fact that it is often more important and highly necessary to treat the macromolecular domain with atomistic descriptions. However, this situation has changed since the introduction of a multidomain formalism,⁶³ which allows a biomolecular complex to be divided into multiple domains and simultaneously treated by multiple physics descriptions. As a result, it is advantageous to include elastic dynamics in certain domains. In our elastic treatment of biomolecular complexes, proteins are assumed to have atomic rigidity or shear modulus. Therefore, a robust method for the extraction of protein atomic flexibility and rigidity information is required. Due to dynamical nature of the CEWAR, the atomic flexibility and rigidity information needs to be extracted in a most efficient manner for both equilibrium and non-equilibrium structures. The present work presents one of the most efficient methods, called flexibility-rigidity index (FRI), for protein B-factor prediction and flexibility analysis. The basic assumption underlying the FRI is that protein functions are entirely determined by the structure of the protein complex. The FRI provides an accurate measure of geometric compactness and topological connectivity of a protein structure at each atom or residue. Physically, the FRI reflects the local interaction strength. As such, it gives rise to accurate prediction of protein B-factors. The proposed FRI method does not require a stringently minimized structure, harmonic assumption, interaction potential, or matrix decomposition, nor does it involve any training procedure as that used in the knowledge based approaches. Its computational complexity is at most of order $\mathcal{O}\left(N^2\right)$.

The rest of this paper is organized as follows. A multiscale, multiphysics, and multidomain model that involves elastic dynamics, electrostatic interactions, molecular mechanics, and chemical potential effects is presented in Sec. 2 to facilitate the discussion on flexibility and rigidity. Equations for the elastic dynamics, elastostatics, and elastic vibration of macromolecular complexes are introduced. In particular, we show how the microscopic analysis of flexibility and rigidity is utilized in the macroscopic analysis of elasticity. A new model for protein flexibility evaluation is introduced in Sec. 3. We first define a diagonal-free correlation matrix to analyze the topological connectivity between protein atoms. Additionally, atomic flexibility and rigidity indices of each protein atom are deduced from the correlation matrix. Molecular rigidity index and averaged molecular rigidity index are proposed. The protein B-factors are directly associated with atomic flexibility indices which give rise to a practical method for B-factor prediction. Finally, a volumetric atomic rigidity function is constructed from the atomic rigidity index. A similar definition is also proposed for the flexibility. In Sec. 4, extensive numerical tests are carried out to validate the proposed method for protein flexibility analysis and B-factor prediction. Careful comparison with experimental data justifies our new approach. The proposed theory and formulation also offer new approaches for the visualization of biomolecular rigidity and flexibility. This paper ends with concluding remarks.

ELASTICITY IN MULTISCALE-MULTIPHYSICS-MULTIDOMAIN MODELING

We consider a multiscale, multiphysics, and multidomain model for biomolecular complexes in solvent where one domain is described by the continuum mechanics of elasticity. Some parts of the biomolecular system are described by using the molecular mechanics. The solvent consists of various charged species and water. Fluid mechanics is used to describe possible fluid motion of the solvent. Electrostatic interactions are considered in the whole computational domain. We first provide a simplified description of the action functional, followed by the derivation of governing equations. Special attention is given to elastic analysis.

The action functionals

Elastic energies

Experimental measurements indicate that protein, DNA, and other biomolecular systems exhibit elasticity, i.e., they are able to deform under prescribed external forces and restore to their original states when the external forces are no longer applied. The amount of deformation under a given external force is determined by internal forces that oppose the deformation. The resistance to the internal force or the stiffness is measured by various elastic moduli, such as Young's modulus, the bulk modulus, and the shear modulus in elasticity theory. For a protein or biomolecule, the internal force or resistance is not uniform and is position dependent. Certain parts of the protein are highly flexible while other parts are highly rigid, as indicated by the variation in protein B-factors.

To analyze the elasticity of arbitrarily shaped biomolecules, we consider the displacement w of a point r to its new position $\overline{\mathbf{r}}$ in ${\mathbb{R}}^3$

$$\mathbf{w}=\overline{\mathbf{r}}-\mathbf{r}.$$ (1)

The difference between the squares of infinitesimal changes is

$$d{\overline{\mathbf{r}}}^2-d{\mathbf{r}}^2=2{\sigma }_{ij}d{\mathbf{w}}_{i}d{\mathbf{w}}_j,$$ (2)

where the Einstein summation notation is used to simplify tensorial quantities and σ_ij is the strain tensor

$$\begin{array}{c}\hfill {\sigma }_{ij}=\frac{1}{2}\left[\left(\frac{\partial {\mathbf{w}}_i}{\partial {\mathbf{r}}_j}+\frac{\partial {\mathbf{w}}_j}{\partial {\mathbf{r}}_i}\right)+\frac{\partial {\mathbf{w}}_k}{\partial {\mathbf{r}}_i}\frac{\partial {\mathbf{w}}_k}{\partial {\mathbf{r}}_j}\right].\end{array}$$ (3)

The strain tensor describes the change of a point between before and after the elastic deformation. For relatively small deformations, one omits the term that is nonlinear in w and obtains a linear strain tensor

$$\begin{array}{c}\hfill {\sigma }_{ij}=\frac{1}{2}\left[\frac{\partial {\mathbf{w}}_i}{\partial {\mathbf{r}}_j}+\frac{\partial {\mathbf{w}}_j}{\partial {\mathbf{r}}_i}\right].\end{array}$$ (4)

Obviously, the linear strain has computational advantages.

We denote the elastic potential energy density in the Einstein notation as

$$\begin{array}{c}\hfill \frac{1}{2}\left[{\lambda }_E{\sigma }_{ii}^2+{\mu }_E{\left({\sigma }_{ij}\right)}^2\right],\end{array}$$ (5)

where λ_E is the lame parameter, describing the compressibility of the elastic macromolecule, and μ_E is the shear modulus, or rigidity, describing the stiffness of the elastic macromolecule under external force. In the present work, an atomistic description of μ_E = μ_E(r) will be provided.

The kinetic energy density of the elastic system is given by $\frac{{\rho }_E}{2}{\dot{\mathbf{w}}}^2,$ where ρ_E is the mass density of the elastic macromolecule and $\dot{\mathbf{w}}=\frac{d\mathbf{w}}{dt}$ denotes the velocity of the displacement. In general, the difference between the kinetic energy density and potential energy density gives rise to the Lagrangian, a functional for variational derivation of governing equations.

Action functional of a multiscale multiphysics and multidomain model

Let us label the continuum solvent, molecular mechanics, and elasticity descriptions, respectively, by S, M, and E so that S_I (I = S, M, and E) are the characteristic functions of the solvent, molecular, and elastic domains. Similarly, p_I, γ_I, ε_I, and ϱ_I are, respectively, pressures, surface tensions, dielectric constants, and charge densities associated with I = S, M, and E. The total action functional of our multiscale multiphysics and multidomain model is given by Ref. 63:

$$\begin{array}{ccc}& & G_{\mathrm{total}}^{\mathrm{MD}-\mathrm{FD}-\mathrm{ED}}\hfill \\ & & =\int \int \int \left\{{\gamma }_M|\nabla S_M|+{\gamma }_E\left|\nabla S_E\right|+p_M{S}_M+p_E{S}_E+S_S{U}^S\right.\hfill \\ & & +S_M\left[-\frac{{\epsilon }_M}{2}{\left|\nabla \Phi \right|}^2+\Phi {\varrho }_M\right]+S_E\left[-\frac{{\epsilon }_E}{2}{\left|\nabla \Phi \right|}^2+\Phi {\varrho }_E\right]\hfill \\ & & +S_S\left[-\frac{{\epsilon }_S}{2}{\left|\nabla \Phi \right|}^2+\Phi \sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha }\right]\hfill \\ & & +S_S\sum _{\alpha }\left[k_{B}T{\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-k_{B}T\left({\rho }_{\alpha }-{\rho }_{\alpha 0}\right)-{\mu }_{\alpha 0}{\rho }_{\alpha }\right]\hfill \\ & & -S_S\left[\rho \frac{{\mathbf{v}}^2}{2}-p_S+\frac{{\mu }_f}{8}{\int }^t{\left(\frac{\partial {\mathbf{v}}_i}{\partial {\mathbf{r}}_j}+\frac{\partial {\mathbf{v}}_j}{\partial {\mathbf{r}}_i}\right)}^{2}d{t}^{\prime }\right]\hfill \\ & & -S_{\mathrm{M}}\sum _j\left[{\rho }_j\frac{{{\dot{\mathbf{z}}}_j}^2}{2}-U^M\left(\mathbf{z}\right)\right]\hfill \\ & & \left.-S_E\left[\frac{{\rho }_E}{2}{\dot{\mathbf{w}}}^2-\frac{1}{2}\left({\lambda }_E{\sigma }_{ii}^2+{\mu }_E{\left({\sigma }_{ij}\right)}^2\right)\right]\right\}d\mathbf{r}d\mathbf{z}dt,\hfill \end{array}$$ (6)

where U^S includes all the non-electrostatic (or nonpolar) interactions involving the solvent,⁶³ Φ is the electrostatic potential, and ρ_α, ρ_α0, q_α, and μ_α0 are, respectively, the density, bulk density, charge, and relative reference chemical potential of αth component of the solvent. Here, ρ = ∑_αρ_α is the total solvent mass density, v is the flow stream velocity, and μ_f is the viscosity of the fluid. The Einstein notation is used in the fluid potential energy. Here, ρ_j = m_jδ(z_j − x_j) is the mass density of the jth atom in a molecular dynamics description, with m_j and x_j being the mass and the macroscopic position of the jth atom, respectively. Here, U^M(z) and ${\rho }_j\frac{{\dot{\mathbf{z}}}_j^2}{2}$ are, respectively, the potential and kinetic energy densities of the jth atom with ${\dot{\mathbf{z}}}_j=\frac{d{\mathbf{z}}_j}{dt}$. We use the short-hand notations $d\mathbf{z}=d{\mathbf{z}}_{1}d{\mathbf{z}}_2...d{\mathbf{z}}_{N_a}$ and $\mathbf{z}=({\mathbf{z}}_1,{\mathbf{z}}_2,...,{\mathbf{z}}_{N_a})\in {\mathbb{R}}^{3N_a}$ with N_a the total number of atoms in the domain of molecular dynamics description. We assume that the potential interactions U^M(z) include all bonding and non-bonding components as used in implicit MD calculations.^{23, 37} The integration is over the macroscopic variable r, microscopic variable z, and time t.

Physically, in Eq. 6, the first is the nonpolar solvation free energy, followed by the electrostatic free energy in the second row, the chemical potential related energy in the third row, the Lagrangian of the fluid dynamics in the fourth row, the Lagrangian of the molecular dynamics in the fifth row, and finally the Lagrangian of the elastic dynamics in the last row.

Governing equations

It has become a standard procedure to derive governing equations by a total variation.^{62, 63} We briefly discuss these equations below.

Generalized Laplace-Beltrami equation

Using the Euler-Lagrange variation, we derive two generalized Laplace-Beltrami equations, respectively, for characteristic functions of molecular mechanics domain and the elastic domain

$$\begin{array}{ccc}\hfill \frac{\partial S_I}{\partial t}& =& |\nabla S_I|\left[\nabla ·\left({\gamma }_I\frac{\nabla S_I}{|\nabla S_I|}\right)+V_I\right],I=M,E,\hfill \end{array}$$ (7)

where driven terms V_M and V_E are, respectively, given by

$$\begin{array}{ccc}\hfill V_M& =& -p_M+U^S+\frac{{\epsilon }_M}{2}{\left|\nabla \Phi \right|}^2-\Phi {\varrho }_M-\frac{{\epsilon }_S}{2}{\left|\nabla \Phi \right|}^2+\Phi \sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha }\hfill \\ & & +\sum _{\alpha }\left[k_{B}T\left({\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-{\rho }_{\alpha }+{\rho }_{\alpha 0}\right)-{\mu }_{\alpha 0}{\rho }_{\alpha }\right]\hfill \\ & & -\left[\rho \frac{{\mathbf{v}}^2}{2}-p_S+\frac{{\mu }_f}{8}{\int }^t{\left(\frac{\partial {\mathbf{v}}_i}{\partial {\mathbf{r}}_j}+\frac{\partial {\mathbf{v}}_j}{\partial {\mathbf{r}}_i}\right)}^{2}d{t}^{\prime }\right]\hfill \\ & & +\sum _j\left[{\rho }_j\frac{{{\dot{\mathbf{z}}}_j}^2}{2}-U^M\left(\mathbf{z}\right)\right]\hfill \end{array}$$ (8)

and

$$\begin{array}{ccc}\hfill V_E& =& -p_E+U^S+\frac{{\epsilon }_E}{2}{\left|\nabla \Phi \right|}^2-\Phi {\varrho }_E-\frac{{\epsilon }_S}{2}{\left|\nabla \Phi \right|}^2+\Phi \sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha }\hfill \\ & & +\sum _{\alpha }\left[k_{B}T\left({\rho }_{\alpha }\ln \frac{{\rho }_{\alpha }}{{\rho }_{\alpha 0}}-{\rho }_{\alpha }+{\rho }_{\alpha 0}\right)-{\mu }_{\alpha 0}{\rho }_{\alpha }\right]\hfill \\ & & -\left[\rho \frac{{\mathbf{v}}^2}{2}-p_S+\frac{{\mu }_f}{8}{\int }^t{\left(\frac{\partial {\mathbf{v}}_i}{\partial {\mathbf{r}}_j}+\frac{\partial {\mathbf{v}}_j}{\partial {\mathbf{r}}_i}\right)}^{2}d{t}^{\prime }\right]\hfill \\ & & +\left[\frac{{\rho }_E}{2}{\dot{\mathbf{w}}}^2-\frac{1}{2}\left({\lambda }_E{\sigma }_{ii}^2+{\mu }_E{\left({\sigma }_{ij}\right)}^2\right)\right].\hfill \end{array}$$ (9)

Surface of the solvent is determined via relation S_S = 1 − S_M − S_E.

Generalized Poisson equation

The electrostatic potential (Φ) is determined by the generalized Poisson equation

$$\begin{array}{c}\hfill -\nabla ·\left(\epsilon \left(S\right)\nabla \Phi \right)=S_M{\varrho }_M+S_E{\varrho }_E+S_S\sum _{\alpha }{\rho }_{\alpha }{q}_{\alpha },\end{array}$$ (10)

where ε(S) = S_Sε_S + S_Mε_M + S_Eε_E is the generalized permittivity function.

Generalized Nernst-Planck equation

The derivation of the generalized Nernst-Planck involves the variation with respect to solvent species ρ_α and the generalized Fick's law^{62, 63, 64}

$$\begin{array}{ccc}\hfill \frac{\partial {\rho }_{\alpha }}{\partial t}+\mathbf{v}·\nabla {\rho }_{\alpha }& =& \nabla ·D_{\alpha }\left[\nabla {\rho }_{\alpha }+\frac{{\rho }_{\alpha }}{k_{B}T}\nabla \left(q_{\alpha }\Phi +U_{\alpha }^S-\frac{{\mathbf{v}}^2}{2}\right)\right]\hfill \\ & & +\sum _j{\overline{\nu }}_{\alpha j}{J}^j,\hfill \end{array}$$ (11)

where ${\overline{\nu }}_{\alpha j}{J}^j$ is the density production of α species per unit volume in the jth chemical reaction.⁶² Equation 11 describes generalized mass conservation law in which the rate of change of each mass density is balanced by convection, diffusion, and reactions.

Generalized Navier-Stokes equation

The total variation of functional 6 gives rise to the generalized Navier-Stokes equation

$$\rho \left(\frac{\partial \mathbf{v}}{\partial t}+\mathbf{v}·\nabla \mathbf{v}\right)=-\nabla p_S+\frac{1}{S_S}\nabla ·S_S\mathbb{T}+{\mathbf{F}}_{\mathrm{E}},$$ (12)

where flow stress tensor T can be expressed as

$$\mathbb{T}=\frac{{\mu }_f}{2}\left(\frac{\partial {\mathbf{v}}_i}{\partial {\mathbf{r}}_j}+\frac{\partial {\mathbf{v}}_j}{\partial {\mathbf{r}}_i}\right)=\frac{{\mu }_f}{2}[\nabla \mathbf{v}+{\left(\nabla \mathbf{v}\right)}^T],$$ (13)

where symbol T denotes the transpose. The force F_E has the form

$$\begin{array}{ccc}\hfill {\mathbf{F}}_{\mathrm{E}}& =& \frac{1}{1-S_M-S_E}\left(-S_M\nabla p_M-S_E\nabla p_E-S_S\sum _{\alpha }{\rho }_{\alpha }\nabla U_{\alpha }^S\right.\hfill \\ & & \left.+{\varrho }_M\nabla \left(S_M\Phi \right)+{\varrho }_E\nabla \left(S_E\Phi \right)\right).\hfill \end{array}$$ (14)

In the inner solvent domain (i.e., S_M = S_E = 0), Eq. 14 reduces to the standard Navier-Stokes equation for incompressible flows except for an extra force term $-{\sum }_{\alpha }{\rho }_{\alpha }\nabla U_{\alpha }^S$ which is due to solvent-solvent interactions. In fact, away from the flow boundary, $-{\sum }_{\alpha }{\rho }_{\alpha }\nabla U_{\alpha }^S$ becomes negligible too.

Generalized Newton equation

As discussed in our earlier work,⁶² the variation with respect to δz_j leads to Newton's equation for the molecular mechanics

$$\begin{array}{c}\hfill {\rho }_j{\ddot{\mathbf{z}}}_j={\mathbf{f}}^j,j=1,2,...,N^a,\end{array}$$ (15)

where the force term is given by

$$\begin{array}{ccc}& & {\mathbf{f}}^j={\mathbf{f}}_{\mathrm{SSI}}^j+{\mathbf{f}}_{\mathrm{RF}}^j+{\mathbf{f}}_{\mathrm{PI}}^j,\hfill \end{array}$$ (16)

$$\begin{array}{ccc}& & {\mathbf{f}}_{\mathrm{SSI}}^j=-\frac{S_S}{S_M}{\nabla }_j{U}^S,\hfill \end{array}$$ (17)

$$\begin{array}{ccc}& & {\mathbf{f}}_{\mathrm{RF}}^j=\frac{1}{S_M}({\varrho }_M{\nabla }_j\left(S_M\Phi \right)+{\varrho }_E{\nabla }_j\left(S_E\Phi \right)),\hfill \end{array}$$ (18)

$$\begin{array}{ccc}& & {\mathbf{f}}_{\mathrm{PI}}^j=-{\nabla }_j{U}^M\left(\mathbf{z}\right).\hfill \end{array}$$ (19)

Here, ${\mathbf{f}}_{\mathrm{SSI}}^j,{\mathbf{f}}_{\mathrm{RF}}^j$, and ${\mathbf{f}}_{\mathrm{PI}}^j$ are, respectively, solvent-solute interaction force, reaction field (RF) force, and potential interaction force due to atomic interactions.

Elastic dynamics

Note that in the present work, the rigidity μ_E = μ_E(r) is continuous function with atomic rigidity information. Considering such a position dependence, the governing equation for the elastic dynamics of the macromolecule can also be derived by variation

$$\begin{array}{c}\hfill {\rho }_E\ddot{\mathbf{w}}=\frac{1}{S_E}\left[\nabla S_E({\lambda }_E+{\mu }_E)\nabla ·\mathbf{w}+\nabla ·S_E{\mu }_E\nabla \mathbf{w}\right]+{\mathbf{f}}^E,\end{array}$$ (20)

where f^E is the total force

$$\begin{array}{c}\hfill {\mathbf{f}}^E={\mathbf{f}}_{\mathrm{FSI}}^E+{\mathbf{f}}_{\mathrm{RF}}^E+{\mathbf{f}}_{\mathrm{HG}}^E,\end{array}$$ (21)

where

$$\begin{array}{ccc}& & {\mathbf{f}}_{\mathrm{FSI}}^E=-\frac{S_S}{S_E}\sum _{\alpha }{\rho }_{\alpha }{\nabla }_{\mathbf{w}}{U}_{\alpha }^S,\hfill \end{array}$$ (22)

$$\begin{array}{ccc}& & {\mathbf{f}}_{\mathrm{RF}}^E=-\frac{1}{S_E}\Phi (S_M{\nabla }_{\mathbf{w}}{\varrho }_M+S_E{\nabla }_{\mathbf{w}}{\varrho }_E),\hfill \end{array}$$ (23)

$$\begin{array}{ccc}& & {\mathbf{f}}_{\mathrm{HG}}^E=-S_E\left[{\left(\nabla ·\mathbf{w}\right)}^2{\nabla }_{\mathbf{w}}\lambda +\frac{1}{4}{(\nabla \mathbf{w}+{\left(\nabla \mathbf{w}\right)}^T)}^2{\nabla }_{\mathbf{w}}\mu \right].\hfill \end{array}$$ (24)

Here, ${\mathbf{f}}_{\mathrm{FSI}}^E$ is the fluid-structure interaction (FSI) force and ${\mathbf{f}}_{\mathrm{RF}}^E$ is the RF force which is due to the charge distributions of biomolecules in the molecular dynamics domain and the elastic domain. Term ${\mathbf{f}}_{\mathrm{HG}}^E$ is the heterogeneous (HG) force due to the inhomogeneity of the biomolecules. If we assume that λ is independent of position (∇_wλ = 0), or the biomolecule is incompressible (∇ · w = 0), we can drop the first part of the HG force. Additionally, in the elastic domain, one has S_E = 1.

To simplify Eq. 20, we make use of the stress tensor of the elastic molecule⁶²

$$\begin{array}{c}\hfill {\mathbb{T}}_{ij}^E={\lambda }_E{\sigma }_{kk}{\delta }_{ij}+2{\mu }_E{\sigma }_{ij}.\end{array}$$ (25)

Obviously, the stress tensor is symmetric with respect to labels i and j. By means of the stress tensor, the elastic dynamics Eq. 20 is

$$\begin{array}{c}\hfill {\rho }_E\ddot{\mathbf{w}}=\frac{1}{S_E}\nabla ·S_E{\mathbb{T}}^E+{\mathbf{f}}^E.\end{array}$$ (26)

Clearly, Eq. 26 is a generalization of the classical elastic dynamics. It is essentially the Newton's equation of motion for elastic molecules and is parallel to the Newton's equation for atomistic molecular dynamics. The product of mass and acceleration $\left({\rho }_E\ddot{\mathbf{w}}\right)$ is balanced by the internal friction $(\frac{1}{S_E}\nabla ·S_E{\mathbb{T}}^E)$, external forces $({\mathbf{f}}_{\mathrm{FSI}}^E$$-\frac{1}{S_E}\Phi S_M{\nabla }_{\mathbf{w}}{\varrho }_M)$, and internal forces ( − Φ∇_wϱ_E, (∇ · w)²∇_wλ, and $\frac{1}{4}{(\nabla \mathbf{w}+{\left(\nabla \mathbf{w}\right)}^T)}^2{\nabla }_{\mathbf{w}}\mu$). The dependent variable in Eq. 26 is a vector in ${\mathbb{R}}^3$, while the spatial dimension of molecular dynamics is 3N_a.

The elastostatic state is given by

$$\begin{array}{c}\hfill \frac{1}{S_E}\nabla ·S_E{\mathbb{T}}^E+{\mathbf{f}}^E=0.\end{array}$$ (27)

Here, Eq. 27 describes the shape of elastic biomolecule at the balance of internal friction and external force. It is meaningful for the equilibrium state but may also be used for a non-equilibrium conformation.

Assume that the elastic dynamics of biomolecules admits a time-harmonic solution, i.e., its time dependence is proportional to e^iωt, we have the following eigenvalue equation:

$$\begin{array}{c}\hfill \frac{1}{S_E}\nabla ·S_E{\mathbb{T}}^E+{\mathbf{f}}^E=-{\rho }_E{\omega }^2\mathbf{w}.\end{array}$$ (28)

Therefore, the diagonalization of the operator $\frac{1}{S_E}\nabla ·S_E{\mathbb{T}}^E+{\mathbf{f}}^E$ in Eq. 28 for biomolecules produces eigenvalues and eigenvectors. The latter can be used to analyze and visualize the vibration of macromolecules. The low order vibrational modes reflect protein collective motions.

In the present multiscale, multiphysics, and multidomain theory, the elastic dynamics 26 is coupled to the generalized Laplace-Beltrami equation 7, Poisson equation 10, Nernst-Planck equation 11, Navier-Stokes equation 12, and Newton's equations 15. There are many ways to simplify this coupled system. For example, one can omit the molecular dynamics by assuming a static conformation in the MD domain, neglect fluid dynamics when there is no flow velocity and disregard the Nernst-Planck equation when there is no ion permeation. In fact, one can also utilize sharp interface and dielectric approximation to skip the Laplace-Beltrami equation. However, more detailed discussion along this line is beyond the scope of the present work and will be carried out in our future work.

FLEXIBILITY AND RIGIDITY

In this section, we present a microscopic theory for molecular rigidity and flexibility in light of CEWAR. We propose a FRI method for protein flexibility analysis and B-factor prediction. The FRI is a structure, or geometry, based method, and does not involve the interaction Hamiltonian used in energy based approaches.

Rigidity

The behavior of the stress tensor 25 determines the dynamics and elastostatics of the biomolecular elasticity. Currently, elastic moduli λ_E and μ_E are taken to be constants in most theoretical modeling and computational experiments.⁵¹ The lame parameter λ_E is typically relatively small for biomolecules because of the incompressibility of macromolecules under physiological condition. The shear modulus μ_E, i.e., rigidity, should vary from position to position so that the continuum elasticity with atomic rigidity can play an important role in the elastic analysis of excessively large macromolecules.

Consider a macromolecule of N particles (or atoms) with a conformation vector $({\mathbf{r}}_1,{\mathbf{r}}_2,...,{\mathbf{r}}_j,...,{\mathbf{r}}_N)\in {\mathbb{R}}^{3N}$, where ${\mathbf{r}}_j\in {\mathbb{R}}^3$ is the position of jth particle or atom. Let us denote ‖r_i − r_j‖ the Euclidean distance between particles r_i and r_j. We assume that the correlation between particles r_i and r_j has the form

$$\begin{array}{c}\hfill C_{ij}=\Phi (\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert ;{\eta }_{ij}),\end{array}$$ (29)

where η_ij are characteristic distances between particles and Φ(‖r_i − r_j‖; η_ij) is a correlation kernel, also called an unnormalized density estimator.⁶¹

In general, the correlation kernel is a real-valued, smooth, and monotonically decreasing function. It has properties

$$\begin{array}{ccc}\hfill \Phi (\Vert {\mathbf{r}}_i-{\mathbf{r}}_i\Vert ;{\eta }_{ii})& =& 1,\hfill \end{array}$$ (30)

$$\begin{array}{ccc}\hfill \Phi (\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert ;{\eta }_{ij})& =& 0\mathrm{as}\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert \to \infty .\hfill \end{array}$$ (31)

Many decaying radial basis functions can be used for correlation kernels. Typical examples include generalized exponential function

$$\begin{array}{c}\hfill \Phi (\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert ;{\eta }_{ij})=e^{-{\left(\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert /{\eta }_{ij}\right)}^{\kappa }},\kappa >0\end{array}$$ (32)

and generalized Lorentz function⁶¹

$$\begin{array}{c}\hfill \Phi (\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert ;{\eta }_{ij})={\left(\frac{{\eta }_{ij}}{{\eta }_{ij}+\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert }\right)}^{\upsilon },\upsilon >0.\end{array}$$ (33)

Certainly, many other alternative choices, such as delta sequence kernels of the positive type discussed in an earlier reference⁶¹ can be employed as well. For example, one can use the product of exponential and Lorentz functions

$${\left(\frac{{\eta }_{ij}}{{\eta }_{ij}+\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert }\right)}^{\upsilon }{e}^{-{\left(\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert /{\eta }_{ij}\right)}^{\kappa }}.$$

We shall not exploit all alternatives at present because our goal is to establish a theoretical framework. The basic idea is that the correlation between any two particles should decay according to their distance.

We construct a N × N symmetric correlation map C = {C_ij}. The correlation map contains topological connectivity between atoms and thus, is also called connectivity. The behavior of the correlation map C is explored in Sec. 4.

For the shear modulus in the continuum elasticity analysis, we need a continuous function defined in the elastic domain (Ω_E = {r|S_E(r) ≠ 0}). To this end, we define the correlation from an arbitrary point r to the jth particle

$$\begin{array}{c}\hfill C_j\left(\mathbf{r}\right)=\Phi (\Vert \mathbf{r}-{\mathbf{r}}_j\Vert ;{\eta }_{ij}),\end{array}$$ (34)

where r is in the proximity of ith particle. We define an atomic rigidity function μ(r) as

$$\begin{array}{c}\hfill \mu \left(\mathbf{r}\right)=\sum _{j=1}^N{w}_j\left(\mathbf{r}\right)\Phi (\Vert \mathbf{r}-{\mathbf{r}}_j\Vert ;{\eta }_{ij}),\mathbf{r}\in {\Omega }_E,\end{array}$$ (35)

where w_j(r) are particle-type related weights. The atomic rigidity function μ(r) measures the local rigidity or local stiffness at point r.

The average rigidity (or averaged rigidity index function) can be calculated by

$$\begin{array}{ccc}\hfill \overline{\mu }& =& \frac{1}{\int S_{E}d\mathbf{r}}\int S_E\mu \left(\mathbf{r}\right)d\mathbf{r}.\hfill \end{array}$$ (36)

Therefore, parameter w_j in Eq. 35 can be determined by a comparison of $\overline{\mu }$ with its experimental value, the shear modulus, for a given macromolecule. This procedure can help the parametrization of w_j in Eq. 35, though w_j should also reflect the difference in different types of atoms in a macromolecule.

It is important to have a discrete representation of rigidity on a set of atoms or particles. To this end, we define an atomic rigidity index as

$$\begin{array}{c}\hfill {\mu }_i=\sum _{j=1}^N{w}_{ij}\Phi (\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert ;{\eta }_{ij}),\end{array}$$ (37)

where w_ij = w_j(r_i). It is convenient to further define the molecular rigidity index as a summation of all the atomic ones

$$\begin{array}{c}\hfill {\mu }_{\mathrm{MRI}}=\sum _{i=1}^N{\mu }_i.\end{array}$$ (38)

Obviously, the molecular rigidity index of a given macromolecule is a direct measure of its total interaction strength in a general sense.

For the purpose of comparison among different molecules, we further define an averaged molecular rigidity index

$$\begin{array}{c}\hfill {\overline{\mu }}_{\mathrm{MRI}}=\frac{1}{N}\sum _{i=1}^N{\mu }_i.\end{array}$$ (39)

Similar to the Wiener index, both the molecular rigidity index and the averaged molecular rigidity index must strongly correlate with many physical properties, such as molecular thermal stability, density (compactness), boiling points of isomers, the ratio of surface area over volume, surface tension, bulk modulus, etc. However, a thorough investigation of these aspects is beyond the scope of the present work and is left for future work.

Flexibility

For polyatomic molecules, we should have μ_i > 0. Therefore, we can define an atomic flexibility index as

$$\begin{array}{c}\hfill f_i=\frac{1}{{\mu }_i},\forall i=1,2,...,N.\end{array}$$ (40)

Atomic flexibility indices {f_i} of a macromolecule must be proportional to its B-factor {B_i}

$$\begin{array}{c}\hfill B_i^t=a{f}_i+b,\forall i=1,2,...,N,\end{array}$$ (41)

where $\left\{B_i^t\right\}$ are theoretically predicted B-factors. Here, constants a and b do not depend on index i and can be determined by a simple linear regression. The procedure outlined above is perhaps the simplest one for B-factor prediction. Unlike ENM, GNM, ANM, and many other methods, the proposed approach by-passes the matrix diagonalization (or decomposition) procedure in conventional B-factor prediction and flexibility analysis. It is well known that the computational complexity of matrix diagonalization is asymptotically close to $\mathcal{O}\left(N^3\right)$, while that of a two-parameter linear regression given in Eq. 41 is asymptotically of $\mathcal{O}\left(N\right)$. The construction of the correlation map C can be made linear in complexity with appropriate spatial index techniques, although the construction of a spatial database may be of $\mathcal{O}\left(N\ln N\right)$ in complexity. Nevertheless, our FRI based B-factor prediction gives rise to a dramatic reduction in the computational complexity compared with conventional approaches. We expect that the proposed method will outperform other methods in computational efficiency and be potentially useful for the flexibility analysis of excessively large macromolecules.

Let us define a molecular flexibility index as a sum of atomic indices

$$\begin{array}{c}\hfill f_{\mathrm{MFI}}=\sum _i\frac{1}{{\mu }_i}\forall i=1,2,...,N,\end{array}$$ (42)

and an averaged molecular flexibility index

$$\begin{array}{c}\hfill {\overline{f}}_{\mathrm{MFI}}=\frac{1}{N}\sum _i\frac{1}{{\mu }_i}\forall i=1,2,...,N.\end{array}$$ (43)

Similar to the Wiener index, the molecular flexibility index or the averaged molecular flexibility index reflects the atomic geometric irrelevance and topological disconnectivity in a molecule, and must strongly correlate with energy and disorderliness. These aspects will be explored in our future work.

Finally, atomic flexibility functions can be defined in two ways. For example, one simply defines

$$\begin{array}{ccc}\hfill F\left(\mathbf{r}\right)& =& \frac{1}{{\sum }_{j=1}^N{w}_j\left(\mathbf{r}\right)\Phi (\Vert \mathbf{r}-{\mathbf{r}}_j\Vert ;{\eta }_{ij})},\mathbf{r}\in {\Omega }_E.\hfill \end{array}$$ (44)

It is reasonable to assume that the atomic rigidity function is non-singular in the domain Ω_E. On the other hand, it is convenient to define the atomic flexibility function by using a set of B-factors {B_j}

$$\begin{array}{ccc}\hfill F_B\left(\mathbf{r}\right)& =& \sum _j{B}_j\Psi (\Vert \mathbf{r}-{\mathbf{r}}_j\Vert ),\mathbf{r}\in {\Omega }_E,\hfill \end{array}$$ (45)

where Ψ(‖r − r_j‖) is a general interpolation kernel. The B-factors can be obtained either from experimental data or from theoretical predictions. When there are different types of atoms, the experimental B-factors should be corrected according to diffraction cross sections before they are interpreted as atomic flexibility. Such a correction can be by-passed when only the same type of atoms, i.e., C_α, is involved.

NUMERICAL EXPERIMENTS

In this section, we validate the concepts, demonstrate the usefulness, and explore the efficiency of the proposed theory and algorithm for flexibility and rigidity analysis. We first analyze the correlation map, which reveals the topological connectivity among atoms in a macromolecule. The prediction of B-factor based on the proposed atomic flexibility index is demonstrated. Finally, we illustrate the use of atomic rigidity function and atomic flexibility function in protein visualization.

In the present experiments, we employ a coarse-grained representation with amino acid residues and consider only C_α atoms. We can set weights w_ij = 1 and assign a common value to characteristic length parameter η_ij = η in Eq. 37

$$\begin{array}{c}\hfill C_{ij}=\Phi (\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert ;\eta ).\end{array}$$ (46)

We consider only the generalized exponential kernel

$$\begin{array}{c}\hfill \Phi (\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert ;\eta )=e^{-{\left(\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert /\eta \right)}^{\kappa }},\kappa >0\end{array}$$ (47)

and the generalized Lorentz kernel in the present numerical experiment

$$\begin{array}{c}\hfill \Phi (\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert ;\eta )={\left(\frac{\eta }{\eta +\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert }\right)}^{\upsilon }.\end{array}$$ (48)

By appropriate selection of power υ, κ, and η, we actually end up with a parameter-free atomic flexibility index

$$\begin{array}{c}\hfill f_i=\frac{1}{{\sum }_j^N\Phi (\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert ;\eta )},\forall i=1,2,...,N.\end{array}$$ (49)

In general, Eqs. 46, 47, 48 are used for computing correlation maps and their combination with Eqs. 40, 41 provides the FRI scheme for B-factor predictions.

To quantitatively assess the performance of the proposed FRI method for the B-factor prediction, we consider the correlation coefficient

$$\begin{array}{c}\hfill C_c=\frac{{\Sigma }_{i=1}^N\left(B_i^e-{\overline{B}}^e\right)\left(B_i^t-{\overline{B}}^t\right)}{{\left[{\Sigma }_{i=1}^N{\left(B_i^e-{\overline{B}}^e\right)}^2{\Sigma }_{i=1}^N{\left(B_i^t-{\overline{B}}^t\right)}^2\right]}^{1/2}},\end{array}$$ (50)

where $\{B_i^t,i=1,2,...,N\}$ are a set of predicted B-factors by using the proposed method and $\{B_i^e,i=1,2,...,N\}$ are a set of experimental B-factors downloaded from the Protein Data Bank (PDB). Here, ${\overline{B}}^t$ and ${\overline{B}}^e$ are the statistical averages of theoretical and experimental B-factors, respectively.

Correlation map

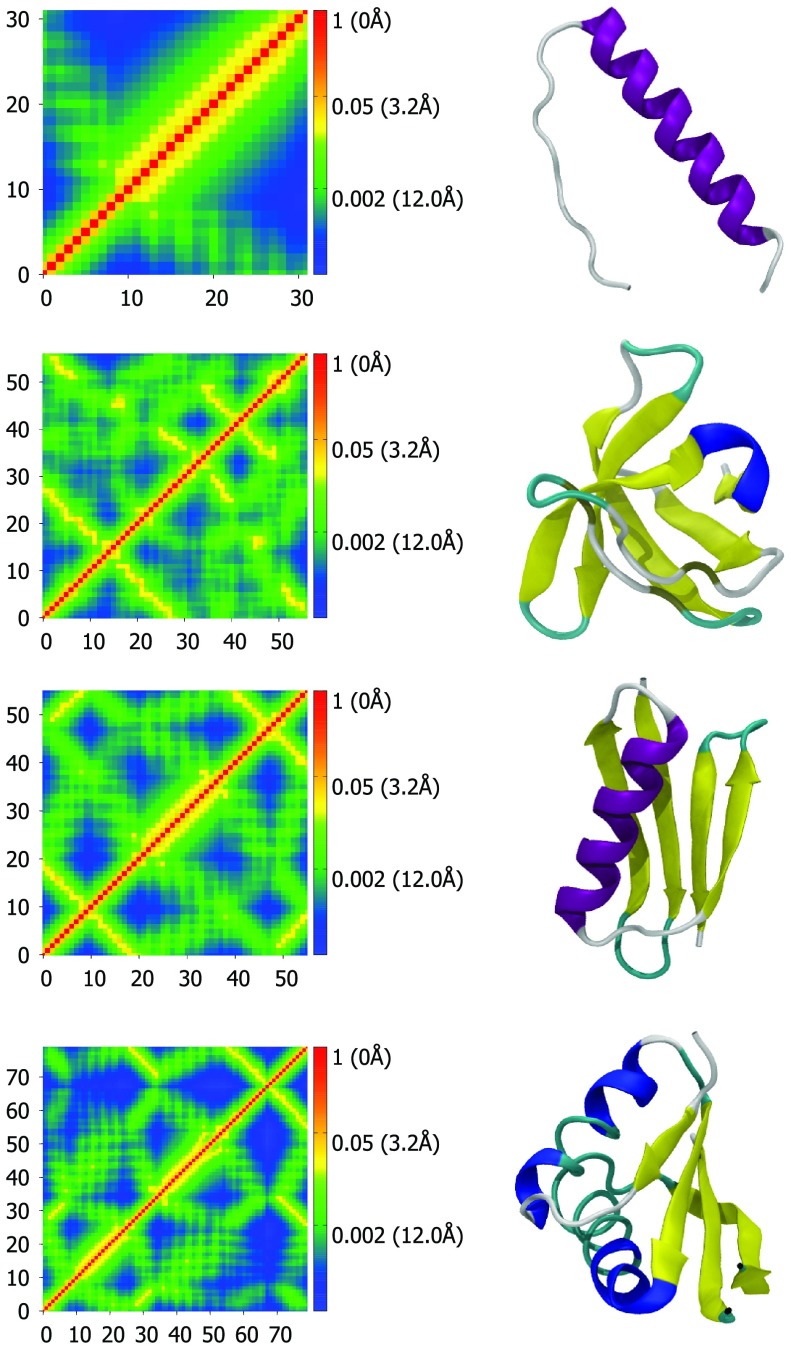
Similar to the cross correlations of the GNM and other methods, FRI correlation maps computed using Eq. 46 qualitatively reflect the three-dimensional structure of a protein. As a consequence, distinct secondary structures such as α helices and β-sheets exhibit characteristic patterns. After some studying of the patterns, it is possible to approximate a protein's secondary and tertiary structures from the patterns of the correlation map alone. However, unlike the cross correlations of the GNM, the FRI correlation maps are able to further offer quantitative structural information. In fact, since the kernel used to generate the map is known, the distances between all atoms can be calculated and the three-dimensional structure can be reconstructed from the correlation map. Figure 1 displays four examples of correlation maps next to their corresponding three-dimensional structure. The scale-bars of the correlation maps include distance values to emphasize the preservation of the 3D structural information.

Figure 1.

Correlation maps (left column) and secondary structure representations (right column) for proteins 1C26, 1BK2, 1PGA, and 1NH9, from top to bottom. Correlation maps are generated using Eq. 48 with υ = 2.5 and η = 1.0 Å. Secondary structure visualizations are generated with VMD.³⁰ Colors represent distance and correlation values for each pair of atoms. Red represents nearby atoms with high correlation values and blue represents distant atoms with low correlation values. The residue numbers for each Cα are listed along the x- and y-axes. The protein are displayed in VMD's “new cartoon” representation and colored by secondary structure determined by STRIDE. The color scheme for secondary structure is: Purple – α helix, blue – 3(10) helix, yellow – β-sheet, cyan – turn, white – coil. The correlation map of an α helix gives rise to a widened diagonal pattern (see the first row). In contrast, the correlation map of paired beta sheets has two patterns. One is a line that is perpendicular to the diagonal with distances around 5-10 Å for a pair of anti-parallel beta sheets (see the first and second beta sheets in the third row). The other is a line that is parallel to the diagonal with distances around 5-10 Å for a pair of parallel beta sheets (see the first and fourth beta sheets in the third row).

As stated previously, each secondary structure exhibits a distinct pattern in our correlation maps. The pattern for an α helix is shown in the first row of Fig. 1. The α helix creates a band of high correlation extending about 4 amino acids in either direction from the diagonal. The correlation has a local maximum at the third neighbor residue, due to the structure of the α helix (3.6 amino acid residues per turn). Therefore, the peak at the third residue serves as another signature of an α helix in the FRI correlation map. An increase in correlation between two such neighboring atoms compared to other neighboring pairs indicates the interaction of the α helix and another component. For example, in the third row of Fig. 1, the correlation strength between 29th C_α and 32th C_α is higher, due to interaction of 29th C_α with the third and fourth beta sheets. This is an example of how this type of correlation kernels reflects tertiary structure information.

Other folds such as β-sheets are also easily identified by distinct patterns. One can easily distinguish parallel β-sheets from anti-parallel β-sheets by their patterns with this method. The second row of Fig. 1 is a good example of the pattern generated by anti-parallel β-sheets. Anti-parallel β-sheets appear as lines that are perpendicular to the diagonal of the map and the intersection of the two lines of high correlation are the turns between each β strand. Parallel β-sheets appear as lines parallel to the diagonal. In the third row of Fig. 1, an anti-parallel β-sheet is formed by the first and last ten amino acids resulting in a line in the top left and bottom right of the correlation matrix.

The last two rows of Fig. 1 both display complex patterns which reflect not only secondary structure information but also the three-dimensional arrangement of the secondary structure features. Clearly, from the last correlation map, the first β-sheet interacts strongly with the first α helix and the second β-sheet in a parallel manner. It also interacts to a lesser degree with the second α helix and with the last β-sheet in an anti-parallel manner. These patterns and the stabilizing forces from the interactions they represent are lost if one uses a contact or Kirchoff matrix based method instead of a monotonically decreasing radial basis function based correlation map.

FRI based B-factor prediction

To further validate our FRI method, we compare the B-factor predictions with the experimental B-factors from protein X-ray crystallography experiments as shown in Eq. 50. A set of 263 proteins was collected from the PDB with preference for high resolution (1.5 Å) protein-only structures that lack structural co-factors. The impact of co-factors on protein stability requires an all atom model and is a topic that will be explored in our future work. The set of 263 proteins was converted to a Cα only format and when atoms have multiple coordinates with occupancy <1.0 the highest occupancy coordinate was kept and all others were discarded. This is a potential source of error in the B-factor predictions. However, some proteins with multiple coordinates for atoms were among the highest scoring which suggests that the impact in most cases is small.

The correlation coefficients of B-factor prediction are displayed in Fig. 2 for both exponential (expo) and Lorentz kernels. Each protein was tested with both the exponential and Lorentz correlation kernels across a range of parameter values of κ and η for the exponential kernel and υ and η for the Lorentz kernel. Correlation coefficient scores for B-factor predictions below 0.5 account for just 19 out of 263 proteins for the Lorentz kernel based FRI and 14 out of 263 for the exponential kernel based FRI and are not shown in Fig. 2. The reasons for these low scores are the subject of future research and are likely related to the influence of crystal packing effects, structural ligands and side-chain effects that are not approximated well by the Cα course grained model. The accuracy of B-factor prediction is also dependent upon the quality of the experimental data. If multiple coordinates are reported for an atom along with multiple B-factors, then we do not have high confidence in the B-factor and thus the prediction will appear to be less accurate.

Figure 2.

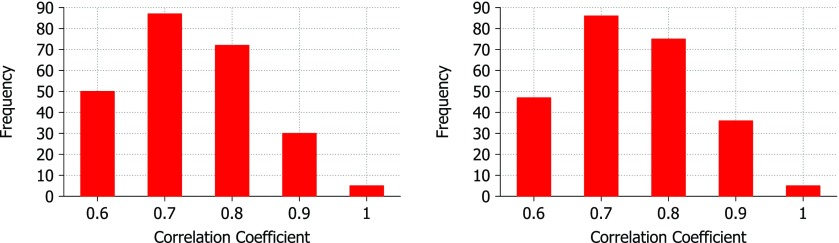
Correlation coefficients for experimental vs predicted B-factors using the Lorentz kernel (left) and exponential (right) kernel. The test set consists of 263 C_α only PDB files. Scores below 0.5 are not shown. For the Lorentz kernel, υ values range from 0.5 to 10.0 at an interval of 0.5 and η values range from 1.0 Å to 40.0 Å at an interval of 1.0 Å. For the exponential kernel, κ values range from 0.5 to 10.0 at an interval of 0.5 and η values range from 0.5 Å to 20.0 Å at an interval of 0.5 Å.

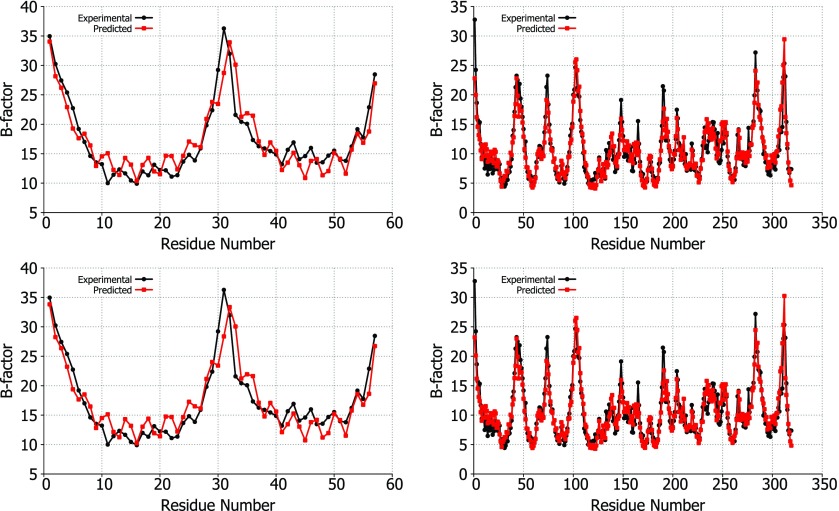
A comparison of the experimental vs predicted B-factors for two proteins, 1DF4 and 2Y7L, is shown in Fig. 3 to demonstrate the accuracy of our FRI method. These two proteins were in the top five highest correlation coefficients for B-factor predictions using the exponential (2Y7L: 0.928, 1DF4: 0.909) and Lorentz (2Y7L: 0.928, 1DF4: 0.917) kernels. It can be seen from the correlation scores and Figs. 23 that both correlation kernels give similar results, especially for these highly accurate predictions.

Figure 3.

Experimental B-factors (black) vs predicted B-factors (red) using the Lorentz (top) and exponential (bottom) correlation kernels. The structures used for comparison are 1DF4 (left) and 2Y7L (right). For these comparisons, the optimal parameters were used for υ, κ, and η based on the parameter searches for each correlation kernel. For the Lorentz kernel, υ = 1.5 and η = 2.0 Å are the parameters used for 1DF4 and υ = 1.5 and η = 19 Å are used for 2Y7L. For the exponential kernel, κ = 0.5 and η = 1.0 Å are employed for 1DF4 and κ = 0.5 and η = 2.5 Å for 2Y7L.

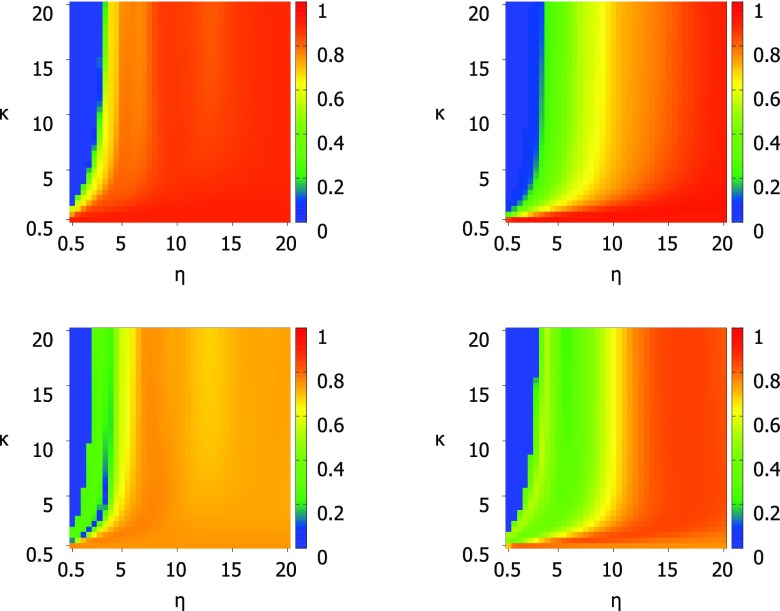
B-factor prediction was calculated for each protein at a range of parameter values in each kernel. The Lorentz kernel requires parameters, υ and η, while the exponential kernel requires κ and η. The aim is to find values for these parameters that are suitable for most or all proteins so that the method may be made parameter free. The parameters which result in the highest correlation coefficient for each protein are displayed in Figs. 46 for the Lorentz and exponential kernels, respectively.

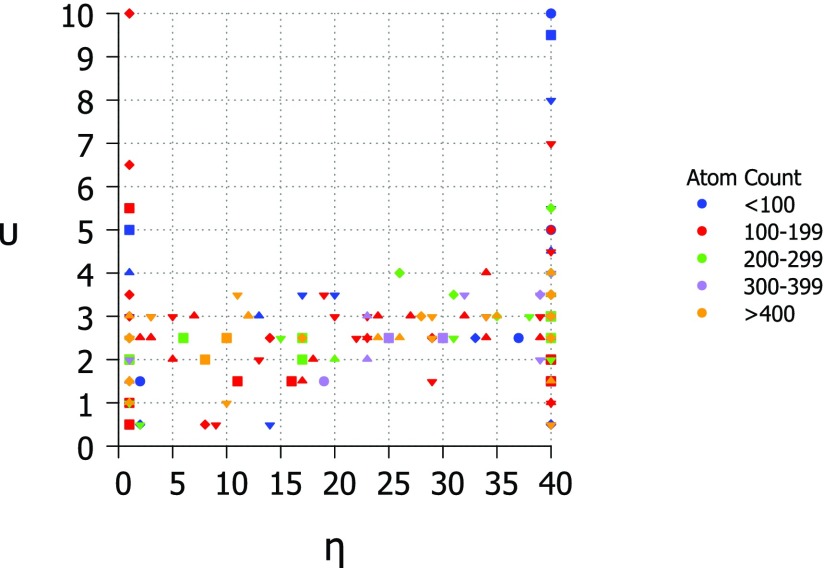
Figure 4.

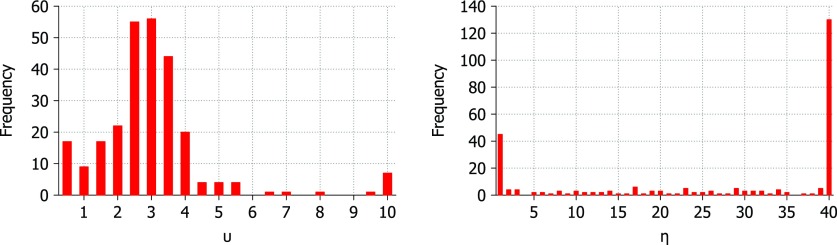
Optimal υ parameter value for 263 proteins using the Lorentz correlation kernel. B-factor prediction was calculated for υ values ranging from 0.5 to 10 at an interval of 0.5 and η values ranging from 1.0 Å to 40.0 Å at an interval of 1.0 Å.

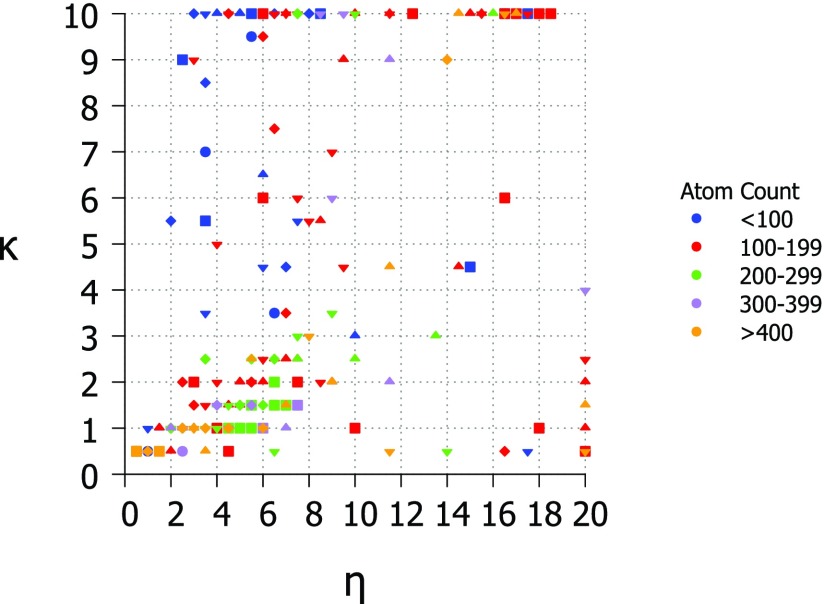
Figure 6.

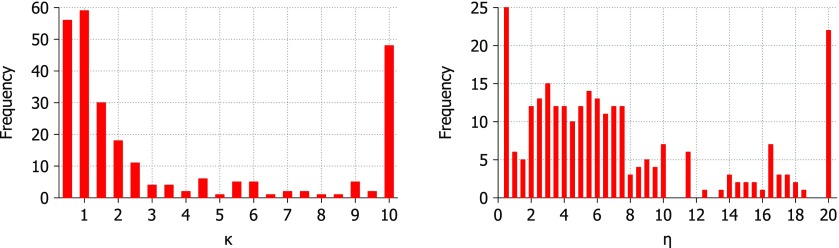
Optimal parameters for 263 structures using the exponential correlation kernel. Here, κ values range from 0.5 to 10.0 at an interval of 0.5. η values range from 0.5 Å to 20.0 Å at an interval of 0.5 Å.

The optimal value for υ in the Lorentz kernel is found to be near 2.5 for most proteins in the test set. The optimal value for η is typically the highest or lowest tested. The results of the parameter search for υ and η are shown in Fig. 4. This result is a close match to the findings of Yang et al.⁶⁷ and their parameter free ENM (pfENM) model. In the pfENM, spring constants are scaled by an inverse power. Yang et al.⁶⁷ tested powers 1-10 and found second and third inverse power relationships were the most accurate for B-factor predictions.⁶⁷ In our study, we also test non-integer powers over the range 0.5-10.0 and come to a similar conclusion. The optimal value for υ is plotted against the optimal value for η and colored by the size of protein in Fig. 5. There is no clear pattern based on protein size except that some smaller proteins (under 100 atoms) prefer very high values of υ which may be due to a lack of long range interactions.

Figure 5.

Phase diagram for Lorentz kernel optimal parameter values υ and η colored by the size of structure and with shapes corresponding to correlation coefficient. Diamond − 0.5, downward triangle − 0.6, upward triangle − 0.7, square − 0.8 , circle − 0.9. υ values range from 0.5 to 10.0 at an interval of 0.5 and η values range from 1.0 Å to 40 Å at an interval of 1.0 Å.

For the exponential kernel, the optimal κ value for most proteins is between 0.5 and 1 while the optimal η values are more spread out with the majority of proteins having optimal η values from 0.5 Å to 8 Å. This ambiguity in the optimal parameter value makes the choice of parameters for a parameter free version difficult, however, the testing of the parameter free exponential kernel method shows that it performs as well as the parameter free Lorentz kernel methods. The optimal values for κ and η for all proteins in the test set are shown in Fig. 6. Optimal values for κ are 0.5 or 1.0 in most cases with a significant peak at κ = 10 which is the highest value tested. Optimal values for η are more varied and there is no clear choice for a parameter free version. There is a large peak at the highest η value tested (η = 20 Å) as there was for κ, however, these two peaks do not correspond to the same set of proteins. This point is illustrated in Fig. 7 which compares κ and η values. Figure 7 also shows that there is no relationship between number of atoms or correlation coefficient and the parameters κ and η. To further inform our choice of parameters for the parameter free exponential method, we look at the patterns of correlation scores for every κ and η value combination in Fig. 8. The parameter maps show that for most proteins the choice of κ is most important and that when κ ⩽ 1 there are many choices for η that result in very similar correlation coefficients.

Figure 7.

Phase diagram for exponential kernel optimal parameter values κ and η colored by the size of structure and with shapes corresponding to correlation coefficient. Diamond − 0.5, downward triangle − 0.6, upward triangle − 0.7, square − 0.8, circle − 0.9. κ values range from 0.5 to 10.0 at an interval of 0.5 and η values range from 0.5 Å to 20 Å at an interval of 0.5 Å.

Figure 8.

Complete results of optimal parameter searches using the exponential correlation kernel for structures 1DF4 (top left), 2Y7L (top right), 2Y9F (bottom left), and 3LAA (bottom right). Structures 1DF4 and 2Y7L (top) represent the high scoring structures, those with scores near 0.9. Structures 2Y7L and 3LAA (bottom) show the typical pattern for correlation scores based on parameter values for the majority of proteins. κ values range from 0.5 to 20.0 at an interval of 0.5 and η values range from 0.5 Å to 20 Å at an interval of 0.5 Å.

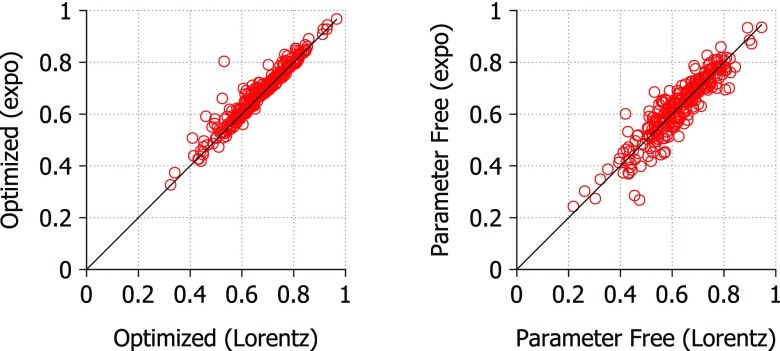
To test parameter free versions of the FRI method, we chose υ = 2.5 and η = 1.0 Å for the Lorentz kernel and κ = 1.5 and η = 5.0 Å for the exponential kernel. These choices were made based on the parameter searches and limited tests of various parameter values. In Fig. 9, we compare the exponential and Lorentz kernel performance based on correlation coefficients from B-factor prediction. The correlation coefficients were highest overall when using the exponential kernel with optimized parameters. The average correlation coefficient of B-factor prediction using the exponential kernel is 0.681 using optimal parameters and 0.627 using the parameter free version. The average correlation coefficient of B-factor prediction using the Lorentz kernel is 0.668 using optimal parameters and 0.627 using the parameter free version. The difference between the exponential and Lorentz kernels is small when using optimized parameters with an average deviation of just 0.0182. The parameter free versions of the kernels also produce very similar correlation coefficients with an average deviation of 0.0365.

Figure 9.

Comparison of correlation coefficients calculated using optimal parameters for both Lorentz and exponential correlation kernels. Average deviation = 0.0182 (left) and 0.0365 (right). For the Lorentz kernel optimal parameter search, υ values range from 0.5 to 10.0 at an interval of 0.5 and η values range from 1.0 Å to 40.0 Å at an interval of 1.0 Å. For the exponential kernel parameter search, κ values range from 0.5 to 10.0 at an interval of 0.5 and η values range from 0.5 Å to 20.0 Å at an interval of 0.5 Å. The parameter free Lorentz kernel uses υ = 2.5 and η = 1.0 Å and the parameter free exponential kernel uses κ = 1.5 and η = 5.0 Å.

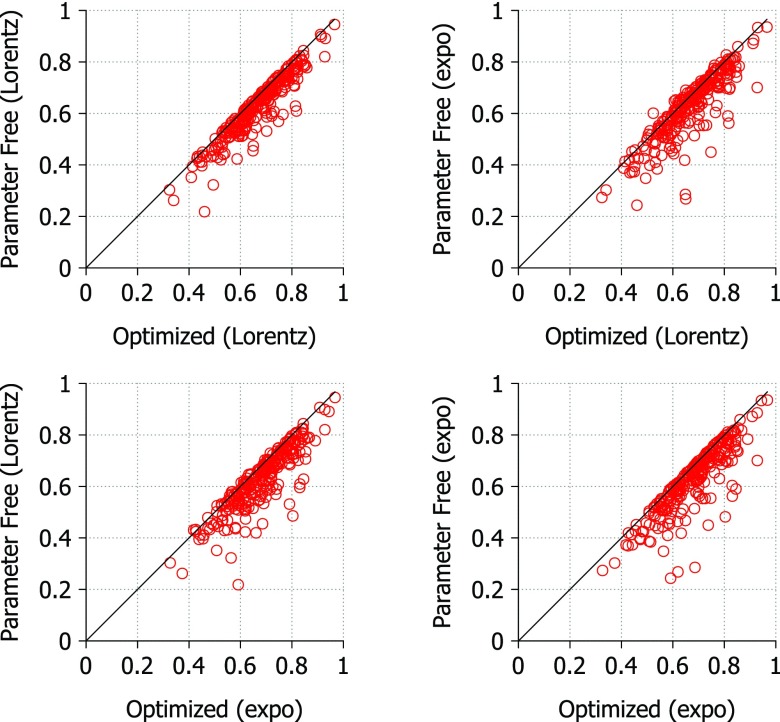
The parameter free Lorentz and exponential kernels appear to have similar performance and these results do not indicate a clear advantage in using either kernel. In Fig. 10, we compare the correlation coefficients from the parameter free and optimized versions of the method for both correlation kernels. In each case, the optimized method outperforms the parameter free method no matter which kernel is used. Again this suggests that neither kernel has an advantage over the other for this method. The maximal average deviation among these methods is 0.0549, meaning that the parameter free exponential kernel captures 94% of the best results generated by optimized Lorentz kernel for this set of proteins. Similarly, the parameter free exponential kernel captures 94% of the best results from the optimized exponential kernel. It is worthwhile to note that the parameter free Lorentz kernel (υ = 2.5 and η = 1.0 Å) is able to capture 95% of the best results generated by either the optimized exponential or Lorentz kernel for this set of proteins. Therefore, it appears that the both parameter free kernels are very robust for practical applications.

Figure 10.

Comparison of correlation coefficients calculated using optimal parameters and parameter free versions of the FRI. The optimized correlation coefficients are the highest scoring from a parameter search. For the Lorentz kernel optimal parameter search, υ values range from 0.5 to 10.0 at an interval of 0.5 and η values range from 1.0 Å to 40.0 Å at an interval of 1.0 Å. For the exponential kernel parameter search, κ values range from 0.5 to 10.0 at an interval of 0.5 and η values range from 0.5 Å to 20.0 Å at an interval of 0.5 Å. The parameter free Lorentz kernel uses υ = 2.5 and η = 1.0 Å and the parameter free exponential kernel uses κ = 1.5 and η = 5.0 Å. The line y = x is shown for reference. Points on the line indicate little or no difference between optimized parameters and the parameter free results. Average deviations are 0.0410, 0.0549, 0.0463, and 0.0540 (from left to right and from top to bottom).

Rigidity and flexibility visualization

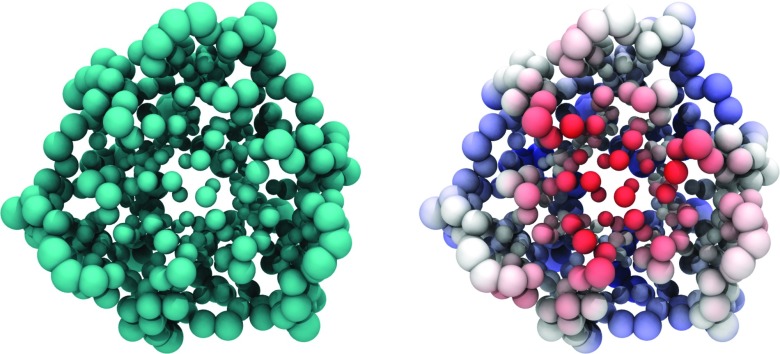
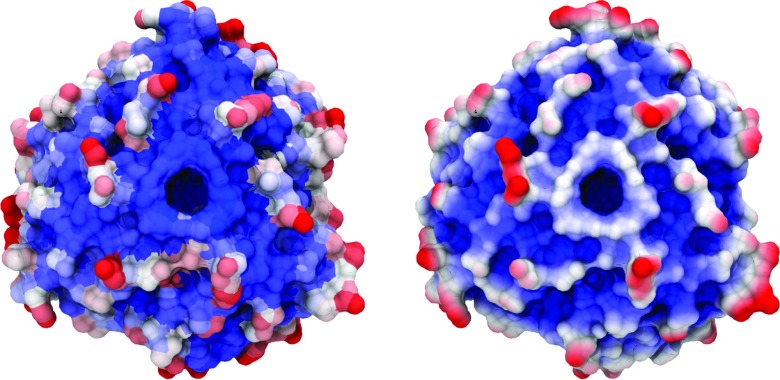
From the above analysis, the rigidity and flexibility indices can be obtained at coordinates of C_α atoms in the protein. Such values can be utilized directly for visualization. For the purpose of visualization, it is sufficient to plot either rigidity or flexibility. A large value of the flexibility index can be represented by a large atomic radius in the visualization while a small flexibility index corresponds a small atomic radius. Therefore, we scale atomic van der Waals radii by their flexibility indices as shown in Fig. 11 for 1QD9. Clearly, C_αs located near molecular boundary are more flexible.

Figure 11.

C_α atoms of 1QD9 in VDW representation scaled by predicted B-factor (both images) and colored with electrostatics (right). Larger VDW radii represent more flexible atoms such as those near the surface of this soluble protein. Smaller VDW radii represent more rigid atoms such as those in the core of the protein. On the right, atoms are colored by electrostatics revealing two charged domains. First, the flexible outer amino acids have some areas of positive charge that interact with the bulk solvent. Second, a highly negatively charged portion of the protein core is highlighted in red. These charges are stabilized by internal water molecules.

Additionally, the flexibility index can be visualized together with electrostatic potential. Specifically, the flexibility is represented by the atomic size while the electrostatics is illustrated by color as shown in the right chart of Fig. 11. There is a correlation between flexibility and partial charge at the protein outer surface—charged residues are more rigid. From these figures we see the image of a typical soluble protein with flexible, partially charged residues on the solvent-solute boundary and a less flexible, rigid core. It is well-known that the partially charged flexible outer protein surface is responsible for many protein functions in enzymes, cell signaling, and ligand binding. Interestingly, this soluble protein has a highly charged core made up of many negatively charged residues interacting with a network of water molecules. This results in a negatively charged, rigid core which is represented by small, red VDW spheres.

Furthermore, in order to study the elastic dynamics, elastostatics, and collective motion of a macromolecule, the continuous atomic rigidity and flexibility functions are required in our multiscale multiphysics multiphysics and multidomain models. The spatially scattered information at each C_α coordinate needs to be interpolated into continuous atomic rigidity and flexibility functions. In this work, we employ the modified Shepard's method to interpolate rigidity and flexibility values at C_α coordinates to build their continuous functions.^{48, 56} The essence of Shepard's method is to blend local interpolants with locally supported weight functions. For example, the atomic flexibility function can be expressed as

$$\begin{array}{c}\hfill F\left(\mathbf{r}\right)=\sum _{i=1}^N{W}_i\left(\mathbf{r}\right)Q_i\left(\mathbf{r}\right),\end{array}$$ (51)

where the locally supported weight function is defined as

$$\begin{array}{ccc}\hfill W_i\left(\mathbf{r}\right)& =& \frac{p_i(\parallel {\mathbf{r}-\mathbf{r}}_i\parallel ;R_i)}{{\sum }_{i=1}^N{p}_i(\parallel {\mathbf{r}-\mathbf{r}}_i\parallel ;R_i)},\hfill \end{array}$$ (52)

$$\begin{array}{ccc}\hfill p_i(\parallel {\mathbf{r}-\mathbf{r}}_i\parallel ;R_i)& =& \left\{\begin{array}{cc}\hfill {\left(\frac{R_i-\parallel {\mathbf{r}-\mathbf{r}}_i\parallel }{R_i\parallel {\mathbf{r}-\mathbf{r}}_i\parallel }\right)}^2,& \hfill \parallel {\mathbf{r}-\mathbf{r}}_i\parallel <R_i,\\ \hfill 0,& \hfill \parallel {\mathbf{r}-\mathbf{r}}_i\parallel \ge R_i.\end{array}\right.\hfill \end{array}$$ (53)

Here, R_i > 0 is a constant radius with ith C_α as its center. Its value varies with i so as to include different numbers of points into its influence domain when it is necessary.⁵⁶

Our input data are a set atomic flexibility indices {f_i} or the predicted B-factors $\left\{B_i^t\right\}$ located at C_αs. We denote r = (x, y, z), r ∈ S_E a general position inside the elastic domain of a macromolecule, and the local interpolant is a nodal function defined as

$$\begin{array}{ccc}\hfill Q_i\left(\mathbf{r}\right)& =& a_{i1}{x}^2+a_{i2}{y}^2+a_{i3}{z}^2+a_{i4}xy+a_{i5}xz+a_{i6}yz\hfill \\ & & +a_{i7}x+a_{i8}y+a_{i9}z+a_{i10},\hfill \end{array}$$ (54)

where a_ij are coefficients and Q_i(r) is a quadratic polynomial function which interpolates the predicted B-factors at neighboring set of C_α locations, namely,

$$\begin{array}{c}\hfill Q_i\left({\mathbf{r}}_j\right)=B_j^t{\delta }_{ij},\end{array}$$ (55)

where δ_ij is the Kronecker delta function. For a given ith C_α, Eq. 55 is repeatedly employed on all C_αs within the given sphere of radius R_i and results in a number of algebraic equations. The algebraic equations are solved by using the weighted least square method, which determines coefficients a_ij. For sufficiently large data, we can choose 32 surrounding atomic flexibility indices to fit coefficients.⁵⁶ Note that the atomic rigidity function (μ(r)) can be constructed in the same manner by replacing $B_j^t$ with μ_j.

In Fig. 12, we compare an atomistic and a continuous representation for flexibility of protein 1QD9. The molecular surface on the left is colored by X-ray B-factors, while the molecular surface on the right is colored by the interpolated flexibility values. Overall, the interpolated values mimic the B-factor pattern closely. However, the predicted flexibility at the inner ring of the structure is higher than that given by X-ray B-factors due to the fact water molecules fill part of the inner core in the full structure. The B-factor color map is discontinuous. In contrast, the flexibility map generated with the FRI method has the advantage of being continuous both on the surface and in the interior of the protein. The atomic rigidity function and atomic flexibility function constructed in the present work will be utilized to study macromolecular elastic dynamics, elastostatics, and elastic vibration in our future work.

Figure 12.

The molecular surface of Protein 1QD9 colored by B-factor (left) and continuous FRI representation (right). The flexibility index is calculated using the Lorentz method with υ = 2.5 and η = 1.0 Å. Images generated by VMD using BWR color bar and scale 10-50 for B-factors and 0.75–0.90 for the flexibility index. In both images, blue regions indicate low flexibility and red regions indicate high flexibility. On the left, B-factor is an atomistic representation of flexibility. On the right, FRI is used to predict flexibility and the continuum representation is mapped to the protein surface. The continuum prediction matches the experimental flexibility pattern closely except for near the core of the protein which contains some structural water not included in our model.

CONCLUSION

This work puts forward a multiscale, multiphysics, and multidomain model for the theoretical description and computer simulation of large macromolecular complexes. The multidomain setting enables the simultaneous multiscale and multiphysical treatment of biomolecular systems. In a special example, we consider a few physical descriptions, including nonpolar solvation, electrostatic interaction, multiple charged species, fluid flow, molecular mechanics, and elasticity. Of these descriptions, molecular mechanics is the only one defined at a microscopic level, while the rest are described using macroscopic theories. The interfaces between various domains are characterized by Laplace-Beltrami flows. The total energy functional is utilized to assemble various physical descriptions on an equal footing. The Euler-Lagrange variation is utilized to derive coupled governing equations for various physical descriptions. Apart from Laplace-Beltrami equations for interfaces, the Poisson-Boltzmann equation, the Navier-Stokes equation, Nernst-Planck equations, the elastic equation, and Newton's equations are obtained, respectively, for electrostatics, fluid flow, ion densities, elastic dynamics, and molecular mechanics in the model. A distinguishing feature of the present theory is that the elasticity theory is made non-uniform. Unlike the usual continuum elasticity analysis which utilizes a uniform shear modulus or rigidity, the present work introduces non-uniform shear modulus based on flexibility and rigidity analysis of macromolecules. This approach, called CEWAR, incorporates microscopic rigidity information in continuum elasticity analysis. The essential idea is to decouple the dynamics complexity of macromolecular system from its static complexity, such that the time-consuming molecular dynamics of the macromolecular system is replaced with a continuum elastic dynamics, while the relatively low-cost static analysis is computed with atomic rigidity.

We propose a FRI to estimate the static property of macromolecules. We utilize monotonically decreasing functions, including delta sequence of positive type,⁶¹ to measure the geometric compactness of a protein and quantify the topological connectivity of atoms or residues in the protein. Physically, the FRI characterizes the total interaction strength at each atom or residue, and thus reflects the atomic rigidity and flexibility. Additionally, we define the total rigidity of a molecule by a summation of atomic rigidities. Furthermore, the spatial varying shear modulus is obtained by an interpolation using atomic rigidities. A practical validation of the proposed FRI is the prediction of B-factors, or temperature factors of proteins, measured by X-ray crystallography. We employ a set of 263 proteins to examine the validity, explore the reliability, and demonstrate the robustness of the proposed FRI method for B-factor prediction. We analyze the performance of two classes of correlation kernels, i.e., the exponential type and the Lorentz type, for the B-factor prediction. The exponential type of correlation kernel involves two parameters, exponential order and characteristic length. The Lorentz type of correlation kernel also involves two parameters, power order and characteristic length. By searching the parameter space for optimal predictions, parameter-free correlation kernels are obtained. It is found that the parameter-free correlation kernel of the Lorentz type is able to retain about 95% accuracy compared to the optimized results.

A basic assumption of the present FRI theory is that the geometry or structure of a given protein together with its specific environment, namely, solvent, assembly, or crystal lattice, completely determines the biological function and properties including flexibility, rigidity, and energy. As such, the present approach bypasses the construction of the Hamiltonian and interaction potentials. A possible drawback of the present method is that the full geometric and topological information of a protein complex is usually not available, which contributes to modeling errors.

The generalization of the present work is underway on a few fronts. First, a comparison of the present FRI and two other state of the art approaches, namely, the GNM and the coarse-grained normal mode analysis (cgNMA) will be carried out for B-factor prediction. Unlike GNM and cgNMA, the FRI does not require matrix diagonalization or decomposition. Its computational complexity is at most $\mathcal{O}\left(N^2\right)$. The performances of FRI, GNM, and cgNMA in terms of accuracy, reliability, and computational efficiency will be examined with a large number of proteins. Additionally, the performance of the present FRI will be improved by the consideration of co-factors, crystal periodicity, and X-ray diffraction cross-section. Moreover, the collective motions of proteins will be studied by solving the eigenvalue problem of the elasticity equation with atomic rigidity. Furthermore, the interaction between elastic domains and other domains will be studied by using the elastostatic equation. Finally, elastic dynamics will be simulated using the theory developed in the present work.