Abstract
Despite tremendous advances in the field of tissue engineering, a number of obstacles is still hindering its successful translation to the clinic. One of these challenges has been to design cell-laden scaffolds that can provide an appropriate environment for cells to successfully synthesize new tissue while providing a mechanical support that can resist physiological loads at the early stage of in situ implementation. A solution to this problem has been to balance tissue growth and scaffold degradation by creating new hydrogel systems that possess both hydrolytic and enzymatic degradation behaviors. Very little is known however, about the complex behavior of these systems, emphasizing the need for a rigorous mathematical approach that can eventually assist and guide experimental advances. This paper introduces a mathematical and numerical formulation based on mixture theory, to describe the degradation, swelling and transport of extracellular matrix (ECM) molecules released by cartilage cells (chondrocytes) within a hydrogel scaffold. The model particularly investigates the relative roles of hydrolytic and enzymatic degradations on ECM diffusion and their impacts on two important outcomes: the extent of ECM transport (and deposition) and the evolution of the scaffold’s mechanical integrity. Numerical results based on finite element show that if properly tuned, enzymatic degradation differs from hydrolytic degradation in that it can create a degradation front that is key to maintaining scaffold stiffness while allowing ECM deposition. These results therefore suggest a hydrogel design that could enable successful in situ cartilage tissue engineering.
Keywords: Biomechanics, Modeling, Tissue engineering, Mixture, Hydrogel, Cartilage
1 Introduction
Degenerative diseases, injuries and aging often lead to organ and tissue failure, which can be fatal or at best, significantly decrease one’s quality of life. To fight this scourge, an efficient strategy consists of injecting the damaged tissue with a population of cells that can stimulate repair mechanisms, growth and restoration of normal function. These cells often need a mechanical support (often referred to as scaffold) that can resist physiological loads and ensure proper tissue development. In this context, the use of hydrogel systems as scaffold materials has provided a very promising solution due to their controllable properties close to that of native tissues [5], their ability to support cell encapsulation and to promote extracellular matrix (ECM) synthesis [57,43]. One limitation, however, resides in the fact that most hydrogels possess a relatively high degree of crosslinks which inhibits the proper diffusion of ECM molecules [43,8] synthesized by cells and restricts tissue development to the immediate region surrounding the cell. This issue was addressed by introducing degradable hydrogels in which crosslink cleavage permits ECM diffusion in time. Although this strategy enables successful tissue growth, gel degradation ultimately results in a loss of the scaffold’s load carrying capacity and the failure of in vivo tissue regeneration. A key challenge in tissue engineering is thus to design scaffolds whose degradation and growth are properly balanced to achieve successful development and sustained mechanical integrity [28].
As we move towards these more complex systems, experimental techniques alone become limited, which precludes significant progress in regenerative medicine [28,25]. Taking the specific example of engineered cartilage, this paper presents a mathematical modeling approach to predict how scaffold structure and degradation dictate the development of functional cartilage, from the molecular to the tissue scale. A challenge in modeling the growth of engineered cartilage is that it involves interactions of multiple phenomena occurring at very distinct length-scale from the molecular to the tissue level. At the molecular scale, growth originates from the chondrocyte-mediated synthesis of two main types of ECM molecules: collagen II and aggrecan subunits, whose subsequent transport and deposition are then strongly affected by the scaffold. In non-degradable hydrogels, the tight polymer mesh keeps ECM molecules in the immediate cellular region and restricts growth to the pericellular domain. In degradable hydrogels, crosslink depletion enables diffusion and leads to a more homogeneous ECM distribution. This stage is then followed by the process of molecular assembly and cross-linking during which ECM units become immobilized, acquire solid-like properties and start participating in the overall stiffness of the tissue. The relative kinetics of ECM synthesis, diffusion and assembly, together with the rate of gel degradation are key players in the development of micro-structural features at the cellular scale.
While current experimental efforts are striving to develop hydrogel systems that balance growth and degradation [43,11,18], the complexity of phenomena and interactions involved during these processes, together with a lack of quantitative understanding, has made this task extremely challenging. There is therefore a pressing need for predictive mathematical models that can provide a clear picture of the mechanisms at play and their effect on macroscale tissue development. From a modeling standpoint, the theory of mixture [3,24] has traditionally provided accurate descriptions of important processes such as hydrogel swelling, the transport of a variety of dissolved phases through the pores [26, 27], as well as solid degradation [53] and matrix deposition [13,16]. However, while this powerful framework has been used to describe cartilage homeostasis and growth at the tissue scale [13,30], no models have so far characterized how they originate from the molecular and cellular scales. In the present work, by considering a uniform cell distribution, it is possible to represent the entire tissue as a small hydrogel domain surrounding a single chondrocyte. The hydrogel degradation and the coupled ECM transport can thus be studied locally around a cell with minimum computational cost. A multiphasic formulation [3,49,55,53] is adopted to describe the molecular diffusion through the porous and deformable hydrogel scaffold. We particularly make two contributions: first, the Flory-Rehner theory [21, 48] is used to accurately describe gel swelling, mesh size and diffusivity and second, we adopt a Michaelis-Menten kinetics [34] to describe changes in hydrogel degradation rates (hydrolytic and enzymatic) with hydrogel structure. The combination of these models enables us to relate molecular quantities such as hydrogel crosslink density, swelling, mesh size and the radius of gyration of ECM molecules to cellular-scale quantities such as scaffold permeability and stiffness. The model thus consists of a spatio-temporal system of differential equations in a spherical domain in which the evolution of ECM distribution in hydrogels (with various degradation kinetics), are computed with the finite element method.
The paper is organized as follows. In the next section, we describe the thermodynamic framework used to model the mechano-chemistry of hydrogel scaffolds. In section 3, the governing equations for the coupled elasticity-degradation-transport problem are discussed, together with appropriate constitutive assumptions. A general finite element formulation is also introduced to obtain a numerical solution of developed partial differential equations. Section 4 then presents a number of benchmark and a thorough investigation of the role of degradation on ECM transport and scaffold mechanics. In section 5, we finally provide a discussion on the concrete implications of this work and address the model’s limitations and potential improvements for future studies.
2 Thermodynamical description of a hydrogel scaffold
Hydrogel scaffolds are made of long polymer chains of repeating chemical units bonded together via chemical and physical crosslinks (Fig. 2). The degree of cross-linking ultimately controls both gel elasticity and permeability (to various interstitial molecules) via the mesh size ξ of the network. Importantly, when interacting with a solvent, solvent molecules that are attracted to the polymer network by entropic and enthalpic forces, fill the space between the chains and ultimately induce swelling of the gel. Swelling tends to increase the hydrogel mesh size and thus promote the permeation of interstitial molecules through the network. It is therefore clear that hydrogel mechanics has significant implications for the transport and deposition of ECM molecules synthesized by cells and as a consequence, on the growth of engineered tissues. We here introduce a theoretical framework describing the elasticity and swelling of hydrogels based on the early work of Flory [15] and more recently Hong et al. in [20].
Fig. 2.

Lattice model of a hydrogel and main contributions of the Gibbs free energy.
2.1 Thermodynamical model
A hydrogel can be described as a mixture of two main phases: the solid polymeric network (represented by the superscript “s”) that constitutes the scaffold and a variety of fluid phase representing the solvent (represented by the superscript “f”) and molecular species produced by embedded cells. In the present study, we consider two such molecular species: a degrading enzyme (represented by the superscript “e”) and ECM molecules (represented by the superscript “m”) that are mostly comprised of collagen and aggrecan molecules. Taking a continuum approach, the equilibrium of the mixture can be studied via the definition of the Gibbs free energy function ΔG as originally introduced by the Flory-Rehner and rubber elasticity theories [15,51]. The energy is typically split into two contributions: an elastic free energy ΔGel(F) and the free energy of mixing ΔGmix(Cs, Cf, Cm, Ce) as follows [10]:
| (1) |
The elastic free energy represents the existence of internal mechanical forces resisting the deformation of the hydrogel described by the deformation gradient F = ∂x/∂X (where δx and δX are infinitesimal material line vectors in the deformed and undeformed configuration, respectively). The entropy of mixing, on the other hand, arises from the tendency of molecules (solvent and other molecular species) to diffuse and fill the space within the polymer network. It is therefore a function of the concentration of the various fluid phases Cα present in the hydrogel, including solvent (α = f), ECM molecules (α = m) and enzymes (α = e). We note here that our lagrangian description implies that concentrations are defined as the number of moles of a specific constituent per reference volume (unswollen hydrogel): Cα= Nα/V0. The elastic contribution of the energy is defined by Flory [15] and Treloar [51], neglecting the phantom network theory [6] for simplicity:
| (2) |
We note that det F = 1 when the transformation is isochoric and thus ΔGel becomes the free energy of a Neo-Hookean material. However, when polymer and solvent are mixed, the term (det F) can significantly increase due to swelling; this can have a strong effect on the mechanical response of the mixture. A factor 2 is placed in front of the term ln (det F) in order to ensure that the volumetric stress vanishes for isochoric deformation. As shown in Eq. (2), the elastic modulus G can be expressed as a function of the specific volume of the solvent ν̄(inverse of density), the crosslink density ρX of the swollen network, the polymer density ρ (dry polymer), the gas constant R and the temperature T. The Gibbs free energy of mixing, in turn contains several contributions as follows:
| (3) |
where H0 denotes the reference enthalpy, ΔHmix is the enthalpy of mixing and ΔSmix is the entropy of mixing. The first term can be written in terms of the reference chemical potentials of each species of the quadriphasic system (polymer, solvent, ECM and enzyme) as:
| (4) |
where V0 is the total volume in the reference configuration (dry unswollen polymer). In turn, the entropy of mixing can be determined by quantifying the various states of the different species in the lattice model [15]; this leads to the conventional expression:
| (5) |
where kB is the Boltzmann constant and φα are the volume fractions of the α–phases (α = f, m, e). Finally, as a hydrogel cannot generally be considered as an ideal solution the energy of mixing must account for physical interactions solvent-polymer as described by the enthalpy of mixing. In the present study, we assume that the concentration of ECM and enzyme are very small compared to that of the solvent, and we therefore only consider the solvent-polymer interactions. Using the Flory lattice model (interactions only occur between nearest neighbors), one can express the enthalpy of mixing of the polymer-solvent system as:
| (6) |
where z is the number of direct neighbors of a polymer molecule in the lattice model. Here, (z −2) denotes the number of neighbors of a polymer segment, neglecting chain ends and Δwsf is the change in interaction energy between a polymer chain and the solvent after mixing. This expression is usually rewritten as:
| (7) |
where χsf = (z − 2) Δwsf/kBT is the binary (polymer-fluid interaction) Flory-Huggins parameter. A positive value of χsf implies that polymer-polymer and solvent-solvent contacts are more energetically favorable than polymer-solvent contacts. Adding contributions from Eq. (4), (5) and (7) leads to the following form of the Gibbs free energy of mixing:
| (8) |
Note that ΔGmix is a volumetric free energy of mixing per unit volume in the unswollen configuration.
2.2 Molecular incompressibility
To express the condition of molecular incompressibility, we first need to introduce the swelling ratio as J = det(F). In other words, J = 1 corresponds to a dry polymer devoided of interstitial constituents. When fluid phases are allowed to diffuse through the polymer network, their contributions to the swelling ratio are taken into account via the molecular incompressibility assumption [20]:
| (9) |
where να is the molar volume of molecules associated with the α–phase. This condition can be enforced by rewriting the total volumetric Gibbs free energy of the system as follows:
| (10) |
where π is a Lagrange multiplier enforcing Eq. (9). It is interesting to note here that the scalar π can be interpreted as the (Cauchy) osmotic pressure in the hydrogel.
3 Governing equations
The processes of hydrogel degradation, swelling and ECM transport are governed by two conservation principles: the balance of linear momentum and the conservation of mass. After discussing the form of these equations for large gel deformations, we introduce a formulation that is able to capture the coupling between the three above processes via appropriate constitutive relations.
3.1 Mechanical equilibrium and stress
For slow processes involved in gel degradation and swelling, the mechanical equilibrium can be expressed by writing the balance of linear momentum with negligible inertial terms. In the context of finite deformation and in the absence of body forces, it can be expressed as:
| (11) |
where P is the first Piola-Kirchhoff stress and ∇X refers to the differential operator defined in the reference con-figuration (i.e. the dry state). The relationship between the above equation and the free energy defined in the previous section is highlighted next.
Stress-strain relationship
It is now useful to invoke the fact that the Piola-Kirchhoff stress P is defined as change in Gibbs free energy due to a deformation F. In other words, one can write:
| (12) |
Using the expression for the elastic and mixing free energy as well as the molecular incompressibility conditions (10), we obtain:
| (13) |
where adj F = JF−T. This expression shows that the total stress in the hydrogel is comprised of two contributions: (a) the elastic stress resulting from the deformation of the polymer network and (b), the hydrostatic pressure π which results from the insertion of incompressible solvent/molecules within the network.
Hydrogel degradation
Hydrogel degradation occurs by the cleavage of crosslinks by two means. The first means, known as hydrolytic degradation, occurs as the crosslinks are degraded by the solvent in time. Because the solvent is homogeneously distributed through the gel, this type of degradation is global, i.e., it is independent of location. The second means, referred to as enzymatic degradation is the result of the cleavage of crosslinks by enzymes (protease) produced by embedded cells. As a consequence, enzymatic degradation occurs in regions where the enzyme concentration is elevated, which gives rise, according to transport processes, to localized degradation. In the present work, we make the following assumptions: (a) hydrolytic degradation is described by a first-order kinetic degradation [40] with rate constant k and (b) enzymatic degradation is modeled with a Michaelis-Menten kinetic model [35], such that the rate of change in crosslink concentration is written:
| (14) |
where k is the hydrolytic degradation rate, k2 and Km are the Michaelis-Menten degradation constants. According to [9], Km can be expressed by using the relation k2/Km = 2.5e5. It is clear here that the presence of enzyme (via the term Ce) tends to increase the effective degrading constant appearing in the parenthesis in Eq. (14). Degradation, by decreasing the crosslink density ρX, decreases the effective elastic modulus of the gel as seen in Eq. (2). Such a decrease in modulus weakens the resistance of the gel to osmotic pressure and induces swelling. As described next, swelling increases the polymer mesh size, improves enzyme transport and in turn, promotes more degradation. The present study aims to understand this non-linear feedback mechanism on ECM deposition.
3.2 Mass conservation and molecular transport
The transport of solvent and molecular species through the gel must satisfy the conservation of mass. It is straightforward to show that this condition can be written in terms of the concentration Cα as:
| (15) |
in which Qα denotes the Lagrangian flux of the α-phase in the reference configuration (number of moles of phase α per surface area of the undeformed, dry polymer), relative to the polymer network [12]. Furthermore, the quantity Ds is the material time derivative taken with respect to the motion of the polymer network. It is written:
| (16) |
where vs is the velocity of the polymer network. Note that contrary to studies in [59,20], the time derivative contains a convection term from solid motion, which can become important when the swelling rate is comparable with the rate at which phase α diffuses through the polymer.
Solvent and molecular fluxes
Using classical thermodynamic arguments, the flux Qα of the α-phase is assumed to be driven by the gradient of chemical potential μα as:
| (17) |
where Dα is the fluid diffusion tensor, or mobility tensor (atomic mobility of the molecules), and μα is related to the free energy density by:
| (18) |
In particular, using Eq. (10), the chemical potential for each phase present in the mixture is given by:
| (19) |
One can see here that the chemical potential of the enzyme and ECM molecules take the form of an ideal solution with an additional pressure term arising from the fact that the hydrogel imposes a pressure on the solution. In contrast, the chemical potential of the solvent contains an additional term that captures the enthalpic interaction between the polymer network and solvent molecules, which is a function of the Flory-Huggins parameter χsf. Substituting the above expressions into Eq. (17) then leads to the following form for the fluxes:
| (20) |
These expressions generally show that the transport of the α–phase is due to a combination of Fickian diffusion (first term driven by the gradient of the concentration) and convection via a Darcy-type law (second term driven by the gradient of the pressure). The term Df ν f Cf/(kB T) can particularly be identified as the permeability of the gel to the solvent. Also note that the term (kB T) coming from Eq. (19) is already included in the diffusivity terms (see Eq. (22), (23)).
Coupling between molecular diffusion and hydrogel deformation
A fundamental aspect of the present study relates to the coupling between gel deformation and the transport of solvent, enzyme and ECM molecules through the polymer network. Indeed, as discussed earlier, the hydrogel mesh size has a large influence on its permeability to solvent and molecules. It is thus important to introduce a relationship between polymer mesh size ξ [19] and the characteristics of the polymer from the work of Bell and Peppas [6] as follows:
| (21) |
Here ξ0 is the mesh size of the dry polymer, l is the average bond length, Cn is the polymer characteristic ratio, and n is the number of bonds between crosslinks. Equation (21) particularly illustrates that the mesh size increases with a decreasing polymer volume fraction φs (and thus with swelling). The dependency of solvent diffusivity on mesh size is driven by two physical quantities, namely the solvent viscosity μ̄f and the tortuosity δ of the hydrogel pore structure. Invoking the work by Holmes and Mow in [19], the diffusivity can then be written:
| (22) |
Regarding the enzyme and ECM molecule transport, Lustig and Peppas [37] have developed a reliable model for the diffusibility of a solute in a crosslinked hydrogel. The proposed diffusivity coefficient of the α-phase is given by:
| (23) |
where rs is the radius of gyration of small matrix molecules and Y is a correction factor. The function g expresses the dependency of the diffusivity on the ratio of the radius of gyration of molecule α and the hydrogel mesh size ξ such that (a) as molecules become larger than the hydrogel mesh size (rs > ξ), molecules transport is prohibited (g = 0) and (b) as the hydrogel mesh size becomes significantly larger than the molecules size (rs ≪ ξ), molecular diffusion is controlled by the diffusivity D∞ characterizing the diffusion of small solutes in a fluid. The latter is commonly described by the Stokes-Einstein equation [6]:
| (24) |
where, again, μ̄f is the solvent viscosity. The coupling between mechanics and transport is therefore established via the mesh size ξ. Indeed, as discussed above, crosslink degradation induces swelling and an increase in mesh size as described by Eq. (21). This rise in mesh size then has a strong effect on the diffusivity on both enzyme and ECM molecules via Eq. (23).
4 Model assumptions and finite element formulation
We now turn to the investigation of the problem of local hydrogel degradation and the coupled ECM molecule transport in a hydrogel scaffold with low cell density. The assumption of low cell density enables us to simplify the problem by concentrating on a representative volume element (RVE) that consists of a single chondrocyte of initial radius Rc = 10μm and the surrounding hydrogel whose radius Rg is dictated by the cell volume fraction fc = (Rc/Rg)3 as shown in Fig 3. In the following, we assume that fc = 0.01 as it constitutes a realistic value for tissue engineering applications. The synthesis and release of enzyme and ECM molecules are then modeled in the form of surface fluxes Qe and Qm on the surface of the cell; these species are subsequently available for diffusion in the scaffold (Fig. 3). As mentioned earlier, we finally make the assumptions that the quantities of enzymes and ECM molecules are small enough compared to the solvent so that:
| (25) |
Fig. 3.
Model idealization and geometrical assumptions. Assuming a scaffold with low density and uniform distribution of cells enables the consideration of a spherical representative volume element (RVE) in centro-symmetric conditions.
This considerably simplifies the molecular incompressibility equation (9) since the solvent is the only fluid phase with an effect on swelling. Besides, Eq. (25) allows to simplify Eq. (17) and to express the flux of α-molecules as a Fickian diffusion only. Mathematically, the problem consists of finding a solution for the following continuum fields in spherical coordinates, under centro-symmetric assumption:
| (26) |
Here the variable u is the radial displacement of the polymer while Cα (α = f, m, e) and π are the concentrations of each fluid phase and the osmotic pressure, respectively. As seen in Eq. (26), these unknowns can be determined by solving the coupled system of differential equations comprised of the balance of momentum (11), the conservation of mass for the fluid phases (15) and the molecular incompressibility (9). In the present work, we choose the finite element method to numerically solve these equations with the associated constitutive relations. The original differential equations are thus turned into an integral weak form via proper multiplication with test functions and integration over the physical domain. After a few derivations, this yields three equations of the form:
| (27) |
| (28) |
and, using assumption (25),
| (29) |
where z, wα and η are the test functions associated with the displacement field, the concentration fields and the osmotic pressure, respectively. We also note that Neumann boundary conditions were applied in the form of a surface traction t0 = P· n0 and a molecular flux Iα = Qα · n0 through the surface of the gel Γ0 (n0 being the unit normal vector in the reference configuration). To obtain the finite element equation, the spherical domain is discretized into N elements, each containing three nodes. The interpolation of continuum fields in the elements was determined via a mixed formulation in which the displacement is approximated with quadratic shape functions Nq (using three nodes) while the concentrations and the osmotic pressure are approximated with linear shape functions Nl (using two nodes), yielding
| (30) |
where [·]e denotes the vector of nodal variables in an element. Spatial derivatives are then approximated by differentiating the shape functions and building the matrices Bq and Bl such that:
| (31) |
Details on the form of the shape functions and associated matrices are given in Appendix A. Using a standard finite element procedure, these approximations are substituted into the weak form equations (27), (28) and (29) and linearized to obtain a final matrix equation for the solution vector y = [u] [Cα] [π] T:
| (32) |
where Fint and Fext are the internal and external forces vectors and are defined in appendix. We also recognize here the damping matrix C and the stiffness matrix K, which, in the present case, take the form:
| (33) |
and
| (34) |
In the above equations, the matrix denotes the mechanical stiffness matrix of the solid phase and includes both the material and geometrical contributions (see Appendix B.1). In a similar way, is related to the diffusivity of the α–phase (solvent, matrix molecules or enzymes) within the gel while the terms and represent coupling terms between mechanics/transport and the molecular incompressibility. Finally, the damping matrix describes the time dependence of the problem, which only arises from the transport equations of the α–phase.
5 Numerical investigation of hydrogel degradation, swelling and their influence on ECM transport and deposition
5.1 Benchmark problems for gel swelling and solvent transport
Before the presented model is applied to the understanding of ECM transport and deposition in a hydrogel scaffold, we first investigate simple situations in which gel swelling is important and compare numerical predictions with known analytical solutions. This preliminary analysis is essential for two reasons: (a) to ensure that the presented numerical scheme gives appropriate results and (b) to help understand more complex behaviors arising in subsequent analyses.
Swelling of a hydrogel under a varying external chemical potential
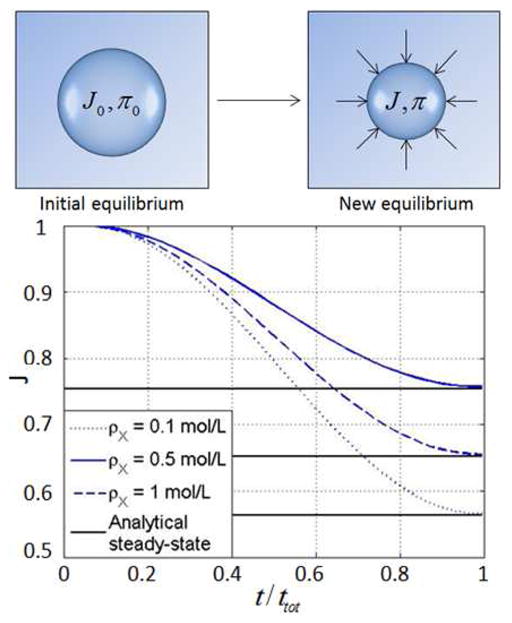
In this example, we consider a hydrogel sphere of radius Rg in the absence of boundary tractions and in contact with a solvent whose chemical potential is μ★. These two conditions translates into a Neumann boundary condition t0 = 0 and a Dirichlet boundary condition for Cf and π such that μ = μ★ on the outer radius (R = Rg) as seen in Fig. 4. We explore the de-formation of the sphere as the external chemical potential suddenly increases from 0 to μ★. This osmotic shock creates an unbalance in chemical forces between the hydrogel and its surrounding which ultimately induces a fluid flow into the gel and a transient swelling. The resulting change of volume is then resisted by the stretch of the polymer network, a process that is dominated by crosslink density. It is possible to analytically determine the equilibrium swelling ratio Jeq by solving for the steady state solution of Eq. (13), (19) and (9) that take the following form under centro-symmetric assumptions:
| (35) |
for three unknowns J, π and Cf under the condition P* = 0. Fig. 4 shows the time evolution of the swelling ratio, as derived from the finite element formulation, for three values of crosslink densities. As expected, the solutions converge to the steady state solution given by Eq. (35) and display an increased swelling with decreasing crosslink density. We note here that the volume of a solvent molecule was taken to be νf = 1e−28m3 as in Zhang et al. [59], and the total time ttot is defined as the time taken for the jacobian to get to the steady state. A large crosslink density suggests that the global stiffness of the gel is higher than for a small crosslink density, and so is the osmotic pressure. As a result, observed swelling is larger for a highly cross-linked gel than for a loosely cross-linked gel.
Fig. 4.

Transient hydrogel swelling under external osmotic shock for different crosslink densities
Mechanical response of a hydrogel under external pressure
In the context of the present study, it is of interest to understand the overall bulk modulus of a hydrogel as it degrades. To computationally assess this quantity, we subject the hydrogel to an external normal load P* and monitor the resulting relative change in gel volume ΔJ. The overall bulk modulus K̄ is then simply determined as:
| (36) |
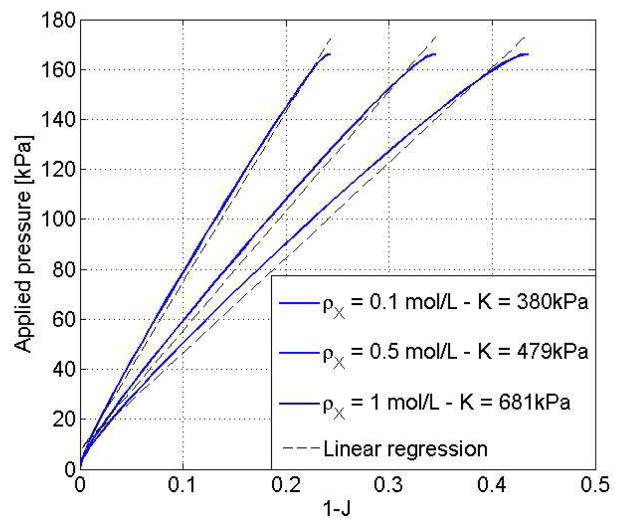
We here derive the solution in two ways. First, the analytical steady state solution is derived by solving the system of three coupled equations for J, π, Cf presented in (35) with varying values of P* and a fixed value of the external chemical potential μ* = 0. Second, the finite element formulation is used to derive the time dependent evolution of the swelling ratio J after a external pressure P* is applied in a step wise fashion at t = 0. The two solutions are displayed in Fig. 5 for an external pressure P* = 160kPa and for three values of crosslink densities ρX = 0.1, 0.5 and 1mol/L. As expected, the transient numerical solution converges to the steady state solution in a time scale that is determined by the permeability of the gel. The hydrogel undergoes a compression (negative change of volume) whose magnitude increases with a decreasing crosslink density. Determination of the overall bulk modulus can then be made by plotting the steady state compression ΔJ = J − 1 in terms of the applied pressure P* as shown in Fig. 6. While the increase in overall stiffness with crosslink density is evident from the original equation, this outlined computational derivation of the bulk modulus is particularly useful when the crosslink density is inhomogeneous, as it will be seen in the next examples.
Fig. 5.
Compression of a hydrogel sphere subjected to a sudden external pressure P* for different crosslink densities.
Fig. 6.
Determination of the overall gel modulus K̄ with the traction test. The bulk modulus can be measured as the slope of the above curves as expressed in (36).
5.2 Role of hydrolytic degradation on hydrogel response and ECM molecules diffusion
In this section, the role of hydrolytic degradation is first investigated without ECM transport and validated with experimental observations. The competition between degradation and ECM diffusion is then explored.
Effect of hydrolytic degradation on hydrogel stiffness and swelling
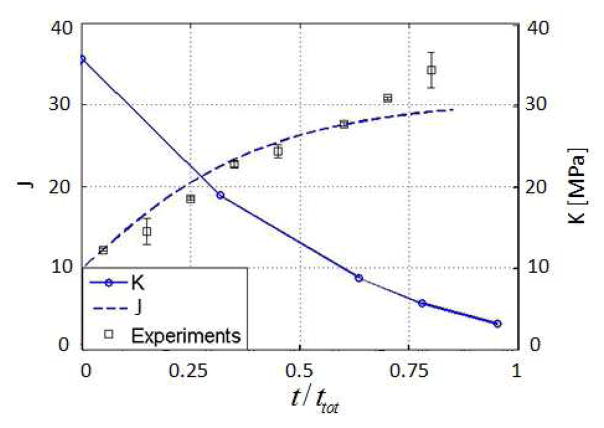
Hydrolytic degradation is commonly used in tissue engineering as a way to smoothly transition from scaffold to tissue. In this case, the Michaelis-Menten constants vanish and Eq. (14) becomes a simple first order kinetic equation of the form DρX/Dt = −kρX. We here choose a hydrolytic degradation rate k = 0.18/day as a realistic value for poly(ethylene glycol) (PEG) hydrogels [12]. Numerical simulations (Fig. 7) of a degrading sphere of gel shows two important consequences of hydrolytic degradation: (a) an increase in gel swelling and (b) a decrease in bulk modulus, both of which are directly linked to the depletion of crosslinks. Note that the evaluation of the bulk modulus was made by performing the above traction test at different times during degradation. Fig. 7 shows that the model provides a fairly accurate description of gel swelling when compared to free swelling experiments. It is also important to note that there exists a critical value of crosslink density, referred to as reverse gelation in several experimental studies [39,40] for which the gel totally loses its mechanical integrity. This aspect is not accounted for in the present study.
Fig. 7.
Evolution of the swelling ratio and the global stiffness of the gel under hydrolytic degradation
Effect of hydrolytic degradation on ECM molecule diffusion
Let us now investigate how hydrolytic degradation affects the diffusion of ECM molecules synthesized by cells. For this, we study a sphere of hydrogel surrounding a cell of radius Rc. The enzyme release at the cell boundary is then modeled assuming that each cell has a reserve of enzyme that remains constant in time. This conditions translates into a Dirichlet boundary condition at R = Rc which implies that as long as the concentration of ECM molecules in the gel at R = Rc is smaller than , the cell releases a flux of molecules Qm that is proportional to the jump in concentration ( ) across the cell membrane. As a consequence, when the ECM concentration Cm in the gel reaches the critical value , ECM is no longer released and the system reaches equilibrium. This assumption aims at capturing the fact that cells can tune their ECM production in time, and in particular, can down-regulate its release as the outside concentration grows larger. The validity of this assumption, however, remains to be verified via experimental measurements. To characterize the competition between gel degradation and ECM diffusion, it is useful to introduce the following non-dimensional parameter:
| (37) |
where rm is the radius of gyration of an ECM molecule and a coefficient 1E9 has been used so that the ratio Φh is of the order of unity. Typically, Φh is small when the rate of degradation is small compared to the diffusion of ECM molecules (reaction limited) and large otherwise (diffusion limited). We note that the ratio of the size of ECM molecules and the initial hydrogel mesh size ξ0 is the driving factor in this competition: large ECM molecules have a restricted diffusivity (Φh is large) while small ECM molecules can easily permeate through the hydrogel mesh (Φh is small). Fig. 8 shows numerical results of the evolution of ECM concentration in the gel for Φh = 1 and Φh = 100 where once again, ttot is the time required to reach the steady state solution. It is clear here that in the first case (Fig. 8.a), ECM diffusion is significantly faster than in the second case (Fig. 8.b). It is important to note that the competition between degradation and diffusion is complex as degradation indirectly affects the mesh size via swelling; this implies that Φh decreases as degradation proceeds. As a consequence, because hydrolytic degradation is spatially homogeneous, the diffusion of large ECM molecules can only occur in either loosely cross-linked or sufficiently degraded gel, which is characterized by a very low bulk modulus. This phenomenon can be observed by assessing the time evolution of the total amount of ECM present in the hydrogel, introduced as:
| (38) |
and compare it to the relative bulk modulus K̄/K̄ini where K̄ini is the bulk modulus before degradation (Fig. 9). The results show that ECM is only present after the hydrogel has greatly degraded (very low bulk modulus). In other words, ECM transport and deposition can only occur in low modulus gels, which may not be able to sustain physiological loads when implanted in situ. This limitation is a strong motivation for the development of hydrogels that can be degraded locally, via enzyme proteolysis.
Fig. 8.
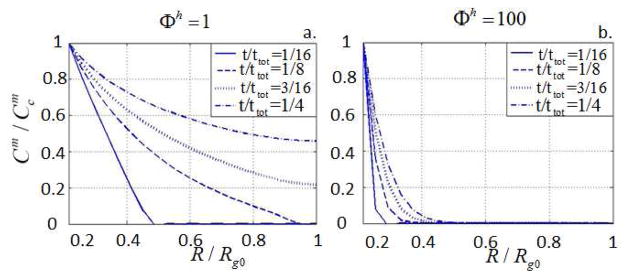
Spatial distribution of matrix molecules ( ) at different times for Φh = 1 and Φh = 100
Fig. 9.
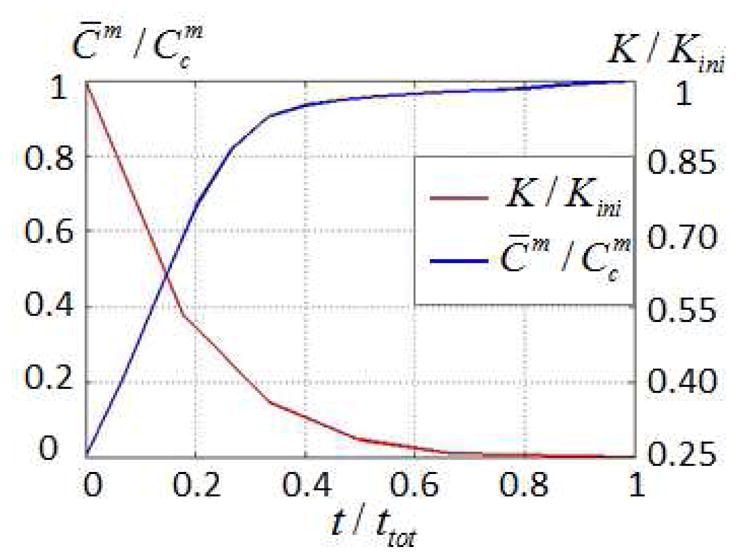
Evolution of ECM molecules diffusion and hydrogel bulk modulus during hydrolytic degradation.
5.3 Role of enzymatic degradation on hydrogel response and ECM molecules diffusion
As opposed to hydrolytic degradation, cell-mediated enzymatic degradation relies on two processes: the diffusion of enzymes in the hydrogel and the resulting inhomogeneous degradation. We investigate this system in two steps: (a) the degradation of the hydrogel without ECM molecules and (b) the combined gel degradation and ECM transport.
Effect of enzymatic degradation on hydrogel stiffness and swelling
Enzymatic degradation is essentially the product of two coupled processes comprising the diffusion of enzymes and the hydrogel degradation according to the Michaelis-Menten kinetics (14). To represent the competition between diffusion and degradation, we introduce a new dimensionless ratio Φe as:
| (39) |
where re is the radius of gyration of an enzyme molecule. On the one hand, as Φe increases, the ability of enzymes to diffuse decreases and the system becomes diffusion-limited. On the other hand, as Φe decreases, the system falls into a reaction-limited regime. Fig. 10 thus depicts the behavior of the system for three characteristic values of Φe (Φe = 1, 10 and 10000). The case Φe = 1 can be interpreted as a situation where the characteristic size of the enzyme is small compared to the hydrogel mesh size. As a results, it can be seen in Fig. 10a that the enzyme diffuses easily in the gel (faster than it degrades it), and crosslink density remains relatively (spatially) homogeneous around the cell (Fig. 10.d). The case Φe = 10000, however, corresponds to a situation in which the enzyme molecules are large compared to the hydrogel mesh size. The consequence is a very slow diffusion (Fig. 10.c) and the appearance of a sharp degradation front separating highly degraded and intact gel regions (Fig. 10.f). This very localized degradation is a feature that is characteristic of enzymatic degradation; its effects on ECM transport and potential in tissue growth are discussed next.
Fig. 10.
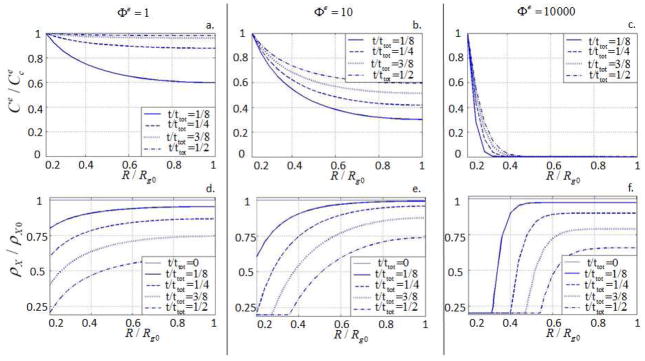
Evolution of the spatial distribution of enzyme concentration and hydrogel crosslink density for different values of Φe.
Effect of enzymatic degradation on the transport of ECM molecules
Similar to hydrolytic degradation, we propose here to characterize the competition between enzymatic degradation and ECM transport with another dimensionless variables Φm defined as
| (40) |
The significance of Φm may be once again understood in terms of the relative size of ECM molecules (to the hydrogel mesh size ξ). Thus, large values of Φm are associated with large ECM molecules for which diffusion is very slow, regardless of the degradation state of the gel. This explains why it appears that ECM diffusion is independent of gel degradation in Fig. 11a. and b. For large values of φe, the presence of a sharp degradation front starts playing a role on ECM distribution. Indeed, in this case, ECM diffusion is facilitated by a degraded gel behind the moving front, but is hindered ahead of the front, as the hydrogel still possesses a smaller mesh size. This coupling between ECM transport and gel degradation becomes more obvious when ECM molecules become smaller (Φm = 10 in Fig. 11). In this situation, ECM molecule diffusion is originally facilitated, but becomes increasingly fast as the gel degrades and the mesh size increases. When a sharp degradation front is present (Fig. 11f.)), we therefore observe that ECM diffusion essentially follows the degradation front. This effect is still present, but becomes milder as Φe decreases, in which case, the degradation front is more spread-out throughout the scaffold (Fig. 11d. and e).
Fig. 11.
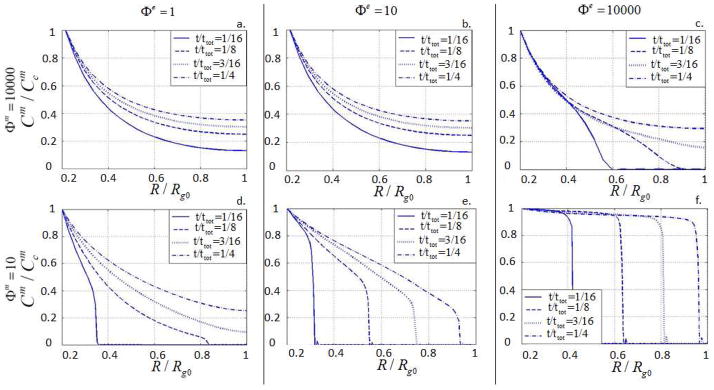
Diffusion of ECM molecules into the gel for different values of Φe and Φm.
This last example therefore clearly shows that when ECM molecules are large compared to the initial hydrogel mesh size, a strong coupling between enzyme diffusion, degradation and ECM diffusion exists. We show here that, due to the inter-dependency between degradation, swelling and transport, it is possible to design the degradation kinetic of a hydrogel in order to control the inhomogeneity of both scaffold degradation and ECM distribution during tissue development. For large Φe and small Φm, we predict a system in which the transition from gel to ECM is very sharp and occurs as a propagating, spherical front around chondrocytes (Fig. 11f.) On the other side of the spectrum, when Φe is small and Φm is large, we predict a system in which gel and ECM are uniformly distributed throughout the scaffold and the degradation occurs in a very homogeneous fashion. This latter situation is reminiscent of a system dominated by hydrolytic degradation.
6 Discussion and concluding remarks
As a summary, this paper presented a mathematical model for the coupled phenomena of hydrogel deformation, degradation and molecular transport with the objective of better understanding how degradation may affect the development of tissue engineered from a cell-laden hydrogel scaffold. A thermodynamical approach was used to incorporate both enthalpic and entropic effects that could explain how the degradation can affect gel elasticity, swelling and permeability. Using a centro-symmetric finite element model, we investigated the effects of two types of degradation (hydrolytic and enzymatic) on loss of scaffold mechanical integrity and ECM diffusion. We particularly showed that, as opposed to hydrolysis, enzyme driven degradation can, in certain circumstances lead to a very localized spherical degradation front around cells and a very inhomogeneous ECM distribution.
To explore the potential effects of these findings on tissue growth, let us assume that the ECM molecules can deposit and acquire mechanical properties only after the hydrogel has lost most of its mechanical properties. To characterize this state, we invoke experimental studies that have shown that reverse gelation (hydrogel loses its solid like properties) occurs when the crosslink density reaches 60–80% of the initial density ρX0 [39]. It is therefore reasonable to assume that the gel is fully degraded, and thus ECM starts participating in the construct’s stiffness, when the cross-link density reaches a critical value ρX = 0.25ρX0. Although it is coarse, this assumption constitutes a realistic scenario for cartilage growth in PEG hydrogels (unpublished communication with Bryant, S.J.). In this context, one can make a rough estimate of the stiffness of the deposited ECM as the ratio of the radius Rfront of the region in which the hydrogel is entirely degraded (and therefore fully occupied by the ECM) and the total radius Rg of the spherical RVE. Thus we write:
| (41) |
where K̂ECM may be thought of as a normalized estimate of the overall ECM stiffness. It verifies K̂ECM = 0 when Rf = Rc, i.e., the gel is intact or only mildly degraded and K̂ECM = 1 when Rf = Rg, i.e. the hydrogel is fully degraded. The balance between hydrogel degradation and ECM deposition can then be explored by plotting both the loss of hydrogel stiffness and gain in ECM stiffness K̂ECM in time for characteristic regimes as summarized in Fig. 12. We note here that the normalized hydrogel stiffness is defined as K̂gel = K̄/K̄ K0 where K̄ was defined in (36) and K̄0 is the value of K̄ when the gel is intact. We can generally make the following observations:
Fig. 12.

Temporal evolution of the loss of hydrogel stiffness K̂ECM versus gain of ECM stiffness K̂gel for different degradation to diffusion ratios. Dashed lines (in blue) correspond to the newly created matrix stiffness, and solid lines (in red) represent the overall stiffness of the hydrogel. The figure indicates the conditions that would preserve total mechanical integrity in time and thus would be most desirable for in situ tissue engineering.
When Φe is small and Φm is large (or when hydrolytic degradation is considered), the degradation is spatially homogeneous and the ECM cannot participate in the overall stiffness before the scaffold is entirely degraded (bottom right in Fig. 12). Since the scaffold needs to be entirely degraded before tissue can form, this scenario is very undesirable from a tissue engineering perspective as the scaffold’s mechanical integrity is not maintained during tissue development.
When Φe and Φm take either small or large values concurrently, the ECM stiffness increases due to the existence of a dispersed front (bottom left and top right in Fig. 12). In these cases, however, the ECM stiffness increases slowly compared to hydrogel degradation, leading to a scaffold that maintains some mechanical integrity, which may not be suffcient to support in vivo physiological during development.
Finally, when Φe is large and Φm is small, the presence of a sharp degradation and ECM front enables two important phenomena (top left in Fig. 12): (a) an optimized ECM stiffness since the hydrogel is entirely degraded behind the front and (b) a postponement of the drop in overall hydrogel bulk modulus. The latter is due to the fact that as the hydrogel degrades locally around the cells, the large volume of intact material left ahead of the front is able to sustain significant loads. Our model predicts here that the scaffold can both preserve its mechanical integrity and promote ECM diffusion and tissue development; this represents a significant improvement compared to current methods based on hydrolytic degradation.
Overall, our theoretical study suggests that enzymatic degradation can provide an excellent alternative to hydrolysis for cartilage tissue engineering. Indeed, its ability to locally degrade the scaffold will potentially make it possible to use hydrogel with higher crosslink densities that can promote tissue development while preserving mechanical integrity throughout tissue development. Our model especially points towards hydrogel design with large Φe and small Φm. In practice, this situation can be achieved by adding a large number of enzymatically degradable crosslinks to the hydrogel to boost the value k2 in the Michaelis-Menten kinetic equation. A large value of k2 (larger than the ratio ) will ensure the creation of a degradation front around cells, which can then promote local ECM molecule diffusion (as Φm will locally decrease). It is finally important to note, that the proposed model is highly idealized and, as such, may sometimes provide an inaccurate picture of the complex physics of scaffold mechanics and degradation. To improve the realism and predictive of the power of the model, future work should concentrate on several important points. First, the assumptions for the cell-mediated release of enzymes and ECM molecules deserve a particular attention as they most likely play a large role into tissue development. In that respect, experimental studies on the role cell sensing and feed-back mechanisms on ECM molecules and enzymes release are greatly needed. Furthermore, very little is known about the mechanisms behind ECM deposition, cross-linking and acquisition of mechanical properties. Direct measurement of these quantities has been very challenging as they are ever changing and difficult to access experimentally. A proper combination of experimental measurements and computer simulations could potentially provide a solution to this problem. Finally, the present analysis has focused on a scaffold with low cell density in which cells were assumed to be periodically distributed. While convenient theoretically, this assumption must be relaxed to obtain more realistic predictions of the overall scaffold stiffness during tissue development. For a random cell distribution at higher density, three-dimensional numerical simulations will thus be necessary to capture a number of phenomena such as the coalescence of ECM islands between adjacent cells. These needs illustrate the fact that the field of computational tissue engineering is still in its infancy and that future successes, notably the development of computer assisted design of tissue scaffolds, will most likely arise from fully integrated experimental/modeling approaches.
Fig. 1.
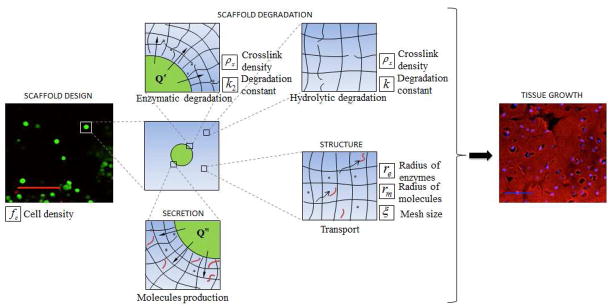
Overview of the processes involved in the early stages of tissue growth from a cell-laden hydrogel scaffold with degradation capabilities. Key model parameters are highlighted for each step in the process. Left picture [12]: scale bar indicates 100 microns. Right picture [12]: scale bar indicates 50 microns.
Table 1.
Inputs and parameters.
| Input name | Notation | Value | Unit | Reference |
|---|---|---|---|---|
|
| ||||
| Polymer density | ρpolymer | 1.07 | g/mL | Estimate |
| Solvent density | ρsolvent | 1 | g/mL | Commonly known |
| Specific volume | ν̄ | 1 | mL/g | Commonly known |
| Polymer charact. ratio | Cn | 4 | - | [38] |
| Average bond length | l | 1.47 | Å | [38] |
| Temperature | T | 310 | K | Physiological temperature |
| Tortuosity | δ | 2 | - | [29] |
| Fluid viscosity | μ̄f | 0.65e−3 | N.s/m2 | [50] |
| Solvent molecules volume | νf | 1e−28 | m3 | [59] |
| Hydrolytic degradation rate | k | 0.18 | /day | Found for experiments fitting |
| Flory-Huggins parameter | χsf | 0.467 | - | [12] |
| Gyration radius of enzymes and ECM molecules | re, rm | 20 | Å | [53] |
Acknowledgments
FJV greatfully acknowledges NIH grant number 1R21AR061011 in support of this work.
A Galerkin form
A mixed formulation is used with three-node elements for the solid phase, and two-node elements for the other phases. The shape functions N and N0 and their derivatives B, B1 and B0 are defined in spherical coordinates (R, θ, ψ). The ψ direction shall not be needed because of the centro -symmetric assumption (same behavior in θ and ψ directions). For example, the first Piola-Kirchhoff stress P can be written .
The shape functions are used to discretize the unknowns and weighting functions to derive weak form of the solid phase, alpha-phase, and the molecular incompressibility. They can be defined in spherical coordinates as:
| (42) |
| (43) |
| (44) |
| (45) |
Discretizing Eq. (27), (28) and (29) is done by injecting Eq. (31) in it. As a result, one can show that the equation of the solid (Eq. (27)) takes the following form:
| (46) |
The alpha phase (Eq. (28)) discretized form is derived:
| (47) |
Finally, the third equation comes from the molecular incompressibility equation (Eq. (29)). Namely:
| (48) |
B Linearized form
In order to solve for the unknown vector y in Eq. (32), Eq. (46), (47) and (48) are linearized. Here,
 , e, nelt and nelt-front denote the assembly operation, element number, number of elements and the number of elements on the boundary (frontier). The unknown vector is written as y =[u [Cα] [π]]T.
, e, nelt and nelt-front denote the assembly operation, element number, number of elements and the number of elements on the boundary (frontier). The unknown vector is written as y =[u [Cα] [π]]T.
B.1 Solid phase
The procedure to linearize the solid expression is to relate the first and the second Piola-Kirchhoff stresses using the expression below, and express the two terms as functions of the unknown fields (Eq (26)):
| (49) |
The latter equation enables to separate the contributions from the material and geometric stiffnesses. The linearized expression thus constitutes the finite element form,
| (50) |
where the stiffness Ks ans the residual vector Rs are defined as
| (51) |
| (52) |
The mechanical stiffness is the summation of the material and geometrical contributions, respectively coming from δS and δF (Eq. (49)). comes from the osmotic pressure term in Eq. (12).
| (53) |
| (54) |
| (55) |
| (56) |
| (57) |
| (58) |
| (59) |
B.2 Alpha phase
The alpha phase equation is linearized after discretization. Thus, Eq. (47) gives
| (60) |
where the damping matrix Cα, stiffness matrix Kα and residual vector Rα are defined as follows
| (61) |
| (62) |
| (63) |
The damping stiffnesses ( and ) come from the time-dependency in Eq. (15), and the stiffness matrices and represent the stiffnesses from Ficks’s and Darcy’s law (Eq. 20).
| (64) |
| (65) |
| (66) |
| (67) |
| (68) |
| (69) |
| (70) |
| (71) |
B.3 Molecular incompressibility
Finally, Eq. (48) linearization results in the last equation:
| (72) |
where the stiffness matrix Kconstr and residual vector Rconstr are defined as follows
| (73) |
| (74) |
The stiffness matrix Kconstr emphasizes that the constraint has an impact on both the solid ( ) and alpha phase ( ). It comes respectively from the term J and ναCα in Eq. (9).
| (75) |
| (76) |
| (77) |
| (78) |
| (79) |
| (80) |
References
- 1.Armstrong CG, Mow VC. Variations in the intrinsic mechanical properties of human articular cartilage with age, degeneration, and water content. The Journal of Bone and Joint Surgery, American volume. 1982;64:88–94. [PubMed] [Google Scholar]
- 2.Ateshian GA, Kim JJ, Grelsamer RP, Mow VC, Warden WH. Finite deformation biphasic material properties of bovine material properties cartilage compression. Journal of Biomechanics. 1997;30(97):1157–1154. doi: 10.1016/s0021-9290(97)85606-0. [DOI] [PubMed] [Google Scholar]
- 3.Ateshian GA. On the theory of reactive mixtures for modeling biological growth. Biomechanics and Modeling in Mechanobiology. 2007;6:423–45. doi: 10.1007/s10237-006-0070-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ateshian GA, Costa KD, Azeloglu EU, Morrison B, Hung CT. Continuum modeling of biological tissue growth by cell division, and alteration of intracellular osmolytes and extracellular fixed charge density. Journal of Biomechanical Engineering. 2009;131:101001. doi: 10.1115/1.3192138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Armstrong CG, Mow VC. Variations in the intrinsic mechanical properties of humanarticular cartilage with age, degeneration, and water content. The Journal of Bone and Joint Surgery. 1982;64:88–94. [PubMed] [Google Scholar]
- 6.Bell CL, Peppas NA. Biomedical membranes from hydrogels and interpolymer complexes. Advances in Polymer Science. 1995;122:125–175. [Google Scholar]
- 7.Boom RM, van den Boomgard Th, Smolders CA. Equilibrium thermodynamics of a quaternary membrane-forming system with two polymers. 1. Calculations. Macromolecules. 1994;27(8):2034–2040. [Google Scholar]
- 8.Bryant SJ, Anseth KS. Hydrogel properties influence ECM production by chondrocytes photoencapsulated in poly(ethylene glycol) hydrogels. Journal of Biomedical Materials Research. 2002;56:63–72. doi: 10.1002/jbm.1217. [DOI] [PubMed] [Google Scholar]
- 9.Chen EI, Kridel SJ, Howard EW, Li W, Godzik A, Smith JW. A unique substrate recognition profile for matrix metalloproteinase-2. The Journal of Biological Chemystry. 2002;277(6):4485–4491. doi: 10.1074/jbc.M109469200. [DOI] [PubMed] [Google Scholar]
- 10.Cowie JMG, Arrighi V. Polymers: Chemistry and physics of modern materials. CRC Press; Boca Raton, Florida: 2008. [Google Scholar]
- 11.Deshmukh M, et al. Biodegradable poly(ethylene glycol) hydrogels based on a self-elimination degradation mechanism. Biomaterials. 2010;31:6675–84. doi: 10.1016/j.biomaterials.2010.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dhote V, Skaalure S, Akalp U, Roberts J, Bryant SJ, Vernerey FJ. On the role of hydrogel structure and degradation in controlling the transport of cell-secreted matrix molecules for engineered cartilage. Journal of the Mechanical Behavior of Biomedical Materials. doi: 10.1016/j.jmbbm.2012.10.016. In Press, Accepted Manuscript, http://dx.doi.org/10.1016/j.jmbbm.2012.10.016 (2012) [DOI] [PMC free article] [PubMed]
- 13.Dimicco MA, Sah RL. Dependence of cartilage matrix composition on biosynthesis, diffusion, and reaction. Transport in Porous Media. 2003;858:57–73. [Google Scholar]
- 14.Farsad M, Vernerey FJ. An XFEM-based numerical strategy to model mechanical interactions between biological cells and a deformable substrate. International Journal of Numerical Methods in Engineering. 2012;92:238–267. [Google Scholar]
- 15.Flory PJ. Principles of polymer chemistry. Cornell University Press; Ithaca, New York: 1953. [Google Scholar]
- 16.Haider MA, Olander JE, Arnold RF, Marous DR, McLamb AJ, Thompson KC, Woodruff WR, et al. A phenomenological mixture model for biosynthesis and linking of cartilage extracellular matrix in scaffolds seeded with chondrocytes. Biomechanics and Modeling in Mechanobiology. 2011;10(6):915–24. doi: 10.1007/s10237-010-0282-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hardingham T. Proteoglycans and glycosaminoglycans. In: Seib MJ, editor. Dynamics of bone and cartilage metabolism. Burlington: 2006. pp. 85–98. [Google Scholar]
- 18.Holland TA, et al. Degradable hydrogel scaffolds for in vivo delivery of single and dual growth factors in cartilage repair. Osteoarthritis and cartilage/OARS, Osteoarthritis Research Society. 2007;15:187–97. doi: 10.1016/j.joca.2006.07.006. [DOI] [PubMed] [Google Scholar]
- 19.Holmes MH, Mow VC. The nonlinear characteristics of soft gels and hydrated connective tissues in ultra-filtration. Journal of Biomechanics. 1990;23(11):1145–56. doi: 10.1016/0021-9290(90)90007-p. [DOI] [PubMed] [Google Scholar]
- 20.Hong W, Zhao X, Suo Z. Large deformation and electro-chemistry of polyelectrolyte gels. Journal of the Mechanics and Physics of Solids. 2010;58:558–577. [Google Scholar]
- 21.Hong W, Liu Z, Suo Z. Inhomogeneous swelling of a gel in equilibrium with a solvent and mechanical load. International Journal of Solids and Structures. 2009;46:3282–3289. [Google Scholar]
- 22.Hootman JM, Helmick CG. Projections of US prevalence of arthritis and associated activity limitations. Arthritis and Rheumatism. 2006;54(1):226–9. doi: 10.1002/art.21562. [DOI] [PubMed] [Google Scholar]
- 23.Horkay F, Tasaki I, Basser PJ. Osmotic swelling of polyacrylate hydrogels in physiological salt solutions. Bio-macromolecules. 2000;1(1):84–90. doi: 10.1021/bm9905031. [DOI] [PubMed] [Google Scholar]
- 24.Humphrey JD, Rajagopal KR, Program BE. A constrained mixture model for growth and remodeling of soft tissues. Mathematical Models and Methods in Applied Sciences. 2002;12:407–430. [Google Scholar]
- 25.Hutmacher DW, Sittinger M, Risbud MV. Scaffold-based tissue engineering: rationale for computer-aided design and solid free-form fabrication systems. Trends in Biotechnology. 2004;22:354–62. doi: 10.1016/j.tibtech.2004.05.005. [DOI] [PubMed] [Google Scholar]
- 26.Huyghe JM, Molenaar MM, Baajens FPT. Poromechanics of compressible charged porous media using the theory of mixtures. Journal of Biomechanical Engineering. 2007;129:776–85. doi: 10.1115/1.2768379. [DOI] [PubMed] [Google Scholar]
- 27.Huyghe JM, Janssen JD. Thermo-chemo-electromechanical formulation of saturated charged porous solids. Journal of Porous Media. 1999;34:129–141. [Google Scholar]
- 28.Ikada Y. Challenges in tissue engineering. Journal of the Royal Society, Interface/the Royal Society. 2006;3:589–601. doi: 10.1098/rsif.2006.0124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kestin J, Khalifa HE, Correia RJ. Tables of the Dynamic and Kinematic Viscosity of Aqueous Nael Solutions in the Temperature Range 20–150 C and the Pressure Range 0.1–35 Mpa. J Phys Chem Ref Data. 1981;10(1):71–87. [Google Scholar]
- 30.Klisch SM, Chen SS, Sah RL, Hoger AA. Growth mixture theory for cartilage with application to growth-related experiments on cartilage explants. Journal of Biomechanical Engineering. 2003;125:169. doi: 10.1115/1.1560144. [DOI] [PubMed] [Google Scholar]
- 31.Klisch SM, Asanbaeva A, Oungoulian SR, Masuda K, Thonar EJ-MA, Sah RL. A cartilage growth mixture model with collagen remodeling: validation protocols. Journal of Biomechanical Engineering. 2008;130(3):031006. doi: 10.1115/1.2907754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kwan MK, Lai WM, Mow VC. A finite deformation theory for cartilage and other soft hydrated connective tissues–I. Equilibrium results. Journal of Biomechanics. 1990;23(2):145–55. doi: 10.1016/0021-9290(90)90348-7. [DOI] [PubMed] [Google Scholar]
- 33.Leddy HA, Awad HA, Guilak F. Molecular diffusion in tissue-engineered cartilage constructs: effects of scaffold material, time, and culture conditions. Journal of Biomedical Materials Research Part B, Applied Biomaterials. 2004;70:397–406. doi: 10.1002/jbm.b.30053. [DOI] [PubMed] [Google Scholar]
- 34.Leskovac V. Comprehensive enzyme kinetics. Kluwer Academic/Plenum Publisheds; New York: 2003. [Google Scholar]
- 35.Lévesque SG, Shoichet MS. Synthesis of enzyme-degradable, peptide-cross-linked dextran hydrogels. Bioconjugate Chemistry. 2007;18:874–85. doi: 10.1021/bc0602127. [DOI] [PubMed] [Google Scholar]
- 36.Li C, Borja RI, Regueiro RA. Dynamics of porous media at finite strain. Computational Methods Appl Mech Engrg. 2004;193:3837–3870. [Google Scholar]
- 37.Lustig SR, Peppas NA. Solute diffusion in swollen membranes. IX. Scaling laws for solute diffusion in gels. Journal of Applied Polymer Science. 1988;36(4):735–747. [Google Scholar]
- 38.Merrill EW, Dennison KA, Sung C. Partitioning and diffbsion of solutes in hydrogels of poly(ethylene oxide) Biomaterials. 1993;14(15):1117–1126. doi: 10.1016/0142-9612(93)90154-t. [DOI] [PubMed] [Google Scholar]
- 39.Metters AT, Anseth KS, Bowman CN. Fundamental studies of a novel, biodegradable PEG-b-PLA hydrogel. Polymer. 2000;41:3993–4004. [Google Scholar]
- 40.Metters AT, Bowman CN, Anseth KS. A Statistical kinetic model for the Bulk Degradation of PLA-b-PEG-b-PLA hydrogel networks. Society. 2000;104:7043–7049. [Google Scholar]
- 41.Metters AT, Bowman CN, Anseth KS. Verification of scaling laws for degrading PLA-b-PEG-b-PLA hydrogels. AIChE Journal. 2001;47(6) [Google Scholar]
- 42.Nicodemus GD, Skaalure SC, Bryant SJ. Gel structure has an impact on pericellular and extracellular matrix deposition, which subsequentely alters metabolic activities in chondrocyteladen PEG hydrogels. Acta Biomateralia. 2011;7:492–504. doi: 10.1016/j.actbio.2010.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nicodemus GD, Bryant SJ. Cell encapsulation in biodegradable hydrogels for tissue engineering applications. Tissue Engineering Part B, Reviews. 2008;14:149–65. doi: 10.1089/ten.teb.2007.0332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nicodemus GD, Bryant SJ. The role of hydrogel structure and dynamic loading on chondrocyte gene expression and matrix formation. Journal of Biomechanics. 2009;41:1528–1536. doi: 10.1016/j.jbiomech.2008.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rubinstein M, Colby RH. Polymer Physics. Oxford University Press; New York: 2003. [Google Scholar]
- 46.Schacht EH. Polymer chemistry and hydrogel systems. Journal of Physics: Conference Series. 2004;3:22–28. [Google Scholar]
- 47.Sengers BG, Van Donkelaar CC, Oomens CWJ, Baaijens FPT. The local matrix distribution and the functional development of tissue engineered cartilage, a finite element study. Annals of Biomedical Engineering. 2004;32(12):1718–27. doi: 10.1007/s10439-004-7824-3. [DOI] [PubMed] [Google Scholar]
- 48.Slaughter BV, Khurshid SS, Fisher OZ, Khademhosseini A, Peppas NA. Hydrogels in regenerative medicine. Advanced Materials. 2009;21(32–33):3307–29. doi: 10.1002/adma.200802106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sun DN, Gu WY, Guo XE, Lai WM, Mow VC. A mixed finite element formulation of triphasic mechano-electrochemical theory for charged hydrated biological soft tissues. International Journal for Numerical Methods in Engineering. 1999;45:1375–1402. [Google Scholar]
- 50.Thorne RG, Hrabetova S, Nicholson C. Diffusion measurements for drug design. Nature Materials. 2005;4:713–714. doi: 10.1038/nmat1489. [DOI] [PubMed] [Google Scholar]
- 51.Treloar LRG. The physics of rubber elasticity. Oxford University Press; New York: 1975. [Google Scholar]
- 52.Trewenack AJ, Please CP, Landman KA. A continuum model for the development of tissue-engineered cartilage around a chondrocyte. Mathematical Medicine and Biology: a journal of the IMA. 2009;26(3):241–62. doi: 10.1093/imammb/dqp013. [DOI] [PubMed] [Google Scholar]
- 53.Vernerey FJ, Greenwald EC, Bryant SJ. Triphasic mixture model of cell-mediated enzymatic degradation of hydrogels. Computer Methods in Biomechanics and Biomedical Engineering. 2011;1:1–14. doi: 10.1080/10255842.2011.585973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Vernerey FJ, Foucard L, Farsad M. Bridging the scales to explore cellular adaptation and remodeling. Bio-nanoScience. 2011;1(3):110–115. [Google Scholar]
- 55.Vernerey FJ, Farsad M. A constrained mixture approach to mechanosensing and force generation in contractile cells. Journal of the Mechanical Behavior of Biomedical Materials. 2011;4(8):1683–1699. doi: 10.1016/j.jmbbm.2011.05.022. [DOI] [PubMed] [Google Scholar]
- 56.Vernerey FJ, Liu WK, Budyn E, Kim JH, To A. Multiresolution mechanics for nano/micro-structured materials. Computational Mechanics. 2007:1–9. [Google Scholar]
- 57.Villanueva I, Hauschulz DS, Mejic D, Bryant SJ. Static and dynamic compressive strains influence nitric oxide production and chondrocyte bioactivity when encapsulated in PEG hydrogels of different crosslinking densities. Osteoarthritis and Cartilage/OARS, Osteoarthritis Research Society. 2008;16:908–18. doi: 10.1016/j.joca.2007.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Yamaoka H, Asato H, Ogasawara T, Nishizawa S, Takahashi T, Nakatsuka T, Koshima I, Nakamura K, Kawaguchi H, Chung U-I, Takato T, Hoshi K. Cartilage tissue engineering using human auricular chondrocytes embedded in different hydrogel materials. Journal of Biomedical Materials Research. 2006;78(1):1–11. doi: 10.1002/jbm.a.30655. [DOI] [PubMed] [Google Scholar]
- 59.Zhang J, Zhao X, Suo Z, Jiang H. A finite element method for transient analysis of concurrent large deformation and mass transport in gels. Journal of Applied Physics. 2009;105:093522. [Google Scholar]