A mathematical model of the coupled mechanisms of cell adhesion, contraction and spreading

Abstract

Recent research has shown that cell spreading is highly dependent on the contractililty of its cytoskeleton and the mechanical properties of the environment it is located in. The dynamics of such process is critical for the development of tissue engineering strategy but is also a key player in wound contraction, tissue maintenance and angiogenesis. To better understand the underlying physics of such phenomena, the paper describes a mathematical formulation of cell spreading and contraction that couples the processes of stress fiber formation, protrusion growth through actin polymerization at the cell edge and dynamics of cross-membrane protein (integrins) enabling cell-substrate attachment. The evolving cell’s cytoskeleton is modeled as a mixture of fluid, proteins and filaments that can exchange mass and generate contraction. In particular, besides self-assembling into stress fibers, actin monomers able to polymerize into an actin meshwork at the cell’s boundary in order to push the membrane forward and generate protrusion. These processes are possible via the development of cell-substrate attachment complexes that arise from the mechano-sensitive equilibrium of membrane proteins, known as integrins. After deriving the governing equation driving the dynamics of cell evolution and spreading, we introduce a numerical solution based on the extended finite element method, combined with a level set formulation. Numerical simulations show that the proposed model is able to capture the dependency of cell spreading and contraction on substrate stiffness and chemistry. The very good agreement between model predictions and experimental observations suggests that mechanics plays a strong role into the coupled mechanisms of contraction, adhesion and spreading of adherent cells.

1 Introduction

Cell spreading and contractions are important players in many biological phenomena such as morphogenesis, wound contraction and tissue maintenance and plays significant roles in certain diseases such as cancer and heart failure [4, 9, 63]. The molecular mechanisms by which cell generate motion and forces depend on a series of highly coordinated events occurring in both the cytoskeleton and at the cell membrane. In the case of adherent cells, membrane proteins, known as integrins, have the ability to mechanically bind to their underlying matrix in the form of large clusters or focal adhesion complexes (FA). A FA typically consists of a complex of integrins and a sub-membrane plaque made of various proteins such as talin and vinculin [16] that are capable of attaching to substrate proteins known as ligands [66, 47]. The formation and stability of FAs has been shown to depend on the mechanical forces exerted on the integrin-ligand complex in a way that increasing the force leads to the growth of FA [70, 58, 8]. These ligand-integrin complexes then provide strong anchor points for the generation of stress fibers, a type of actin filament that is able to generate mechanical forces through acto-myosin interactions at the molecular level [24, 69]. Stress fibers assemble from a variety of proteins present in the cytosol such as globular actin and non-muscle myosin, a process that is now known to be driven by the nature of a cell’s mechanical environment [84, 56, 29, 12]. On stiff substrates, cells develop strong focal adhesions and stress fibers while the opposite trend is observed in soft environments [24, 69]. While cell adhesion and contraction are ultimately dependent on one another, they also have a strong influence on the phenomenon of cell spreading. In a nutshell, the presence of adhesion complexes influences spreading by enabling cells to extend a branched network of actin filaments (the lamellipodia) beneath its membrane [13, 27, 53, 59] and pushes it forward [15, 19, 53, 59]. As a result, cell growth and spreading are highly sensitive on the mechanical properties of the cell’s substrate [14, 60, 61, 66]; this is particularly apparent in experiments showing that cell area and rate of spreading increase in a nonlinear fashion with substrate stiffness and ligand density. Overall, the above observations have been extremely useful at highlighting the fact that contraction, spreading and adhesion are strongly interconnected mechanisms whose interactions determine the ways by which cells can sense and react to their mechanical environment. There are still, however, many questions regarding the nature of these interactions and how they can explain the myriad of mechano-responsive behaviors (including contraction, spreading, migration as well as matrix degradation and production [28, 73, 72]) displayed by adherent cells in both healthy and diseased states.

Mathematical models have been very useful at quantifying a number of chemical and mechanical processes of cell contraction and migration. For instance, the mechanisms of stress fiber orientation with mechanical forces have been assessed by variety of models, some based on purely thermodynamical arguments [25, 68] and some based on biochemically arguments including signalling pathways [11]. At the cellular level, the development of global stress fibers organization, contraction and adhesion have recently been the object of a formulation [18] based on empirical relationship describing the mechanically driven dissociation of stress fibers and integrin dynamics. A similar continuum approach was later introduced within the framework of mixture theory [78, 75], therefore providing a more natural formulation to describe growth and mass exchanges between constituents in the cell. Similarly, the complex phenomenon of cell adhesion has been the object of a number of modeling studies in the context of cell migration [19], focal adhesion assembly [65, 51, 5, 6], and mechano-sensitivity [80], but has not, so far, been incorporated in a global cell model accounting for contraction and spreading. In turn, the problem of protrusion growth has traditionally been studied by considering the force induced by polymerization of new actin filaments beneath the membrane [57, 42], leading the Brownian ratchet model. It is particularly interesting to note here that application of the above mechanisms at the level of a whole cell has recently been successful at reproducing the shape transition from a spherical fibroblast to a polarized cell possessing the attributes of a migrating fish keratocyte [33]. The physics of single filopodia growth was also investigated with mathematical models in [49] by similarly invoking force balance between actin polymerization and membrane resistance and the interplay between growth and membrane proteins was investigated in the context of cell crawling [38]. More recently, Li et al. [46] introduced a formulation for cell spreading in which the Brownian Ratchet model was extended to account for the existence of a pulling force that facilitates actin filament growth. This approach was successful at predicting the overall increase in cell spreading with bond density as well as the power-law relationship between contact radius and time. It did not, however, capture the effect of substrate stiffness on cell contraction and spreading dynamics. More generally, while the above models have successully captured distinct aspects of cell behaviors, the relationship between protrusion growth, cell contraction and substrate properties has, to the knowledge of the authors, not been established.

The present work is therefore an attempt to capture, in a unified fashion, the coupled dynamics of adhesion, contraction and spreading via the introduction of a thermodynamic model that accounts for the various cross-talks between mechanics and chemistry occuring in adherent cells. The model is based on three important features: (i) the chemo-mechanical interactions responsible for the formation and contraction of stress fibers, (ii) the transport and attachment of integrins to the ligand of their underlying substrate and (iii) a force dependent membrane protrusion growth. The attractiveness of the model lies in the simplicity of its assumptions, its physical motivations and its ability to describe various features observed in adherent cells. For instance, the model of stress fiber organization has previously shown that it could capture their complex orientation and formation under varying substrate stiffness as well as constant and cyclic stretch [25]. To assess the outcomes of the model, we further introduce a numerical formulation that can naturally handle the moving boundary problem associated with cell growth. The formulation is then used to assess model prediction in terms of cell’s sensitivity to its mechanical environment. We find that cell contraction, adhesion and spreading are strongly determined by factors such as substrate stiffness and ligand density. Model predictions are in very good agreement with experimental observation, which suggests that some key mechanisms of cell spreading have been captured by the model.

The paper is organized as follows: we first introduce the mathematical formulation based on the chemical and mechanical equilibrium of the cytoskeleton and its surrounding membrane. A numerical strategy is then presented to solve the system of differential equations and a strategy based on the level set method is proposed to capture cell growth. We then assess the soundness of the model by investigating a few biologically relevant problems and providing comparisons with experimental results. We finally conclude by providing a brief summary of the work and future perspectives.

2 Mathematical model of cell contraction, adhesion and growth

The following study concentrates on the case of a thin, circular cell laying on an isotropic, linear elastic substrate with variable stiffness. The isotropy assumptions imply that the cell remains circular during growth and that the original three-dimensional problem can be reduced into a one-dimensional plane-stress axisymmetric approach (Fig. 1). Experimental observations [32] indeed suggest that cells on two-dimensional substrate usually display a relatively small thickness (1–5 microns) compared to their in-plane dimensions (tens to hundreds of microns) and that stress-fibers are mostly oriented in the plane of the substrate and localize towards the bottom of the cell. This implies that forces are mostly oriented in plane and net zero out-of plane stress components can be assumed, consistent with plane-stress assumptions. Although they do not affect the generality of the formulation, these assumptions will greatly improve the clarity and simplicity of the model. We also emphasize that the one-dimensional equation presented in the paper are derived from the original three-dimensional geometry, which is subjected to the axisymmetric and plane stress assumptions. It is in this context that we next introduce the general equations governing the phenomena of cell contraction, adhesion and growth by invoking the thermodynamic equilibrium of various cell constituents.

Figure 1.

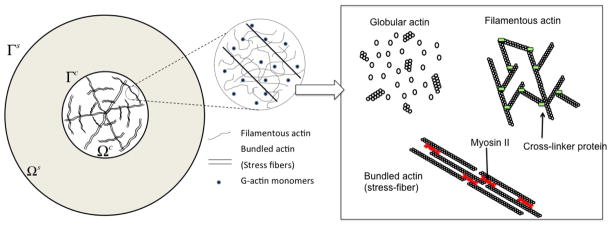
General configuration of an circular cell located on an elastic substrate with a representation of the three forms of actin considered in this study: globular, filamentous and bundled (stress fibers).

2.1 Cytoskeleton dynamics and equilibrium

The highly dynamic and responsive behavior of the cytoskeleton arise from the fact that its principal constituent, actin, is never at equilibrium and constantly consumes chemical energy in the form of adenosine triphosphate (ATP) [39]. ATP is responsible for numerous important phenomena in the cytoskeleton such as actin filament treadmilling and the generation of mechanical work by myosin II (which induce contractile force in actin filament bundles (e.g. stress-fibers)). The present study only attempts to represent these molecular processes in an average sense by describing the actin cytoskeleton as a mixture of four major constituents representing the cytosol and actin in three different forms: globular, filamentous, and bundled (Fig. 1). In its globular form, actin easily diffuses throughout the cytoskeleton and thus, may be represented as a fluid phase in the present study. In its filamentous form, however, actin may be thought of as a solid-like chemical gel that is cross-linked by other cytoskeletal proteins such as filamin dimers. Finally, in its bundled form (interpreted here as stress fibers), actin usually combines with myosin II motors such that a contractile stress often arises in the bundle’s direction. This is a direct consequence of the non-equilibrium processes at the molecular scale.

In our study, the dynamics of actin assembly/disassembly is particularly important in two situations. (a) Within the cytoskeleton, the actin turn-over is responsible for the formation of stress fibers, a process that, we will see, depends on nature of mechanical constraints provided by the underlying substrate. It is assumed that the turn-over rate is fast compared to the rate of cell spreading, which allows us to consider that the actin cytoskeleton is in a state of dynamic equilibrium at all time. (b) Near the cell periphery, the dynamics of actin assembly are resisted by mechanical forces arising from membrane stretching, bending and adhesion. In other words, it is the difference between the driving force for actin assembly and the above mechanical forces that determine the rate of cell spreading. Detailed discussions of these processes in the context of cell motility are provided in [49, 10, 62]

2.1.1 Chemical equilibrium in the cytoskeleton

While the actin cytoskeleton is a non-equilibrium polymer, we assume here that, at larger length scales, it may reach a state of dynamic equilibrium. In other words, while changes of phase between actin in its different forms continuously occur, these reactions may reach a steady state at which the overall volume fractions of each constituent ceases to change. This dynamic equilibrium can be studied by describing the evolution of the cytoskeleton in terms of the different constituent’s volume fractions φ^f, φ^m, φ^c and ${\phi }_i^{SF}$ where superscripts f, m, c and SF denotes the fluid cytosol, G-actin, the passive cytoskeleton (made of elements such as microtubules and intermiediate filaments) and stress fibers, respectively. In particular, because of their directionality, the volume fraction ${\phi }_i^{SF}$ of stress fibers contains two contributions: one representing stress fibers oriented in the radial direction (i = r) and one representing them in the circumferential direction (i = θ). The above constituents may exchange mass with one-another in a way that they decrease their free energy. Following a similar approach as Shemesh et al. [64], the dynamic equilibrium between actin monomers in their “free” and “stress-fiber” phase can be determined by stating that their respective chemical potentials μ^m and μ^SF remain equal at all time, i.e.:

$${\mu }^m={\mu }^{SF}.$$ (1)

As actin monomers form a dilute solution in the cytosol, it is possible to evaluate their chemical potential in terms of the volume fraction ${\phi }_f^m={\phi }^m/{\phi }^f$ in the fluid phase as follows:

$${\mu }^m={\mu }_0^m+k_{B}Tln({\phi }_f^m)$$ (2)

where T is the thermodynamic temperature, ${\mu }_0^m$ is the reference chemical potential of globular actin (evaluated at ${\phi }_f^m=1$) and k_B is the Boltzman constant. The aggregation of actin into filament and stress fibers is known to be strongly influenced by mechanics [81, 67, 31, 45]; this motivated the introduction of thermodynamical models [25, 64] in which filament stability is promoted with contractile work and decreased with stored elastic energy. Following this model and considering stress fibers as anisotropic filaments with no translational entropy, the chemical potential of actin monomers in a stress fiber aligned in direction i (i = r, θ) can be written as:

$${\mu }_i^{SF}={\mu }_0^{SF}+\frac{1}{2}{E}_1{\epsilon }_i^2-T^{\ast }{\epsilon }_i$$ (3)

where ${\mu }_0^{SF}$ is the reference potential and the last two terms denote the mechanical contribution of the chemical potential in which E₁, T^* and ε_i are the stiffness, contractile stress and strain experienced by stress fibers, respectively. These terms indicates that the chemical potential actin monomers in a stress fiber increases with its stored elastic energy while it decreases with acto-myosin contraction T^* if positive stretch is applied (ε_i > 0). This model is critical to describe the dependence of stress-fiber stability on substrate stiffness. For instance, when a cell adheres to a stiff substrate, stress fiber contraction generates very little deformation (ε_i is negligible) and the chemical potential ${\mu }_i^{SF}$ is unaffected. However, when it adheres onto soft substrates, cell contractions may generate significant compaction (negative strain ε_i). In this case, the last two terms in (3) trigger a rise in ${\mu }_i^{SF}$ which ultimately results in a drop in stress-fiber concentration. A more extensive discussion of these processes is provided in [25].

2.1.2 Protein transport and mass exchange

To reach chemical equilibrium, constituents may decrease or increase their chemical potentials by exchanging mass with one another. For instance, actin monomers can self-assemble (or disassemble) into either the filamentous cytoskeleton or stress fibers during the process of remodeling. These processes are usually accompanied with monomer transport through the cytosol, a phenomena that can influence the rate of cell evolution. Mathematically, mass exchange and transport phenomena are described by mass conservation equations and constitutive relations for actin and cytosol flux. In the context of incompressible constituents, the mass balance of each constituent can be written in terms of their volume fractions as follows:

$$\frac{D{\phi }^{\alpha }}{Dt}+{\phi }^{\alpha }\nabla ·{\mathbf{v}}^c+\nabla ·{\mathbf{J}}^{\alpha }=\frac{{\rho }^{\alpha }{\mathrm{\Pi }}^{\alpha }}{{\rho }_T^{\alpha }}\alpha =m,f$$ (4)

$$\frac{D{\phi }^{SF}}{DT}+{\phi }_i^{SF}\nabla ·{\mathbf{v}}^c=\frac{{\rho }^{SF}{\mathrm{\Pi }}_i^{SF}}{{\rho }_T^{SF}}$$ (5)

$$\frac{D{\phi }^c}{Dt}+{\phi }^c\nabla ·{\mathbf{v}}^c=0$$ (6)

where D ·/Dt denotes the material time derivative with respect to the solid phase while v^α and J^α = φ^α(v^α−v^c) are the velocity of constituent α and the relative fluxes of monomer and cytosol through the cell, respectively. We have also introduced two types of mass densities. On the one hand, the true mass density ${\rho }_T^{\alpha }$ is the mass per unit volume of pure constituent α and is related to the specific volume ν^α of phase α via ${\rho }_T^{\alpha }=1/{\nu }^{\alpha }$. On the other hand, the partial mass density ρ^α is defined the mass of constituent α per unit volume of mixture. To allow mass exchange between constituents, we have finally invoked the quantity ρ^αΠ^α as rate of mass formation of constituent α per total mixture volume. For the sake of simplicity, we assume here that the net mass exchange only occurs between globular actin and stress fibers, i.e., neither the cytosol nor the passive cytoskeleton are allowed to exchange mass with other constituents (Π^f = Π^c = 0). This assumption is motivated by the fact that G-actin first polymerizes into a filamentous form, which then can bundle into stress fibers. In this process, while the filamentous actin present in the passive cytoskeleton is constantly renewed in time, its net mass generation remains invariant. It is important to note that this assumption does not imply that the volume fraction φ^c is constant. In fact, as can be seen in (6) that the quantity φ^c can undergo large changes as a result of volumetric deformations of the cytoskeleton, represented by the term ∇ · v^c.

Three assumptions can then be made to simplify the formulation. First, the mixture is saturated, i.e., ${\phi }^c+{\phi }_r^{SF}+{\phi }_{\theta }^{SF}+{\phi }^m+{\phi }^f=1$. Second, the true mass density of actin is constant, regardless of its phase, i.e, ${\rho }_T^c={\rho }_T^{SF}={\rho }_T^m$. Third and finally, the total mass of the mixture is conserved, which directly implies that Σρ^αΠ^α = ρ^mΠ^m + ρ^SFΠ^SF = 0. Applying these assumptions and after some calculations, one can show that the mass conservation of the cytosol, mixture and passive cytoskeleton, respectively, along with the saturation constraint can be written (under plane stress and asymmetric assumptions):

$${\stackrel{.}{\phi }}^f+\alpha {\phi }^f\left(\frac{\partial v^c}{\partial r}+\frac{v^c}{r}\right)+\beta {\phi }^f\stackrel{.}{p}+\left(\frac{\partial J^f}{\partial r}+\frac{J^f}{r}\right)=0$$ (7)

$$\alpha \left(\frac{\partial v^c}{\partial r}+\frac{v^c}{r}\right)+\beta \stackrel{.}{p}+\left(\frac{\partial J^f}{\partial r}+\frac{J^f}{r}\right)+\left(\frac{\partial J^m}{\partial r}+\frac{J^m}{r}\right)=0$$ (8)

$${\stackrel{.}{\phi }}^c+\alpha {\phi }^c\left(\frac{\partial v^c}{\partial r}+\frac{v^c}{r}\right)+\beta {\phi }^c\stackrel{.}{p}=0$$ (9)

$${\stackrel{.}{\phi }}^f+\frac{1}{1+{\phi }_f^m}\left({\phi }^f{\stackrel{.}{\phi }}_f^m+{\stackrel{.}{\phi }}^c+{\stackrel{.}{\phi }}^{SF}\right)=0$$ (10)

where all velocities and fluxes are in the radial direction (circumferential directions vanish due to the problem’s symmetry). Furthermore, we introduced p as the fluid pressure and the coefficients α = (1 − 2ν^c)/(1 − ν^c) and β = (1 + ν^c)(1 − 2ν^c)/(E^c(1 − ν^c)) are obtained by applying plane stress conditions (see appendix 7.1 for details). It is important to note that although the rates of mass exchange between actin in its monomer and fiber form (represented by Π^m and Π^SF) have disappeared from the system, mass transfer still occurs and is captured by the instantaneous equilibrium in chemical potential (1). This statement is, of course, only accurate in the case where chemical reactions occur at a much faster rate than molecular diffusion within the cell. To capture the phenomenon of molecular transport of cytosol and actin monomers, we however need to specify constitutive equations relating radial fluxes J^f and J^m to the gradient of fluid pressure and monomer concentrations. Following Darcy’s law and Fick’s law of particle diffusion in a fluid, we can derive the following expressions [78]:

$$J^f=-\frac{\kappa }{\mu }\nabla p,J^m=-{\phi }_f^m\frac{\kappa }{\mu }\nabla p-{\phi }^{f}D\nabla {\phi }_f^m$$ (11)

in which κ, μ, and D are the cytoskeleton permeability, cytosol viscosity, and G-actin diffusion constant in the cytosol, respectively.

2.1.3 Mechanical equilibrium, stress and deformation

In addition to constantly remodeling their cytoskeleton, adherent cells are able to contract, deform and apply relatively large forces to their surroundings. Such processes can typically be described by the concepts of stress, strains and the associated momentum balance equations.

The deformation of the cytoskeleton arises from the interplay between a variety of forces that originate from stress fiber contraction and the resistance of the underlying substrate via focal adhesion. To mathematically represent each contribution, it is useful to introduce the total stress T as the overall internal force per unit area of mixture. Under our specific assumptions, T is represented by two components, T_r and T_θ, in the radial and circumferential directions, respectively and using mixture assumptions, one can decompose the stress as

$$\mathbf{T}={\mathbf{T}}^c+{\mathbf{T}}^{SF}-p\mathbf{I}$$ (12)

where I = [1 1]^T, p is the cytosol pressure, T^c the partial stress in the passive cytoskeleton and T^SF the partial stress induced by stress fiber. We note here that the term “passive cytoskeleton” was used on a broad sense as it represents a number of possible components contributing to the cell elasticity. This includes for instance, microtubules, intermediate filaments and the membrane located on top and the bottom of a planar cell. Assuming small deformation (strains are typically less than 10% in the problem of interest), a linear elastic relation can be used to describe the passive cytoskeleton response:

$$T_i^c=\frac{E^c}{1-{\nu }^{c2}}\left(a_i{\epsilon }_r^c+a_j{\epsilon }_{\theta }^c\right)+\frac{{\nu }^c}{1-{\nu }^c}pi=r,\theta \text{and}j=\theta ,r$$ (13)

where a_r = 1 and a_θ = ν^c. The material parameters E^c and ν^c represent the Young’s modulus and Poisson’s ratio, respectively while the radial and circumferential linear strains ε_r and ε_θ are related to the radial displacement u by ε_r = ∂u/∂r and ε_θ = u/r. As discussed in more detail in [78], the partial stress T^SF of stress fibers is proportional to the volume fractions ${\phi }_i^{SF}$ and arises from two different sources: active contraction and passive elastic response. We therefore write:

$$T_i^{SF}={\phi }_i^{SF}(E_1{\epsilon }_i+T^{\ast })i=r,\theta$$ (14)

where the coefficient E₁ denotes the stiffness of stress fibers while the contractile stress T^* is the result of acto-myosin cross-bridge dynamics at the sarcomeric level [78]. Although sarcomere force is known to depend on the rate of contraction as predicted by the Hill model [35], we choose to neglect this aspect for the present study and consider that the contractile stress is constant and equal to that found in a state of isometric contraction. This assumption is motivated by the fact that cell spreading is a slow process compared to the characteristic time-scale of cross-bridge dynamics and is therefore insensitive to the rate of elongation of sarcomeres. Finally, force equilibrium in the mixture follows from the balance of linear momentum. Under axisymmetric and plane-stress conditions, this yields:

$$\frac{\partial T_r}{\partial r}+\frac{1}{r}(T_r-T_{\theta })-\frac{t^i}{h}=0$$ (15)

In above equation, h denote the thickness of the cell and tⁱ represents the distributed traction force on the membrane arising from the interaction with the underlying substrate via focal adhesion. While this force is applied at the bottom of a cell through its membrane, it is equivalent to consider it as a tangential body force applied to the cytoskeleton by invoking plane stress assumptions. To finally characterize the behavior of the underlying substrate, it is first useful to note that its thickness is usually much larger than that of cells. In this situation, stress variations are expected in a direction perpendicular to the plane, rendering plane-stress assumptions inappropriate. However, a precise study of substrate stresses is beyond the scope of this study; we therefore choose to simplify the formulation by considering a substrate thin enough for plane stress conditions to be applicable. While they do not affect the applicability of the model, these considerations significantly simplify its formulation and capture the main trends exhibited by a three-dimensional substrate, i.e., variable stiffness and ligand density. We note that the extension to finite thickness substrates will not present any major difficulty and is left for future studies. In this context, the elasticity of the substrate is characterized by its Young’s modulus E^s and Poisson’s ratio ν^s such that the stress T^s is expressed in terms of the substrate strain ε^s via an equation similar to (13). Substrate equilibrium then takes a similar form that of the cell’s equilibrium:

$$\frac{\partial T_r^s}{\partial r}+\frac{1}{r^s}\left(T_r^s-T_{\theta }^s\right)+\frac{t^i}{h}=0.$$ (16)

Note that the main different between (15) and (16) is that the forces tⁱ applied by the cell on the substrate have the same magnitude but opposite direction as those applied by the substrate on the cell.

2.2 Cell membrane and membrane proteins

Cytoskeleton remodeling and contraction cannot proceed without the existence of physical links that anchor adherent cells to their underlying substrate. In turn, the existence of such links is driven by the dynamics and equilibrium of the phospho-lipid membrane on which a population of proteins, known as integrins, may diffuse and self-assemble into large focal adhesion complexes [44]. A mathematical model for the chemical equilibrium, transport and mechanical role of these surface proteins is provided below.

2.2.1 Chemical equilibrium of integrins

Integrins can usually be found in two states (Fig. 3): (1) an active (or high-affinity) state in which they take a straight configuration and can bind to substrate ligands and (2) an inactive (or low affinity) state in which they take a bent configuration and are unable to attach to ligands. To investigate the chemical equilibrium between these two states, we take a thermodynamical approach (similar to that introduced for the cytoskeleton) in which the chemical potentials μ^H and μ^L of high and low affinity integrins must verify:

$${\mu }^H={\mu }^L$$ (17)

at equilibrium. At low concentration, unbound low affinity integrins can typically be viewed as a dilute solution in the fluid phospho-lipid membrane such that their chemical potential increases with their area density c^L as follows:

$${\mu }^L={\mu }_0^L+k_{B}Tln\left(\frac{c^L}{c_0^I}\right)$$ (18)

where ${\mu }_0^L$ and $c_0^I$ are the free energy and concentration of low-affinity integrin in standard condition, respectively. The chemical stability of high affinity integrins is known to depend on the amount of tensile forces they are subjected to [65, 58, 70]. In other words, when integrins physically attach to substrate ligands, cell contraction (from stress fiber) triggers a stretching force on the integrins which tends to increase their stability. To capture this phenomenon, it is first important to consider the existence of high infinity integrins in two conditions: those which are bound (with concentration c^BH) and those which are unbound (with concentration c^UH) to substrate ligands. Following [44], the concentration of bound integrins can be expressed as a function of the underlying ligand concentration c^lg as follows:

$$c^{BH}=\frac{c^{lg}}{1+c^{lg}}{c}^H.$$ (19)

Figure 3.

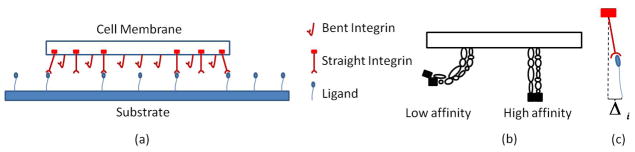
Integrin-ligand complexes: a) ligands, low affinity integrins, and bound/unbound high-affinity integrins, b) integrin states, c) relative displacement between two sides of integrin-ligand complex.

This expression clearly shows how increasing the ligand concentration tends to promote the attachment of integrins to the substrate. The stabilization of integrins with stretch has then led to the following form of their chemical potential [16]:

$${\mu }^{UH}={\mu }_0^H+k_{B}Tln\left(\frac{c^H}{c_0^I}\right)$$ (20)

$${\mu }^{BH}={\mu }_0^H+k_{B}Tln\left(\frac{c^H}{c_0^I}\right)-\frac{1}{2}{\lambda }_s{\mathrm{\Delta }}_i^2$$ (21)

where ${\mu }_0^H$ is the standard chemical potential of high affinity integrins. These equations show that when unbound, integrins do not stretch and therefore cannot be stabilized by mechanical forces. However, when bound, integrins may decrease their chemical potential by increasing their elastic energy, represented here by the term $\frac{1}{2}{\lambda }_s{\mathrm{\Delta }}_i^2$, (in which Δ_i is the integrin stretch and λ_s is the stiffness of the bond). This feature is responsible for the formation of focal complexes in regions subjected to large forces. We are now in a position to express the total chemical potential μ^H of high infinity integrins by realising that μ^H = φ^UHμ^UH + φ^BHμ^BH, where φ^UH and φ^BH are the fractions of undbound and bound, respectively. Further using (19) and the facts that φ^BH = c^BH/c^H and φ^UH = 1 − φ^BH, we obtain:

$${\mu }^H={\mu }_0^{\ast }+k_{B}Tln\left(\frac{c^H}{c_0^I}\right)-\frac{c^{lg}}{2(1+c^{lg})}{\lambda }_s{\mathrm{\Delta }}_i^2$$ (22)

where the constant ${\mu }_0^{\ast }$ is given by ${\mu }_0^{\ast }={\mu }_0^H+k_{B}T\left[c^{lg}ln(c^{lg})/(1+c^{lg})-ln(1+c^{lg})\right]$. Generally, because of their straight configuration, unbound high affinity integrins are less stable than low infinity integrins ( ${\mu }_0^{\ast }>{\mu }_0^L$); this implies that only bound and stretched high infinity integrins remain stable while others quickly convert to their low affinity state. Equation (22) suggests that ligand concentration c^lg has an important role in this equilibrium. For instance, for low ligand density, mechanical stabilization of integrins is greatly reduced and cells are not able to properly attach to the substrate; this has significant consequences during contraction and spreading as discussed in the result section.

2.2.2 Integrin transport and attachment

Let us now investigate the transport and mass exchange between integrins in their respective states. The diffusion of integrins on the phospho-lipid membrane is very sensitive to their state; when assuming a bent configuration, integrins can easily diffuse through the membrane. However, when assuming a straight configuration, their motion is strongly impeded; this translate into the fact that their flux J^H can generally be neglected. Based on this argument, the mass balance of integrins on the cell membrane is only written in terms of the flux J^L of low affinity integrins as:

$$\frac{{Dc}^L}{Dt}+c^L\nabla ·v^c+\nabla ·J^L=c^L{\mathrm{\Pi }}^L$$ (23)

$$\frac{{Dc}^H}{Dt}+c^H\nabla ·v^c=c^H{\mathrm{\Pi }}^H$$ (24)

where c^LΠ^L and c^HΠ^H define the rate of convertion between high and low-affinity integrins per unit membrane area and vice versa. Note that in the above equation, we have considered that the membrane velocity is that same as that of the underlying cytoskeleton v^c. This is consistent with the plane-stress assumptions that in-plane velocities (cytoskeleton and membrane) do not vary across the infinitesimal cell thickness. Conservation of the total number of integrins may then be invoked (c^LΠ^L + c^HΠ^H = 0) in order to write the mass balance of the entire integrin population as follows:

$$\frac{D(c^L+c^H)}{Dt}+\left(c^L+c^H\right)\left(\frac{\partial v^c}{\partial r}+\frac{v^c}{r}\right)+\left(\frac{\partial J^L}{\partial r}+\frac{J^L}{r}\right)=0.$$ (25)

It can be seen here that the rate of mass exchange Π^H and Π^L do no longer appear in the mass balance. Instead, equation (17) is invoked to ensure that the relative concentrations of low and high affinity integrins satisfy chemical equilibrium at all time. The flux J^L of low affinity integrins can finally be written in terms of their (surface) gradient as [44]:

$$J^L=-m\nabla c^L$$ (26)

where m is the mobility coefficient. As discussed above, cell-substrate attachment forces are entirely defined by the local concentration of bound integrin. It is therefore possible to evaluate the force tⁱ (appearing in (15) and (16)) exert by integrins on the elastic substrate from the knowledge of the concentration c^BH of bound high affinity integrins. In particular, the focal adhesion traction (per unit area) may simply be calculated as follows:

$$t^i=c^{BH}{\lambda }_s{\mathrm{\Delta }}_i$$ (27)

where λ_s is the complex stiffness (with unit of force per length) and Δ_i = u^c−u^s is the relative cell-substrate deformation (Fig. 3c). The above equation clearly states that deformation coupling between a cell and its substrate is strongly influenced by integrin clustering at focal adhesion.

2.2.3 Membrane mechanics and deformation

A major contributor to cell deformation and evolution, especially when growth is involved, is the effect the membrane tension, represented by a circumferential stress T^σ. Here, we simplify the analysis by representing the membrane as a circular elastic film surrounding the cell, undergoing a stretching deformation as the cell spreads. In that respect, it is important to note that although deformations remain relatively small in the actin cytoskeleton (the change in cell area mostly arises from surface growth), the strains in the surrounding membrane can become fairly large as a result of the potentially significant increase in cell circumference [61, 66]. For this reason, we use a large strain measure, namely the Green-Lagrange strain, to capture the membrane deformation. For our plane-stress axisymmetric geometry, this strain is directly related to the increase in cell radius from its original value $a_0^c$ to its current value a^c as:

$$E^{\sigma }=\frac{1}{2}\left({\left(\frac{a^c}{a_0^c}\right)}^2-1\right)$$ (28)

To characterize the membrane elasticity, it is useful to introduce the elastic potential ψ(E^σ) such that the membrane stress reads:

$$T^{\sigma }=\frac{\partial \psi }{\partial E^{\sigma }}F\text{and}\psi (E^{\sigma })=T_0^{\sigma }{E}^{\sigma }+\frac{1}{2}{k}^{\sigma }{(E^{\sigma })}^2$$ (29)

Here F = a/a₀ is the deformation gradient, $T_0^{\sigma }$ is the pre-existing surface tension and k^σ is the stiffness of the cell membrane. The mechanical equilibrium of the membrane with cytoskeleton stresses is then given by the standard equation [77, 76]:

$$\mathbf{T}·\mathbf{n}={\nabla }_{\sigma }·{\mathbf{T}}^{\sigma }\Rightarrow T_r^{\mathrm{\Gamma }}=-\frac{T^{\sigma }}{a^c}$$ (30)

where T is the stress tensor in the cytoskeleton, n is the outward normal to the cell, ∇_σ is the surface gradient operator and T^σ = T^σe_θ is the surface tension vector. It can be shown that due to our axisymmetric assumptions, this equation reduced to the simpler form shown in the right end side of (30) in which $T_r^{\mathrm{\Gamma }}$ denotes the radial stress on the boundary Γ.

2.3 Membrane protrusion and cell growth

Let us now concentrate on the the phenomenon of membrane protrusion from a physical viewpoint. This aspect of cell mechanics is known to involve strong interplays between actin polymerization at the cell’s edge and membrane resistance [15, 19, 53, 59, 74, 79, 83]. Similar to the previous section, such chemo-mechanical couplings can be mathematically addressed by considering the chemical equilibrium of the cytoskeleton at the cell edge and how it is affected by mechanical forces exerted by the cell membrane. We therefore consider a simple thermodynamical model based on the work of Hill [36], that describes the kinetic of actin filament assembly against a physical force (provided by the membrane). The rate of assembly of actin filaments is the result of simultaneous addition and removal of G-actin monomers onto an aggregate occurring at rates k_on and k_off, respectively. Referring to Fig. 4, the velocity V at which a filament grows can then be related to the half-monomer size δ as:

$$V=\delta \left(k_{on}{\phi }_f^m-k_{\mathit{off}}\right)$$ (31)

Figure 4.

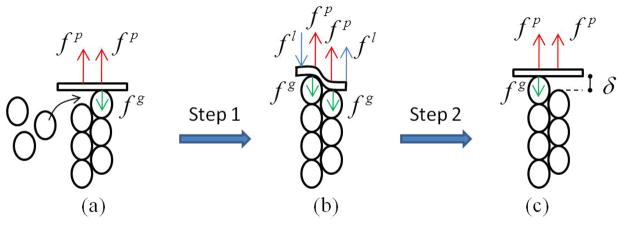
A cycle of actin polymerization beneath the cell membrane: a) G-actin monomers inserts between the existing filament and cell membrane, b) cell membrane is bent such that one monomer is bound at the end of the existing filament, and c) cell membrane returns to its unbent configuration.

The rate constants are, of course, dependent on the resisting force of the membrane, as well as the forces exerted by integrins on the membrane. These effects are discussed next.

2.3.1 Effect of membrane and integrin forces on actin aggregation

Protrusion growth is the result of the chemo-mechanical equilibrium of a system composed of growing actin filaments and a resisting membrane. Experimental observations showing that actin polymerization at the cell edge are concentrated near focal adhesion [55, 54] has led us to consider the effect of integrins pulling force on the membrane as a contributing factor to this chemical equilibrium. To understand the effect of this force, we consider the growth of an actin filament as the two-step process shown in Fig. 4.

In the first step, shown in Fig. 4b, an actin monomer is added to an existing filament in contact with the membrane. There are several forces resisting (or helping) this polymer-ization step: (a) the membrane bending force f^l resists the insertion of the monomer by increasing the energy of the system by an amount f^lδ where δ is the half monomer size. As shown in Fig. 4b, these “bending forces” represent the couple moment generated by the local membrane curvatures arising from the insertion of an actin monomer. (b) the membrane stretching force f^g similarly resists polymerization by contributing an elastic energy f^gδ and (c) the pulling force f^p of integrins tend to promote polymerization as they are oriented in the direction of polymerization. With the addition of a new monomers, this force decreases the energy of the system by an amount f^pδ. Globally, the first step tends to change the free energy of the system by an amount:

$$\mathrm{\Delta }{\mu }_I^c=f^l\delta +f^g\delta -f^p\delta .$$ (32)

The second step of actin polymerization involves the partial detachment of the membrane as depicted in Fig. 4c. This process is thermodynamically favorable as it enables the membrane to return to its unbent configuration and recover the elastic energy f^lδ. In addition, the pulling force f^p tends to promote this process by contributing to the released energy by an amount f^pδ. As a consequence, the total change in free energy during the second step is:

$$\mathrm{\Delta }{\mu }_{II}^c=-f^l\delta -f^p\delta .$$ (33)

The total change of free energy during an entire polymerization cycle can then be estimated by adding contributions from steps 1 and 2. This yields:

$$\mathrm{\Delta }{\mu }_{\mathit{tot}}^c=\delta (f^g-2f^p).$$ (34)

2.3.2 Rate of cell protrusion

We are now in a position to write the chemical potential of actin monomers in their aggregated form accounting for the effect of membrane and integrin forces as follows [36]:

$${\mu }_{\mathrm{\Gamma }}^c={\mu }_0^c+\mathrm{\Delta }{\mu }_{\mathit{tot}}^c={\mu }_0^c+\delta (f^g-2f^p)$$ (35)

Note that the change in free energy from the presence of physical forces was added to the original chemical potential ${\mu }_0^c$ since $\mathrm{\Delta }{\mu }_{\mathit{tot}}^c$ is interpreted as an energy consumed by the actin cytoskeleton during a polymerization step. When the system is at equilibrium, the chemical potentials of G-actin and actin filaments (aggregated actin) are equal ( ${\mu }_{\mathrm{\Gamma }}^c={\mu }^m$) and we obtain:

$${\mu }_0^c+\delta (f^g-2f^p)={\mu }_0^m+k_B\mathit{Tln}(r)\text{with}r=\frac{k_{\mathit{off}}}{k_{on}}$$ (36)

Here, we used the fact that the volume fraction of actin monomer at equilibrium is equal to k_off/k_on by setting V = 0 in (31). Now introducing the “on” and “off” rate constants $k_{on}^0$ and $k_{\mathit{off}}^0$ of actin polymerization in the absence of physical forces, (36) takes the form:

$${\mu }_0^c={\mu }_0^m+k_B\mathit{Tln}(r^0)\text{with}{r}^0=\frac{k_{\mathit{off}}^0}{k_{on}^0}$$ (37)

We can now use a combination of (36) and (37) in order to obtain the following relationship between rate constants and physical forces:

$$r=r^{0}exp\left(\frac{\delta (f^g-2f^p)}{k_{B}T}\right)$$ (38)

More specifically, the above relation allows us to define a fraction coefficient α (0 < α < 1) describing the split between the effect of physical forces on the “on” and “off” rates such that [36]:

$$k_{on}=k_{on}^{0}exp\left(\frac{-\alpha \delta (f^g-2f^p)}{k_{B}T}\right)$$ (39)

$$k_{\mathit{off}}=k_{\mathit{off}}^{0}exp\left(\frac{(1-\alpha )\delta (f^g-2f^p)}{k_{B}T}\right)$$ (40)

While the coefficient α is generally a function of the magnitude of participating forces (see discussion in [36]), we consider it here as a constant (α = 1/2) for simplicity. In other words, we assume that physical forces affect the “on” and “off” rates equally. Using (39) and (31), it is then possible to obtain the velocity V of cell spreading (or the rate of actin filament growth below the membrane) as:

$$V=k_{on}^0\left({\phi }_f^m-r\right)\delta exp\left(-\frac{\alpha \delta (f^g-2f^p)}{k_{B}T}\right)$$ (41)

where r is the force dependent concentration of G-actin at equilibrium defined in (38). The above equation captures many features of cell spreading. In particular, one sees that in (41) that the membrane resisting force f^g tend to decrease the rate of growth while the pulling force f^p increases it. Since the integrin pulling force is directly related to cell contraction, (41) captures the coupling between cell contraction and spreading: the more contraction, the faster the spreading. Furthermore, the equation clearly shows when the monomer concentration reaches its equilibrium values r, the rate of filament assembly comes to an end. Alternatively, when ${\phi }_f^m>r$, k becomes positive and the cell spreads; when ${\phi }_f^m<r$, the rate constant k becomes negative, and the cell depolymerizes actin at the edge and decreases its surface area. As a consequence, the phenomenon of monomer transport (addressed in (11)) is expected to play an major role in the dynamics of cell spreading. It should be emphasized that the main contribution of this work is the consideration of the integrin pulling force into the mechanisms of cell growth and spreading. It is therefore interesting to find that, when those effects are neglected, i.e., f^p and f^l vanish, the rate of spreading takes a similar form as the well-known Brownian-Ratchet model originally introduced by Peskin and co-workers in [57]:

$$V=k\delta \mathit{exp}\left(-\frac{\alpha f^g\delta }{k_{B}T}\right)$$ (42)

where $k=k_{on}^0({\phi }_f^m-r)$.

2.3.3 Relationship between protrusion forces, integrin forces and surface elasticity

To complete the model, we now need to relate the pulling force f^p and the membrane resisting force f^g to stress measures defined in section 2. One the one hand, the membrane resisting force f^p arises from the normal radial stress on $T_r^{\mathrm{\Gamma }}$ arising from membrane tension T^σ (defined in (30)). As shown in Fig. 5, the contribution of the stress $T_r^{\mathrm{\Gamma }}$ on an effective area A = 4δh^c defined by two monomers spanning the cell height h^c leads to the force:

$$f^g=2\delta h^c{T}_r^{\mathrm{\Gamma }}=\frac{2\delta h^c}{a^c}{T}^{\sigma }$$ (43)

where (30) was used to obtain the last term. We note that in the above equation, f^g represents the force applied on a single actin monomer. On the other hand, the integrin pulling force f^p may be thought of as the resulting force of distributed integrin traction tⁱ on a portion of the cell edge whose length is the averaged distance ℓ between two advancing actin filaments. This length can then be calculated from the actin volume fraction φ^c at the cell edge by $\ell =4\delta /\sqrt{{\phi }^c}$ (Fig. 5). This leads to the estimation of the pulling force as:

$$f^p=\frac{1}{2}{t}_{\mathrm{\Gamma }}^i\ell h^c=\frac{2\delta h^c}{\sqrt{{\phi }^c}}{t}_{\mathrm{\Gamma }}^i$$ (44)

where $t_{\mathrm{\Gamma }}^i$ is the integrin force at the cell perimeter Γ and the product ℓh^c is the effective area on which the integin traction helps the polymerization of a single filament. Note that (43) and (44) provide a clear relationship between the mechanics of integrins, the membrane stress and the rate of cell growth in (41).

Figure 5.

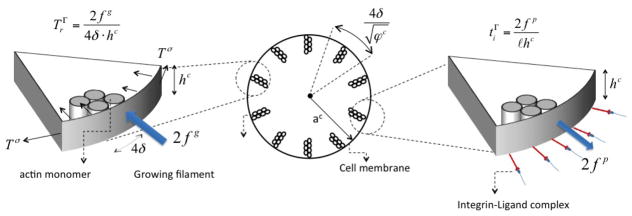
Relationship between the membrane protrusion forces f^p and f^g and integrin force tⁱ and membrane tension t^σ.

3 Numerical solution based on the finite element and level set methods

The above thermodynamical formulation yields a coupled system of partial differential equations that usually does not lead to an analytical solution. To investigate model prediction though, a solution can usually be determined numerically using a non-linear finite element solver as described in [23, 76, 22]. A potential issue, however, is that the phenomenon of growth leads to a moving boundary problem that usually is a problem with the conventional finite-element formalism. Here, we circumvent this issue by coupling the finite-element method with the level set method, known to be very efficient at capturing the motion of the arbitrary boundaries with time. The result is a general, unified formulation that can potentially be extended to study cell growth in many conditions. Before we present the numerical strategy, it is first important to summarize the principal variables and equations describing the contraction and spreading of a cell on an elastic substrate. For clarity, we decompose the variables into those associated with (a) the cytoskeleton, (b) the cell membrane and (c) the elastic substrate. First, the state of the cytoskeleton is fully described by three independent volume fractions φ^f, φ^c and ${\phi }_i^{SF}$, the fluid pressure p and the radial displacement u^c. The state of the cell membrane is given in terms of the integrin fractions φ^L and φ^H and finally, the deformation of the substrate is entirely known via the knowledge of its radial displacement u^s. The above eight variables may be determined through the following eight equations derived in the previous section:

Chemical equilibrium

$$\text{Stress}\text{fibers}{\mu }^m={\mu }_i^{SF}\text{in}\mathrm{\Omega }$$ (45)

$$\text{actin}\text{filaments}{\mu }^m={\mu }_{\mathrm{\Gamma }}^c\text{on}\mathrm{\Gamma }$$ (46)

$$\text{Cell}\text{membrane}{\mu }^H={\mu }^L\text{in}\mathrm{\Omega }$$ (47)

Mass conservation

$$\text{Cytosol}{\stackrel{.}{\phi }}^f+\alpha {\phi }^f\left(\frac{\partial v^c}{\partial r}+\frac{v^c}{r}\right)+\beta {\phi }^f\stackrel{.}{p}+\left(\frac{\partial J^f}{\partial r}+\frac{J^f}{r}\right)=0$$ (48)

$$\text{Mixture}\alpha \left(\frac{\partial v^c}{\partial r}+\frac{v^c}{r}\right)+\beta \stackrel{.}{p}+\left(\frac{\partial J^f}{\partial r}+\frac{J^f}{r}\right)+\left(\frac{\partial J^m}{\partial r}+\frac{J^m}{r}\right)=0$$ (49)

$$\text{Integrins}\frac{D\left(c^L+c^H\right)}{Dt}+\left(c^L+c^H\right)\left(\frac{\partial v^c}{\partial r}+\frac{v^c}{r}\right)+\left(\frac{\partial J^L}{\partial r}+\frac{J^L}{r}\right)=0$$ (50)

Mechanical equilibrium

$$\text{Cell}\frac{\partial T_r^c}{\partial r}+\frac{1}{r}(T_r^c-T_{\theta })+\frac{\partial T_r^{SF}}{\partial r}+\frac{1}{r}(T_r^{SF}-T_{\theta }^{SF})-\frac{\partial p}{\partial r}-t^i=0$$ (51)

$$\text{Substrate}\frac{\partial T_r^s}{\partial r}+\frac{(T_r^s-T_{\theta }^s)}{r}+t^i=0$$ (52)

These equations are complemented by the five boundary conditions (corresponding to the above five differential equations) and initial conditions, specifying the state of the cell at the begning of the simulations. These conditions are such that the cell and substrate are initially undeformed and unpressurized:

$$u^c(r,0)=0u^s(r,0)=0p(r,0)=0$$ (53)

In addition, it is assumed that the composition of the cell consists of 25% volume fraction of elements comprising the passive cytoskeleton, 5% volume fraction of actin monomers and no initial stress fibers (references for these numbers are given in Table 1).

Table 1.

Parameters used in the simulations.

Definition	Symbol	Value	unit	Reference
Cytosol volume fraction	φf	70	%	[2]
Cytoskeleton volume fraction	φc	25	%	n/a
SF+G-actin volume fraction	φm + φSF	5	%	[1, 41]
Straight+bent integrin concentration	cH + cL	5e15	#/m2	[16]
Cytoskeleton permeability	κ/μ	1e–15	m4/N · sec	[30]
G-actin diffusion constant	D	5e–12	m2/sec	[52]
L-integrin mobility coefficient	m	10e–12	m2/sec	[44]
Cytoskeleton Young’s modulus	Ec	1	kPa	[66]
Cytoskeleton Poisson’s ratio	νc	0.3		[17]
Substrate Young’s modulus	Es	1 – 10000	kPa	[66]
Substrate Poisson’s ratio	νs	0.3		[17]
Stress fiber maximum tensile stress	T*	10	kPa	[82, 43, 71]
Stress fiber Young’s modulus	E1	100	kPa	[40]
Integrin-ligand complex stiffness	λs	0.15	nN/μm	[16]
membrane stiffness	kσ	0.01	N/m	[37]
Absolute temperature	T	310	K	[16]
Membrane surface tension	$T_0^{\sigma }$	1e–2	N/m	n/a
Filament - G-actin standard potential	$\mathrm{\Delta }{\mu }_0^p$	1kBT	J	[25]
Straight - bent integrin standard potential	$\mathrm{\Delta }{\mu }_0^I$	5kBT	J	[16]
Cell initial radius	$a_0^c$	14	μm	[66]
Substrate initial radius	$a_0^s$	30	μm	n/a
Rate of actin polymerization (“on” and “off”)	$k_{on}^0$ and $k_{\mathit{off}}^0$	280 and 50	sec−1	[57]
Cell and substrate thichness	h	1	μm	[16]

$${\phi }^c(r,0)=0.25{\phi }^m(r,0)=0.05{\phi }_i^{SF}(r,0)=0$$ (54)

and all integrins are originally in their low affinity state (see table 1 for references):

$$c^L(r,0)=5e^{15}{c}^H(r,0)=0$$ (55)

Concerning the boundary conditions, we assume that there are no fluxes of cytosol and actin monomers across the cell membrane and no low affinity integrins are allowed to enter the system. Invoking equations (11) and (26), we can thus write:

$$\frac{\partial p}{\partial r}({\mathrm{\Gamma }}^c)=0,\frac{\partial {\phi }^m}{\partial r}({\mathrm{\Gamma }}^c)=0\text{and}\frac{\partial c^L}{\partial r}({\mathrm{\Gamma }}^c)=0$$ (56)

Furthermore, we consider the following two mechanical boundary conditions: (a) the substrate boundary is not subjected to traction forces and (b) the actin cytoskeleton is subjected to the membrane forces determined in (30). This is written:

$$T_r^s({\mathrm{\Gamma }}^s)=0\text{and}{T}_r({\mathrm{\Gamma }}^c)=-\frac{T^{\sigma }}{a^c}$$ (57)

where the quantity T^σ was defined as the tensile stress in the membrane. Finally, the above system of equations is coupled with the growth equation (41) in order to determine the motion of the cell boundary in time. The numerical approach to solve (48–52) is discussed below.

3.1 Cell-substrate equilibrium

In order to determine the spatial and time evolution of the various continuum fields, the physical domains (representing cell and substrate) must be discretized in a finite number of elements and nodes. A potential issue with the present problem is that cell growth involves a moving boundary; this implies that the computational domain Ω^c constantly changes, and thus must be regularly redefined, with time. Since the traditional finite-element method requires that the mesh follows the domain boundary at any time, it automatically implies that the discretization needs to be redefined at each time step during a simulation. This type of schemes, usually labeled as “moving mesh methods” are extremely cumbersome and computationally costly, especially when the problem is translated into two and three dimensions. In order to remedy these issues, we here choose to discretize the cell and substrate domains with a single mesh and introduce a level set function to specify the location of the cell boundary (Fig. 6). The moving boundary can thus be naturally modeled via a level set evolution equation, circumventing the computational difficulties associated with remeshing schemes. For the one-dimensional axisymmetric problem considered in this paper, the level set is represented as a linear sign distance function φ(r) that takes a zero value at the cell boundary. With this definition, material points inside the cell domain are associated with a negative value of φ while points outside the cell are associated with a positive value. Thus, referring to Fig. 6a), when φ < 0, nodes are associated with both cell and substrate and thus contain degrees of freedom u^c, u^s, p, φ^c, φ^m, ${\phi }_i^{SF}$, c^L, and c^H. However, when φ > 0, nodes are outside the cell domain Ω^c and are thus only associated with substrate displacements u^s. One of the potential problem with this formulation is that most fields are discontinuous across the cell membrane, yet conventional finite element interpolation functions can only describe continuous variations.

Figure 6.

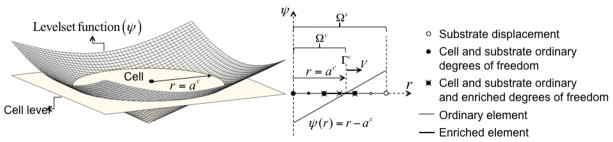
Illustration of the level set function describing the cell boundary and the degrees of freedom associated with nodes in the computational domain.

This obstacle can naturally be overcome by using the extended finite element framework [20, 34], a method that has proven very efficient in capturing various types of discontinuities in a continuum field within an element [48, 7, 23]. In this context (Fig. 6), elements that are cut by the level set are enriched by additional fictitious degrees of freedom and interpolation functions to capture the discontinuities. Here, the interpolation of a continuum field f in a discontinuous element is written:

$$\stackrel{\sim }{f}(r)=\sum _{I=1}^n{N}_I(r)f_I+\sum _{J=1}^m{N}_J(r)(H(r)-H(r_J)){\overline{f}}_J+\sum _{J=1}^m{N}_J(r)(\chi (r)-\chi (r_J)){\overline{\overline{f}}}_J$$ (58)

where n and m denote the total number of nodes and number of enriched nodes of an element. Furthermore, the nodal variables f_I are the conventional (continuous) degrees of freedom at node I while f̄_I and ${\overline{\overline{f}}}_I$ are the fictitious degrees of freedom to describe strong and weak discontinuities, respectively. We also introduced ordinary interpolation functions N_I and their enrichment with the strongly discontinuous Heaviside function H(r) and the weakly discontinuous ridge function χ(r) = |φ(r)| illustrated in Fig. 7. In our particular case, the function H(r) is used to introduce a jump in the fields u̇^c, ṗ, φ̇^c, φ̇^m, ${\stackrel{.}{\phi }}_r^{SF},{\stackrel{.}{\phi }}_{\theta }^{SF}$, ċ^L and ċ^H across the cell’s membrane, whereas the ridge function is used to define discontinuities in the spatial derivatives of u̇^s and u̇^c ([48, 50]). Indeed, discontinuities in strain across the cell membrane typically arise from the existence of membrane surface tension [23].

Figure 7.

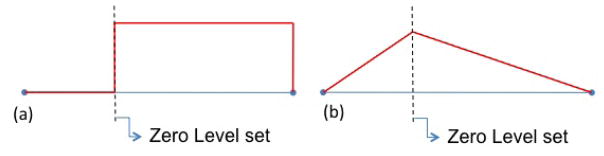
(a) Heaviside function and (b) ridge function used to describe discontinuities across the cell membrane.

To obtain the finite element equations, the system of equation (48–52) is converted to its weak Galerkin form in a similar fashion as shown in [78]. The computational domain is then discretized into three-node, quadratic elements whose nodal degrees of freedom ${\mathbf{U}}_I^e$ are given by the vector:

$${\mathbf{U}}_I^e={\left[\begin{array}{ccc}{\mathbf{u}}_I^e& {\overline{\mathbf{u}}}_I^e& {\overline{\overline{\mathbf{u}}}}_I^e\end{array}\right]}^T$$ (59)

where

$${\mathbf{u}}_I^e={\left[\begin{array}{ccccccccc}{u}_I^{s,e}& u_I^{c,e}& p_I^e& {\phi }_I^{m,e}& {\phi }_I^{c,e}& {\phi }_{r,I}^{SF,e}& {\phi }_{\theta ,I}^{SF,e}& c_I^{L,e}& c_I^{H,e}\end{array}\right]}^T$$ (60)

$${\overline{\mathbf{u}}}_I^e={\left[\begin{array}{cccccccc}{\overline{u}}_I^{c,e}& {\overline{p}}_I^e& {\overline{\phi }}_I^{m,e}& {\overline{\phi }}_I^{c,e}& {\overline{\phi }}_{r,I}^{SF,e}& {\overline{\phi }}_{\theta ,I}^{FS,e}& {\overline{c}}_I^{L,e}& {\overline{c}}_I^{H,e}\end{array}\right]}^T$$ (61)

$${\overline{\overline{\mathbf{u}}}}_I^e={\left[\begin{array}{cc}{\overline{\overline{u}}}_I^{s,e}& {\overline{\overline{u}}}_I^{c,e}\end{array}\right]}^T.$$ (62)

Here I = 1, 2, 3 denotes the local node number for each element and the terms ${\overline{\mathbf{u}}}_I^e$ and ${\overline{\overline{\mathbf{u}}}}_I^e$ correspond to strong and weak degrees of freedom that vanish for non-enriched elements. Substituting the finite interpolation (58) in the weak form and linearizing the equations, one can show that the problem reduces to solving the following algebraic iterative problem:

$$\mathbf{C}\stackrel{.}{\mathbf{U}}+\mathbf{K}\delta \mathbf{U}+\mathbf{F}=\mathbf{0}$$ (63)

where U denotes the vector containing global degrees of freedom, while C, K and F are the damping matrix, stiffness matrix and force vector, respectively (see appendix 7.2 for a more detailed explanation). Equation (63) is solved at each time step using a Newton-Raphson procedure and a backward Euler integration method is used to compute the unknown fields at each time step as follows:

$$\delta \mathbf{U}=\delta \stackrel{.}{\mathbf{U}}·\mathrm{\Delta }t$$ (64)

where Δt denotes the time increment. Upon obtaining a solution at time increement t, the method consists of computing the rate U̇ at the next time step t + Δt

$${\stackrel{.}{\mathbf{U}}}^i(t+\mathrm{\Delta }t)={\stackrel{.}{\mathbf{U}}}^{i-1}(t+\mathrm{\Delta }t)+\delta {\stackrel{.}{\mathbf{U}}}^i$$ (65)

where the value δU̇ⁱ is computed for each iteration by substituting equations (64) and (65) into equation (63). This leads to the following equation:

$$\left({\mathbf{C}}_{t+\mathrm{\Delta }t}^{i-1}+\mathrm{\Delta }t.{\mathbf{K}}_{t+\mathrm{\Delta }t}^{i-1}\right).\delta {\stackrel{.}{\mathbf{U}}}^i=-\left({\mathbf{F}}_{t+\mathrm{\Delta }t}^{i-1}+{\mathbf{C}}_{t+\mathrm{\Delta }t}^{i-1}·{\stackrel{.}{\mathbf{U}}}_{t+\mathrm{\Delta }t}^{i-1}\right).$$ (66)

Iterations are then repeated until the norm of the vector |δUⁱ| is smaller than a small tolerance.

3.2 Cell growth and level set evolution

To model cell growth, results from the equilibrium equations at each time-step can be used to estimate the pulling and membrane resistance forces appearing in (41). Since the cell radius is defined in terms of the level set function φ, its rate of change in time can simply be expressed in terms of the traditional level set evolution equation [21]:

$$\frac{D\phi }{Dt}=\frac{\partial \phi }{\partial t}+V\frac{\partial \phi }{\partial r}=0$$ (67)

where V is cell boundary velocity computed in (41). Defining the level set as a sign-distance function (i.e. $\frac{\partial \phi }{\partial r}=1$), we can find the expression of the level set function at time step t + Δt as:

$${\phi }^{t+\mathrm{\Delta }t}={\phi }^t+V·\mathrm{\Delta }t.$$ (68)

Growth typically involves the creation of new material points, whose composition is unknown, at the cell boundary. It is thus necessary to make some assumption regarding the state of the mixture at the new cell edge in terms of the constituent’s volume fractions. To ensure the continuity of both a continuum field and its derivative during cell growth, a realistic assumption [3] consists of approximating a field f at the new boundary by:

$$f^{\mathrm{\Gamma }}=f^{{\mathrm{\Gamma }}^{\mathit{old}}}+\frac{\partial f^{{\mathrm{\Gamma }}^{\mathit{old}}}}{\partial r}·\left(r-a^{\mathit{old}}\right)$$ (69)

where f^Γ represents the continuum fields u^c, p, φ^c, φ^m, ${\phi }_r^{SF},{\phi }_{\theta }^{SF}$, and the superscript old denotes the value of the same field at the previous time step. Applying the boundary conditions shown in (56) and (57), it is straightforward to show that in our particular situation, the last term in (69) vanishes and f^Γ = f^Γold for all continuum fields listed above.

4 Results

There are number of experimental studies that have measured various aspects of cell spreading, including rate of spreading and final cell area in terms of substrate stiffness and ligand density. These results provide a very useful dataset onto which one can assess the soundness of the proposed model. Due to our axisymmetric assumptions, the following results are valid for isotropic cell spreading and the implications of the model for anisotropic cell spreading and morphology changes are left for future studies. The physical parameters used in the following simulations are listed in Table 1.

4.1 Coupled mechanisms of cell contraction and spreading

For illustration purposes, we first perform the simulation of cell spreading on a substrate whose stiffness can be characterized as soft and stiff, respectively. We then investigate the key mechanisms at play as the cell adheres to the substrate, contracts and spreads.

Stress-fiber assembly and contraction

The thermodynamical model presented in section 2.1 implies that stress fiber stability is negatively affected by the contracile work T^*ε_i when ε_i < 0. In other words, stress fibers are stable whenever there is a non-negligible resistance to their contraction. This resistance is present under two conditions; first when the cell is firmly attached to the ligands of the substrate, and second, when the substrate is stiff enough to resist compaction. As a result (Fig. 8), the model predicts an increase in stress fiber concentration φ^SF and overall contraction with substrate stiffness, a behavior that is observed experimentally [26]. Furthermore the model predicts that stress-fiber formation is limited by the pool of contractile proteins in the cell; this explains why cell contraction eventually levels off and reaches a maximum value (Fig. 8), regardless of substrate stiffness.

Figure 8.

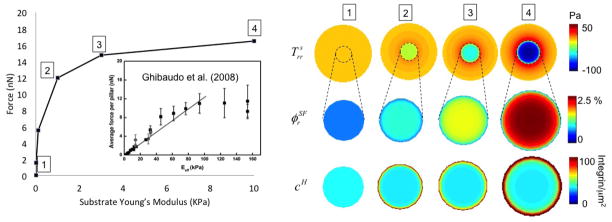
Left: Relationship between cell contraction and cell area for different substrate stiffness. The model predicts a nonlinear relationship between contraction and substrate stiffness in agreement with experiments on micropillars [26]. For comparison purposes, the simulated force in the ordinate is equal to the total computed integrin force divided by the number of pillars from experimental images and multiplied by the ratio of cell areas obtained from experiments and simulations. Right: The evolution of radial stress $T_{rr}^s$ in the substrate, volume fraction ${\phi }_r^{SF}$ of stress fibers in the radial direction and the concentration c^H of high affinity integrins are also shown for different substrate stiffness.

Cell adhesion

Cell adhesion is provided by the clustering of intregin-ligand complex resulting from the chemical equilibrium described in section 2.2. Cell contraction triggers a radial separation between its membrane and the underlying substrate, such that the separation reaches a maximum at the cell’s periphery. When ligands are present, the integrins resisting this separation are subjected to large stretching forces in this region, which leads to their stabilization (according to (22)). This explains the accumulation of high affinity integrins at the cell’s periphery observed in Fig. 8.

Cell spreading

According to the model introduced in section 2.3, the phenomenon of cell spreading is strongly related to the integrin pulling force and thus, to cell contraction. Large contractions leads to large pulling force f^p and the promotion of actin polymerization by creating extra-space below the cell membrane. Cell growth may thus proceed as long as the driving force for actin polymerization is larger than the resisting force f^g of the stretched membrane. This mechanism is illustrated in Fig. 9 where the spreading rate, pulling force and membrane resisting force are depicted as a function of time. It is seen that the spreading rate is a function of the difference between f^p and f^g such that when f^p – f^g vanishes (the two curves meet), the velocity of spreading becomes quasi-negligible. Another effect of the pulling force is to increase the rate of spreading by raising the activation energy. The model therefore predicts a rise in both cell area and spreading rate with contraction and substrate stiffness as shown by the fact that the cell area becomes larger as one moves to the right in Fig 8.

Figure 9.

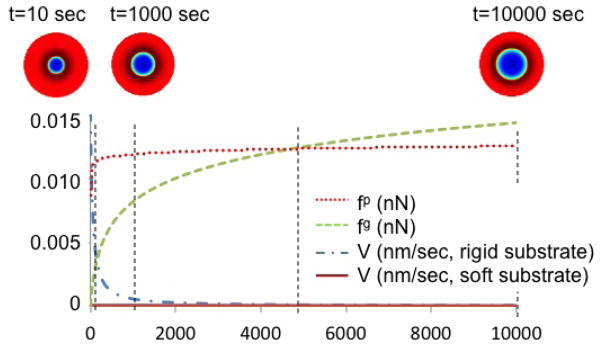
Evolution of pulling force, membrane resistance force and cell area in time

The model particularly predicts that the three above mechanisms are strongly interrelated and dependent on substrate stiffness and ligand density. We next assess the soundness of the model by comparing numerical predictions and experimental measurements from the literature.

4.2 Effect of substrate stiffness on cell area

Experimental studies on fibroblasts have shown that cell area [66] increases with substrate stiffness in a nonlinear fashion (Fig. 10). Here, we investigate this dependency by considering an elastic substrate whose ligand concentration is infinitely large (c^lg → ∞) to ensure that cell spreading is only affected by stiffness. To investigate cell spreading, we start from an original cell configuration of surface area A₀ ≈ 600μm² in which no stress fibers and high affinity integrins are present. Since this system is originally out of equilibrium, we observe a time dependent stress fiber formation, integrin-ligand adhesion and cell spreading that eventually reaches a steady state. Fig. 10 depicts the predicted relationship between final cell area and substrate stiffness, together with an illustration of cell size and integrin distribution for three typical cases. We futher note that these predictions are in very good agreement with experimental results by Solon et al.[66] depicted in the figure. Our model suggests that the dependency of cell area on substrate stiffness is explained by the fact that increasing substrate stiffness induces stress fiber stabilization and increased contraction. In turn, contraction affects the magnitude of the intregrin pulling force f^p and thus cell spreading. However, the increase in cell spreading with substrate stiffness has a limit, which depends on two mechanisms that act against actin polymerization. First, stress fibers eventually reach a maximum concentration, which limits the contraction a cell can exert on its surrounding and thus the pulling force. Second, according to (41), the rate of spreading is controlled by the competition between the pulling and the resisting force. As observed in Fig. 9, the resisting force, while originally weak, increases at a much faster rate than the pulling force and eventually become the dominating factor; this puts an end to cell spreading.

Figure 10.

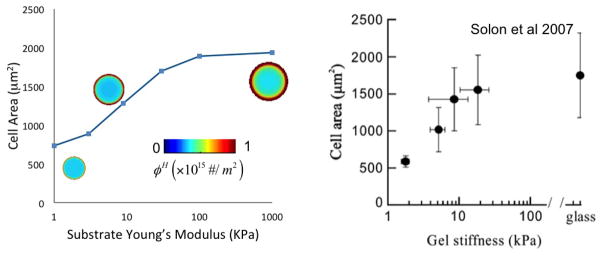
Changes of cell area and high-affinity integrin concentration at steady state for different substrate stiffness, and comparison with experimental results of [66]

4.3 Rate of cell spreading

When deposited on elastic susbtrate, fibroblasts also exhibit a pronounced mechano-sensitivity in their rate of spreading; more particularly, they tend to spread faster in stiffer environment [66]. To investigate this response, we simulate the spreading of a cell, with a no original adhesion and stress-fiber, subjected to a substrate stiffness that varies between 100Pa and 10MPa. We then computed the rate of cell spreading by plotting the polymerization velocity V (given in (41)) as a function of time for different stiffness (Fig. 11). Consistent with experimental results [66], the model predicts an increase in spreading rate with substrate stiffness. This phenomenon can then be explained as follows. The rate of cell spreading is governed by the rate of actin polymerization, which itself is a function of the integrin pulling force. Since this force increases with cell contraction and substrate rigidity, stiff substrates create an ideal environment to promote actin polymerization beneath the membrane and increase spreading speed. Interestingly, the model captures a fast spreading rate at early times and a steady decrease in velocity at longer times. This behavior can be attributed by the nonlinearly increasing membrane resisting force f^p with cell area.

Figure 11.

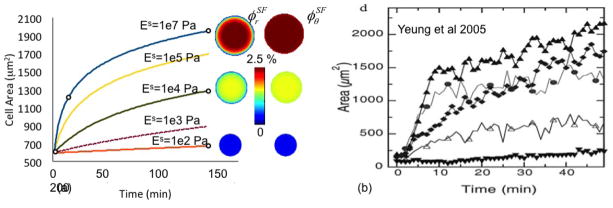
(a) Changes of cell area and stress fiber volume fraction during growth for different substrate stiffness, and (b) experimental results of reference [84].

4.4 Effect of ligand concentration

The effect of ligand concentration was experimentally assessed by Reinhart and co-workers [61] on very stiff substrate. Concentrating on RGD peptides, the study showed that cell area was a linear function of ligand density within concentrations that ranged from 0.001 mg/ml to 1 mg/ml. To know whether the proposed model could reproduce this trend, we considered a cell lying on a substrate of given stiffness and varied the ligand concentration from 0.001 ligand/μm² to 1000 ligand/μm². As depicted in Fig. 12, the model predicts a nonlinear relationship between ligand density and cell area. While this result may seem contradictory with experimental trends, there are several explanations for the observed discrepancy. First, it should be noted that the range of ligand concentration considered in the simulation is much greater than that investigated experimentally. In fact, if one compares trends within the same concentration range, the predicted increase in cell area is very close to the linear relationship seen in experiments. Furthermore, outside of this range, model predictions are perfectly sound as it is known that cell area cannot continuously increase and must reach a maximum, regardless of the concentration of ligand. Similarly, when no ligands are present, cell area must converge to a small but finite value. This justifies the fact that cell area has horizontal asymptotes as ligand density tends to zero and infinity. Finally, the increase of cell area with ligand concentration can be explained on the basis of (22). On the one hand, when ligand density vanishes, integrins cannot attach to the substrate; this precludes the existence of a pulling force and the associated increase in cell area. On the other hand, when ligand density is high, cells can attach to the substrate and generate contraction; this produces an integrin pulling force promoting spreading. Between these two limits, there is an almost linear transition region that are in good agreement with experimental results [61] (Fig. 12).

Figure 12.

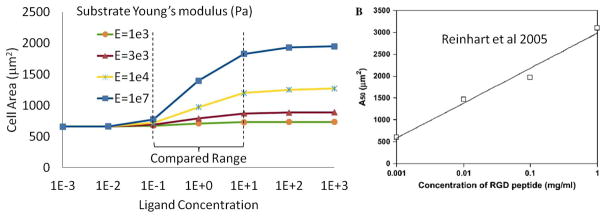
Changes of cell area at steady state for different ligand concentration, and comparison with experimental results of [61]

5 Summary and concluding remarks

As a summary, this paper presented a mathematical model of cell contraction spreading by considering the chemical and mechanical equilibrium of various constituents in the cytoskeleton and on the plasma membrane. In particular, the model considers the interplay between three key phenomena: cell contraction, cell adhesion and protrusion growth. Contraction is governed by the assembly of stress fibers under conditions in which contractile deformation is resisted. In a similar fashion, the stability of integrin-ligand attachment on the plasma membrane is promoted by large intregrin pulling force and tends to reinforce both contraction and adhesion on stiff substrates. Finally, the phenomenon of protrusion growth is the result of an interplay between two opposite forces: the integrin pulling force at the edge of the cell and the stretching and bending resistance of the cell membrane. These mechanisms have been presented within a thermodynamically consistent framework that obey fundamental principles such as mass and momentum balance. The final problem consisted in a number of coupled nonlinear differential equations that can be solved within the framework of nonlinear finite-element. In particular, we introduced a strategy based on the extended finite element and level set method, by which one can naturally describe the phenomenon of cell growth without numerical complications. Our simulation showed that spreading, contraction and adhesion are strongly coupled mechanisms that rely on the nature of the underlying substrate, both mechanically (stiffness) and chemically (ligand concentration). Model predictions were generally in very good agreement with existing experimental data; suggesting that it likely captures some fundamental mechanisms that drives the mechanical behavior of adherent cells. Although the present work concentrated on the growth of a single, circular cell on an elastic substrate, the model is general and can easily be extended to study more complex situations, in which substrate anisotropy, inhomogeneous ligand distribution and substrate stretch may exist. Such studies will enable validation of the model against more experimental observations before it can be used to predict certain behaviors that are key to tissue engineering and biological processes including cell migration, wound contraction and disease.

Figure 2.

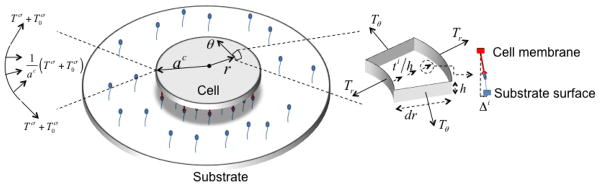
Illustration of the forces equilibrium in the spreading cell.

7 Appendix

7.1 Plane-stress conditions elasticity equations for cell

In this paper, it is assumed that the cell’s geometry can be described as a very thin plate such that two-dimensional plane-stress conditions can be applied. This implies that the total stress T verifies T_xz = T_yz = 0, T_zz = 0. Since stress fibers do not exert forces in the z-direction, the last equation can be written $T_{zz}^c-p=0$, where p is the cytosol pressure. Writting the three-dimensional stress-strain relation for the actin filament network as:

$$\left[\begin{array}{c}{T}_{xx}^c\\ T_{yy}^c\\ T_{zz}^c\\ T_{yz}^c\\ T_{xz}^c\\ T_{xy}^c\end{array}\right]=\left[\begin{array}{cccccc}2\mu +\lambda & \lambda & \lambda & 0& 0& 0\\ \lambda & 2\mu +\lambda & \lambda & 0& 0& 0\\ \lambda & \lambda & 2\mu +\lambda & 0& 0& 0\\ 0& 0& 0& \mu & 0& 0\\ 0& 0& 0& 0& \mu & 0\\ 0& 0& 0& 0& 0& \mu \end{array}\right]\left[\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\epsilon }_{zz}\\ 2{\epsilon }_{yz}\\ 2{\epsilon }_{xz}\\ 2{\epsilon }_{xy}\end{array}\right],$$ (70)

and enforcing the fact that $T_{zz}^c=p$, we obtain the following expression for ε_zz:

$${\epsilon }_{zz}=\frac{1}{1-\nu }\left[\frac{p}{E}(1+\nu )(1-2\nu )-\nu ({\epsilon }_{xx}+{\epsilon }_{yy})\right]$$ (71)

where E and ν are the Young’s modulus and Poisson’s ratio of the actin filament network. Their relationship with Lame’s constants appearing in (70) is given below:

$$E=\frac{{\mu }^{\prime }(3\lambda +2{\mu }^{\prime })}{\lambda +{\mu }^{\prime }};\text{and}\nu =\frac{\lambda }{2(\lambda +{\mu }^{\prime })}$$ (72)

We now wish to express the divergence ∇ · v^c of the velocity field v^c for substitution in the equations of mass balance (4–6). For a three dimensional problem, the divergence reads ∇·v^c = ε̇_xx + ε̇_yy + ε̇_zz where a superimposed dot is used to denote a time derivative. Using the fact that:

$${\stackrel{.}{\epsilon }}_{zz}=\frac{1}{1-\nu }\left[\frac{\stackrel{.}{p}}{E}(1+\nu )(1-2\nu )-\nu ({\stackrel{.}{\epsilon }}_{xx}+{\stackrel{.}{\epsilon }}_{yy})\right]$$ (73)

from (71), we can rewrite:

$$\nabla ·{\mathbf{v}}^c=\alpha {\nabla }^{(2)}·\mathbf{v}+\beta \stackrel{.}{p}$$ (74)

where ∇⁽²⁾ · v = ∂v_x/∂x + ∂v_y/∂y = ε̇_xx + ε̇_yy represents the divergence of the velocity v in the two-dimensional plane xy while constants α and β can be found to be:

$$\alpha =\frac{1-2\nu }{1-\nu };\text{and}\beta =\frac{(1+\nu )(1-2\nu )}{E(1-\nu )}$$ (75)

In the particular case of axisymmetric conditions, (74) becomes:

$$\nabla ·{\mathbf{v}}^c=\alpha \left(\frac{\partial v^c}{\partial r}+\frac{v^c}{r}\right)+\beta \stackrel{.}{p}$$ (76)

This result is used to obtain equation (7) and (8) in the present study.

7.2 Stiffness and damping matrices

It can be shown, through a standard finite-element procedure, that the force vector, damping matrix and stiffness matrix appearing in Eq. (63) take the following form:

$$\mathbf{F}={\mathcal{A}}_{e=1}^{\mathit{nel}}{\mathbf{F}}^e\mathbf{K}={\mathcal{A}}_{e=1}^{\mathit{nel}}{\mathbf{K}}^e\text{and}\mathbf{C}={\mathcal{A}}_{e=1}^{\mathit{nel}}{\mathbf{C}}^e.$$ (77)

where the superscript e denotes quantities associated with individual finite element e and the symbol denotes the assembly operator. The final force vector, damping matrix, and stiffness matrix finally take the forms:

$$\mathbf{F}={\left[{\mathbf{F}}^{u^s},{\mathbf{F}}^{u^c},{\mathbf{F}}^f,{\mathbf{F}}^m,{\mathbf{F}}^c,{\mathbf{F}}^{SF,r},{\mathbf{F}}^{SF,\theta },{\mathbf{F}}^L,{\mathbf{F}}^H\right]}^T,$$ (78)

$$\mathbf{C}=\left[\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& {\mathbf{C}}^{fu}& {\mathbf{C}}^{ff}& {\mathbf{C}}^{fm}& {\mathbf{C}}^{fc}& {\mathbf{C}}^{fr}& {\mathbf{C}}^{f\theta }& 0& 0\\ 0& {\mathbf{C}}^{mu}& {\mathbf{C}}^{mf}& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& {\mathbf{C}}^{Lu}& 0& 0& 0& 0& 0& {\mathbf{C}}^{LL}& {\mathbf{C}}^{LH}\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$ (79)

and

$$\mathbf{K}=\left[\begin{array}{ccccccccc}{\mathbf{K}}^{ss}& {\mathbf{K}}^{su}& 0& 0& 0& 0& 0& 0& {\mathbf{K}}^{sH}\\ {\mathbf{K}}^{us}& {\mathbf{K}}^{uu}& {\mathbf{K}}^{uf}& 0& 0& {\mathbf{K}}^{ur}& {\mathbf{K}}^{u\theta }& 0& {\mathbf{K}}^{uH}\\ 0& 0& {\mathbf{K}}^{ff}& 0& 0& 0& 0& 0& 0\\ 0& 0& {\mathbf{K}}^{mf}& {\mathbf{K}}^{mm}& {\mathbf{K}}^{mc}& {\mathbf{K}}^{mr}& {\mathbf{K}}^{m\theta }& 0& 0\\ 0& 0& 0& {\mathbf{K}}^{cm}& {\mathbf{K}}^{cc}& 0& 0& 0& 0\\ 0& {\mathbf{K}}^{ru}& 0& {\mathbf{K}}^{rm}& 0& {\mathbf{K}}^{rr}& 0& 0& 0\\ 0& {\mathbf{K}}^{\theta u}& 0& {\mathbf{K}}^{\theta m}& 0& 0& {\mathbf{K}}^{\theta \theta }& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& {\mathbf{K}}^{LL}& 0\\ {\mathbf{K}}^{Hs}& {\mathbf{K}}^{Hu}& 0& 0& 0& 0& 0& {\mathbf{K}}^{HL}& {\mathbf{K}}^{HH}\end{array}\right]$$ (80)

where the superscripts ij is used to designate a matrix representing the interactions between component i and component j.