Fast non-iterative calibration of an external motion tracking device

Abstract

Purpose

Prospective motion correction of MR scans commonly uses an external device, such as a camera, to track the pose of the organ of interest. However, in order for external tracking data to be translated into the MR scanner reference frame, the pose of the camera relative to the MR scanner must be known accurately. Here, we describe a fast, accurate, non-iterative technique to determine the position of an external tracking device de novo relative to the MR reference frame.

Theory and Methods

The method relies on imaging a sparse object that allows simultaneous tracking of arbitrary rigid body transformations in the reference frame of the MRI machine and that of the external tracking device.

Results

Large motions in the MRI reference frame can be measured using a sparse phantom with an accuracy of 0.2 mm, or approximately 1/10 of the voxel size. By using a dual quaternion algorithm to solve the calibration problem, a good camera calibration can be achieved with fewer than 6 measurements. Further refinements can be achieved by applying the method iteratively and using motion correction feedback.

Conclusion

Independent tracking of a series of movements in two reference frames allows for an analytical solution to the hand-eye-calibration problem for various motion tracking setups in MRI.

Introduction

Motion-related problems during MRI scans can be addressed with prospective motion correction (PMC). PMC techniques rely on real-time measurement of the pose (translations and rotations) of a subject’s body parts during scans, and applying continuous corrections to the medical imaging device to attenuate or eliminate the detrimental effects of motion. There are many advantages to having an external tracking system that operates independently from the MRI scanner, such as an optical camera tracking motion of the head. First, external tracking systems do not interfere with the MR imaging process, and therefore do not reduce the time available for medical imaging. Additionally, some external tracking systems, such as those based on cameras, can readily provide tracking information at approximately 100 frames per second (1, 2), which is almost impossible to achieve with MRI.

However, one distinct disadvantage of external tracking systems is that the primary motion measurement occurs in a coordinate frame that is different from that of the medical imaging device. In contrast, active MR marker approaches detect motion directly in the MR frame, using MR devices (3, 4). In order to translate original motion data from an external tracking device into data in the scanner frame, the pose of the tracking device in MR coordinates has to be known accurately. The process of determining the homogeneous transform that connects the two reference frames will be referred to as cross calibration, or as Hand-Eye-Calibration in robotics applications.

The unknown cross calibration transform relating a camera and a scanner frame can be calculated from at least two motions (i.e. 3 positions) where the transforms in both frames are known (5). The algorithm presented in (5) describes rigid body motion and coordinate transforms with the help of dual quaternions (see appendix), which make it possible to solve the cross calibration problem analytically.

Assuming that arbitrary rigid body motions can be measured by the tracking device with high precision, the challenge in the calibration procedure is to provide independent accurate measurements of the motion in the MRI reference frame with the gradient isocenter as the origin of the coordinate system. Since the isocenter is well defined in MR images reconstructed by the scanner, it is intuitive to acquire images of a structured rigid object in various positions and estimate the motion by co-registration. A variety of image based co-registration algorithms, such as FSL (6), SPM (www.fil.ion.ucl.ac.uk/spm) or PACE (7), estimate motion parameters by iteratively minimizing voxel-wise differences between the reference and transformed images. An iterative calibration scheme based on this approach was proposed in (8). To find an initial calibration for the iterative method, a series of small motions of a structured phantom was tracked using PACE and simultaneously recorded by the camera (9). The cross calibration is given as the transformation that describes the motion in the camera and scanner frame in a least squares sense.

Another cross calibration method is to use a device that is both visible to the camera and the MR scanner, where the relative position between the camera marker and the MR marker is precisely known (1, 10, 11). The internal calibration has to be performed during construction of the dual-visible device.

To overcome some limitations of these prior cross-calibration procedures, such as being complex, time-consuming, and non-deterministic, we developed a method that allows accurate and unambiguous measurements of arbitrary and large rigid body movements / transforms in the reference frame of an MRI machine. This is achieved by measuring the absolute position of the imaged phantom in the reference frame defined by the gradient system. Importantly, a sparse phantom is used, which makes it possible to represent the information encoded in the image space by a few vectors. The transform relating two sets of vectors at various phantom positions can then be found analytically. The method allows the non-iterative and precise determination of the position of an external tracking device relative to the MRI reference frame. Furthermore, we show how PMC can be used to further refine an initial cross calibration by using a feedback loop based on the residuals of motion corrected scans. We encourage the use of dual quaternions to describe rigid-body motion and provide the mathematical basis for iterative and non-iterative cross calibration procedures.

Theory

Sparsity condition and center-of-gravity (COG) encoded phantom position

An object can be considered sparse and rigid in terms of MRI if it has the following properties:

1. Only a small fraction of pixels in the imaging volume generate an MR-signal above the noise level.

2. The object consists of N signal-generating regions that are isolated (not connected in space) and have fixed relative positions.

3. The MR image of each individual region is invariant during rotations and translations, i.e. the shape of the object must not change during movements.

Given a volumetric MR image of such an object, its position in image space can be represented by N point coordinate triples (center-of-gravities, or COGs) plus the center-of-gravity of all regions combined. Since the goal is to describe motion in the scanner reference frame (defined by the imaging gradients) based on reconstructed images, the internal reference frame of the images (voxel frame) has to be known and aligned with the scanner frame. The homogeneous transform that maps voxel coordinates to their position in space is known as the voxel-to-world transform, and is either assumed to be known or can be found by a series of pre-scans with well-defined rotations. For the remainder of the manuscript, we assume that the voxel frame and any other voxel representation based on that frame are aligned with the scanner frame.

The following steps were performed to convert a voxel-intensity representation of the object (i.e. an MRI scan) to a point or COG representation.

1. Create a binary mask of pixels whose intensities are above the noise level

2. Based on the binary mask identify each connected region (labeling step) and calculate the center of gravity g_i of each region.

3. Calculate the center of mass of the object now consisting of N regions.

4. Sort the points g_i by their Euclidian distance from the center of mass. This process uniquely identifies each region, since the center of mass and the relative distances of the regions are invariant under rigid body motions. If necessary, additional unique sorting criteria can be applied, such as volume or signal intensity of each region.

In our implementation, step 1 involved creation of a binary mask of voxels whose intensities are 10 times above the noise level (average signal of noisy pixels). Based on the binary mask, the N regions (spheres) are identified using a labeling algorithm. From the labeled mask the COG g_i of each sphere is calculated. We used the MATLAB functions bwlabeln to perform the labeling operation and regionprops to determine various properties of each region, such as the COG coordinates and the total number of pixels. In the next step, the N center-of-gravity values are used to calculate the total center-of-mass g̅ of the phantom: $\mathit{g̅}=N^{-1}{\sum }_i^N{\mathit{g}}_i$.

The last step is to sort the set of {g_i} according to a set of criteria that are unique for each region and invariant under arbitrary spatial transformations. Since our phantom was designed carefully to possess unique relative distances of regions (see Methods section for details) and no intrinsic spatial symmetry, the sorting criterion was the relative distance d_i of each region to the center of mass. Both are invariant under rigid body transformations. The final result is an ordered list of (N+1) 3- dimensional positions {g̅, g_i} in the reference frame of the MR scanner which is referred to as COG representation

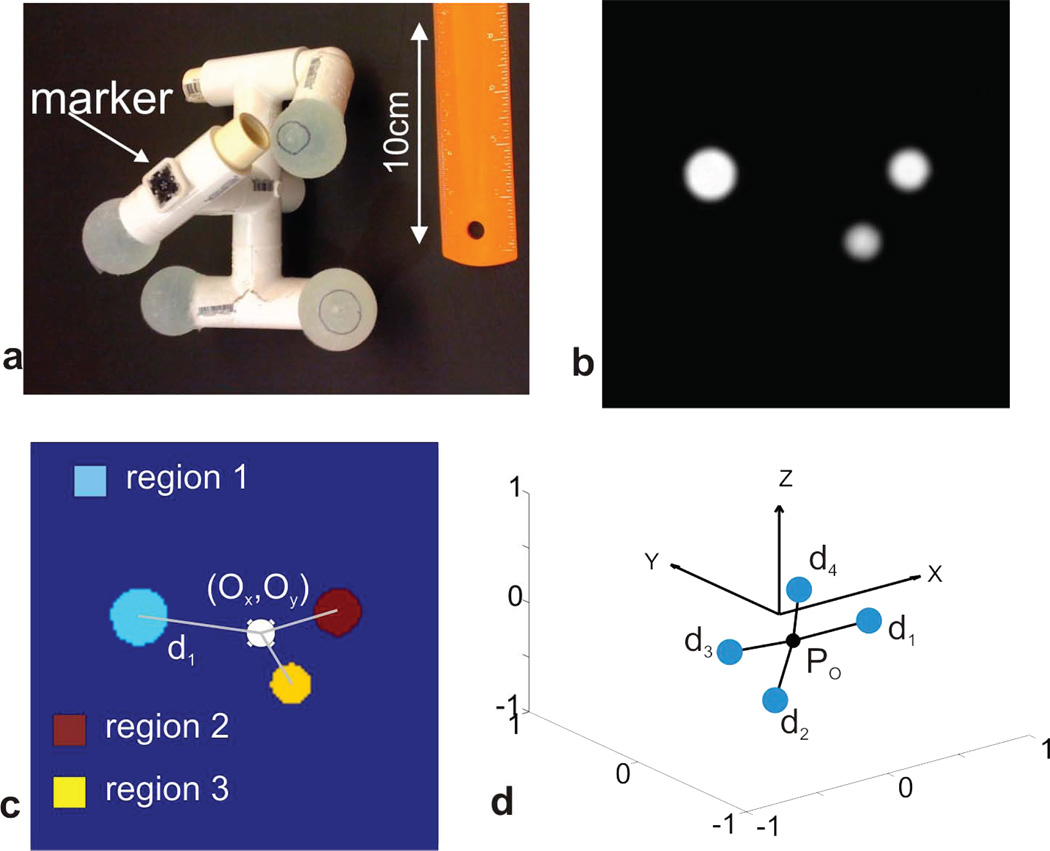
Figure 1 illustrates the major steps involved in creating a set of coordinate triples in the scanner frame from the physical phantom. Figure 1a shows a photograph of the phantom with the optical tracking marker attached (“marker”). Figure 1b displays a grayscale image of a slice through the acquired GRE volume, with 3 of the 4 spheres visible. Figure 1c shows the labeled mask, together with the center-of-mass and the distances to the origin. In Figure 1d, the position of the phantom in the reference frame of the scanner is visualized by plotting the center of mass in black and the COGs of the four spheres as blue circles.

Figure 1.

Sparse phantom with attached MPT marker (a). Transversal cross section through the 3D GRE acquisition of the phantom is shown in b. From the raw images in b, the center-of-gravity is found by a masking and image labeling operation, depicted in c. Different colors in c represent connected regions with signal intensities significantly above the noise level. The absolute position of the sparse phantom in the reference frame defined by the gradient system is displayed in d.

Motion estimation between COG encoded phantom positions

Motion estimation follows the approach in (12). First, a pair of volumetric scans at two positions, referred to as V₁ and V₂, is transformed from pixel-intensity to COG-representation according to the previous section, yielding two sets of points P₁ = {n̅, n_i} and P₂ = {m̅, m_i} for V₁ and V₂. The aim is to find the homogenous transformation T(R, t) = T_{P1 → P2} that maps {n̅, n_i} onto {m̅, m_i}: P₂ = TP₁.

Separating the rotational and translational part, the transformation is given by

$${\mathit{m}}_{\mathit{i}}=R*{\mathit{n}}_{\mathit{i}}+\mathit{t}+{\mathit{v}}_{\mathit{i}}$$ [1]

with the 3×3 rotation matrix R, the translation vector t and an additional noise vector v_i.

The translation part t of the homogeneous transformation can be removed from the equation by placing both objects relative to the origin of the coordinate system. Using m̃_i = m_i − m̅ and ñ_i= n_i − n̅, Eq.[1] is split into two sub-problems

$${\mathit{m̃}}_{\mathit{i}}=R{\mathit{ñ}}_{\mathit{i}}+{\mathit{v}}_{\mathit{i}}$$ [2]

$$\mathit{t}=-R\mathit{n̅}+\mathit{m̅}$$ [3]

which can be solved in succession.

This operation corresponds to a shift of the object’s center of mass to the origin. In this representation, only the rotational component of the homogeneous transform remains, which is subjected to a least squares error criterion

$$\text{min}{\mathrm{\Sigma }}^2={\sum }_{i=1}^N\Vert {\mathit{m̃}}_{\mathit{i}}-R*{\mathit{ñ}}_{\mathit{i}}{\Vert }^2$$ [4]

Calculating the quadratic sum leads to

$${\mathrm{\Sigma }}^2={\sum }_{i=1}^N({\mathit{m̃}}_{\mathit{i}}^{\mathit{T}}{\mathit{m̃}}_{\mathit{i}}+{\mathit{ñ}}_{\mathit{i}}^{\mathit{T}}{\mathit{ñ}}_{\mathit{i}}-2{\mathit{m̃}}_{\mathit{i}}R{\mathit{ñ}}_{\mathit{i}})$$ [5]

Since the first 2 terms in Eq. 5 are independent of R, Σ is minimized by maximizing the last part of the sum which is equivalent to maximizing the trace of RH where H is a correlation matrix given by the outer vector product $H={\sum }_{i=1}^N{\mathit{ñ}}_i{\mathit{m̃}}_i^T$.

Singular value decomposition of H yields: $H\stackrel{SVD}{\to }H=US{V}^T$, and the optimal rotation matrix which minimizes Eq. [5] is then given as R = VU^T. After the optimal rotation is determined, the translation can be computed using Eq. [3]. Minimizing Eq. [4] is known as the orthogonal Procrustes problem (OPP) and the singular value decomposition based solution (SVD-OPP) is given in (13). A review of algorithms for solving Eq.[4] can be found in (14), and a method involving unit quaternions is given in (15).

Non-iterative cross-calibration using dual quaternions

As noted, cross calibration refers to the process of finding the camera (tracking device) position in the reference frame of the MRI scanner. Given two reference frames related by the transform X = X_{A → B} and the respective motions A and B therein, the following equations hold:

$$AX=XB\leftrightarrow B=X^{-1}AX$$ [6]

Therefore, motion as observed in reference frame A is transformed into a different reference frame (B) by this so-called “sandwich equation”. The ultimate goal of every calibration method is to find the transform X that connects the camera and the scanner frame (X can be interpreted as the pose of the camera in the scanner frame). For the rest of this work we assume that for arbitrary phantom motions a noise and error free description in the camera frame is available.

The phantom is imaged by the MRI scanner, and its position simultaneously measured by the tracking system, for a series of M different poses in space. For each pose of the phantom, the COG-representation is determined as described above. From M poses, the (M − 1) rigid body transformations B_i connecting the poses can be determined using the SVD-OPP method.

In parallel, the tracking system will follow the various movements of the phantom, using its own marker, yielding a second set of (M-1) rigid body transformations A_i. Using the 2 sets of motions, it is possible to determine the position of the tracking device relative to the imaging device, and vice versa. Based on Eq. [6], the calibration problem is solved in a least-squares sense by minimizing

$$X_{\mathit{\text{optim}}}=\mathit{\text{min}}{\mathrm{\Sigma }}_i\Vert B_i-X^{-1}{A}_{i}X\Vert$$ [7]

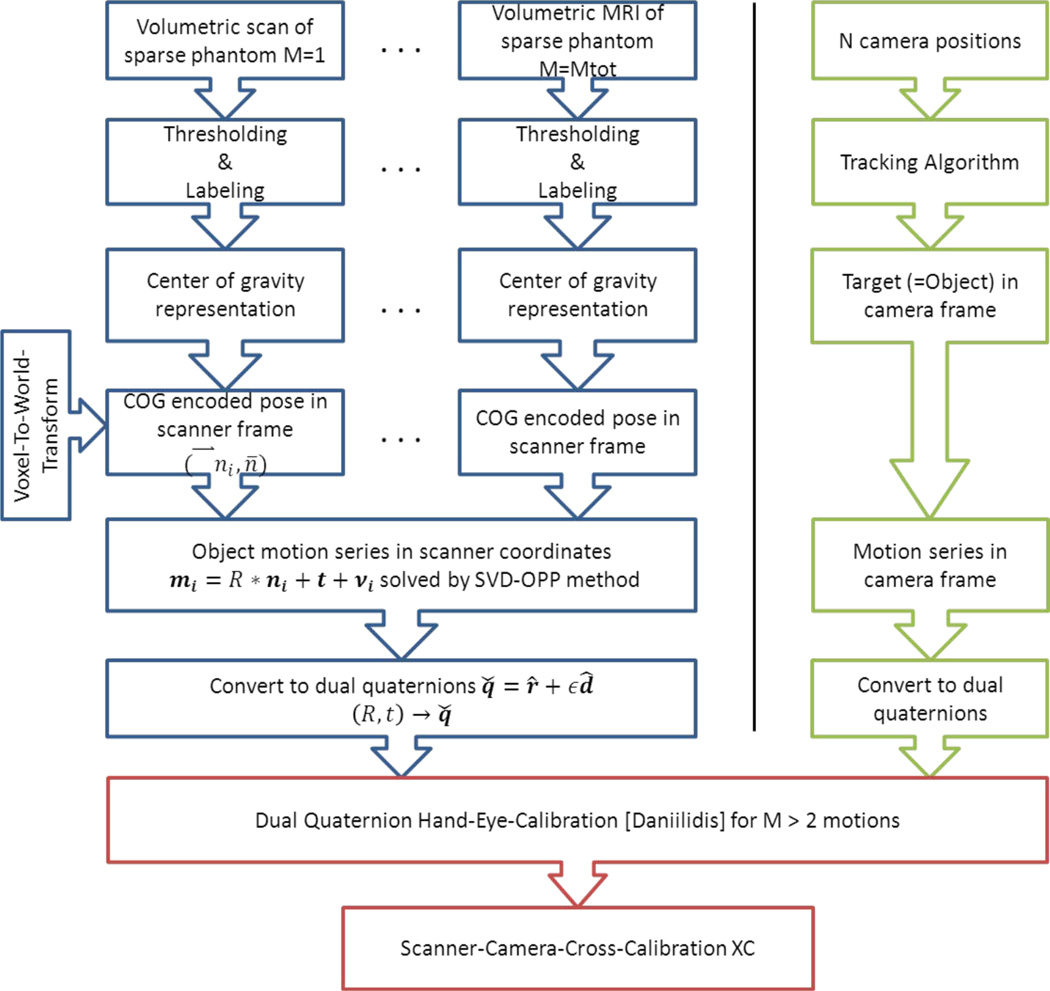
We implemented an algorithm that makes use of dual quaternions to describe the rotations and translations in a compact and closed form [“Dual Quaternion Hand Eye Calibration”, or DQHEC, algorithm; (5)]. This approach allows fitting of all available motions in a non-iterative and analytical way, and is superior in terms of precision and reliability over all previous methods (which separately solved for rotations and translations). An overview of how motion is described with the help of dual quaternions and how to transform a homogeneous matrix into the corresponding dual quaternion is given in the Appendix. The steps necessary to perform the DQHEC algorithm are summarized as a workflow chart in Figure 2. Of note, there are many approaches to solving the operator equations [6]–[12] (use of dual quaternions being one of them). A review of other methods and representations is provided in (16).

Figure 2.

Overview of the suggested steps for a non-iterative camera-scanner cross calibration using dual quaternions based on a series of motions.

Input data accuracy and removal of outliers

A series of unit dual quaternions describes motion in the camera and the scanner coordinate frames. Since both modalities observe the same physical motion, the absolute rotation angle and the total displacement must be preserved. In the dual quaternion formalism this means that the scalar values (first coefficient) of the rotational and the displacement quaternion must be identical in both coordinate systems (see appendix A2 and the proof in (5)). Mutual deviations above the expected noise level are a strong indication for a systematic error during the motion measurement in one of the reference frames. Given the limited number of motion pairs used in minimizing Eq. [7], incorrect motions can lead to severe degradation of the quality of the fit. Pairs of motion in the camera and scanner frame were therefore excluded from further analysis if the deviation in scalar values was greater than 1 %.

Assessing the quality of the hand-eye calibration algorithm

Performing a series of motions, recording them in the scanner and the camera frames, and applying the cross calibration algorithm result in an initial estimate of the camera-scanner transform. The quality of this initial calibration can be evaluated by comparing the theoretical scanner motions (synthesized with the initial cross calibration) with the actually measured scanner motions. Specifically, the homogeneous transforms between each of the measured and the synthesized data were calculated, and the total displacement and the total rotation angle were defined as translational and angular errors (mm and degree).

Refining the cross calibration using prospective motion correction feedback

The algorithm described above determined the camera position in the MRI reference frame (the cross calibration) without using feedback from an actual prospective motion correction implementation (i.e. PMC was “OFF”). However, PMC can be used to assess the quality of a camera calibration by measuring the difference between an object’s initial position and its “corrected” position after motion (in MRI coordinates). In case of perfect cross calibration and sequence implementation, motion correction would be perfect and no difference in the detected position should occur in the presence of any motion. Conversely, residual motion with prospective correction suggests calibration errors. We demonstrate how a series of measured correction residuals can be used to further improve the cross calibration. The initially estimated cross calibration can be expressed as a product of the true (unknown) calibration X_true with an error term E

$$X_{\mathit{\text{est}}}=E{X}_{\mathit{\text{true}}}$$ [8]

The estimated motion in the scanner frame is then the true motion sandwiched by the error term

$$B_{\mathit{\text{est}}}=E{B}_{\mathit{\text{true}}}{E}^{-1}$$ [9]

If a series of estimated {(B_est)_i} and true motions{(B_true)_i} is known, the error term can be calculated using the hand-eye-calibration algorithm. The (B_est)_i are derived from the motions A_i detected by the tracking device and the initial calibration. Any single scan i is described by

$$B_{\mathit{\text{est}}}=X_{\mathit{\text{est}}}A{X}_{\mathit{\text{est}}}^{-1}$$ [10]

Based on the residual motion D between the original phantom position P₀ and the motion corrected scan $P_i^{\mathit{\text{corr}}}$, the true motion can be derived.

$$D=P_1^{\mathit{\text{corr}}}{P}_0^{-1}=B_{\mathit{\text{est}}}^{-1}{P}_1{P}_0^{-1}=B_{\mathit{\text{est}}}^{-1}{B}_{\mathit{\text{true}}}{P}_0{P}_0^{-1}=B_{\mathit{\text{est}}}^{-1}{B}_{\mathit{\text{true}}}$$ [11]

With the estimated motion from Eq.[10] and the measured deviation D, the true motion, necessary to solve Eq. [9], is calculated as

$$B_{\mathit{\text{true}}}=B_{\mathit{\text{est}}}D$$ [12]

After the error term E is calculated by using the DQHEC method, the true calibration is given by inverting Eq. [8]. If necessary, the newly calculated “true” transform can again be subjected to a further residuum-based optimization step. A pictorial description of the transformations involved in the iterative calibration steps is given in Figure 3. We refer to the procedure described in this section as closed-loop cross calibration since it is based on residuals (feedback) of the motion correction implementation. As noted, it may be applied iteratively.

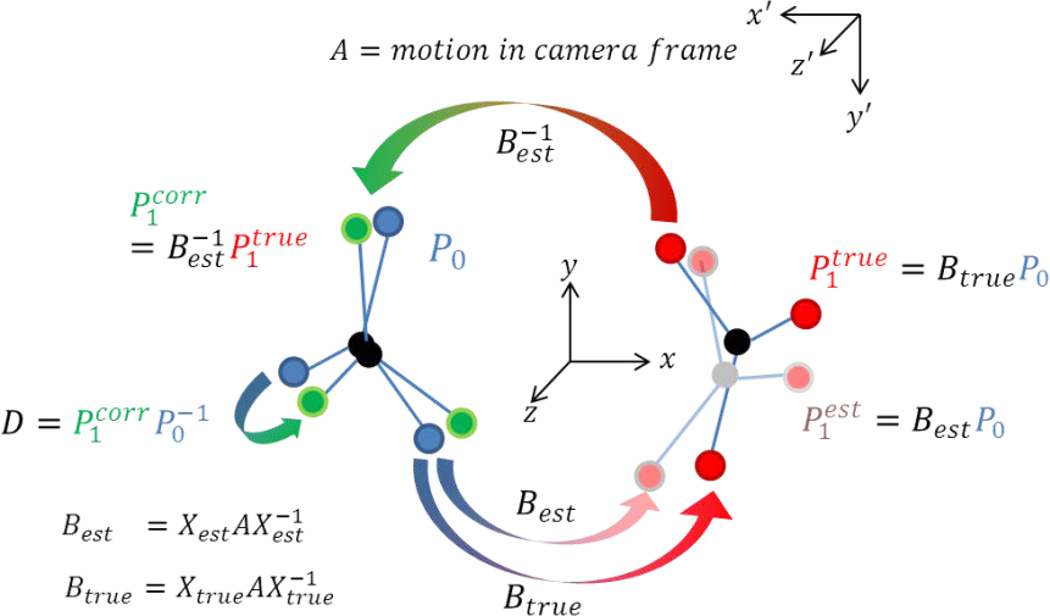
Figure 3.

Pictorial description of the closed-loop calibration step. The initial cross calibration X_est causes errors in the motion estimate in the scanner frame based on the motion in the camera frame (A). The inaccurate motion is then inversely applied to the true pose of the object leading to an error in corrected pose P_corr. The residual D between the initial pose and the corrected pose P1corr can be measured using the sparse phantom, SVD-OPP method. This allows the calculation of the unknown true motion and in a second step the calculation of the correct cross calibration.

Methods

Experiments were performed on a 3T Tim Trio system (Siemens Erlangen, Germany) equipped with a prototype in-bore camera optical motion tracking system based on Moiré-Phase-Tracking (MPT) of a single marker (15mm) that can be attached to the object to be imaged (17). The tracking system can operate at up to 85 frames per second, and has an absolute accuracy of <0.1mm and <0.1 degrees over the entire measurement range (Metria Innovation, Milwaukee, WI, vendor specification).

Prospective motion correction was performed using a gradient echo sequence capable of adapting the scan geometry according to object motion in real time (8). The communication interface between the sequence and the camera was provided by the XPACE library (8). Cross-calibration was first performed using the non-iterative approach (Eq. [6]). For the closed-loop calibration step, the pose of the initial phantom orientation was stored and used as the reference pose for subsequent scans with the phantom in various orientations and PMC enabled. Additionally, the closed-loop algorithm was applied to an existing cross-calibration of moderate accuracy.

The sparse phantom was built from 4 plastic spheres with a diameter of 30mm, filled with CuSO₄ doped water, which were rigidly attached to a plastic frame (see Fig.1a with the marker attached at an arbitrary position). The ordered distances of the individual spheres relative to the center-of-gravity of the complete phantom are given as 67.5, 62.8, 60.8, 56.0 mm. At least 4 spheres not lying within a plane are necessary to encode arbitrary rigid body motion. Care was taken to ensure that no residual air bubbles were present inside the liquid filled spheres, since moving air bubbles would violate the rigidity condition for the phantom. For the initial scan in each experiment, one of the spheres was at the magnet isocenter to facilitate automatic resonance frequency adjustments.

For the calibration measurements, between 7 and 10 phantom motions were performed, with arbitrary rotations between 90 and 180° and translations between 10–30mm. All algorithms and a class handling dual quaternions were implemented in MatLab (Mathworks, Natick, Massachusetts). Volume imaging was performed with a 3D GRE sequence with the following parameters: TR/TE = 7.5/2ms; FOV = 256×256×256 mm³ ; 2×2×2mm³ spatial resolution; matrix size 128×128×128 flip angle = 25°, total acquisition time 2min. The imaging volume was always symmetric about MRI isocenter in order to prevent off-center rotations. The scanner raw data were exported and reconstructed offline in MatLab using a simple Fourier Transform. The images were reoriented to match the scanner reference frame.

The intrinsic accuracy of the sparse phantom SVD-OPP method was estimated using a Rayleigh distribution $f(x,\sigma )=\frac{x}{{\sigma }^2}\text{exp}\left(\frac{-x^2}{2{\sigma }^2}\right)$ for x > 0 which describes the magnitude of a vector where the each component is uncorrelated and normally distributed with zero mean and equal variance. The residual Euclidian Distances of each sphere in its initial position and after reversing an estimated transform are assumed to be Rayleigh distributed. The variance of the Rayleigh distribution is assumed to reflect the intrinsic accuracy of the sparse phantom SVD-OPP method based on GRE images with 2mm isotropic spatial resolution

Results

Accuracy estimation for COG encoded motion measurements

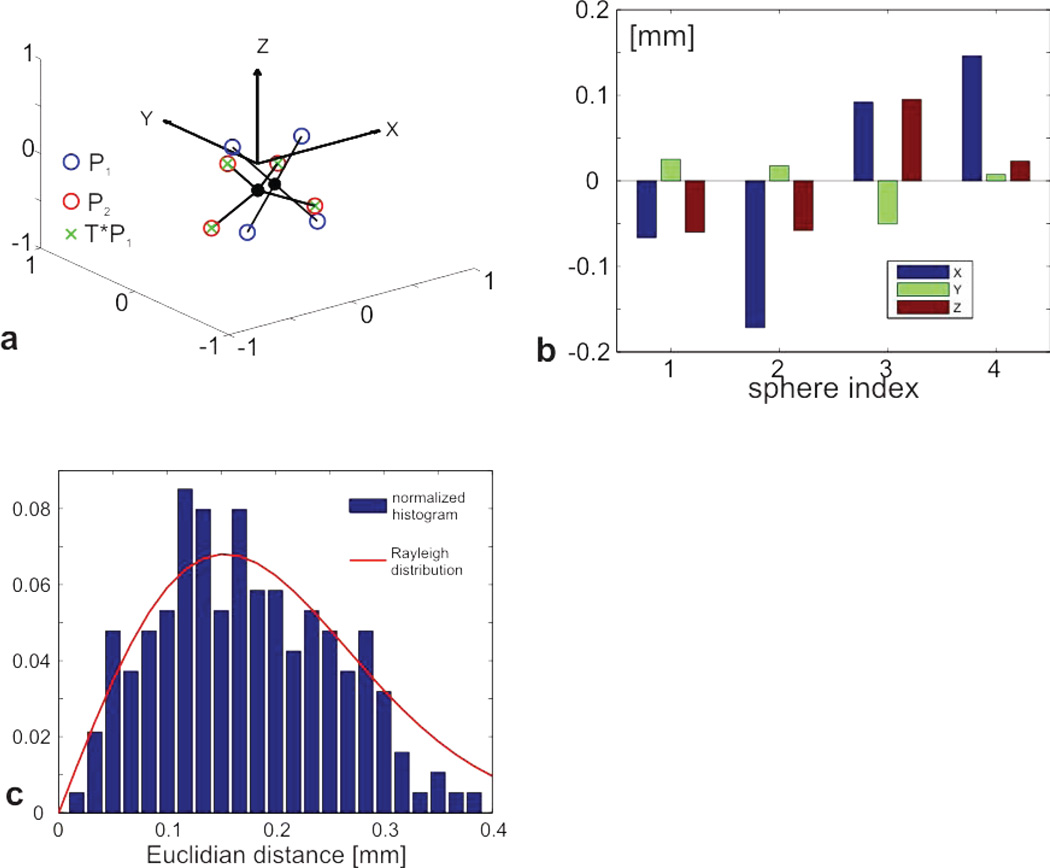
The application of the SVD-OPP method on COG encoded phantom poses is shown in Figure 4a. The blue circles represent the initial phantom position P₁ and the red circles display the pose P₂ after an arbitrary phantom motion. The green crosses display the resulting transform T applied to P₁. The almost perfect match between the red circles and green crosses is an indication for an accurate estimation of the true transformation. For each of the 4 spheres, the difference in the xyz-components between the second pose P₂ and the transformed pose P_trans = TP₁ was calculated and plotted (Figure 4b). The error in the individual components is below 0.2mm for all spheres and axes. Based on xyz-components for the second pose P₂ and the transformed pose P_trans (using the transformation found by the SVD-OPP method), the Euclidian distance between the spheres was calculated for a total number of n=47 large motions. The normalized histogram for all 4×47 Euclidian Distances is plotted in Figure 4c, and can be approximated by a Rayleigh distribution with a variance of σ = 0.15 mm (red line in Figure 4c). Importantly, GRE images with 1mm spatial resolution did not substantially improve the accuracy of the SVD-OPP algorithm. We also compared the COG representation derived from the GRE scan to that derived from a fast spin echo sequence and found the differences to be less than 1/10^th of the voxel size.

Figure 4.

Application of the SVD-OPP method to arbitrary motion is shown in a. The blue circles represent the initial phantom position P₁ and the red circles display the transformed position P₂. The green crosses display the resulting transform T applied to P₁. The almost perfect match between the red circles and green crosses is an indication for a very accurate estimation of the true transformation. The residual xyz components for a single motion are plotted in b. The distribution of Euclidian distances between original and transformed poses is displayed in c. The normalized histogram matches a Rayleigh distribution with σ = 0.15 mm.

Non-iterative calibration using the hand-eye-calibration algorithm

Table 1 shows the total rotation angle θ and the displacement d for 7 motions in the camera and the scanner frames derived from the dual quaternion’s scalar values.

Table 1.

Total rotation angle in degree and the total displacement in mm for 7 motions as seen in the camera and in the scanner frame. The deviation Δ is calculated as the difference between camera and scanner frame.

Motion number	#1	#2	#3	#4	#5	#6	#7
θMPT [deg]	164.48	90.41	20.13	105.84	166.12	70.19	34.27
θscanner [deg]	164.23	90.50	20.22	105.83	166.21	69.83	34.24
Δθ [deg]	0.25	−0.09	−0.09	0.01	−0.09	0.36	0.03
dMPT [mm]	1.77	0.93	12.11	3.36	25.25	5.24	11.19
dscanner [mm]	1.63	1.02	12.07	3.33	25.51	5.11	10.90
Δd [mm]	0.14	−0.09	0.04	0.03	−0.26	0.13	0.29

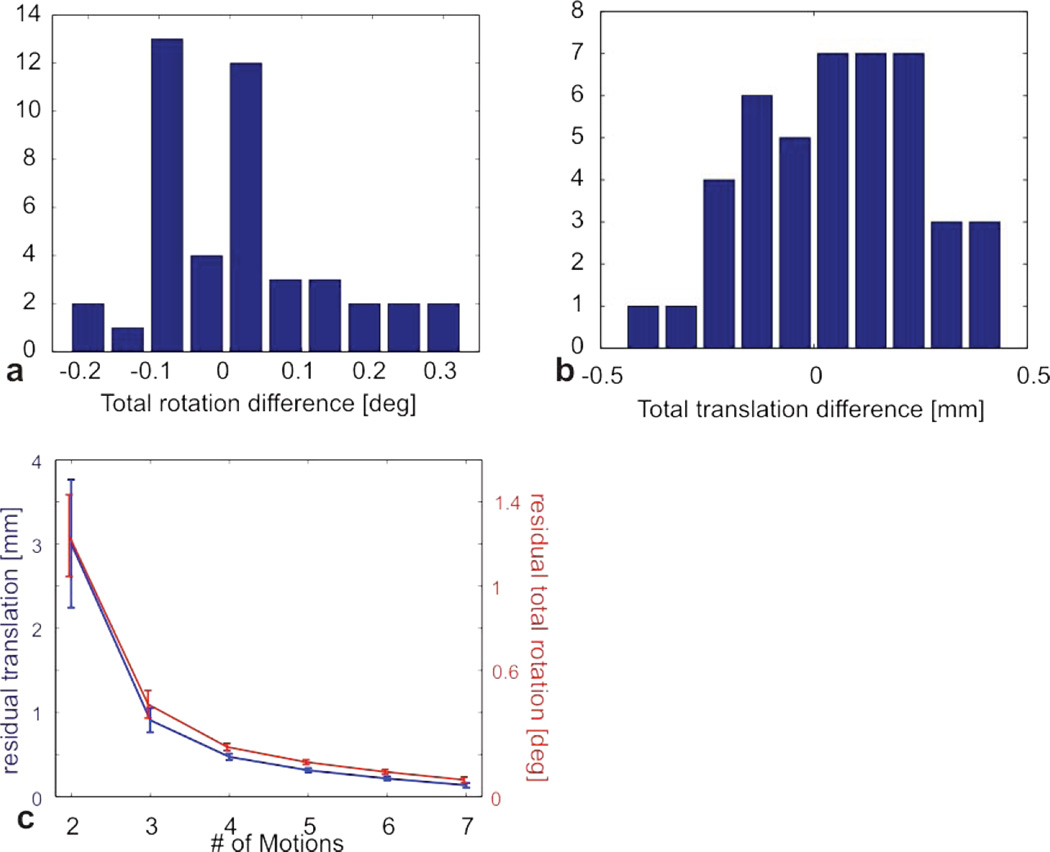
The maximum rotational deviation between the optical tracking system and the sparse phantom SVD-OPP method is 0.5%, with most of the values considerably lower. The maximum translational deviation is < 0.3 mm. For the n=47 motions, the difference in the total rotation angle (in degree) and the total translation (in mm) between the camera and the SVD-OPP method was calculated and plotted as histograms in Figure 5a and b, respectively. The majority of deviations are around 0.1 degree and below 0.3mm. Based on these values it is possible to define a threshold which allows excluding obvious outliers from the fitting procedure and thereby improving the accuracy of the fitted cross calibration.

Figure 5.

Difference between the total rotation angle measured by the camera and measured by the SVD-OPP method for a series of 47 motions. The difference in the total translation is calculated as well. The histograms of the respective differences are shown in a and b. Figure 4 c shows the convergence of the DQHEC algorithm as a function of the number of poses used to calculate the cross calibration.

Convergence behavior of the DQHEC-algorithm

In case of noise free measurements, the cross calibration can be computed from only two nonparallel motions. In order to estimate how many motions are needed in a real world scenario that includes measurement errors, we calculated the cross calibration from subsets of an available motion series with increasing length M. For every subset with 2 <= M < 8 the cross calibration was computed for all possible permutations and averaged. The cross calibration for M=8 was assumed to represent the true value and taken as a reference. Figure 5c displays the deviation from the reference calibration in terms of the total rotation angle and the residual translations for all subsets. The deviation curve converges quickly to the reference value, with negligible error (below 0.3 degree and 0.3mm) for more than 5 motions.

Closed-loop calibration step using prospective motion correction

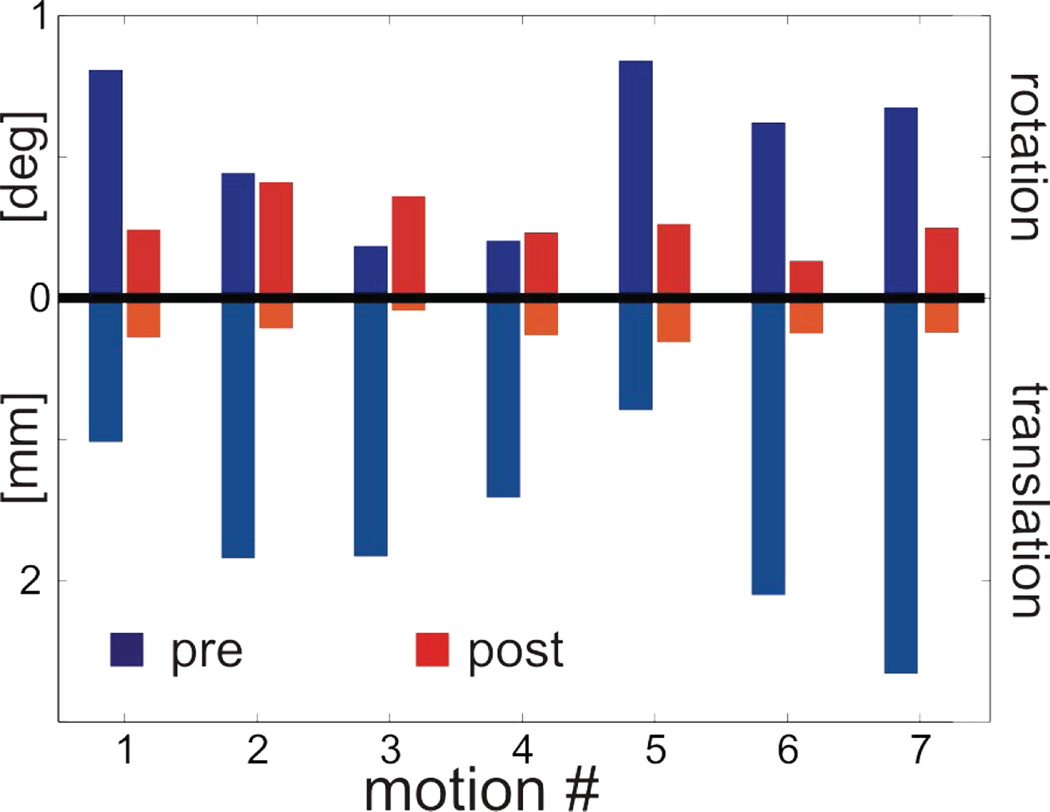
The non-iterative approach from the previous section generally yields an initial camera-scanner cross calibration with reasonable accuracy, but systematic errors are generally not removed by the fitting process and may cause degradation of the cross calibration accuracy. By applying the closed-loop calibration method, the actual performance of a motion corrected sequence is used as a feedback to further refine the calibration accuracy. For 7 arbitrary motions, data were acquired twice, using a sequence with PMC switched on. The initial pose was taken as a reference for the other scans with the phantom in various (physical) poses. The deviations D between the corrected and the reference scan were calculated and plotted for each scan as the residual rotation and translation; values were below 2mm and 1 degree (blue bars in Figure 6). Based on the measured deviations D, the closed-loop DQHEC algorithm was applied and the camera cross calibration file was then updated. The phantom was then put back in its initial reference pose and the 7 motions were repeated with approximately identical motion parameters (within 5–10 degree and 10mm accuracy), again using PMC relative to the first pose. The residual deviations after the iterative calibration step are displayed as red bars in Figure 6, and are below 0.3mm and 0.4 degree. Therefore, the motion correction clearly benefits from the closed-loop calibration step, with residual errors now in the range of measurement accuracy of the sparse phantom method.

Figure 6.

Results of a closed-loop calibration step. The blue bars show the residual translations and rotations for 7 arbitrary motions using an imaging sequence with adaptive motion correction. From these residuals, a new cross calibration was calculated and the 7 motions were repeated. The red bars display the residual rotations and translations with the updated cross calibration transform.

Imperfect calibration

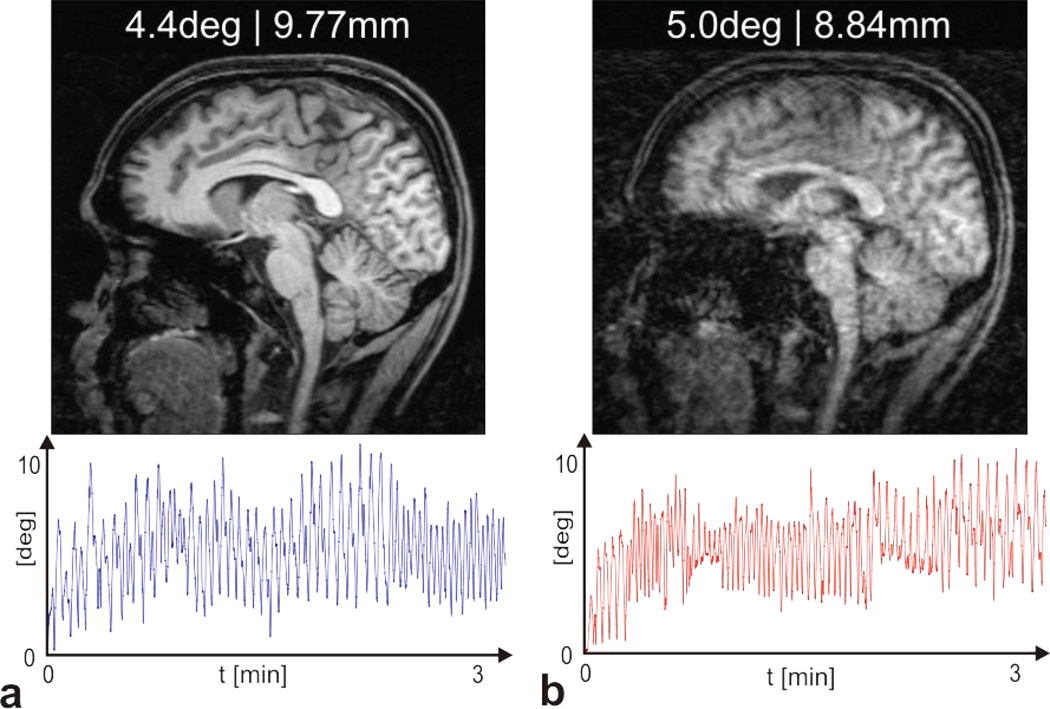
The effect of insufficient calibration accuracy on the outcome of PMC applied to moderate and continuous head movements during the 3min acquisition of a T1-weighted structural scan (MPRAGE) is shown in Figure 7. For the sagittal slice in a, the cross calibration transform after the closed loop calibration step was used, and is assumed to be optimal. Prospective motion correction is able to compensate for the rather larger head movement and yields an undistorted scan (Fig. 7a). For the scan in b, the subject performed a similar head motion (see motion traces) as in a. However, the cross-calibration transform was deliberately altered by 3 degrees and translated by 5mm prior to the MR acquisition. The resulting slice in Figure 7b, acquired with the false calibration, shows substantially more residual motion artifacts than the scan acquired with optimal calibration (7a).

Figure 7.

Effect of a poor calibration on the outcome of prospective motion correction. Two T1-weighted structural scans (MPRAGE) were acquired with comparable and continuous head motion (3min acquisition time). The motion traces for the rotational component are displayed under the sagittal slices. The average rotational deviation was 4.4 degree and 5.0 degree for a and b, respectively. The averaged translation was 9.77mm for a and 8.84mm for b. For the scan in a an optimal camera cross-calibration was used which results in an almost undistorted image despite the rather larger motion. For b, the optimal calibration was deliberately rotated and translated by 5degree and 5mm, respectively, resulting in a significantly more distorted scan.

Discussion

We present a method that allows accurate and relatively fast cross calibration between an external tracking device (optical camera) and an MR scanner or other medical imaging device de novo (without any prior information). The method relies on imaging a sparse phantom that allows tracking of arbitrary and large rigid body transformations in the reference frame of the scanner. Based on the dual quaternion approach, the cross calibration is computed (fitted) analytically from a series of rigid body motions observed both in the camera and in the scanner frames. Dual quaternions provide a compact and numerically favorable way to describe homogeneous transforms since the axis and the rotation angle/displacement are algebraically separated. No non-linear minimization step is involved, which ensures that the computed value is optimal in that it minimizes Eq. [7].

The calibration method in (9) differs from our method by using image registration based techniques to assess the motion in the scanner frame. As a result, it requires relatively small (<15 degree) rotations, which ultimately limits the performance of the fitting algorithm. The limitation of small rotations may be overcome by using PMC during the calibration process (8), as long as large physical rotations result in residual rotations (with PMC on) that fall within the sensitive range of the image registration procedure. By feeding back the residuals and updating the camera-scanner transform at each step, this method iteratively converges to a cross calibration (18). The disadvantage of this iterative approach is that only a limited number of degrees of freedom (for instance, a rotation about one axis) are subject to minimization at each step, which may result in poor convergence. For instance, calibration errors parallel to the actual rotation axis can be arbitrarily large without affecting the correction of rotations about that particular axis.

In contrast, our method makes use of all six degrees of freedom to determine the transformation. Likewise, the dual quaternion algorithm minimizes the rotational and translational components of Eq. [7] in a single step. This is advantageous over methods where the two components are solved separately (16) and the result from the first step is used to solve the remaining component, since residual errors from the first minimization step can degrade the numerical accuracy of the second step. An overview of dual quaternion properties is given in the appendix and a detailed discussion can be found in (5) and (19).

Another advantage of the new method presented is that it is robust and can unambiguously and non-iteratively determine phantom movements even for large rotations Conversely, prior approaches that rely on image registration of a complex phantom (using existing registration packages) generally fail to estimate arbitrarily large motions, since the differential norm of a structured image that is rotated relative to its initial position has an unpredictable number of local minima. Furthermore, our COG procedure relies on binarized images of a few separate regions, and may therefore be less sensitive to the effect of B1-inhomogeneties than registration-based approaches (which ultimately align spatial alterations in signal intensity). Furthermore, compared to larger liquid-filled phantoms, the sparse phantom proposed appears to be less prone to the occurrence of eddies, which may cause signal alterations and interfere with conventional registration algorithms.

The initial non-interative step of the method does not require feedback (or cross-talk) between the camera and the scanner. If the motions span a reasonable large fraction of the unit circle, a good initial calibration with errors below 1 degree and 1mm can be obtained from fewer than 6 measurements in less than 10 minutes. The non-iterative method eliminates randomly distributed errors that are inevitably associated with each camera/MRI motion data pair. Possible sources for these errors are gradient non-linearity and magnetic field inhomogeneities resulting in spatial distortions in MR images, imperfections in the camera or lens, violation of the rigid-body assumption of the phantom, and random errors. However, certain systematic errors that can be described as a transformation to a slightly different but consistent reference frame (either camera or scanner), such as an incorrect voxel-to-world- transform of the image reconstruction method, are not eliminated by the non-iterative method.

By using the closed-loop, feedback-based method, some of these errors can be eliminated because they are explicitly modeled as an error term in the fitting equation.

The intrinsic accuracy of the sparse phantom SVD-OPP method of 0.15mm is well below the actual spatial resolution of the underlying images (2mm). This result is in general agreement with the literature, where the achievable accuracy of a Centroid algorithm with simple thresholding is estimated to be approximately 1/10 of the pixel resolution (20). In (20) it is also shown that the centroid detection problem for binary raw images benefits only moderately from increased spatial resolution, which is in agreement with our observation that GRE images with 1mm spatial resolution do not substantially improve the accuracy of the SVD-OPP algorithm. In general, a wide range of imaging sequences is feasible as long as it is insensitive to effects of global shim variations and local inhomogeneities (susceptibility changes) at the region borders.

However, the accuracy of the method is ultimately limited by the accuracy of the MRI scanner. Gradient nonlinearities and B₀ inhomogeneities can cause incorrect registration of pixel intensities as a function of pixel position, causing deviations from the rigid body assumption when applying the SVD-OPP algorithm. Additionally, although the accuracy of the camera tracking system is assumed to be somewhat better than MRI based methods (<0.1mm and <0.1°), tracking errors may still contribute to the total error of the calibration method at the level observed.

Our method may be modified to perform a single scan recalibration of an external tracking system. After rigidly attaching the marker to the sparse phantom, the marker position relative to the phantom coordinate system (COG-representation) can be derived and stored. Since the absolute position of the sparse phantom relative to the scanner frame can be measured in a single scan, and since the camera position relative to the marker is provided by the tracking data, the camera position relative to the scanner frame can be calculated. This might be useful for implementations with variable camera mounting points. Furthermore, our approach is well suited for quick routine checks if the motion correction feedback still achieves the necessary accuracy to actually improve imaging results in case of patient motion. Finally, although our manuscript demonstrates the calibration of a camera tracking system relative to an MRI scanner, the principles described in this work may also be applied to other tomographic imaging modalities, such as computer tomography (CT).

Appendix

A1 Dual Numbers

Dual numbers were invented by Clifford (1873) and are defined as

$$ž=r+\epsilon d\mathit{\text{ with }}{\epsilon }^2=0$$ [A1.1]

with the real and dual part r and d, respectively. The imaginary unit ε has the property ε² = 0 in analogy to complex numbers where the imaginary unit has the property i² = −1.

Multiplication of dual numbers is defined as

$$ž\times \mathrm{w̌}=(z_r+\epsilon z_d)\times (w_r+\epsilon w_d)=z_r{w}_r+\epsilon (z_r{w}_d+z_d{w}_r)$$ [A1.2]

Dual number multiplication is associative but non-commutative (ž× w̌ ≠ w̌ × ž).

A2 Unit quaternion representation of rotations

Unit quaternions provide a convenient and compact representation of rotations. A unit quaternion r̂ is defined as r̂ = s + ix + jy + kz with the imaginary units i, j, k with i² = j² = k² = ijk = −1

A quaternion with $\Vert \mathit{r̂}\Vert =\sqrt{s^2+x^2+y^2+z^2}=1$ is called a unit quaternion and represents a rotation with rotation angle θ around an axis with direction n⃗ = (x, y, z) where the so called scalar value s is given as $\text{cos}\frac{\theta }{2}$. A unit quaternion can therefore be written in an axis-angle representation $(\text{cos}\frac{\theta }{2},\text{sin}\frac{\theta }{2}\overrightarrow{n})$ which algebraically separates the rotation angle and axis.

A3.1 Dual quaternions

Dual quaternions are defined in analogy to dual numbers as

$$\mathit{q̌}=\mathit{r̂}+\epsilon \mathit{d̂}$$ [A3.1]

where r and d are ordinary quaternions that can be used to describe the rotational and translational part of a coordinate system transform or rigid body motion.

Dual quaternions can also be represented by a scalar and a vector part as it is possible for quaternions. In that case the scalar part is a dual number and the vector part a dual vector with three dual number components.

The following basic arithmetic operations are defined

Addition

$${\mathit{q̌}}_1+{\mathit{q̌}}_2=({\mathit{r̂}}_1+\epsilon {\mathit{d̂}}_1)+({\mathit{r̂}}_2+\epsilon {\mathit{d̂}}_2)=({\mathit{r̂}}_1+{\mathit{r̂}}_2)+\epsilon ({\mathit{d̂}}_1+{\mathit{d̂}}_2)$$ [A3.2]

Multiplication

$${\mathit{q̌}}_1\times {\mathit{q̌}}_2=({\mathit{r̂}}_1+\epsilon {\mathit{d̂}}_1)\times ({\mathit{r̂}}_2+\epsilon {\mathit{d̂}}_2)={\mathit{r̂}}_1{\mathit{r̂}}_2+\epsilon ({\mathit{r̂}}_1{\mathit{d̂}}_2+{\mathit{d̂}}_1{\mathit{r̂}}_2)$$ [A3.3]

Conjugation

$${\mathit{q̌}}^{*}={(\mathit{r̂}+\epsilon \mathit{d̂})}^{*}={\mathit{r̂}}^{*}+\epsilon {\mathit{d̂}}^{*}$$ [A3.4]

Norm

$${\Vert \mathit{q̌}\Vert }^2=\mathit{q̌}{\mathit{q̌}}^{*}=$$ [A3.5]

Inversion

$${\mathit{q̌}}^{-1}=\frac{{\mathit{q̌}}^{*}}{\Vert \mathit{q̌}\Vert }$$ [A3.6]

In case of a unit dual quaternion with ‖q̌‖ = 1, inversion corresponds to conjugation

Scalar value and constants of motion

The scalar value of a unit dual quaternion is a dual number and can be calculated by

$$\check{sc}=\frac{1}{2}(\mathit{q̌}+{\mathit{q̌}}^{*})$$

It represents a constant of motion (independent of the reference frame) and is related to the total rotation angle θ and the length of the displacement vector d (see Figure 7) by

$$\theta =2{\text{cos}}^{-1}\mathit{\text{real}}[\check{sc}]$$

And

$$d=\frac{-2\mathit{\text{dual}}[\check{sc}]}{\text{sin}\frac{\theta }{2}}$$

where real[] and dual[] stand for the operation of extracting the real and dual part of a dual quaternion, respectively.

A3.2 Switching between homogeneous transform matrices and dual quaternions

If a homogeneous transform is given as a rotation matrix R and a translation vector t⃑ the corresponding unit dual quaternion q̌ = r̂ + εd̂ is constructed as follows. The first component r̂ is simply given by the quaternion representation of the rotation matrix R. The quaternion representing the displacement is given by writing the translation vector t⃑ as a quaternion with zero scalar part t̂ = (0, t⃑) and multiplying it with r̂:

$$\mathit{d̂}=\frac{1}{2}\mathit{t̂}\mathit{r̂}$$

The backward transformation is given as t̂ = 2d̂;r̂⁻¹ and extracting the vector part of the quaternion t̂. The rotation matrix is given by a conventional quaternion-to-discrete-cosine-matrix transform.

The translation t = ‖t‖ in [mm] of a unit dual quaternion is then given as

$$t=\Vert \stackrel{\rightharpoonup }{\mathit{t}}\Vert =\Vert \mathit{t̂}\Vert =\sqrt{\mathit{t̂}{\mathit{t̂}}^{*}}=2\sqrt{\mathit{d̂}{\mathit{d̂}}^{*}}=2\Vert \mathit{d̂}\Vert$$

A3.3 Example of hand eye calibration using dual quaternions

We assume that the camera calibration (i.e. camera position) X can be described as a 90deg rotation about the y-axis n⃗ = (0,1,0) and a shift of 40mm along the x-axis t̂ = (0,40,0,0) relative to the scanner frame. The corresponding dual quaternion is then given as

$$X_{dq}^{\mathit{\text{true}}}=\mathit{r̂}+\epsilon \mathit{d̂}\text{with}\mathit{r̂}=(\text{cos}\frac{{90}^{°}}{2};\text{sin}\frac{{90}^{°}}{2}\overrightarrow{n});\mathit{d̂}=\frac{1}{2}\mathit{t̂}\mathit{r̂}=\frac{1}{2}(0,40,0,0)\times (\text{cos}\frac{{90}^{°}}{2};\text{sin}\frac{{90}^{°}}{2}\overrightarrow{n})\to X_{dq}^{\mathit{\text{true}}}=\{\sqrt{2}/2;0;\sqrt{2}/2;0\}+\epsilon \{0;14.14;0;14.14\}$$

At least two motions are necessary to calculate X. Assume the two motions in frame A are a 180 degree rotation around the z-axis and a shift of 5mm along x, and a 90 degree rotation around×and a shift of 2mm along z for A₁ and A₂, respectively.

$$A_1=\{0;0;0;1\}+\epsilon \{0;0;-2.5;0\}\text{and}{A}_2=\{\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{2};0;0\}+\epsilon \{0;0;\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{2}\}$$

The same motions seen in reference frame B are then given as $B_i={(x_{dq}^{\mathit{\text{true}}})}^{-1}{A}_i(X_{dq}^{\mathit{\text{true}}})$:

$$B_1=\{0;-1;0;0\}+\epsilon \{0;0;37.5;0\}\text{and}{B}_2=\{\frac{\sqrt{2}}{2};0;0;\frac{\sqrt{2}}{2}\}+\epsilon \{0;-\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{2};0\}$$

It can easily verified that the scalar values of A₁, B₁ and A₂, B₂ are identical. By applying the algorithm from Daniilidis et al. (5) the underlying transform $X_{dq}^{\mathit{\text{true}}}$ can be calculated from A_i and B_i even in the presence of noise. A detailed explanation of the complex algorithm in (5) is beyond the scope of this paper.