Periodic migration in a physical model of cells on micropatterns

Abstract

We extend a model for the morphology and dynamics of a crawling eukaryotic cell to describe cells on micropatterned substrates. This model couples cell morphology, adhesion, and cytoskeletal flow in response to active stresses induced by actin and myosin. We propose that protrusive stresses are only generated where the cell adheres, leading to the cell's effective confinement to the pattern. Consistent with experimental results, simulated cells exhibit a broad range of behaviors, including steady motion, turning, bipedal motion, and periodic migration, in which the cell crawls persistently in one direction before reversing periodically. We show that periodic motion emerges naturally from the coupling of cell polarization to cell shape by reducing the model to a simplified one-dimensional form that can be understood analytically.

Cultured cells on two-dimensional substrates are often used as a convenient proxy for more biologically relevant situations, such as cells within three-dimensional extracellular matrix (ECM). However, cells in ECM often exhibit qualitatively different modes of migration than those on substrates [1–4]. A remarkable example of this is the discovery of periodic migration in zyxin-depleted cells in collagen matrix [5]. Understanding cell motility in ECM may be profoundly important for the study of cancer invasion [6]. Interestingly, features of cell morphology and dynamics in matrix are recapitulated in cells on micropatterned adhesive substrates, including cell speed, shape, dependence on myosin [1] and periodic migration [5]. Other micropatterns induce cell polarization and directed cell motion [7–9] and sorting of cells from one- to two-dimensional regions of micropatterns [10]. In this Letter, we study the influence of micropatterns on cell motility using an extension of a computational model of eukaryotic cell crawling [11, 12] and observe a wide range of dynamic behaviors including periodic migration. To our knowledge, ours is the first cell crawling simulation to display periodic migration.

It would be natural to expect that periodic migration [5] requires underlying oscillatory protein dynamics, as in Min oscillations in E. coli [13]. Surprisingly, this is not the case; periodic migration and other complex behaviors appear with only minimal alteration to the model for freely crawling cells. We study periodic migration in detail, and show that it is a consequence of feedback between the cell's shape and its biochemical polarization, i.e. how proteins are segregated to one side of the cell. We use sharp interface theory to reduce our model to a simplified one-dimensional (1D) model that is analytically tractable. Periodic migration exemplifies how coupling between cell shape and chemical polarity can lead to unexpected cell behavior.

Model summary

We describe the cell's cytoskeleton as a viscous, compressible fluid driven by active stresses from actin polymerization and myosin contraction. This is appropriate for the long time scales of keratocyte and fibroblast migration on which the cytoskeleton can rearrange, see e.g. [14]. Our model is one of a broad spectrum of active matter [15, 16] models of motility in which active stresses drive deformation [14, 17-26]. Details of the model are available in Ref. [12]; we review it briefly to highlight changes made to study cells on micropatterns. It has four modules: 1) cell shape, tracked by a phase field ϕ(r,t), 2) the cytoskeleton as an active viscous compressible fluid [14, 27], 3) actin promoter (e.g. Rac or Cdc42) and myosin concentrations obeying reaction-diffusion-advection equations, and 4) adhesions between cell and substrate, tracked individually.

Cell shape is tracked by a “phase field” ϕ(r,t) that is zero outside and unity inside the cell [11, 28-33]. ϕ varies smoothly across the cell boundary, which is implicitly set by ϕ = 1/2. ϕ(r,t) obeys

$${\partial }_t\varphi +\mathbf{u}\cdot \nabla \varphi =\mathrm{\Gamma }(\mathit{\in }{\nabla }^2\varphi -G^{\prime }(\varphi )/\mathit{\in }+c\mathit{\in }|\nabla \varphi |)$$ (1)

where u is the cytoskeletal velocity, Γ a relaxation coefficient, $c=\nabla \cdot \left(\frac{\nabla \varphi }{|\nabla \varphi |}\right)$ is the local interface curvature, ∈ the interface width,and G(ϕ) = 18ϕ²(1 − ϕ)².

We describe cytoskeletal flow with a Stokes equation including active forces from actin and myosin and forces induced by membrane curvature and cell-substrate adhesion:

$$\nabla \cdot \left[\nu \left(\nabla \mathbf{u}+\nabla {\mathbf{u}}^T\right)\right]+\nabla \cdot ({\sigma }_{\text{poly}}+{\sigma }_{\text{myo}})+{\mathbf{F}}_{\text{mem}}+{\mathbf{F}}_{\text{adh}}-\xi \mathbf{u}=0$$ (2)

where ν(ϕ) = ν₀ϕ is the viscosity. ξ does not vary over the substrate i.e. ξu is a hydrodynamic drag [34], not friction from adhesive binding [35]. Individual adhesions lead to F_adh; F_mem comes from membrane deformations (see Appendix). We neglect the pressure term arising from coupling between cytoskeletal mesh and cytoplasm [14]. Eq. 2 is solved numerically with a semi-implicit finite difference spectral method; other equations are stepped explicitly (see Appendix).

Our central hypothesis for the effect of the adhesive micropattern is that protrusive stress from actin polymerization, σ_poly, is only generated where the cell contacts the micropattern,

$${\sigma }_{\text{poly}}=-{\eta }_a^0\chi (\mathbf{r})\varphi {\rho }_a{\delta }_{\mathit{\in }}\widehat{\mathbf{n}}\widehat{\mathbf{n}}$$ (3)

where χ(r) is one inside the pattern and zero outside, ${\delta }_{\mathit{\in }}(\varphi )=\mathit{\in }|\nabla \varphi {|}^2,\widehat{\mathbf{n}}$ is the normal to the cell surface, ρ_a the actin promoter density on the membrane, and ${\eta }_a^0$ a protrusion coefficient. Our assumption is supported by experimental work showing that fibroblasts preferentially protrude processes from points near newly formed adhesions, which only form on the pattern [36]. Others have proposed active stresses proportional to cell-substrate adhesion [37]. Our pattern is a stripe, $\chi (\mathbf{r})=\frac{1}{2}\left[1+tan\mathrm{h}\left(3\left\{\frac{\omega }{2}-|x|\right\}/\mathit{\in }\right)\right]$, with w the stripe width. The contractile stress is ${\sigma }_{\text{myo}}={\eta }_m^0\varphi {\rho }_m\mathbf{I}$ with ρ_m the myosin density, ${\eta }_m^0$ the myosin contractility coefficient, and I the identity tensor.

Cell polarization arises from ρ_a, which follows a wave-pinning model [38]. Actin promoter exchanges between active membrane-bound (ρ_a) and inactive cytosolic $({\rho }_a^{\text{cyt}})$ states; membrane-bound promoter catalyzes binding to the membrane. Fronts between high ρ_a and low ρ_a can stall (“pin”), leading to a steady polarization [38].

Actin promoter and myosin processes only occur inside the cell; the phase field method is ideally suited to handle reaction-diffusion-advection equations within moving cells [11, 19,31–33]. The reaction-diffusion-advection equations for actin promoter and myosin are

$${\partial }_t\left(\varphi {\rho }_a\right)+\nabla \cdot \left(\varphi {\rho }_a\mathbf{u}\right)=\nabla \cdot \left[\varphi D_a\nabla {\rho }_a\right]+\varphi f$$ (4)

$${\partial }_t\left(\varphi {\rho }_m\right)+\nabla \cdot \left(\varphi {\rho }_m\mathbf{u}\right)=\nabla \cdot \left[\varphi D_m\left({\rho }_a\right)\nabla {\rho }_m\right].$$ (5)

Actin promoter diffuses with coefficient D_a on the membrane; at this level of modeling, we do not distinguish between membrane and cytoskeleton velocity, and so ρ_a is advected with the cytoskeletal velocity u. Myosin binds and unbinds from the cytoskeleton, which we model as a ρ_a-dependent diffusion coefficient $D_m({\rho }_a)=D_m^0/(1+{\rho }_a/K_D)$ [12]. The nonlinear reaction term $f({\rho }_a,{\rho }_a^{\text{cyt}})$ for promoter membrane-cytosol exchange is in the Appendix. ${\rho }_a^{\text{cyt}}$ is well-mixed (constant) and set by the conservation of ρ_a, i.e. ${\displaystyle \int d^{2}r\varphi (\mathbf{r})\left[{\rho }_a(\mathbf{r})+{\rho }_a^{\text{cyt}}\right]}=N_a^{\text{tot}}$ is constant.

Adhesions between cell and substrate are formed, age, and transition between modes as in [12]. However, adhesions may only form on the micropattern [36]; adhesions that leave the micropattern are destroyed (see Appendix). The number of adhesions is fixed. We do not enforce symmetry, unlike [12].

Simulation of periodic migration

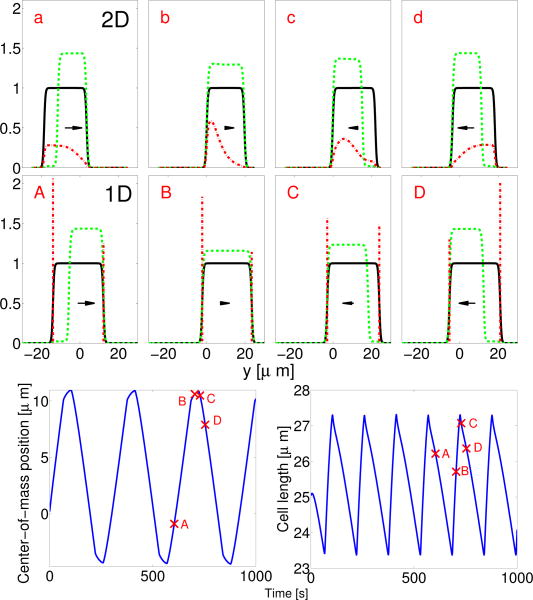
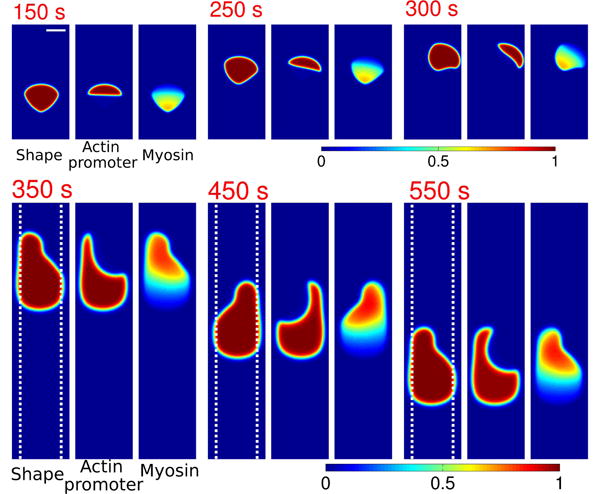
Numerical evaluation of Eqs. 1-5 shows spontaneous emergence of periodic motion. An initially circular cell contracts to the stripe, polarizes, migrates one way, then reverses and migrates in the other direction. We present one reversal in Fig. 1. When the cell is polarized (ρ_a is segregated on one side), the cell contracts while crawling in the direction of its polarization (point a in Fig. 1). As the cell contracts, it depolarizes (b). The unpolarized cell expands quickly, but does not crawl significantly. As the cell grows, it suddenly re-polarizes (c) and begins to travel in the direction opposite to its initial direction. As the cell moves, myosin localizes to the cell rear [39], and the cell begins to contract again (d). Each reversal corresponds to one peak in cell area.

Fig. 1.

TOP: Cell shape (ϕ), actin promoter (ρ_aϕ), and myosin (ρ_mϕ) distribution during a reversal event in periodic migration. Color plots are rescaled by 1,1.4μm^–2, and 0.55μm^–2 respectively. Cell velocity is indicated by an arrow. Total width of stripe is w = 6 μm; (dashed lines). BOTTOM: Center-of-mass position $(\overline{y}=\frac{1}{A}\int d^{2}ry\varphi (x,y))$ and area $(A=\int d^{2}r\varphi )$ of cell as a function of time. Full parameters for all simulations are listed in the Appendix

Several questions arise: 1) How does cell polarization control the cell's growth and contraction? 2) Why does the cell depolarize at small areas and repolarize at large ones? 3) Why does the cell repolarize in a direction opposite to its original motion? We address these questions by reducing our model to a significantly simpler 1D one.

Reduction to 1D model

We neglect adhesions and advection of ρ_a. The latter is not strictly justified, as the Peclet number Pe = V_cellL_cell/D_a is of order unity (L_cell is the cell length and V_cell its velocity), but we reproduce the essential aspects of the two-dimensional simulation without fluid flow. In migrating cells, myosin accumulates at the back while actin is enriched at the front [39]. We model these myosin dynamics phenomenologically by letting myosin go to the cell rear (where ρ_a is low) with time lag τ. The simplified model for ρ_a and ρ_m is

$${\partial }_t\left(\varphi {\rho }_a\right)={\partial }_y\left[\varphi D_a{\partial }_y{\rho }_a\right]+\varphi f\left({\rho }_a,{\rho }_a^{\text{cyt}}\right)$$ (6)

$${\partial }_t{\rho }_m^{f,b}=-{\tau }^{-1}\left[{\rho }_m^{f,b}-\left(m_0-{\rho }_a^{f,b}\right)\right]$$ (7)

where ${\rho }_{a,m}^{f,b}={\rho }_{a,m}\left(y_{f,b}\right)$ and m₀ is the equilibrium myosin when ρ_a is zero. The cell “front” is defined by y_f > y_b. The cell shape is $\varphi (y,t)=\frac{1}{2}\left[tan\mathrm{h}\frac{3(y-y_b)}{\mathit{\in }}-tan\mathrm{h}\frac{3(y-y_f)}{\in }\right].$ Actin polymerization causes local protrusion; myosin contraction causes local contraction. The simplest form for the normal velocity of the edge is thus ${\mathbf{v}}_{\text{edge}}\cdot \widehat{\mathbf{n}}=\alpha {\rho }_a-\beta {\rho }_m$, i.e.

$${\partial }_t{y}_{f,b}=\pm (\alpha {\rho }_a^{f,b}-\beta {\rho }_m^{f,b})$$ (8)

This result can be rigorously justified in some limits by solving the Stokes equation (Eq. 2) in the presence of a planar front. If ∈/ℓ_h ≪ 1 (sharp interface limit) and L_cell ≫ ℓ_h, where ${\ell }_h=\sqrt{2{\nu }_0/\xi }$, we find $\alpha =\frac{{\eta }_a^0}{4{\nu }_0}$ and $\beta =\frac{{\eta }_m^0{\ell }_h}{2{\nu }_0}$ (Appendix).

This limit is not necessarily applicable, as we have ℓ_h ≈ 63µm > L_cell. Nevertheless, Eqs. 6-8 capture the essential features of periodic migration in Fig. 1. We simulate them (Fig. 2) and compare the 1D simulation to the centerline of Fig. 1.

Fig. 2.

Two- and one-dimensional models show highly similar behavior. TOP: Centerline of Fig. 1 a-d with ϕ (black solid line), ϕρ_a (green dashed line), and ϕρ_m (red dash-dotted line); axis is shifted for comparison to middle plot, MIDDLE: 1D model at comparable points in the periodic cycle (A-D). BOTTOM: Plot of position and size of periodically migrating 1D cell.

Our 1D model shows how the cell's shape changes and polarization are coupled. The cell shrinks if ${\partial }_t{L}_{\text{cell}}={\partial }_t(y_f-y_b)=\alpha ({\rho }_a^f+{\rho }_a^b)-\beta ({\rho }_m^f+{\rho }_m^b)$ is negative. To find when this is true, we need ${\rho }_a^{f,b}$. We use the analysis of Mori et al. [38, 40], who proposed the wave-pinning reaction-diffusion model we apply in Eq. 6. Their solutions would be exact if ∈ → 0 (sharp interface limit) and the cell were slow-moving, Pe ≪ 1. Pe is not small, but these solutions provide a valuable qualitative guide to the cell's polarization as a function of its size. We use the simplified reaction kinetics $\stackrel{\sim }{f}({\rho }_a,{\rho }_a^{\text{cyt}})\equiv -k{\rho }_a({\rho }_a-h)({\rho }_a-m{\rho }_a^{\text{cyt}})$ which reproduce the phenomenology of the full kinetics and permit analytical solutions. h and m are parameters related to the steady states of ρ_a [38]. Mori et al. find two homogeneous and linearly stable steady states, ρ_a(y) = 0 ${\rho }_a(y)=\frac{m{N}_a^{\text{tot}}}{L_{\text{cell}}(1+m)}$, where $N_a^{\text{tot}}={\displaystyle {\int }_0^{L}dy}({\rho }_a+{\rho }_a^{\text{cyt}})$ is the conserved total number of actin promoter molecules in either membrane-bound or cytosolic form ( $N_a^{\text{tot}}={\displaystyle \int d^{d}r({\rho }_a+{\rho }_a^{\text{cyt}})\varphi }$ in the phase field model). Ref. [38] also finds a polarized state with a stationary front connecting a region with ρ_a= 2h to ρ_a= 0; the length of the region with large ρ_a is $y_p=\frac{N_a^{\text{tot}}}{2h}-\frac{L_{\text{cell}}}{m}.$ The cell can only polarize if y_p < L_cell, i.e. L_cell > $L_{\text{depol}}\equiv \frac{m{N}_a^{\text{tot}}}{2h(m+1)}$. This causes the cell to depolarize at small lengths, partially answering Question 2 above.

Why doesn't the cell immediately repolarize when L_cell > L_depol? The homogeneous state ${\rho }_a(y)=\frac{m{N}_a^{\text{tot}}}{L_{\text{cell}}(1+m)}$ is linearly stable; even though the cell can support a polarized state if L_cell> L_depol, it will not reach that state without a perturbation beyond a certain threshold. Numerically evaluating Eq. 6 in a cell of fixed size, we find that this threshold decreases with increasing cell size; larger cells are easier to polarize. (For the full kinetics $f({\rho }_a,{\rho }_a^{\text{cyt}})$, this threshold can decrease to zero [40]). Others [41–43] have also suggested that cell shape influences signaling, polarization, and response to stimuli.

What perturbation causes the cell's repolarization? Within the 1D model the only possibility is the moving edge. If a cell edge expands faster than ρ_a can be transported by diffusion or converted from cytosolic form, ρ_a will be depleted near the expanding edge. Explicitly: if we numerically solve Eq. 6 for an initially homogeneous cell with one edge expanding, the cell always polarizes to a state with low ρ_a near the expanding edge. Depletion sets the direction in which the repolarization occurs. As the cell expands, both edges have high ρ_a but one has lower ρ_m (Figs. 1,2). Edge normal velocity is set by Eq. 8: actin polymerization causes expansion, but local contraction from myosin decreases the edge's velocity. Therefore, the edge with low ρ_m expands faster, leading to more depletion of ρ_a near that edge. When this depletion crosses the threshold of patterning, a polarized state forms with low ρ_a near the quickly-moving edge, and high ρ_a near the slowly-moving edge: the cell polarizes in the direction of higher myosin. Myosin keeps the memory of the cell's direction: if it becomes uniform before the cell repolarizes, this information is lost.

We have now answered our questions: 1) Cell shape is set by ρ_a and ρ_m via Eq. 8, and this is controlled by the cell polarization. 2) At small cell sizes, Eq. 6 does not support a polarized state, but as the cell expands, the polarized state and homogeneous state are both stable. Polarization requires a perturbation to ρ_a larger than a threshold, which decreases as the cell grows. 3) Repolarization is initiated by depletion of ρ_a near an expanding cell boundary; myosin makes the previous “back” of the cell expand more slowly, ensuring the cell polarizes in a direction opposite to its previous movement.

We calculate the amplitude of periodic migration analytically by using the results of [38] and making some additional assumptions. We assume the cell depolarizes at length L_depol as above and repolarizes in the direction of high myosin at a critical length L*. The value of L* would depend on the details of the cell's motion, the diffusion coefficient D_a, and the threshold for perturbations. We expect that the dominant contribution to the cell's displacement over time will be the distance that it crawls while polarized; when the cell is polarized, it contracts. We can then approximate the amplitude of periodic migration as A = υ_cmt_contract where υ_cm is the cell center of mass velocity in the contraction phase, and t_contract the time required to contract from L* to L_depol. Using Eq. 8 and the results of [38], we find that in the polarized state, ∂_tL_cell ≈ 2hα − β(2m₀−2h) (assuming the myosin is at its equilibrium value ρ_m= m₀ − ρ_a). Similarly, υ_cm ≈ h(α + β). We find

$$A=\left(\frac{L^{\ast }-L_{\text{depol}}}{2}\right)\frac{\gamma +1}{{\gamma }_c-\gamma }$$ (9)

where γ = α/β and γ_c=(m₀– h)/h. For the cell to contract while polarized, γ < γ_c. The cell must also grow while unpolarized for periodic migration to occur; this condition depends on $N_a^{\text{tot}}$.

For the amplitude of periodic migration to become large, protrusion and retraction must be balanced so that γ – γ_c is small. However, this requirement can be weakened by the cell's internal dynamics, which we have mostly neglected in deriving Eq. 9. If we assume a large viscous resistance to changes in size, we suppress the rate of contraction and expansion by a factor λ, where λ ≪ 1. If the cell's contraction is slowed, but crawling is not, the amplitude of periodic migration increases significantly, as t_contract∼ 1/λ, and A ≈ t_contractυ_cm, so A ∼ 1/λ becomes large.

Additional emergent behaviors

Depending on initial conditions and micropattern width, other behaviors are observed. These include steady crawling, turning, and bipedal motion (see Appendix). The bipedal motion resembles that seen theoretically and experimentally by Barnhart et al. [44]. Turning has been studied by Rubinstein et al. [45, 46]; see also [19]. We plan to address the origin of these effects within our model in future work.

If periodic migration in [5] arose through precisely the mechanism we have described, the cell area would oscillate with a period half that of the cell's migration and myosin reorientation would lag the reversal of cell direction (Figs. 1-2). It would be interesting to experimentally quantify total surface area and myosin localization of periodically migrating cells. We present this study primarily as an example of complex behaviors that develop when cell polarization is coupled to cell shape. However, our mechanism of periodic migration may be more general if cell polarization is coupled to other mechanical properties. Cell-surface adhesion is a natural choice, as periodic motion arises in [5] when the adhesion protein zyxin is depleted. If cells only polarize when sufficiently adherent to the surface, and this adhesion changes with cell motion, our periodic migration scheme may be recapitulated with adhesion in place of cell area.

Periodic migration as observed in our simulations is a new, interesting, and tractable example of the complex dynamics resulting from coupling cell shape and polarity. Periodic migration requires a balance between contraction and protrusion (Eq. 9), but its existence is robust to many model details. Within our larger model, individual adhesions can be neglected, as can the ρ_a -dependence of D_m. In the 1D model, we have ignored hydrodynamics entirely. Removing features or varying parameters (Appendix) changes migration amplitude, but if the fundamental aspects illustrated by the 1D model are present, periodic migration exists. Therefore, we believe periodic migration could be observed in other models of eukaryotic cell motility that couple polarity and cell shape [11, 26, 32, 43, 47], especially those using the wave-pinning polarity mechanism [38]. Randomly-occurring reversals without periodicity have been observed by Ziebert and Aronson [48]; their model may only lack a memory. Our one-dimensional model suggests the essential elements required for periodic migration, and emphasizes the role of myosin in preserving the memory of the cell's initial direction. Our model for cells on adhesive micropatterns and the analytical tools we developed to study periodic migration may be useful in understanding more complex behavior on micropatterns, including “dimension sensing” [10], response of fibroblasts to cross-hatched patterns [1], and polarization in response to asymmetric micropatterns [7–9]. In all of these cases, cell polarity is coupled to the underlying micropattern. The coupling of micropattern shape, cell shape, and cell polarization studied here will be essential to a deeper understanding of these problems.

Appendix B: Sharp interface derivation

We will derive the sharp interface results presented in the text. These are that the front and back interface velocities are given by $\pm \alpha {\rho }_a^{f,b}\mp \beta {\rho }_m^{f,b}$ with

$$\alpha =\frac{{\eta }_a^0}{4{\nu }_0},\beta =\frac{{\eta }_m^0{\ell }_h}{2{\nu }_0},$$ (B1)

where ${\ell }_h^2=2{\nu }_0/\xi$. In order to get these results, we will assume the sharp interface limit ∈/ℓ_h≪1, and also that the cell's size L_cell is much larger than ℓ_h. We will also assume that the interface's curvature is not relevant.

Our Stokes equation for the cell's cytoskeletal velocity u is

$$\nabla \cdot \left[\nu \left(\varphi \right)\left(\nabla \mathbf{u}+\nabla {\mathbf{u}}^T\right)\right]+\nabla \cdot {\sigma }_{\text{myo}}+\nabla \cdot {\sigma }_{\text{poly}}+{\mathbf{F}}_{\text{mem}}+{\mathbf{F}}_{\text{adh}}-\xi \mathbf{u}=0$$ (B2)

where ν(ϕ) = ν₀ϕ(r) and the active stresses are given by

$${\sigma }_{\text{myo}}={\eta }_m^0\varphi {\rho }_m\mathbf{I}$$ (B3)

$${\sigma }_{\text{poly}}=-{\eta }_a^0\varphi {\rho }_a{\delta }_{\mathit{\in }}\widehat{\mathbf{n}}\widehat{\mathbf{n}}$$ (B4)

where I is the identity tensor, δ_∈ = ∈(∇ ϕ)², and $\widehat{\mathbf{n}}$ is the unit normal vector to the cell boundary. F_adh contains stochastic adhesion forces, which we ignore. We note that these adhesion forces may in some limits only renormalize ξ [35], so it may be appropriate to think of the ξ as an effective value larger than that given in the simulation. The membrane forces are derived from a phase field approximation to the Helfrich energy and surface tension (see, e.g. [12, 49]), F_mem = F_tension + F_bend with

$${\mathbf{F}}_{\text{tension}}=-\gamma \left(\mathit{\in }{\nabla }^2\varphi -\frac{G^{\prime }}{\mathit{\in }}\right)\nabla \varphi$$ (B5)

$${\mathbf{F}}_{\text{bend}}=k\mathit{\in }\left({\nabla }^2-\frac{G^{″}}{{\mathit{\in }}^2}\right)\left({\nabla }^2\varphi -\frac{G^{\prime }}{{\mathit{\in }}^2}\right)\nabla \varphi$$ (B6)

where G(ϕ) = 18ϕ² (1 − ϕ)² and G′ and G″ denote derivatives of G with respect to ϕ.

We are interested in creating an effectively one-dimensional model. We approximate our cell's complex shape by an effectively one-dimensional front that minimizes the tension and bending energies (i.e. F_tension = F_bend = 0). This will be true if $\mathit{\in }{\nabla }^2\varphi =\frac{G\text{'}}{\mathit{\in }}$, or (for a front in the y direction)

$${\varphi }_I\left(y\right)=\frac{1}{2}(1+tan\mathrm{h}(3y/\mathit{\in }))$$ (B7)

Under this assumption, the Stokes equation becomes

$$\stackrel{\sim }{\nu }{\partial }_y\left[{\varphi }_I\left(y\right){\partial }_{y}u\right]+F_{\text{myo}}\left[{\varphi }_I\right]+F_{\text{poly}}\left[{\varphi }_I\right]-\xi u=0$$ (B8)

Where $\stackrel{\sim }{\nu }=2{\nu }_0$, $F_{\text{poly}}\equiv {\partial }_y{\sigma }_{\text{poly}}$ and $F_{\text{myo}}\equiv {\partial }_y{\sigma }_{\text{myo}}$ We will look at the two force terms separately, since this equation is linear and we can superimpose the two resulting velocity fields. We will also assume that the densities ρ_a and ρ_m do not vary quickly at the front, so that $F_{\text{poly}}\approx -{\eta }_a^0{\rho }_a{\partial }_y({\varphi }_I{\delta }_{\mathit{\epsilon }})$ and $F_{\text{myo}}\approx {\eta }_m^0{\rho }_m{\partial }_y{\varphi }_I$. We illustrate the resulting field ϕ_I and the forces in Fig.4 below.

Fig. 4.

We show the phase field and active forces at the interface at y = 0. Here the phase field $\varphi I=\frac{1}{2}\left(1+tan\mathrm{h}(3y/\mathit{\in })\right)$. The active force due to actin polymerization is $F_{\text{poly}}\approx -{\eta }_a^0{\rho }_a{\partial }_y({\varphi }_I{\delta }_{\mathit{\in }})$ and the active force due to myosin contractility is $F_{\text{myo}}\approx {\eta }_m^0{\rho }_m{\partial }_y{\varphi }_{I\cdot }\mathit{\in }=2\mathrm{\mu }\mathrm{m}$ in this figure.

1. Active force due to actin polymerization

We start by rewriting Eq. B8 with $F_{\text{poly}}=-{\eta }_a^0{\rho }_a{\partial }_y({\varphi }_I{\delta }_{\mathit{\in }})$ and F_myo= 0. (We will use linearity to rescue the complete result later.) Rescaling our lengths to r = y/(l_h) where ${\ell }_h^2=\stackrel{\sim }{\nu }/\xi$ and defining δ = ∈/3ℓ_h, we find

$${\partial }_r\left[\right\{1+tan\mathrm{h}\left(r/\delta \right)\left\}{\partial }_{r}u\right]-\frac{\chi }{\delta }{\partial }_r\left[\left\{1+tan\mathrm{h}(r/\delta )\right\}{sec\mathrm{h}}^4(r/\delta )\right]-2u=0$$ (B9)

where $\chi =\frac{3}{4}{\eta }_a^0{\rho }_a/\stackrel{\sim }{\nu }$. We can't solve this equation exactly, but can develop an asymptotic approximation in the sharp interface limit of ∈≪ℓ_h (δ ≪ 1). In particular, we can see that in the sharp interface limit, the term sech⁴r/δ can be neglected everywhere but near the front position, r = O(δ). Moving to the stretched variable z = r/δ, and defining U(z)= u(r) for convenience,

$${\partial }_z\left[\left(1+tan\mathrm{h}z\right){\partial }_{z}U\right]-\chi {\partial }_z\left[\left(1+tan\mathrm{h}z\right){sec\mathrm{h}}^{4}z\right]-2{\delta }^{2}U=0$$ (B10)

To O(δ⁰), we can neglect the last term on the right. The remaining ODE can be directly integrated:

$$U\left(z\right)=A\left(z-\frac{1}{2}{e}^{-2z}\right)+B+\chi \left\{\frac{4}{{\left(1+e^{-2z}\right)}^2}-\frac{8}{3{\left(1+e^{-2z}\right)}^3}\right\}$$ (B11)

We cannot consistently apply the boundary conditions u(r → ±∞) = 0 to this solution; we need to match it to the solution in the outer region. However, the outer regions to the right and left of the front have two distinctly different characters. For r ≪ δ,1 + tanh(r/δ) ≈ 2, and the outer expansion is

$${\partial }_r^2{u}_R-u_R=0$$ (B12)

and we can immediately determine u_r= Ce^–r, neglecting the solution that diverges as r →∞. Matching to the interior solution yields the requirement $C=B+\frac{4}{3}\chi$ and A = − δC. However, for r ≪ − δ,1+tanh (r/δ) approaches zero; δ is a singular perturbation to the outer equation in the left region. For r ≪ – δ,1+tanh(r/δ) ≈ 2e^2r/δ, and so

$${\partial }_r\left(e^{2r/\delta }{\partial }_r{u}_L\right)-u_L=0$$ (B13)

which can be solved to find

$$u_L=D{e}^{-r/\delta }{K}_1\left(\delta e^{-r/\delta }\right)$$ (B14)

where K₁ is the modified Bessel function of order 1, and we have dropped the solution that diverges as r → −∞. To match this to the interior solution, we choose r = δz_c with z_c fixed but large (and negative), and look at the behavior as δ → 0:

$$u_L~D\left[\frac{1}{\delta }+\frac{e^{-2z_c}}{2}\delta \{ln\delta -z_c-ln2+{\gamma }_E-1/2\}\right]$$ (B15)

$$~D\left[\frac{1}{\delta }+\frac{e^{-2z_c}}{2}\delta ln\delta \right]$$ (B16)

where γE is the Euler gamma, γE = 0.5772…. We match to the interior solution at z = z_c with z_c ≪ −1,

$$U~-\frac{1}{2}A{e}^{-2z_c}+B$$ (B17)

Matching then requires that -A = Dδ ln δ and B = D/δ. Combining this with our earlier matching requirements, $C=B+\frac{4}{3}\chi$ and A = −δC, we find:

$$A/\chi =\frac{4}{3}\frac{{\delta }^{2}ln\delta }{1-\delta ln\delta }$$ (B18)

$$B/\chi =-\frac{4}{3}\frac{1}{1-\delta ln\delta }$$ (B19)

$$C/\chi =-\frac{4}{3}\frac{\delta ln\delta }{1-\delta ln\delta }$$ (B20)

$$D/\chi =-\frac{4}{3}\frac{\delta }{1-\delta ln\delta }$$ (B21)

Importantly, because C → 0 as δ → 0, in the sharp interface limit, there is no long-range velocity induced by the actin promoter at the interface.

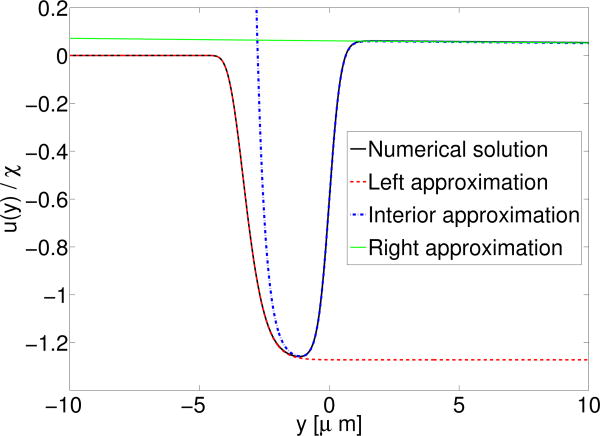
Our asymptotics provide an excellent approximation to the full numerical solution (Fig. 5). It also allows us to determine the interface velocity, u (0) (using the interior solution). We find in the sharp interface limit that

Fig. 5.

Velocity of fluid due to the presence of actin promoter at the cell boundary. Interface is at y = 0 as above, i.e. $\varphi =\frac{1}{2}\left[1+tan\mathrm{h}(3y/\mathit{\in })\right].$Here ∈ = 2 μm, ℓ_h = 63 μm, i.e. δ ≈ 0.001.

$$u_{\text{interface}}=-\frac{2}{3}\chi \equiv -\alpha {\rho }_a$$ (B22)

where

$$\alpha =\frac{{\eta }_a^0}{2\stackrel{\sim }{\nu }}=\frac{{\eta }_a^0}{4{\nu }_0}.$$ (B23)

This is the result given in the main paper. It is only the leading order term; higher-order terms that depend on δ can also be obtained from the solution above. The process for myosin is very similar, but we will find that a long-range (on the order of ℓ_h) velocity will be induced, unlike the actin promoter case.

2. Myosin force

We start by rewriting Eq. B8 with $F_{\text{myo}}={\eta }_m^0{\rho }_m{\partial }_y\varphi$ and F_poly = 0. Rescaling our lengths to r = y/(ℓ_h) where ${\ell }_h^2=\stackrel{\sim }{\nu }/\xi$ and defining δ = ∈/3ℓ_h, we find

$${\partial }_r\left[\left\{1+tan\mathrm{h}(r/\delta )\right\}{\partial }_{r}u\right]+\mu {\partial }_r\left[1+tan\mathrm{h}(r/\delta )\right]-2u=0$$ (B24)

where $\mu ={\eta }_m^0{\rho }_m{\ell }_h/\stackrel{\sim }{\nu }.$ Note that unlike χ in the actin promoter case, μ does have an explicit dependence on the hydrodynamic length scale ℓ_h.

We develop an asymptotic approximation in the sharp interface limit of ∈ ≪ ℓ_h(δ≪1) Moving to the stretched variable z = r/δ, and defining U(z) = u(r),

$${\partial }_z\left[\left(1+tan\mathrm{h}z\right){\partial }_{z}U\right]+\mu \delta {\partial }_z\left[1+tan\mathrm{h}z\right]-2{\delta }^{2}U=0$$ (B25)

To linear order in δ, the last term can be dropped, and the remaining equation can be easily integrated to find

$$U(z)=A\left(z-\frac{1}{2}{e}^{-2z}\right)+B-\frac{\mu \delta }{2}{e}^{-2z}$$ (B26)

The outer limits are the same as in the actin promoter case. We then get the matching conditions D/δ = B, A + μδ = -Dδ ln δ, B = C, and A = -δC. These can be solved to find

$$A/\mu =-\frac{\delta }{1-\delta In\delta }$$ (B27)

$$B/\mu =\frac{1}{1-\delta In\delta }$$ (B28)

$$C/\mu =\frac{1}{1-\delta In\delta }$$ (B29)

$$D/\mu =\frac{\delta }{1-\delta In\delta }$$ (B30)

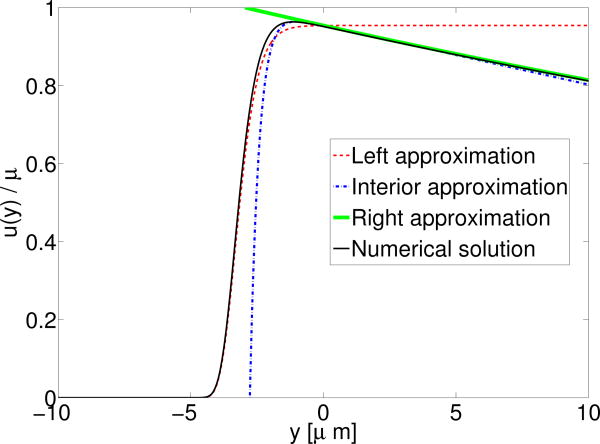
Note that C does not vanish in the sharp interface limit: the presence of myosin at the interface leads to a velocity far away from the interface, u(r) ≈ μe^-r. Our asymptotic approximations are again an excellent approximation to the full numerical solution (Fig.6).

Fig. 6.

Velocity of fluid due to the presence of myosin at the cell boundary. Interface is at y = 0 as above, i.e. $\varphi =\frac{1}{2}[1+tan\mathrm{h}(3y/\mathit{\in })]$ Here ∈ = 2 μm, i.e. δ ≈ 0.001. Note that even though δ is small, the velocity to the right of the interface is not small since C is O (δ⁰).

In the sharp interface limit, u(0) becomes

$$u_{\text{intrface}}=\mu \equiv \beta {\rho }_m$$ (B31)

where

$$\beta =\frac{{\eta }_m^0{\ell }_h}{\stackrel{\sim }{\nu }}=\frac{{\eta }_m^0{\ell }_h}{2{\nu }_0}$$ (B32)

3. When can we apply the sharp interface result?

We argue that in the limit L_cell ≫ ℓ_h, we can neglect correlations between the cell edges. We have been attempting to determine the velocity of the cell interface using only the actin promoter and myosin densities at the interface, but no information about the actin promoter and myosin throughout the cell, or the other interface of the cell. When is this appropriate? We have seen above that myosin at the cell interface induces a velocity in the cell body with a dependence of position of $e^{-y/{\ell }_h}$; if L_cell ≫ ℓ_h, one interface will not affect the other. We have also neglected forces coming from internal gradients of the myosin-induced stress; once again, the characteristic length scale for these forces is ℓ_h, and so they should not affect the velocity of the interfaces if L_cell ≫ ℓ_h. The sharp interface results could be generalized to include all of these effects, but they produce additional complications, such as the need to track the details of myosin within the cell.

Appendix C: Tables of parameters used

1. Parameters used for all two-dimensional phase field simulations

We mark with an asterisk the parameters that have been changed from the simulations presented in Ref. [12]. Parameters were originally chosen in [12] to ensure that the cell velocity, actin flow velocity, and midline stress were close to experimentally reported values for keratocytes; in general, we have attempted not to change these values. Where possible, we have given literature justification for these parameters.

a. Phase field and cell boundary properties

Parameter	Description	Value	Justification
γ	Cell tension coefficient	20 pN	Order-of-magnitude set in [11]
К	Cell bending coefficient	20 pN μm2	Order-of-magnitude set in [11]
∊	Phase field width	2 μm	Chosen to ensure smooth variation in ϕ
Γ	Phase field relaxation parameter	0.4 μm/s	Set in [12]

b. Cytoskeletal flow parameters

Parameter	Description	Value	Justification
ν0	Viscosity of cytoskeletal flow	103 pN s / μm	Set roughly by [50]; see also [14]
${\eta }_a^0$	Protrusion coefficient	560 pN μm 2	Chosen to reproduce shapes and other features in [12]
${\eta }_m^0$	Myosin contractility coefficient	60-61 pN μm *	Similar to that of [14]; tuned to increase periodic migration amplitude
ξ	Substrate friction coefficient	0.5 Pa s / μm	Value arising from cell sitting on layer of water with height 2 nm [34]

c. Reaction-diffusion parameters

In the same wave-pinning kinetics as [12] for the reaction term in the actin promoter equation,

$$f\left({\rho }_a,{\rho }_a^{\text{cyt}}\right)=k_b\left(\frac{{\rho }_a^2}{K_a^2+{\rho }_a^2}+k_a\right){\rho }_a^{\text{cyt}}-k_c{\rho }_a$$ (C1)

where, by the conservation of total actin promoter, ${\displaystyle \int d^{2}r}({\rho }_a(\mathbf{r})+{\rho }_a^{\text{cyt}})\varphi (\mathbf{r})=N_a^{\text{tot}}$, or, assuming the cytosolic actin promoter is well-mixed (uniform),

$${\rho }_a^{\text{cyt}}=\frac{N_a^{\text{tot}}-{\displaystyle \int d^{2}r{\rho }_a(\mathbf{r})\varphi \left(\mathbf{r}\right)}}{{\displaystyle \int d^2}r\varphi \left(\mathbf{r}\right)}.$$ (C2)

We note that this formula was written incorrectly in the Supplementary Material of Ref. [12].

Parameter	Description	Value	Justification
ka	Unitless base activation rate	0.01 [51]	Order-of-magnitude from [38]
kb	Overall activation rate	10 s–1	Order-of-magnitude from [38]
kc	Deactivation rate	10 s–1	Order-of-magnitude from [38]
Ka	Positive feedback threshold for actin promoter concentration	1 μm –2	Order-of-magnitude from [38]
Da	Actin promoter diffusion coefficient	0.8 μm 2/s	Typical membrane-bound protein diffusion coefficient [52]
$D_m^0$	Myosin diffusion coefficient at zero actin concentration	2 μm 2/s	Chosen in [12]
KD	Myosin diffusion threshold, $D_m=D_m^0/(1+{\rho }_a/K_D)$	0.5 μm –2[53]	Chosen in [12]
$N_a^{\text{tot}}$	Total amount of actin promoter	485* [54]	Roughly rescaled by cell size from value chosen in [12] proportional to cell area
${\rho }_m^0$	Initial density of myosin	0.3 μm –2	Chosen such that myosin stress corresponds to that estimated in [14]

d. Adhesion parameters

Parameter	Description	Value	Justification
Nadh	Number of adhesions	1000* [55]	Roughly rescaled from value chosen in [12] proportional to cell area
$F_{\text{grip}}^0$	Characteristic gripping stress for gripping-slipping rupture	5 Pa	Chosen in [12] to reproduce traction forces and shape of keratocytes
$k_{\text{grip}}^0$	Gripping coefficient	2.5 Pa / (s μm)	Chosen in [12] to reproduce traction forces and shape of keratocytes
$k_{\text{slip}}^0$	Slipping coefficient	0.25 Pa / μm	Chosen in [12] to reproduce traction forces and shape of keratocytes
ron	Rate of transition from slipping to gripping state	0.005 s–1	Chosen in [12] to reproduce traction forces and shape of keratocytes
$r_{\text{off}}^0$	Rate of transition from gripping to slipping state (at zero force)	0.002 s–1	Chosen in [12] to reproduce traction forces and shape of keratocytes
rdie	Rate of slipping site death	0.2 s–1	Chosen in [12] to reproduce traction forces and shape of keratocytes

e. Numerical evaluation parameters

Parameter	Description	Value
n × m	Number of (horizontal, vertical) grid points	256 × 256
Lx×Ly	Box size	50μm×50μm
∇t	Time step	2 × 10–3 s*
λ	Cutoff for evaluating phase field equations	10–4

2. Parameters used for each figure

a. Figure 1

For the oscillation in Fig. 1, we start with an initial state of a circular cell with radius 6 μm. We choose ${\eta }_m^0=61\mathrm{p}\mathrm{N}\mathrm{\mu }\mathrm{m}$, and have an adhesive stripe of total width w = 6μm, i.e. $\chi (\mathbf{r})=\frac{1}{2}\left[1+tan\mathrm{h}\left(3\left\{\frac{w}{2}-\left|x\right|\right\}/\mathit{\in }\right)\right].$ All other parameters are as written in the tables above.

b. Figure 2

We think of our one-dimensional model as describing a slice down the center of a two-dimensional cell with width w, but with ρ_a uniform across the x direction. Parameters for the actin promoter reaction-diffusion part of the one-dimensional model are exactly the same as for the two-dimensional model of Fig. 1; however, the conservation law follows a slightly different form:

$${\displaystyle {\int }_{-\omega /2}^{\omega /2}dx}{\displaystyle {\int }_{-L/2}^{L_y/2}\left[{\rho }_a\left(y\right)+{\rho }_a^{\text{cyt}}\right]\varphi \left(y\right)=N_a^{\text{tot}}}$$ (C3)

or, equivalently,

$${\rho }_a^{\text{cyt}}=\frac{N_a^{\text{tot}}/\omega -{\displaystyle \int dy{\rho }_a(y)\varphi \left(y\right)}}{{\displaystyle \int dy\varphi \left(y\right)}}.$$ (C4)

The parameters unique to the one-dimensional model are α = 0.14μm³/s and β = 0.068μm³/s, m₀ = 2.43μm^–2 and τ = 30 s. The value for α is determined by the sharp interface result, $\alpha ={\eta }_a^0/4{\nu }_0$, using the two-dimensional simulation parameters. We have set β, m₀, and τ so that the cell oscillates similarly to the two-dimensional simulation. The one-dimensional model is evaluated on a grid of 512 points with L_y= 100 μm, with Δt = 0.01 s.

c. Figure 3

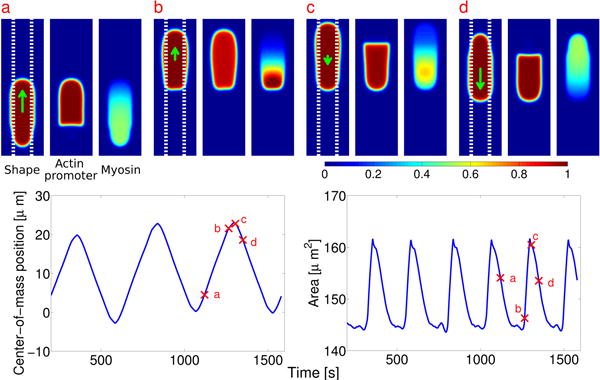
Fig. 3.

Many types of cell crawling appear, including bipedal motion and turning. Cell shape (phase field ϕ), actin promoter (ρ_aϕ), and myosin (ρ_mϕ) of cells at different times. Color plots are rescaled by 1, 1.4 μm^–2, and 0.8 μm^–2, respectively. TOP: Cell turning; total width of stripe is w = 40 μm (not in image; scale bar indicates 10 um). BOTTOM: Bipedal motion. Total width of stripe is w = 10 μm (dashed lines).

For the turning motion (Fig. 3 top), we start with an initial state of a circular cell with radius 8 μm. We choose ${\eta }_m^0=60\mathrm{p}\mathrm{N}\mathrm{\mu }\mathrm{m}$, and have an adhesive stripe of total width w = 40 μm, i.e. $\chi (\mathbf{r})=\frac{1}{2}\left[1+tan\mathrm{h}\left(3\left\{\frac{w}{2}-\left|x\right|\right\}/\mathit{\in }\right)\right]$. For the bipedal motion (Fig. 3 bottom), we choose exactly the same parameters, except that we take w = 10 μm. All other parameters are as written in the tables above.

3. Robustness of periodic migration to variation in parameters

The bulk of our parameters have been set by comparison with experiments on keratocytes, and are identical to those used in [12]; they were not selected to observe periodic migration. However, some parameters have been changed in order to ensure that the cells polarize and migrate on stripes. In particular, we changed $N_a^{\text{tot}}$ and N_adh because the cells we study are significantly smaller in area than those in [12]. We also changed ${\eta }_m^0$ to change the contraction speed and vary the amplitude of periodic migration. Initial simulations have shown that periodic migration can be observed over wider ranges of parameters as well; varying one parameter at a time, we see periodic migration at N_adh= 700, or ${\eta }_m^0=80\mathrm{p}\mathrm{N}\mathrm{\mu }\mathrm{m}$, or $N_a^{\text{tot}}=400$ These parameters can be changed more if we change multiple parameters at once. Our experience with altering the model suggests that periodic migration can be re-created as long as the central polarization mechanism is in place, the contraction and protrusion are closely balanced, and the myosin effectively keeps the memory.

Appendix D: Details of numerical algorithm

1. Time-stepping and discretization

Our goal is to numerically solve the system of equations

$${\partial }_t\varphi +\mathbf{u}\cdot \nabla \varphi =\mathrm{\Gamma }\left(\mathit{\in }{\nabla }^2\varphi -G^{\prime }\left(\varphi \right)/\mathit{\in }+\mathit{\in }c|\nabla \varphi |\right)$$ (D1)

$${\partial }_t\left(\varphi {\rho }_a\right)+\nabla \cdot \left(\varphi {\rho }_a\mathbf{u}\right)=\nabla \cdot \left(\varphi D_a\nabla {\rho }_a\right)+\varphi f\left({\rho }_a,{\rho }_a^{\text{cyt}}\right)$$ (D2)

$${\partial }_t\left(\varphi {\rho }_m\right)+\nabla \cdot \left(\varphi {\rho }_m\mathbf{u}\right)=\nabla \cdot \left(\varphi D_m\left({\rho }_a\right)\nabla {\rho }_a\right)$$ (D3)

$$\nabla \cdot \left[{\nu }_0\varphi \left(\nabla \mathbf{u}+\nabla {\mathbf{u}}^T\right)\right]+\nabla \cdot \left({\sigma }_{\text{poly}}+{\sigma }_{\text{myo}}\right)+{\mathbf{F}}_{\text{mem}}+{\mathbf{F}}_{\text{adh}}-\xi \mathbf{u}=0$$ (D4)

We fix a uniform spatial grid with grid sizes Δx, Δy. We also use a fixed time step Δt to march these equations forward from initial conditions ϕ⁽⁰⁾, u⁽⁰⁾, ${\rho }_a^{(0)},{\rho }_m^{(0)}$. We denote the state of the system at time t = nΔt by ϕ⁽ⁿ⁾, u⁽ⁿ⁾, ${\rho }_a^{(n)},{\rho }_m^{(n)}$. Suppose we have obtained all these quantities at the time nΔt. We then solve all the equations (D1)–(D3) to obtain these quantities at the time (n + 1)Δt.

We first obtain ϕ⁽ⁿ⁺¹⁾ from the ϕ-equation (D1) with the forward Euler scheme:

$${\varphi }^{\left(n+1\right)}={\varphi }^{(n)}-\mathrm{\Delta }t{\mathbf{u}}^{\left(n\right)}\cdot \nabla {\varphi }^{\left(n\right)}+\mathrm{\Delta }t\mathrm{\Gamma }\left[\mathit{\in }{\nabla }^2{\varphi }^{\left(n\right)}-G^{\prime }({\varphi }^{\left(n\right)})/\mathit{\in }+\mathit{\in }{c}^{\left(n\right)}|\nabla {\varphi }^{\left(n\right)}|\right].$$

On the right-hand side of this equation, ∇ϕ⁽ⁿ⁾ is calculated with a central difference scheme, ∇²ϕ⁽ⁿ⁾ is calculated by five-point finite difference scheme, and the curvature term c⁽ⁿ⁾ is calculated by

$$c^{\left(n\right)}=\nabla \cdot \frac{\nabla {\varphi }^{\left(n\right)}}{|\nabla {\varphi }^{\left(n\right)}|}$$

when |∇ϕ⁽ⁿ⁾ | > 0.01, and set to be zero otherwise.

we next solve (Eq. D2) and (Eq. D3) to obtain ${\rho }_a^{(n+1)}\text{and}{\rho }_m^{(n+1)}$, respectively. We apply the forward Euler scheme to the reaction-diffusion-advection equation (D2):

$${\varphi }^{\left(n\right)}\frac{{\rho }_a^{(n+1)}-{\rho }_a^{(n)}}{\mathrm{\Delta }t}+\frac{{\varphi }^{\left(n+1\right)}-{\varphi }^{\left(n\right)}}{\mathrm{\Delta }t}{\rho }_a^{(n)}=-\nabla \cdot ({\varphi }^{\left(n\right)}{\rho }_a^{(n)}{\mathbf{u}}^{\left(n\right)})+\nabla \cdot \left({\varphi }^{\left(n\right)}{D}_a\nabla {\rho }_a^{\left(n\right)}\right)+{\varphi }^{\left(n\right)}{f}^{\left(n\right)}$$

Equivalently,

$${\rho }_a^{(n+1)}=\frac{(2\varphi {}^{(n)}-{\varphi }^{(n+1)})}{{\varphi }^{(n)}}{\rho }_a^{(n)}-\mathrm{\Delta }t\frac{\nabla \cdot ({\varphi }^{(n)}{\rho }_a^{(n)}{\mathbf{u}}^{(n)})}{{\varphi }^{(n)}}+\mathrm{\Delta }t\frac{\nabla \cdot ({\varphi }^{(n)}{D}_a\nabla {\rho }_a^{(n)})}{{\varphi }^{(n)}}+\mathrm{\Delta }t{f}^{(n)}$$ (D5)

we only divide by ϕ⁽ⁿ⁾ in the region where ϕ⁽ⁿ⁾ ≥ λ, where λ = 10^-4. Outside of this region, we keep ${\rho }_a^{(n+1)}={\rho }_a^{(n)}$. More specifically, we have use the following discretization:

$$\begin{array}{l}{\left[\nabla \cdot ({\varphi }^{(n)}{\rho }_a^{(n)}{\mathbf{u}}^{(n)})\right]}_{ij}=\left[{\varphi }_{i+1/2,j}^{(n)}{\rho }_{a,i+1/2,j}^{(n)}{u}_{i+1/2,j}^{(n)}-{\varphi }_{i-1/2,j}^{(n)}{\rho }_{a,i-1/2,j}^{(n)}{u}_{i-1/2,j}^{(n)}\right]/\mathrm{\Delta }x+\left[{\varphi }_{i,j+1/2}^{(n)}{\rho }_{a,i,j+1/2}^{(n)}{\upsilon }_{i,j+1/2}^{(n)}-{\varphi }_{i,j-1/2}^{(n)}+{\rho }_{a,i,j-1/2}^{(n)}{\upsilon }_{i,j-1/2}^{(n)}\right]/\mathrm{\Delta }y\\ {\left[\nabla \cdot ({\varphi }^{(n)}{D}_a\nabla {\rho }_a^{(n)})\right]}_{ij}=D_a\left[{\varphi }_{i+1/2,j}^{(n)}\frac{{\rho }_{a,i+1,j}^{(n)}-{\rho }_{a,ij}^{(n)}}{\mathrm{\Delta }x}-{\varphi }_{i-1/2,j}^{(n)}\frac{{\rho }_{a,ij}^{(n)}-{\rho }_{a,i-1,j}^{(n)}}{\mathrm{\Delta }x}\right]/\mathrm{\Delta }x+D_a\left[{\varphi }_{i,j+1/2}^{(n)}\frac{{\rho }_{a,i,j+1}^{(n)}-{\rho }_{a,ij}^{(n)}}{\mathrm{\Delta }y}-{\varphi }_{i,j-1/2}^{(n)}\frac{{\rho }_{a,ij}^{(n)}-{\rho }_{a,i,j-1}^{(n)}}{\mathrm{\Delta }y}\right]/\mathrm{\Delta }y\end{array}$$

where ${\mathbf{u}}_{ij}^{(n)}=\left(u_{ij}^{(n)},{\upsilon }_{ij}^{(n)}\right)$. We apply the analogous forward Euler scheme to the ρ_m-equation (D3). Since the diffusion coefficient D_m= D_m(ρ_a) depends on ρ_a, we discretize the diffusion term at a grid point labeled by (i, j) as follows

$${\left[\nabla \cdot ({\varphi }^{(n)}{D}_m^{(n)}\nabla {\rho }_a^{(n)})\right]}_{ij}=\left[\frac{{\varphi }_{ij}^{(n)}{D}_{m,ij}^{(n)}+{\varphi }_{i+1,j}^{(n)}{D}_{m,i+1,j}^{(n)}}{2}\cdot \frac{{\rho }_{a,i+1,j}^{(n)}-{\rho }_{a,ij}^{(n)}}{\mathrm{\Delta }x}-\frac{{\varphi }_{ij}^{(n)}{D}_{m,ij}^{(n)}+{\varphi }_{i-1,j}^{(n)}{D}_{m,i-1,j}^{(n)}}{2}\cdot \frac{{\rho }_{a,ij}^{(n)}-{\rho }_{a,i-1,j}^{(n)}}{\mathrm{\Delta }x}\right]/\mathrm{\Delta }x+\left[\frac{{\varphi }_{ij}^{(n)}{D}_{m,ij}^{(n)}+{\varphi }_{i,j+1}^{(n)}{D}_{m,i,j+1}^{(n)}}{2}\cdot \frac{{\rho }_{a,i,j+1}^{(n)}-{\rho }_{a,ij}^{(n)}}{\mathrm{\Delta }y}-\frac{{\varphi }_{ij}^{(n)}{D}_{m,ij}^{(n)}+{\varphi }_{i,j-1}^{(n)}{D}_{m,i,j-1}^{(n)}}{2}\cdot \frac{{\rho }_{a,ij}^{(n)}-{\rho }_{a,i,j-1}^{(n)}}{\mathrm{\Delta }y}\right]/\mathrm{\Delta }y$$

where $D_{m,ij}^{(n)}=D_m\left({\rho }_{a,ij}^{(n)}\right)$. To keep ρ_m conserved and reduce its drift, we rescale ρ_m at each time step so that the total integral of ρ_m is kept a constant. We note that we have corrected the position of the non-constant diffusion coefficient in the ρ_m equation in [12].

Finally, we solve the Stokes equation (D4) with a semi-implicit Fourier spectral scheme to obtain u⁽ⁿ⁺¹⁾. To do so, we first subtract the term ${\nu }_0\stackrel{\sim }{\varphi }{\nabla }^2\mathbf{u}$ from both sides of the Stokes equation (D4) with ϕ a constant (e.g., $\stackrel{\sim }{\varphi }=2$) to yield

$$\xi \mathbf{u}-{\nu }_0\stackrel{\sim }{\varphi }{\nabla }^2\mathbf{u}=\nabla \cdot \left[{\nu }_0(\varphi -\stackrel{\sim }{\varphi })\nabla \mathbf{u}+{\nu }_0\varphi \nabla {\mathbf{u}}^T)\right]+\nabla \cdot ({\sigma }_{\text{poly}}+{\sigma }_{\text{myo}})+{\mathbf{F}}_{\text{mem}}+{\mathbf{F}}_{\text{adh}}\equiv \text{RHS}(\mathbf{u},\varphi ,{\rho }_a,{\rho }_m)$$

To obtain u⁽ⁿ⁺¹⁾, we set ${\mathbf{u}}_0^{(n+1)}={\mathbf{u}}^{(n)}$ and solve the following equation iteratively using the spectral Fourier method:

$$\xi {\mathbf{u}}_{k+1}^{(n+1)}-{\nu }_0\stackrel{\sim }{\varphi }{\nabla }^2{\mathbf{u}}_{k+1}^{(n+1)}=\text{RHS}({\mathbf{u}}_k^{(n+1)},{\varphi }^{(n+1)},{\rho }_a^{(n+1)},{\rho }_m^{(n+1)})k=0,1,\dots ,m$$

and set ${\mathbf{u}}^{(n+1)}={\mathbf{u}}_m^{(n+1)}$. The calculations of ∇. (σ_poly+ σ_myo), F_mem and F_adh are performed as in [12]. The number of steps m in this iteration is set to be m = 10 or set by

$$max\left|{\mathbf{u}}_m^{(n+1)}-{\mathbf{u}}_{m-1}^{(n+1)}\right|<0.001max\left|{\mathbf{u}}_m^{(n+1)}\right|.$$

Shifting of the simulation box when the cell approaches the box edges is performed as in [11, 12].

2. Adhesion dynamics and calculation of adhesion force

The adhesion dynamics are precisely as given in [12], except that adhesions do not form off of the adhesive stripe, and are destroyed if they leave the stripe. For completeness, we summarize these dynamics here.

Adhesions between the cell and substrate are tracked individually; there are a fixed number N_adh of adhesions, and if one is destroyed, another one is created. The probability of adhesion formation is proportional to ρ_a and to ϕ, resulting in nascent adhesions being more likely to form at the front of the cell. We compute the initial adhesion location by a rejection method: we propose an adhesion location r₀ distributed uniformly in the region $\left|x\right|\le \frac{w}{2}$, where w is the total width of the adhesive stripe, and accept that adhesion location with probability p = ρ_a(r₀)ϕ/max(ρ_a). Adhesions are destroyed if they leave the stripe(i.e. have $\left|x\right|\le \frac{w}{2}$) or if ϕ < 1/2 at the adhesion location.

Adhesions are advected by the cytoskeletal flow, u; in practice, we choose the adhesion velocity to be the velocity u at the nearest grid point to the adhesion location.

Adhesions have two modes: “slipping” and “gripping.” Adhesions are formed in gripping mode. When an adhesion is formed or transitions into gripping mode, its initial position r₀ is noted. The gripping adhesion acts as a spring stretched from its initial location (where the adhesion attaches to the substrate) to its current location. It thus exerts a force on the cell of

$${\mathbf{F}}_{\text{grip}}=-k_{\text{grip}}(\mathbf{r}-{\mathbf{r}}_0)$$ (D6)

By contrast, a slipping adhesion exerts a force

$${\mathbf{F}}_{\text{slip}}=-k_{\text{slip}}\mathbf{u}(\mathbf{r})$$ (D7)

where r is the adhesion position. We assume that the adhesions mature over time: $k_{\text{grip}}=k_{\text{grip}}^0{t}_{\text{adh}}$ and $k_{\text{slip}}=k_{\text{slip}}^0{t}_{\text{adh}}$ where t_adh is the age of the adhesion site. Adhesions may transition between slipping and gripping, and slipping adhesions may disappear. Gripping adhesions rupture and become slipping adhesions with a force-dependent rate $r_{\text{off}}=r_{\text{off}}^{0}exp\left(\left|{\mathbf{F}}_{\text{grip}}\right|/F_0\right)$, with F₀ the gripping strength scale. Slipping adhesions may return to gripping mode with a rate r_on, and disappear with a rate r_die. To calculate the force density F_adh that enters into the Stokes equation, forces on adhesions are distributed to the nearest grid point; we therefore list the appropriate units in terms of forces per unit area. (We note that [12] incorrectly describes the force as being spread over the closest four grid points.)