Spatial Modeling for Groundwater Arsenic Levels in North Carolina

Abstract

To examine environmental and geologic determinants of arsenic in groundwater, detailed geologic data were integrated with well water arsenic concentration data and well construction data for 471 private wells in Orange County, NC, via a geographic information system. For the statistical analysis, the geologic units were simplified into four generalized categories based on rock type and interpreted mode of deposition/emplacement. The geologic transitions from rocks of a primary pyroclastic origin to rocks of volcaniclastic sedimentary origin were designated as polylines. The data were fitted to a left-censored regression model to identify key determinants of arsenic levels in groundwater. A Bayesian spatial random effects model was then developed to capture any spatial patterns in groundwater arsenic residuals into model estimation. Statistical model results indicate (1) wells close to a transition zone or fault are more likely to contain detectible arsenic; (2) welded tuffs and hydrothermal quartz bodies are associated with relatively higher groundwater arsenic concentrations and even higher for those proximal to a pluton; and (3) wells of greater depth are more likely to contain elevated arsenic. This modeling effort informs policy intervention by creating three-dimensional maps of predicted arsenic levels in groundwater for any location and depth in the area.

INTRODUCTION

Arsenic (As) is a naturally occurring element contained in rocks, soil, water, and air, but human ingestion is primarily from drinking water.¹ A growing body of research shows that long-term exposure to arsenic in drinking water can cause serious health effects including adverse pregnancy outcomes,^2,3 disrupted neuropsychological development,⁴ vascular disease,⁵ skin lesion,⁶ and cancer.⁷ Research also shows that elevated levels of dissolved arsenic tend to be more prevalent in groundwater than in surface water.⁸

Arsenic concentration in public drinking water supplies is regulated by the U.S. Environmental Protection Agency (EPA). In 2001, the EPA lowered the public drinking-water standard from 0.05 to 0.01 mg/L (equivalent to 10 ppb) to sufficiently protect the public from long-term exposure.⁹ Some argue that the EPA arsenic standard for drinking water should be revised downward to no higher than 0.003 mg/L due to potential cancer and other health risks.¹⁰ The EPA’s maximum contaminant level goal (MCLG) is set to 0 mg/L, and North Carolina’s drinking water health risk evaluations use a health-based maximum Ccontaminant level (MCL) of 0.00002 mg/L.¹¹

As groundwater from private wells is still a primary source of drinking water for many people in rural areas in developing and developed countries,¹² understanding which private wells are at risk for potentially high levels of arsenic is a critical environmental and public health concern. Approximately 15% of U.S. citizens receive their drinking water from private wells, but the EPA does not regulate private wells.¹³ Environmental determinants have been identified in past global,¹⁴ regional,^15–18 and local^19–23 studies of the distribution of naturally occurring arsenic. However, little is yet known about the environmental determinants of arsenic in groundwater or the nature of its spatial pattern in the Piedmont of North Carolina.

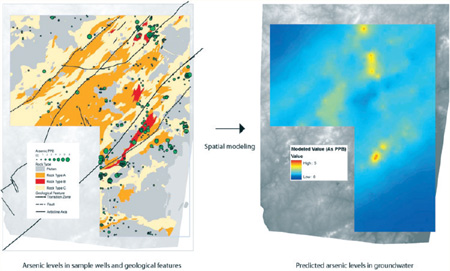
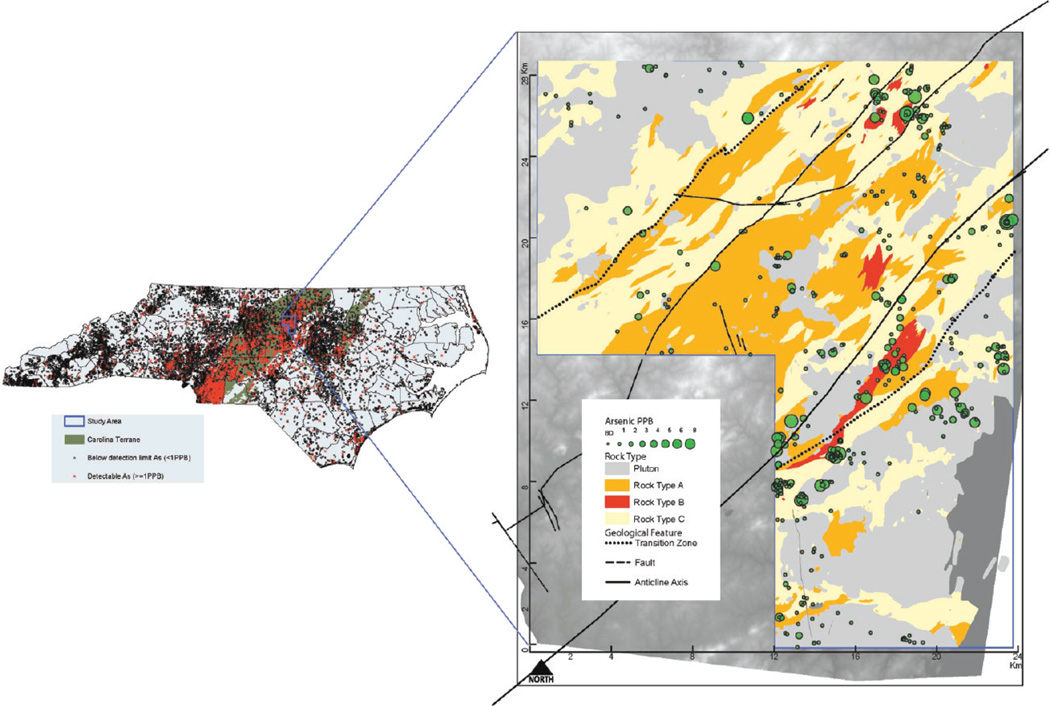
Naturally occurring dissolved arsenic in groundwater is a growing concern in the North Carolina Piedmont.¹¹ Currently, the minimum detection limit (MDL) of arsenic in the North Carolina Department of Health and Human Services (NCDHHS) Laboratory is 0.001 mg/L. The left map of Figure 1 shows that arsenic-detected wells above the current MDL of arsenic (shown as red) exhibit a clear spatial pattern in North Carolina: they concentrate in the Carolina terrane (formerly known as the Carolina slate belt) located in the North Carolina Piedmont, including Guilford, Montgomery, Moore, Orange, Randolph, Stanly, and Union Counties.

Figure 1.

Arsenic levels in 471 sample wells and geological features in study area.

The distribution of naturally occurring arsenic is controlled by regional and local geology. Abundant literature exists detailing the distribution of arsenic contamination of groundwater from metallic sulfide mining activities or other anthroprogenic sources.^24–28 Reports on the spatial distribution of naturally occurring arsenic contamination of groundwater supplies in nonmined areas have been reported in the bedrock aquifers of the eastern U.S. and elsewhere.^{14–23,29–31} Pippin¹¹ compiled groundwater arsenic data from North Carolina and plotted its spatial distribution throughout the state. This study performed a simple probability analysis to identify potential “hot spot” areas with elevated groundwater arsenic. Specific areas of the Piedmont of North Carolina underlain by metavolcanic or metavolcaniclastic rocks were identified as the areas of greatest potential for groundwater arsenic problems. Pippin’s analysis narrowed the focus of elevated arsenic distribution to more localized areas (tens of square miles).

Extensive research into the local distribution of groundwater arsenic has occurred in Bangladesh,^32,33 Wisconsin,^34,35 Michigan,²¹ and other localities. Groundwater arsenic in Bangladesh, Wisconsin, and Michigan occurs in sedimentary basins in which the local geology is relatively well understood through subsurface investigations. Past studies in crystalline rock terranes^{15–20,22,23} range from regional in scope (covering areas of several thousand square miles) to local (several square mile area) but rely on low resolution geologic data (1:100 000 to 1:500 000).

Research into the distribution of groundwater arsenic in areas of complex geology with unconfined fractured bedrock aquifers, as present in parts of North Carolina, using high resolution geologic data (e.g., 1:24 000 scale) is less common.³⁶ This Article is one of the first attempts to utilize detailed 1:24 000 scale geologic data in a GIS platform coupled with geolocated groundwater arsenic data to the parcel level in a folded crystalline rock area to produce highly resolved modeling on the spatial distribution of arsenic. Our statistical approach enables us to attach uncertainty to both the significance of the determinants as well as to predicted levels of arsenic at any location and depth. The results from these analyses illustrate the potential for developing guidelines for environmental sampling and public health intervention.

MATERIALS AND METHODS

This study integrated detailed geologic data with groundwater arsenic concentration data, well construction data, and tax parcel data for portions of Orange County, NC (area inside blue polygon in Figure 1) into a GIS. All data were obtained from publicly available data files. Well sampling data from Orange County, which lies in the NC piedmont, indicate multiple locations with detectable levels (greater than or equal to 0.001 mg/L) of arsenic. This, in combination with the availability of 1:24 000 scale geologic data, makes Orange County an especially attractive location for exploring potential predictors of arsenic in well water. Modeling was implemented using a spatial random effects model in a Bayesian computational framework.

Geologic Data

Detailed geological data were provided by the North Carolina Geological Survey for the Chapel Hill, Hillsborough, and Efland 7.5 min (1:24 000 scale) quadrangles.^37–39 The detailed geologic mapping separated the study area into over 45 geologic units. For the statistical analysis, the geologic units were simplified into four generalized categories based on rock type and interpreted mode of deposition/emplacement. The generalized rock types are (1) plutons/intrusive, (2) felsic and mafic lavas and tuffs (“rock type A”), (3) welded tuffs and hydrothermal quartz bodies (“rock type B”), and (4) air fall tuffs and epiclastic rocks (“rock type C”). Welded tuffs and hydrothermal quartz bodies were included into their own category to differentiate them from air fall tuffs and epiclastic rocks based on their temperature of emplacement. Welded tuffs and hydrothermal quartz bodies are emplaced at temperature >200 °C, whereas air fall tuffs are emplaced at temperatures around 25 °C.⁴⁰

In addition to generalized rock types, the geologic data include line elements (line shapefiles) depicting the location of faults and lines termed “transition zones”. The “transition zones” mark zones that indicate a rock type transition from an area dominated by tuffs (also known as primary pyroclastic rocks) and lavas to an area dominated by epiclastic (also known as volcaniclastic sedimentary) rocks. “Transition zones” are incorporated into the statistical model because geologic models of volcanic massive sulfide and disseminated gold-pyrite deposits (deposits that have abundant hydrothermally altered rock and/or arsenic bearing rock) indicate that favorable horizons for economic mineral deposits occur at the transition from an environment dominated by primary pyroclastic rocks and lavas to an environment dominated by volcaniclastic sedimentary rocks.⁴¹

Groundwater Arsenic and Groundwater Well Construction Data

Groundwater chemistry data were obtained from the NCDHHS laboratory. The data derive from water samples collected in Orange County, NC and analyzed between 1999 and 2005. Orange County private well construction data were provided by the Orange County Health Department, including information on well depth, water flow, and age of well.

Water samples from both public and private water systems were examined for chemical and/or physical parameters. Arsenic is one of the routinely analyzed inorganic contaminants, and the detection limit is 0.001 mg/L. Wells drilled before July 2008 are tested only on request by the Orange County Environmental Health staff for a fee of $35.⁴² A private water system (homeowner) can obtain chemical analyses from the State Laboratory only if the sample is submitted through the local health department.

There are 2178 arsenic measurement records between 1999 and 2006 in Orange County from the North Carolina inorganic chemistry data. Some of the records represent repeat sampling of the same well to track arsenic concentration over time. Therefore, only the maximum recorded value was kept from the wells with multiple test results to reflect potential groundwater concentrations, which reduced the data set to 1788 records. Only about 10% of wells had multiple test results, and, of these, most had only two records. Among these, 543 records were spatially joined to parcels in the study area where well construction data were available using a standard batch geocoding protocol developed by the Children’s Environmental Health Initiative at Duke University.⁴³ The 68 records collected under the older detection limit (0.01 mg/L) were discarded. After dropping 4 records that do not belong to our rock type categories, 471 records were included in the final data set for analysis. Finally, arsenic, well construction, and geologic data were integrated into a comprehensive geographic information system.

Statistical Modeling

Statistical modeling was performed to (1) measure the effect of environmental and geologic factors on groundwater arsenic levels; (2) determine if any spatial patterns in groundwater arsenic detections were present; and (3) predict actual arsenic level at any location and depth in the study area. Recent studies suggest that arsenic concentrations in groundwater may be spatially positively correlated.^19,21,44 We developed spatial statistical models that borrow information from nearby wells to estimate arsenic levels in nondetect and nonsampled wells. Spatial modeling also helps identify spatial patterns in the determinants, which affect not only arsenic levels in a well but also levels in neighboring wells. Moreover, spatial techniques can capture the spatial dependence in arsenic levels. Such dependence is ignored in standard models, including regression analyses that assume independence among observations.

We also take a Bayesian approach to implement full and exact inference in analyzing data, particularly with regard to uncertainty, which is useful for decision-making purposes.^45–48 It gives explicit posterior probability distributions for all parameters and for any predicted outcomes, conditioned on the observed data, and revises the probabilities as new information becomes available.⁴⁹ Posterior probabilities produced by Bayesian methods can be used to calculate expected risks associated with arsenic concentrations along with the levels of uncertainty. In addition, credible intervals (which are similar to confidence intervals in classical statistics) provide direct probability statements with regard to a parameter falling within certain bounds.

In our data, arsenic levels in the wells with nondetect results are coded as zero, although the actual arsenic levels would be between 0 and 1 ppb (equivalent to 0.001 mg/L). Hence, the observed data can be represented as Y(s, d) = A(s, d)1(A(s, d) ≥1), where, at location s and depth d, A(s, d) is the actual arsenic level, Y(s, d) is the measurable arsenic level, the conditional function 1(•) returns one if the inside condition is true and zero otherwise, and the scale is in ppb with 1 ppb the detectable limit. To accommodate the right skewness in the data due to the 328 nondetects in the data set, we model arsenic on the log scale. We first provide a nonspatial model where the data are viewed as independent given their means. That is:

$$Z(s,d)=\text{log}A(s,d)=X{(s,d)}^{\mathrm{T}}\beta +{\beta }_d·d+\epsilon (s,d)$$ (1)

where ε(s,d) ≈ N(0, τ²). Here, X(s, d) is the design vector incorporating 10 geological covariates, including a continuous variable for distance to the closest transition zone or fault (in feet), and nine dummy variables for underground rock types and distance to pluton. The dummy variables indicate the full combination between three categories of underground rock types where the well is located (i.e., rock types A, B, and C) and three categories of Euclidean distance to the closest pluton from the well (i.e., “less than 200 feet”, “200–1000 feet”, and “over 1000 feet”) with pluton as reference. The depth of a well is introduced into the model linearly (other forms were considered, but the linear version appears to be adequate). β is the coefficient vector associated with the explanatory variables and β_d is the coefficient associated with depth. Therefore, the observed arsenic measurements at location s and depth d (Y(s,d)) become:

$$Y(s,d)=\{\begin{array}{cc}\text{exp}(Z(s,d))\hfill & \text{if}Z(s,d)\ge 0\hfill \\ 0\hfill & \text{if}Z(s,d)<0\hfill \end{array}$$ (2)

where Z(s,d) are independently distributed N(X(s,d)^Tβ + β_dd, τ²).

Next, we introduce spatial dependence in the form of a hierarchical spatial random effects model where the spatial random effects are modeled assuming a stationary Gaussian spatial process so that now:

$$Z(s,d)\approx N(X{(s,d)}^T\beta +{\beta }_d·d+W(s),{\tau }^{2}I)W(s)\approx N(0,{\sigma }^{2}H(\varphi ))$$ (3)

Here, W(s) is the spatial random effect at location s arising from a Gaussian process with mean 0 and covariance function, cov(W(s),W(s′)) = ρ(s − s′;ϕ). In particular, for simplicity, we adopt the isotropic exponential covariance function, ρ(s − s′;ϕ) = σ² exp{−ϕ‖s − s′‖}. The isotropic exponential covariance function is introduced to explain the spatial random effects in the residuals adjusted for the explanatory variables. The exponential covariance function is commonly used to model spatial random effects. Hence, we assume additive effects of three components to arsenic levels: (1) geological determinants (X); (2) well depth (d); and (3) spatial random effect (W). As a result, adjusted for covariates, the effects of space and depth on arsenic are separable and additive. To obtain the posterior distribution of each parameter, we use the Markov Chain Monte Carlo (MCMC) model fitting in the form of a Gibbs sampler⁵⁰ employing a Metropolis–Hastings algorithm.⁵¹

RESULTS AND DISCUSSION

Exploratory Analysis

The distribution of arsenic measurements in the combined data is positively skewed with an approximate 70% of the data under the detection limit of 1 ppb. Arsenic was detected in 143 of 471 unique wells, and the maximum arsenic level was 8 ppb. Because it is analytically unattractive to ignore such a high proportion of sites (328 sites) or to assign an arbitrary level less than 1 ppb to the nondetect sites,⁵² we introduce a left-censored data model.⁵³ The right map of Figure 1 displays the spatial distribution of arsenic levels in the 471 wells in the data (BDL = below detection limit). A majority of the wells with relatively high arsenic levels are clustered around a diagonal axis from northeast to southwest. Wells with nondetect results are distributed throughout the study area. The map also illustrates the geological features in the study area, including the geological transition zones and faults (dotted and dashed lines, respectively), anticline axis (solid line), and generalized rock types.

Figure 1 suggests that geological features may be associated with groundwater arsenic levels; we hypothesize that wells with elevated arsenic levels are more likely to be located near transition zones or faults and at felsic/mafic lavas and tuffs (rock type A) or welded tuffs and hydrothermal quartz bodies (rock type B). Because arsenic levels are measured at varying well depth, we also hypothesize that deeper wells are more likely to contain higher levels of arsenic. Well depths are non-normally distributed and right skewed, with an average of 318 feet, and range of 105–925 feet.

Multivariable Analysis

The results for the spatial random effects model are compared to those for the nonspatial model. Both nonspatial and spatial models converge well with 40 000 MCMC iterations. The first 30 000 burn-in iterations were dropped. To achieve roughly independent posterior samples, we used only the results from every 10th remaining iteration for posterior inference. The mean estimate for σ² is 0.79 with a 95% credible interval of (0.03, 3.39), while the mean estimate for τ² is 1.31 with a 95% credible interval of (0.01, 5.24). The posterior probabilities for the three values of ϕ are 0.43 (small), 0.34 (middle), and 0.23 (large).

As presented in Table 1, both nonspatial and spatial models show that well depth is positively associated with relatively high arsenic levels. As expected from Figure 1, distance to the closest transition zone or fault is negatively associated with elevated arsenic levels. These results indicate that wells that are deeper and closer to a transition zone or fault are more likely to contain higher levels of arsenic. The models also show that only one of nine dummy variables for combinations of rock types and distance-to-pluton categories is significantly associated with arsenic in groundwater (i.e., wells located on welded tuffs and hydrothermal quartz bodies (rock type B) and closer to plutons). This result indicates that welded tuffs and hydrothermal quartz bodies are associated with relatively higher groundwater arsenic concentrations, and welded tuffs proximal to a pluton appear to exhibit even higher groundwater arsenic concentrations. These results correspond well with the initial hypotheses that variations in arsenic concentrations may be related to the effects of hydrothermal alteration and the spatial relationships to geologic transition zones described in geological models of volcanic massive sulfide and disseminated gold-pyrite deposits.^40,41

Table 1.

Results of Nonspatial and Spatial Models^b

	nonspatial model			spatial random effects model
variable	mean (β)	SD (β)	prob (β > 0)	mean (β)	SD (β)	prob (β > 0)
well depth (ft)	0.0007	0.0003	0.997	0.001	0.0005	0.961
distance to closest transition zone or fault (ft)	−0.00001	0.000007	0.986a	−0.00005	0.00003	0.982a
rock type A and less than 500 ft from pluton	0.013	0.180	0.522	−0.060	0.259	0.374
rock type A and 500–2000 ft from pluton	−0.005	0.129	0.484	−0.116	0.215	0.323
rock type A and over 2000 ft from pluton	0.038	0.130	0.612	−0.125	0.275	0.311
rock type B and less than 500 ft from pluton	0.476	0.289	0.951	0.851	0.377	0.993
rock type B and 500–2000 ft from pluton	0.131	0.192	0.755	0.285	0.288	0.865
rock type B and over 2000 ft from pluton	0.269	0.215	0.893	0.134	0.339	0.642
rock type C and less than 500 ft from pluton	−0.191	0.237	0.211	−0.156	0.326	0.313
rock type C and 500–2000 ft from pluton	−0.085	0.214	0.348	−0.052	0.344	0.452
rock type C and over 2000 ft from pluton	−0.111	0.260	0.329	0.254	0.417	0.776

^aProb (β < 0).

^bSignificant variables are in bold.

We note that the effects of these significant variables appear to be accentuated in the spatial random effects model as compared to the nonspatial model. For instance, the negative effect of distance to the closest transition zone or fault in the spatial model is 5 times larger than that in the nonspatial model. The key difference between the two models lies in the estimation of arsenic values for the nondetect wells. We found that the estimated arsenic levels from the nonspatial model cluster toward one, while those from the spatial model vary more in the entire interval between zero and one. Such difference in estimating actual arsenic levels for nondetect wells indicates that the spatial model depends not only on the observed values in arsenic-detected wells, but also on the spatial correlation structure of observed and estimated arsenic levels for all wells in the sample.

Model Validation

To validate the performance of both the nonspatial and the spatial random effects models in predicting arsenic levels, two follow-up analyses were designed to (1) calculate predicted mean squared errors (MSE) for both models, and (2) assess empirical coverage of the models. For such analyses, we randomly selected 20 wells out of 143 wells with detected arsenic levels and held out those wells from the model fitting. We fit the model to the remaining wells and used the fitted model to predict arsenic levels at the hold-out wells.

By calculating predicted MSE, we compared what was observed at each of the 20 hold-out wells with the posterior mean from fitting the model at that well (i.e., the average of the posterior samples from the predictive distribution for that well). The predictive MSE for the spatial model is 0.25, and that for the nonspatial model is 0.47. By checking empirical coverage, we obtained 80%, 90%, and 95% predictive intervals for the arsenic levels, calculating the proportion of times the intervals contain the observed value. The term 90% empirical coverage refers to the proportion of times a predictive interval is correct for data that were held out from the model fitting. For a satisfactory model, the observed or empirical proportion should be approximately the nominal probability (in this case 0.9). We found that the empirical coverage for the spatial model was consistently larger than that for the nonspatial model. For instance, the empirical coverage for 90% nominal coverage is 100% for the spatial model (i.e., all 20 hold-out samples are contained by the 90% predictive intervals), while it is only 85% for the nonspatial model (i.e., 17 out of 20 hold-out samples are contained by the 90% predictive intervals). The results of these hold-out analyses indicate that the spatial random effects model outperforms the nonspatial model in predicting arsenic levels in groundwater in the study area.

Arsenic Mapping

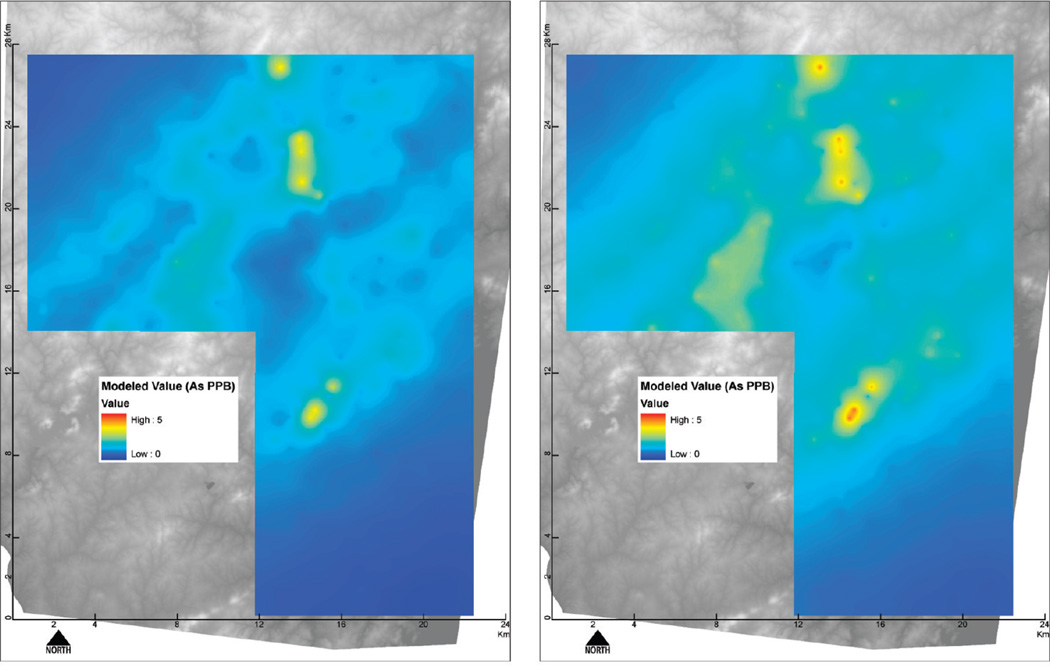
Using the results of the spatial random effects model, we predicted arsenic levels for 500 new locations, which were determined using a regular grid superimposed on the map of the entire study area. We constructed the data for all of the covariates used in the multivariate model for the new locations and predicted an arsenic level for each location, using the coefficient vector of the spatial model along with the covariate data for the new locations. Separate predictions are made at each location assuming that wells are installed to a depth of 150 feet or, alternatively, to a depth of 400 feet. Once we completed prediction for the 500 locations, a simple kriging interpolation method in the ESRI’s ArcGIS program was used to create the predicted arsenic surfaces for 150 and 400 foot wells. This neighborhood interpolation was done solely for display purposes and is unrelated to the results of the statistical modeling. Because of the large changes in observed arsenic values over short distances, the mapping process is limited.

Figure 2 provides a map of predicted arsenic surface at each well depth, interpolated to the entire study area. Several hotspots for arsenic-affected groundwater are observed in these maps, and arsenic levels in the areas are higher for deeper wells. This result implies that greater concern for arsenic concentrations should be given to deeper wells, especially for those located in the hotspot areas.

Figure 2.

Predicted arsenic levels in groundwater: 150 feet and 400 feet deep.

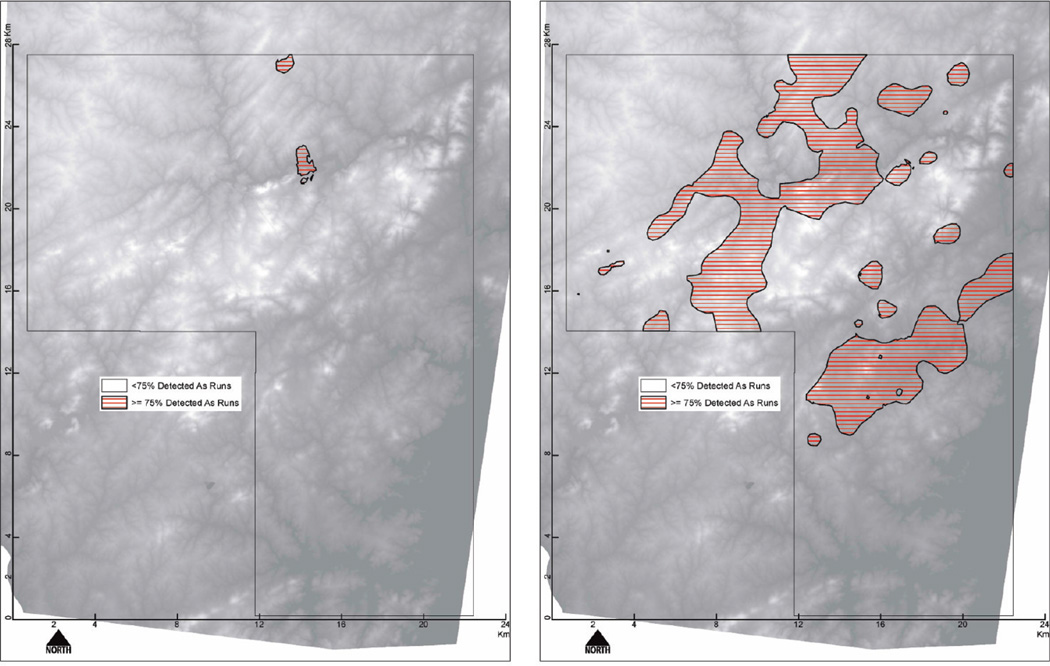
Figure 3 displays the areas of hotspots for each of the two well depths, where the posterior probability of arsenic being detected is greater than 0.75 (i.e., predicted arsenic levels are found to be greater than 1 ppb for three-fourths of the simulated samples). We note that the hotspot areas are located around transition zones and faults and are larger for deeper wells. Considering high well-to-well variability of arsenic concentrations in the data, it would be possible that a low level of arsenic is observed within a hotspot and arsenic is a problem even in low risk areas. However, these maps could be used as a guideline for environmental and health intervention in this area, such as instruction for new well locations, health education of households consuming water from wells with potential arsenic risks, and selection/design guidelines for additional water testing for arsenic.

Figure 3.

Arsenic hotspots (posterior probability of arsenic detected >0.75).

Limitations and Future Work

Our analytical work has four major limitations in that it (1) assumes there is no interaction effect between well location and well depth on arsenic levels; (2) uses simplified categories for underground geological features such as rock type and transition zone; (3) ignores data uncertainty around polylines and polygons; and (4) employs interval-censored instruments measuring arsenic levels above detection limit as integers which potentially creates a measurement error. Moreover, due to the apparent high variability in groundwater arsenic concentrations from well to well, spatial estimation and mapping is limited to some extent. In addition, the analysis relies on detailed geologic data, which may not be available in other locations.

In future research, the spatial model can be refined to capture the interaction effects of two-dimensional spaces (easting and northing) and depth on arsenic levels in groundwater by allowing spatial random effects to vary by depth. This approach would allow us to map out the full three-dimensional surface for arsenic in groundwater in the study area. Furthermore, sensitivity analyses can be performed to evaluate the models by examining how the model results vary with different categorizations of geological features and uncertainty levels of geological data.

Detailed geologic data used in the statistical model runs were collected up to 2006, and additional detailed geologic data have been collected by the North Carolina Geological Survey in Orange County. Additionally, new regulations, enacted in 2006, mandate that all newly constructed private groundwater wells be tested for numerous inorganic parameters including arsenic. As such, new unbiased arsenic groundwater data are available from Orange County. A reanalysis of the statistical model incorporating the newly available geologic data and arsenic data would provide more robust model results.

In summary, the results of the Bayesian spatial random effects model for the left-censored arsenic data identified three major determinants of arsenic levels in groundwater: (1) wells close to a transition zone or a fault are more likely to contain detectable arsenic; (2) welded tuffs and hydrothermal quartz bodies, especially proximal to a pluton, are associated with relatively higher groundwater arsenic concentrations; and (3) deeper wells are more likely to contain arsenic-affected water. Our spatial modeling work provides initial evidence of the potential environmental determinants of groundwater arsenic levels. The resulting three-dimensional maps showing spatial patterns of predicted groundwater arsenic levels could be used as a partial basis for public health intervention.