Abstract
This paper focuses on the geometric modeling and computational algorithm development of biomolecular structures from two data sources: Protein Data Bank (PDB) and Electron Microscopy Data Bank (EMDB) in the Eulerian (or Cartesian) representation. Molecular surface (MS) contains non-smooth geometric singularities, such as cusps, tips and self-intersecting facets, which often lead to computational instabilities in molecular simulations, and violate the physical principle of surface free energy minimization. Variational multiscale surface definitions are proposed based on geometric flows and solvation analysis of biomolecular systems. Our approach leads to geometric and potential driven Laplace-Beltrami flows for biomolecular surface evolution and formation. The resulting surfaces are free of geometric singularities and minimize the total free energy of the biomolecular system. High order partial differential equation (PDE)-based nonlinear filters are employed for EMDB data processing. We show the efficacy of this approach in feature-preserving noise reduction. After the construction of protein multiresolution surfaces, we explore the analysis and characterization of surface morphology by using a variety of curvature definitions. Apart from the classical Gaussian curvature and mean curvature, maximum curvature, minimum curvature, shape index, and curvedness are also applied to macromolecular surface analysis for the first time. Our curvature analysis is uniquely coupled to the analysis of electrostatic surface potential, which is a by-product of our variational multiscale solvation models. As an expository investigation, we particularly emphasize the numerical algorithms and computational protocols for practical applications of the above multiscale geometric models. Such information may otherwise be scattered over the vast literature on this topic. Based on the curvature and electrostatic analysis from our multiresolution surfaces, we introduce a new concept, the polarized curvature, for the prediction of protein binding sites.
Keywords: Protein characterization, Variational multiscale surfaces, Curvature analysis, High order geometric PDEs, Free energy functional, EMDataBank, Protein data bank
1 Introduction
Structural biology is an essential part of modern biological sciences. A basic role of structural biology is to provide structural information of biological macromolecules, especially proteins and nucleic acids, and the interpretation of macromolecular structures, namely, structure-function correlations. Typically, macromolecular structures are determined via macromolecular crystallography, NMR, EPR, etc. Macromolecular structural data are deposited at the Protein Data Bank (PDB), which is a source for much biophysical modeling, simulation and analysis. One most important new trend in structural biology is the study of large protein complexes and subcellular organelles, which plays an essential role in many key biological processes, including genome replication, transcription, translation, protein-folding, signal transduction, and viral infection. The structural information of large protein complexes and subcellular organelles is crucial for exploring the molecular mechanisms behind complex biological processes. Unfortunately, most conventional experimental means and imaging modalities well-suited for relatively small proteins do not work well for multiprotein complexes and subcellular organelles. Recently, electron tomography, especially cryo-electron microscopy (cryo-EM), has become a powerful tool for revealing three-dimensional (3D) structures of macromolecular complexes in different functional or biological states. The feasible resolution of cryo-EMs ranges from 80 to 2Å, capable of bridging the gap between live-cell imaging and atomic resolution structures. Structures determined by cryo-EMs are deposited at the EMDataBank (EMDB), a significant resource for global deposition and retrieval of cryo-EM data. Unlike PDB, which usually contains information about structures of proteins, nucleic acids, and complex assemblies obtained from X-ray crystallography or NMR spectroscopy at the atomic level resolution, EMDB typically provides information about multiproteins, organelles, cell and tissue from cryo-EMs at the molecular level resolution.
It remains a great challenge to quantitatively model and predict the structure, function, dynamics and transport of complex self-organizing biological systems. Geometric modeling not only bridges the gap between biomolecular data and biological conceptualization and interpretation, but also provides a basis for mathematical modeling, analysis and computation [78, 22]. In 1953, Corey and Pauling proposed the atom and bond model of molecules [18], which has since become a cornerstone in physical science. Numerous other models, including the van der Waals surface, the solvent-excluded surface (SES) (also known as molecular surface (MS)), and the solvent-accessible surface have been proposed [36, 46]. The combination of these biomolecular surfaces with the calculated electrostatic potentials on and around them, has become an important procedure in the analysis of biomolecular structure, function, and interaction, such as ligand-receptor binding, protein specification, drug design, macromolecular assembly, protein-nucleic acid and protein-protein interactions, and enzymatic mechanism [47]. A variety of physical and graphical models are developed during the past few decades.
The widely applied biomolecular surfaces, especially SESs, have well-known drawbacks in their definitions. One of these problems is the admission of geometric singularities, i.e., tips, cusps and self-intersecting facets, which lead to computational instabilities and induce numerical errors [17, 20, 32, 50]. Another defect is that these surfaces are simply ad hoc divisions of a biomolecule from its surroundings, without the consideration of the physical laws of surface energy minimization and surface evolution under the interaction with the aqueous environment. At the fundamental level, there is no sharp division between solvent and solute because their electron densities overlap with each other. In the past few years, many theoretical models have been proposed to address these problems [67, 5, 6, 7, 4, 82].
In the past two decades, geometric flows, particularly the mean curvature flows, have received much attention. Geometric flows have had much impact in image processing and data analysis, particularly for feature-preserving noise reduction [40, 51, 55]. Historically, Witkin pioneered diffusion equation based image denoising in 1983 [71]. In 1990, Perona and Malik proposed an anisotropic diffusion equation [43], in which the diffusion coefficient is controlled by image gradients. The Perona and Malik equation can remove the noise without blurring the image edges. Osher and Sethian invented the level set method, which was applied far beyond the scope of image processing, to computer graphics, computational geometry, optimization, and computational fluid dynamics [51, 41]. Other related mathematical techniques include Mumford-Shah variational functional [39], total variation models designed by Rudin, Osher, and Fatemi [49], and Willmore flow formulation [69, 53, 9, 19]. Because high order partial differential equation (PDE) can more efficiently suppress the noisy component, Wei introduced the first family of arbitrarily high order nonlinear PDEs for noisy image restoration in 1999 [63]. Most geometric PDEs are designed as low-pass filters. The first nonlinear PDE based high-pass filter was proposed in 2002 [66]. Recently, PDE transform has been introduced for functional mode decomposition based on the iterative applications of Wei’s high order nonlinear PDE filters [62, 61].
To overcome geometric singularity in classical macromolecular surfaces, Wei and his co-workers introduced one of the first geometric flow approaches for molecular surface generation in 2005 [67]. Bates, Wei and Zhao incorporated the energy minimization principle into macromolecular surface generation, and proposed one of the first variational frameworks for biomolecular surfaces [5, 6]. Basically, a free energy functional of the biomolecular surface model is defined. Through the Euler-Lagrange equation of surface free energy minimization, a generalized mean curvature flow equation is attained. The resulting molecular surface, called the minimal molecular surface (MMS), is then constructed by the mean curvature flow [7]. PDE algorithms for biomolecular surface generation have become a popular topic in theoretical biology [75, 79, 4]. Both aforementioned arbitrarily high-order geometric PDEs and PDE transform have been applied to biomolecular surface construction [4, 82]. Similar approaches were employed by Cheng et al. [15] to extract biomolecular surfaces from a variational solvation model.
In a physiological environment, up to 65%–90% of human cellular mass is water. Consequently, almost all the biological processes in cell, such as signal transduction, transcription, translation, protein folding, protein ligand binding, and charge and mass transport, occur in aqueous surroundings. Therefore, the understanding of the solvation is of fundamental importance for quantitative modeling and analysis of all the above-mentioned processes. Explicit solvent models and implicit solvent models are two major approaches for solvation analysis [48, 52, 54]. For explicit solvent models, both the solvent and the solute are described in atomic detail and extensive sampling is required. Implicit solvent models are designed to reduce the number of degrees of freedom by using a dielectric continuum to describe the solvent while admitting a microscopic atomic description for the biomolecules [74, 3, 8]. Due to their fewer degree of freedom, implicit solvent models, such as the Poisson-Boltzmann (PB) model or the Poisson equation (PE) model when there is no salt in the solvent, are widely used [1, 2, 45]. The coupling of the PB or PE with the generalized Laplace-Beltrami flow has the potential of describing the formation of molecular surface in realistic solvation environments. Conceptually, a solvation free energy can be divided into two major parts: a nonpolar part associated with inserting an uncharged solute into the solvent [14] and a polar part associated with charging the solute in vacuum and solvent [38, 11]. The nonpolar free energy and polar free energy can be represented by a total free energy functional [63]. By using the variational principle, a new geometric flow equation is generated that controls the biomolecular surface formation and evolution via curvature and potential driven [4, 11, 12, 13]. This model takes into consideration of the surface energy minimization and also the solvent-solute interaction, and gives a multiresolution representation of biomolecular surfaces in their native environment. Additionally, the external potential term can be used to incorporate different kinds of effects, such as chemical reaction, fluid flow, and elastic description of marcomolecules [68, 65].
The objective of the present paper is to provide an expository investigation and summary of tools, algorithms and methodologies for geometric modeling of biomolecules. We particularly focus on tools, algorithms and methodologies required for biophysical models in the Eulerian representation. Although Eulerian formation [11] and Lagrangian formation [12] of biomolecular surfaces can be formally equivalent, they depend on different tools, algorithms and methodologies. The starting points of our discussions are experimental data from either the PDB or the EMDB. For the latter, the high order PDEs are introduced to perform noise reduction. Geometric features, such as Gaussian curvatures, mean curvatures, and shape index, are employed to describe the geometric properties of biomolecular multiresolution surfaces generated by generalized geometric flows and from the EMDB for the first time.
The rest of this paper is organized as follows. Section 2 is devoted to computational algorithms. We discuss in great detail data sources, related softwares, and computational techniques for surface construction, quality improvement, and geometric characterization. We provide advanced interface methods for the evaluation of surface area and surface enclosed volume in the Cartesian representation. Efficient algorithms for calculating various curvature properties, such as Gaussian curvature, mean curvature, maximum and minimum principal curvatures, shape index, and curvedness are developed. The performance of these algorithms is compared. Mathematical models are presented in Appendix A. Two variational models for macromolecular surface generation from PDB data are introduced. We make use of the differential geometry theory of surfaces and geometric measure theory to formulate protein surfaces in conjugation with electrostatic analysis. Additionally, geometric flow based methods are utilized to render high quality macromolecular surfaces from EMDB data. Finally, methods for characterizing geometric features of macromolecules are also proposed. This paper ends with concluding remarks.
2 Computational algorithms
2.1 PDB data processing and surface generation
The PDB is a repository for the 3D structural data of macromolecules, usually obtained by X-ray crystallography or NMR spectroscopy. Most data downloaded from the PDB need to be processed for preparing structures used in theoretical analysis and modeling [10]. Visualization is of great importance to our understanding and conceptualization of the biomolecular systems. Many softwares can be employed to generate triangular surface meshes for biomolecules. An example is the MSMS package. However, the MSMS surface cannot be directly used in Cartesian domain modeling and computation as discussed below.
2.1.1 Lagrangian to Eulerian transformation
The molecular surface generated from the MSMS software is in the Lagrangian representation, i.e., triangle meshes are used to describe the surface. In order to generate the Cartesian representation for finite difference type of methods, one needs to carry out the transformation from Lagrangian to Eulerian representation, i.e., to immerse the 2D surface obtained from the Lagrangian representation into a bounded 3D domain with the Cartesian grid. In this process, one needs to extract interface information from the triangle mesh representation, including the coordinates of intersecting points between the surface and Cartesian mesh lines, and surface normal directions at these intersecting points.
For example, if we have a surface mesh in .vert and .face files, usually, the .vert file stores the point coordinates in the form of v = (υx, υy, υz), and the .face file contains the connectivity information with each triangle represented by three vertex indices. The bounded box to encompass the protein can be constructed by expanding the tightest axis-aligned bounding box, i.e., by decreasing (increasing) the minimal (maximal) values of surface coordinates, by a certain value denoted as dc. The new Cartesian mesh domain is thus [xl, xr] × [yl, yr] × [zl, zr], and can be obtained from,
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where Nt is the total number of the node points in the Lagrangian representation of the protein surface. One can specify the mesh spacing, i.e., the size of each grid, as h, and coordinates of Cartesian mesh nodes can be calculated and represented as {(xi, yj, zk)|i = 1, …, Nx; j = 1, …, Ny; k = 1, …, Nz}, with Nx, Ny and Nz standing for the total node numbers in each dimension. It can be seen that xl = x1 and xr = xNx. Similar relations exist for y and z coordinates.
As the goal is to find the intersection points of each triangle with grid lines, we first find the plane equation. For each mesh triangle, one has the coordinates for its three vertices (v1, v2 and v3). The 2D plane that the triangle belongs to is
| (7) |
The norm for the triangle is the same for the plane, represented as
| (8) |
We find the intersection points by testing grid edges within the bounding box of the triangle. It is easy to find the coordinate ranges for all the relevant grid edges, e.g. in x coordinate,
| (9) |
| (10) |
For all the points within the triangle, the values of x coordinate should fall in the range [xs, xb]. For any Cartesian grid line with x-coordinate xi in {xi|xs ≤ xi ≤ xb}, the index i satisfies the restriction i0 ≤ i ≤ i1, where i0 = [xs/h] and i1 = [xb/h] with h being the grid spacing. Similarly, one can find similar lower and upper limit integers for the other two coordinates, j0 ≤ j ≤ j1, k0 ≤ k ≤ k1. Thus, to find an intersection between a surface triangle and a grid line along x direction, one can choose two arbitrary index (j, k) within the corresponded ranges, with their associated coordinates defined as (yj, zk), and calculate the related point in the triangle plane. The related coordinates are denoted as (xo, yj, zk), and evaluated from
| (11) |
The intersecting points form a set, which is the collection of only three possible types of points:
| (12) |
| (13) |
| (14) |
The only task left to do is to determine whether the planar point we calculate falls within the triangle. The points located outside the triangle are discarded. If the point located on the boundary edges or the interior of the triangle, it is indeed a point where the interface intersects with the Cartesian grid lines. The normal vector for this interface intersecting point is defined to be the same as that of the triangle, or for efficiency, it can be computed as the linear interpolations of vertex normals. The normals and coordinates are then stored in the sequence of their related Cartesian nodes.
We test our method on a sphere with radius r = 2. Using the MSMS software, we generate the Lagrangian representation of the surface with 100 vertices for each 1 × 1 area. The Cartesian representation is set with a mesh spacing h and the interface-mesh intersecting points are calculated and the average error is evaluated by
| (15) |
where (xo, yo, zo) are the calculated interface-mesh intersecting points and No are the total number of such intersecting points. The errors of Lagrangian to Eulerian transformation are illustrated in Table 1. It can be seen from the table that second order accuracy is attained.
Table 1.
Test of the convergence of the proposed method for Lagrangian to Eulerian transformation.
| h | Error | Order |
|---|---|---|
| 2.500e-1 | 7.985e-4 | |
| 1.250e-1 | 2.651e-4 | 1.59 |
| 6.250e-2 | 7.265e-5 | 1.87 |
| 3.125e-2 | 1.979e-5 | 1.88 |
2.1.2 Surface generation in the Cartesian representation
The basic idea for surface generation is to embed an enlarged van der Waals surface in a 3D domain and evolve this hypersurface under a geometric and potential driven flow under certain biological constraint. Note that directly evolving the geometric flow equation in the Lagrangian representation for a protein may be unstable due to the possible topological changes during the surface evolution. In the Cartesian setting, some basic information of the protein is needed, including atom positions xi, i = 1, ⋯, n, atom radii ri, i = 1, ⋯, n and also the atomic charges information for electrostatic analysis when a full solvation model is used; see description in Appendix A. Here n is the total number of the atoms in the protein molecule. To set up the initial conditions, two domains are defined, one is Dχ representing the domain enclosed by the van der Waals surface; the other is an enlarged domain D:
| (16) |
| (17) |
Here we choose a factor of 1.3 to guarantee the formation of properly connected surfaces. In fact, this special parameter can be adjusted to give different scales of the molecular surface, which may lead to dramatically different geometric features [22]. We denote S as the Cartesian representation of the hypersurface. For the initial value of S, we consider two functions,
| (18) |
| (19) |
The characteristic function χ(x, y, z) is used to protect the van der Waals surface during the surface evolution. The Dirichlet boundary condition is used in the computation, the boundary value is S = 0. The formation of surface is driven only by the generalized Laplace-Beltrami equation (83) in Appendix A. We spell out all the terms involved,
| (20) |
where γ is the surface tension and V1 is a general potential driven term due to other effects. We treat protein surface tension as a fitting parameter in the free energy calculation of a set of molecules [11, 12]. To take into consideration the biological constraints, we modify the evolution equation and incorporate the characteristic function χ(x, y, z),
| (21) |
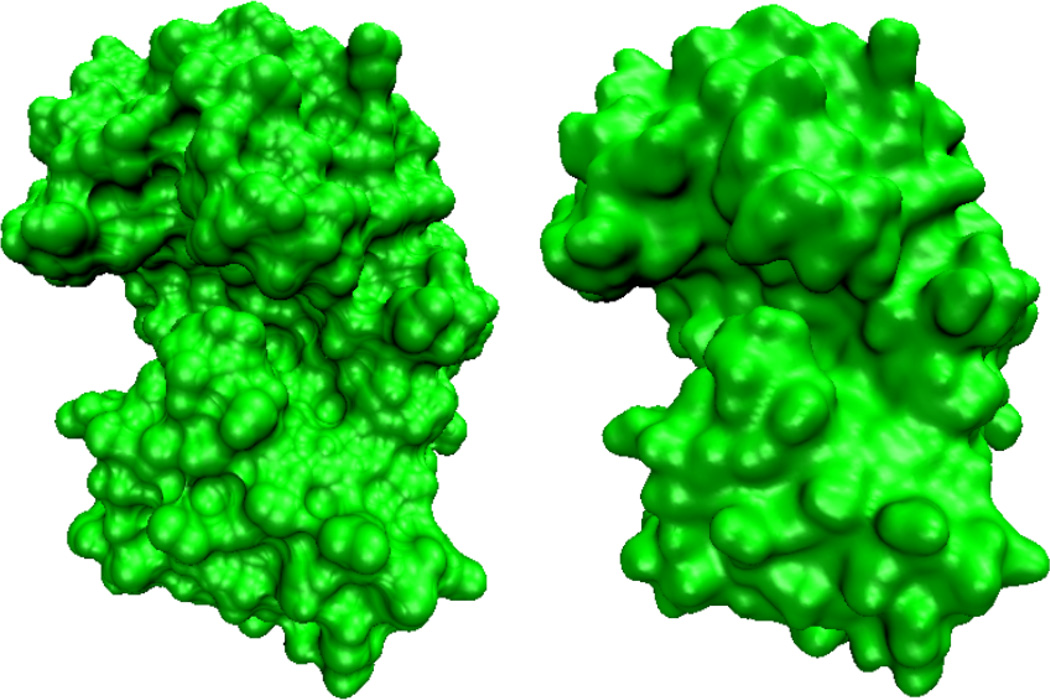
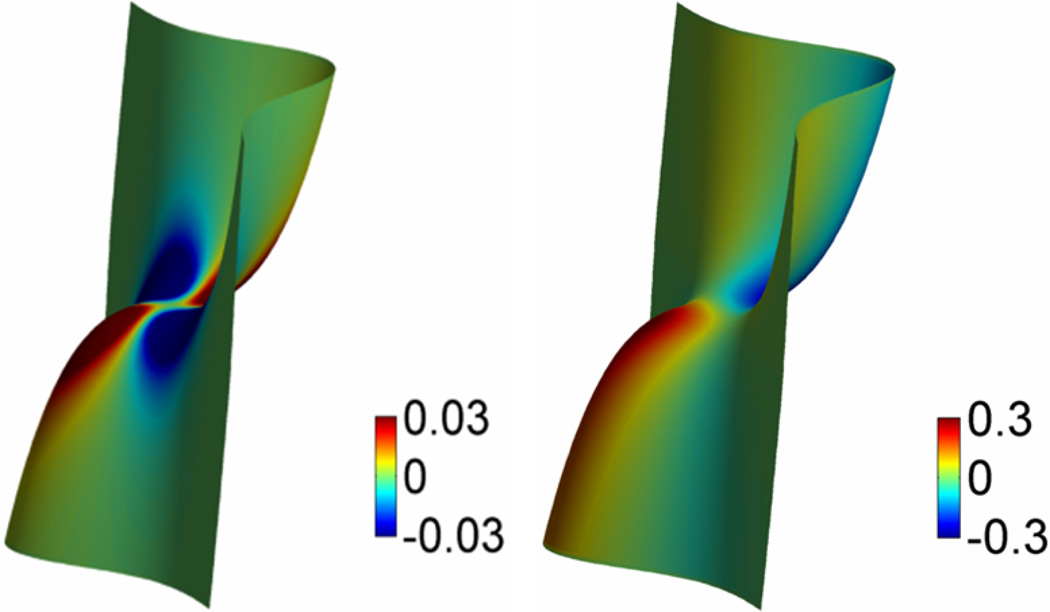
The approximated steady state solution of S(x, y, z, t) is obtained after certain large iteration time, t = T0. It is a smooth function with relatively rapid changes near the protected atomic boundaries of Dχ. However, the hypersurface S(x, y, z, T0) gives rise to a family of isosurfaces. It is easy to extract an isosurface by setting S(x, y, z, T0) = C, where C is a value between 0 and 1. The value of C can be adjusted to achieve the effect of multiresolution surfaces. However, by choosing C = 0.5, one can attain a better accuracy in the calculations of the surface area and surface enclosed volume. For all the surfaces demonstrated in this paper, we choose C = 0.5. Figure 1 gives an example of the comparison between the molecular surface and the surface generated from the Laplace-Beltrami flow. It can be seen from the figure that the surface evolved from the Laplace-Beltrami is free from singularities.
Figure 1.
Comparison of the solvent excluded surface (Left) of protein 1PPL and surface generated by the Laplace-Beltrami flow with V1 = 0 (Right). The latter is free from geometric singularity. In the generation of 1PPL MMS, an outer layer of 1.7Å is used to immerse the protein in solvent. The comptational domain for protein 1PPL is [−14.7, 57.8]*[−16.7,41.3]*[−8.2,39.8]. We set the grid size to be 0.5 Å, and 100 iterations are carried out.
When there are external potentials (V1 ≠ 0), the surface generation is usually coupled with the calculation of other physical variables governed by other equations. These coupled equations should be solved iteratively. For example, to take into consideration the electrostatic effect, the PB model is commonly employed. Due to the vastly different quantities of the dielectric constants in solute and solvent domains, the elliptic interface problems are frequently updated in the geometric and potential driven models.
2.2 EMDB data processing and surface generation
2.2.1 EMDB Data
As the data from the cryo-EM accumulated, EMDataBank.org was established to create a global deposition and retrieval network for cryo-EM maps and associated metadata. It also serves as a portal of software tools for standardized map format conversion, segmentation, model assessment, visualization, and data integration. A list of EM software packages can be found in the website http://emdatabank.org/emsoftware.html. MRC (Medical Research Council) is the file format used in cryo-EM data, in which the data are stored on a 3D grid of voxels (volumetric cells) with values corresponding to the density of electrons. It was developed by the MRC Laboratory of Molecular Biology, and is supported by almost every molecular graphics software package that supports volumetric data, such as, visual molecular dynamics (VMD), PyMOL, and UCSF Chimera. A detailed specification of the MRC file format can be found at the website http://ami.scripps.edu/software/mrctools/mrc_specification.php. The Matlab code for extracting the voxel value information is also mentioned in the above webpage. Here we modify the code and incorporate a simple procedure to store the values in the “.dat” format for further use. For example, if we want to extract the information of “emd_1048.map”, the related Matlab code is given in Appendix D.
To avoid any confusion, here “emd_1048.map” contains the data directly downloaded from EMDataBank’s website http://www.ebi.ac.uk/pdbe-srv/emsearch/form and is stored in the standard MRC format. With VMD, one can visualize the data directly. In the VMD, when loading the data, one needs to select the “CCP4,MRC density map” option for “Determine file type”. In the “Graphical representation”, the “Drawing method” is chosen to be “Isosurface”. For the “isovalue” option, one needs to key in the recommended iso-values found in the webpage of the map data. One can select the “ColorID” in the “Coloring method” and adjust the value to render the surface with a specific color.
2.2.2 Noise reduction of EMD
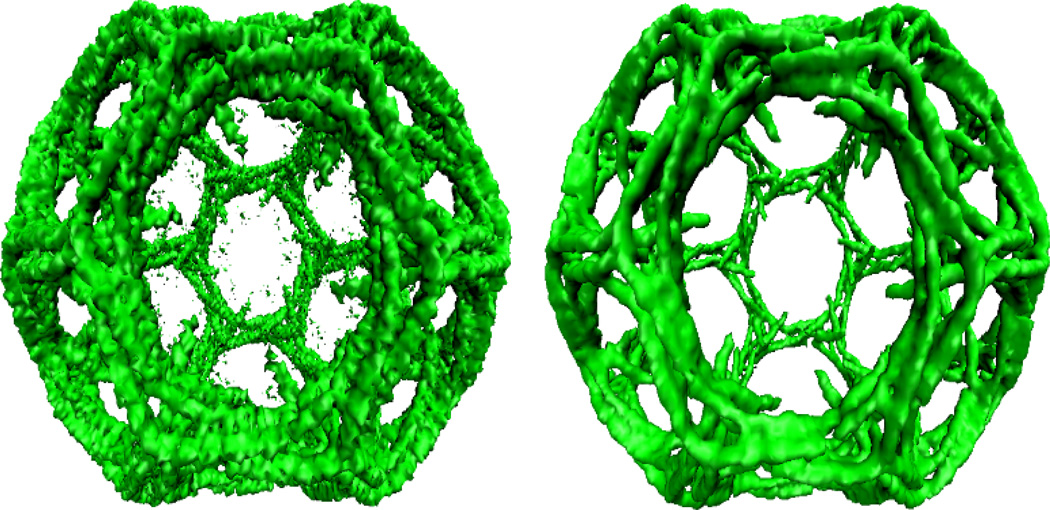
It is seen from the left chart in Fig. 2 that electron tomography sometimes produces extremely noisy and low contrast 3D density maps. The poor signal-to-noise ratio (SNR) hinders visualization and interpretation. Therefore, noise filtering techniques are indispensable when treating EM data. There are a number of effective methods and schemes for this task, like wavelet transform techniques, nonlinear anisotropic diffusions, Beltrami flow, bilateral filter, and iterative median filtering [58, 25, 24, 59, 33, 42, 60].
Figure 2.
Noise reduction for emd5119. The left chart shows the noisy image from the original density maps; The right chart shows the image free from the noise.
To further improve the noise reduction efficiency, high order geometric PDEs are employed, see Appendix C. We can control the process by three parameters, the integration time t, the PDE order q, and the external term P(u, |∇u|). For the protein surface generation from the PDB, a proper combination of the PDE order and integration time is required to deliver high-quality surface [81, 22, 23]. If the solvation process is considered, the potential driven term should incorporate both the nonpolar and polar effects. In our noise reduction procedure for EMDB data, the external term is omitted. The integration time is adjusted to give different levels of noise amplitude and image construction. Figure 2 demonstrates an example of noise removal of EMD5119. To be specific, left chart in Fig. 2 is generated with the suggested contour level value 0.25 from the original noisy data. The right chart is produced with same contour level value but from the processed data. The noise is reduced efficiently, while the salient edges are preserved very well.
2.3 Surface electrostatic analysis
One of the most important problems in biological sciences is the understanding of electrostatic interactions in biomolecules. Electrostatic interactions are ubiquitous in any system of charged or polar molecules, such as proteins, nucleic acids, lipid bilayers, and sugars. The importance of electrostatics in biomolecular systems is due to the fact that electrostatic interactions frequently dominate other forces and determine the structure, function, stability, dynamics and transport of macromolecular systems. As shown in Section A.2, electrostatic analysis is readily coupled with surface analysis. Electrostatic potential can be obtained by solving the Poisson-Boltzmann equation. The surface electrostatic potential, obtained by the projection of electrostatic potential on a surface, is important for the understanding of protein-protein interactions, ligand binding, solvation, and drug design.
From the mathematical point of view, solvent-solute boundary can be treated as an interface. If we use the Poisson equation or the PB equation to describe the electrostatic potential with the different dielectric constants in the solvent and solute domains, an elliptic interface problem is constructed. The well-posedness of this equation relies on the interface information, which usually involves the jump conditions of the function values and the derivatives with respect to normal directions on the interface.
| (22) |
| (23) |
where Γ denotes the interface, and vector n is the normal direction. Here u+, and β+ denote the limiting values of from one subdomain Ω+, and u−, and β− from the other Ω−. The total computational domain Ω = Ω+∪Ω−, and interface Γ = Ω+∪Ω−. In the PB model, the variable u is replaced by the electrostatic potential Φ. Due to the continuity of electrostatic potential and its flux density, the right terms in the jump condition equals zero, that is, Ψ1 = Ψ2 = 0.
2.3.1 Extraction of interface information from volumetric data
Interface information is required for both electrostatic analysis and geometric analysis. To extract interface information from volumetric data, one needs to know the isovalues (or level set values) at the Cartesian grid nodes. The volumetric data can be treated as a surface function on a grid with one value assigned to each grid node. When a new Cartesian mesh is employed in computation, the isovalues on the new grid nodes need to be evaluated for further applications in elliptic interface schemes and curvature analysis. For instance, if one has volumetric data {Sυ}320×320×320, the Cartesian mesh size is set to Nx × Ny × Nz (21 × 21 × 21 in the example), and {Sυ} should be sampled on the grid to produce {S}Nx × Ny × Nz. Here {S}Nx × Ny × Nz can be seen as the discrete representation of the trilinearly interpolated surface function S(x, y, z). We provide details for the trilinear interpolation below. First, we assume the domain for given volumetric data as Ωυ = [1, 320] × [1, 320] × [1, 320], and denote the coordinates of node (i, j, k) on target Cartesian grid by (xi, yj, zk), expressed as
| (24) |
Then, we denote the integer part of (xi, yj, zk) as (it, jt, kt), and the fractional part as (xd, yd, zd). The Cartesian mesh node (i, j, k) can be viewed as a point in Ωυ, and encompassed by the cube formed by eight original grid nodes, with coordinates (vm)m=1,…,8. It is seen that the coordinates for diagonal two nodes are v1 = (it, jt, kt) and v8 = (it + 1, jt + 1, kt + 1). If the isovalues on these grid nodes are denoted as Sυ(vm)m=1,…,8, to calculate the isovalues Si,j,k, eight weights W(m)m=1,…,8 are needed in the interpolation form,
| (25) |
One can certainly choose more than 8 points to carry out the evaluation and also the weights are by no means unique. Here we just make use of the Lagrangian shape functions on cubes, and map the original cube to a logical cube with the coordinate of the diagonal two nodes as (−1, −1, −1) and (1, 1, 1). The mesh point (i, j, k) is then projected to a new node with coordinate (ξ η ζ)
| (26) |
The weight functions corresponded to cubic nodes can be represented as
| (27) |
where (ξm, ηm, ζm) are the nodal coordinates of the logical cube.
For volumetric data, a recommended isovalue is given to define the interface, denoted as Γ. Therefore, the region with isovalues bigger than the recommended one is specified as the biomolecular subdomain, which we usually denote as Ω+ and with the opposite Ω−. Each mesh node is assigned to a region. For a given node, when its surrounding six nodes are in the same subdomain, this node is defined as a regular node. Otherwise if any of its six surrounding nodes is located in the other subdomain, the node is an irregular node. Irregular nodes usually occur in pairs.
The real physical domain for the voxel data can be also found from the EMDB data description. The unit is usually in angstrom or nanometer. It is easy to interpolate the physical coordinates into Cartesian mesh nodes. To avoid heavy notation, we still use (xi, yj, zk) to represent the coordinate of node (i, j, k). However, it is now assumed to be in the real physical domain.
In the matched interface boundary (MIB) algorithm, in order to implement the jump conditions, we need to know the interface information between the pair of irregular nodes. For example, if nodes (i, j, k) and (i+1, j, k) are located in two different subdomains, the coordinate of the interface intersecting with the mesh is specified as vo = (xo, yo, zo),
| (28) |
where S0 stands for the recommended isovalue of the interface, and Si,j,k represents the isovalue at node (i, j, k). The normal direction is interpolated from the expression,
| (29) |
where no is the normal direction at interface intersecting with mesh line point. The value of ni+1,j,k can be evaluated from
| (30) |
The value for ni,j,k can be calculated in the same manner.
In the MIB algorithm, the Cartesian grid is employed and jump conditions are only implemented at points where the interface intersects with grid lines. However, in the MIB Galerkin method, to guarantee the reversibility of the matrix, for the special geometric singularity situations, one needs to enforce jump conditions not only at points where interface intersects with grid lines but also on the interface off grid lines. Therefore, new schemes are needed. For example, two irregular points can be located in the different subdomains and near the node where the fictitious value is evaluated. The coordinates for these two nodes are v1 and v2, and the distance between these two nodes is
| (31) |
The interface point between these two nodes can be interpolated as
| (32) |
| (33) |
| (34) |
and the normal is
| (35) |
In the MIB Galerkin method [73, 72], the mesh is based on the Cartesian grid, while the definition of irregular points is slightly different from that of the traditional definition in the MIB collocation method [83, 84, 76, 77, 29, 80]. Basically, the irregular points do not necessarily come in pairs. It can be seen that the MIB Galerkin method is a Galerkin implementation of the MIB ideas.
2.3.2 Solution of the Poisson-Boltzmann equation
In the MIB method, the Cartesian grid is employed. In its numerical schemes, the interface jump conditions are employed only at the intersecting points between the interface and the mesh lines. If the interface is analytically given, for instance, a sphere with certain radius, the coordinates of intersecting points can be easily determined when the mesh size is specified. However, for volumetric data from EMDataBank, an interpolation procedure is required. A detailed description is given below.
The MIB method has been developed to solve the elliptic interface problems with geometric singularities [83, 84, 76, 77, 29, 80]. It delivers the second order accuracy in solving the PB equation with complex protein interfaces, possible geometric singularities and charge singularities. The essential ideas of the MIB method are the following: The standard finite difference schemes are used on the simple Cartesian grids; the fictitious values are employed near the interface as a smooth extension of the non-smooth functions; interface jump conditions are incorporated into the calculation of the fictitious values; and to construct high-order schemes, the lowest order jump conditions are used repeatedly. For the PB equation, one more challenge is the charge singularities, which represent the partial charges of protein atoms assigned by the CHARMM or AMBER force field. In the PB equation, partial charges are represented by Dirac delta functions in the source term. Through the use of the Green’s function formulation, the charge singularities are transformed into interface flux jump conditions, which are integrated into the geometric singularities framework [29].
When the Laplace-Beltrami equation is coupled with the PB equation, they should be solved iteratively until self-consistency is reached [11, 12]. Two approaches have been employed. One approach is a simple relaxation algorithm: the characteristic function S and electrostatic potential ϕ is updated by a linear combination of the previous ones and the new ones. Basically, we start with the initial condition of hypersurface function S0. This value is used in the PB equation to calculate a temporary electrostatic potential ϕ. The calculated ϕ value is then used in the Laplace-Beltrami equation to evaluate the new S. Instead of using this new S as the new input in the PB equation, we use a weighted average as described below,
| (36) |
where Sn+1,new is the one applied to the evaluation of the electrostatic potential ϕn+1,old. Once we have ϕn+1,old, the electrostatic potential is updated with as,
| (37) |
Relaxation coefficients are denoted as α and α′. Again, the updated ϕn+1,new is used in Laplace-Beltrami equation to update the hypersurface function to Sn+2,old.
The other approach is to refresh the electrostatic potential at a lower frequency than that for updating the surface function. Basically, after a number of iterations (in our tests, 10 to 100 steps) of the generalized Laplace Beltrami equation, the electrostatic potential is then updated. By adaptively changing the number of iterations, one can increase the computational efficiency especially when the change in the surface function during each iteration step is very small.
The coupled system of Laplace-Beltrami equation and PB equation is highly nonlinear. To our best knowledge, there is no rigorous mathematical proof of the existence and uniqueness of the solution. In order to validate our model and algorithm, we evaluate the solvation free energy and compare it with the experimental results [11, 12]. We also check the volume and area of the protein structure calculated from the model during the iteration, and ensure that the convergence to the steady state is observed [12, 68]. In our algorithm, the solvation free energy is often used as an indication of the steady state. Its value can be obtained from minimizing the nonpolar part, polar part and homogeneous energy part as follows
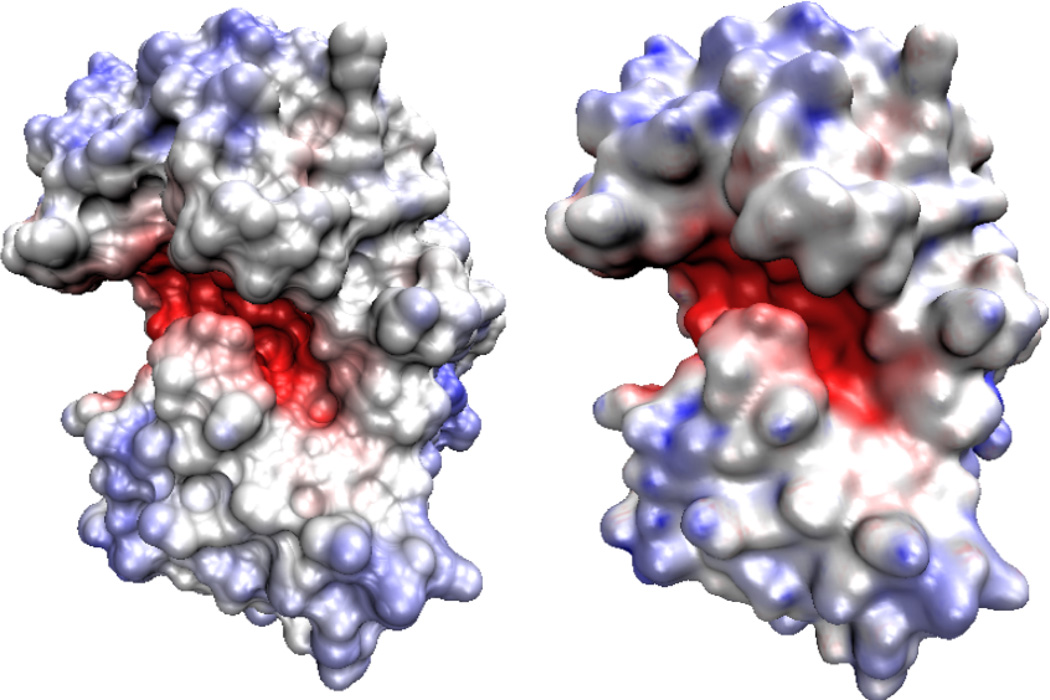
where the nonpolar part is from Eq. (76), and ϕ0(ri) is the electrostatic potential for the homogeneous environment condition at ith atomic position. Figure 3 gives a comparison of electrostatic surface potentials on the molecular surface and the surface obtained from a generalized Laplace-Beltrami flow.
Figure 3.
Comparison of electrostatic potential distributions on a molecular surface (Left) and a surface generated from a generalized Laplace Beltrami equation (Right) for protein 1PPL.
2.4 Computational aspects of geometric features
We have introduced the procedure building the characteristic function representing the surface based on PDB data. For EMDB data, the surface is extracted from the volumetric data after noise reduction. Therefore, the protein surfaces from these two data banks are all in the Cartesian representation. To evaluate the surface properties, Cartesian representation based algorithms are needed. In this section, the computational methods for the calculating basic geometric features are presented and their potential applications are discussed.
2.4.1 Surface area and volume calculation
Based on PDB data and volumetric data from EMDB, the biomolecular surface can be represented by using characteristic functions in two ways: one is the sharp interface by extracting certain iso-values; and the other is the smeared interface that varies in a certain iso-value range. The smeared interface (smooth surface function) is more physical as the radius of the atom is indeed obtained by the probability measure of the electron cloud around the atomic nucleus. Mathematically, the sharp interface is simpler and straightforward.
In the Cartesian representation, the area of a sharp surface can be evaluated as [28, 12]
| (38) |
where R is the set of intersection points located inside the protein domain. Here no = (no, x, no, y, no, z) are the normal for the intersection point. As the surface information is in the Cartesian representation, interpolation is used to evaluate the interface coordinates and norms, see Section 2.3.1 for details.
In a smeared surface representation, the mean surface area and the related coarea formula are defined in Eq. (69)
| (39) |
where the surface integration is converted to a volume integration, which is easier to evaluate in the Cartesian representation.
We can obtain a similar expression for the volume calculation. When the protein surface is defined as a sharp interface, a simple summation is used [12],
| (40) |
where χ̃(i, j, k) is a characteristic function with value 1 inside the protein domain and value 0 for the other. For a smooth surface function, the volume is computed as
| (41) |
where S ∈ [0, 1] is the surface characteristic function.
The scheme for computing sharp surface area in the Cartesian representation is tested with an analytical example. We use a sphere with the analytical expression of x2 + y2 + z2 = 4 in the domain [−5, 5] × [−5, 5] × [−5, 5]. The second order central finite difference scheme is used in our computation. The error is defined as the absolute value of the difference between the analytical surface area and the calculated surface area. The result is presented in Table 2. It is seen that second order accuracy is attained.
Table 2.
Test of the convergence of the proposed method for the surface area of a sharp interface in the Cartesian representation.
| Nx × Ny | Error | Order |
|---|---|---|
| 21× 21 | 3.391 | |
| 41× 41 | 9.390e-1 | 1.85 |
| 81× 81 | 2.026e-1 | 2.21 |
| 161× 161 | 5.498e-2 | 1.88 |
2.4.2 Curvature evaluation
The evaluation of curvature properties from iso-surface embedded volumetric data has been thoroughly studied in geometric modeling. There are a variety of elegant methods in the literature. Essentially, the first and second fundamental forms in the differential geometry are involved in the definition and evaluation of the curvatures. We give a brief introduction of the mathematical background [56, 7].
The surface of interest can be extracted from a level set with iso-value S0, i.e., S(x, y, z) = S0. We assume S to be non-degenerate, i.e., the norm of its gradient is non-zero when it is equal to S0. Without loss of generality, we further assume that its projection onto z is non-zero. According to the implicit function theorem, locally, there exists a function z = f(x, y), which parameterize the surface as S(x, y) = (x, y, f(x, y)). One has the relation S(x, y, f(x, y)) = S0. The differentiation with respect to x and y produces two more equations
| (42) |
| (43) |
Thus fx(x, y) and fy(x, y) can be expressed as:
| (44) |
| (45) |
We define E(x, y, z), F(x, y, z), G(x, y, z), L(x, y, z), M(x, y, z) and N(x, y, z) below to be the coefficients in the first and second fundamental forms. For simplicity, we omit parameter parts. Their values for surface S = (x, y, f) can be given as
| (46) |
| (47) |
| (48) |
| (49) |
| (50) |
| (51) |
where and the normal direction . As the Gaussian curvature can be represented as the ratio of the determinants of the second and first fundamental forms, it can be given by
| (52) |
The mean curvature is the average second derivative with respect to the normal direction,
| (53) |
An alternative algorithm for the curvature extraction from volumetric data is the Hessian matrix method [34]. For volumetric data S(x, y, z), we define the surface gradient g and surface norm n.
| (54) |
| (55) |
The Hessian matrix, H, is given by
| (56) |
The two principal curvatures can be evaluated by the following procedure.
Calculate matrix P = I − nnT, here I is the identity matrix and T denotes the transpose;
- Evaluate matrix ,
(57) - Calculate the trace t and Frobenius norm f of matrix G;
(58) (59) (60) (61)
When the two principal curvatures are available, the Gaussian curvature K and mean curvature H can be easily calculated,
| (62) |
| (63) |
Essentially, the Hessian matrix method generates the same results as the above algorithm derived from the first and second fundamental form.
Numerical test for analytical cases
We use the second order central difference scheme to do the discretization. Two analytical examples are considered. We denote L∞ and L2 the L∞ error and L2 error.
Case 1. We set the domain as [−10, 10] × [−10, 10] × [−10, 10], and define a surface as
| (64) |
Basically, the volumetric data f(x, y, z) are defined as f(x, y, z) = z − Z(x, y). Therefore, the analytical surface can be extracted by setting f(x, y, z) = 0. The analytical expressions for Gaussian curvature and mean curvature can be calculated,
| (65) |
| (66) |
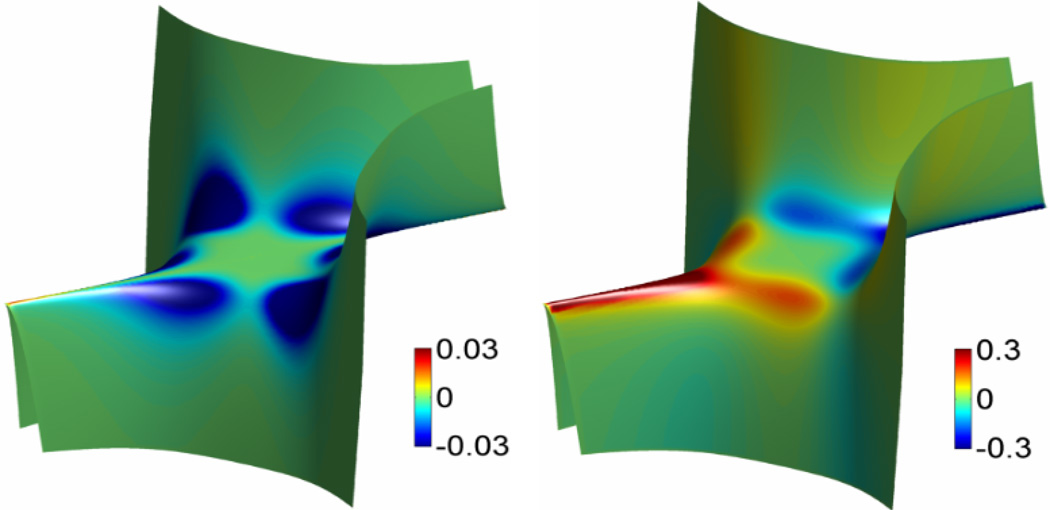
The numerical results are demonstrated in Fig. 4. Tables 3 and 4 give the error and associated convergence order. As we use the second order finite difference scheme to evaluate the derivatives, the second order accuracy is obtained. We also tested the Hessian matrix method, it generates the same results.
Figure 4.
Computational results of Gaussian curvature and mean curvature for test Case 1.
Table 3.
Numerical errors and convergence orders for calculating Gaussian curvature (Case 1).
| nx × ny | L∞ | Order | L2 | Order |
|---|---|---|---|---|
| 21 × 21 | 1.483e-1 | 1.543e-2 | ||
| 41 × 41 | 7.049e-2 | 1.07 | 4.280e-3 | 1.85 |
| 81 × 81 | 2.028e-2 | 1.80 | 8.494e-4 | 2.33 |
| 161 × 161 | 5.348e-3 | 1.92 | 1.816e-4 | 2.23 |
Table 4.
Numerical errors and convergence orders for calculating mean curvature (Case 1).
| nx × ny | L∞ | Order | L2 | Order |
|---|---|---|---|---|
| 21 × 21 | 4.498e-1 | 3.735e-2 | ||
| 41 × 41 | 4.057e-2 | 3.47 | 2.667e-3 | 3.81 |
| 81 × 81 | 2.231e-3 | 4.18 | 5.262e-4 | 2.34 |
| 161 × 161 | 6.893e-4 | 1.69 | 1.343e-4 | 1.97 |
Case 2. In this case the domain is set as [−10, 10] × [−10, 10] × [−10, 10], and a surface is defined as
| (67) |
The volumetric data f(x, y, z) are defined as f(x, y, z) = z − Z(x, y). Therefore, the analytical surface can be extracted by setting f(x, y, z) = 0. We can calculate the analytical solution for the Gaussian curvature and the mean curvature using Eqs. 65 and 66. Fig. 5 demonstrates the numerical results. The error and associated convergence order are listed in Tables 5 and 6. The Hessian matrix method gives the same results and both methods achieve the second order accuracy.
Figure 5.
Computational results of Gaussian curvature and mean curvature for test Case 2.
Table 5.
Numerical errors and convergence orders for Gaussian curvature (Case 2).
| nx × ny | L∞ | Order | L2 | Order |
|---|---|---|---|---|
| 11 × 11 | 2.682e-2 | 6.295e-3 | ||
| 21 × 21 | 7.268e-3 | 1.88 | 1.420e-3 | 2.15 |
| 41 × 41 | 1.846e-3 | 1.98 | 3.528e-4 | 2.01 |
| 81 × 81 | 4.927e-4 | 1.91 | 8.751e-5 | 2.01 |
Table 6.
Numerical errors and convergence orders for calculating mean curvature (Case 2).
| nx × ny | L∞ | Order | L2 | Order |
|---|---|---|---|---|
| 11 × 11 | 4.451e-2 | 1.009e-2 | ||
| 21 × 21 | 1.146e-2 | 1.96 | 2.415e-3 | 2.06 |
| 41 × 41 | 2.923e-3 | 1.97 | 5.942e-4 | 2.02 |
| 81 × 81 | 7.604e-4 | 1.94 | 1.470e-4 | 2.02 |
Numerical test for protein data
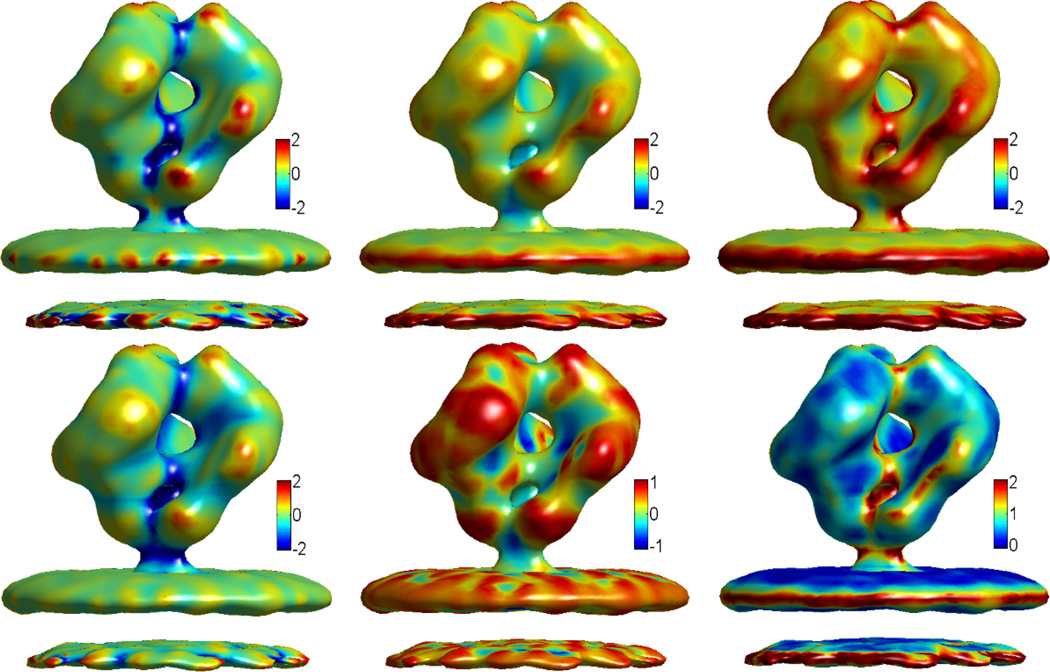
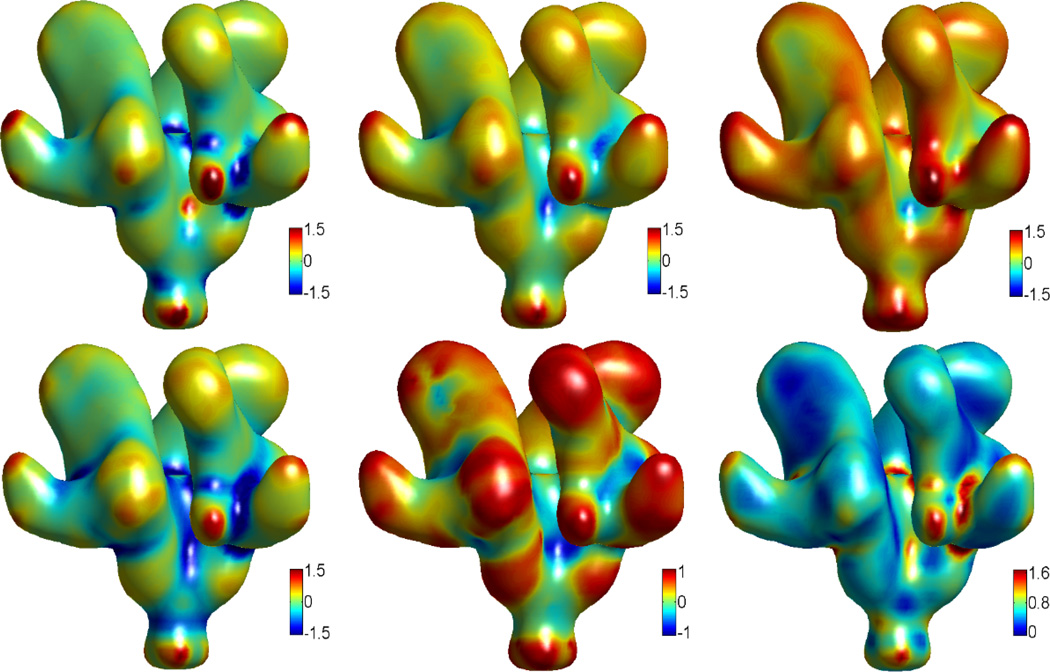
Having validated the two methods for curvature evaluation, we apply them to calculation of the structural features of proteins. Three protein structures are considered, two are from EMDB, i.e., EMD5273 and EMD5020, and the other one is from PDB with ID:1PPL. Figures 6, 7 and 8 demonstrate our results. All the protein surfaces generated in this section are extracted with the isovalue C=0.5. The data size for 1PPL is 146 × 117 × 97. EMD5273 and EMD5020 have the same data size of 100 × 100 × 100. As curvature evaluation algorithms involve only simple interpolation, the computation cost is very small. On a PC with Pentium 4 CPU 3.60GHz and 1.00 GB RAM, the computation times are about 4.2, 2.1 and 2.2 second for proteins EMD5273, EMD5020 and 1PPL, respectively.
Figure 6.
Curvature analysis of Protein 1PPL. From top left to bottom right: Gaussian curvature, mean curvature, maximum curvature, minimum curvature, shape index, and curvedness.
Figure 7.
EMD5273 curvature properties. From top left to bottom right: Gaussian curvature, mean curvature, maximum curvature, minimum curvature, shape index, and curvedness.
Figure 8.
EMD5020 curvature properties. From top left to bottom right: Gaussian curvature, mean curvature, maximum curvature, minimum curvature, shape index, and curvedness.
These curvatures describe the concave and convex properties of the protein surface, see Appendix C. It is well known that in drug design and protein-protein interaction, the surface geometry is of significant importance [16]. Usually, the geometry of the drug should match to a concave region of the protein just like the key and lock relation. The same applies when two proteins interact with each other, or when a substrate binds to the active site of an enzyme. The quantitative measurement of curvatures has a great potential for further modeling and analysis of the geometric impact on biomolecular interactions.
Gaussian curvature characterizes the topological property of a surface. When integrated over the surface, Gaussian curvature gives rise to the information of the genus number, which is, loosely speaking, the number of “holes” in the biomolecule. The genus number can be applied to systems like ion channel proteins, whose open state and close state have different genus numbers. From the minimum curvature and shape index, we can obtain a rather clear picture of concave regions. Actually, the concaveness can be quantitatively characterized by the values of minimum curvature and shape index. Similarly, the convexity can be parameterized by the maximum curvature and shape index. The curvedness provides the information about the amplitude of the curvature, e.g., a large value usually indicates a sharp edge and/or corner.
The traditional MS suffers from geometric singularities, for which curvatures are undefined. Computationally, near geometric singularities, curvatures tend to have much dramatic local variations and the accuracy of computational results is reduced. In our MMS and surface generated from geometric and potential driven geometric flows, the geometric singularities are removed, and the surface is smooth with less local curvature uctuations. Further, a multiresolution model is proposed in our recent work [22]. Obtained with an adjustable parameter, a family of multiresolution surfaces can be designed to reduce local curvature variations. Consequently, concave regions and convex regions reflect the molecular morphology, instead of local atomic characteristics. In differential geometry based multiscale multiresolution models, the electrostatic potential is also coupled with the molecular surface generation. With polar and nonpolar areas defined by electrostatic potential, and concave and convex regions evaluated by the above curvature schemes, our approaches have a great potential for the prediction of protein active sites and/or binding sites.
2.5 Polarized curvature and binding site prediction
Based on the above curvature analysis and electrostatic characterization, it is clear that a potential protein binding site should be both electrostatically favorable and geometrically favorable. To combine these compatibilities, we propose polarized curvatures as the products of electrostatic potentials and curvatures. Specifically, the maximal curvature κ1 and minimal curvature κ2 are employed to construct their products with positive electrostatic surface potential Φ+ and negative electrostatic surface potential Φ−. Large amplitudes of these products indicate four different potential binding sites as summarized in Table 7. For example, a large amplitude of Φ+ × κ1 on a certain region of a protein surface indicates a potential binding site for a negatively charged protein or virus, while a large amplitude of Φ+ × κ2 indicates a potential binding site for a negatively charged small ligand. Similar behavior can be stated for the products of Φ− × κ2 and Φ− × κ1.
Table 7.
Polarized curvatures as binding indicators of protein surfaces. Maximal curvature (κ1), minimal curvature (κ2), positive electrostatic surface potential (Φ+) and negative electrostatic surface potential (Φ−) are combined to indicate potential binding sites.
| κ1 > 0 | κ2 < 0 | |
|---|---|---|
| Φ+ > 0 | site for negatively charged protein | site for negatively charged small ligand |
| Φ− < 0 | site for positively charged protein | site for positively charged small ligand |
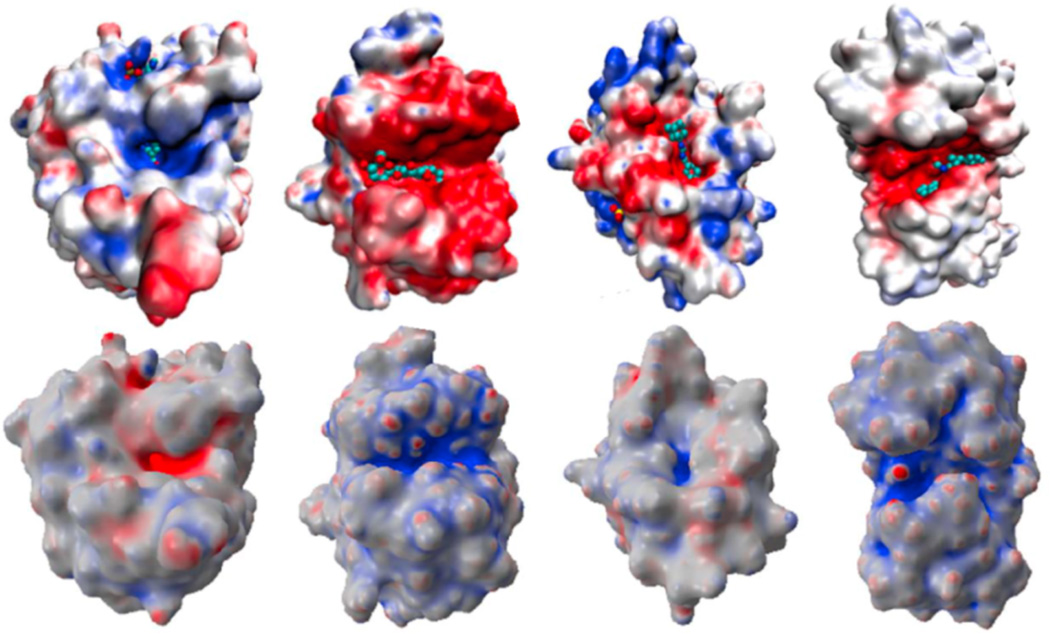
Figure 9 demonstrates the effectiveness of our proposed polarized curvature analysis. The top row illustrates the electrostatic surface maps and (small ligand) binding sites of four proteins. The bottom row displays the predictions of polarized curvatures (Φ × κ2). In these cases, the minimal curvature (κ2) is used to predict the concave regions of protein surfaces for potential binding sites of small ligands. The protein on the left chart is positively charged at its binding site and the rest of proteins are all negatively charged at their binding sites. The polarized curvatures shown in the bottom row give correct predictions for all binding sites.
Figure 9.
Polarized curvature based binding site prediction for four proteins (Left to right:1ADS, 1BYH, 1EJN, 2WEB). Top row: Protein-ligand complexes displayed with electrostatic surface potential; Bottom row: Polarized curvature maps (Φ × κ2) indicating the binding sites.
In our future work, we will combine the polarized curvature analysis and the binding affinity analysis readily available in our multiscale solvation model [12] for more accurate prediction of protein-ligand binding, protein-DNA specificity and protein-protein interactions. We will make this approach automatic and robust.
3 Conclusion
Geometric modeling has widespread applications in the visualization, analysis and characterization of the macromolecules. For proteins, their structural features are intrinsically associated with their functions and molecular mechanisms. The exploration of the geometric features of a protein molecular surface enhances our understanding of molecular morphology and molecular mechanism, and allows significant applications to drug design and protein-protein interaction. This is particularly true when the geometric modeling is associated with the electrostatic analysis. The present work offers expository investigation and comprehensive summary of tools, algorithms and methodologies for geometric modeling of macromolecules.
Our study is based on two major biomolecular structure sources collected from experiments: the Protein Data bank (PDB) and the Electron Microscopy Data Bank (EMDB). The PDB contains information about structures obtained mainly by using X-ray crystallography and NMR spectroscopy at the atomic level resolution. Whereas, EMDB provides information mainly about multiproteins, organelles, viruses, and subcellular complexes obtained mostly from cryo-Electron Microscopy (cryo-EM) at the molecular level resolution. In the present paper, based on data from the PDB and the EMDB, related geometric modeling methods, software packages and visualization tools are provided and discussed in great detail.
The protein data from the PDB are in atomic resolution, so that crucial information like atom positions, van der Walls radius and partial charges can be obtained either directly or indirectly. Different definitions of the macromolecular surface have been proposed and constructed based on experimental data. However, the resulting surfaces usually suffer from geometric singularities (i.e., tips, cusps and self-intersecting facets) and violate the energy minimization principle, due to the fact that they are just ad hoc divisions of the protein and its surroundings. The minimal molecular surface (MMS) is proposed as a surface that minimizes the surface free energy. This variational formulation based biomolecular surface fulfills the principle of energy minimization, while producing a smooth surface through Laplace-Beltrami flows obtained from the Euler-Lagrange equation. As the solvation process is of fundamental importance to biomolecular systems, it should be considered in the surface modeling. By adding the solvation energy, which is composed of nonpolar and polar parts, into the total free energy functional and by using the Euler-Lagrange equation, the geometric and potential driven Laplace-Beltrami flow is formulated. Essentially, the external potential term incorporates various solvation effects, except the surface tension. Further, in different types of biomolecular systems, other related effects, such as chemical potential and fluid flow, are accounted in external potential terms as well. In this paper, we explore all the surface generation related geometric aspects, including surface modeling, computational methods, algorithms and techniques.
The data from the EMDB, in contrast, is in a volumetric format and usually without detailed atomic information. These data often have a poor signal to noise ratio (SNR) and a noise reduction process is required. High order geometric PDEs can suppress the high-frequency components efficiently. In this paper, for the first time, the high order geometric PDEs are applied to the EMD noise removal. With the suitable PDE order and iteration time, the noise is drastically reduced, while image features are preserved.
Curvature properties indicate the concave or convex regions, which are likely to be the potential binding sites or active sites. Within the framework of the Cartesian representation, we tested second order computational algorithms for curvature evaluation. Six different curvature descriptors, including Gaussian curvature, mean curvature, maximum curvature, minimum curvature, shape index, and curvedness, are employed for the first time to the two types of protein surfaces, variational surfaces generated from PDB data and surfaces extracted from denoised EMDB data. An interesting feature of our work is that the curvature analysis for surfaces generated from our variational model is paired with the electrostatic analysis resulted from the same model. Such a feature enables us to introduce polarized curvatures for the screen of protein-ligand binding and protein-protein interaction sites. We demonstrate that newly proposed polarized curvatures give rise to a good prediction of protein-ligand binding sites.
Acknowledgments
This work was supported in part by NSF grants IIS-0953096, IIS-1302285 and DMS-1160352, and NIH grant R01GM-090208. GWW acknowledges the Mathematical Biosciences Institute for hosting valuable workshops.
Appendices
A Mathematical models for surface generation
In this appendix, the theoretical models for surface generation are presented based on two experimental data sources, the PDB and the EMDB.
A.1 Minimal molecular surface
The minimal molecular surface (MMS) was introduced to construct surfaces free of geometric singularities via the variational principle [5, 7]. Although the original derivation was pursued in the Lagrangian formulation, we offer an Eulerian description in the present work. In this approach, a hypersurface S is defined to represent the biomolecular surface. Basically, we assign each point with coordinate (x, y, z) a value S(x, y, z), which represents the domain information. It can be viewed as a characteristic function of the solute domain. It is also known as a surface function. In Fig. 10, we illustrate this surface function by its 1D projection. By using geometric measure theory, the surface energy functional can be expressed as [64]
| (68) |
where γ is the surface tension. As it is convenient for us to set up the total free functional as a 3D integral in ℝ3, we make use of the concept of a mean surface area [64, 13] and the coarea formula [21] on a smooth surface
| (69) |
Here hypersurface function S is distributed between 0 and 1, S−1 (c) represents the inverse function of S and Ω is defined as the whole domain. The variation of Eq. (68) with respect to S leads to the vanishing of surface-tension weighted mean curvature . The energy minimization of Eq. (68) can be realized by the introduction of an artificial time to obtain a generalized Laplace-Beltrami equation
| (70) |
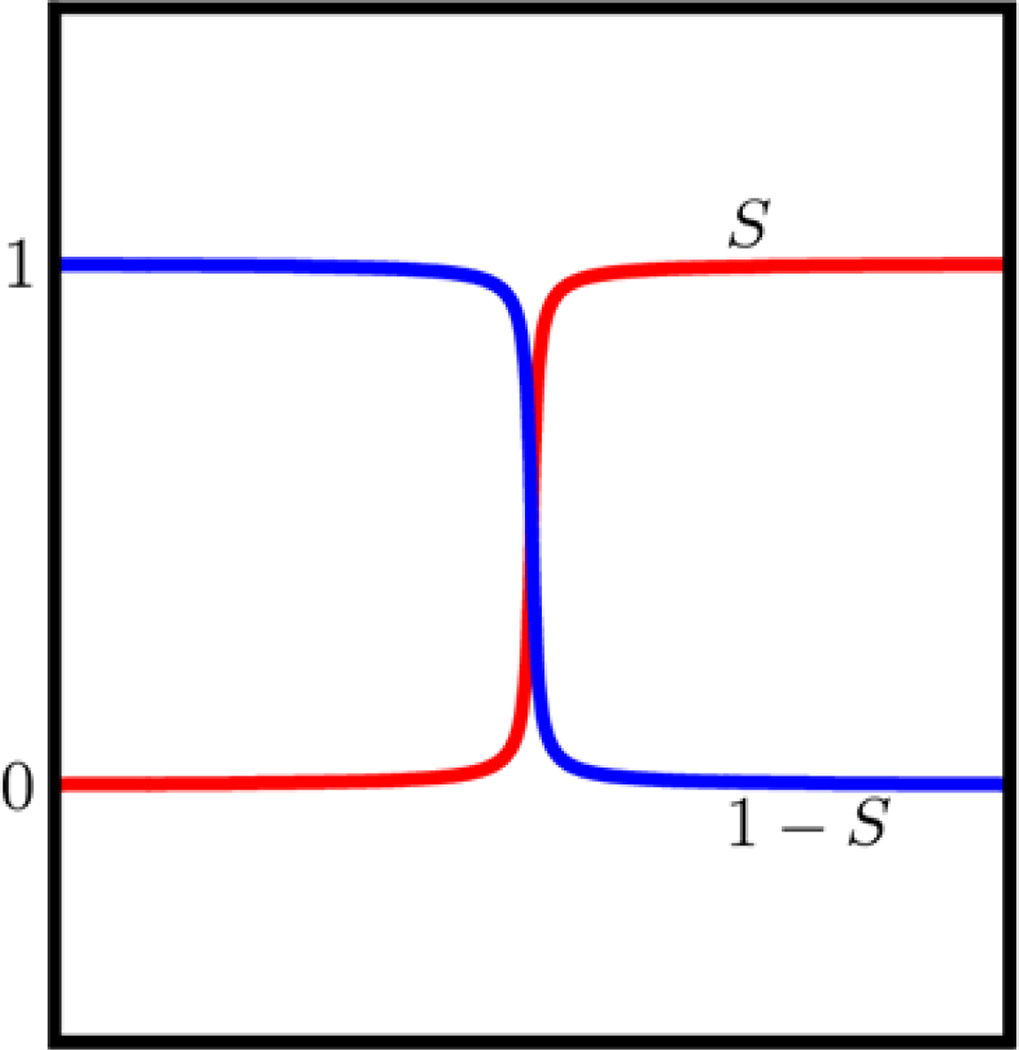
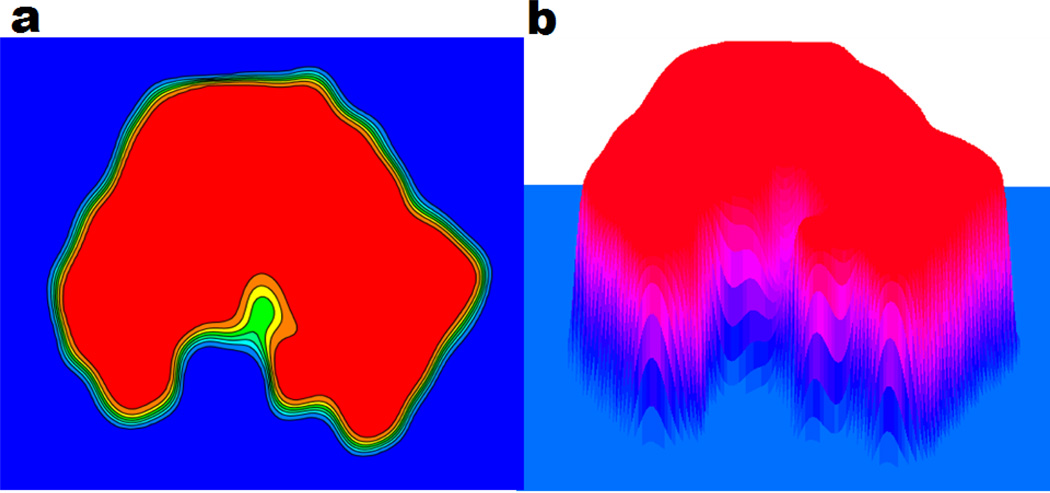
The final MMS, which is free of geometric singularity, is obtained by extracting an iso-surface from the steady state hypersurface function. During each iteration, we keep the value in the van der Waals surface enclosed domain unchanged. The computational details are described in Section 2. A cross section of the characteristic function S for protein 1PPL is demonstrated in Fig. 11. It can be seen that all contour lines between 0 and 1 can be chosen to extract isosurfaces. The MMS is often chosen to be S = 0.5, which has been found to be near optimal.
Figure 10.
Characteristic functions S and 1 − S projected in 1D.
Figure 11.
A contour plot (a) and a mesh plot (b) of a cross section of the characteristic function S for protein 1PPL. The blue color and red color represent value 0 and 1, respectively in (a). All contour lines between 0 and 1 can be chosen to extract isosurfaces.
A.2 Variational multiscale models
To account for the local variations near the biomolecular surfaces due to interactions between solvent and solute molecules, solvation models are needed. It is well known that water contributes to more than half of the human cell mass. Essentially all the biological processes in a human cell occurred in aqueous environment. Therefore, solvation process is of tremendous importance for biomolecular systems. Phenomenologically, solvation processes can be described as the creation of a cavity in the solvent, the hydrogen bond breaking and formation at the solvent-solute interface, the surface reconstruction of the solute molecule, and entropy effect due to the solvent-solute mixing. Solute-solvent interactions are usually described by solvation energy, which can be decomposed into polar and nonpolar contributions. Due to the extensive sampling of the explicit methods, implicit approaches are commonly employed for solvation analysis and computation. Among them, the scaled particle theory (SPT) describes the surface free energy and the mechanical work of creating a cavity of the solute size in the solvent [57, 44]. To account for the solvent-solute dispersive interaction, an improved nonpolar solvation free energy functional is defined as
| (71) |
where p is the hydrodynamic pressure, and U denotes the solvent-solute non-electrostatic interactions, such as the van der Waals interaction. The final integration is over the whole solvent domain Ωs. We define S as the characteristic function of the solute domain as in Section A.1. Keep in mind that the biomolecular surface can be viewed from two aspects, that is, it can be represented as a sharp interface by extracting certain iso-values from the hypersurface function, or it can be treated as a smooth interface between the solvent and the solute. The volume term can be easily defined as
| (72) |
where Ωm is the solute domain. On the other hand, 1 − S can be viewed as the characteristic function of the solvent domain. Therefore, the last term in Eq. (71) can be rewritten as
| (73) |
When there are multiple species in the aqueous environment, under the assumption of pairwise solvent-solute interactions, U can be expressed as a summation over all the interactions of the solvent species with each solute atom near the interface [68]
| (74) |
| (75) |
where ρα (r) is the density of αth solvent component, and Uα is the interaction potential of αth solvent species, which can be further divided into the summation of Uαj, namely, the interaction potentials between the jth atom of the solute and the αth component of the solvent, and the summation of Uαβ, i.e., the interaction potentials between the αth component of the solvent and the βth component of the solvent.
Therefore, the total nonpolar solvation free energy can be rewritten as
| (76) |
The Poisson-Boltzmann theory is of great significance in the analysis of polar solvation free energy. When there are multiple charge species in the aqueous surrounding, their concentration profiles can be represented by Boltzmann distributions [81]. For example, density of the αth solvent component can be expressed as an integral equation of density functional theory (DFT) type
| (77) |
where kB is the Boltzmann constant, T is the temperature, ρα0 denotes the reference bulk concentration of the αth charged species, and qα denotes the valence of the αth charged species and Φ is the electrostatic potential. The term μα0 is a relative reference chemical potential. Physically, for different charge species, i.e., ρα ≠ ρβ, given that ρα0 = ρβ0, μα0 describes the difference in their equilibrium concentrations. The Boltzmann distribution is an efficient way to avoid more expensive description of the solvent. Note that Eq. (77) is a statement that the chemical potential vanishes at equilibrium [68].
Using the Boltzmann distribution, the polar solvation free energy can be expressed as [64, 68]
| (78) |
where εs and εm are the dielectric constants of the solvent and solute, respectively, and ρm represents the fixed charge density of the solute. It is important to realize that the polar/nonpolar decomposition is by no means unique but rather arbitrary [11]. The Boltzmann distribution in Eq. (77) has the term Uα, and takes into account the energy of this solvent-solute non-electrostatic interactions. One should not double count these interactions when summarizing all the energy contributions. Thus, the total free energy functional for the solvation system can be described as
| (79) |
The total solvation free energy in Eq. (79) is expressed as a functional of the surface function S and the electrostatic potential Φ. By applying the variational principle to minimize the total solvation free energy with respect to Φ and S, we obtain two equations
| (80) |
and
| (81) |
From Eq. (80), the generalized Poisson-Boltzmann equation is obtained
| (82) |
where ε(S) = (1 − S)εs + Sεm is the generalized permittivity function. Based on our earlier related work [7, 64, 11, 12], we introduce an artificial time to Eq. (81) and obtain a generalized Laplace-Beltrami equation
| (83) |
where the potential driven term V1 is given by
| (84) |
The generalized Laplace-Beltrami equation (83) describes the surface formation and evolution under the geometric and potential driven flow. The potential flow part consists of both the polar and nonpolar energy effects, and the solvation process is naturally involved in the surface generation. The final solvent-solute interface can be extracted from the steady state, and will be free from geometric singularities.
Noted that by appropriate selections of the evolution time, one can generate a multiresolution representation of biomolecular surfaces. Such a multiresolution representation can be tuned to emphasize desirable features, namely, the binding sites of different scales, on a protein surface.
B High order geometric PDEs for the treatment of noisy EMDB data
The cryo-EM data in the EMDB suffer from the poor signal-to-noise ratio (SNR). Noise reduction is an indispensable process for the visualization, analysis and modeling of the cryo-EM data. Many elegant methods and techniques have been proposed or introduced, including wavelet transform techniques [58], bilateral filtering [59, 33, 42], and iterative median filtering [60], nonlinear anisotropic diffusion equations [27, 26] and Beltrami flow [24]. As high order geometric PDEs can suppress high-frequency components more efficiently [63], here we apply them to edge-preserving noise reduction of the EMD.
The arbitrarily high order nonlinear PDEs can be constructed using Fick’s law [63]. Basically, we can design a nonlinear hyperflux,
| (85) |
where r ∈ ℝn, , u(r, t) can be viewed as the surface functions, and dq(u(r, t), |∇u(r, t)|, t) are edge sensitive diffusion coefficients. The high order diffusion PDEs can be expressed as
| (86) |
where e(u(r, t), |∇u(r, t)|, t) is a nonlinear operator. It can be viewed as an external potential term and can be used to influence the behavior of the hyperflux. We can obtain the Perona-Malik equation by setting q = 0. The original data are used as an initial condition with suitable boundary conditions. The diffusion coefficients can be designed to be inhomogeneous or anisotropic, so as to remove the noise more efficiently while preserving the features. The Gaussian distribution is a widely used choice,
| (87) |
where dq0 reflects the noise amplitude, σ0 and σ1 are variance of u and ∇u in the neighborhood of a certain position r,
| (88) |
The notation stands for the average of Y (r) in the neighborhood around position r. High order nonlinear diffusion PDEs have been applied to many areas [63, 37, 31, 30].
Another option is the high order geometric PDEs [4],
| (89) |
where g(|∇∇2qS|) = 1 + |∇∇2qS|2 is the generalized Gram determinant. When q = 0, we have the potential driven mean curvature flow [4]
| (90) |
This equation is also related to the geometric flow equations derived from solvation analysis in Section A.2.
Computationally, due to the stiffness of high order nonlinear PDEs, the construction of suitable algorithms is an important issue. The common approach is alternating direction implicit (ADI) schemes [70, 4]. Through the splitting of the spatial dimensions, they managed to improve the efficiency and stability.
C Geometric features
Geometric features include surface area, volume, Gaussian curvature, mean curvature, shape index, and curvedness. The evaluation of surface area and surface enclosed volume is quite straightforward in the Lagrangian representation. However, in the Eulerian representation, their accurate evaluation is non-trivial. The details of the evaluation in the Eulerian representation have been described in Section 2.4.
The curvatures, on the contrary, involve more intrinsic or extrinsic information than area or volume. When a 2D surface is embedded in the 3D space, curvatures at each point measure how fast the normal direction changes from this point to nearby points. A normal plane at a certain point is spanned by the normal vector and a chosen tangent vector. This plane intersects with the surface along a planar curve, which has a unique curvature at the given point. Therefore, for this point, different curvatures can be obtained along different tangent directions. Among them, two principal curvatures, the maximum curvature and the minimum curvature are the maximum and the minimum values of these curvatures, respectively. The tangent directions related to principal curvatures are called principal directions. Note that these two tangent directions are always orthogonal to each other. From the point of view of eigenvalue decomposition of the shape operator matrix (Jacobian of the normal field), principal curvatures are just eigenvalues, and the principal directions are associated eigenvectors. The sign of the curvature can be defined as follows: bending towards the normal direction indicates negative curvature and bending away form the normal direction implies a positive curvature.
Gaussian curvature and mean curvature are popular shape descriptors as they are invariants under the rotation of the tangent plane. The Gaussian curvature is defined as the product of the two principal curvatures κ1κ2, while the mean curvature is defined as the average of the two principal curvatures . Based on the signs of the Gaussian curvature and mean curvature, the local shape near a certain point can be classified into eight different surface types: pit, valley, saddle valley, flat, minimal surface, saddle ridge, ridge and peak. Table 8 demonstrates these different situations and summarizes the details of the definition. There is an intuitive way to understand this special classification — we locally approximate a surface in a specific coordinate system aligned to the principal directions and the normal direction (Darboux frame) as
where the values of two principal curvatures κ1 and κ2 are chosen from the representative set in the sequence of ascending values. For instance, for the surface type of pit, their values are both −1.
Table 8.
The figure gives surface types classified according to Gaussian curvature (K) and mean curvature (H). From top left to bottom right: pit, valley, saddle valley, flat, minimal surface, saddle ridge, ridge and peak, respectively. The table lists surface types based on signs of Gaussian curvature (K) and mean curvature (H).
 | |||
|---|---|---|---|
| K > 0 | K = 0 | K < 0 | |
| H > 0 | peak | ridge | saddle ridge |
| H = 0 | none | flat | minimal surface |
| H < 0 | pit | valley | saddle valley |
Koenderink and van Doorn developed a single-value, angular measure to describe a local surface type instead of the principal curvatures [35]. It is called the shape index and defined as:
The shape index describes the relation between the principal curvatures and gives an intuitive representation of the local surface shape. An important surface parameter complementary to the shape index is called curvedness, defined as:
These two surface indication parameters are also used in image processing, computer-aided design, and experimental data segmentation. In the present work, we introduce them to the biomolecular surface analysis.
D Matlab code for MRC data extraction
A Matlab code is given for extracting the voxel value information from the MRC (or CCP4) data. The output data are stored in “.dat” format for further use. The example here is for “EMD1048” with the input data “emd_.map” and output data “EMD1048.dat”. A detail specification of the MRC file format can be found on the website http://ami.scripps.edu/software/mrctools/mrc_specification.php.
function a= readMRCfile(fname)
% readMRCfile readMRCfile (fname)
[fid,message]=fopen(’emd_1048.map’,’r’);
if fid == −1
error(’can’’t open file’);
a= −1;
return;
end
nx=fread(fid,1,’long’);
ny=fread(fid,1,’long’);
nz=fread(fid,1,’long’);
type= fread(fid,1,’long’);
fprintf(1,’nx= %d ny= %d nz= %d type= %d’, nx, ny,nz,type)
% Seek to start of data
status=fseek(fid,1024,−1);
% Shorts
if type== 1
a=fread(fid,nx*ny*nz,’int16’);
end
%floats
if type == 2
a=fread(fid,nx*ny*nz,’float32’);
end
fclose( fid);
a= reshape(a, [nx ny nz]);
if nz == 1
a= reshape(a, [nx ny]);
end
bb=reshape(a,[nx*ny*nz,1]);
save(’EMD1048.dat’,’bb’, ’−ASCII’);
References
- 1.Baker NA. Biomolecular applications of Poisson-Boltzmann methods. In: Lipkowitz KB, Larter R, Cundari TR, editors. Reviews in Computational Chemistry. volume 21. Hoboken, NJ: John Wiley and Sons; 2005. [Google Scholar]
- 2.Baker NA, Bashford D, Case DA. Implicit solvent electrostatics in biomolecular simulation. In: Leimkuhler B, Chipot C, Elber R, Laaksonen A, Mark A, Schlick T, Schutte C, Skeel R, editors. New Algorithms for Macromolecular Simulation. Springer; 2006. [Google Scholar]
- 3.Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Electrostatics of nanosystems: Application to microtubules and the ribosome. Proceedings of the National Academy of Sciences of the United States of America. 2001;98(18):10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bates PW, Chen Z, Sun YH, Wei GW, Zhao S. Geometric and potential driving formation and evolution of biomolecular surfaces. J. Math. Biol. 2009;59:193–231. doi: 10.1007/s00285-008-0226-7. [DOI] [PubMed] [Google Scholar]
- 5.Bates PW, Wei GW, Zhao S. The minimal molecular surface. arXiv:q-bio/0610038v1, [q-bio.BM] 2006 [Google Scholar]
- 6.Bates PW, Wei GW, Zhao S. Midwest Quantitative Biology Conference. Mackinac Island, MI: Mission Point Resort; 2006. Sep-Oct. The minimal molecular surface. [Google Scholar]
- 7.Bates PW, Wei GW, Zhao S. Minimal molecular surfaces and their applications. Journal of Computational Chemistry. 2008;29(3):380–391. doi: 10.1002/jcc.20796. [DOI] [PubMed] [Google Scholar]
- 8.Bertonati C, Honig B, Alexov E. Poisson-Boltzmann calculations of nonspecific salt effects on protein-protein binding free energy. Biophysical Journal. 2007;92:1891–1899. doi: 10.1529/biophysj.106.092122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bobenko AI, Schröder P. Discrete willmore flow; Symp. on Geometry Processing; 2005. Jul, pp. 101–110. [Google Scholar]
- 10.Chen D, Chen Z, Chen C, Geng WH, Wei GW. MIBPB: A software package for electrostatic analysis. J. Comput. Chem. 2011;32:657–670. doi: 10.1002/jcc.21646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen Z, Baker NA, Wei GW. Differential geometry based solvation models I: Eulerian formulation. J. Comput. Phys. 2010;229:8231–8258. doi: 10.1016/j.jcp.2010.06.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen Z, Baker NA, Wei GW. Differential geometry based solvation models II: Lagrangian formulation. J. Math. Biol. 2011;63:1139–1200. doi: 10.1007/s00285-011-0402-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen Z, Wei GW. Differential geometry based solvation models III: Quantum formulation. J. Chem. Phys. 2011;135(194108) doi: 10.1063/1.3660212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen Z, Zhao S, Chun J, Thomas DG, Baker NA, Bates PB, Wei GW. Variational approach for nonpolar solvation analysis. Journal of Chemical Physics. 2012;137(084101) doi: 10.1063/1.4745084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cheng LT, Dzubiella J, McCammon AJ, Li B. Application of the level-set method to the implicit solvation of nonpolar molecules. Journal of Chemical Physics. 2007;127(8) doi: 10.1063/1.2757169. [DOI] [PubMed] [Google Scholar]
- 16.Cipriano G, Phillips GN, Jr, Gleicher M. Multi-scale surface descriptors. IEEE Transactions on Visualization and Computer Graphics. 2009;15:1201–1208. doi: 10.1109/TVCG.2009.168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Connolly ML. Depth buffer algorithms for molecular modeling. J. Mol. Graphics. 1985;3:19–24. [Google Scholar]
- 18.Corey RB, Pauling L. Molecular models of amino acids, peptides and proteins. Rev. Sci. Instr. 1953;24:621–627. [Google Scholar]
- 19.Droske M, Rumpf M. A level set formulation for willmore flow. Interfaces and Free Boundaries. 2004;6(3):361–378. [Google Scholar]
- 20.Eisenhaber F, Argos P. Improved strategy in analytic surface calculation for molecular systems: Handling of singularities and computational efficiency. J. Comput. Chem. 1993;14:1272–1280. [Google Scholar]
- 21.Federer H. Curvature Measures. Trans. Amer. Math. Soc. 1959;93:418–491. [Google Scholar]
- 22.Feng X, Xia K, Tong Y, Wei G-W. Geometric modeling of subcellular structures, organelles and large multiprotein complexes. International Journal for Numerical Methods in Biomedical Engineering. 2012;28:1198–1223. doi: 10.1002/cnm.2532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Feng X, Xia KL, Chen Z, Tong YY, Wei GW. Multiscale geometric modeling of macromolecules II: Lagrangian representation. Journal of Computational Chemistry. 2013 doi: 10.1002/jcc.23364. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fernandez J. Tomobflow: feature-preserving noise filtering for electron tomography. BMC Bioinformatics. 2009;178:1–10. doi: 10.1186/1471-2105-10-178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fernandez J, Li S, Lucic V. Three-dimensional anisotropic noise reduction with automated parameter tuning: Application to electron cryotomography. Current Topics in Artificial Intelligence. 2007;volume 4788:60–69. [Google Scholar]
- 26.Fernandez S, Li JJ. An improved algorithm for anisotropic nonlinear diffusion for denoising cryo-tomograms. J. Struct. Biol. 2003;144:152–161. doi: 10.1016/j.jsb.2003.09.010. [DOI] [PubMed] [Google Scholar]
- 27.Frangakis AS, Hegerl R. Noise reduction in electron tomographic reconstructions using nonlinear anisotropic diffusion. J. Struct. Biol. 2001;135:239–250. doi: 10.1006/jsbi.2001.4406. [DOI] [PubMed] [Google Scholar]
- 28.Geng W, Wei GW. Multiscale molecular dynamics using the matched interface and boundary method. J Comput. Phys. 2011;230(2):435–457. doi: 10.1016/j.jcp.2010.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Geng W, Yu S, Wei GW. Treatment of charge singularities in implicit solvent models. Journal of Chemical Physics. 2007;127:114106. doi: 10.1063/1.2768064. [DOI] [PubMed] [Google Scholar]
- 30.Gilboa G, Sochen N, Zeevi YY. Forward-and-backward diffusion processes for adaptive image enhancement and denoising. IEEE Transactions on Image Processing. 2002;11(7):689–703. doi: 10.1109/TIP.2002.800883. [DOI] [PubMed] [Google Scholar]
- 31.Gilboa G, Sochen N, Zeevi YY. Image sharpening by flows based on triple well potentials. Journal of Mathematical Imaging and Vision. 2004;20(1–2):121–131. [Google Scholar]
- 32.Gogonea V, Osawa EE. Implementation of solvent effect in molecular mechanics. 1. model development and analytical algorithm for the solvent -accessible surface area. Supramol. Chem. 1994;3:303–317. [Google Scholar]
- 33.Jiang W, Baker ML, Wu Q, Bajaj C, Chiu W. Applications of a bilateral denoising filter in biological electron microscopy. J. Struct. Biol. 2003;144:114–122. doi: 10.1016/j.jsb.2003.09.028. [DOI] [PubMed] [Google Scholar]
- 34.Kindlmann G, Whitaker R, Tasdizen T, Möller T. Curvature-based transfer functions for direct volume rendering: methods and applications. Proc. IEEE Visualization. 2003 [Google Scholar]
- 35.Koenderink JJ, van Doorn AJ. Surface shape and curvature scales. Image and Vision Computing. 1992 Oct.10(8):557–564. [Google Scholar]
- 36.Lee B, Richards FM. The interpretation of protein structures: estimation of static accessibility. J Mol Biol. 1971;55(3):379–400. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
- 37.Lysaker M, Lundervold A, Tai XC. Noise removal using fourth-order partial differential equation with application to medical magnetic resonance images in space and time. IEEE Transactions on Image Processing. 2003;12(12):1579–1590. doi: 10.1109/TIP.2003.819229. [DOI] [PubMed] [Google Scholar]
- 38.Marenich AV, Cramer CJ, Truhlar DG. Perspective on foundations of solvation modeling: The electrostatic contribution to the free energy of solvation. Journal of Chemical Theory and Computation. 2008;4(6):877–887. doi: 10.1021/ct800029c. [DOI] [PubMed] [Google Scholar]
- 39.Mumford D, Shah J. Optimal approximations by piecewise smooth functions and associated variational problems. Communications on Pure and Applied Mathematics. 1989;42(5):577–685. [Google Scholar]
- 40.Osher S, Fedkiw RP. Level set methods: An overview and some recent results. J. Comput. Phys. 2001;169(2):463–502. [Google Scholar]
- 41.Osher S, Sethian J. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations. Journal of computational physics. 1988;79(1):12–49. [Google Scholar]
- 42.Pantelic RS, Rothnagel CY, Huang R, Muller D, Woolford D, Landsberg MJ, McDowall A, Pailthorpe B, Young PR, Banks J, Hankamer B, Ericksson G. The discriminative bilateral filter: An enhanced denoising filter for electron microscopy data. J. Struct. Biol. 2006;155:395–408. doi: 10.1016/j.jsb.2006.03.030. [DOI] [PubMed] [Google Scholar]
- 43.Perona P, Malik J. Scale-space and edge-detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1990;12(7):629–639. [Google Scholar]
- 44.Pierotti RA. A scaled particle theory of aqueous and nonaqeous solutions. Chemical Reviews. 1976;76(6):717–726. [Google Scholar]
- 45.Prabhu NV, Zhu P, Sharp KA. Implementation and testing of stable, fast implicit solvation in molecular dynamics using the smooth-permittivity finite difference Poisson-Boltzmann method. Journal of Computational Chemistry. 2004;25(16):2049–2064. doi: 10.1002/jcc.20138. [DOI] [PubMed] [Google Scholar]
- 46.Richards FM. Areas, volumes, packing, and protein structure. Annual Review of Biophysics and Bioengineering. 1977;6(1):151–176. doi: 10.1146/annurev.bb.06.060177.001055. [DOI] [PubMed] [Google Scholar]
- 47.Rocchia W, Sridharan S, Nicholls A, Alexov E, Chiabrera A, Honig B. Rapid grid-based construction of the molecular surface and the use of induced surface charge to calculate reaction field energies: Applications to the molecular systems and geometric objects. Journal of Computational Chemistry. 2002;23:128–137. doi: 10.1002/jcc.1161. [DOI] [PubMed] [Google Scholar]
- 48.Roux B, Simonson T. Implicit solvent models. Biophysical Chemistry. 1999;78(1–2):1–20. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- 49.Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Proceedings of the eleventh annual international conference of the Center for Nonlinear Studies on Experimental mathematics : computational issues in nonlinear science; Elsevier North-Holland, Inc; Amsterdam, The Netherlands, The Netherlands. 1992. p. 259.p. 268. [Google Scholar]
- 50.Sanner MF, Olson AJ, Spehner JC. Reduced surface: An efficient way to compute molecular surfaces. Biopolymers. 1996;38:305–320. doi: 10.1002/(SICI)1097-0282(199603)38:3%3C305::AID-BIP4%3E3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 51.Sethian JA. Evolution, implementation, and application of level set and fast marching methods for advancing fronts. J. Comput. Phys. 2001;169(2):503–555. [Google Scholar]
- 52.Sharp KA, Honig B. Electrostatic interactions in macromolecules - theory and applications. Annual Review of Biophysics and Biophysical Chemistry. 1990;19:301–332. doi: 10.1146/annurev.bb.19.060190.001505. [DOI] [PubMed] [Google Scholar]
- 53.Simonett G. The willmore flow for near spheres. Differential and Integral Equations. 2001;14:1005–1014. [Google Scholar]
- 54.Simonson T. Macromolecular electrostatics: continuum models and their growing pains. Current Opinion in Structural Biology. 2001;11(2):243–252. doi: 10.1016/s0959-440x(00)00197-4. [DOI] [PubMed] [Google Scholar]
- 55.Sochen N, Kimmel R, Malladi R. A general framework for low level vision. Image Processing, IEEE Transactions on. 1998;7(3):310–318. doi: 10.1109/83.661181. [DOI] [PubMed] [Google Scholar]
- 56.Soldea O, Elber G, Rivlin E. Global segmentation and curvature analysis of volumetric data sets using trivariate b-spline functions. IEEE Trans. on PAMI. 2006;28(2):265–278. doi: 10.1109/TPAMI.2006.36. [DOI] [PubMed] [Google Scholar]
- 57.Stillinger FH. Structure in aqueous solutions of nonpolar solutes from the standpoint of scaled-particle theory. J. Solution Chem. 1973;2:141–158. [Google Scholar]
- 58.Stoschek A, Hegerl R. Denoising of electron tomographic reconstructions using multiscale transformations. J. Struct. Biol. 1997;120:257–265. doi: 10.1006/jsbi.1997.3925. [DOI] [PubMed] [Google Scholar]
- 59.Tomasi C, Manduchi R. Bilateral filtering for gray and color images. Proc. ICCV. 1998;98:839–846. [Google Scholar]
- 60.van der Heide P, Xu XP, Marsh BJ, Hanein D, Volkmann N. Efficient automatic noise reduction of electron tomographic reconstructions based on iterative median filtering. J. Struct. Biol. 2007;158:196–204. doi: 10.1016/j.jsb.2006.10.030. [DOI] [PubMed] [Google Scholar]
- 61.Wang Y, Wei GW, Yang S-Y. Partial differential equation transform – Variational formulation and Fourier analysis. International Journal for Numerical Methods in Biomedical Engineering. 2011;27:1996–2020. doi: 10.1002/cnm.1452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Wang Y, Wei GW, Yang S-Y. Mode decomposition evolution equations. Journal of Scientific Computing. 2012;50:495–518. doi: 10.1007/s10915-011-9509-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Wei GW. Generalized Perona-Malik equation for image restoration. IEEE Signal Processing Lett. 1999;6:165–167. [Google Scholar]
- 64.Wei GW. Differential geometry based multiscale models. Bulletin of Mathematical Biology. 2010;72:1562–1622. doi: 10.1007/s11538-010-9511-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Wei G-W. Multiscale multiphysics and multidomain models I: Basic theory. Journal of Theoretical and Computational Chemistry. 2013;12(8):1341006. doi: 10.1142/S021963361341006X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Wei GW, Jia YQ. Synchronization-based image edge detection. Europhysics Letters. 2002;59(6):814–819. [Google Scholar]
- 67.Wei GW, Sun YH, Zhou YC, Feig M. Molecular multiresolution surfaces. arXiv:math-ph/0511001v1. 2005:1–11. [Google Scholar]
- 68.Wei G-W, Zheng Q, Chen Z, Xia K. Variational multiscale models for charge transport. SIAM Review. 2012;54(4):699–754. doi: 10.1137/110845690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Willmore TJ. Riemannian Geometry. USA: Oxford University Press; 1997. [Google Scholar]
- 70.Witelski TP, Bowen M. ADI schemes for higher-order nonlinear diffusion equations. Applied Numerical Mathematics. 2003;45(2–3):331–351. [Google Scholar]
- 71.Witkin A. Scale-space filtering: A new approach to multi-scale description. Proceedings of IEEE International Conference on Acoustic Speech Signal Processing. 1984;9:150–153. [Google Scholar]
- 72.Xia KL, Wei GW. Three-dimensional MIB galerkin method for elliptic interface problems. submitted to Journal of Computational Physics. 2013 doi: 10.1016/j.cam.2014.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Xia KL, Zhan M, Wei GW. MIB galerkin method for elliptic interface problems. Journal of Computational Physics. 2013 doi: 10.1016/j.cam.2014.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Xie D, Jiang Y, Brune P, Scott LR. A fast solver for a nonlocal dielectric continuum model. SIAM Journal on Scientific Computing. 2012;34:B107–B126. [Google Scholar]
- 75.Xu G, Pan Q, Bajaj CL. Discrete surface modeling using partial differential equations. Computer Aided Geometric Design. 2006;23(2):125–145. doi: 10.1016/j.cagd.2005.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Yu SN, Geng WH, Wei GW. Treatment of geometric singularities in implicit solvent models. Journal of Chemical Physics. 2007;126:244108. doi: 10.1063/1.2743020. [DOI] [PubMed] [Google Scholar]
- 77.Yu SN, Wei GW. Three-dimensional matched interface and boundary (MIB) method for treating geometric singularities. J. Comput. Phys. 2007;227:602–632. [Google Scholar]
- 78.Yu ZY, Holst M, Cheng Y, McCammon JA. Feature-preserving adaptive mesh generation for molecular shape modeling and simulation. Journal of Molecular Graphics and Modeling. 2008;26:1370–1380. doi: 10.1016/j.jmgm.2008.01.007. [DOI] [PubMed] [Google Scholar]
- 79.Zhang Y, Bajaj C, Xu G. Surface smoothing and quality improvement of quadrilateral/hexahedral meshes with geometric flow. Communications in Numerical Methods in Engineering. 2009;25:1–18. doi: 10.1002/cnm.1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Zhao S. High order matched interface and boundary methods for the helmholtz equation in media with arbitrarily curved interfaces. J. Comput. Phys. 2010;229:3155–3170. [Google Scholar]
- 81.Zheng Q, Wei GW. Poisson-Boltzmann-Nernst-Planck model. Journal of Chemical Physics. 2011;134:194101. doi: 10.1063/1.3581031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Zheng Q, Yang SY, Wei GW. Molecular surface generation using PDE transform. International Journal for Numerical Methods in Biomedical Engineering. 2012;28:291–316. doi: 10.1002/cnm.1469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Zhou YC, Wei GW. On the fictitious-domain and interpolation formulations of the matched interface and boundary (MIB) method. J. Comput. Phys. 2006;219(1):228–246. [Google Scholar]
- 84.Zhou YC, Zhao S, Feig M, Wei GW. High order matched interface and boundary method for elliptic equations with discontinuous coefficients and singular sources. J. Comput. Phys. 2006;213(1):1–30. [Google Scholar]