Integrating Risk Adjustment and Enrollee Premiums in Health Plan Payment

Abstract

In two important health policy contexts – private plans in Medicare and the new state-run “Exchanges” created as part of the Affordable Care Act (ACA) – plan payments come from two sources: risk-adjusted payments from a Regulator and premiums charged to individual enrollees. This paper derives principles for integrating risk-adjusted payments and premium policy in individual health insurance markets based on fitting total plan payments to health plan costs per person as closely as possible. A least squares regression including both health status and variables used in premiums reveals the weights a Regulator should put on risk adjusters when markets determine premiums. We apply the methods to an Exchange-eligible population drawn from the Medical Expenditure Panel Survey (MEPS).

1. Introduction

Payments to health plans often come from just one source. In individual commercial health insurance markets to date, all plan revenue has come from enrollee premiums. In employer-based health insurance, the employer pays plans (even though the employer recoups some of its costs by requiring employee contributions).¹ However, in important health policy contexts, for example, the Medicare Advantage (MA) program offering private plans in Medicare and the new state-run “Exchanges” created as part of the Affordable Care Act (ACA), plan payments come from two sources at once: risk-adjusted payments from a Regulator and premiums charged to individual enrollees. Paying plans from two sources raises issues in payment system design. This paper derives principles for integrating risk-adjusted payments and premium policy in individual and small group health insurance markets. We apply these to risk adjustment and premium setting for potential Exchange participants. We describe how a Regulator should risk adjust plan payments when plans also charge and collect premiums from enrollees or employers. Specifically, we describe how a Regulator should determine weights on risk-adjustment factors in the presence of premiums.

The relationship between risk adjustment and premiums is reciprocal. Suppose the Regulator subsidizes and risk adjusts 75 percent of costs with enrollee premiums paying for the other 25 percent; the premiums are conditioned on age, smoking status, and geography. The key insight is that the risk adjustment mechanism adopted by the Regulator affects premiums, because what a plan would want to (from profit-maximization) and would be able to (due to competition) charge enrollees as a premium depends on how the regulator sets risk-adjusted payments. To set the desired risk adjustment scheme, however, the Regulator needs to consider the effect of the risk adjustment on premiums. The Regulator’s problem in this case differs from the case when the Regulator simply pays for 75 percent of health costs and the remaining 25 percent are financed by a flat enrollee premium that is specified in statute, as in Medicare Part B.

Section 2 describes plan payment policy in Medicare and the Exchanges and relates our paper to the existing literature on risk adjustment. Section 3 presents a model of individual health insurance in which a Regulator seeks to make total plan payments for an enrollee (Regulator payments plus premiums) approximate health plan costs for the enrollee as closely as possible. The Regulator has a fixed budget with which to subsidize all plans; in addition, the regulator risk adjusts payments to each. We assume the adjustment will be based on a measure of health status of enrollees. Constrained by market forces, plans set premiums on another, possibly overlapping set of personal enrollee characteristics. Section 4 characterizes how the Regulator should assign risk adjustment weights to a predetermined set of risk adjustment factors such as age, gender, and previous diagnoses. We show that simple modifications of least squares methods reveal the best-fitting weights. Specifically, an ordinary least squares regression on costs using risk adjustment and premium categories as variables solves the Regulator’s problem because of the equivalence between two important sets of relations, the “normal equations” in a least squares regression and the “zero-profit” conditions in competitive markets. This equivalence means that the coefficient weights from a least squares regression using premium categories are the same as would emerge in a competitive market. This is the central point of this paper: a least squares regression that includes both premiums and risk adjustment variables tells the Regulator how to set the risk-adjustment weights.

Section 5 applies the methods for risk adjustment to a potential Exchange population drawn from several panels of the Medical Expenditure Panel Survey (MEPS), basing risk adjustment on Hierarchical Condition Categories (HCCs).² We demonstrate the practical utility of least squares methods with three applications: setting a per-person budget for risk adjustment; incorporating the age-band restrictions specified in the ACA; and estimating risk adjustment weights when some of the population has a “history” that can be used for diagnosis-based risk adjustment and some of the population does not. These applications, which use constrained least squares regressions, build upon one another so our final least squares model instructs the Regulator in setting risk adjustment weights when facing a budget in which the balance of costs will be covered by premiums set in a market, with a target premium ratio, and with some enrollees without a diagnostic history.

Section 6 concludes the paper with some comments on next steps for applying the methods developed here to Exchange and Medicare contexts. We discuss there some of the significant issues not confronted in this paper, including imperfect competition in insurance markets; multiple types of plans (Bronze, Silver, etc.); and service-level selection.

2. Policy Background and Literature Review

In Medicare presently and in the new state-level Exchanges shortly, health plans will be paid by a combination of risk-adjusted payments and premiums chosen by the plans. The risk-adjustment formula is chosen by regulation, as are the terms on which premiums can be set. This section sets the policy contexts for the analysis, and then briefly reviews some of the literature on risk adjustment methods.

2.1 Medicare Advantage

Part C of Medicare, in existence for almost 30 years, created Medicare Advantage (MA) plans as an alternative to traditional Medicare (TM), with the intention of creating choice of health insurance for beneficiaries and reducing Medicare costs through the economies of managed care.³ TM is composed of Parts A and B which pay for facility and professional services, and a voluntary Part D, implemented in 2006, which covers prescription drugs and which relies on competing private insurers to manage drug costs. About 27% of Medicare beneficiaries chose MA plans as of March 2012 (Gold et al., 2012). Part C has been disappointing throughout its history. Choices for beneficiaries are very limited in some regions and probably too numerous and confusing in others (McWilliams et al., 2011). Our recent review of the payment history of Part C concluded that the program has never succeeded in saving Medicare funds (McGuire, Newhouse and Sinaiko, 2011). Glazer and McGuire (forthcoming) argue that one of the fundamental problems with MA is Medicare’s “single premium” policy that leads to an inefficient sorting of beneficiaries between MA and TM.⁴ As cost pressures on Medicare intensify, beneficiaries are likely to be asked to pay higher premiums for both MA and TM, giving Medicare the opportunity to reform its premium policy.

One potential strategy for reform, known as premium support, would shift Medicare from a defined benefit to a defined contribution program. First proposed in the mid-1990s (Aaron and Reischauer, 1995), premium support is gaining attention from budget-minded policymakers (Debt Reduction Task Force, 2010; Wyden and Ryan, 2011). Under a premium support policy, beneficiaries would receive a risk-adjusted voucher to use to purchase health insurance coverage from among a set of competing private health plans that may or may not include traditional fee-for-service Medicare. While the details of specific proposals vary, in most cases the voucher would be set to cover the cost of enrolling in one of the lower-cost plans, and beneficiaries who choose alternatives would be responsible for paying any differential between plan premium and the voucher.

MA plans are paid predominantly by risk-adjusted payments from Medicare, and partly by premiums chosen by the plan.⁵ Medicare’s MA payments are based on a Medicare “benchmark” rate set for each county and the plan’s “bid.” Until 2011, the benchmark was based on the maximum of (1) the CMS estimate of Medicare costs for a typical beneficiary in Parts A and B, (2) a minimum or “floor” payment, and (3) the past payment rate for the county trended forward at national average Medicare cost growth rates. We are now (2012) in transition to a new system wherein by 2017, the benchmark will be based on the quartile of a county’s TM spending and it quality rankings.⁶ A plan’s bid is the plan’s estimate of what regular benefits from Part A and B would cost the plan for a beneficiary of average health status plus whatever margin it adds. If a plan bids above the benchmark, Medicare pays the plan the benchmark and the beneficiary pays the differential. If the bid falls below the benchmark, Medicare pays the bid plus a 50%, 65%, or 70% share of the difference between the bid and the benchmark, depending on the plan’s quality rating. The idea is that Medicare gets a share of any “savings” (difference between benchmark and bid) and the plan must use the balance of the difference to reduce beneficiary premiums or provide additional coverage and benefits.⁷ Finally, the base payment from Medicare to the plan is risk adjusted by applying the CMS Hierarchical Condition Categories model (CMS-HCC), derived from a linear regression of 24 age-gender cells, 70 HCC indicators, an indicator for Medicaid status in the base year, and an indicator if the beneficiary was originally enrolled in Medicare because of disability.⁸

The premiums that beneficiaries pay to MA plans depend on the type of MA plan in which one chooses to enroll. All beneficiaries in MA plans must pay the Part B premium (which goes to Medicare),⁹ and MA plans can charge a premium above this. Many plans, however, are “zero-premium” plans, meaning they charge nothing above the Part B premium.¹⁰ In 2011, about half of beneficiaries in HMOs paid zero additional premium. A small percentage of plans reduce the beneficiary’s Part B premium obligation. Most MA beneficiaries also choose to enroll in MA-PD plans, which means their plan provides coverage for prescription drugs that is at least equivalent to that provided through Part D of Medicare. The average monthly premium for an MA-PD plan (across all plan types, and on top of the Medicare Part B premium) was $50 per month, unweighted by enrollment (KFF, 2011).

MA premiums need to be understood in the context of what beneficiaries must pay in TM for comparable coverage. To bring TM coverage in line with what is offered in a typical MA-PD plan, the beneficiary needs to buy Part D coverage, averaging $38 per month in 2011, and a supplemental Medigap plan averaging $167, assuming the beneficiary is not one of the 30 percent who currently has supplemental insurance through a prior employer or the 18 percent who are eligible for Medicaid (Glazer and McGuire, 2011b).

2.2 State Exchanges in the ACA

The Patient Protection and Affordable Care Act of 2010 (ACA) creates new state-level health insurance markets referred to as “Exchanges” as one pillar of its effort to reduce the number of uninsured and underinsured in the U.S and make individual and small group markets more efficient. Under the ACA, beginning in January 2014, U.S. citizens and legal residents who are not eligible for employer-sponsored or public coverage will be able to purchase health insurance through new Exchanges. States can choose to operate their own state-based Exchange or choose instead to rely on the Federal government to perform the function (known as a Federally-Facilitated Exchange). As of November, 2012, 18 states and the District of Columbia have declared that they will establish a state-based Exchange; 6 states plan to establish a state-federal partnership Exchange, and 16 states are planning to default to a federally run exchange (Kaiser Family Foundation, 2012). Small businesses will be able to purchase coverage through a separate exchange, although states have the option and many may choose to combine their individual and small group exchanges. Exchanges will consolidate and regulate the market for individual insurance, as plans offered through the Exchanges must cover a state-defined “essential benefit package,” and be classified into one of four cost-sharing tiers (platinum, gold, silver or bronze) that are defined by actuarial value. Premium and cost-sharing subsidies will apply on a sliding scale for individuals and families earning up to 400% of poverty; in the Exchange, individuals will pay a premium directly to their health plan. The Congressional Budget Office estimates 24 million people will purchase an insurance policy (in some cases subsidized) through these Exchanges (CBO, 2010).

Several provisions of the ACA are designed to minimize adverse selection in Exchanges, including a requirement that insurers must offer at least one plan in each of the gold and silver tiers, that income-based premium and cost-sharing subsidies only be available for plans purchased through the Exchange, and that insurers charge the same premium rates for a health plan whether it is purchased through the Exchange or through the outside individual market. Exchange plans will be able to condition premiums on age, family size, smoking status, and geography, though the age-based premium variation is limited to a ratio of no more than 3-to-1. Open questions on plan premiums remain however, such as whether there will be restrictions on the ratio of premiums across coverage tiers (e.g., Gold vs. Silver plans).

To further minimize the effects of risk selection, the ACA also mandates that Exchanges engage in risk adjustment and implement temporary risk corridors and reinsurance programs. The reinsurance and risk corridor programs are to operate from 2014 – 2016 and are intended to create stability in Exchange markets during the early transition years (when healthier individuals may delay enrolling in Exchange plans). In contrast, risk adjustment is permanent. Section 1343 of the ACA requires risk-adjustment to be budget neutral: health plans with an enrollee population that has lower than average health risk will be required to make payments to the state and plans with higher than average health risk will receive supplementary payments. These adjustments will take place at the insurance carrier level, based on insurers’ aggregate risks across an entire state.¹¹

Many of the specific details around the risk adjustment program are yet to be determined; in July 2011, DHHS released the first set of proposed regulations relating to risk adjustment in the Exchanges.¹² The regulations give states flexibility to choose whether to administer risk-adjustment or to have the Federal government perform that function; any state that chooses to implement risk adjustment must have their risk adjustment methodology approved and certified by DHHS. Risk adjustment may be implemented retroactively (with a suggested time-lag of six months following completion of a benefit year). Insurers will be required to submit raw claims data to the state (or to HHS in case of the Federalexchange) to determine risk adjusted payments (as opposed to submitting an aggregated risk profile).

2.3 Research on Risk Adjustment and Enrollee Premiums

National health policy in a number of countries finds inspiration in the research of Enthoven and colleagues who advocated “managed competition” among competing private health insurers (Enthoven, 1988; Enthoven and Kronick, 1989). Public policy in both Medicare and Exchanges can be traced to these ideas.¹³ Risk adjustment and enrollee premiums each play an important role in the managed competition model. Risk adjustment pays more for the sick so plans would be willing to accept and provide care for more costly enrollees. This requires a Regulator or tax authority to collect and pool individual contributions (perhaps financed by taxes) and redistribute them to plans according to the risk adjustment formula. Plans would also set and collect a premium, so plan competition occurs on the basis of cost (price) as well as on the “quality” of the insurance product. The idea is that consumers would choose plans on the basis of both cost and quality, leading to an efficient level of health care spending (Pizer et al., 2003).

In spite of the necessary integration of risk adjustment and premium policy within managed competition, research on risk adjustment and premiums has largely proceeded on independent tracks. One strand of research in risk adjustment has been empirical and statistical; this work has focused on identifying suitable risk adjustment variables (they need to be routinely available in medical data, clinically meaningful, contribute to model fit, not gameable) and applying regression techniques to maximize some measure of fit such as R². Comprehensive review chapters in Volumes 1 and 2 of the Handbook of Health Economics deal with risk variation and risk adjustment. Van de Ven and Ellis (2000) cover many of the econometric issues associated with constructing a risk adjustment formula. Breyer, Bundorf and Pauly (2012) discuss the attributes of good risk adjuster variables, and update the use of risk adjustment in health care systems around the world.¹⁴

Another strand in risk adjustment research introduces an objective of a Regulator in deriving rules for risk adjustment. Objectives are typically to reduce market failures associated with adverse selection. For example, if health plans engage in what Breyer, Bundorf and Pauly (2012, p 729) refer to as “indirect selection” and skimp on certain service offerings (e.g. network quality among cancer specialists) to attract good risks, risk adjustment weights can counter by paying more for enrollees who would make use of the services subject to these incentives. Glazer and McGuire (2002) derive the optimal risk adjustment weights to counter skimping and show how they can be found by a constrained least squares regression.¹⁵

Research on health plan premiums recognizes several social objectives for premiums: fairness, risk spreading, and efficiency in the market for plan choice. Fairness, as defined by the European term, “solidarity,” implies that sick should no pay more than the healthy (though fairness does not rule out and may require higher income groups paying more than lower income groups). Maximum risk spreading also requires premiums not differ by health state, since full risk spreading protects consumers against the risk of change in health status or having a child with a costly health condition. These objectives conflict, however, with short-term efficiency in health insurance markets which calls for premiums for each individual to reflect the incremental marginal cost associated with their choice of alternative health plans (Keeler, Carter, Newhouse, 1998). If a sick person has higher incremental cost in a Gold plan over a Silver plan than a healthy person, the efficient premium difference between the two plans should be higher for the sick than for the healthy. Bundorf, Levin and Mahoney (2009) reiterate this point and show that in general any single premium would not lead to efficient sorting among plan offerings. Glazer and McGuire (2011a) analyze the conditions in which risk adjustment, taxes, and subsidies can complement premium policy to achieve objectives of both efficient sorting among plans and solidarity within a model of managed competition. In general, as with taxes, policy makers face a tradeoff between using premiums to promote efficiency or achieve solidarity (and protect against health status risk). This tension between fairness and efficiency is evident in premium regulations within Exchanges where the more expensive old are allowed to be charged only a limited amount more than the young.

3. Costs and Payments in an Individual Health Insurance Market

This section starts from the premise that a Regulator seeks to use available information to design a payment system for an individual health insurance market to fit payments to health care costs as closely as possible. The assumptions we make about the market and the role of the Regulator share some features of ACA Exchanges (premiums can be conditioned on personal characteristics), some features of Medicare Part D and proposals for premium support (a budget for subsidies and risk adjustment), and some features of both Medicare and Exchanges (some enrollees have no history to use as a basis for risk adjustment). Our purpose is to employ a simple and general context to illustrate the versatility of least squares methods. The key feature shared by all of these applications is that a Regulator controls risk adjustment and can regulate the terms on which private plans compete on premiums.

3.1 Population Characteristics and Health Care Costs

Let the total number of people be N and health care costs of individual i be x_i, with an overall average of x̄. People vary in two observable dimensions, according to health status, the basis of risk adjustment, and according to another set of characteristics we refer to as “personal,” the basis of premiums. Health status is indexed by h, h = 1,…,H; personal characteristics are indexed by t, t = 1,…,T. For notational simplicity, we assume that each of these categorizations is one dimensional and the information is mutually exclusive so that each person is characterized by an (h,t) pair we will refer to together as a “type.” Later we relax this assumption and allow multiple dimensions of h and t with potentially overlapping information (like age). Hence, while we initially assume there is a single index for health status and personal characteristics, there could be more than one variable behind the index.¹⁶

Define x_ht to be the average cost of person of type (h,t), and n_ht to be the number of people of type (h,t). Health care costs also vary within each (h,t) pair. Health care costs are plan costs (which must be covered by plan payments) and are fixed (do not depend on risk adjustment or premiums).¹⁷ For simplicity we assume the market is competitive and plans have access to the same technology and input prices, so that all plans earn the same margin, which we ignore.¹⁸ There is one type of insurance plan with fixed coverage and health care management practices.

We further define:

$$\begin{array}{ll}{\text{n}}_{\text{h}}=\sum _{\text{t}}{\text{n}}_{\text{ht}}\hfill & \text{number}\text{of}\text{people}\text{with}\text{health}\text{status}\text{h}.\hfill \\ {\text{n}}_{\text{t}}=\sum _{\text{h}}{\text{n}}_{\text{ht}}\hfill & \text{number}\text{of}\text{people}\text{of}\text{with}\text{personal}\text{characteristics}\text{t}.\hfill \\ {\text{x}}_{\text{h}}=\frac{1}{{\text{n}}_{\text{h}}}\sum _{\text{t}}{\text{n}}_{\text{ht}}{\text{x}}_{\text{ht}}\hfill & \text{average}\text{cost}\text{of}\text{person}\text{of}\text{health}\text{status}\text{h}.\hfill \\ {\text{x}}_{\text{t}}=\frac{1}{{\text{n}}_{\text{t}}}\sum _{\text{h}}{\text{n}}_{\text{ht}}{\text{x}}_{\text{ht}}\hfill & \text{average}\text{cost}\text{of}\text{person}\text{with}\text{personal}\text{characteristics}\text{t}.\hfill \end{array}$$

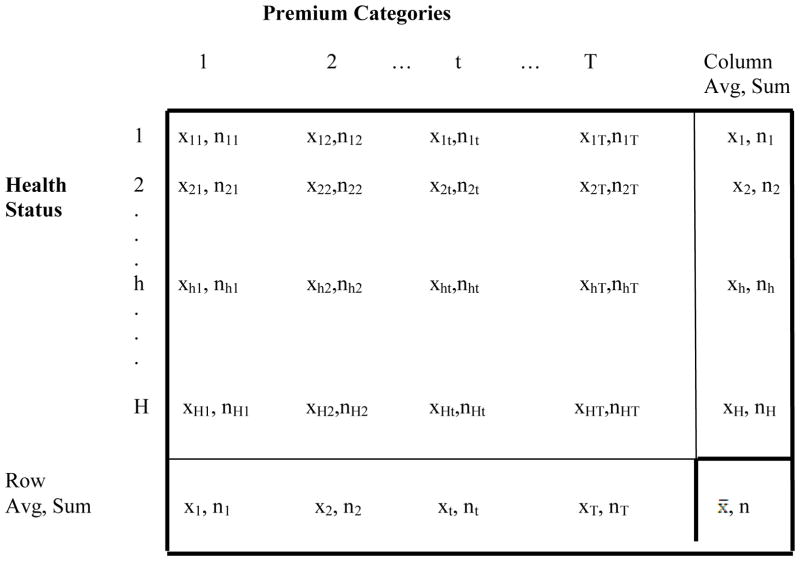
Table 1 depicts the data on the population and health care costs and summarizes the definitons used.

Table 1.

Health Care Cost and Population

Definitions:

• x_t average health care costs of person of personal characteristics t (column average)
• n_t sum of people of with personal characteristics t (column sum)
• x_h average health care costs of person of health status h (row average)
• n_h sum of people of health status h (row sum)
• x̄ overall average health care costs
• n total population

3.2 Payment System

Plans are financed by risk-adjusted payments from a Regulator and premiums paid by enrollees. We assume risk adjustment can only be based on health status. Premiums can only be based on personal characteristics. r_h is the risk-adjusted payment to plan for enrollee health status h, and p_t is the premium paid by enrollee with personal characteristics t. r_h is the sum of any subsidy plus or minus the risk adjustment payment. Thus, for a person of type (h,t), the plan gets r_h + p_t in revenue and incurs, on average, x_ht in health costs.

3.3 Regulator’s Objective

The Regulator seeks to fit payments to costs as closely as possible. We measure fit by the sum of squares of the deviation between payments and costs, with better fit corresponding to a lower residual sum of squares. This approach is consistent with most of the risk adjustment literature which contends that a better statistical fit reduces problems related to risk and adverse selection.¹⁹ An explicit formulation of the connection between payment system incentives and plan and enrollee behavior can lead to different answers about risk adjustment, a direction of analysis we discuss in Section 6.

Formally, the Regulator minimizes the residual sum of squares (RSS) with respect to choice of weights, r_h, on the h risk adjustment categories:

$$\text{RSS}=\sum _{\text{h}}\sum _{\text{t}}\sum _{\text{i}\in \{\text{ht}\}}{({\text{r}}_{\text{h}}+{\text{p}}_{\text{t}}-{\text{x}}_{\text{i}})}^2,$$ (1)

where {ht}is the set of all individuals whose type is (h,t). The Regulator faces at least two sets of constraints on this minimization, one from a budget constraint on funds available for risk adjustment, and another imposed by plans’ behavior setting premiums in the market. We consider additional constraints in our empirical application section.

3.4 Budget Constraint

The Regulator has a fixed budget per person, b, to be used for risk-adjusted payments to plans. The budget constraint can be expressed as (2):

$$\sum _{\text{h}}{\text{n}}_{\text{h}}({\text{r}}_{\text{h}}-\text{b})=0.$$ (2)

3.5 Premiums Set in a Market

The Regulator limits the variables used for premiums, and may otherwise restrict premiums, but within such regulation, private health plans can set premiums in their own interest. We assume that competition leads plans to set premiums at costs for each premium category, taking into account any revenue received through risk adjusted payments. Thus, competition implies:

$$\sum _{\text{h}}{\text{n}}_{\text{ht}}({\text{r}}_{\text{h}}+{\text{p}}_{\text{t}}-{\text{x}}_{\text{ht}})=0\text{for}\text{all}\text{t}$$ (3)

(3) is a system of t equations describing the vector of premiums, p_t, that lead to zero profit for each premium category, taking into account the health costs and risk-adjusted payments for the people within premium category t. From the Regulator’s point of view, (3) describes how risk-adjusted payments determine market premiums.

4. Methods for Setting Risk Adjusted Payments and Premiums

We begin by characterizing payment systems that rely only on enrollee premiums or only on health status risk-adjusted payments to pay plans. We then consider an integrated approach.

4.1 Premiums Only – Competitive Market

In a market without Regulator payments, competition leads plans to set premiums equal to average costs for each premium category. From (3), with r_h = 0, p_t = x_t, for all t.

4.2 Risk-Adjusted Payments Only – Conventional Risk Adjustment

In a market without premiums, the Regulator must cover costs with risk-adjusted payments, and the budget constraint must be set aside.²⁰ The Regulator minimizes the RSS from (4) with respect to choice of r_h:

$$\sum _{\text{h}}\sum _{\text{i}\in \{\text{h}\}}{({\text{r}}_{\text{h}}-{\text{x}}_{\text{i}})}^2,$$ (4)

where{h}is the set of individuals with health status h. In (4), (p_t =0). The solution for r_h is the set of means conditional on health status: r_h = x_h, for all h, equivalent to the estimates from an ordinary least squares (OLS) regression of health costs on mutually exclusive categorical health status variables. An OLS regression with (0,1) risk adjustment variables (which are not mutually exclusive) is in fact used to set the risk-adjustment weights in Medicare Advantage and in Part D.

Notably, the zero-profit condition from competition yields the same form of solution as an OLS regression with mutually exclusive categories minimizing unexplained variance. Competition on premiums sets premiums equal to average cost conditional on t: p_t = x_t. A regression maximizing fit sets risk adjusted payments equal to average cost conditional on h: r_h = x_h. Analogous results, from in one case economic forces and the other from a statistical criterion, are the basis of the main result of the paper, contained in the next section.

4.3 Simultaneous Choice of Risk-Adjusted Payments and Premiums

In practice, risk adjusted payments and premiums in Medicare (Parts C and D) and in the Exchanges will be determined in a two-step process. In the first step, the Regulator specifies the risk adjustment methodology, and announces some rules for premiums. Rules include enumeration of the variables that are permissible for premium setting, and possibly the portion of total costs to be risk adjusted and restrictions on rate bands, for example, as in the Exchanges, that the ratio between premiums for the oldest and youngest groups can be no greater than three-to-one. Then, in a second step, plans will set premiums in recognition of the risk adjusted payments and subject to the regulations on premium structure.

One might expect that finding the Regulator’s best set of risk adjustment weights in this two-step institutional context would require solving a principal-agent problem. However, as previewed in Sections 4.1 and 4.2, the similarity in the form of a competitive and statistical solution for weights on indicator variables implies that the constraints imposed by competitive premium setting are embedded in the statistical solution of the least squares regression. Thus, least squares also solves the principal-agent problem. Additional constraints can be also incorporated as part of a constrained least squares estimator.

We show in this section that the best Regulator policy for risk adjustment can be found by a least squares regression of health care costs on risk adjustment and premium categories. Specifically, the least squares solution satisfies constraints imposed by the market on premiums, and since least squares estimates maximize fit, this choice of risk adjustment weights is the optimal policy for the Regulator.

We begin by a formal restatement of the problem: the Regulator seeks to maximize fit of the payment system (equivalent to minimizing the RSS from (1)) with respect to choice of the risk adjustment weights r_h on the h health status factors, subject to a per-person budget for risk adjustment b shown in (2) and subject to how the market will set premiums to be zero profit conditional on risk adjustment (3).

Consider the following constrained regression equation for health care costs x to be estimated by least squares (omitting the i subscripts):

$$\text{x}={\sum }_{\text{h}}{\text{r}}_{\text{h}}{I}_{\text{h}}+{\sum }_{\text{t}}{\text{p}}_{\text{t}}{I}_{\text{t}}+\epsilon ,\text{h}=1,\dots ,\text{H},\text{and}\text{t}=1,\dots \text{T}\text{subject}\text{to}{\sum }_{\text{h}}{\text{n}}_{\text{h}}({\text{r}}_{\text{h}}-\text{b})=0.$$ (5)

In (5), I_h and I_t are indicator variables that take the value of 1 when person i has health status h and person characteristics t, respectively, and are zero otherwise. r_h is the coefficient to be estimated for each health status indicator, and constitutes the risk adjusted payment for health status category h. p_t constitutes the premium level for a person with characteristics t. Equation (5) contains no constant term. ε is the error term.²¹ Finally, the linear constraint is the budget for risk adjustment, (2).

Let r_h* and p_t* refer to the least squares estimates obtained from (5). “Least squares” refers to minimizing the RSS (equation (1)), subject to the constraint. The least squares solution is consistent with zero profitability for premium categories. We know from the normal equations of least squares that for each premium category t:²²

$$\sum _{\text{h}}\sum _{\text{i}\in \{\text{h}\}}{I}_{\text{t}}({\text{r}}_{\text{h}}^{\ast }+{\text{p}}_{\text{t}}^{\ast }-{\text{x}}_{\text{i}})=0,$$ (6)

Since the number of people with personal characteristics t is n_t = Σ_hn_ht, and noting the definition of x_ht, we can rewrite (6) as

$$\sum _{\text{h}}{\text{n}}_{\text{ht}}({\text{r}}_{\text{h}}^{\ast }+{\text{p}}_{\text{t}}^{\ast }-{\text{x}}_{\text{ht}})=0$$ (6′)

(6′) is equivalent to (3), implying that the zero-profit constraint on premiums is satisfied at (r_h*, p_t*). Put another way, if the Regulator chooses r_h* (subject to the constraint affecting the least squares estimate for the risk adjustment weights), the market responds with p_t*.

The main result can be summarized as follows:

Main Result

Coefficients from a least squares regression including variables representing risk adjusters and premiums and incorporating a budget constraint for risk adjustment yield the risk adjustment weights that maximize fit of the payment system, given premiums set in a market.²³

4.4 Incorporating Additional Constraints on Premiums

Premiums are often regulated to accomplish objectives associated with fairness. “Fair” premiums limit the information premiums can be conditioned upon (e.g. ruling out “pre-existing conditions”) or force subsidization of older enrollees by limiting age bands. The ACA limits the ratio of premiums in the Exchanges of the oldest group to the youngest group to be no greater than three-to-one. In the extreme, “community rating” regulation imposes equality in premiums across groups that may have very different expected health care costs even after risk adjustment on health status of some part of plan payments.

Least squares methods turn out to be extremely versatile in this context. Because of the budget constraint on funds for risk adjustment, estimating (5) requires a constrained least squares regression model.²⁴ Additional constraints on premium estimates can easily be added. An old-young premium ratio, for example, is a linear constraint (one for each geographic area.) When premiums for two groups are tethered by such a constraint, we also have to constrain profits to be zero for the paired groups. That is, competition implies the plan sets a premium for the old-young pair such that profits are zero (given risk adjustment) if it draws a random distribution of young and old.

Another practical problem faced by a Regulator in both a Medicare and Exchange context is the absence of claims history for some enrollees, for example Medicare beneficiaries just turning 65 or Exchange participants new to the market. Least squares can also accommodate setting risk adjustment weights when only some of enrollees have an observable history of medical events.

In the following section, our empirical application layers these constraints atop the market-determined premiums and the budget constraint affecting the average risk adjusted payment. Our final model (Model 5 below) incorporates all of the additional constraints mentioned above: premiums set in a market, a budget constraint on risk-adjusted payments, a 2:1 old-young ratio, and half the potential enrollees coming without a history. Although the ACA specifies that the premium spread by age cannot exceed 3:1, we use 2:1 since 3:1 is not binding in our data and we wanted to illustrate how a binding constraint could be incorporated. Even with all these constraints, a single least squares regression continues to find the best risk adjustment weights.²⁵

5. Empirical Application

5.1 Data

To provide a worked example of our methods we use data from the Medical Expenditure Panel Survey (MEPS), a nationally representative survey of the civilian non-institutionalized U.S. population conducted annually since 1996. Each year MEPS surveys approximately 15,000 households, enlisting a new panel of respondents followed for two years. Data are collected in five rounds of interviews covering the two-year period. The Household Component (HC) is the source of data for personal and household characteristics, including insurance coverage and self-reported health and health conditions and health care utilization. The MEPS Medical Provider Component (MPC), based on phone surveys of hospitals and physician offices that provide care to MEPS respondents, is the primary source of data on health care expenses including sources of payment. The MEPS collects data in similar fashion for respondents in all types of health insurance coverage, including the uninsured. We use Panels 9 (2004/05) through 13 (2008/09), requiring participation in both years of the panel (dropping those who die during their first survey year.) We take advantage of the two-year panel structure of MEPS to implement risk adjustment; our first year of study for expenditures will be 2005, since we need data on medical events (analogous to claims) by individuals in 2004 (the first year of Panel 9) to predict spending in the study year. Medical spending in the second year is total spending from all sources for health care services that would be covered in a typical private health insurance plan.²⁶

5.2 The Exchange Population

We select a population of individuals and families who would be eligible to enroll in state-level Exchanges under current law based on their income, insurance and employment status. We identify adult, non-elderly individuals (aged 18–64) in households earning at least 138% of the federal poverty level and children in households with income of at least 205% of the federal poverty level.²⁷ We select the Exchange population from these groups who are, or in the case of children, those who live in a household where an adult is: ever uninsured, a holder of a non-group insurance policy, self-employed, employed by a small employer, paying an out-of-pocket premium for their employer-sponsored health insurance (ESI) plan that is deemed to be unaffordable (as defined in the ACA).²⁸

5.3 Risk Adjustment with the CMS-HCC Model

We base risk adjustment on the Center for Medicare and Medicaid Services Hierarchical Condition Category (CMS-HCC) model, which uses individual demographics and information on major medical conditions in a base year to predict an individual’s health care expenditure for the next year. The model maps individual diagnoses from ICD-9 codes (those related to Office-based Medical Provider Visits, Outpatient Department Visits and Inpatient Hospital Stays) into one of 70 hierarchical condition categories (HCCs) to predict costs. Diseases within an HCC are similar clinically. Each individual is given a (0,1) indicator for each of 70 HCCs, and these become part of a linear regression model predicting cost. The coefficients from this model are the “weights” on age, gender, HCC and other factors used in risk adjustment (Pope et al., 2011).

Our implementation of the risk adjustment model diverges from the CMS model in a several ways to accommodate the MEPS Exchange population. First, we apply the same age-gender categories as in the CMS-HCC model, but we have fewer age cells since we include only people 18–64. Second, our risk adjustment model excludes variables indicating Medicaid and disability status, and interaction variables related to them, as these are not applicable to the population that will be insured through the new Exchanges. Third, whereas the CMS-HCC model uses 5-digit ICD-9 diagnosis code to classify diagnoses into CCs, the MEPS public use files do not include 5-digit ICD-9 codes to protect respondent confidentiality. We use the 3-digit ICD-9 codes which are publicly available.²⁹ Documentation of the CMS-HCC model indicates that moving from 3 to 5-digit classification does little to improve model fit in MEPS.³⁰ In MEPS, diagnostic data come from household reports which lack the specificity and precision of physician reports (AHRQ 2011). Finally, we do not include the full set of 70 HCC indicators because of limitations of our sample size. All HCCs with more than 20 observations are entered in the model. The remaining HCCs are aggregated into one of two categories based on the average health expenditure of individuals in the HCC: high if average expenditure is larger than $10,000, and low otherwise. Dummy variables indicating these expenditure categorizations are included in our model. Table A in the Appendix lists average spending per person by the HCCs that we include in our risk adjustment model. For convenience, we will refer to the risk adjustment system we use as CMS-HCCs, even though it is modified in the ways just described.³¹

5.4 Premiums in the Simulated Exchange

As discussed above, the ACA allows premiums to be conditioned on age, smoking status, and geography. We group age into two categories: young (18–49) and old (50–64). In a preliminary analysis, annual expenditures differed little by smoking status in this young population, so we did not include smoking as a premium variable. State exchanges would use within-state location for purposes of premiums; here we use geographic variables available in MEPS: four census regions, and an urban rural indicator. With two age categories, four regions, and urban-rural, there are 2×4×2=16 premium categories.

5.5 Models

We estimate the following models by least-squares regression.³² None includes a constant:

Model 1: Basic premium model

This model contains sixteen indicator variables used as the basis of premiums, the combinations of young-old, four regions and urban-rural. The coefficient estimates from this model can be interpreted as the zero-profit premiums.

Model 2: Basic risk adjustment model

This model contains the full set of CMS-HCC sex-age indicators applicable to our 18–64 year-old population. In addition, as described above, it includes HCCs except those with few observations. “No-HCC” is an omitted category. This model corresponds to the conventional approach to risk adjustment. Note that the indicators are not mutually exclusive. Coefficient estimates for the HCCs can be interpreted as the additional dollar payment a plan would receive if an enrollee has a positive indicator for that HCC.

Model 3: Combined model with budget constraint

This model combines the CMS-HCC model with premium variables.³³ We set the budget constraint for risk adjustment at $2,000 per person by imposing a single linear constraint on the coefficients, as follows. The CMS-HCC model is a set of zero-one indicators. The constraint is that the sum of the product of these indicators times the proportion of the sample with the indicator equal to one equals $2,000. The estimated risk adjustment weights will obviously be affected by including the premium variables, particularly for those risk adjustment variables highly correlated with premium categories.³⁴

Model 4: Combined model with budget constraint and ratio constraints on premiums

Eight constraints are added to Model 3, such that within in each of the eight geographic areas, the ratio of the premium for the old is twice the premium for the young. In addition, four zero-profit constraints characterize the level of the old-young premiums that would emerge in a competitive market.

Model 5: Combined model with no history for part of participating population, a budget constraint and a ratio constraint on premiums

Model 5 incorporates the budget and premium ratio constraints while stripping history from half of the Exchange population. “History” or “no-history” is assigned with a random-number generator. The risk adjustment weights for those with a history encompass age-gender indicators from the CMS-HCC model as well as the HCC weights. These payments are constrained to average $2,000. For those without a history, payments can only be based on age and gender. These payments are also constrained to be $2,000 but obviously require different weights on the age-gender indicators. Premiums, however, are constrained to be the same for those with and without a history. ³⁵ All of these parameters are simultaneously estimated in a single least squares model. We impose separate budget constraints on those with and without a history confining their average risk adjusted payment to be $2,000.³⁶

5.6 Results

Table 2 summarizes the risk adjustment and premium variables for the Exchange-eligible population and shows the average expenditure for each group. In total, MEPS yields 11,568 Exchange eligible adult respondents from five panels. Average total spending is $3,410 per year (in $2009), with spending by males slightly lower than females. The older group, age 50 and up, spends more than twice but less than three times the younger group. The Midwest is the highest cost region and the West the lowest. In this sample there is little difference in average spending between those in and outside of metropolitan areas.

Table 2.

Exchange Population Characteristics

	Percent	Expenditures ($2009)
		Mean	Standard error
Gender
Male	42.2%	$3,207	$178
Female	57.8%	$3,558	$97
Premium Variables
Age
Age 18–49	68.1%	$2,460	$74
Age 50–64	31.9%	$5,437	$246
Region
Northeast	15.2%	$3,472	$225
Midwest	21.6%	$3,713	$273
South	37.0%	$3,447	$141
West	26.2%	$3,070	$147
Live in Metropolitan Area
No	16.6%	$3,628	$188
Yes	83.4%	$3,366	$106
CMS-HCC Variables
CMS-HCC Age Categories
Female 0–34	19.3%	$2,546	$112
Female 35–44	12.7%	$2,810	$147
Female 45–54	15.0%	$3,804	$210
Female 55–59	6.2%	$5,007	$341
Female 60–64	4.6%	$7,108	$628
Male 0–34	13.0%	$1,170	$106
Male 35–44	9.9%	$2,186	$197
Male 45–54	10.9%	$4,248	$379
Male 55–59	5.0%	$6,023	$1,054
Male 60–64	3.4%	$6,525	$682
Number of HCC’s
0	74.5%	$2,403	$67
1	20.8%	$5,282	$326
2	3.8%	$9,542	$803
3+	0.9%	$16,971	$2,199
Overall sample	100%	$3,410	$94

Source: Medical Expenditures Panel Survey (MEPS) 2005–2009; N=11,568

Note: CMS-HCC models are estimated with individual HCC indicators.

Turning to the CMS-HCC variables, we first show average spending by all of the age-gender categories used in the CMS-HCC model. An age gradient in spending is evident for both males and females, steepening for both at the older age categories. Spending rises with number of HCCs. Notably, the large majority of likely Exchange participants have no HCC from among the set of 70 in the CMS-HCC model, even with one full year’s recorded experience. Few have more than one. (Table A in the Appendix reports average spending by individual HCC.)

Selected coefficient estimates from the least squares regressions are reported in Table 3. CMS-HCC demographic weights are shown for female age categories, but not males. Individual HCC weights are also not shown. On the premium side, urban weights for four regions and two ages are shown. The eight rural categories are not. Appendix B contains the full set of estimates for all models. The set of variables reported in Table 3 is sufficient to show how a combined model works to identify best risk adjustment weights for the Regulator and the effect of the restrictions.

Table 3.

Risk Adjustment and Premium Regression Results

	Model 1 Premiums only	Model 2 Risk Adjustment only	Model 3 Combined	Model 4 Combined	Model 5 Combined
Constraints*	None	None	RA budget	RA budget & premium ratio	RA budget, premium ratio, & half with no history
CMS-HCC Model Weights					History	no history
Female 0–34		$2,122	$953	$1,050	$1,326	$1,189
Female 35–44		$2,054	$877	$994	$1,225	$1,502
Female 45–54		$2,654	$1,138	$1,087	$1,031	$2,330
Female 55–59		$3,309	$1,407	$1,183	$1,041	$3,093
Female 60–64		$5,518	$3,227	$3,002	$3,246	$5,247
Premiums
young_n_urban	$2,319		$1,027	$999	$945
young_m_urban	$2,780		$1,407	$1,363	$1,411
young_s_urban	$2,314		$1,039	$1,014	$1,028
young_w_urban	$2,295		$1,118	$977	$939
old_n_urban	$5,550		$1,930	$1,999	$1,889
old_m_urban	$6,166		$2,639	$2,725	$2,823
old_s_urban	$5,540		$1,978	$2,027	$2,056
old_w_urban	$5,034		$1,649	$1,954	$1,878
R-squared	0.12	0.169	0.171	0.17	0.15

Source: Medical Expenditure Panel Survey, 2005–2009; Sample size =11,568

Notes: Estimates reported in $2009. HCC variable weights, male CMS-HCC weights and rural premiums not shown. Full results are contained in Appendix B. All estimates significant at p=.001 or better, except Female 55–59, w/history (Model 5), which is significant at p=.05 For the premium variables, the geographic regions are n=Northeast, m=Midwest, s=South, and w=West, interacted with urban and rural indicators.

^*RA budget constraint imposes that the average risk adjusted payment equal $2000. Premium ratio requires that within geographic regions, the ratio of premiums for older enrollees to younger enrollees be no more than 2:1. Half with no history implies that health status information is missing for (a randomly selected) half of the sample.

Model 1 contains estimates for premium variables only from a regression with just the 16 premium variables. In all regions, for the urban participants, the total premium for the old is more than twice that for the young. These sixteen indicators alone produce an R-squared of .120. Model 2 is our equivalent of the CMS-HCC model, with an R-squared of .169. Premiums use geography, which is not part of risk adjustment, and risk adjustment uses previous conditions, which are not part of premiums. Age-gender categories do much of the work in the CMS-HCC model for an exchange population, since most of the participants are relatively healthy and do not have an HCC.³⁷

Model 3 is the first of three combined models. Model 3 constrains the risk adjusted payments to plans on the basis of the CMS-HCC model to average $2,000 per person. The fit of the payment system – premiums plus risk adjusted payments -- goes up very modestly, to .171, in comparison with Model 2, the CMS-HCC model. The key results in Model 3 are the weights on the CMS-HCC variables. Model 3 shows the weights the Regulator should put on these categories to hit the budget target and in recognition that the balance of costs (e.g., on average $1,410 = $3,410 – $2,000) will be covered by premiums set in the market. For example, $953 is the weight on females 0–34. These weights are different than the conventional risk adjustment model (Model 2). When age-related premiums are doing some of the work, risk adjustment weights on age factors emphasize the large uptick in expected costs associated with being 60+. As would be expected, the difference in estimated weights on the clinical factors included in both Models 2 and 3 are not so great since health status is not a premium variable.

Model 4 adds eight premium ratio constraints to Model 3, and the corresponding zero-profit constraints for the tethered premiums. Restricting the premium for the old in Northeast urban areas to be just twice the premium for young in the same geographic area results in premiums for the two groups of $1,999 and $999 respectively. This ratio holds in all the premium estimates in Model 4. In terms of the normal equations of least squares, with the premium constraint there is one variable with respect to which fit is maximized. The first-order condition corresponds to the following “zero-profit constraint:” a plan attracting a representative population of young and old from a region would make zero profit. This is the natural competitive constraint since the plan also can essentially select one variable, the level of premiums, which must then move in a certain ratio. Model 4 shows the weights for the CMS-HCC variables that are incentive-compatible with these premiums (i.e., those that would lead plans to set them in this ratio in their own interest in competition) and which yield the best overall fit for the payment system. The R² for Model 4, 0.170, is very slightly smaller than that of 0.171 from Model 3, indicating that, if risk adjustment weights are set correctly, the sacrifice in fit due to the premium ratio restrictions is negligible.

Finally, Model 5 maintains the constraints from Model 4 and adds the realistic feature that the Regulator must set risk adjustment weights when past history is available for only part of the population. Model 5 results are reported in two columns for the CMS-HCC demographic indicators, reflecting that the Regulator needs two sets of population weights, one for the population with a history and one for the population without. The decisions about weighting demographic factors for the groups with and without histories are linked together because premiums enrollees pay to plans are the same for members of each group (i.e., premiums do not depend on whether the individual has a history or not).³⁸ The single least squares Model 5 instructs the Regulator how best to set weights for the history and no-history populations for age and gender and for the HCCs in the history population. As expected, the population “without history” features a much steeper age gradient in weights than the “with history” population where the Regulator can also use the HCCs from the previous year to set payment. The R² for the overall fit has fallen to .148, a value that refers to the fit for the entire population.

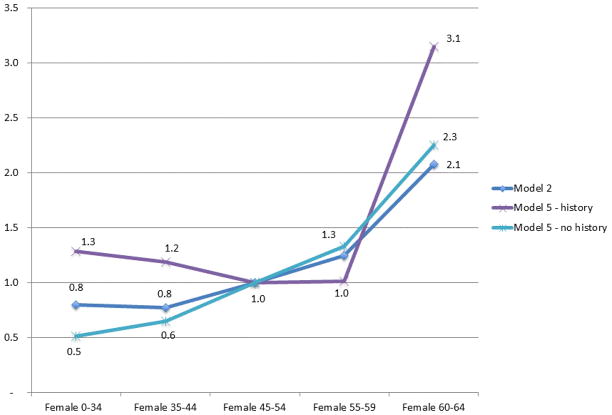
As a way to illustrate the quantitative importance of including premium variables and constraints within the least squares estimates, Figure 1 shows the relative weights for female age categories across selected risk adjustment models. Model 2 represents the weights from “conventional risk adjustment.” (There are no risk adjustment weights in Model 1.) Relative weights in the other models are affected by the presence of premiums and the constraints, with the sharpest contrast with the weights from Model 5. These are contrasted with conventional risk adjustment weights in Figure 1. “Without history” enrollees call for monotonically and substantially increasing weights with age. For enrollees “with history” (e.g., HCC indicators), the HCCs capture differences in expected costs for the four lower age categories. When HCCs are available (and premiums are partly conditioned on age), the weight in risk adjustment needs only to be higher for the oldest female age category. Premiums are doing some of the work in fitting payments to costs, altering the weights on age in the CMS-HCC model.

Figure 1.

Risk Adjustment Relative Weights

Source: Author’s analysis of risk-adjustment regression results. Model 2 includes risk-adjustment variables only. Model 5 imposes budget and age ratio constraints; no-history indicates health status information is missing.

6. Discussion

The primary purpose of our paper is to demonstrate the versatility of least squares methods for risk adjustment in individual health insurance markets with enrollee premiums. Development of actual risk adjustment weights should be done with different and ideally state-specific data, and account for the rules about flows of funds and premium setting in Exchanges. Methods from our paper could be also be modified to estimation of risk adjustment weights for a premium-support policy in Medicare Part C.

The relation between age and gender and HCC indicators (or other risk adjuster variables) and next year’s health care cost is likely to vary a great deal across states. The vast literature on “geographic variations” supports this notion as does the importance of local data in actuarial methods. The easy-to-use feature of least squares makes it feasible for states to use their own data to weight the risk adjuster variables in the CMS-HCC system or any modification of it.

Generally, risk adjustment is intended to counter problems related to adverse selection. Fitting payments (premiums plus risk adjusted payments) to a measure of costs is a step in the right direction, but as is well-recognized, leaves many issues unresolved. Costs are measured with error that is known to plans. In reality cost is not fixed because it is subject to medical management, and the efficacy of that can vary across plans. Enrollees may know more about their likely costs and use beyond the factors captured in risk adjustment. For example, factors related to costs may be unknown or impossible to incorporate in any ex ante risk adjustment policy, but be revealed to a plan as experience accumulates with a beneficiary. The plan will then have incentives to discourage such beneficiaries from continuing to enroll. To the degree that selection-related problems can be recognized and quantified, modification of risk adjustment and payment policy may be of some help. Practically speaking, targetted efficiency corrections will have to fit in with the governing framework of empirical risk adjustment research, to fit expected costs as best as possible.

A number of factors beyond those addressed here need consideration in development of a risk adjustment policy. We acknowledge some of them here and briefly comment on how they could be accommodated within the methods developed here.

Moral hazard

Health care utilization is endogenous to insurance coverage. The health care use by the population studied here is likely to increase following their transition to insurance. It would be possible in MEPS, where coverage is known, to factor use up or down with an assumption about demand response and according to whether coverage in an Exchange plan was likely to be better or worse than the person’s current coverage.

Mulitiple plan types

Exchanges will have four plan types with varying degrees of coverage; coverage in the Bronze plans will be most basic. Risk adjustment policy must decide how much of costs to include in risk adjustment and whether the payment for an enrollee should differ across plan types, perhaps in anticipation of more expensive enrollees selecting into better coverage. Efficient sorting of enrollees among plan types requires that enrollees face their “incremental marginal cost” across plans, which differs by enrollee type, and should not include average cost differences due to selection. Conditioning risk adjustment payments on type of plan selected may be necessary to offset selection.

Service-level selection

Health plans may distort service offerings to attract good risks and deter bad risks. Services for predictable services used by enrollees with high total health care costs are particularly subject to strict rationing (Ellis and McGuire, 2007). One way to address service-level selection incentives is to include additional constraints derived from plan profit maximization that characterize the risk adjustment weights that lead a plan to allocate a budget efficiently across services (Glazer and McGuire, 2002).

Imperfect competition in health insurance markets

Premiums charged by private insurers exceed costs due to the presence of administrative and sales costs, and potentially super-competitive profits. Even in this context the least squares regression can still be interpreted as derivation of risk adjustment weights in relation to the claims cost portion of premiums. Restrictions on premiums, such as the premium ratio, would need to be rewritten if cost and profit markups do not have a proportionate effect on all premiums.

Information to use in risk adjustment and premiums

In this paper we take as given the set of factors used as the basis of risk adjustment and premiums. One natural question is, given a factor that can be used in a payment system (e.g., geography), what are the considerations relevant to using it for risk adjustment or premiums (or both)? Premium discrimination has fairness implications as well as affecting plan choice. Risk adjustment has another set of effects directed towards plan behavior.

Other payment system features

Actual payment systems in Medicare and the Exchanges features such as reinsurance and risk-sharing that affect fit and plan incentives. Calculation of risk adjustment weights and consideration of any incentive properties of payment systems should incorporate the other elements of a payment system in addition to premiums and risk adjustment.

Medicare has always used least squares regression methods to assign weights to risk adjuster variables. In addition to being easy to use, the statistical criterion of “least squares” corresponds to a policy interest in the “best fit” of a payment system to deal with risk and selection. As this paper shows, least squares methods have another attractive property when enrollee premiums share the burden of paying for health care costs with risk adjusted payments. The “normal equations” in least squares correspond to the “zero-profit” conditions that govern premium setting in a competitive market. Thus, least squares methods embody both the Regulator’s objective – payment system fit – and a simultaneous solution to the problem of setting risk adjustment weights in the presence of premiums. Furthermore, when the Regulator is constrained by a budget, by premium targets, by having health history on only part of the population, least squares methods retain their easy-to-use feature and maximize payment system fit subject to these constraints.

Appendix Tables

Table A.

Sample Size and Spending for HCCs Included in the Empirical Analysis

HCC	Obs.	Mean($)	S.D.($)	Min($)	Max($)
1 HIV/AIDS	102	5291	10600	0	66413
2 Septicemia/Shock	27	5304	7282	0	28607
5 Opportunistic Infections	160	3267	5062	0	39006
7 Metastatic Cancer and Acute Leukemia	22	20032	32241	624	115175
10 Breast, Prostate, Colorectal and Other Cancers and Tumors	247	6129	12350	0	78955
19 Diabetes without Complication	718	8351	14501	0	154657
27 Chronic Hepatitis	23	6913	9352	0	28218
31 Intestinal Obstruction/Perforation	32	2326	3580	0	18253
33 Inflammatory Bowel Disease	25	4638	6117	0	25189
37 Bone/Joint/Muscle Infections/Necrosis	90	4604	8677	0	63474
38 Rheumatoid Arthritis and Inflammatory Connective Tissue Disease	105	8321	13127	0	72020
44 Severe Hematological Disorders	20	10228	22578	0	92289
52 Drug/Alcohol Dependence	25	2549	2716	0	11130
55 Major Depressive, Bipolar, and Paranoid Disorders	62	8304	13203	0	99372
74 Seizure Disorders and Convulsions	20	4515	5610	106	21139
75 Coma, Brain Compression/Anoxic Damage	373	6050	11148	0	104611
77 Respirator Dependence/Tracheostomy Status	33	2713	3140	0	11468
80 Congestive Heart Failure	95	9955	19673	0	158424
82 Unstable Angina and Other Acute Ischemic Heart Disease	65	12248	26593	0	168243
83 Angina Pectoris/Old Myocardial Infarction	32	8812	11048	471	45428
92 Specified Heart Arrhythmias	64	6731	12532	0	92289
96 Ischemic or Unspecified Stroke	35	16763	38536	5	168243
104 Vascular Disease with Complications	122	8486	19556	0	168243
108 Chronic Obstructive Pulmonary Disease	318	7713	17080	0	174984
119 Proliferative Diabetic Retinopathy and Vitreous Hemorrhage	99	11600	56091	0	546121
131 Renal Failure	20	21015	26563	0	92289
155 Major Head Injury	32	4793	11441	0	60260
157 Vertebral Fractures without Spinal Cord Injury	88	6552	10990	0	74920
164 Major Complications of Medical Care and Trauma	20	7180	9338	0	34621
176 Artificial Openings for Feeding or Elimination	349	6299	11093	0	82733
HCC high expenditure group*	126	13246	27356	0	226946
HCC low expenditure group**	92	6807	10074	0	50814
No HCC	8614	2403	6220	0	213339

Source: MEPS 2005–2009. All spending reported in $2009, N=11,568

^*This category includes HCCs for which there are fewer than 20 observations in the category and mean spending is greater than $10,000 per year. It includes hcc8, hcc9, hcc26, hcc45, hcc72, hcc79, hcc100, hcc105, hcc111, hcc130, hcc132, hcc158 and hcc174.

^**This category includes HCCs for which there are fewer than 20 observations in the category and mean spending less than $10,000 per year. It includes hcc32, hcc54, hcc68, hcc69, hcc70, hcc71, hcc73, hcc95, hcc107, hcc148, hcc177.

Table B.

Full Regression Results

	Model 1	Model 2	Model 3	Model 4	Model 5**
Constraints*	Premiums	Risk Adjustment	Combined	Combined	Combined
	None	None	RA budget	RA budget Premium ratio	RA budget Premium ratio Half with no history
CMS-HCC Model Weights					w/history	w/o history
Female 0–34		$2,122 (10.10)	$953 (4.30)	$1,050 (5.54)	$1,326 (4.85)	$1,189 (4.48)
Female 35–44		$2,054 (7.97)	$877 (3.28)	$994 (4.12)	$1,225 (3.47)	$1,502 (4.51)
Female 45–54		$2,654 (10.99)	$1,138 (4.92)	$1,087 (4.86)	$1,031 (3.27)	$2,330 (7.39)
Female 55–59		$3,309 (8.82)	$1,407 (3.23)	$1,183 (3.25)	$1,041 (1.99)	$3,093 (6.14)
Female 60–64		$5,118 (11.74)	$3,227 (6.60)	$3,002 (7.04)	$3,246 (5.31)	$5,247 (8.93)
Male 0–34		$720 (2.84)	−$451 (−1.71)	−$349 (1.48)	−$232 (0.69)	$31 (0.09)
Male 35–44		$1,470 (5.06)	$289 (0.97)	$404 (1.46)	$422 (1.09)	$1,007 (2.51)
Male 45–54		$3,154 (11.26)	$1,606 (5.90)	$1,558 (5.88)	$1,743 (4.56)	$2,473 (6.71)
Male 55–59		$4,315 (10.38)	$2,428 (5.15)	$2,197 (5.42)	$1,017 (1.81)	$5,553 (9.40)
Male 60–64		$4,200 (8.33)	$2,336 (4.24)	$2,105 (4.24)	$1,659 (2.38)	$4,706 (6.63)
Premiums
young_n_urban	$2,319 (7.49)		$1,027 (3.25)	$999 (88.40)	$945 (78.39)
young_m_urban	$2,780 (10.04)		$1,407 (4.90)	$1,363 (114.46)	$1,411 (135.86)
young_s_urban	$2,314 (11.22)		$1,039 (4.66)	$1,014 (149.53)	$1,028 (129.48)
young_w_urban	$2,295 (10.10)		$1,118 (4.61)	$977 (95.43)	$939 (84.22)
old_n_urban	$5,550 (12.57)		$1,930 (4.04)	$1,999 (88.40)	$1,889 (78.39)
old_m_urban	$6,166 (14.69)		$2,639 (5.78)	$2,725 (114.46)	$2,823 (135.86)
old_s_urban	$5,540 (18.09)		$1,978 (5.45)	$2,028 (149.53)	$2,056 (129.48)
old_w_urban	$5,034 (14.47)		$1,649 (4.18)	$1,954 (95.43)	$1,878 (84.22)
young_n_rural	$4,120 (4.63)		$2,443 (2.81)	$1,272 (39.02)	$1,388 (42.01)
young_m_rural	$2,425 (4.81)		$1,180 (2.37)	$1,039 (57.08)	$1,037 (54.90)
young_s_rural	$2,813 (6.46)		$1,390 (3.20)	$1,195 (64.65)	$1,245 (57.46)
young_w_rural	$2,518 (3.24)		$1,440 (1.89)	$571 (22.70)	$515 (19.17)
old_n_rural	$4,270 (3.46)		$253 (0.21)	$2,543 (39.02)	$2,777 (42.01)
old_m_rural	$5,155 (7.80)		$1,795 (2.66)	$2,079 (57.08)	$2,074 (54.90)
old_s_rural	$5,872 (10.45)		$2,025 (3.46)	$2,390 (64.65)	$2,490 (57.46)
old_w_rural	$2,771 (2.65)		−$467 (−0.45)	$1,143 (22.70)	$1,030 (19.17)
HCC
hcc_high_exp		$8,146 (9.26)	$8,164 (9.28)	$8,132 (9.24)	$10,614 (8.68)
hcc_low_exp		$2,574 (2.51)	$2,530 (2.47)	$2,564 (2.50)	$4,089 (2.74)
hcc1		$2,076 (2.13)	$2,082 (2.14)	$2,065 (2.12)	$1,230 (0.85)
hcc2		$2,398 (1.28)	$2,436 (1.30)	$2,441 (1.30)	$1,791 (0.63)
hcc5		−$257 (−0.33)	−$292 (−0.37)	−$305 (0.39)	−$334 (0.31)
hcc7		$13,959 (6.67)	$13,817 (6.60)	$13,770 (6.58)	$20,749 (6.18)
hcc10		$1,816 (2.88)	$1,781 (2.82)	$1,776 (2.82)	$1,563 (1.73)
hcc19		$3,792 (9.84)	$3,772 (9.77)	$3,761 (9.76)	$4,406 (8.04)
hcc27		$2,642 (1.29)	$2,673 (1.31)	$2,703 (1.32)	−$1,385 (0.50)
hcc31		−$2,743 (−1.58)	−$2,770 (−1.60)	−$2,758 (1.59)	−$2,888 (1.09)
hcc33		$984 (0.50)	$904 (0.46)	$952 (0.49)	$2,848 (1.08)
hcc37		$609 (0.59)	$666 (0.64)	$683 (0.66)	$2,489 (1.77)
hcc38		$3,466 (3.61)	$3,416 (3.55)	$3,373 (3.51)	$2,187 (1.65)
hcc44		$3,364 (1.53)	$3,431 (1.56)	$3,339 (1.52)	−$965 (0.19)
hcc52		−$577 (−0.29)	−$645 (−0.33)	−$605 (0.31)	−$1,554 (0.50)
hcc55		$4,906 (3.94)	$4,916 (3.95)	$4,927 (3.96)	$4,110 (2.48)
hcc74		$812 (0.37)	$779 (0.36)	$762 (0.35)	$2,352 (0.63)
hcc75		$2,035 (3.95)	$2,019 (3.92)	$2,032 (3.94)	$2,043 (2.84)
hcc77		−$1,451 (−0.85)	−$1,526 (−0.90)	−$1,543 (0.91)	−$925 (0.39)
hcc80		$3,617 (3.56)	$3,602 (3.54)	$3,576 (3.52)	$2,702 (1.85)
hcc82		$5,847 (4.77)	$5,746 (4.69)	$5,738 (4.68)	$7,927 (4.27)
hcc83		$2,347 (1.35)	$2,235 (1.29)	$2,287 (1.32)	−$475 (0.18)
hcc92		$1,411 (1.15)	$1,266 (1.03)	$1,294 (1.05)	$1,646 (0.96)
hcc96		$10,950 (6.60)	$10,788 (6.50)	$10,842 (6.53)	$4,926 (1.91)
hcc104		$3,153 (3.52)	$3,125 (3.49)	$3,135 (3.50)	$2,771 (1.87)
hcc108		$3,205 (5.74)	$3,218 (5.75)	$3,179 (5.69)	$4,361 (5.45)
hcc119		$7,280 (7.37)	$7,246 (7.33)	$7,243 (7.33)	$1,705 (1.27)
hcc131		$12,533 (5.68)	$12,514 (5.67)	$12,461 (5.65)	−$4,749 (1.06)
hcc155		$1,361 (0.79)	$1,296 (0.75)	$1,268 (0.73)	−$725 (0.32)
hcc157		$1,081 (1.03)	$1,122 (1.06)	$1,077 (1.02)	$328 (0.24)
hcc164		$1,538 (0.70)	$1,417 (0.65)	$1,439 (0.66)	$2,608 (0.82)
hcc176		$2,323 (4.35)	$2,306 (4.32)	$2,324 (4.35)	$1,492 (1.99)
RA budget constraint			0 -	−36,706 (0.28)	−56,129 (0.43)
RA budget constraint					−1,900 (0.01)
Age rating constraint				−31,460 (0.23)	−165,055 (0.91)
Age rating constraint				−90,784 (0.51)	96,215 (0.58)
Age rating constraint				94,962 (0.58)	102,971 (2.14)
Age rating constraint				104,715 (2.20)	19,990 (0.23)
Age rating constraint				21,436 (0.25)	32,327 (0.33)
Age rating constraint				47,244 (0.49)	85,705 (1.54)
Age rating constraint				98,093 (1.79)	161 (1.71)
Age rating constraint				18 (1.03)	−138 (1.50)
Restrict zero profit in region				−543 (0.73)	−534 (0.71)
Restrict zero profit in region				−34 (0.08)	−32 (0.08)
Restrict zero profit in region				−56 (0.16)	−38 (0.11)
Restrict zero profit in region				−380 (0.59)	−332 (0.51)
Restrict zero profit in region				24 (0.09)	36 (0.14)
Restrict zero profit in region				17 (0.07)	1 0.00
Restrict zero profit in region				26 (0.15)	48 (0.27)
Restrict zero profit in region				−34 (0.18)	−35 (0.18)
R square	0.120	0.169	0.171	0.167	0.146

Source: MEPS, 2005–2009. N = 11,568, All dollar estimates reported in $2009, t-statistics in parentheses.

For the premium variables, the geographic regions are n=North, m=Midwest, s=South, and w=West, interacted with urban and rural indicators. Probability computed using beta distribution for restrictions.

^*RA budget constraint imposes that the average risk adjusted payment equal $2000. Premium ratio requires that within geographic regions, the ratio of premiums for older enrollees to younger enrollees be no more than 2:1. Half with no history implies that health status information is missing for (a randomly selected) half of the sample.

^**There are two budget constraints for model 5, one for people with history and the other for people without history.