Can Drugs Enhance Hypofractionated Radiotherapy? A Novel Method of Modeling Radiosensitization Using in Vitro Data

Abstract

Background

Hypofractionated radiotherapy (hRT) is being explored for a number of malignancies. The potential benefit of giving concurrent chemotherapy with hRT is not known. We seek to predict the effects of combined modality treatment using mathematical models derived from laboratory data.

Methods

Data from 26 published clonogenic survival assays for cancer cell lines without and with the use of radiosensitizing chemotherapy were collected.

The first three data points of the radiotherapy (RT) arm of each assay were used to derive parameters for the Linear Quadratic (LQ) Model, the Multitarget (MT) Model, and the Generalized Linear Quadratic (gLQ) Model. For each assay and model, the difference between the predicted and observed surviving fraction at the highest tested RT dose was calculated.

The gLQ model was fit to all of the data from each RT cell survival assay, and the biologically equivalent doses in 2-Gy fractions (EQD2s) of clinically-relevant hRT regimens were calculated. The increase in cell kill conferred by the addition of chemotherapy was used to estimate the EQD2 of hRT along with a radiosensitizing agent. For comparison, this was repeated using conventionally-fractionated RT regimens.

Results

At a mean RT dose of 8.0 Gy, the average errors for the LQ, MT, and gLQ models were 1.63, 0.83, and 0.56 log units, respectively, favoring the gLQ model (p<0.05). Radiosensitizing chemotherapy increased the EQD2 of hRT schedules by an average of 28% to 82%, depending on disease site. This was similar to the gains predicted for the addition of chemotherapy to conventionally-fractionated RT.

Conclusions

Based on published in vitro assays, the gLQ equation is superior to the LQ and MT models in predicting cell kill at high doses of RT. Modeling exercises demonstrate that significant increases in biologically equivalent dose may be achieved with the addition of radiosensitizing agents to hRT. Clinical study of this approach is warranted.

Introduction

The majority of patients receiving radiotherapy (RT) are treated with small, daily fractions over a number of weeks. In general, this approach maximizes tumor cell kill while limiting normal tissue toxicity. In recent years, technological advances in target definition, treatment planning, and setup verification have led to increased interest in the use hypofractionated radiotherapy (hRT) for a number of malignancies. For some diseases, RT delivered in one or a few fractions has already shown promise as being safe and effective.(1–4) In other situations where adequate clinical experience is lacking, clinicians often attempt to predict the likelihood of tumor control and normal tissue complications with a novel RT regimen by calculating its biologically effective dose (BED) or biologically equivalent dose in 2-Gy fractions (EQD2).

In practice, calculation of BED or EQD2 is most commonly performed using the linear quadratic (LQ) model.(5) This formula was initially derived to fit experimental observations of the effects of RT dose on cell survival in vitro. There is concern, however, that the LQ model is ill-suited to predict cell survival after high doses of RT.(6) The ability of the LQ model to predict clinical outcomes with hRT schedules has also been questioned.(7)

The addition of radiosensitizing chemotherapy to conventionally-fractionated RT has been shown to improve local control and overall survival for a number of disease sites.(8–14) In diseases where outcomes remain poor, further therapeutic gains may be possible through the combination of hRT and radiosensitizing agents. This will be an active area of study in coming years.

In this study we use published clonogenic assay data to compare the performance of several cell survival models at high doses of RT. We then utilize data from in vitro studies of radiosensitizing agents to quantify the potential gains in EQD2 that may be made through the combination of systemic therapy and hRT.

Methods

Evaluating Cell Survival Models

A literature search for publications containing clonogenic cell survival assay data for glioblastoma (GBM), head and neck cancer (HNC), pancreatic cancer, or non-small cell lung cancer (NSCLC) cell lines with and without the use of a clinically-used radiosensitizing agent was performed. Survival curves with four or more data points were included for this analysis.

Based on statistical considerations (see below), data from 26 experiments was collected. For papers in which numerical data were not provided, a customized script in MATLAB (Mathworks, Natick, MA) was used to extract data from digitized graphical survival curves.

The first portion of this study tested the accuracy of various cell survival models at high RT doses. The three models that were assessed were the LQ model(5), the multi-target (MT) model(6), and the generalized linear-quadratic (gLQ) model for constant dose-rate irradiation.(15) For this portion of the study, RT only data (no chemotherapy) was utilized.

1. Linear Quadratic Model: $\mathrm{S}={\mathrm{e}}^{-\mathrm{\alpha }\mathrm{d}-\mathrm{\beta }\mathrm{d}^2}$

2. Multi-target Model: $\mathrm{S}=1-{[1-{\mathrm{e}}^{(-\mathrm{d}/\mathrm{D}0)}]}^{\mathrm{n}}$

3. Generalized Linear Quadratic Model: $\mathrm{S}={\mathrm{e}}^{-\mathrm{\alpha }\mathrm{d}-\mathrm{\beta }\text{Gd}^2}$, where

   G = 2 [εT−1+e^−εT]/ε²T²,

   ε = μ + β₂I₀,

   μ = ln(2)/T_r,

   β₂ = sqrt(β), and

   I₀ = d/T

   S is surviving fraction; d is radiation dose in Gy. For model (3), values of 20 minutes for treatment time(T) and 24 minutes(15–21) for repair half-time(T_r) were used.

For each data set and model, least-squares optimization was performed on a log-linear plot of surviving fraction v. dose, using only the first three data points of each cell survival curve (RT only). Values for the parameters (α, β) for models (1) and (3) and (D0) for model (2) were restricted to be ≥ 0. In model (2), n was restricted to be ≥ 1.

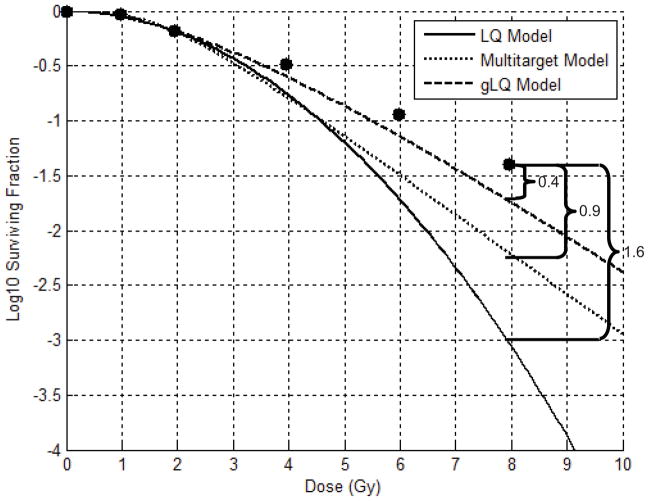
For each survival curve and model, the difference (in log units) between the predicted surviving fraction and the actual surviving fraction at the highest tested dose was recorded as the model error. (Figure 1) Assuming a standard deviation for model error of 0.75 log units, it was calculated that 26 survival assays should be utilized to provide a 90% probability of detecting a difference in mean error between models of 1 log unit.

Figure 1.

Example (data from van Bree, et al [46]) of Determining Model Errors: Each cell survival model is fit to only the first three data points from a clonogenic cell assay (radiotherapy only). At the highest tested dose (8 Gy), the Linear Quadratic (LQ), Multi-target, and Generalized Linear Quadratic (gLQ) models overestimate cell kill by 1.6, 0.9, and 0.4 log units, respectively.

To test for systematic error in each model, unpaired Student’s t-test was used to evaluate the hypothesis that the mean model error was equal to 0. To test the models against one another, paired Student’s t-test was utilized to compare the absolute value of the model errors.

Estimating EQD2 of hRT without and with drug

In the second portion of this study, we quantified the potential benefit of the addition of established radiosensitizing systemic agents to hRT. For each disease site, we evaluated a conventionally-fractionated radiotherapy regimen as well as one hRT regimen that has been utilized in published clinical reports. The selected RT schedules are listed in Table 3.

Table 3.

Biologically equivalent doses of conventional and hypofractionated radiotherapy regimens, with and without the addition of chemotherapy

Disease	RT Schedule [reference]	RT: Mean EQD2 (95% CI)	RT+Chemo: Mean EQD2 (95% CI)	Mean EQD2 increase	p
GBM	2.0 Gy x 30 fx = 60 Gy(8)	60.0 Gy (NA)	121.3 Gy (97.9 to 144.7 Gy)	102%	0.002
GBM	6.0 Gy x 5 fx = 30 Gy(51)	51.6 Gy (40.6 to 62.6 Gy)	77.8 Gy (72.3 to 83.3 Gy)	39%	0.015
HNC	2.0 Gy x 35 fx = 70 Gy(52)	70.0 Gy (NA)	105.2 Gy (81.3 to 129.1 Gy)	50%	0.034
HNC	5.0 Gy x 6 fx = 30 Gy(53, 54)	38.4 Gy (32.3 to 44.6 Gy)	49.7 Gy (39.5 to 59.9 Gy)	28%	0.045
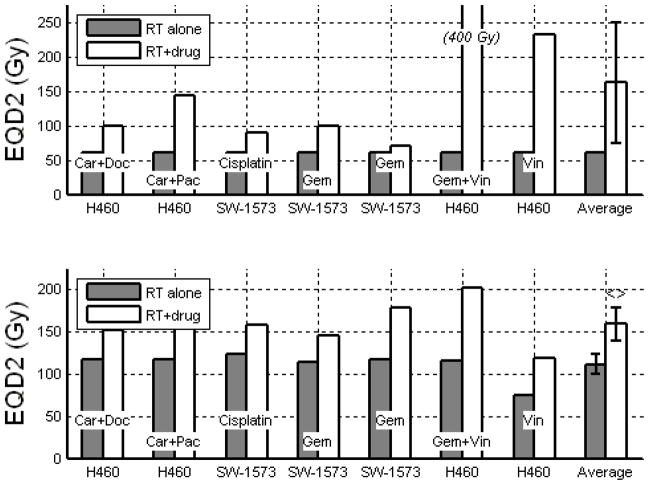
NSCLC	2.0 Gy x 30 fx = 60 Gy(10)	60.0 Gy (NA)	161.6 Gy (74.1 to 249.2 Gy)	169%	0.063
NSCLC	10.0 Gy x 5 fx = 50 Gy(55, 56)	111.5 Gy (99.4 to 123.5 Gy)	159.3 Gy (139.9 to 178.6 Gy)	42%	0.001
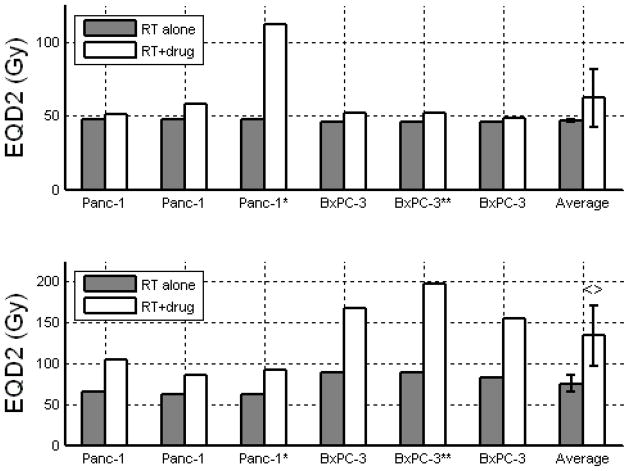
Pancreas	1.8 Gy x 28 fx = 50.4 Gy(57)	46.8 Gy (46.2 to 47.4 Gy)	62.4 Gy (42.8 Gy to 82.1 Gy)	34%	0.175
Pancreas	10.0 Gy x 3 fx = 30 Gy(58)	75.2 Gy (64.6 to 85.7 Gy)	133.8 Gy (97.1 to 170.5 Gy)	82%	0.007

Modeled radiotherapy (RT) fractionation schedules. (fx = fraction, EQD2 = biologically equivalent dose of RT given in 2 Gy fractions, NA = not applicable)

Based on the findings from the first portion of this study (see below), we utilized the gLQ model for the remainder of this analysis. For each survival curve (RT alone, all data points), least-squares optimization was performed on a log-linear plot of surviving fraction v. dose to determine values of α and β. Again, α and β were restricted to be ≥ 0.

For each data set and RT regimen, EQD2 was determined as follows:

$$\begin{array}{l}\mathrm{S}={({\mathrm{e}}^{-\mathrm{\alpha }\mathrm{d}-\mathrm{\beta }\text{Gd}^2})}^{\mathrm{D}/\mathrm{d}}\\ {\mathrm{S}}_2=({\mathrm{e}}^{-2\mathrm{\alpha }-4\mathrm{\beta }\mathrm{G}})\\ \text{EQD}2=ln(\mathrm{S})/ln({\mathrm{S}}_2)\ast 2\text{Gy}\end{array}$$

S₂ is surviving fraction after 2 Gy of irradiation; EQD2 is the biologically equivalent dose of RT given in 2 Gy fractions. Note that for RT schedules with a fraction size of 2 Gy, EQD2 will simply be equal to the prescription dose, D.

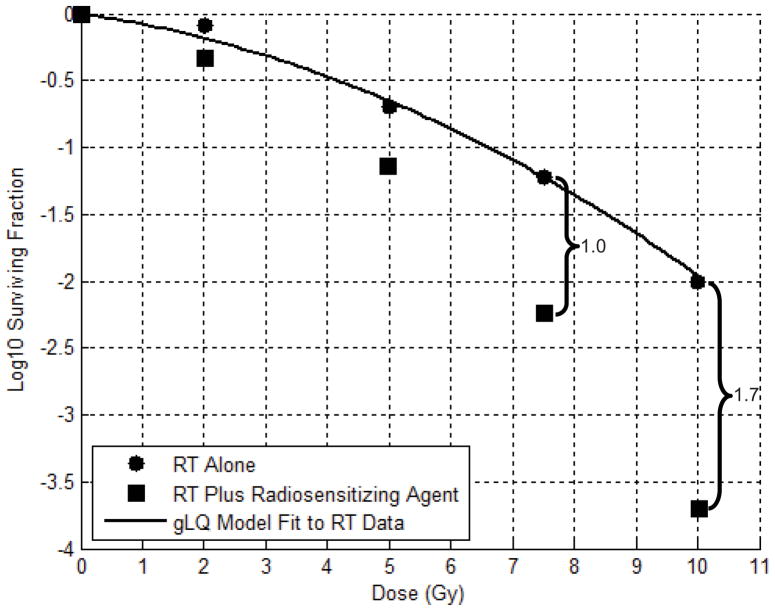
To determine the potential effects of adding radiosensitizing agents to RT, we first estimated the dose enhancement factor (DEF), defined as the increase in log cell kill, for each survival curve at each proposed fraction size. As DEF tends to increase with fraction size, a conservative estimate was made for each proposed fractionation scheme by using the DEF calculated using the surviving fraction values at the closest lower tested RT fraction size. (See Figure 2) Biologically equivalent dose for each data set and proposed chemoradiotherapy regimen was then calculated as follows:

$$\begin{array}{l}{\mathrm{S}}_{\mathrm{d}}={({10}^{-\text{DEF}}\ast {\mathrm{e}}^{-\mathrm{\alpha }\mathrm{d}-\mathrm{\beta }\text{Gd}^2})}^{\mathrm{D}/\mathrm{d}}\\ \text{EQD}2=ln({\mathrm{S}}_{\mathrm{d}})/ln({\mathrm{S}}_2)\ast 2\text{Gy}\end{array}$$

Figure 2.

Example of determining biologically equivalent dose (EQD2) and dose enhancement factor (DEF): After fitting the Generalized Linear Quadratic (gLQ) model to survival assay data, estimates of log cell kill at 2 Gy and 10 Gy are 0.2 and 2.0, respectively. The EQD2 of a single fraction of 10 Gy is therefore 20 Gy. To determine EQD2 for chemoradiation, the DEF is defined as the increase in log cell kill at the closest lower tested radiotherapy (RT) dose. For example, a DEF of 1.0 would be used for fraction sizes between 7.5 and 10 Gy. For fraction sizes of 10 Gy or higher, a DEF of 1.7 is used. The EQD2 of a single fraction of 10 Gy with a radiosensitizing agent in this example is 37 Gy.

D is the total RT dose, d is the dose per fraction, S_d is the surviving fraction after chemoradiotherapy, and EQD2 is the biologically effective dose of chemoradiotherapy in 2 Gy fractions.

Results

Details regarding the 26 survival assays used in this analysis are provided in Table 1. The RT survival curves had a mean of 5.5 data points (range 5–7). The assays tested RT doses up to an average of 8.0 Gy (range 5.0–10.0 Gy). Least squares optimization was performed on all available data points from the RT alone (no radiosensitizing agent) survival curves to generate the model parameters listed in Table 1.

Table 1.

Cell survival assays utilized, survival model parameters using radiotherapy-only data, and average chemotherapy dose enhancement factors.

Reference	Disease	Cell Line	Alpha (LQ)	Beta (LQ)	Alpha (gLQ)	Beta (gLQ)	D0 (MT)	n(MT)	Drug	Mean DEF
Charkravarti (38)	GBM	UN10	0.2	0.00	0.20	0.00	4.60	1.0	TMZ	0.757
Charkravarti (38)	GBM	UN11	0.2	0.00	0.20	0.00	4.60	1.0	TMZ	0.748
Kil (39)	GBM	U251	0.1	0.08	0.00	0.26	1.00	9.6	TMZ	0.333
van Nifterik (40)	GBM	VU-122	0.08	0.07	0.00	0.18	1.40	4.2	TMZ	0.198
van Nifterik (40)	GBM	VU-109	0.1	0.04	0.04	0.10	2.00	2.6	TMZ	0.077
van Nifterik (40)	GBM	AMC 3046	0.03	0.06	0.00	0.13	1.60	4.4	TMZ	0.200
van Rijn (41)	GBM	D384	0.1	0.06	0.01	0.16	1.60	3.2	TMZ	0.206
Pekkola-Heino (42)	HNC	UM-SCC-1	0.45	0.00	0.45	0.00	2.20	1.0	Cis	0.331
Pekkola-Heino (42)	HNC	UM-SCC-14A	0.3	0.15	0.00	0.58	0.70	6.6	Cis	0.535
Zhang (43)	HNC	UT-SCC-29	0.45	0.01	0.45	0.02	1.80	1.2	Cis	0.067
Zhang (43)	HNC	UT-SCC-29	0.45	0.01	0.45	0.02	1.80	1.2	Cis+Cet	0.043
Zhang (43)	HNC	UT-SCC-24A	0.2	0.04	0.15	0.10	1.60	2.6	Cis	0.102
Zhang (43)	HNC	UT-SCC-24A	0.2	0.04	0.15	0.10	1.60	2.6	Cis+Cet	0.127
Amorino (44)	NSCLC	H460	0	0.12	0.00	0.25	0.90	12.5	Car+Doc	0.454
Amorino (44)	NSCLC	H460	0	0.12	0.00	0.25	0.90	12.0	Car+Pac	0.689
Bergs (45)	NSCLC	SW-1573	0.1	0.06	0.00	0.19	1.20	7.6	Cis	0.315
van Bree (46)	NSCLC	SW-1573	0.25	0.03	0.06	0.13	1.60	3.0	Gem	0.291
van Bree (46)	NSCLC	SW-1573	0.1	0.04	0.05	0.10	2.00	2.4	Gem	0.420
Zhang (47)	NSCLC	H460	0.35	0.04	0.00	0.26	1.00	9.2	Gem+ Vin	1.353
Zhang (47)	NSCLC	H460	0.55	0.03	0.40	0.12	1.00	3.6	Vin	1.185
Lawrence (48)	Pancreas	Panc-1	0.3	0.02	0.08	0.11	1.60	3.4	Gem	0.647
Morgan (49)	Pancreas	Panc-1	0.4	0.04	0.08	0.23	1.00	7.4	Gem	0.353
Morgan (49)	Pancreas	Panc-1	0.4	0.04	0.08	0.23	1.00	7.4	Gem+Ox	0.671
Morgan (49)	Pancreas	BxPC-3	0.05	0.03	0.00	0.08	1.80	7.8	Gem	0.593
Morgan (49)	Pancreas	BxPC-3	0.05	0.03	0.00	0.08	1.80	7.8	Gem+Erl	0.712
Symon (50)	Pancreas	BxPC-3	0.15	0.03	0.00	0.12	1.60	5.6	Gem	0.668

LQ = linear quadratic model, gLQ = generalized linear quadratic model, MT = multi-target model, TMZ = Temozolomide, Cis = Cisplatin, Cet = Cetuxmiab, Car = Carboplatin, Doc = Docetaxel, Pac = Paclitaxel, Gem = Gemcitabine, Vin = Vinorelbine, Ox = Oxaliplatin, Erl = Erlotinib, DEF=dose enhancement factor

Determining Model Errors

Fitting the three cell survival models to the first three data points of each radiotherapy survival curve yielded mean errors at the last data point of −1.49, −0.44, and −0.18 log units for the LQ, MT, and gLQ models, respectively. (Table 2a) One sample Student’s t-test demonstrated that the mean error for the LQ model was significantly (p<0.05) lower than zero, indicating a systematic error (i.e. overestimation of cell kill by the LQ model). This was not the case for the gLQ or MT models.

Table 2a.

Mean differences between predicted (using models fit to low-dose RT data) and actual cell kill with high dose RT

Model	Mean Error	95% CI	p
LQ	−1.49	−2.60 to −0.38	0.01
MT	−0.44	−1.00 to 0.12	0.12
gLQ	−0.19	−0.54 to 0.16	0.26

The mean absolute errors of the LQ, MT, and gLQ models were 1.63, 0.83, and 0.56 log units, respectively. Compared to the LQ model, both the gLQ and MT models demonstrated significantly lower absolute errors on paired Student’s t-test (p=0.01). Additionally, the absolute errors of the gLQ model were significantly lower than those of the MT model (p=0.02). The gLQ model was consequently chosen for the second portion of this study.

Estimating EQD2 of hRT without and with radiosensitizing chemotherapy

‘Mean DEF’, or the average gain in cell kill with the addition of drug to RT for each survival assay, ranged from 0.04 to 1.35 log units. Mean DEF for GBM, HNC, pancreatic cancer, and NSCLC cell lines averaged 0.36, 0.20, 0.61, and 0.67 log units, respectively. Mean DEF was significantly lower (p<0.05) for HNC cell lines than for pancreatic cancer or NSCLC on unpaired Student’s t test.

The average EQD2 values for each RT regimen and disease site, with and without radiosensitizing chemotherapy, are listed in Table 3. For conventionally-fractionated RT, the addition of chemotherapy yielded average EQD2 increases of 102%, 50%, 169%, and 34%, for GBM, HNC, NSCLC, and pancreatic cancer cell lines, respectively (mean: 89%). For the hRT regimens, corresponding EQD2 increases with the addition of chemotherapy were 39%, 28%, 42%, and 82% (mean: 48%). There was no statistically significant difference in the projected EQD2 increase using hRT compared to conventionally-fractionated RT (p = 0.345, using paired Students’ t-test). Of note, the predicted EQD2 gain when chemotherapy is added to hRT for pancreatic cancer was actually larger than that predicted for the combination of chemotherapy and conventionally-fractionated RT (mean 82% v. 34%, p<0.001 using paired Students’ t-test). This was not the case for other disease sites.

Discussion

We have demonstrated that, when fit to data from the low-dose range of clonogenic cell survival assays, the gLQ model outperforms both the LQ and MT models in predicting surviving fraction at higher radiotherapy doses. Our findings support the hypothesis, already established with a smaller sample size, (15) that the LQ model systematically overestimates cell kill at high fraction sizes. We have also shown that the effects of radiosensitizing chemotherapy seen in vitro, if reproduced in a clinical setting, would significantly increase the biologically equivalent dose delivered by commonly used hRT schema.

It has long been recognized that the LQ model is not well-suited to fit clonogenic cell survival assay data at high doses of RT.(22) In essence, the LQ equation predicts a cell survival curve that is continuously bending downward on a log-linear graph, while experimental data demonstrates a linear relationship between log cell kill and dose after an initial shoulder.(22, 23) This discrepancy has been addressed with the proposal of several novel cell survival models. These include the Lethal and Potentially Lethal (LPL) model, the Linear-Quadratic-Cubic (LQC) model, the Modified LQ (MLQ) model, the Universal Survival Curve (USC), and the gLQ model.(15, 24–28) For this exercise, we chose to compare the LQ model to the more traditional Multitarget (MT) model. The formulation of this equation, which assumes that a number of critical targets must be inactivated to kill each cell, generates a survival curve that is linear in the high dose range when plotted on a log-linear graph.

Radiotherapy works by damaging the DNA of tumor cells. One reason that the LQ model gained popularity over prior models, including the MT model, is that its parameters may be construed to reflect the formation of single- and double-strand breaks in DNA. We chose to test the gLQ model in this exercise because it maintains the form and mechanistic implications of the LQ model, with the addition of a factor to diminish the predicted cell kill at high fraction sizes. This attenuation of cell kill accounts for the fact that, at high RT fraction sizes, a large fraction of sublethal lesions are converted to lethal damage, and sublethal damage is essentially depleted.(15)

In the second portion of this study, we determined that, over a range of disease sites and hRT schedules, the addition of radiosensitizing chemotherapy would increase EQD2 by approximately 50%. This was similar to the increase in EQD2 predicted for the addition of chemotherapy to conventionally-fractionated RT schedules. As chemotherapy is commonly administered with conventionally-fractionated RT for HNC, NSCLC, pancreatic cancer, and GBM, this suggests that clinically-relevant gains may also be achieved with the addition of radiosensitizing agents to hRT.

In the case of HNC, data from randomized clinical trials has been used to estimate that the gain in local tumor control from the addition of chemotherapy to conventionally-fractionated RT equates to an increase in RT dose of 10–14%. (29, 30) This is significantly less than the 50% increase in EQD2 predicted by applying our methodology to in vitro data from HNC cell lines. Among the many potential explanations for the relatively modest gains seen in patients are the concepts that:

1. Tumor repopulation may accelerate during a lengthy treatment course and counteract gains in tumor control probability conferred by radiosensitizing agents.

2. Each fraction of a daily radiotherapy course may not be enhanced equally by intravenous chemotherapy that is administered every 3 weeks.

3. In vitro experiments cannot account for factors such as tumor oxygenation, therapeutic effects on stromal cells, and spatial variations of drug concentration within a tumor that likely affect tumor control.

Of note, limitations (1) and (2) may both be mitigated by a shift to a hypofractionated RT schedule. Modeling techniques to account for both accelerated repopulation and variations in radiosensitizing drug bioavailability have been described (29, 31, 32) but were beyond the scope of this analysis. Some investigators have also suggested that the effectiveness of hRT is enhanced by its effects on tumor microenvironment, particularly endothelial cells. (33–35) This is a potential mechanism by which tumor control rates with hRT may exceed those predicted based on clonogenic cell survival assays.

There are also reasons why a shift to hRT may not provide clinical benefit. Hypoxic cells are known to be relatively resistant to ionizing radiation.(6) Carlson et al have pointed out that the presence of transitory hypoxia will be more detrimental to the effectiveness of hRT than to that of conventionally-fractionated RT. (36) One solution may be to incorporate a hypoxic radiosensitizing agent, as suggested by the Stanford group. (37) Another approach might be to combine hRT with systemic anti-cancer agents that are equally active against hypoxic and normoxic cells.

An important limitation of our study is its dependence on in-vitro data and the consequent disregard of micro-environmental factors such as hypoxia. While it is important that we acknowledge these radiobiologic considerations, only careful clinical study can confirm if the combination of hRT and radiosensitizing chemotherapy will provide gains in tumor control.

The gLQ equation is superior to traditional cell survival models in predicting in vitro cell kill at high doses of RT. Mathematical modeling suggests that the addition of radiosensitizing agents to hRT may lead to clinically-significant gains in tumor control. These hypothesis-generating findings support the careful clinical investigation of hRT with concurrent systemic therapy.

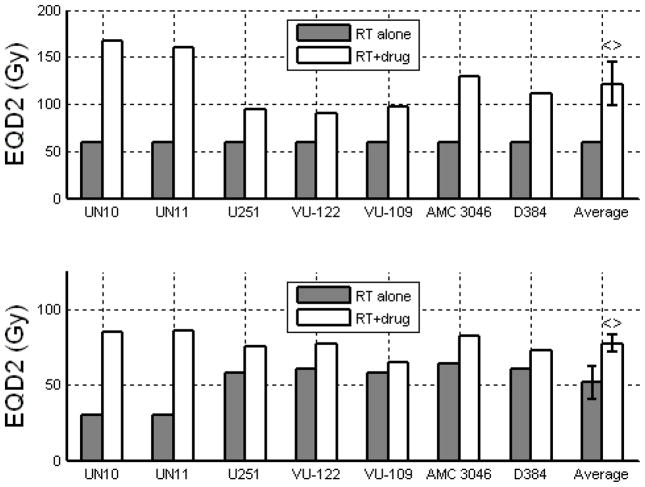
Figure 3.

EQD2 for GBM cell lines treated with 2.0 Gy x 30 (top) and 6 Gy x 5 (bottom), with and without concurrent temozolomide. Error bars indicate 95% confidence intervals. <> denotes a significant (p<0.05) increase in EQD2 with the addition of drug using paired Student’s t-test.

Figure 4.

EQD2 for HNC cell lines treated with 2.0 Gy x 35 (top) and 5.0 Gy x 6 (bottom), with and without concurrent cisplatin. * denotes addition of cetuximab. Error bars indicate 95% confidence intervals. <> denotes a significant (p<0.05) increase in EQD2 with the addition of drug using paired Student’s t-test.

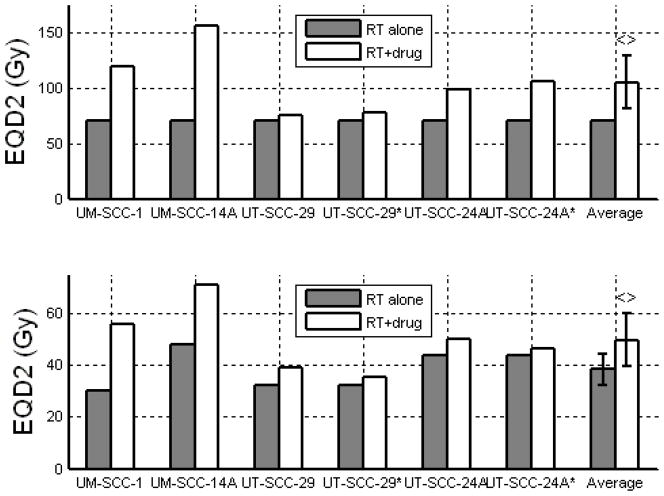
Figure 5.

EQD2 for NSCLC cell lines treated with 2.0 Gy x 30 (top) and 10.0 Gy x 5 (bottom). Car = Carboplatin, Doc = Docetaxel, Pac = Paclitaxel, Gem = Gemcitabine, Vin = Vinorelbine. Error bars indicate 95% confidence intervals. <> denotes a significant (p<0.05) increase in EQD2 with the addition of drug using paired Student’s t-test.

Figure 6.

EQD2 for Pancreatic cancer cell lines treated with 1.8 Gy x 28 (top) and 10 Gy x 3 (bottom), with and without concurrent gemcitabine. * denotes addition of oxaliplatin. ** denotes addition of erlotinib. Error bars indicate 95% confidence intervals. <> denotes a significant (p<0.05) increase in EQD2 with the addition of drug using paired Student’s t-test.

Table 2b.

Mean absolute differences between predicted (using models fit to low-dose RT data) and actual cell kill with high dose RT

Model	Mean Absolute Error	95% CI
LQ	1.63	0.55 to 2.70
MT*	0.83	0.36 to 1.31
gLQ*,**	0.56	0.28 to 0.83

^*p<0.05 compared to LQ model;

^**p<0.05 compared to MT model