Cartography and Connectomes Perspective article for Neuron 25^th Anniversary Issue

Abstract

The past 25 years have seen great progress in parcellating the cerebral cortex into a mosaic of many distinct areas in mice, monkeys, and humans. Quantitative studies of inter-areal connectivity have revealed unexpectedly many pathways and a wide range of connection strengths in mouse and macaque cortex. In humans, advances in analyzing ‘structural’ and ‘functional’ connectivity using powerful but indirect noninvasive neuroimaging methods are yielding intriguing insights about brain circuits, their variability across individuals, and their relationship to behavior.

Introduction

In recent years there has been an explosion of interest in mapping the brain and its connections systematically across a range of spatial scales and in a number of species. This is embodied in the concept of a connectome as a “comprehensive” map of brain connectivity (Sporns et al., 2005). However, a truly comprehensive connectome that charts all synaptic connections in all neurons over an entire brain is currently feasible only for tiny invertebrates such as the nematode; at the other extreme, such an achievement may not ever be feasible for the human brain. Instead, methodological constraints lead to a natural division of labor (and enthusiasm) across three complementary domains of the connectome landscape: the micro-, meso-, and macro-connectomes (Akil et al., 2011). Each domain aims to map connectivity down to the spatial resolution of the available methodologies, and over as large a spatial expanse as is technically feasible.

Every brain is an extremely complex network. Two fundamental and complementary levels of description are those of maps and connections. Maps refer to the spatial arrangement of brain parts (parcels), along with countless types of information that can be associated with each spatial location or each parcel. This is the domain of brain cartography – how maps are generated, visualized, and navigated, and what information can be represented on them. Connections are, in essence, pairwise relationships indicating the existence, strength, and/or polarity of links between different locations or different parcels as determined directly using anatomical methods or as inferred using one or another indirect imaging method. When the analysis aims to be comprehensive rather than piecemeal, connectivity studies fall into the realm of connectomics.

Why is connectomics important? Skeptics can correctly point out that knowing a complete wiring diagram will not on its own tell us how the brain works. For example, the availability of a complete nematode connectome (White et al., 1986; Varshney et al., 2011) leaves open many mysteries of how its nervous system actually processes information – i.e., how it ‘computes’. A starting counterpoint is to invoke the analogy of the genome: knowing the precise sequence of 3 billion base pairs in the human genome on its own tells us precious little about how our bodies and brains are assembled and regulated by genes and regulatory sequences. Yet the early skeptics of the Human Genome Project have largely been quieted by the awesome success of modern genomics - even though it remains humbling to realize how much is not yet understood about the workings of the genome. However, the reasons for mapping connectomes arguably goes deeper, because the precise wiring of the brain is fundamental in constraining what it can (and cannot!) compute. The brain is not a general-purpose computer that can support a variety of operating systems and software applications. Instead, the software (functions) and hardware (the squishy stuff) are intimately co-embedded with one another.

This essay focuses on brain cartography and connectomics in three intensively studied species: human, macaque monkey, and mouse. The emphasis is on cerebral cortex, owing to its physical dominance as well as the special challenges it poses, but subcortical and cerebellar domains are considered as well. Throughout the nearly four decades that I have been involved in brain mapping, methodological advances have played a transformative role in accelerating progress and deepening our understanding of brain circuits and function. The focus here is also on macroscopic cartography and connectomics, while recognizing that there have been exciting discoveries and methods development on the meso- and micro-connectome front as well.

Special emphasis is placed on the Human Connectome Project (HCP), an ambitious endeavor to chart brain connectivity and its variability in a large number of healthy adults. The HCP has already achieved a coordinated set of advances in acquiring, analyzing, visualizing, and sharing large amounts of exceptionally high quality brain imaging data along with extensive behavioral data (Van Essen et al., 2013a). This includes information about brain connectivity provided by the complementary imaging modalities of resting-state fMRI (rfMRI) and diffusion imaging (dMRI). Both modalities are powerful and have been substantially improved through advances made by the HCP, yet both have major limitations that are not always adequately appreciated. The HCP is also acquiring data using additional modalities that provide information about brain function (task-evoked fMRI and magnetoencephalography) and brain architecture (high-resolution structural MRI and cortical myelin maps derived from them). Ongoing analyses of HCP data, while still at an early stage, are already reshaping our understanding of human brain cartography, connectivity, and function, as well as their relationship to behavior.

Cartography. (Van Essen et al., 2013a; Van Essen et al., 2013b)

Cartography

An earthly comparison

The history of earth cartography provides a useful context for the ensuing discussion of brain cartography. Classical earth maps have used physical media (e.g., parchment sheets, book atlases, 3D globes) whose size limitations force tradeoffs between spatial resolution (detail) and overall spatial extent that can be represented on a given map. These restrictions do not apply to computerized maps enabled by the digital revolution. Earth maps can now cover the globe yet be exquisitely detailed, using copious computer memory to store vast amounts of information acquired by satellite imagery and other imaging methods. In parallel, the Global Positioning System has transformed the centuries-old concept of latitude and longitude into a spatial coordinate system that is precise within a few meters. This information is fed into devices and software (e.g. Google Earth, Google Maps) that have transformed our daily lives. Digital earth maps can represent countless types of information overlaid dynamically in flexible combinations that include the broad categories of geographical features (continents, mountains, rivers, etc) and political/cultural features (countries, states, etc., based on the activities and affiliations of human populations).

Earth cartographers map changes over a wide range of time scales, but there is only one earth and one spatial coordinate system. In contrast, brain cartographers must cope with the diversity of individual brains within a given species, dramatic changes in structure and function of every brain over the lifespan, and large differences between species. Nonetheless, brain cartography has undergone a parallel set of advances, including a transition from paper-based to computerized brain maps that provide increasingly powerful and flexible navigation capabilities. We first consider brain geography (shapes and physical features) and then brain parcellations that represent functionally distinct subdivisions (akin to the political subdivisions on earth maps).

Sheets and blobs; slices and surfaces

As every neuroanatomy student knows, gray matter in the mammalian brain includes the sheet-like cerebral and cerebellar cortex plus a diverse collection of blob-like subcortical nuclei. Historically, neuroscientists have tended to visualize brain anatomy mainly using slice-based representations. In classical neuroanatomy, the primary data comes from sectioning postmortem brains histologically. For MRI-based neuroimaging studies, the primary data are typically stored as 3D volumes - stacks of ‘voxels’ that are most readily visualized in slices through the volume. For example, Figure 1 (top row) shows slices of mouse, macaque, and human brains in a parasagittal slice plane that includes cerebral and cerebellar cortex plus several sub-cortical nuclei. While planar slices are invaluable for many aspects of analysis and visualization, they do not respect cortical topology and can obscure key spatial relationships between neighboring locations in the cerebral and cerebellar sheets.

Figure 1.

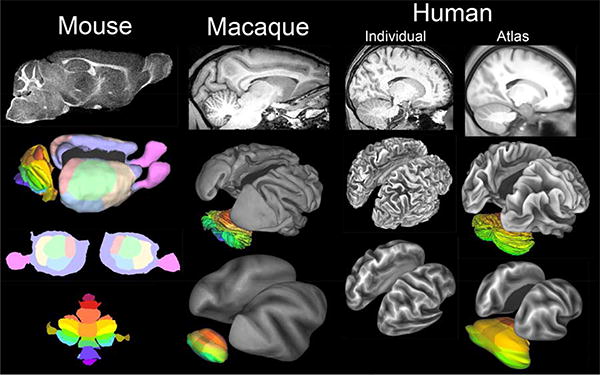
Volume and surface representations of mouse, macaque, and human brains. Top row: Parasagittal slices of high-resolution T1w scans from 3 species. The mouse and macaque data are described in Van Essen (2002a,b). The human individual and group average (120 subjects) are from HCP scans acquired at high spatial resolution (0.7 mm) rather than the 1 mm isotropic voxels conventionally used, Lower panels: Surface reconstructions are shown as midthickness surfaces (all 3) and inflated surfaces (flatmaps for the mouse). Cortical lobes are colored on the mouse surfaces; cerebellar lobules are colored for all 3 species. The mouse surface includes the olfactory bulb. The HCP surface reconstructions benefitted from refinements to standard FreeSurfer processing (Glasser et al., 2013b; Glasser et al., 2013c). The human cerebellar surface is from the Colin individual MRI atlas (Van Essen, 2002b).

A key to circumventing this difficulty is to use surface-based representations that respect the sheet-like topology of cortical structures. This is obvious nowadays, especially when aided by attractive images such as those in Figure 1. However, it assuredly was not obvious to the field when I started working on monkey visual cortex several decades ago at University College London. I quickly became frustrated by the limitations of the traditional slice-based approach to analyzing anatomical data. Consequently, much of my postdoctoral year was spent fiddling with pencil and tracing paper, until I successfully developed a manual method of making flat maps of macaque extrastriate visual cortex (Van Essen and Zeki, 1978). After I joined the faculty at Caltech, John Maunsell and I extended this approach to the entire macaque hemisphere (Van Essen and Maunsell, 1980). However, this quaint manual approach to map-making was tedious and was impractical to extend to the highly convoluted human cerebral cortex. It was clear that generating and manipulating cortical surfaces was a job far better suited for computers than humans; indeed I started on that effort in the 1970's (see Van Essen, 2012). However, the transition took decades (and is still ongoing), because it required more powerful computers, automated segmentation and surface reconstruction algorithms, and the emergence of structural MRI as a reliable way to distinguish between gray and white matter (e.g., Dale and Sereno, 1993; Van Essen et al., 2001a; see also Fischl, 2012; Van Essen, 2012). The lower panels in Figure 1 show 3D surface reconstructions of cerebral cortex (the cortical midthickness, approximately in layer 4) for mouse, macaque, and human as well as inflated surfaces and flat maps. The surface area of the two cerebral hemispheres combined varies over several orders of magnitude, smaller than a dime for a mouse (~1.8 cm²), cookie-sized in a macaque (~200 cm²), to pizza-sized in humans (2,000 cm² = two 13-inch pizzas) (Van Essen, 2002a; Van Essen et al., 2012a; Van Essen et al., 2012b).

Cerebellar cortex is very difficult to segment because it is so thin (~1/3 the thickness of neocortex) and has very little underlying white matter (owing to the absence of cortico-cortical connections) (Fig. 1A-C). To date, the only accurate surface cerebellar reconstructions are for the three individual mouse, macaque, and human cases illustrated in Figure 1 (Van Essen, 2002b). The human cerebellar surface is from the ‘Colin’ individual atlas and was generated by a labor of love, in which I spent hundreds of hours manually editing the initial segmentation in order to achieve a topologically correct and reasonably faithful representation! The two cerebellar hemispheres are connected across the midline to form a single sheet, whose surface area is comparable to that of a single cerebral hemisphere: ~0.8 cm² for the mouse cerebellum, ~60-80 cm² for the macaque, and ~1100 cm² for humans (Sultan and Braitenberg, 1993; Van Essen, 2002b), but these values are lower bounds because the surface reconstructions failed to capture most of the fine cerebellar folia.

Surface reconstructions serve three vital and complementary functions. (i) Visualization. In gyrencephalic species, cortical inflation or flattening exposes buried regions while preserving neighborhood relationships within the convoluted cortical sheet. Figure 1 (lower panels) includes inflated maps for the gyrencephalic macaque and human cerebral and cerebellar cortex, plus flat maps for all three species. Shape information (cortical “geography”) can be preserved on the smoothed surfaces using maps of “sulcal depth” to denote buried (darker) vs. gyral (lighter) regions. (ii) Within-subject data analysis. Mathematical operations such as spatial smoothing and computing spatial gradients are best carried out on surfaces when dealing with data that is specific to the cortical gray matter. Regrettably, the alternative of using volume-based 3D smoothing remains widespread in many neuroimaging studies, even though this leads to undesirable blurring between gray and white matter and across gray matter on opposite banks of (sometimes deep) sulci. Surface-constrained smoothing improves signal strength and spatial specificity (Jo et al., 2007), particularly when analyzing high-resolution data such as that from the HCP (Glasser et al, 2013c). (iii) Intersubject registration. The convolutions of human cerebral cortex are highly variable across individuals in many regions (Ono et al., 1990). In order to compensate for this variability and thereby enable accurate intersubject comparisons, it is vital to register each individual to a common atlas target. For the mouse and macaque, an individual brain is reasonable for an atlas target (Fig. 1, columns 1-2), though MRI-based population-average atlases are available as volumes (Kovacevic et al., 2005; McLaren et al., 2009) and surfaces (Glasser et al., 2012a; Glasser et al., 2013a). For human cortex, early surface-based atlases used individual brains (Van Essen and Drury, 1997; Van Essen, 2002a) but these have been supplanted by population-average atlases. Volume registration achieves accurate intersubject alignment of sub-cortical nuclei, as shown by the group average of 120 HCP subjects (Fig. 1D), blurring of cortical sulci and gyri is variable even when using high dimensional nonlinear registration. Instead, surface-based cortical registration provides clear advantages (Fischl et al., 1999a; Fischl et al., 1999b; van essen, 2005; Fischl et al., 2008; Yeo et al., 2010; Van Essen et al., 2012a; Van Essen et al., 2012b; Glasser et al., 2013a; Glasser et al., 2013b). For cerebral cortex, registration to a population-average surface-based template avoids biases associated with the idiosyncratic convolutions of any individual subject. One widely used atlas template is FreeSurfer's ‘fsaverage’, which uses an energy-based registration method to align individual folding patterns to a population average map based on the pattern of folding (Fischl et al. 1999, 2008). A recent extension of this is the ‘fs_LR’ surface mesh and the ‘Conte69′ atlas, which capitalize on FreeSurfer's energy-based registration but achieve geographic correspondence between left and right hemispheres using landmark-constrained interhemispheric registration (Van Essen et al., 2012b). In the average midthickness surfaces from 120 HCP subjects (Fig. 1, right column), only the major sulci and gyri are visible; the distinctive secondary and tertiary folds of individual subjects are not well preserved owing to imperfect alignment, especially in regions of high variability.(Glasser et al., 2012b)

The cerebellar atlas surfaces shown in Figure 1 are useful for surface-based visualization, but unfortunately not for surface-based analysis (e.g., smoothing) or intersubject alignment. Higher quality structural images and cerebellum-specific segmentation algorithms will be needed in order to enable cerebellar surface reconstructions in individual subjects as a matter of routine.

Subcortical nuclei

Subcortical nuclei constitute a major fraction of the mouse brain, but progressively much smaller fractions of the macaque and human (Fig. 1, top row). Despite their critical roles in brain function, subcortical nuclei are only ~8% of total human brain volume and even more modest in neuronal count because of their low neuronal density; they contain ~1% of total neurons in humans (Azevedo et al., 2009). The relatively modest expansion of subcortical structures compared to the evolutionary explosion of cortical structures suggests that the evolutionary changes in subcortical organization may have been modest.

Cortical parcellation

A holy grail for systems neuroscience is to identify and accurately chart the mosaic of distinct cortical areas in humans and key laboratory mammals. This is as fundamental to brain cartography as the charting of major political boundaries is to earth cartography. However, cortical parcellation has proven to be a remarkably challenging problem, owing to a combination of neurobiological and methodological complexities.

In general, cortical parcellation has been powered by four conceptually distinct approaches. Architectonics is the oldest, starting with cytoarchitecture and myeloarchitecture a century ago. This was followed by physiological and anatomical methods for mapping topographic organization of sensory and motor areas (e.g., retinotopy, somatotopy). When the modern era of systems neuroscience began in the 1970's, two additional approaches came into vogue, one that identifies areas based on pattern of connectivity and the other based on their distinctive functional characteristics. Using these approaches in isolation or in combination, evidence for a large number of cortical areas has been reported in many mammalian species. Ideally, each cortical area and each parcellation scheme would be validated by demonstrating agreement across multiple approaches. The poster child for this is area V1 in the macaque, which is readily identifiable by its distinctive architecture (e.g., the stria of Gennari), connectivity (e.g., geniculo-cortical terminations in layer 4C and projections from layer 4B to area MT), functional signature (orientation and ocular dominance columns), and precise retinotopy. Unfortunately, V1 is the exception rather than the rule. Consequently, many competing schemes coexist, and a consensus pan-hemispheric parcellation has yet to be achieved for any species. Before summarizing the current state of mouse, macaque, and human cortical parcellation efforts, it is useful to comment on four general obstacles to accurate parcellation that reflect a combination of neurobiological and methodological considerations.

(i) Noise and bias. The transitions in features that distinguish neighboring cortical areas are typically rather subtle. Identification of these transitions is often impeded by the distortions induced by cortical folding and by various artifacts and noise associated with any given parcellation method. (ii) Within-area heterogeneity. A conceptually deeper challenge arises from genuine heterogeneity in connectivity found within some cortical areas. For example, within-area heterogeneity has been reported for V1 and V2 in the macaque, where central vs peripheral parts of the visual field representation differ in their connectivity with parietal and temporal cortex (Baizer et al., 1991; Falchier et al., 2002); in primary motor cortex, the head and leg regions are connected with different areas (Tokuno et al., 1997; Hatanaka et al., 2001). In human cortex, internal heterogeneity within a single area can exceed the connectivity differences between corresponding topographic locations in neighboring areas; as illustrated below this can result in marked differences in boundaries revealed by connectivity vs architectonic methods. (iii) Topographic complexity. Topographic organization is precise and orderly in early sensory areas (e.g., visual area V1). It becomes coarser and more disorderly in regions areas progressively farther from the primary area; some areas also have an incomplete or biased representation of the contralateral sensory space (Maunsell and Van Essen, 1987; Hansen et al., 2007; Kolster et al., 2009; Kolster et al., 2010). Genuine irregularities in topographic organization make it difficult to delineate areal boundaries, and this can be compounded by methodological noise or bias. (iii) Individual variability. Comparisons across individuals are vital for crossmodal validation and for assessing the consistency of any given parcellation scheme. However, such comparisons must cope with individual variability in the size (surface area) of each cortical area and in its location relative to cortical folds. Well-defined cortical areas such as V1 vary in areal size by two-fold or more in humans and nonhuman primates (Andrews et al., 1997; Amunts et al., 1999; Amunts et al., 2000). The relationship of areal boundaries to gyral and sulcal folds is reasonably consistent in the moderately gyrencephalic macaque (Van Essen et al., 2012a) but is much more variable in humans, especially in regions of high folding variability (Amunts et al., 1999; Van Essen et al., 2012b) A corollary of this observation is that perfect alignment of cortical areas (and hence cortical function) cannot be achieved using any registration method that relies exclusively on folding pattern or other shape features. Fortunately, novel approaches now enable registration based on function and other areal features (see below).

The next three subsections provide an update on cortical parcellations in the mouse, macaque, and human, along with reference to key historical milestones in order to provide perspective. Visual cortex warrants special consideration owing to the recent identification of many more visual areas than envisioned in classical schemes.

Mouse

Early studies of rodent visual cortex suggested that area V1 was surrounded by only one or two neighboring retinotopically organized visual areas (Wagor et al., 1977). This simplistic view has been overturned by studies from Andreas Burkhalter's lab that identified 10 retinotopic visual areas in the mouse (plus additional non-retinotopic visual areas) based on focal tracer injections combined with neurophysiological mapping (Wang et al., 2007, 2011). A multimodal analysis applied to all of cortex (neocortex, transitional cortex, and part of hippocampal cortex) provides evidence for a total of 40 areas (Wang et al., 2012) as displayed in Figure 2A on a tangentially sliced section of physically flattened cortex. This cortical parcellation differs in a number of ways from that of Paxinos and Franklin (2000) and also the Allen mouse atlas (http://atlas.brain-map.org/; Dong, 2008), which are both based on cytoarchitectonics using conventional histological sections.

Figure 2.

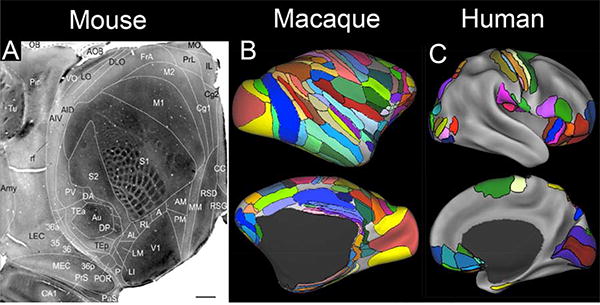
Parcellations of mouse, macaque, and human cortex. A. A 40-area parcellation of mouse cortex illustrated on a cytochrome-oxidase stained tangential section of flattened mouse cortex. (Reproduced, with permission, from Wang et al., 2012). B. A composite parcellation of macaque cortex (Van Essen et al., 2012a) showing 130 areas of neocortex and transitional cortex, based on architectonic schemes of Lewis and Van Essen (2000b), Ferry et al. (2000), and Paxinos et al., (2000) and displayed on the inflated F99 atlas surface. C. A composite parcellation of 52 cortical areas spanning ~1/3 of human neocortex, based on published architectonic and retinotopic maps and displayed on the inflated Conte69 atlas surface (Van Essen et al., 2012a).(Ferry et al., 2000; Paxinos et al., 2000; Lewis and Van Essen, 2000b)

Macaque

Studies that address one or another aspect of cortical parcellation in the macaque and other nonhuman primates now number in the thousands. Classical architectonic maps of the old world monkeys contained three concentrically organized visual areas in occipital cortex and a total of only 28 areas or 25 areas (Brodmann, 1905; von Bonin and Bailey, 1947). The evidence for a more complex cortical organization emerged gradually, starting in the 1970's with the discovery of multiple retinotopic extrastriate visual areas in the macaque (Zeki, 1978) and owl monkey (Allman, 1977). Over ensuing decades, evidence accumulated for many additional visual areas, but comparisons across studies were impeded by the lack of a suitable atlas framework. One early step in addressing this need was a summary map of 32 visual areas plus dozens of other cortical areas (Felleman and Van Essen, 1991) generated using tools available at the time: a new manual flatmap to serve as an atlas combined with ‘eyeballing’ to transfer data from other studies onto the map using gyral and sulcal features as landmarks. The transition to an atlas based on high-resolution MRI scans occurred a decade later with the introduction of the surface-based ‘F99′ macaque atlas (Van Essen, 2002a) (See Fig. 1B). Another key part of the growing toolkit was a surface-based registration algorithm for aligning different parcellation schemes to the atlas using geographic landmarks (gyral and sulcal folds) as registration constraints (Van Essen et al., 2001b; Van Essen et al., 2005). More recently we used an improved landmark-based registration method and generated a composite macaque parcellation scheme containing 130 cortical areas (Fig. 2B) based on regions considered most reliable from three independent architectonic parcellations (Van Essen et al., 2012a). Undoubtedly there will be further revisions and refinements, but this macaque parcellation provides a reasonable estimate of the approximate number of neocortical and transitional areas in the macaque. (Van Essen, 1979)

Human cortical parcellations

As in the macaque, human cortical parcellation began with classical architectonic parcellations a century ago, including a map of 44 neocortical cytoarchitectonic areas proposed by Brodmann (1909) and a larger number (185) of myeloarchitectonic areas proposed by C. and O. Vogt (see Nieuwenhuys, 2013). Advances in parcellating human cortex have come from a combination of postmortem histological and in vivo neuroimaging approaches, mainly in the past two decades. Here, the focus is on analyses that use surface reconstructions of individual subjects followed by registration to a surface-based atlas in order to cope with the complexity of human cortical convolutions and the variability in areal boundaries relative to these folds. Figure 2C illustrates a summary map (Van Essen et al., 2012b) that includes 52 surface-mapped cortical areas derived from three parcellation approaches: (i) observer-independent architectonic methods (Schleicher et al., 2005, 2009; Fischl et al., 2008); (ii) combined architectonic approaches involving cyto-, myelo-, and chemo-architecture in the same individual (Ongur et al., 2000); and (iii) retinotopic visual areas from four fMRI studies, all registered to the Conte69/fs_LR atlas. In comparing the human and macaque parcellations, there are many similarities and likely homologies between the two species, but there are also significant interspecies differences in the arrangement of retinotopic and other areas. Some of these are likely to reflect genuine evolutionary divergence in cortical organization, but others may reflect inaccuracy or incompleteness in one or both of the illustrated parcellation schemes. In the case of retinotopic areas, there are many similarities but also some clear species differences (Kolster et al., 2009, 2010). The composite 52-area human parcellation (Fig. 2c) some covers only 1/3 of cerebral neocortex, suggesting that the total number of areas may be ~150, or even more if cortical areas are on average smaller in the portions of frontal, parietal, and temporal cortex yet to be accurately mapped. Relative to the estimate of 130-140 areas in the macaque, the total number of human cortical areas may modestly exceed that in the macaque. There are good prospects for filling in many of the gaps and addressing these issues using high resolution data and improved analysis methods emerging from the HCP (see below). However, it is unlikely that a consensus parcellation will emerge soon, owing to of the subtlety of many areal boundaries and the challenges associated with individual variability.

Cerebellum and subcortical nuclei

The cerebellum represents a fascinating cartographer's challenge for several reasons. (i) It contains ‘fractured’ somatosensory maps (Shambes et al., 1978) rather than a one-to-one mapping of sensory surfaces that characterize neocortical sensory areas. (ii) It is very difficult to accurately and systematically map properties across the full cerebellar sheet using currently available neurophysiological, neuroanatomical, or neuroimaging methods owing to its thin and highly convoluted configuration, even in rodents. (iii) A large portion of cerebellar cortex in primates is implicated in higher cognitive processes (Strick et al., 2009) rather than being predominantly involved in sensori-motor coordination as traditionally thought. Human fMRI studies have revealed functional cerebellar networks that are systematically related to cerebral networks at a relatively coarse level (Buckner et al., 2011). However, until methods improve to the point that accurate surface-based mapping can be done in individual subjects, it seems likely that important organizational principles for the cerebellum may be hidden from view.

Regarding subcortical structures, conventional in vivo neuroimaging enables visualization and analysis of the larger nuclei; accurate automated segmentation of these nuclei (e.g., using FreeSurfer) is facilitated by their low degree of individual variability. However, there are many small subnuclei (e.g. of the hypothalamus) that cannot be discerned using conventional structural scans (e.g., T1w and T2w scans). On the other hand, conventional histological atlases can be complemented by specialized MR-based imaging that reveals considerably greater neuroanatomical detail using ultra-high field strength (7T or higher), specialized pulse sequences such as susceptibility-weighted imaging (Abosch et al., 2010), and/or postmortem scans (e.g. Augustinack et al., 2013) (Abosch et al., 2010; Augustinack et al., 2013)

Connectomics

Our understanding of the amazing complexity of long-range neural connections in the mammalian brain has evolved dramatically in recent decades. Key recurring themes that have emerged are (i) an unexpectedly large number of identified pathways, implying a dense rather than sparse connectivity matrix at the level of area-to-area connections; (ii) a range of interareal connection strengths that is remarkably broad but conforms to a stereotyped statistical distribution; and (iii) organization into highly distributed and interconnected networks and subnetworks. As in the cartography section, the focus here is on cerebral cortex, starting with the macaque and mouse. These are of great interest in their own right, but they also provide a vital form of ‘ground truth’ when considering human brain circuits that can only be explored using indirect methods. Quantitative ‘parcellated connectomes’ have recently been reported for all 3 species, representing major progress even though the connectomes remain incomplete for the mouse and macaque and are indirect for the human brain.

Macaque

Early studies using classical axonal degeneration-based methods suggested that each cortical area was directly connected to only a handful of other cortical areas (Van Essen, 1979). The advent of modern anterograde and retrograde tracers starting in the 1970's gradually revealed that connectivity pattern are far more complex. The finding that most pathways are bidirectional but asymmetric in their laminar pattern led Rockland and Pandya (1979) to propose that laminar pattern could be used to distinguish between feedforward and feedback directions of information flow. This in turn led John Maunsell to propose an anatomically based cortical hierarchy (Maunsell and Van Essen, 1983). Dan Felleman and I expanded this hierarchy by drawing from the available literature on macaque cortico-cortical connectivity. After countless hours scouring papers (and frequent visits to the library – another quaint habit!), we assembled evidence for the presence of several hundred pathways interconnecting 32 visual areas (an average of ~10 inputs and 10 outputs per area). This distributed hierarchical system (Felleman and Van Essen, 1991) was presented as a colorful as a ‘subway-map’ version that has come to symbolize the complexity of cortical circuitry as it was known at the time. We also illustrated the same data as a 32 × 32 binary connectivity matrix that in retrospect can be considered the first ‘parcellated connectome’ for macaque visual cortex. Another theme that emerged around that time was the realization that visual processing is associated with multiple processing streams (Desimone and Ungerleider, 1989) that show distinct pattern of convergence and divergence at different hierarchical levels (DeYoe and Van Essen, 1988). (DeYoe and Van Essen, 1988). (Rockland and Pandya, 1979)

For many years, it was frustrating that very little quantitative connectivity data was reported in the literature, even though cortico-cortical connections were well known to vary widely in strength. When Jim Lewis joined my lab, we put a major effort into quantifying the distribution of retrogradely labeled neurons after tracer injections, assigning their connections to different cortical areas, and registering the data to an atlas surface (Lewis and Van Essen, 2000a; Lewis and Van Essen, 2000b; Van Essen et al., 2001b). However, further efforts at quantifying cortico-cortical connectivity were rare until recently, when Henry Kennedy's lab undertook major steps to remedy this deficit. They used a 91-area cortical parcellation (Fig. 3A, top panel) and retrograde tracer injections placed into 29 different areas (second panel) in followed by quantitative analyses of the complete pattern of retrogradely labeled neurons (Markov et al., 2011; Markov et al., 2012; Markov et al., 2013a; Markov et al., 2013b). Panel 3 shows the spatial pattern of the 32 areas that project to area V2, colored according to a logarithmic scale for the projection strength. At the other extreme in terms of number of inputs is area 8L, which receives input from 87 areas out of the 90 possible (Fig. 3A, row 4). Key findings include: (i) a total of 1,615 cortical pathways (average of 55 inputs per injected area), including many new-found pathways (Fig. 3E); (ii) a distribution of connection strengths that spans 5 orders of magnitude and conforms to a lognormal distribution for all injections; (iii) consistency across individuals of ~ 1 order of magnitude when injections are placed in similar regions of a given area; and (iv) an exponential distance rule, in which the strongest predictor of connection strength is the inter-areal separation within the white matter (Ercsey-Ravasz et al., 2013). While these studies represent a major milestone, they also point to the need for further advances. This includes tracer injections placed into even more areas and within different subregions of areas having connection heterogeneity, the use of finer-grained cortical parcellations (see above, Fig. 2B), and quantifying connection strengths across the entire cortical sheet, irrespective of any particular parcellation.

Figure 3.

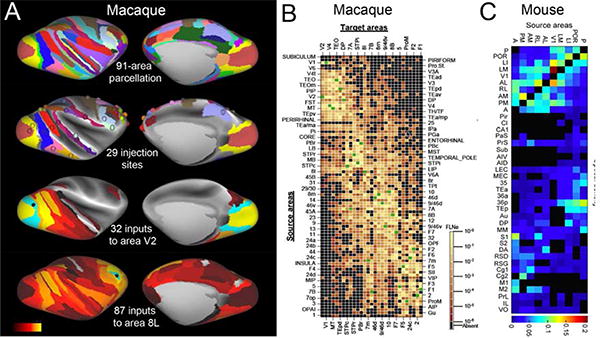
Parcellated connectomes for the macaque and mouse. Left column: Top row: 91-area parcellation of Markov et al. (2012). Row 2: 29 injected areas with each injected area colored on a dot placed on the estimated injection site. Row 3: Connectivity profile for area V2 (31 inputs). Row 4: Connectivity profile for area 8L (87 inputs). B. The 29×91 macaque connectome based on retrograde tracer injections, with 1,615 pathways. Reproduced, with permission, from Markov et al. (2012). C. The mouse connectome is based on anterograde tracers and the 40 area parcellation shown in Fig. 2. Reproduced, with permission, from Wang et al. (2012).

When considered as a binary interareal connectivity matrix, the macaque parcellated connectome is a dense (highly interconnected) graph (67% of all possible connections exist in the 29×91 matrix), which is incompatible with the small-world network architecture previously hypothesized. However, viewed in a different way, macaque cortex contains ~1.4 billion cortical neurons (Collins et al., 2010) and approximately10⁴ synapses/neuron (Beaulieu and Colonnier, 1985; Braitenberg and Schuz, 1991). This suggests a sparsity of ~10^-5 of individual neurons. At an intermediate level of ~1mm³ (i.e., the approximate voxel size for whole-brain neuroimaging) cortico-cortical connectivity), each patch of cortical neurons may be directly linked to a domain that may be roughly 10-20% of the cortical sheet (based on supplemental figures in Markov et al., 2012), but it would be valuable to refine such estimates.

Mouse

Systematic studies of cortico-cortical connectivity in rodents languished until recently, despite its simpler cortical organization. Major progress has come from a recent study that quantified projection pattern from anterograde tracer injections into 10 visual areas in a 40-area parcellation of mouse cortex, that includes transitional and archicortical subdivisions (Wang et al., 2012). Virtually all of the 10 visual areas are interconnected reciprocally with one another, and the overall binary graph density in the 10 × 40 connectivity matrix they studied (Fig. 3F) exceeds that noted above for the macaque. Connection strengths span at least three orders of magnitude (at a minimum, as estimates were limited by the sensitivity of the method), and they follow a lognormal distribution similar to that reported in the macaque. Thus, important principles apply to rodents and primates despite major differences in the total number and arrangement of cortical areas.

The Allen Brain Institute has taken the systematic analysis of long-distance connectivity in the mouse to a new level through a publicly accessible connectivity atlas that currently includes 1010 anterograde tracer injections (http://connectivity.brain-map.org). By using sensitive viral tracers, whole-brain data acquisition via serial 2-photon microscopy, and standardized experimental and analysis protocols that enable quantification of projection strengths, this project will serve as an invaluable resource that greatly enhances our understanding of the mouse meso-connectome.

Human structural and functional connectivity

Classical studies involving postmortem blunt dissection of white matter (e.g., Gluhbegovic, 1980) provided a few key insights about the relatively coherent trajectories of macroscopic fiber bundles within deep white matter. However, most of what is currently known about long-distance pathways in the human brain derive from two complementary neuroimaging approaches: analyses of ‘structural connectivity’ based on diffusion imaging (dMRI) and analyses of ‘functional connectivity’ (fcMRI) based on resting state fMRI (rfMRI) scans. Both approaches emerged in the 1990's and have subsequently been improved dramatically, which is greatly enhancing our understanding of human brain circuits. However, the methods also remain indirect and subject to substantial limitations that are inadequately recognized. Here, the focus is on results from recent efforts by the HCP to improve the acquisition and analysis of structural and functional connectivity data and to enable comparisons with other modalities, including maps of function based on task-fMRI and maps of architecture (e.g., myelin maps) in individuals and group averages. One of the most important advances has been the use of improved scanning protocols, especially “multiband” pulse sequences that acquire data many slices at a time, thereby enabling better spatial and temporal resolution (Ugurbil et al., 2013).(Gluhbegovic, 1980)

Diffusion MRI (dMRI) relies on the preferential diffusion of water along the length of axons in order to estimate fiber bundle orientations in each voxel. This includes not only the primary (dominant) fiber bundle, but also the secondary and even tertiary fiber orientations that can be detected in many voxels. The HCP has achieved improved dMRI data acquisition by refining the pulse sequences, using a customized 3 Tesla scanner (with a more powerful ‘gradient insert’), and scanning each participant for a full hour (Sotiropoulos et al., 2013; Ugurbil et al., 2013). This yields excellent data quality with high spatial resolution: 1.25 mm voxels instead of the conventional 2 mm voxels. Data preprocessing and analysis (distortion correction, fiber orientation modeling, and probabilistic tractography) have been improved, as has the capability for visualizing the results of tractography analyses. As an example, Figure 4 illustrates state-of-the-art analysis and visualization of the probabilistic fiber trajectories, starting from a seed point on the inferior temporal gyrus (Fig. 4A) and viewed in a coronal slice (Fig. 4B) and as a 3D trajectory through the volume (Fig. 4C). Obviously, a major strength of tractography is that it provides evidence for the 3D probabilistic trajectories within the white matter. Information about the trajectories of major tracts is of interest for a variety of reasons. However, the white matter represents the ‘cables’ of the brain's communications infrastructure, and for many purposes it is of particular interest to know the gray-matter origins and terminations of long-distance pathways that can be inferred from tractography. For example, Fig. 4D illustrates the estimated pattern of structural connectivity with other cortical gray matter locations from the inferior temporal seed location shown in Fig. 4A. It includes many anatomically plausible connections, but there are many sources of bias and noise that can introduce false positives and false negatives. Hence, caution is warranted in interpreting tractography results without independent validation.

Figure 4.

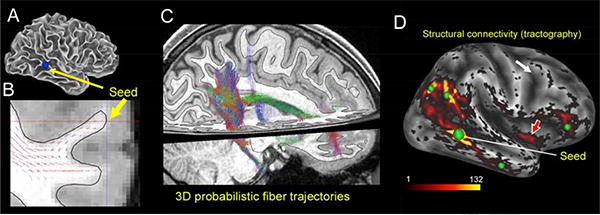
Diffusion MRI and probabilistic tractography results in an individual HCP subject. A. Lateral view of the ‘gray/white’ surface, showing a seed location in the inferior frontal gyrus (IFG, blue dot). B. Probabilistic streamlines in white matter on a coronal slice that intersects the IFG seed point. C. Probabilistic trajectories from the IFG seed point viewed in a 3D volume. D. Structural connectivity from the IFG seed point (large green dot) viewed on the inflated cortical surface. Smaller green dots indicate the approximate centers of patches showing high structural connectivity with the seed point. Red arrow indicates a likely false positive patch in insular cortex. Adapted, with permission, from Van Essen et al., 2013).

One set of limitations arises from a prominent ‘gyral bias’ that occurs because fiber bundles in white matter blades point strongly towards gyral crowns (Van Essen et al., 2013b). Another source of complexity is the presumed ‘traffic jam’ of crisscrossing as well as gradually diverging fiber bundles deep within white matter. A possible simplifying hypothesis proposes a grid-like organization of fiber trajectories underlying the organization of brain circuits (Wedeen et al., 2012). However, this hypothesis is controversial on methodological grounds (Catani et al., 2012) and is difficult to reconcile with the sheer complexity of wiring demanded by the many thousands of inter-areal pathways in the primate parcellated connectome (Fig. 3A). In order to resolve these issues, it is important to complement diffusion imaging with high resolution anatomical methods that provide direct evidence on the statistical pattern of fiber fanning, dispersion, branching, and/or sharp angles that characterize long-distance pathways. One such approach involves comparing tracer injections in the macaque directly with tractography results (Jbabdi et al., 2013), a topic my lab is actively exploring. Novel optical imaging methods such as CLARITY (Chung et al., 2013) as well as ultrastructural reconstructions may provide critical information needed for better ‘anatomical priors’ that can inform the modeling of dMRI data. However, these will likely be most informative in primates; rodents will be of limited value because they have a very modest amount of white matter, and many cortico-cortical pathways are likely to travel directly through the unconvoluted gray matter. As the next section illustrates, a different approach involves functional connectivity, which is also highly informative in complementary ways.

Functional connectivity MRI (fcMRI) is based on BOLD fMRI signal fluctuations in the resting state that show a complex pattern of spatial correlations with nearby and distant regions. In the macaque, fcMRI correlations are strongest between anatomically connected regions (Vincent et al., 2007), but the correlations likely reflect a combination of indirect as well as anatomical connectivity, and they also may be influenced by more complex aspects of neurovascular coupling. The HCP fcMRI data benefit from high resolution in space (2 mm voxels time (0.7s ‘frame rate’), and time (0.7s TR), and in many analysis steps. An important component of preprocessing is the removal of spatially structured and unstructured noise, as only an estimated ~4-6% of the variance of the unprocessed data represents neurobiologically genuine signal (Marcus et al., 2013). Removal of spatially structured noise has been greatly improved by an automated “FIX” denoising algorithm (Smith et al., 2013b).

The fMRI data of interest are restricted to gray matter (white matter and non-brain voxels are largely irrelevant to this analysis). At the 2mm spatial resolution appropriate for the fMRI data, there are ~90,000 ‘grayordinates’ (surface vertices for cortex and voxels for subcortical domains). Analysis of functional connectivity entails computing the correlation of timeseries data for 90,000 × 90,000 grayordinates. This amounts to ~33 GB of data when stored in the recently introduced “CIFTI” grayordinate × grayordinate file format; the data files would be ~6-fold larger if stored in a conventional voxel-based volumetric format (Glasser et al., 2013a). More generally, the CIFTI format provides efficient and flexible way of representing many types of data used by the HCP, including task-fMRI and dMRI results.

One widely used way to analyze fcMRI data involves seed-based correlations, which reveals the spatial pattern associated with any given region of interest (ROI), be it a single seed point or a larger collection of grayordinates or conventional voxels. For example, Figure 5 compares the fcMRI seed-based correlations (column 2) in individual (top row) and a group average (generated from 120 subjects). The selected seed in parietal cortex (black dot, green arrows) reveals a pattern of strong correlations and anti-correlations in several distant regions of frontal, occipital and temporal cortex (arrows). The high quality of HCP data acquisition and analysis provides notably fine spatial detail for a single grayordinate seed in each individual subject with minimal smoothing of the data. The group average pattern is similar to the individual, but is much blurrier, because the alignment is imperfect but also presumably because there is noise in each of the individual subject maps, as well as biological variation between individuals. One way to examine the specificity is by cross-modal comparisons, using cortical myelin maps (column 3) and task-fMRI (column 4), that are part of standard HCP data acquisition and processing. The fcMRI patches correspond with patches of heavy cortical myelin (Fig. 5C, black dots, arrows). There is also a correlation with the task fMRI results in Figure 5D, which shows the activation pattern from viewing faces in the HCP ‘Emotion’ state.

Figure 5.

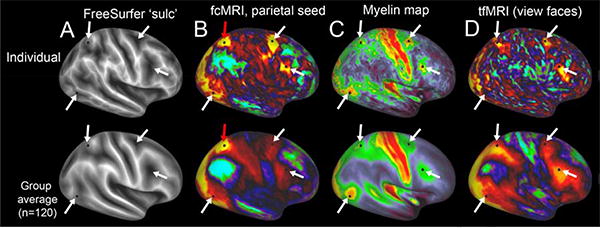
Multimodal analysis of HCP data in individuals and group averages for functional connectivity, myelin maps, and task-fMRI. A: Maps of cortical shape (FreeSurfer ‘sulc’ map) in an individual (top row) and a group average (bottom row, subjects) after FreeSurfer shape-based registration. B: Functional connectivity maps from a seed (black spot, red arrow) in parietal cortex, with hotspots in two patches in prefrontal cortex (arrows). C: Myelin maps, demonstrating myelin hotspots at the parietal seed location, in the area MT+ complex, and in the frontal eye fields and a nearby prefrontal patch (arrows). D: task-fMRI activation when viewing expressive faces in the HCP Emotion task, with activation foci that overlap with the parietal and prefrontal foci from the preceding panels.

The intersubject registration used in Figure 5 was based only on shape features, using FreeSurfer's ‘sulc’ maps and registration algorithm (column 1). Alignment can be further improved using a novel multimodal surface matching (MSM) algorithm (Robinson et al., 2013a; Robinson et al., 2013b) that can capitalize on multiple additional modalities, including myelin maps as well as resting state network maps (Glasser et al., 2013b; Smith et al., 2013b).

From dense to parcellated connectomes

The sheer size of each dense connectome (33 GB) makes them unwieldy for many analyses that instead can benefit from compact representations of connectivity between regions defined by one or another parcellation. It is obviously preferable to use a parcellation having relatively homogeneous connectivity within the parcels rather than, say, a geographically-based parcellation having demonstrably heterogeneous connectivity profiles. Accordingly, the fcMRI data provide the best available evidence on which to derive an objective brainwide connectivity-based parcellation.

There are several complementary ways to analyze fcMRI data in order to infer or identify parcels that reflect functionally distinct regions (Cohen et al., 2008; Wig et al., 2011; Power et al., 2012; Blumensath et al., 2013; Wig et al., 2013; Smith et al., 2013a). One powerful approach uses ICA analysis applied to group-average data (concatenated fMRI timeseries) in order to identify grayordinates that share similar fMRI timecourses (Smith et al., 2013). The left half of Figure 6 shows three representative components (network “nodes”) from a 98- component ICA decomposition using data from 120 HCP subjects.

Figure 6.

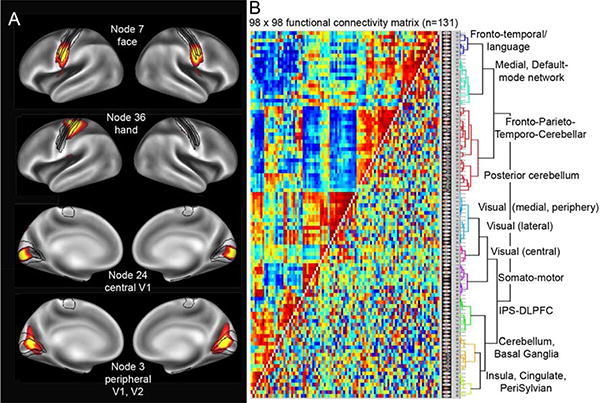
ICA-based analysis of group-average functional connectivity. A. Four ICA-based components (“nodes”) from an analysis of 120 HCP subjects, registered using multimodal surface matching (Robinson et al., 2013b; Smith et al., 2013b). Top row: node 7 in the bilateral face representation of somato-motor cortex. Row 2: node 36, in the left hemisphere hand representation. Black contours show boundaries of areas 4a, 4p. 3a, 3b, and 1 (Van Essen et al., 2012b). Bottom panels: node 24 (bilateral central V1, row 3) and node 3 (bilateral peripheral V1, V2, row 4). B. Functional connectivity matrix for a 98 × 98 ICA analysis of data from 131 HCP subjects. The full correlation is shown above the diagonal and the partial correlation below the diagonal. Adapted, with permission, from Smith et al. (2013b).

These fcMRI derived nodes are analogous to previously published resting state networks (e.g. Yeo et al., 2011), but are much smaller and reveal much finer detail. Two distinctive characteristics warrant mention. (i) Many nodes include topologically noncontiguous portions, making them unlike classically defined cortical areas. (This is particularly the case at lower ICA dimensionalities. The noncontiguous segments usually involve symmetric portions of the two hemispheres, often involve both cerebellum and cerebral cortex, and often involve dispersed regions within a single cerebral hemisphere. This reflects the physically dispersed nature of network and sub-network components defined by similarities in fMRI time-series. (ii) In relation to topographically organized sensory and motor areas, some nodes cross multiple areal boundaries but occupy only part of the topographic map of each area. In Figure 6A (top row), node 7 includes the face region of somatomotor cortex bilaterally, and extends across areas 1, 3a, 3b, 4a, and 4b. In row 2, node 36 includes the hand region only in the left hemisphere. In rows 3 and 4 nodes 24 occupies central area V1, respecting the V1/V2 boundary; node 3 includes the peripheral representation of both area V1 and V2. These observations drive home the point made previously that connectivity based parcels and architectonic parcels can differ markedly because they reflect fundamentally different aspects of cortical organization.

Figure 6B shows the 98 × 98 connectivity matrix that results from correlating the timeseries of each ICA spatial component with one another (n=131 subjects). The full correlation matrix is above the diagonal; below the diagonal is the partial correlation matrix, after regressing out all common components. The components are clustered based on similarity of the full correlation values; the hierarchical cluster analysis shown on the right reveals 10 major networks in the geographical domains indicated. This type of group-based fcMRI analysis can be extended to single-subject analyses that enable comparisons between functional connectivity and behavioral measures; it can also be used to assess the heritability of brain connectivity, given that the HCP subjects came from twins and nontwin siblings (Smith et al., 2013b). Importantly, while the full correlation and partial correlation provide quantitative values, neither provides a direct measure of anatomical connection strengths. Given the indirect nature of neurovascular coupling and the complexity of the many analysis steps, the correlation values that are expressed as ‘functional connectivity’ need to be interpreted cautiously in terms of their neurobiological underpinnings.

On navigating the human brain

Returning to the analogy of earth maps, humans are increasingly reliant in our daily lives on information based on GPS-based spatial coordinates as we navigate our environment, yet most of us are blissfully ignorant of such basics as the latitude and longitude of our home city. For the brain, spatial coordinates provide an objective way to express precise locations in an individual or an atlas brain. Traditionally, this has been done using stereotaxic (x,y,z) coordinates, such as the famous Talairach coordinate system or the more commonly used MNI stereotaxic space. A decade ago spherical coordinates of latitude and longitude were introduced for specifying locations in cerebral cortex (Van Essen et al., 2001; Drury et al., 2009; Fischl et al., 2009). However, spherical coordinates have not caught on widely, in part because it is not intuitive to think about brain locations on a spherical map. An attractive alternative is to use the aforementioned grayordinates as an efficient basis for describing gray-matter locations in individuals and atlases. It allows a single machine-readable number (the CIFTI grayordinate index) to specify brain locations accurately and objectively. That being said, the accuracy of CIFTI-based analyses will depend heavily on the quality of the surface registration method used to bring the data into standard grayordinates space. (Drury et al., 1999)

Concluding Remarks

The remainder of this essay touches on six ancillary topics that are relevant to the core issues of cartography and connectomics: data sharing, the resurgence of neuroanatomy, cortical development, brain disorders, cortical evolution, and computational neuroscience. I have been active in each of these domains and comment on them from a distinctly personal perspective.

Data sharing

A culture and practice of widespread data sharing has been vital for rapid progress in many fields, from astronomy to genomics. This has been very slow to occur for neuroscience in general, even though the potential benefits of data sharing are large. Efforts to promote data sharing in neuroscience date back to the 1990's when the Human Brain Project was launched. The impediments along the way have been both technical and sociological (Koslow, 2002). My lab's contribution to the data sharing enterprise started with the SumsDB database as a vehicle for sharing neuroimaging data (Dickson et al., 2001); Van Essen et al., 2005), including stereotaxic neuroimaging coordinates (Van Essen, 2009). Our experience and that of others (e.g., the BrainMap database - (Fox and Lancaster, 2002) was that neuroscientists appreciate having data available in a public database, but relatively few are motivated to contribute to a database if it entails significant effort on their part. In the past several years the data sharing tide has begun to turn, driven by several factors (Akil et al., 2011). The Neuroscience Information Framework (NIF, www.neuinfo.org/) has demonstrated the breadth of currently available resources as well as the value of ‘one-stop-shopping’ for exploring these resources (Gardner et al., 2008; Cachat et al., 2012).

One domain that is especially well suited to data sharing involves large-scale projects such as the Allen Institute for Brain Sciences (AIBS) and the HCP. The AIBS (http://www.alleninstitute.org) has demonstrated the power of high-throughput, high quality analyses of gene expression patterns in different species and different developmental stages, especially when the data are freely shared through user-friendly interfaces for data visualization and mining. Data sharing is also an integral part of the HCP mission, and our experience in this process has driven home several lessons. One is the importance of well-organized, systematically processed data in order to make the HPC data highly useful to the community. This includes pipelines and a database structure that are systematically and consistently organized in order to facilitate a wide variety of analyses (Glasser et al, 2013a, Marcus et al., 2013). As of September, 2013, the HCP had released three large datasets, each containing data acquired in an earlier quarter and then carefully processed and organized. The unprocessed datasets are available for investigators who prefer to start from scratch. However, the great majority of users have heeded our recommendation to download the ‘minimally preprocessed’ datasets, thereby capitalizing on many analysis steps that represent improvements relative to conventional methods. Future HCP data releases will include additional types of extensively processed data and will also support additional capabilities for data mining. The various preprocessing and analysis pipeline scripts will also be made available, along with the ConnectomeDB database infrastructure, so that investigators at other institutions will have the option to apply HCP-like approaches to their own neuroimaging projects.

A corollary observation is that most neuroscientists (myself included!) would benefit from better data organization and management for the smaller-scale projects carried out in our own labs, whether or not the data are later made freely available. If individual labs become more efficient in managing their data, it will lower the practical barriers to data sharing. It is encouraging that the need for data sharing is receiving attention from funding agencies and also in the advisory report on the BRAIN Initiative (http://www.nih.gov/science/brain/).

The rebirth of neuroanatomy

During the 1990's, many of my neuroanatomy colleagues bemoaned the decline of systems neuroanatomy. It was increasingly hard to get funding and to recruit graduate students to the field. While I shared the concern, my instincts were that a resurgence was essential for the vitality of neuroscience more broadly, and that the pendulum would swing with the advent of more powerful and efficient neuroanatomical methods. However, never in my wildest turn-of-the-century dreams did I countenance the amazing explosion of interest in matters neuroanatomical that now engage a broad spectrum of investigators, including hard-core molecular neuroscientists who now appreciate the importance of delving into the intricacies of neuroanatomy. To paraphrase Mark Twain, reports of the death of neuroanatomy were greatly exaggerated. The field has undergone an amazing resurgence, fueled by advances on many fronts. In animal models, this includes optogenetics and labeling of neuronal subtypes and their projections genetically tractable species like mouse zebrafish and Drosophila (Schnitzer and Deisseroth, this issue). In monkeys and humans, this includes the powerful neuroimaging methods discussed in this essay.

Cortical development

My interests in neural development are deeply rooted but have followed a circuitous trajectory that intersects with the cartography and connectomic themes of this essay. While at Caltech, my lab pursued parallel, highly disparate lines of research on synapse elimination at the neuromuscular junction and on the functional organization of primate visual cortex. After moving to Washington University in 1992, my developmental focus shifted to cerebral cortex. We used postmortem anatomical methods to show that connections between macaque areas V1 and V2 initially form around the time that cortical gyrification occurs (Coogan and Van Essen, 1996). This prompted me to think mechanistically about how cortical folding brings the retinotopic maps of areas V1 and V2 into register. In my favorite ‘light-bulb’ moment of an entire scientific career, it occurred to me one evening that cortical folding might arise if axons generated mechanical tension that pulled strongly connected locations closer to one another. This notion quickly generalized into a theory of tension-based morphogenesis that can account for many other key features of nervous system development (Van Essen, 1997). For example, mechanical tension in apical dendrites may account for the sheet-like structure of cerebral and cerebellar cortex. Given that neurites in vitro in fact exert mechanical tension (Lamoureux et al., 1989; Heidemann and Buxbaum, 1990), the anisotropic orientation of neuronal and glial processes in vivo are well positioned to have powerful morphogenetic influences that are distinctive for each brain region. These ideas extend to the nervous system D'Arcy Thompson's classic thesis that competing forces of tension and pressure drive the morphogenesis of plant and animal forms in general (D'ArcyThompson, 1917)

Tension-based cortical folding is a very attractive hypothesis, but it has been devilishly difficult to obtain incisive evidence in favor or against it. Like many major other developmental phenomena, cortical folding likely arises from more than a single mechanism. For example, regional differences in neuronal proliferation within the subventricular zone (Kriegstein et al., 2006; Reillo et al., 2011) may contribute to early stages of gyrification, but it seems very unlikely that this could account for the complexity and variability of secondary and tertiary convolutions in humans (Van Essen, 2006, 2007). Other hypotheses for cortical folding continue to be promulgated, including differential tangential expansion (Ronan et al., 2013) and even a completely countervailing notion of ‘axonal pushing’ as a mechanism of gyrification (Nie et al., 2012). However, the empirical evidence for these alternatives is tenuous in this author's opinion. Hence, on encountering the statement “While the axonal-tension theory provides a description of how gyrification arises, the evidence that it is incorrect, as previously discussed, is convincing” (Ronan et al., 2013), my reaction is to again invoke Mark Twain and counter that reports of the death of tension-based cortical folding are greatly exaggerated! (Reillo et al., 2011)

Studies of human twins provide an interesting perspective on cortical folding that is relevant to these mechanistic considerations. A starting point is that the convolutions in identical twins differ from one another almost as much as in unrelated individuals. I learned this firsthand in a friendly competition among collaborators to predict twin status based on visual inspection of cortical folding patterns (while blinded to the identity of 14 twin pairs). I lost the competition (performing no better than chance!); the hands-down winner was a computer algorithm that did the matching perfectly, suggesting that cortical folding patterns are indeed heritable, but only to a modest degree (Botteron et al., 2008). These questions are now amenable to a much more detailed analysis because the HCP is acquiring data from twins and their nontwin siblings. Our initial analyses of the HCP data indicate that functional connectivity is inherited to a significant degree (Smith et al, 2013b). It will be of great interest to see whether future analyses using larger HCP datasets informs the debate about the mechanisms of cortical folding.

Brain Disorders

A growing number of investigators who were trained as basic neuroscientists have become engaged in projects that relate to specific brain diseases and disorders. In part, this reflects pressure from NIH and other funding agencies to promote research related to the core mission of improving health. However, I believe that first and foremost this trend reflects the tremendous progress in the field that enables meaningful attacks on key disease-related problems, using a variety of animal models as well as human patient populations. In my case, I was drawn into disease-related research about a decade ago when a serendipitous opportunity arose to collaborate in applying our cortical cartography tools (Caret software) to a study of children with Williams Syndrome. We identified dozens of cortical folding abnormalities in Williams Syndrome and hypothesized that these folding abnormalities might be caused by underlying circuit abnormalities via the aforementioned tension-based folding hypothesis (Van Essen et al., 2006). Soon thereafter, I struck up a collaboration with pediatric neurologists Terrie Inder and Jeff Neil to study cortical development using structural MRI scans in infants, including those born prematurely. This is extremely important clinically, because of the disturbingly high incidence of various behavioral disorders in children born prematurely (Bos and Roze, 2011). It is also provides a fascinating window on a period of rapid development, when gyrification is in full swing and the cortex is expanding rapidly. In comparing healthy term-born infants to adults, we discovered that postnatal cortical expansion is strikingly nonuniform, with the greatest expansion occurring in lateral temporal, prefrontal, and parietal regions that are implicated in cognitive function (Hill et al., 2010).

Evolution

Earlier sections have already emphasized the importance of studying nonhuman primates, especially the macaque, as model systems for better understanding the human brain. However, human cerebral cortex is not only larger (by 10-fold) and far more convoluted than the macaque, but it is far from being a scale model even after smoothing out the wrinkles (see Fig. 2B, C). The need for objective and quantitative comparisons in the face of large interspecies differences poses an interesting cartographer's challenge. Years ago I realized that the surface-based registration methods we had developed for within-species registration could be adapted to registration between species. By assigning landmarks to areas known as suspected to be homologous in the macaque and human, registration constrained by these landmarks indicates that lateral temporal, parietal regions expanded 20-fold or more in the human lineage compared to the macaque, whereas early sensory areas expanded far less (Van Essen and Dierker, 2007; see also (Chaplin et al., 2013)). Intriguingly, the regions of high evolutionary expansion overlap strongly with the aforementioned regions that expand the most in postnatal human maturation (Hill et al., 2010).

Surface-based cartography also provides a window on our closest living relatives, the great apes, whose cerebral cortex is about one-third that of human cortex. The cortical myelin maps illustrated above for human cortex (Fig. 5C) have also been generated for chimpanzees and macaques (Glasser et al., 2013c). In all three species, the early sensory and motor areas are heavily myelinated, whereas lateral temporal, parietal, and prefrontal regions presumed to be cognitive in function are lightly myelinated. Quantitative comparisons between the three species may provide interesting insights about the way in which specializations for cognitive function have evolved in the primate lineage.

Computational Connectomics

My scientific training was as a neuroanatomist and neurophysiologist, but I became convinced in the 1980's that computational approaches were essential in order to deepen our interpretation and understanding of brain function. It has been heartening to see the once-small ‘fringe’ field of computational neuroscience blossom in the ensuing decades, to the point that it is now a vibrant part of mainstream neuroscience. In the context of this essay, it is interesting to consider the evolving relationships among neural computation, cartography and connectomes.

A starting point is to acknowledge that connectivity data (be it of a micro-, meso-, or macro-connectome flavor) while providing extremely important constraints on the nature of the underlying computations, doesn't on its own explain what or how the brain and its component networks actually compute. Insights can be greatly strengthened when information about neural activity is available (be it macroscopic as derived from fMRI, MEG, or EEG, or microscopic as derived from neurophysiological or optical methods). Ambitious methodological advances may enable comprehensive mapping of brain activity at the single-neuron level in model organisms (Alivisatos et al., 2012). However, such ‘brain activity maps’ on their own will not answer critical questions of how and what the brain computes. Computational neuroscience comes into play by providing a framework for generating and evaluating computational models that test our understanding of what is going on ‘under the hood’.

Contemporary computational neuroscience includes a diversity of theoretical and methodological approaches. This diversity will surely increase as new approaches emerge that can make good use of massive datasets involving connectomic and/or brain activity data at one or another spatial scale. Indeed, a new specialty of computational connectomics may emerge, analogous to how computational genomics evolved to enable analysis of massive genomic datasets. From my perspective, an important consideration for progress computational neuroscience relates to the belief that nervous systems are exquisitely well-engineered to carry out the computations that mediate species-specific behaviors, because they are driven by intense evolutionary pressures. Accordingly, it is important that computational models themselves be grounded in sound neural engineering principles that impact how the models are framed, implemented, and interpreted (Eliasmith and Anderson, 2004; Eliasmith, 2013).