Quantifying the local tissue volume and composition in individual brains with MRI

Abstract

We describe a quantitative neuroimaging method to estimate the macromolecular tissue volume (MTV), a fundamental measure of brain anatomy. By making measurements over a range of field strengths and scan parameters, we tested the key assumptions and the robustness of the method. The measurements confirm that a consistent, quantitative estimate of macromolecular volume can be obtained across a range of scanners. MTV estimates are sufficiently precise to enable a comparison between data obtained from an individual subject with control population data. We describe two applications. First, we show that MTV estimates can be combined with T1 and diffusion measurements to augment our understanding of the tissue properties. Second we show that MTV provides a sensitive measure of disease status in individual patients with multiple sclerosis. The MTV maps are obtained using short clinically appropriate scans that can reveal how tissue changes influence behavior and cognition.

Introduction

Magnetic resonance imaging (MRI) signals are often designed to reveal qualitative tissue contrast, but there are clinical and scientific advantages for designing quantitative MRI (qMRI) methods^1–4. Just as we measure body temperature or blood pressure, clinicians can use qMRI to assess brain tissue. QMRI is well-suited for clinical trials measurements at different sites and different points in time. QMRI is also critical for research of the neural and cellular basis of development, behavior, or disease. Yet, current diagnostic practice is rarely based on qMRI due to practical limitations (e.g. long scan duration, low signal-to-noise ratio, low accuracy and unique non-clinical scan sequences).

Tissue volume is a valuable target to evaluate a variety of clinical disorders^1,5–7. But the widely used methods of voxel based morphometry⁸ and cortical thickness^9,10 are qualitative; they are derived from a statistical analysis of uncalibrated T1-weighted images that depend on multiple biological factors, including regional brain size and shape, thickness of the cortex and myelination. Changes in these parameters reflect development across the lifespan, disease impairment, and are correlated with behavior and cognition^10–13 but the conclusions drawn from these analyses do not point to a specific biological property¹⁴.

We describe a quantitative neuroimaging method to estimate the brain macromolecular tissue volume (MTV). The brain macromolecules are principally cell membranes and proteins; in white matter approximately ~50% are myelin sheaths¹⁵. Along with MTV, the method measures a quantitative T1 map. T1 values depend on the MTV as well as the physico-chemical environment of the macromolecules surfaces^16–18. We describe ways of combining MTV and T1 that measure the macromolecular composition. Further, we show that combining MTV with diffusion measurement provides insight about macroscopic tissue organization. We test the accuracy of the methods for individual clinical assessment across a range of MR scanners, field strengths, RF coils and time points. Finally, we describe measurements of white matter in individuals with multiple sclerosis.

Results

Measurement of MTV

MTV quantifies the non-water volume in each voxel and the complementary volume is water. The amount of water in a voxel is estimated from the proton density (PD) signal. The PD-values are proportional to the amount of water, with an unknown constant of proportionality. We approximate CSF voxels as entirely filled with water, thus for each voxel the water volume fraction (WVF) is the ratio of the PD and CSF value. The voxel MTV fraction (MTVF) is MTVF=1−WVF (for glossary see supplemental Table 1).

To estimate the voxel MTV, we estimate instrumental biases from the data. The PD and T1 values are then derived from the signal equation of the spoiled gradient echo (GE) clinical sequence^17,19 (see online Methods for the fully automatic post-processing technique that is implemented in the software we distribute (https://github.com/mezera/mrQ), and summarized in the pipeline-diagram in Supplementary Figure 1). The transmit-coil inhomogeneity is corrected by combining the spoiled-GE with a set of unbiased spin-echo-inversion-recovery scans (Supplementary Figure 2). The receive-coil inhomogeneity is estimated using the logic developed for parallel imaging algorithms. The key idea is to separate the coil effects from the brain signal using data from the individual coils (Supplementary Figure 3). The data acquisition is straightforward, relying on vendor-supplied sequences and takes about 12 minutes for clinical (2mm³) and 25 minutes for sub-millimeter resolutions.

Validating MTV accuracy and reliability

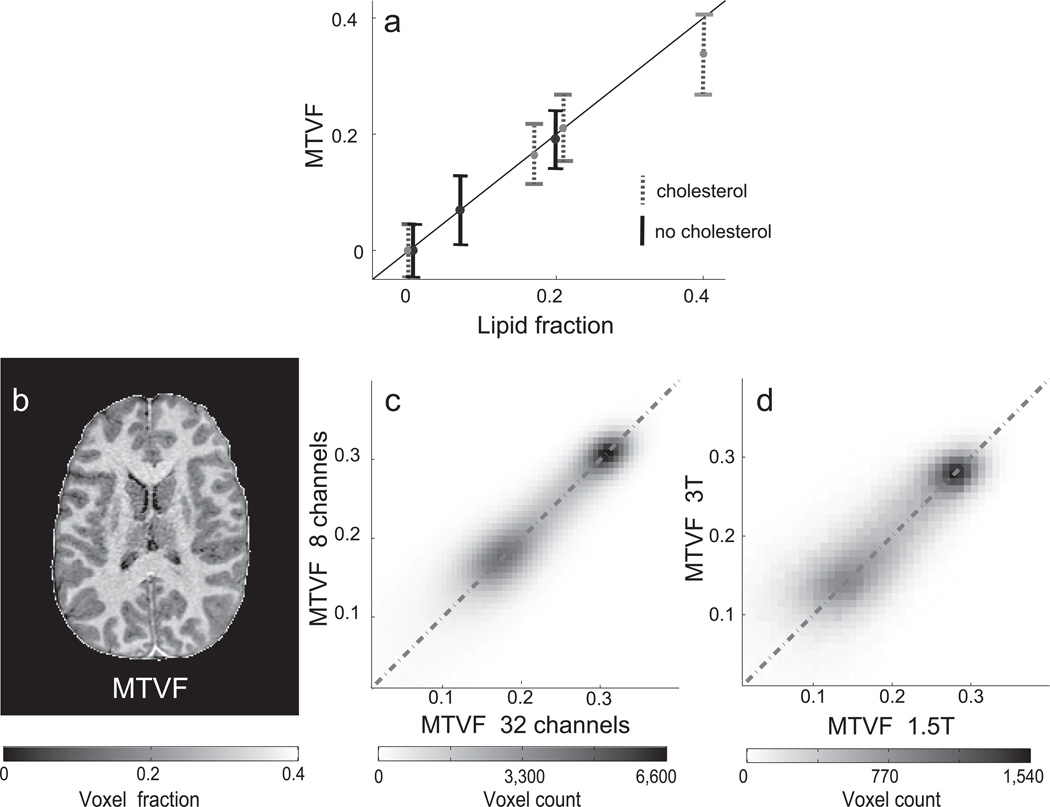
In the first experiments we estimated MTV in phantoms with controlled volumes. We mix phosphatidylcholine lipid, cholesterol and water with different volume levels. The MTV reliably quantifies the lipid volume (Figure 1a).The accuracy of the MTV estimates show that the coil inhomogeneities that influence the raw measurements are corrected. The cholesterol content changes the T1 of the lipid substantially^20,21. Hence, MTV value is estimated independent of the cholesterol content.

Figure 1.

Assessment of macromolecular tissue volume fraction (MTVF) accuracy and reliability. (a) The MTVF was measured using two types of lipid mixtures: one with cholesterol (30% weight, gray dotted lines) and one without cholesterol (black lines) embedded in the lipid membranes. The lipid fraction and estimated MTVF are both given in fraction of the voxel, and these values agree well. The vertical bars are ± 1 standard deviation, and the average standard deviation is 0.053. (b) An axial brain slice showing MTV map. (c) Comparison of MTV values in the gray and white matter measured twice in the same subject but with two different RF-coils, 8- and a 32-channel (R²=0.84). The two regions represent values from the gray and white matter (higher MTVF). (d) Comparison of MTVF values in the same brain measured in a 1.5T and 3.0T magnet (R²=0.67). The scans in panel c were acquired on the same day; six months passed between the two scans compared in panel d.

Next we evaluate the instrumental independence of the MTV estimates. Figure 1b shows a MTV map. Figure 1c d compares MTV estimates from this brain obtained with different coils at 3T and from 1.5T and 3.0T magnets. The scans in panel c were done on the same day while six months passed between the two scans in panel d. Along with MTV, we obtain a T1-observed map. The stability of these T1 maps across different field strengths, coils, TR, TE and flip angle parameters is shown in Supplementary Figures 2, 4–6. The consistency of both maps across the wide variety of measurement conditions validates the accuracy of the methods for removing coil bias and the model assumptions (for further discussion see Supplementary information).

Variation in MTV between brain structures

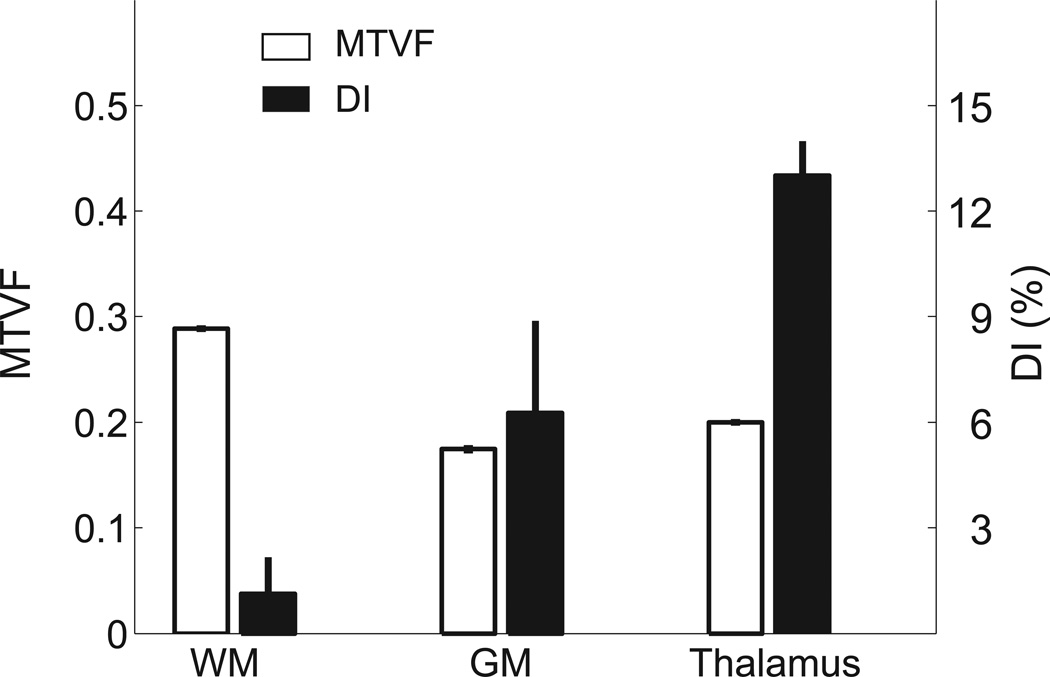
The MTV values differ between parts of the brain; MTV values are summarized for three large brain regions (n=16, Figure 2). These values are in good agreement with post-mortem measurements (Tables 4.2 in Ref¹). The summary measures show that the MTV values averaged across these large brain regions are extremely similar between subjects. The difference between gray and white matter is substantial (35%), but the thalamus region values are close to the gray matter values. These comparisons are spatially coarse; a more details example for the corpus callosum (CC) is given below. We will report more spatially resolved analyses of gray and white matter in a separate investigation.

Figure 2.

The MTVF and Dissimilarity Index (DI) in different brain regions. The mean MTVF (left axis, open bars) and DI (right axis, filled bars) are averages from three large regions of interest (ROI, n=15) defined by FreeSurfer⁹. The voxels within each ROI that border other regions were excluded. Error bars are ±1 SEM.

The CC comprises a set of tracts that carry signals between different functional regions of cortex. Histological and MRI measurements show that along the anterior-posterior axis the CC axons differ in size, number^22,23 and potentially also in axonal packing density²⁴. We compared the MTV values in distinct zones within the CC that contain axons with terminals in different cortical regions (Figure 3a). Using tractography, we identified three CC zones: the body, the splenium, and the genu-rostrum. These zones include axons from motor, visual, and orbito-frontal cortex respectively.

Figure 3.

The mean MTVF values near the mid-line of three callosal tracts. (a) Mid-sagittal T1-weighted images are shown from three subjects. The images are overlaid by three callosal fibers tracts estimated using deterministic DTI tractography: motor fibers, blue; visual fibers, green; orbito-frontal fibers, purple. The tracts segment the CC into three distinct zones: the body, the splenium, and the genu-rostrum, respectively. (b) The mean MTVF values within a 5mm portion of each tract on either side of the mid-sagittal plane (n=15). The MTVF values in the body are significantly smaller than the MTVF values within the other regions, and the genu-rostrum values are the largest. Error bars are ±1 SEM.

The mean MTV values in these three regions (Figure 3b) are smallest in the body where axonal diameters are largest²², larger in the splenium, and largest in the genu-rostrum. The MTV differences are quite substantial: the body is separated by about 10 SEM from the genu-rostrum and by about 8 SEM from splenium.

Combining MTV and diffusion imaging

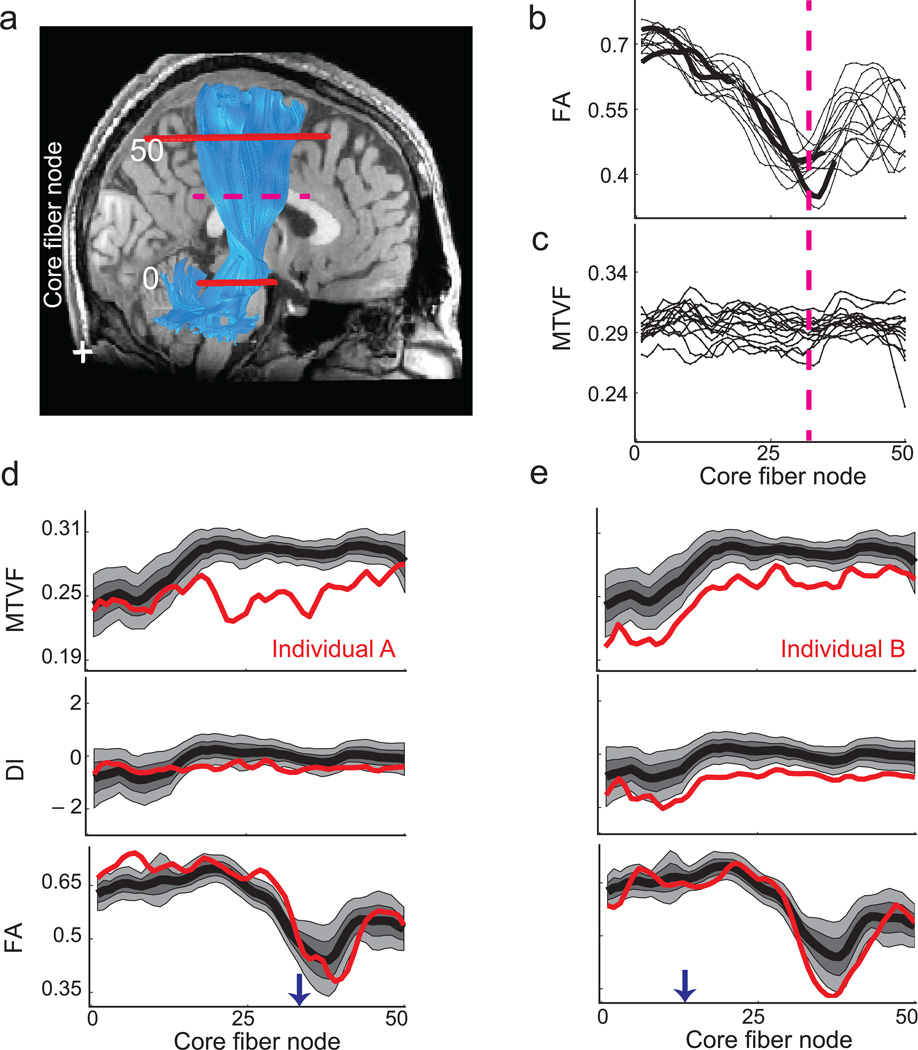
Diffusion weighted imaging measures the intra-voxel water diffusion in multiple orientations. The diffusion orientation distribution function is clinically modeled by a tensor, which is summarized by its fractional anisotropy (FA)²⁵. The FA value combines a range of geometric and microstructural factors, and it would be valuable to distinguish between these biological factors^26,27. Hence, there is potential benefit of combining MTV and diffusion measures to clarify the contributions of different tissue properties. To illustrate one benefit, consider the MTV and FA values along the corticospinal tract (CST). We identified each subject’s CST core fiber (n=15), and measured the FA and MTV along it using the AFQ software²⁸ .The FA value drops significantly in the region where fibers from the CC pass through the CST, reducing fiber direction coherence (Figure 4a, dashed-line). This region is within the centrum semiovale where there are known to be many crossing fibers²⁹. This drop in FA is consistent across all subjects (Figure 4b). The MTV values on the other hand are constant along the CST (Figure 4c). Importantly the crossing fibers do not significantly affect the MTV. This example illustrates that FA and MTV values inform us about complementary aspects of the white matter tracts. Combining the two measurements help discriminate between different mechanisms that influence FA. For example, if MTV and FA change together, we would be inclined to explain the change as an axon packing difference. If MTV were constant but FA changes, we would be inclined to explain the change by mechanisms such as differences in axon coherence.

Figure 4.

Corticospinal tract (CST) measurements in controls and two individuals with multiple sclerosis. (a) The estimated right CST (blue) is overlaid on a sagittal T1-weighted image. The two solid red lines show axial planes that bound the measurement region; the centroid of the tract (core fiber) is calculated and sampled into 50 nodes. (b, c) The curves show FA and MTVF values measured at different nodes along the CST from different control subjects (n=15). The FA value declines in the region where the CST intersects callosal fibers (dotted red line). (d) The MTVF, DI and FA values along the left CST in individual-A with multiple sclerosis (red) are compared with the distribution of measurements from the controls. The black curve represents the control mean, and the lighter shades show the [25, 75] and [10, 90] percentiles. In individual-A the MTVF values are substantially below the control values in the superior portion of the CST. The DI and FA values are close to the control range throughout. An arrow indicates the core fiber node corresponding to the axial plane further analyzed in Supplementary Figure 12. (e) In individual-B the MTVF and the DI values are consistently below the distribution of control values. The CST region appears normal in the diagnostic images shown in Supplementary Figure 12.

The pattern of the data in Figure 4 is typical of another difference between diffusion and tissue property measures. The MTV standard deviation between subject tracts is thirty percent greater than the difference within each subject’s tract (7.5 × 10⁻⁴ vs. 1.1 × 10⁻³). The situation is reversed for FA (9.8 × 10⁻² vs. 4.6 × 10⁻²). Therefore MTV values, which are highly reliable across instruments and repetitions, may be a particularly useful measure to distinguish individuals.

Combining MTV and T1 mapping

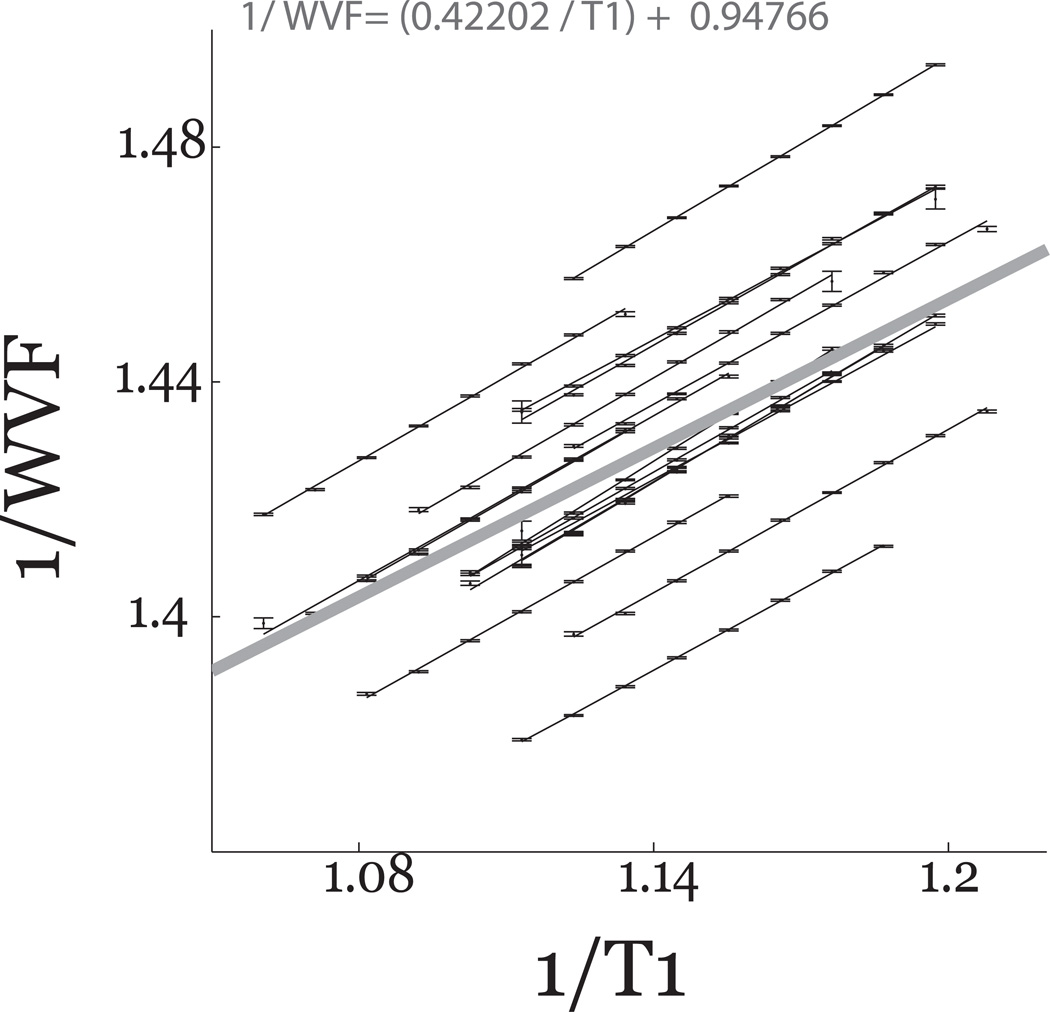
The brain T1 depends on both the density of macromolecules and the local physico-chemical environment^16–18. Consequently, there should be a relationship between the measured T1 and MTV values. Earlier work showed^5,30 a linear relationship between 1/(1−MTVF) and 1/T1. We confirm this relationship using the data from all the white matter of individual subjects (Figure 5). It is useful to provide a summary of the linear relationship based on the data from all subjects (thick line). This average is given by Equation-1:

$$\frac{1}{(1-\mathit{\text{MTVF}})}=\frac{0.42202}{T1}+0.94766$$ 1.0

Figure 5.

The relationship between T1 and WVF in white matter. The white matter R1 (1/T1) plotted against 1/WVF (water volume fraction (WVF=1−MTVF, n =16). The R1 values are pooled into bins separated by 0.05sec⁻¹. The mean number of voxels in each bin is 1.5 × 10⁵ ± 5.5×10³. Data from individual subjects are fitted accurately by lines. Error bars are ±1 SEM. The linear fit combining data from all the subjects is shown as the thick gray line, and the formula for that line is in the Equation.

The slope and intercept are close to the values reported elsewhere^5,30.

While the linear relationship characterizes the main effect, deviations from the line contribute additional information about the local physico-chemical environment. Early work showed that observed T1 depends on both the ensemble^20,21 and compartmentalization of the macromolecules³¹. To measure this information we compute a dissimilarity index (DI) between the measured and predicted R1=(1/T1) (Equation-1) using the equation:

$$\mathit{\text{DI}}=100\times \frac{R{1}_{\mathit{\text{measured}}}-R{1}_{\mathit{\text{predicted}}}}{R{1}_{\mathit{\text{measured}}}}$$

If two voxels differ only in MTV, and their physico-chemical environment is equal, DI should be zero. Measured DI values differ substantially when comparing white matter, gray matter and thalamus (Figure 2, black bars). For example, the gray matter and thalamus regions have similar MTV values (0.18–0.20), but the DI values differ by a significant amount (6% in GM and 12% in thalamus). These measurements show that MTV within a single tissue class (white matter) predict the T1, but the same prediction does not extend to different brain tissue (gray matter and thalamus). Hence, comparing T1 and MTV values between tissues is informative about the local physico-chemical environment of the macromolecules.

The DI measure is based on the observed T1 without any assumption regarding the biophysical source. In the Supplementary Materials, we review the T1 literature and develop a biophysical framework, which explains the brain T1 value differences. The model develops a formula that transforms the MTV and T1 values (seconds), to a tissue property, which we name ‘the apparent volume of the interacting water protons’ (VIP). In a nutshell, this model assumes that the tissue’s T1 relaxation time may be explained by both the amount of the tissue water interface and the water-surface interaction rate (SIR). This model assumes a fast exchange between proton pools and neglects effects of slow exchange. We analyze the likely size of slow exchange effects (Supplementary figure 7).

In Figure 1 we show that adding cholesterol to a lipid mixture does not change the MTV estimate; therefore MTV is independent of measure of the type of macromolecule. Supplementary Figure 8 shows that SIR does depend on the lipid cholesterol. Hence, SIR measures the local physico-chemical environments. Supplementary figure 9 shows that SIR estimates are independent over a range of clinically relevant field strengths (0.5T–3T).

Multiple sclerosis

A clinical application for MTV and T1 measurements is the identification and monitoring of brain tissue changes. Specifically, a reliable MRI approach for the assessments of demyelinating disorders such as multiple sclerosis has yet to be standardized^32–34. In clinical practice^32–34, lesions are typically monitored with conventional MR metrics that identify (a) hyperintensities in T2-weighted images and/or gadolinium enhancement on T1-weighted images as markers of disease activity, and (b) hypointensities in T1-weighted images as a marker of neuronal degeneration. Quantitative MTV measures can be used to compare individual subjects with respect to control populations over time and across MR centers and scanners, serving as a noninvasive biomarker for both disease monitoring and drug design. Other qMRI methods such as magnetization transfer (MT) and T2 mapping also detect lesions (see review³⁵). These protocols are not part of the current clinical assessment because of the long scan time required to achieve satisfactory resolution and reliability. The MTV is highly correlated with quantitative MT (r=0.9) in the white matter tracks and with T2 myelin water fraction (r=0.79, for additional details see Supplementary information and Supplementary Figure 10).

We compare the MTV, DI and FA levels of ten individual subjects with relapsing remitting multiple sclerosis with the same measures in a group of control subjects (n=16). We observed reliable quantitative differences between individual patients and the controls in specific white matter tracts. We describe two individuals, who both have CST tissue abnormalities (Figure 4d,e; further examples in Supplementary Figure 11). Both subjects have FA values in the CST within the normal range. In subject-A MTV values in the superior portion the tract are below the control population distribution, while in subject-B the MTV values along the entire CST are below the control population distribution. The FLAIR and T1-weighted diagnostic images (Supplementary Figure 12) show a localized abnormality for subject-A, but the images appear normal for subject-B.

Multiple sclerosis postmortem histology shows both a reduction in macromolecular volume and a change in tissue characteristics³⁶. In both subjects there is a reduction in the MTV. But only in subject-B there is a variation in DI suggesting also a change in the tissue macromolecular from typical white matter.

The MTV measurements identify abnormal regions and quantify the size of these deviations in normal appearing white matter. The DI measure adds information about changes in the tissue physico-chemical environment.

Discussion

The MR signal arises from protons that probe tissue properties at nanometer scale³⁷. MTV is the most basic MR measurement, assessing the volume of water and non-water in each voxel. The consistency of the MR estimates derived by our methods across field strengths, coils and time with histology and lipid phantoms supports the method accuracy. Combining MTV with diffusion signal distinguishes between variation in tissue orientations and tissue density, while combining with T1 mapping informs us about variations local physico-chemical environments. We found tissue differences between brain regions as well as between individuals with multiple sclerosis and controls, bringing in-vivo human imaging a step closer to the biochemistry and biophysics of the underlying brain tissue.

Contrast measurements are sufficient for investigations aiming to identify only the location of unusual tissue. The next goal in MRI is to obtain quantitatively assess specific tissue properties. This goal is challenging because MR-scanners generally operate with incomplete calibrations. Some procedures like taking the ratio of two images with a common bias, say T1 and T2³⁸, or calculating a MT ratio¹, removes some biases. Another approach is to reduce the biases through statistical smoothing procedures^39,40 or to combine data sets from multiple subjects^8,9. Our method goes beyond these procedures by using absolute calibration procedures to eliminate both receive- and excite- RF coil inhomogeneities.

The measurements are limited by the same technical challenges that limit imaging of all large volumes: Imperfections in the main field and coil corrections both bias the estimates. Further, deviations from the main fitting assumptions might limit the accuracy of the estimates. We assume that the images are free from $T_2^{*}$ -weighting, given the chosen TE. Our confidence in the assumption comes from the agreement of the MTV values with prior measurements using different methods and between our measures in different magnetic fields. To explain the T1 properties of different tissues we suggest a biophysical model in the Supplementary information yet further investigation is needed to establish the biophysical interpretation of the DI measures.

The MTV and T1 mapping makes use of a short straightforward clinical sequence supplied by most MR vendors. The acquisition time is about 12 minutes for clinical relevant resolution (2mm³) and 25 minutes for sub-millimeter resolution. The computations use simple and robust formulae that derived membrane and macromolecular properties with high-quality signal-to-noise ratio and spatial resolution as the spoiled-GE images. Together, these advantages make it possible to apply the MTV and T1 methods in novel scientific and clinical applications and facilitate comparison of data across multiple sites and enable comparisons of individual participants to a control population, and the same individual across time.

Online Methods

Lipids

Phantom construction

Large multilamellar vesicles (referred to hereafter as vesicles) consisting of L-α-phosphatidylcholine (Egg PC from soy extract, Avanti Polar Lipids, Alabaster, USA) with or without cholesterol were prepared by the sonication method. For all the analytical phantom measurements described here, we used a 10 mM PBS buffer solution [pH 7.5] with 150 mM NaCl. All solutions were prepared in 18.2 MΩ·cm MilliQ water (MilliPore, Oregon, USA). Lipid films were first prepared by drying the as-supplied lipids dissolved in chloroform under a gentle stream of nitrogen air at room temperature. The resulting lipid film was then stored under vacuum overnight to remove residual chloroform. Vesicles were prepared by swelling the lipid film in an aqueous solution, followed by vortexing periodically for ten minutes. The resulting vesicle solution was next sonicated with a probe tip sonicator in order to produce uniform lipids solubility. Vesicles were generally used within three days of preparation. The mixtures were made with different lipid concentrations (see figure 1a). To calculate the lipid mixture volume, we determined the number of lipid molecules based on the molecular mass and volume (~1875 ų) of a single lipid^41–43. For mixture with cholesterol we assume that the cholesterol volume is negligible, according to the free space theory⁴⁴. The different vesicle mixtures were poured into 3ml cuvettes and glued to a plastic vessel. The vessel was filled with PBS buffer and sealed.

MR image acquisition

Data were obtained using a 1.5T GE Signa MRI scanner. Spoiled gradient echo (GE) images were acquired with parameters similar to those used with human subjects (see below). The data processing was identical to the human MR data processing with two exceptions. First, the coil biases were estimated by a single set of 3D 2nd order polynomial approximate over homogenous region (the vessel was filled with PBS). Second, the receive-coil inhomogeneity correction was scaled so that the water fraction (WF) of the PBS region was 1. The transmit-coil inhomogeneity correction was scaled so that the T1 of the PBS region was equal to the T1 of water at room temperature.

Human anatomical mapping

Subjects

Human measurements were performed on sixteen healthy adult volunteers. In addition, 10 volunteers with relapsing remitting multiple sclerosis (diagnosed based on revised McDonald’s Criteria⁴⁵). The disease duration was 2–17 years with Expanded Disability Status scale values of <3.0⁴⁶. All patients were on disease modifying treatments (2 natalizumab, 1 glatiramer acetate, 7 interferon beta–1a) and free of steroids for at least 3 months at time of MR imaging. All studies were performed with the informed written consent of subjects. The Stanford University Institutional Review Board approved all procedures for medical research involving human subjects.

MR-Image acquisition

Data were obtained from five MR scanners: a 0.5T GE-Signa SP (N=2), two different 1.5T GE-Signa (N=4) and two different 3T GE Signa MRI scanner (N=26). At 1.5T, we used two different 8-channel receive-only head coils. At 3T, in one magnet we used an 8-channel receive-only head coil and in the other we used a 32-channel receive-only head coil.

The quantitative T1 and MTV parameters were measured from spoiled-GE images acquired with different flip angles (á = 4°, 10°, 20°, 30°, TR = 20 ms, TE = 2.4 ms). The scan resolutions at different field strengths were: 0.5T, 1.5×1.5×3 mm³; 1.5T, 1.5 mm³; 3T, 0.9375×0.9375×1 mm³.

For T1 calibration, all subjects measured at 1.5T and 3T were also scanned using spin echo inversion recovery with an EPI read-out (SEIR-epi). This scan was done with a slab inversion pulse. For SEIR-epi the TR was 3 sec at 3T and 2.5 sec at 1.5T. The echo time was set to minimum full; inversion times were 50, 400, 1200, 2400 msec. We used 2mm² inplane resolution with a slice thickness of 4 mm. The EPI readout was performed using 2× acceleration at 3T and no acceleration at 1.5T.

To enable the use of post-scan calibration (below), we made sure that the manufacturer’s pre-scan was performed only for the first scan. We assured that these parameters were used for the remaining scans.

T1 mapping- transmit-coil inhomogeneity correction

The MTV values are estimated from measures of two fundamental MR maps: T1 and proton density (PD). T1 and PD can be derived from a set of spoiled-GE images. The images signal equation (Equation 1.1)^17,19 depends on three tissue-related MR constants, observed T1 and $T_2^{*}$ relaxation times and PD. The equation also depends on four acquisition parameters TR, TE flip-angle (α) and coil inhomogeneity.

$$S(\alpha )=M_0\text{ sin}(\alpha )\left(\frac{1-e^{\frac{-\mathit{\text{TR}}}{T_1}}}{1-\text{cos}(\alpha )e^{\frac{-\mathit{\text{TR}}}{T_1}}}\right)$$ 1.1

The M₀ term combines g, a scale factor that characterizes receive-coil inhomogeneity gain, arbitrary instrument scaling, PD, and the $T_2^{*}$ decay constant (equation 1.2).

$$M_0=\mathrm{g}{\mathit{\text{PDe}}}^{\frac{-\mathrm{\text{TE}}}{T_2^{*}}}\approx \mathrm{g}\mathrm{\text{PD}}$$ 1.2

In principle T1 and M₀ can be estimated by collecting measurements with at least two flip angles. In practice the receive coil and the transmit coil are not perfectly calibrated. The receive-coil imperfection influences only the M₀ term. While, the transmit-coil imperfection prevents us from knowing the true α at each brain voxel, which results in erroneous estimates of both T1 and M₀. Consequently, we must estimate both transmit and receive-coil inhomogeneity to derive the T1 and PD maps accurately.

Our strategy to overcome the transmit-coil calibration errors is as follows. We first use SEIR-epi to measure an unbiased, low resolution, T1 map of the whole brain. We calculate T1 from SEIR data using the method described by Barrel et al.⁴⁷. We then align the T1 data with a matched, low-resolution representation of the spoiled-GE data. From the T1 and several flip-angle spoiled-GE values, we use a nonlinear least-squares (NLS) solver and estimate the transmit-coil inhomogeneity and M₀ (Equation 1.1). Next we interpolate the low-resolution transmit-coil inhomogeneity data to the resolution of the original spoiled-GE measurements. We assume that the transmit-coil inhomogeneities are smooth and can be estimated by local regressions of hyper-planes (3D). We derive the hyper-plane coefficients using the whole-brain data, although we exclude certain voxels that are likely to be outliers. First, we exclude voxels with a T1 value higher than 2 second to exclude CSF voxels⁴⁷. Second, we exclude voxels with transmit coil inhomogeneity values more than two standard deviations from the mean transmit-coil values. Using the fitted polynomial, we interpolate the transmit-coil inhomogeneity estimates to the high-resolution spoiled-GE. Regions in the high-resolution spoiled-GE that are not covered by the low-resolution bias map are estimated by extrapolation using a 2nd order 3D polynomial that spans the target volume.

We use the estimated transmit-coil inhomogeneity and the several flip-angle spoiled-GE measurements to derive the high-resolution T1 and maps. These were calculated using a nonlinear least-squares (NLS) fitting procedure⁴⁸ to minimize the difference between the data and the signal equation predictions (Equation 1.1).

Proton density mapping - receive coil inhomogeneity correction

At each point in the volume, PD is proportional to M₀. But the M₀ data are contaminated with $T_2^{*}$ decay and receive-coil imperfections and an arbitrary instrument-scaling factor (see Equation 1.2). For short TE measurements, the $T_2^{*}$ decay can be neglected. Hence, the main challenge we face is removal of the receive-coil inhomogeneity.

We estimated the receive coil inhomogeneity by combining data obtained from the individual coil elements. Just as in parallel imaging algorithms, the estimation procedure relies on the fact that multiple coils measure the same PD, but with different coil gains. The estimation algorithm is described as below.

The brain image was gridded into a set of partially overlapping volumes, each approximately 20mm³ with 50% overlap of neighboring volumes. The volumes were processed independently. For the i^th coil we estimated M_0,i(α) from the measured signal S_i(α) and, the estimated T1 map and the corrected α (above) using Equation 1.1

$$M_{0,i}(\alpha )=\frac{S_i(\alpha )(1-\text{cos}(\alpha )e^{\frac{-\mathit{\text{TR}}}{T_1}})}{\text{sin}(\alpha )(1-e^{\frac{-\mathit{\text{TR}}}{T_1}})}$$

We use the average of these estimates over α as the mean M_0,i for that volume and coil. We assumed that within each volume the gain (g_i) is a 2nd order polynomial spanning the volume^39,40,49. The fitting procedure is constrained to assume that all M_0,i images share the same PD component. From g_i and M_0,i, each coil estimates a PD_i (Equation 1.2). We solve for the polynomials g_i that produce the greatest agreement between the PD_i estimates from the different coils

$$\underset{{\mathrm{g}}_i}{\text{min}}\left\{{\displaystyle \sum }{({\mathit{\text{PD}}}_i-\overline{{\mathit{\text{PD}}}_i})}^2\right\}$$

To regularize the search across the polynomial coefficients we further require that the correlations between the g_i does not exceed the correlations between M_0,i and g_i > 0.

The last step is to combine the $\overline{\mathit{\text{PD}}}$ maps estimated from each of the gridded estimation volumes. We set the mean in overlapping volumes to be equal and then average the measures across volumes.

Volume calculations

We derive the water and macromolecular tissue volume (WV and MTV) in each voxel from the PD map. We use the calculated PD values in CSF as a baseline to indicate a voxel with only water. Hence, to derive the fraction of the voxel volume that is water we normalize the map by the mean value from a region of interest (ROI) in the cerebrospinal fluid (CSF). The CSF was identified using the FreeSurfer segmentation algorithm⁹ and was limited to voxels with a T1 in the range 4–5 s⁵⁰. Aside from water, the molecules present in CSF are in relatively low concentration, so the assumption that the normalized measures water fraction is reasonable. The normalized PD values are between 0 and 1, and the few locations greater than 1 are clipped. These normalized PD maps measure water volume fraction (WVF) in each voxel. The macromolecular tissue volume fraction is 1−WVF and both can be expressed in volume units when we multiply the fraction by the voxel volume.

Map Reliability

Phantom

A homogenous agar phantom was used to evaluate the quality of the RF-coil inhomogeneity correction. To estimate the RF-excite homogeneity we measured the T1 using SEIR-epi. We compared the phantom T1 map using SEIR-epi with a gold standard SEIR⁴⁷.

To evaluate the receive homogeneity correction we measured thevalue in the homogenous phantom. The standard deviation of the value measures the reliability of the receive -coil measurements.

Human

To measure the T1 estimation error, one of the subjects was scanned 12 times at 1.5T scanner with a large set of flip angles (α = 4° 10° 20° 30° 30° 20° 10° 4° 10° 20° 30° 4° 20° 4° 10° 30°]) and 2mm³ voxel size, using the same TR and TE. We performed a bootstrap analysis of these scans, randomly selecting a set of flip angles = [4° 10° 20° 30°] in a thousand repeats to estimate the T1 map using a linear approximation¹⁹. The T1 estimation error was defined as the standard deviation of the estimated T1 values.

To further characterize the effect of flip angles, the same subject was scanned with slightly different flip angles [3° 5° 9° 11° 18° 22° 26° 34°]. The T1 value was estimated again with a set of values higher [5° 11° 22° 34°] and lower [3° 9° 18° 26°] than the standard flip angle set. The estimated T1 values from these two sets were compared to the T1 values derived from the standard flip angle set.

To characterize the effects of TR and TE on the estimation another subject was scanned at 1.5T scanner using TR = [20, 80] ms; TE = [2, 12] ms; α = [4°, 18°]; voxel size = 2mm³.

To estimate the reliability and generalization of the maps in humans, we performed multiple scans on different scanners using the parameters listed above. To estimate reliability within instruments, two subjects had three measurements in the same 1.5T scanner and two subjects were scanned twice in the same 3T scanner using different receive coils. To estimate reliability across instruments two subjects had two measurements in two different 1.5T scanners, and two subjects had two measurements in two different 3T scanners. Three of the subjects scanned at the 1.5T scanner were also scanned at a 3T scanner.

Additional MR methods

Data alignment

We either collected high-resolution T1-weighted anatomical images for each subject using an 8-minute sagittal 3D- spoiled-GE sequence (1mm³ voxel size) or synthesized an equivalent T1-weighted image from the accrued acquired multi-flip angle spoiled-GE images⁵¹. For alignment several anatomical landmarks were manually defined in the T1 images: the anterior commissure (AC), the posterior commissure (PC), and the mid-sagittal plane. Using these landmarks, we calculated a rigid-body transform to convert the T1-weighted images to the conventional AC-PC aligned space. This T1-weighted image was then used as a common reference for alignment of the T1, PD, MTV, VIP, MT and DTI maps.

Co-registration of multiple scans of the same subject

When brain volumes from the same subject were compared, the two volumes were co-registered using affine transformations determined using semi-automatic procedures with cubic interpolation implemented in-house software.

0.5T T1 mapping

Two subjects were scanned at a 0.5T GE Signa SP, with a quadrature head coil. The spoiled-GE parameter was similar to the one in 1.5T and 3T. The scan resolution at 0.5T was 1.5×1.5×3 mm³. At 0.5T the T1 data were acquired using a combined transmit-receive quadrature head coil. On this instrument the multi-coil images and the specific SEIR-epi sequence used for transmit correction are not available. Hence, the coil corrections applied to the 1.5T and 3T data is not applicable at this low field strength. In this case we assume that there is minimal transmit-coil inhomogeneity. These data were used only for comparison of T1 values at different field strengths.

T1 estimation with spin-echo inversion recovery (gold standard)

Two subjects in 1.5T and four subjects at 3T were scanned with these parameters: one to three slices were acquired using the SE-IR sequence, a receive-only head coil and the following parameters: TR = 2550 ms, TE = 10 ms, TI = [50, 400, 1100, 2500] ms, BW = ±32 kHz, FOV = 24 × 18 cm², slice thickness = 5mm⁴⁷.

Magnetization transfer measurements

For five of the subjects the T1 mapping procedure was followed by magnetization transfer spoiled-GE scans with variable offset frequency (TR = 32 ms, TE = 2.4 ms, α = 10°, Δ = [3, 6, 9, 12] kHz)⁵².

Fluid attenuated inversion recovery

We collected fluid attenuated inversion recovery (FLAIR) scans from each of the MS patients (TR = 8 sec, TE = 129ms, inversion time = 2250ms, inplane resolution = 0.43 mm², slice thickness = 5 mm).

Diffusion tensor imaging and tractography

Whole-brain DTI measurements were performed using a diffusion-weighted spin-echo EPI sequence with isotropic 2mm³ resolution. We measured 96 diffusion directions with a b-value of 2.0 ms/µm² and eight repeats of the same sequence with no diffusion weighting. We used 2.5× ASSET acceleration to reduce EPI distortions.

Fiber tracts were estimated using a deterministic streamlined tracking algorithm^53,54. The methods are described in detail elsewhere^24,55. The tract were identified in each individual by restricting fibers to two way-point ROIs (shown in figures 4a) that were defined based on a DTI atlas of human white matter⁵⁶.

For both fiber tracts of interest in this study, tractography algorithms estimated a dense set of core pathways along with a small proportion of pathways that are outliers. To minimize the influence of the outliers we combine data from different voxels in a weighted fashion, assigning greater weight to voxels near the core of the estimated tract⁵⁷.

The algorithm for calculating the weights is the following. All fibers were clipped to the portion spanning the two way-point ROIs such that each fiber was approximately the same length. Then the fiber groups were resampled to equal numbers of nodes; in this case we used 50 nodes along the track. We computed the mean position of each of the 50 nodes, and defined this as the fiber tract core. We specified the diffusion at each node of the fiber group core as a weighted average of the diffusion measured near the equivalent node of each individual fiber in the group. The contribution of a given fiber is weighted by its distance from the tract core. We measure the distance from the node to a voxel using the covariance matrix of the node position. Specifically, if a voxel position is X, the mean position is X0, and the covariance matrix of the 3D node position is C, then we calculate the Mahalanobis distance, d, as:

$$d=\sqrt{{(X-X_0)}^t{C}^{-1}(X-X_0)}$$

The weight assigned to data from a voxel is the inverse of its distance, d. This procedure assigns higher weights to fibers near the bundle core as describe in details by Yeatman et. al.²⁸.