Digital Correction of Motion Artifacts in Microscopy Image Sequences Collected from Living Animals Using Rigid and Non-Rigid Registration

Abstract

Digital image analysis is a fundamental component of quantitative microscopy. However, intravital microscopy presents many challenges for digital image analysis. In general, microscopy volumes are inherently anisotropic, suffer from decreasing contrast with tissue depth, lack object edge detail, and characteristically have low signal levels. Intravital microscopy introduces the additional problem of motion artifacts, resulting from respiratory motion and heartbeat from specimens imaged in vivo. This paper describes an image registration technique for use with sequences of intravital microscopy images collected in time-series or in 3D volumes. Our registration method involves both rigid and non-rigid components. The rigid registration component corrects global image translations, while the non-rigid component manipulates a uniform grid of control points defined by B-splines. Each control point is optimized by minimizing a cost function consisting of two parts: a term to define image similarity, and a term to ensure deformation grid smoothness. Experimental results indicate that this approach is promising based on the analysis of several image volumes collected from the kidney, lung, and salivary gland of living rodents.

1 Introduction

Optical microscopy has become one of the most powerful techniques in biomedical research. Among the most exciting forms of microscopy is “intravital microscopy,” a termed coined by Ellinger and Hirt (Ellinger & Hirt, 1929, 1930) for the technique of microscopic imaging of living animals. It is perhaps surprising that intravital microscopy has been conducted for much more than 100 years, first used to observe the behavior of leukocytes in frogs (Dutrochet, 1824; Cohnheim, 1889; Wagner, 1839). Increasingly applied throughout the 20th century, intravital microscopy experienced a quantum boost in 1990 with the invention of multiphoton microscopy, a technique that facilitates imaging hundreds of microns into biological tissues at subcellular resolution (Denk, Strickler & Webb, 1990).

Intravital multiphoton microscopy has since been used to obtain unique insights into the in vivo cell biology of the brain (Svoboda & Yasuda, 2006; Skoch, Hickey, Kajdasz, Hyman & Bacskai, 2005), the immune system (Zarbock & Ley, 2009; Sumen, Mempel, Mazo & von Andrian, 2004; Hickey & Kubes, 2009), and cancer (Lunt, Gray, Reyes-Aldasoro, Matcher & Tozer, 2010; Condeelis & Segall, 2003; Fukumura, Duda, Munn & Jain, 2003). Intravital microscopy also has a long history of productive application to visceral organs, such as the liver (Irwin & MacDonald, 1953; Clemens, McDonagh, Chaudry & Baue, 1985) and the kidney (Ghiron, 1912; Steinhausen & Tanner, 1976). However, multiphoton microscopy of visceral organs is generally complicated by motion resulting from respiration and heartbeat. Amounts of sample motion that are acceptable for lower-resolution techniques are intolerable in multiphoton microscopy, whose sub-micron resolution is completely spoiled with even the slightest motion in the tissue.

To some extent, motion artifacts can be minimized by immobilizing the organ or coordinating image capture with respiration. In many cases, these approaches are sufficiently effective to facilitate high-resolution multiphoton fluorescence microscopy of the kidney (Dunn, Sandoval, Kelly, Dagher, Tanner, Atkinson, Bacallao & Molitoris, 2002; Russo, Sandoval, McKee, Osicka, Collins, Brown, Molitoris & Comper, 2007; Peti-Peterdi, Toma, Sipos & Vargas, 2009), the liver (Li, Liu, Huang, Chiou, Liang, Sun, Dong & Lee, May 2009; Theruvath, Snoddy, Zhong & Lemasters, 2008), and even the lung (Kreisel, Nava, Li, Zinselmeyer, Wang, Lai, Pless, Gelman, Krupnick & Miller, 2010). However, these methods are by no means foolproof, so that imaging studies are frequently plagued with residual motion artifacts. Here, we describe an image processing method that effectively corrects for motion artifacts in sequences of intravital microscopy images collected in time-series or in three-dimensional volumes, based upon a combined rigid and non-rigid registration technique using B-splines. This image registration method will aid in future segmentation and other image analysis techniques. In particular, the proposed image registration method consists of two distinct components: a rigid registration component that corrects global translations, and a non-rigid registration component utilizing B-splines to correct localized, non-linear motion artifacts. We demonstrate that this registration technique is effective for correcting motion artifacts in image sequences collected in time-series or in 3D, using image volumes collected from the kidney, lung, and salivary gland of living rodents.

2 Methods

2.1 Image Collection

Images were collected using multiphoton fluorescence excitation, using a BioRad MRC1024 confocal/multiphoton microscope system equipped with a Nikon 60X NA1.2 water immersion objective (for images of the kidney) or an Olympus Fluoview 1000 confocal/multiphoton microscope system equipped with an Olympus 20X, NA 0.95 water immersion objective (for images of the lung) or an Olympus 60X, NA1.2 water immersion objective (for images of the salivary gland). Images were kindly provided by Ruben Sandoval and Bruce Molitoris (rat kidney), Irina Petrache and Robert Presson (rat lung), and Roberto Weigert (mouse salivary gland). Images were collected at a rate of approximately one frame per second.

2.2 Rigid Registration

Image registration is the task of finding a function that maps coordinates from a moving test image to corresponding coordinates in a reference image (Zitová & Flusser, 2003). It is often desirable to transform information obtained from multiple images into a single common coordinate system encompassing the knowledge available from all the various source images (Hajnal, Hill & Hawkes, 2001). Current registration methods generally consider registering only a single pair of reference and moving images. Using medical image registration on stacks containing hundreds of images is still an ongoing field of research.

Rigid registration is first performed to correct global translations throughout the image sequence before non-rigid registration so that the non-rigid process focuses solely on localized motion rather than both local and global motion. The particular registration parameters selected for this approach include a Neumann boundary condition, where pixel values outside of the image boundary are given the values of the nearest pixel within the image boundary. Additionally, registration is performed using nearest-neighbor interpolation. Furthermore, an exhaustive search is not performed to compute the registration solution; instead, several optimization methods have been studied (Arnold, Fink, Grove, Hind & Sweeney, 2005; Swisher, Hyden, Jacobson & Schruben, 2000). Our registration implementation employs the well-known quasi-Newton BFGS (Broyden-Fletcher-Goldfarb-Shanno) optimizer. This optimization method greatly reduces computational complexity by estimating the Hessian matrix rather than computing it directly. As a result, the error metric is evaluated for only a small subset of all possible registered offset locations (Ibáñez, Ng, Gee & Aylward, 2002).

The registration metric used was mean squared error:

$$(u,v)=\underset{(u,v)}{\mathrm{argmin}}\left\{\sum _m\sum _n{\left(x_{i-1}\right(m,n)-x_i(m-u,n-v\left)\right)}^2\right\}$$ (1)

where i denotes the current image number, x_i–1(m, n) and x_i(m, n) denote the pixels at location (m, n) within the reference image x_i–1 and moving image x_i respectively, and (u, v) denotes the obtained registration offset distances. The mean squared error metric is a common metric with a large capture radius (Brown, 1992). In order to register an entire stack of images, the moving test image was chosen to be the current image, and the reference image was chosen to be the previous (unregistered) image. If the registration of the current image in reference to the previous image is denoted as r(x_i, x_i–1) = x_i ○ x_i–1, the output of the registration process in terms of the first image can be represented as a concatenation of all previous registrations:

$$\mathrm{r}(x_i,x_1)=\mathrm{r}(x_i,x_{i-1})\circ \mathrm{r}(x_{i-1},x_{i-2})\circ \cdots \circ \mathrm{r}(x_2,x_1)$$ (2)

as was similarly performed in (Kim, Yang, Le Baccon, Heard, Chen, Spector, Kappel, Eils & Rohr, 2007). This was found to greatly improve registration performance instead of using the first image in the stack as the reference image, as well as reduce the computational complexity and consequently the time required to analyze the entire series. In fact, the current image may contain few of the same structures also visible in the first image if the sequence has already significantly progressed into the stack of images. This result was especially true for three-dimensional/volumetric data, or image sequences corresponding with increasing tissue depth. Using a pre-selected image in the stack as the reference image has undergone experimentation using time-series data, or image sequences corresponding with increasing time instances, as the same cellular objects are expected to be in view for every image in the sequence. However, no noticeable improvement was observed.

In addition to the mean squared error metric used, the following metrics have been evaluated:

$$\begin{array}{cc}\hfill (u,v)=& \underset{(u,v)}{\text{argmax}}\left\{\sum _m\sum _n{x}_{i-1}(m,n)x_i(m-u,n-v)\right\}\hfill \\ \hfill (u,v)=& \underset{(u,v)}{\text{argmin}}\left\{\sum _m\sum _n\mid x_{i-1}(m,n)-x_i(m-u,n-v)\mid \right\}\hfill \end{array}$$ (3)

where x_i–1(m, n) and x_i(m, n) denote the pixels at location (m, n) within the reference image and moving image, respectively. Registration was performed using both metrics, and the results were observed to be visually identical to those using the mean squared error metric. Furthermore, the use of mutual information as a metric has been evaluated (Pluim, Maintz & Viergever, 2003). This consisted of maximizing the following:

$$(u,v)=\underset{(u,v)}{\text{argmax}}\left\{\mathit{MI}\right(x_{i-1}(m,n),x_i(m-u,n-v)\left)\right\}$$ (4)

where

$$\mathit{MI}\left(x\right(m,n),y(m-u,n-v\left)\right)=H\left(x\right(m,n\left)\right)+H\left(y\right(m-u,n-v\left)\right)-H\left(x\right(m,n),y(m-u,n-v\left)\right)$$ (5)

is the mutual information between x(m, n) and y(m – u, n – v), and H denotes Shannon entropy (Cover & Thomas, 2006). The mutual information implementation from (Mattes, Haynor, Vesselle, Lewellen & Eubank, 2001) has been used here. However, results using mutual information were poorer than those obtained using the mean squared error metric. It has been extensively shown that metrics based on the evaluation of mutual information are well suited for overcoming the difficulties of multi-modality registration, where images to be registered are acquired using different imaging techniques such that pixel intensities for the same objects are not correlated across images. Since our data sets are all single modality, having mutual information perform poorly is not surprising.

Additionally, this rigid registration method assumes grayscale single channel images, not multi-channel images. Therefore, for multi-channel data sets, a particular channel must be selected to perform registration on. Simply using one of the multiple channels directly may be enticing due to its simplicity. However, using only one of the channels and discarding the remaining channels omits much information which may cause improper image registration in these discarded channels. Indeed, for the datasets we show here, we have obtained better results using a composite gray channel, x_gray, that is similar to the luminance component of each image. This new gray image used with our registration method is given as:

$$x_{\mathit{gray}}=\frac{r}{r+g+b}{x}_{\mathit{red}}+\frac{g}{r+g+b}{x}_{\mathit{green}}+\frac{b}{r+g+b}{x}_{\mathit{blue}}$$ (6)

where

$$\begin{array}{cc}\hfill r=& \sum _m\sum _n{x}_{\mathit{red}}(m,n)\hfill \\ \hfill g=& \sum _m\sum _n{x}_{\mathit{green}}(m,n)\hfill \\ \hfill b=& \sum _m\sum _n{x}_{\mathit{blue}}(m,n)\hfill \end{array}$$ (7)

and where x_red, x_green, and x_blue denote the red, green, and blue components of the input image x, respectively. Even though a linear combination of the three channels has no biological significance, using gray composite images for registration has corrected significantly more motion artifacts than using any individual channel for the images that we have evaluated thus far, as the composite gray image contains and uses information from the entire image. However, one can easily imagine situations in which a particular channel might provide better registration results, as these results will depend upon the particular data being analyzed. Lastly, after translation results are obtained using the gray image, these offsets are then replicated across all channels when obtaining the registered image.

If the system is not required to be real-time when the entire stack of images is available, the system can be implemented using non-causal methods. In our rigid-registration approach, the output image size is unknown unless the maximum total displacement due to registration is known. However, this information is not available until the entire data set has been analyzed. For the system to be causal, an assumption about the output image size must be made, and the placement of the first image in the output image must be chosen. However, with a non-causal approach, the system has the advantage of being able to analyze the entire data set before producing any output images. After all images have been analyzed, the maximum displacement across all images can be determined to set the output image size so that no source images are truncated. For the sake of simplicity, we will assume the system is not utilized in a real-time scenario, and is implemented using non-causal methods.

2.3 Non-Rigid Registration

In this section, we will now address how to circumvent the localized motion artifacts and non-linear distortions caused by respiration and heartbeat. Here, we will investigate a non-rigid registration technique using B-splines, an extension of the work proposed in (Rueckert, Sonoda, Hayes, Hill, Leach & Hawkes, 1999). This method also allows for easy visualization of the distortion via deformation grids.

This non-rigid registration method deforms an image by first establishing an underlying mesh of control points, and then manipulates these control points in a manner that maintains a smooth and continuous transformation. To begin, a grid of control points, ϕ_i,j, is initially constructed with equal spacings δ_x and δ_y between points, in the horizontal and vertical directions, respectively. The non-rigid transformation T of a point (x, y) in the moving image to the corresponding point (x’, y’) in the reference image is given by the mapping T(x, y) → (x’, y’) (Mazaheri, Bokacheva, Kroon, Akin, Hricak, Chamudot, Fine & Koutcher, 2010):

$$\mathbf{T}(x,y)=\sum _{l=0}^3\sum _{m=0}^3{B}_l\left(u\right)B_m\left(v\right){\varphi }_{i+l,j+m}$$ (8)

where i = ⌊x/δ_x⌋ – 1 and j = ⌊y/δ_y⌋ – 1 are the indices of the nearest control point ϕ_i,j above and to the left of (x, y), and u = x/δ_x – ⌊x/δ_x⌋ and ν = y/δ_y – ⌊y/δ_y⌋ are such that (u, v) is the relative position of (x, y) relative to ϕ_i,j. Additionally, B_l represents the l-th basis function of the B-spline (Lee, Wolberg & Shin, 1997; Unser, 1999):

$$\begin{array}{cc}\hfill B_0\left(t\right)& ={(1-t)}^3∕6\hfill \\ \hfill B_1\left(t\right)& =(3t^3-6t^2+4)∕6\hfill \\ \hfill B_2\left(t\right)& =(-3t^3+3t^2+3t+1)∕6\hfill \\ \hfill B_3\left(t\right)& =t^3∕6\hfill \end{array}$$ (9)

As previously stated, in addition to the non-rigid deformation maximizing the similarity between the registered image and the reference image, the deformation must be realistic and smooth. To constrain the deformation field to be smooth, a penalty term that regularizes the transformation is introduced into the cost function as (Sorzano, Thévenaz & Unser, 2005; Rohlfing, Maurer Jr., Bluemke & Jacobs, 2003):

$$C_{\mathit{smooth}}=\frac{1}{A}{\int }_0^X{\int }_0^Y\left[{\left(\frac{{\partial }^2\mathbf{T}}{\partial x^2}\right)}^2+{\left(\frac{{\partial }^2\mathbf{T}}{\partial y^2}\right)}^2+2{\left(\frac{{\partial }^2\mathbf{T}}{\partial x\partial y}\right)}^2\right]\mathit{dx}\mathit{dy}$$ (10)

This regularization is necessary because each pixel in the image is free to move independently. As such, in an extreme case, it is possible that all pixels with one particular intensity in the moving image may map to a single pixel having this same intensity in the reference image, causing the resulting deformation field to be unrealistic (Pennec, Cachier & Ayache, 1999). This is one of the primary reasons why non-rigid image registration is considered difficult, as an appropriate balance and compromise must be reached between allowing large amounts of independent movement and ensuring smoothness of the transformation.

The optimal deformation of the grid of control points is found by optimizing a cost function. This cost function includes two terms with two competing goals. The first goal is to maximize the similarity and alignment between the reference image and the deformed moving or registered image. The second goal is to smooth and regularize the deformation to create a realistic transformation. This cost function is written as:

$$C_{\mathit{total}}=C_{\mathit{similarity}}\left(I_{n-1}^{\prime }\right(x,y),I_n(\mathbf{T}(x,y)\left)\right)+\lambda C_{\mathit{smooth}}\left(\mathbf{T}\right)$$ (11)

where n denotes the current image number, I’ denotes the registered image, and λ is a weighting coefficient which defines the trade-off between the two competing cost terms. In our work, we have chosen Csimilarity to have decreasing value for increasingly similar images (i.e. two identical images have C_similarity = 0). With such an approach, and by also wanting to minimize sharp warping elements of the transformation T defined in C_smooth, we desire to minimize C_total as well. The similarity metric, C_similarity, may be defined as one of numerous possibilities, including sum of squared differences, sum of absolute differences, or normalized mutual information, whichever may fit the particular image set best. In our case, we use sum of log of absolute differences:

$$C_{\mathit{similarity}}(I_x,I_y)=\frac{1}{M\ast N}\sum _m\sum _n\mathit{log}(\mid I_x(m,n)-I_y(m,n)\mid +1)$$ (12)

Our experiments have shown that this similarity metric has significantly outperformed any of the aforementioned similarity metrics for our particular data sets, both from a qualitative viewpoint (from visual inspection) and from a quantitative viewpoint (using sum of squared differences to evaluate registration accuracy).

The degree of deformation allowed is also affected by the resolution of the grid of control points used, and hence affects how readily C_similarity may be minimized. A large, sparse spacing of control points corresponds with a more global non-rigid deformation, which may not allow C_similarity to reach values near zero. Alternatively, a small, dense spacing of control points corresponds with highly local non-rigid deformations and more readily allows C_similarity to reach values near zero, but may also encourage more unrealistic deformations. In our work, we have experimented with various grid spacing values, and have found that values that work well are highly dependent on image size, the content of these images, and the degree of motion artifacts present throughout the stack of images. As a result, grid spacing values are currently chosen empirically.

Similar to the rigid registration method, the non-rigid B-spline registration method also assumes grayscale, single channel images, not multi-channel (multiple component) images. Therefore, we use the same composite gray channel constructed previously to use with this registration method. More specifically, the resulting grayscale image from the rigid registration method is used as the input image to the non-rigid registration method. Then, for each image, a final deformation field based on the gray image is obtained. This deformation field is then used to transform all channels of the image.

Since the data set to be registered consists of an entire stack of images, non-rigid registration is again performed on an image by image basis. In this case, the current image’s (the current image will be designated as the moving image) reference image is simply not the prior image in the stack. Instead, the reference image used is the registered or warped prior image. This is in contrast to the rigid registration method previously described which corrected for translations. In the rigid registration case, the moving test image was the current image and the static reference image was the original previous image. A cumulative sum of the incremental translations obtained from rigid registration is then used to register the current image. Using this approach with the non-rigid registration method was shown to produce very poor results. The cumulative sum of incremental deformation fields created unrealistic final deformation fields. This is because the deformation field is not necessarily twice continuously differentiable after the summation operation. Therefore, the current image, after it has experienced rigid registration, is registered against the previous image that has already undergone both rigid followed by non-rigid registration, ensuring that the resulting deformation field is smooth, continuous, and realistic. The combined rigid translation and non-rigid deformation obtained for this grayscale image is used to transform all channels of the multi-channel image.

2.4 Validation and “Ground Truth” Data

In general, objective evaluation of registration results proves to be difficult due to the lack of “ground truth” data, for which the true shape and position of each object in each image is known. In fact, ground truth is impossible to obtain in intravital microscopy, since both the shape and position of an object are fluid in living animals, and are inevitably altered in the process of isolating and fixing tissues. Thus, to the degree that the concept of a single “true” structure is meaningful, it is unknown and unknowable. However, we can make the assumption that shapes of structures remain relatively constant over time, and seek to reduce changes. In this section, we will describe a means based on block motion estimation by which a more objective and quantitative evaluation and validation of our results is performed. In addition, a subjective evaluation of our results will also be presented in the form of overlay images, maximum projection images, and line scan projection images. A more objective and quantitative evaluation and validation of our results is described here.

Block motion compensation has been used with video coding for decades. The overall idea is that block motion estimation provides localized information about direction and magnitude of motion throughout each image in a data set. The method proceeds as follows (Jain & Jain, 1981): The current image is divided into an array of equally sized blocks of pixels. Each block is then compared with its corresponding equally sized block and its adjacent neighbors in the previous image. The block in the previous image that is most similar to the block in the current image creates a motion vector that predicts the movement of this block from one location in the previous image to its new location in the current image. A motion vector is computed for each block in the entire image. The search area of adjacent neighboring blocks in the previous image is constrained to p pixels in all four directions, and will create a (2p + 1) × (2p + 1) search window. A larger p is necessary to correctly predict larger motion, but at the same time, this also increases computational complexity.

Block motion estimation has the strong ability to identify localized motion patterns from one image to the next, and also allows for easy visualization of this localized motion. However, even though this method is able to identify and visualize these highly local motion patterns, a consequence of dividing the image into equally sized blocks is that it does not provide an easy and obvious way to correct these motions and produce a viable and realistically registered image. Traditionally, following block motion estimation, a motion compensated image is created by displacing each block in the image by its associated motion vector. This may increase the similarity between the motion compensated image and the original image according to some defined cost metric. However, the motion compensated image has obvious block artifacts, creating an unrealistic image.

Although block motion estimation does not lend itself well to image registration directly, we will use this method in an attempt to objectively gauge the performance of our non-rigid B-spline registration method. Since block motion estimation does lend itself well to visualization, we can objectively compare the quantity and angle of motion vectors before and after non-rigid registration.

In our work, we have specified a 31 × 31 search window. Searching for the maximum similarity between two blocks is determined by minimizing a cost function. Here, we specify mean squared error (MSE) as our cost function:

$$\mathit{MSE}=\frac{1}{N^2}\sum _{i=0}^{N-1}\sum _{j=0}^{N-1}{(C_{\mathit{ij}}-R_{\mathit{ij}})}^2$$ (13)

where N is our chosen block size, and C_ij and R_ij are the pixels being compared in the current and reference blocks, respectively. Several methods have been developed to reduce the computational complexity of this motion estimation process. However, since we are currently more concerned with accuracy and correctness of our results rather than computational complexity, we utilize the exhaustive search, or full search, method to find the best possible match. This method computes the cost function for every block in the search window, requiring (2p + 1)² comparisons with blocks having N² pixels.

3 Experimental Results

As described above, motion artifacts can be considered to consist of two components: a rigid component in which sequential images exhibit a translational offset from one another, and a non-rigid component which features non-linear distortions within each image. Many software applications have been developed for addressing global linear and orthogonal registration of microscopy images (e.g. Metamorph and various plugins for ImageJ), since this has been an ongoing problem in microscopy of living cells in culture. We first show an example of a dataset in which motion artifacts consist primarily of rigid translations.

Figure 1(A) shows one of a series of images collected over time from the kidney of a living rat, following intravenous injection with fluorescent dextran. The motion of the sample is apparent in Figure 1(B), which shows a maximum projection of the entire time-series, in which the motion results in a smearing in the images of the renal capillaries. The significant reduction of motion artifacts is shown in the projection of this time-series after rigid registration, shown in Figure 1(C). The effectiveness of the correction is more apparent in Video 1, which shows the side-by-side comparison of the sequences of the raw and registered images. The effective elimination of specimen translation by the registration technique is also shown in Figure 1(D)-(E), which shows sequences of single lines from the images before and after registration, respectively. In these images, the intensity profile of each line is arrayed horizontally and the time sequence arrayed vertically.

Figure 1.

(A) Example image from kidney vascular flow data set. (B) Maximum projection of entire series of images before rigid registration. (C) Maximum projection of entire series of images after rigid registration. (D) Line scan projection image before rigid registration. (E) Line scan projection image after rigid registration. Image field before registration is 205 microns wide. Image field after registration is wider because the field has shifted over the time of collection to include more area. Image sequence contains 200 frames.

However, as previously discussed, intravital microscopy introduces a completely different type of registration problem in which there is intrascene motion resulting from motion in the sample during collection of an individual image. Common image registration approaches are based upon a rigid frame translation, but because of the slow frame rate of laser point scanning microscope systems, images collected from living animals typically have complex intrascene distortions that are not corrected with rigid translations. In a scanning multiphoton fluorescence microscope, a two-dimensional image is assembled by sequentially scanning a series of horizontal lines across a sample. Because of the method of scanning, adjacent pixels are collected only microseconds apart in the horizontal direction, but are collected milliseconds apart in the vertical direction. For this reason, motion artifacts frequently appear in horizontal banding patterns. In fact, motion artifacts will be apparent at any frame rate, differing only in their relative manifestation as distortions between or within frames. Correcting these artifacts is significantly more challenging. We will now demonstrate the effectiveness of our non-rigid registration technique on several data sets consisting of images of the lung, kidney, and salivary gland collected in living rodents.

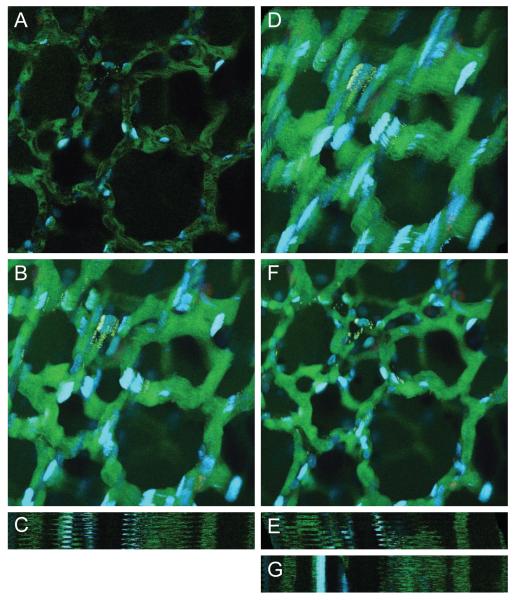
Figure 2(A) shows a single image from a time-series of images collected from the lung of a living rat following injection with fluorescein dextran (which fluoresces green in the vasculature) and Hoechst 33342 (which labels cell nuclei blue). We initially perform the rigid registration method as was performed previously with the sequence of rat kidney images. By comparing maximum projection and line scan projection images from before and after rigid registration shown in Figure 2(B)-(E), these images indicate that rigid registration has barely corrected the motion artifacts. In fact, one may argue that the registration has even exacerbated the motion artifacts compared to the raw images.

Figure 2.

(A) Example image from lung tissue data set. (B) Maximum projection of entire series of images before registration. (C) Line scan projection image before registration. (D) Maximum projection of entire series of images after rigid registration. (E) Line scan projection image after rigid registration. (F) Maximum projection of entire series of images after non-rigid registration. (G) Line scan projection image after non-rigid registration. Image field is 205 microns wide. Image sequence contains 50 frames. Non-rigid registration was performed using λ = 0.02 and a B-spline control point grid spacing of δ_x = δ_y = 64 pixels, and using a limited memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) optimizer to determine the final B-spline control points.

By now utilizing our combined rigid and non-rigid registration method using B-splines, we see in Figure 2(F)-(G) that the maximum projection and line scan projection images show extraordinary reduction of the motion artifacts. This clearly illustrates the deficiencies of rigid registration for correction of respiration and heartbeat motion artifacts, while non-rigid registration using B-splines is very promising in this application. The effectiveness of the non-rigid registration is extraordinarily convincing in Video 2, which shows the side-by-side comparison of the sequences of the raw and registered lung tissue images.

To present a more quantitative measure of registration success, one may consider evaluating a well-established metric such as Target Registration Error, or TRE (Fitzpatrick, West & Maurer Jr., 1998). However, this registration evaluation metric requires manually identifying fiducial points in corresponding pairs of images. This is quite impractical and labor intensive for image sequences that contain hundreds of images. Therefore, as a more automated quantitative evaluation, we compute an average of sum of squared differences (SSD) of pixel intensities across all images in the sequence. Normalizing this value by the number of pixels in the image is not appropriate because the registered image sequence has a larger field of view. Since each image in the registered sequence contains more matching black pixels, a normalized value would show an improvement in alignment even if no registration had been performed. Results for this image sequence of lung tissue are shown in Table 1, which compares SSD values before registration, after rigid registration, and after both rigid and non-rigid registration. Even though Figure 2(D) may show a worsening of image alignment, rigid registration has marginally improved image alignment according to the SSD metric. However, non-rigid registration has drastically improved image alignment, according to both a quantitative SSD standpoint and a visual standpoint.

Table 1.

Image Sequence	Average SSD per Image	Percent Improvement
Lung without registration	7329.7	—
Lung with rigid registration	7190.5	1.9%
Lung with rigid and non-rigid registration	2739.8	62.6%
Kidney without registration	13208	—
Kidney with rigid registration	12938	2.0%
Kidney with rigid and non-rigid registration	6026	54.4%
Salivary gland without registration	273.0	—
Salivary gland with rigid registration	246.9	9.6%
Salivary gland with rigid and non-rigid registration	124.2	54.5%

As we have seen, SSD quantitative evaluation does not necessarily match visual evaluation of image alignment. Therefore, in addition to projection images, we also utilize the motion vector analysis described previously as a validation technique. This attempts to identify any distinct motion patterns within the motion vector field prior to and subsequent to registration. Computation of motion vectors was performed for all images in the sequence, and weighted histograms of motion vector angles with non-zero magnitudes were generated for each image. These histograms are created with 36 bins, and motion vector angles are weighted by motion vector magnitudes. A weighted histogram for one particular image in the lung tissue sequence is shown in Figure 3(A). The histogram for the unregistered image is shown in blue, while the histogram for the corresponding registered image is shown in red. As can be seen, the unregistered image has dominant motion to the upper-right and lower-left with respect to its previous image. However, the magnitudes of the motion vectors for the registered image shown in red are significantly reduced compared to the unregistered image. Furthermore, not only are the magnitudes of motion vectors reduced, but the distribution of motion vector angles is significantly more uniform compared to the unregistered image, indicating that motion is not apparent in any particular direction. Comparing magnitude and angle distribution of motion vectors from before and after registration demonstrates that our non-rigid B-spline registration technique has successfully corrected a large portion of the motion artifacts.

Figure 3.

Motion vector analysis for lung tissue data set shown in Figure 2. (A) Weighted histogram of motion vector angles for one slice. Histogram for unregistered image is show in blue, while histogram for registered image is shown in red. Motion vector analysis was performed using a 31×31 search window and 16×16 blocks size. (B) 3D distribution plot of motion vector displacements before registration. (C) 3D distribution plot of motion vector displacements after registration.

Since these weighted histograms omit motion vectors with zero magnitude, we can include these in a 3D distribution plot of all motion vectors for the same image as shown in Figure 3(B)-(C). For the unregistered image, the 3D distribution plot contains many large peaks across the entire search window, indicating that significant motion has been identified throughout the image. Peaks in the 3D distribution plot indicate that the image contains many motion vectors with the corresponding magnitude and orientation. In contrast, for the registered image, the vast majority of the motion vectors are concentrated at the origin, suggesting no motion. Again, this comparison indicates that the non-rigid B-spline registration technique has successfully corrected a large portion of the motion artifacts.

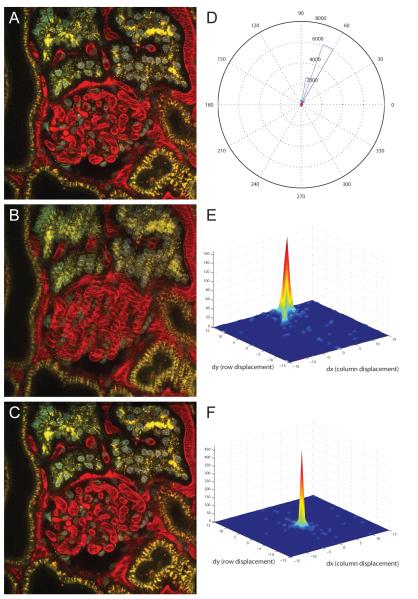
We previously mentioned that our combined rigid and non-rigid registration method is robust and effective on both time-series and three-dimensional data. After demonstrating our non-rigid registration technique on images collected in time-series, we will now demonstrate its effectiveness on three-dimensional sequences of images. Consecutive images in a three-dimensional sequence of images share enough content such that the registration process performs well. Figure 4(A) shows a single image from a three-dimensional image volume collected from the kidney of a living rat injected intravenously with Hoechst 33342, which labels cell nuclei (blue), a large molecular weight dextran that fluoresces red in the vasculature of the glomerulus (center of image) and a small molecular weight dextran that is internalized into endosomes of proximal tubule cells (appearing as fine yellow spots). Specimen motion occurring during collection of this volume is apparent as the smeared appearance in the overlay of two consecutive images shown in Figure 4(B).

Figure 4.

(A) Example image from renal tissue data set. (B) Overlay of consecutive unregistered images. (C) Overlay of consecutive registered images. Image field is 205 microns wide. Image sequence contains 56 frames. Non-rigid registration was performed using λ = 0.02 and a B-spline control point grid spacing of δ_x = δ_y = 64 pixels, and using a limited memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) optimizer to determine the final B-spline control points. (D) Weighted histogram of motion vector angles for one slice. Histogram for unregistered image is show in blue, while histogram for registered image is shown in red. Motion vector analysis was performed using a 31 × 31 search window and 16 × 16 blocks size. (E) 3D distribution plot of motion vector displacements before registration. (F) 3D distribution plot of motion vector displacements after registration.

We illustrate the effectiveness of our combined rigid and non-rigid registration method by showing the overlay of the corresponding two consecutive images after registration shown in Figure 4(C). Ghosting artifacts resulting from significant misalignment of objects are obvious in the original volume, but are vastly improved following registration. Therefore, this visual inspection of the registration results confirms that the motion artifacts have largely been corrected. Again, this motion reduction is more apparent in Video 3, which shows the side-by-side comparison of the sequences of the raw and registered three-dimensional kidney tissue images.

Again, quantitative SSD values to evaluate registration success are shown in Table 1 for this image sequence of kidney tissue. Similar to the lung, rigid registration has marginally improved image alignment according to the SSD metric, while non-rigid registration has drastically improved image alignment. Motion vector analysis was again performed as an additional validation technique. A weighted histogram for one particular image in the kidney tissue sequence is shown in Figure 4(D). The histogram for the unregistered image is shown in blue, while the histogram for the corresponding registered image is shown in red. As can be seen, the unregistered image has an extremely distinct motion to the upper-right with respect to its previous image. However, the histogram in red shows the near elimination of all motion in the registered image, as all of the histogram bins are near zero and dwarfed by the histogram bins from the unregistered image. Again, this simple comparison indicates that the non-rigid B-spline registration technique has successfully corrected essentially all of the motion artifacts.

All motion vectors computed across the same image in the sequence are quantified in a 3D distribution plot and are shown in Figure 4(E)-(F). For the unregistered image, the 3D distribution plot contains one large peak at the edge of the plot, confirming that the majority of the motion vectors suggest upward motion. In contrast, for the registered image, essentially all of the motion vectors are concentrated at the origin, suggesting no motion. Again, this comparison indicates that the non-rigid B-spline registration technique has successfully corrected the vast majority of the motion artifacts.

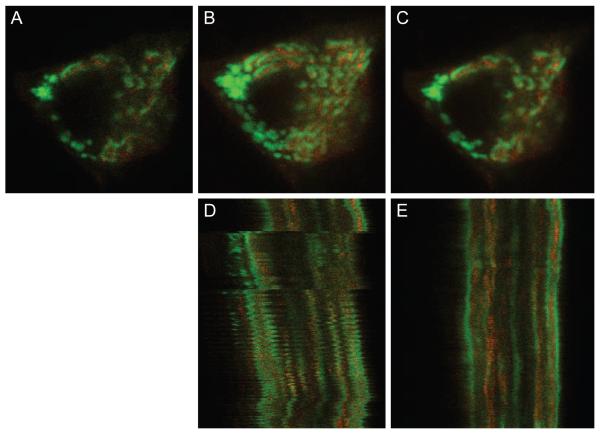
Our last example shows the effectiveness of motion artifact correction even at the sub-cellular level. Figure 5(A) shows a single image from a time-series of images of a single cell in the salivary gland of a living mouse. The mouse cell is expressing EGFP-clathrin in endosomes and the trans-Golgi network and mCherry-TGN38 in the trans-Golgi network. Since even the slightest motion will compromise the ability to distinguish intracellular organelles, motion artifacts present a serious challenge to intravital microscopy of subcellular processes.

Figure 5.

(A) Example image from salivary gland data set. (B) Maximum projection of 15 images before registration. (C) Maximum projection of 15 images after registration. (D) Line scan projection image before registration. (E) Line scan projection image after registration. Image field before registration is 25 microns wide. Image field after registration is wider because the field has shifted over the time of collection to include more area. Image sequence contains 310 frames. Non-rigid registration was performed using λ = 0.005 and a B-spline control point grid spacing of δ_x = δ_y = 16 pixels, and using a limited memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) optimizer to determine the final B-spline control points.

Due to the decreased image resolution and image scale along with more intense motion artifacts compared to the previous image sequences, the smoothness penalty coefficient in the cost function has been reduced by a factor of 4, and the B-spline control point grid spacing has been increased by a factor of 4. A smaller and more dense B-spline control point grid along with a decreased smoothness constraint coefficient allows for more bending and warping in the registration process to correct more intense motion artifacts, both spatially and temporally. Maximum projection images across 15 sequential image planes from before and after registration are shown in Figure 5(B)-(C), respectively, demonstrating that registration accomplishes a significant reduction in the motion artifact of the original image series. The correction is somewhat obscured in these images by the fact that the intracellular vesicles actually are in motion. The success of the correction is more apparent in Video 4. Viewers of the video will notice that the registration performs better toward the end of the video where there is more pronounced subcellular motion compared to the beginning of the video sequence. Perhaps contrary to intuition, the non-rigid registration method will more closely register a pair of images that contain a greater misalignment—up to a certain threshold. If two images are too similar, the smoothness constraint term in the cost function will overpower the similarity metric term. Therefore, for the beginning of the video sequence, where consecutive images are already much more closely aligned, tiny misalignments are allowed to propagate through the registration process. The correction is also apparent in comparison of line scan images from before and after registration shown in Figure 5(D)-(E), in which the disjointed subcellular objects of the original image series have been properly aligned into solid, continuous objects through the time series.

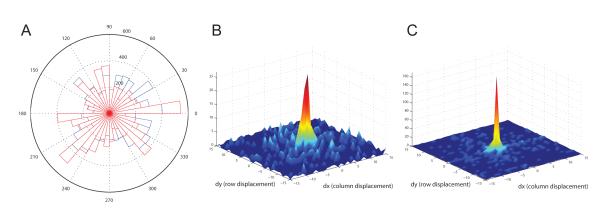
Lastly, quantitative SSD values to evaluate registration success are again shown in Table 1 for this image sequence of salivary gland tissue. Similar to both the lung and kidney, rigid registration has marginally improved image alignment, while non-rigid registration has drastically improved image alignment. Motion vector analysis is performed to validate the subcellular non-rigid registration results as well. A weighted histogram for one particular image in the salivary gland tissue sequence is shown in Figure 6(A). The histogram for the unregistered image is shown in blue, while the histogram for the corresponding registered image is shown in red. The histogram bins for the registered and unregistered images show little distinction between each other. However, the comparison of the 3D distribution plots for both unregistered and registered images shown in Figure 6(B)-(C) is much more convincing. Motion vectors for the registered sequence are much more concentrated at the origin compared to those for the unregistered image. This comparison indicates that the non-rigid B-spline registration technique has successfully corrected a large portion of the motion artifacts at the subcellular level as well.

Figure 6.

Motion vector analysis for salivary gland data set shown in Figure 5. (A) Weighted histogram of motion vector angles for one slice. Histogram for unregistered image is show in blue, while histogram for registered image is shown in red. Motion vector analysis was performed using a 31 × 31 search window and 8 × 8 blocks size. (B) 3D distribution plot of motion vector displacements before registration. (C) 3D distribution plot of motion vector displacements after registration.

4 Discussion

While intravital microscopy has made it possible to apply many of the same techniques that have been productively used in microscopic studies of cultured cells to studies of single cells in vivo, quantitative analysis is frequently limited by motion artifacts, which—with the notable exception of the brain—are ubiquitous to intravital microscopy. Motion artifacts, resulting from respiration and heartbeat, limit resolution and preclude segmentation, which is prerequisite to image quantification. In addition, many other well-known challenges complicate quantitative analysis of fluorescence images collected from living animals. Microscopy volumes are inherently anisotropic, with aberrations and distortions that vary in different axes. At a larger scale, contrast decreases with depth in biological tissues. This contrast decrease aggravates a general problem of fluorescence images, which characteristically have low signal levels (Dufour, Shinin, Tajbakhsh, Guillen-Aghion, Olivo-Marin & Zimmer, 2005). Signal levels are further decreased by the need for high image capture rates necessary to image dynamic biological structures. It has been demonstrated that image registration can significantly improve image segmentation performance, especially with volumetric data (Pohl, Fisher, Levitt, Shenton, Kikinis, Grimson & Wells, 2005). However, images with poor contrast and low resolution generally preclude registration methods involving landmarks, and decrease the ability of intensity-based registration methods to properly identify corresponding objects across images. Furthermore, biological structures often consist of many different kinds of irregular and complicated structures that are frequently incompletely delineated with fluorescent probes. With edges of biological structures sparse and poorly defined, gradient- and edge-based error metrics used in the registration method will perform poorly. Low contrast and small intensity gradients in multiphoton image volumes cause image analysis and rendering results to be very sensitive to small changes in parameters, resulting in the failure of typical image registration methods. Despite all of the challenges discussed, we have demonstrated that a combination of rigid and non-rigid registration techniques is capable of significantly improving the quality of microscope images collected in time series or in three dimensions from living animals.

The non-rigid registration method using B-splines discussed in this paper is sufficiently robust to overcome many of the challenges outlined above, and is paramount to any image analysis to follow. Experimental results indicated that this method is promising in registering images in time-series data sets as well as data sets comprised of images acquired at increasing tissue depths. Additionally, the registration method has performed well for image sequences of kidney, lung, and salivary gland of living animals. With the one exception of the subcellular salivary gland images, all image sequences utilized identical sets of registration parameters, including grid point spacing and smoothness penalty cost coefficient. This demonstrates that a default set of parameters can be chosen to perform reasonably well to register a wide variety of image sequences. Furthermore, the rigid registration section of our method has a wide capture radius and has a strong ability to correct large displacements. The non-rigid registration section of our method is able to correct small to medium discontinuities. As a result, with the combination of the two, we are able to correct a wide range of discontinuities. Therefore, this registration method demonstrates profound versatility and robustness.

Previously developed and well-established registration methods may be used to process stacks consisting of multiple images (Thévenaz, Ruttimann & Unser, 1995, 1998). However, these methods implement an affine registration. Affine registrations account for transformations including translation, rotation, scaling, and shearing. However, these transformations alone are insufficient to register image sequences collected in vivo. The dynamic motion from living animals introduced from respiration and heartbeat cannot be described with an affine transformation.

Objective evaluation of our results proves to be difficult due to the lack of ground truth data. Evaluation of results has been initially addressed subjectively by evaluating overlay images, maximum projection images, and line scan projection images, and objectively by using using block motion estimation vectors. Even with the lack of ground truth, the results from these images along with side-by-side video comparisons all contribute to demonstrating the efficacy of our non-rigid registration method using B-splines. However, evaluation of accuracy in contrast to precision remains difficult as judgments are significantly more subjective and less objective.

In summary, intravital microscopy is a powerful technique for studying physiological processes in the most relevant context, in the living animal. However, developing assays of physiological function will require developing novel methods of digital image analysis that will support quantitative analysis. Insofar as accurate image registration is prerequisite to quantitative analysis of time-series and volumetric image data, the development of effective methods of image registration is fundamentally important to realizing the potential of intravital microscopy as a tool for understanding and treating human diseases. The techniques described here will enable new studies that were previously impossible. Readers interested in using the tools described in this paper can contact us (psalama@iupui.edu) concerning the availability of the software. At the time of development, computational runtime was a secondary concern compared to registration performance and accuracy. However, the software to be provided to end users is being rewritten for efficiency and runtime improvements. Future work will involve developing registration approaches using more 3D techniques, as surrounding images provide additional information useful in distinguishing the degree of distortion from motion artifacts.