Computational approaches to predicting the impact of novel bases on RNA structure and stability

Abstract

The use of computational modelling techniques to gain insight into nucleobase interactions has been a challenging endeavor to date. Accurate treatment requires the tackling of many challenges, but also holds the promise of great rewards. The development of effective computational approaches to predict the binding affinities of nucleobases and analogs can, for example, streamline the process of developing novel nucleobase modifications, which should facilitate the development of new RNAi-based therapeutics, for example. This brief review focuses on available computational approaches to predicting base pairing affinity in RNA-based contexts such as nucleobase-nucleobase interactions in duplexes and nucleobase-protein interactions. The challenges associated with such modelling along with potential future directions for the field are highlighted.

Introduction

Chemical biologists are increasingly captivated by the study of ribonucleic acid (RNA) both for its chemical properties and its diverse biological functions.^(1–5) RNAs can adopt complex three-dimensional shapes and can catalyze a wide range of different chemical reactions.⁽⁶⁾ Functional RNAs can also be small and accessible by total chemical synthesis.⁽⁷⁾ In addition, RNAs have wide-ranging biological properties as essential structural components of cells, information storage and retrieval systems, catalysts and regulators of gene expression. The basic structural component of folded RNAs is the Watson-Crick base-paired double helix (double-stranded RNA, dsRNA) (Figure 1). While dsDNA tends to adopt the familiar B-form helix with well-defined major and minor grooves, dsRNA’s structure is different. Duplex RNA favors the A′-form helical structure, where the minor groove is very shallow and wider than the major groove, which is now quite narrow but deep (Figure 1). RNA also regularly adopts structures with loops and single-stranded regions. The base pairs in A′-form RNA are twisted with respect to one another, and are not perpendicular to the primary axis (as in B form DNA). Furthermore, some base pairs in RNA involve non-canonical interactions or protonated bases,^{(8, 9)} and, in addition to the common four ribonucleosides A, G, C and U, naturally occurring RNAs frequently contain nucleoside analogs (Figure 2).^{(10, 11)} These modifications of the typical RNA structure extend the functional properties of the RNA beyond those possible without them. Chemists have also introduced nonnatural nucleosides into RNA that impart properties not possible with the native RNA structure alone. This has become even more common recently with increased focus on the therapeutic potential of small RNAs (e.g. siRNAs that induce target knockdown via RNAi) that are easily prepared by chemical synthesis.⁽²⁾ Given the nearly infinite chemical space that could be explored in the development of nucleoside analogs for use in RNA, there is a need for rapid methods that can be used to filter structures prior to testing. In addition, our fundamental understanding of how changes in nucleoside structure translate into changes in the RNA fold and/or stability is still limited. Thus, the question arises: Can currently available computational methods be helpful in predicting the effects on RNA structure and stability of modified nucleotides, particularly those with novel nucleobase structures that may alter base pairing interactions? Here we review methods that one might consider when trying to address this question and highlight particularly promising approaches.

Figure 1.

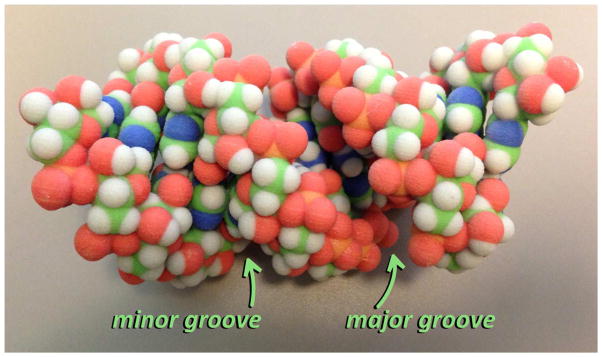
A 3D model⁽¹²⁾ of dsRNA, showing the minor and major grooves (PDB ID: 1R9F).⁽¹³⁾

Figure 2.

A naturally occurring nucleobase analog with unique base-pairing properties. The cytidine analog agmatidine preferentially base pairs with adenosine (over guanosine) in the archael tRNA₂^Ile-mRNA duplex formed during decoding in the ribosome.⁽¹⁴⁾

Available Computational Methods

Bioinformatics

There is a wealth of literature describing attempts to use computational methods to provide understanding of the physical factors that control RNA structure.^(15–17) One approach to predicting various RNA-related phenomena (structures and reactivities),⁽¹⁸⁾ is to make use of statistical/data-mining/informatics methods.^(19–22) These methods, however, are only able to make effective predictions when large enough databases of relevant experimental information are available. Along these lines, much effort has gone toward prediction of the thermodynamics of RNA folding, i.e., predicting secondary structure preferences based on sequences, although the ability to predict secondary structure without the guidance of some experimental data is limited.^(23–29) A recent success in secondary structure prediction is the development of CONTRAfold, which makes use of “fully-automated statistical learning algorithms”⁽³⁰⁾

Explicit Interactions—General Concerns

We focus herein, however, on computational chemistry approaches aimed at predicting base-pairing proficiencies by explicitly taking into account interatomic interactions. The primary challenge in this area is that the systems under investigation are very large (by computational standards), necessitating the use of small model systems (which may unintentionally lack important structural features) or fast computational methods (which may not be able to answer all questions of interest with sufficient accuracy). For example, molecular mechanics (MM) and MM-based molecular dynamics (MD) calculations allow for the investigation of full-sized RNA oligomers, but these methods are based on classical mechanics, and as such, neglect or approximate interactions of quantum mechanical (QM) origin. There are many QM methods that can be used to treat these interactions, but these require considerable computational resources (especially, time).

Classical Mechanics

MM and MD methods have been applied successfully to modeling DNA and RNA.^(31–40) Issues facing these approaches, however, include appropriate treatment of nucleobase polarizability and subtle electrostatic effects.^{(41, 42)} Although well-parameterized MM force-field methods can faithfully reproduce higher order interaction energies,⁽⁴³⁾ there is room for improvement in accurate prediction of RNA macrostructure.⁽⁴⁴⁾ Without a doubt, improvements to these methods will help facilitate the rapid computation of key properties of RNA oligomers.⁽⁴⁵⁾

Quantum Mechanics

Among the QM approaches available for studying RNA, semi-empirical QM methods have been found to be less successful than ab initio and density functional theory (DFT) methods for many systems, while providing extremely accurate results for some specific cases.^(46–50) Various high-level quantum mechanical (e.g., post-Hartree Fock) methods can very accurately capture features that depend on, for example, electron correlation and dispersion effects,^{(51, 52)} but due to computational expense, most investigations have so far utilized small model systems, containing only one or two base pairs, designed to capture specific effects (e.g., π-stacking,^{(53, 54)} hydrogen bonding,⁽⁵⁵⁾ sterics/shape⁽⁵⁶⁾, electrostatics),^{(51, 57, 58)} rather than the combination of these effects that is manifested experimentally. Proper modeling of these combined effects are no small task, and ongoing efforts have been led by the Šponer and Hobza laboratories for both RNA and DNA systems, among others.^(59–61) Even these “small” model systems are large enough to prohibit the use of the highest levels of theory, and studies aimed at determining which methods are appropriate for probing which interactions are ongoing.^{(62, 63)}

Nonetheless, these studies have provided key insights into the forces that contribute to RNA structure, for example, in the area of π-stacking, an important contributor to the total interaction energies between nucleobases. For example, utilizing very high levels of theory (coupled cluster methods) on the interaction of benzene dimers, Sinnokrot and Sherrill obtained benchmark-quality data to be used in the creation of more accurate force-fields.⁽²⁷⁾ In addition, some DFT methods can reproduce π-stacking interactions with accuracy comparable to that from much higher levels of theory, at least in select cases.⁽⁶⁰⁾

There have also been some successes in the reproduction of base pair affinities using approaches that neglect the sugar-phosphate backbone but focus only on particular free nucleobases. In the case of known base pairs, only small changes to geometric features associated with hydrogen-bonding and π-stacking compared to diffraction data have been found when using such models.⁽⁵⁵⁾ The essential role of hydrogen-bonding in nucleic acid structure has also been amply demonstrated using very high level QM methods.⁽⁶⁴⁾ Nonetheless, further work is needed on larger systems that incorporate structural features beyond the base pair in order to account for distortions (e.g., helical strain, propeller twist) imposed by the larger superstructure of the RNA duplex^{(57, 65)}—distortions that likely contribute not only to magnitudes of interaction energies between bases, but also to base-pairing specificity and sequence effects.⁽⁶⁶⁾

Recent Successes

Interaction Energies from QM Using Experimentally Determined Nucleobase Geometries

Recently, Znosko, Lewis and co-workers described a study that appears to dispel two myths in the field of RNA (and DNA) structure prediction: 1) average fiber diffraction data does not provide reliable geometries for predicting interaction energies between bases, and 2) stacking energies from QM calculations are not accurate enough to predict RNA structures.⁽⁶⁷⁾ Using nucleobase geometries from average diffraction data and QM (MP2) energy calculations, these researchers were able to demonstrate a correlation between predicted and experimental nearest-neighbor binding energies. Although additional work will be required to make such predictions quantitatively accurate, this approach appears to have promise for the prediction of not only base-pairing partners, but also stacking preferences, however this has not been without debate.^{(68, 69)}

Kamya and Muchall utilized a similar approach (X-ray crystal structure data for nucleobase geometries and the PBE0 DFT method for energy calculations, along with QTAIM⁽⁷⁰⁾ [Quantum Theory of Atoms In Molecules] analysis of electron density) to quantify hydrogen bonding and π-stacking interactions.⁽⁷¹⁾ On the basis of their results, these researchers suggested that conflicting experimental and computational evidence on the relative strengths of A•T and A•U base pairs⁽⁶⁴⁾ is likely a manifestation of sequence effects, i.e., the context in which such base pairs occur can tip the balance.

Together, these studies demonstrate the benefits of employing experimental structural information in QM-based calculations on base-pairing affinities. By doing so, approximations associated with using MM methods to predict geometries of large systems or using small model systems for geometry optimization with QM methods are avoided. The structural consequences of the many small interactions contributing to stable base pairing are present in the experimentally determined geometries, which can then be analyzed utilizing a reliable QM method. The ever-growing library of experimentally characterized RNA structures will allow such approaches to be further refined, opening the door toward a richer understanding of the fundamental interactions at play.

Automated Docking

While the approaches just described are very useful for teasing out the origins of base pairing affinities, they are still computationally demanding. If one wishes to survey a wide variety of nucleobase analogs (experimentally available or proposed) so as to predict their binding propensities in particular contexts, then a more rapid and computationally tractable approach is required. Automated computational docking may provide such an approach.^{(72, 73)} Since such methods are often utilized, for example, to screen large libraries of potential drug leads, they are fast. Consequently, these methods generally employ MM force fields, of varying sophistication, to assign scores to small molecule-protein binding orientations (poses). The application of such methods to problems in nucleic acid chemistry,^(74–76) however, is an under-explored area that appears to have potential.

In one recent application, Brenk and co-workers used a computational docking approach (DOCK 3.5.54 with small modifications for RNA) to predict the binding of a variety of nucleobase analogs to adenine-binding riboswitches whose structures had been determined using X-ray crystallography.⁽⁷⁷⁾ Binding modes for analog-riboswitch complexes that had already been determined experimentally were successfully reproduced via docking. The docking calculations were also able to distinguish known binders from structurally related decoy molecules, although not infallibly. A strong correlation between docking scores and known dissociation constants was not observed, but this is a problem that is not particular to docking with RNA receptors. Some successful predictions of commercially available compounds that might bind to these riboswitches were also made. Studies of this type show that docking of nucleobases and nucleobase analogs into RNA binding sites is feasible, even using docking software not designed specifically for use with RNA.^{(57, 65, 66, 78–82)}

Desirable Data

The types of calculations highlighted above require experimental structures as starting points limiting the number of systems that can be explored using computational methods. There is obviously a need for additional structural data if new nucleobase analogs with desired functions are to be designed rationally or obtained from molecular docking screens. For instance, recent reports of the structure of human Ago2, the key nuclease of the RNAi pathway, bound to guide strand RNA provide an opportunity for siRNA optimization using computational screening for nucleoside analogs that bind well to this protein (Figure 3).⁽⁸⁵⁾ At this point, although relatively few structures are available, different duplex RNA structures have been reported, including some that contain nucleobase analogs.⁽⁵⁾ For instance, structural studies and UV melting (T_M) data for duplex RNAs containing the uridine mimic ribo-2,4-difluorotoluyl indicate that this modification is destabilizing opposite A and induces numerous local structural changes that subtly effect the geometry of the RNA duplex; this modified nucleotide does, however, appear to bind more tightly to G, in which case less structural distortion is observed (Figure 4).^{(83, 84)} This experimental work fed directly into computational work, as this study also described QM (MP2) calculations on difluorotoluyl-containing base pairs; these calculations reproduced the order of base pair stabilities determined experimentally.⁽⁷⁶⁾ The availability of additional structural and thermodynamic data of this type will no doubt facilitate computational approaches aimed at identifying new nucleoside analogs that can be used to deepen our understanding of these fundamental interactions.

Figure 3.

Crystal structure of human Ago2 bound to guide RNA (PDB ID: 4EI1).⁽⁸⁵⁾

Figure 4.

Portion of crystal structure of an RNA dodecamer duplex containing a difluorotoluyl•••G base pair (F atoms highlighted in green; putative F•••HN and CH•••O interactions highlighted in yellow), which affects silencing despite not displaying major disruptions to the duplex structure (PDB ID: 2Q10).⁽⁷⁶⁾

Computational Approaches for the Future

While the work of Brenk and coworkers showed that computational docking could be applied to RNA to discover new ligands for an RNA-based receptor, the question remains whether such tools can be used to predict how well a nucleobase analog attached covalently in place of a particular nucleobase will bind to its neighbors. One can envision many possible computational approaches to this problem. For example, a layered approach could be used in which the geometries of the analog and the nucleobases interacting directly with it are optimized with QM methods, leaving the rest of the duplex frozen to an experimentally determined geometry. Šponer and co-workers recently have made methodological advances toward this approach.⁽⁶⁶⁾ Alternatively, one could utilize the recently described fragment-based⁽⁸⁶⁾ QM approaches developed by Raghavachari and co-workers (and others) for treating large molecules such as DNA oligomers.⁽⁸⁷⁾ A third option would be to repurpose existing computational docking software to predict the binding proficiency of a nucleobase analog. Finally, with better coding and faster computers, high-level dynamical approaches will become more viable. While there are challenges to overcome with each of these methods, computational (bio)chemistry will likely play an important role in the future development of new nucleobase analogs capable of stable and specific pairing in RNA.

Keywords

Nucleobase

structural component of a nucleic acid often involved in base pairing

RNAi

RNA interference, the process of cleavage and ultimately degradation of a specifically targeted RNA induced by an added RNA duplex containing a strand matching the target sequence

Ago2

nuclease responsible for cleavage of target RNA in RNAi, binds one of the strands of a short interfering RNA duplex and uses it as a guide for target identification

Riboswitch

an RNA species involved in regulation of gene expression containing a ligand-binding aptamer domain and expression platform

DFT

Density functional theory, a quantum mechanical method that uses the electron density to calculate molecular properties, as opposed to calculation of the wavefunction in ab initio methods

Classical Mechanics

Method for description of objects, including molecules, using Newton’s laws of motion. This could be a description using potential energy (MM) only, or potential and kinetic energy together (MD)

Quantum Mechanics

Class of methods for describing the properties of molecules using the principles of quantum physics

Automated Docking

Computational methods (usually molecular mechanics-based) designed to describe and predict interactions between small and large molecules