Pathway-based Approaches for Sequencing-based Genome-wide Association Studies

Abstract

For analyzing complex trait association with sequencing data, most current studies test aggregated effects of variants in a gene or genomic region. While gene-based tests have insufficient power even for moderately sized samples, pathway-based analyses combine information across multiple genes in biological pathways and may offer additional insight. However, most existing pathway association methods are originally designed for genome-wide association studies (GWAS), and are not comprehensively evaluated for sequencing data. Moreover, region-based rare variant association methods, although potentially applicable to pathway-based analysis by extending their region definition to gene sets, have never been rigorously tested.

In the context of exome-based studies, we use simulated and real data sets to evaluate pathway-based association tests. Our simulation strategy adopts a genome-wide genetic model that distributes total genetic effects hierarchically into pathways, genes, and individual variants, allowing the evaluation of pathway-based methods with realistic quantifiable assumptions on the underlying genetic architectures.

The results show that, while no single pathway-based association method offers superior performance in all simulated scenarios, a modification of GSEA approach using statistics from single-marker tests without gene-level collapsing (WKS-Variant method) is consistently powerful. Interestingly, directly applying rare variant association tests (e.g., SKAT) to pathway analysis offers a similar power, but its results are sensitive to assumptions of genetic architecture. We applied pathway association analysis to an exome sequencing data of the chronic obstructive pulmonary disease (COPD), and found that the WKS-Variant method confirms associated genes previously published.

Introduction

Exome sequencing has been proven to be a powerful and economical technology for identifying protein-coding variants [Ng, et al. 2009]. Encouraged by its success in identifying genes associated with rare Mendelian diseases (RMDs) [Kiezun, et al. 2012], researchers are now applying exome sequencing to large epidemiological cohorts in the hope that it will identify rare variants that may explain part of the missing heritability of complex traits [Maher 2008; Manolio, et al. 2009]. Compared with RMDs, complex traits are often caused by joint effects of multiple variants scattered in many genes. Genomic sequencing identifies genetic variants across the entire allele frequency spectrum, with a majority of the variants called being rare variants [Tennessen, et al. 2012a]. Since single SNP association tests are underpowered for rare variants, current association tests for sequencing data are mainly gene based or region based [Asimit and Zeggini 2010; Bansal, et al. 2010]. These methods combine information across multiple variants in a gene, and thus offer higher power than single variant tests.

However, because of the severe multiple testing problem, it is unlikely that these gene-based methods alone will be powerful enough to pinpoint individual genes in whole exome analysis for moderately-sized studies. Theoretical studies [Kiezun, et al. 2012; Kryukov, et al. 2009; Liu and Leal 2010; Tennessen, et al. 2012a] and candidate gene sequencing studies [Ahituv, et al. 2007; Cohen, et al. 2004; Harismendy, et al. 2010] suggest that these gene-based rare variant tests may not be sufficiently powered unless sample sizes are as large as n>10,000, as genome-wide significance requires strict Bonferroni correction (p-value < 2.5×10⁻⁶ for 20,000 genes). However, because the cost of exome sequencing is still significantly higher than microarray-based genotyping, most GWAS-exome projects are only able to afford a smaller sample size than GWAS. In addition, many variants identified by exome sequencing are rare variants, whose effects are even more difficult to estimate [Park, et al. 2010; Yi and Zhi 2011].

In such case, a pathway-based test may find useful biological information from exome sequencing data sets that are often underpowered for gene-based tests. Just as gene-based tests combine signals from multiple single variant association tests, so too do pathway-based tests combine signals from multiple gene-based association tests. If a complex trait is affected by multiple causal genes in a biological pathway, pathway-based tests will likely have higher power. Moreover, pathway-based methods consider the biologically meaningful gene sets, and may help to interpret the association results and decipher the biological mechanisms. It is noted that pathway level analysis, as a complement of variant and gene level analyses, relies on specific trait’s biological knowledge and researchers’ hypotheses.

There are two main approaches for pathway-based tests for sequencing data. The first approach is to extend the gene-set analysis methods that have been developed in GWAS data [Holden, et al. 2008; Luo, et al. 2010; Wang, et al. 2007; Wang, et al. 2010a; Wang, et al. 2011] to exome-sequencing data. However, there are intrinsic differences between GWAS and exome-sequencing genotyping data. Exome sequencing is gene-centric by design while most GWAS designs, especially early platforms, often ignore gene structures. There are several important distinctive characteristics of exomic data compared to array-based GWAS data. First, the gene membership of exomic variants is typically clearly defined while GWAS variants can often fall in intergenic regions. Secondly, annotation of exomic variants is often more informative, as our ability to interpret the impact of protein coding variants is far more advanced than for non-coding variants which are also often identified as the most significantly associated SNPs in regions identified in GWAS studies. Thirdly, exome sequencing provides a complete catalogue of coding variants. Thus, there is a good chance that the true causal variants, if protein-coding, are directly observed. This is in contrast to GWAS association signals that are often ‘tags’ of the true underlying causal variants, and this tagging is less accurate for rare variants.

The second approach is to apply region-based rare variant association methods directly to regions that are defined as the union of all genic regions in a pathway. While in the context of rare variant association methods, regions primarily refer to gene regions; there is no methodological hurdle preventing the extended definition of regions. The main differences, however, are that regions of gene sets may contain a very large number of variants, many of which may not be relevant to the trait of interest. In addition, it may not be the case that most of the causal variants affect the trait in the same direction. Therefore, variance-based tests may be more appropriate than burden tests in the context of pathway tests.

However, there have been few rigorous evaluations of pathway-based methods for genome-wide genetic associations. In recent years, rigorous simulations have been instrumental in shaping the methodological developments of gene-based rare variant association tests. Li and Leal [Li and Leal 2008] evaluated type-I error rates and power for gene-based rare variant association methods under realistic simulations of various population attributable risks (PARs), number of variants, allele frequency, mis-classification of causal and non-causal variants, different proportions of variants being causal, and contributions from common variants. Later developments also considered variants of different effect sizes, opposite effects of variants, and a realistic allele frequency spectrum from a population genetics simulation [Ionita-Laza, et al. 2011; Wu, et al. 2011] or real sequence data [Daye, et al. 2012]. Interestingly, to the best of our knowledge, there are no rigorous evaluations on pathway-based methods, either for microarray-based GWAS or for exome sequencing data with complex traits.

In this work, we conduct an extensive simulation-based evaluation of various strategies for pathway-based association tests for exome sequencing data. We use real genotype data from the 1000 Genomes Project [The 1000 Genomes Project Consortium 2010] and simulated traits with various genome-wide genetic architectures. We evaluate the type-I errors and powers for 11 pathway-association methods, including variations of the pathway-based association originally designed for GWAS data and variance-based region test originally designed for gene-based rare variant tests. In addition, we present the results of using pathway-based methods in the analysis of a real exome sequencing data set for chronic obstructive pulmonary disease.

Materials and methods

1. Genotype data used in simulation

We use the whole exome sequencing genotype data of the 1000 Genomes Project (1000G) Phase 1 study intermediate release 20110810 (ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/technical/working/20110810_exome_consensus_snps/) in simulation. This data set contains 822 individuals and is available as 13 HapMap population specific VCF files. The pipeline of alignment and genotype calling, as well as quality control procedures are documented in details in projects’ supplementary materials [The 1000 Genomes Project Consortium 2010] and website (http://www.1000genomes.org/data). We use VCFtools 0.1.9 [Danecek, et al. 2011] to merge different populations’ genotype data together. Then we use ANNOVAR (version 2011Dec20) [Wang, et al. 2010b] with the hg19 human genome databases to obtain the genomic annotations of these variants. After excluding synonymous and intronic variants and variants with non-coding RNA, we focuse our analysis on protein-changing coding variants. Furthermore, we exclude indel genotypes, and keep only biallellic SNP variations. Finally, because we are focusing on pathway-based analyses, we exclude genes which do not belong to any of the pathways we used (See Subsection 2 Pathway annotation). As a result, our data set contains the genotype information for 40,918 coding variants.

There are two technical issues with 1000G data in simulation: population stratification and missing genotypes. Population stratification is often an important confounder in genetic association studies[Kiezun, et al. 2012], when samples come from multiple populations or admixed populations. Usually principal component analysis (PCA) or mixed models are used to correct for population stratification [Edwards and Gao 2012]. Here we apply PCA to the 822 individuals’ genotypes. The results are consistent with known ethnic PCs in previous literature [Biffi, et al. 2010]. The top 2 principal components (PCs) accounts for 14% variations within the whole genome sequencing data (Supplementary Figure S1A) while there is a radical decrease at 3^rd PC (which accounts for 0.9% variations). However, the 3rd PC shows (Supplementary Figure S1B) the distinction of MXL population (Mexican Ancestry in Los Angeles) [The 1000 Genomes Project Consortium 2010]. The 4^th and following PCs (each accounts for less than 0.5% variations) seem reflecting intra-population variability. We thus include the top 3 PCs as covariates in regression analyses to adjust for the population stratification.

Missing genotypes is a common problem in sequencing data. However, in this multi-population 1000G dataset, all missing genotypes are of such a pattern that a variant is consistently missing throughout all individuals in one or several populations, but fully genotyped in other populations. We assumed that the missing genotype occurs in one whole population because the reference allele fixed at the locus for the population. For this reason, we imputed the missing genotype to be the reference allele accordingly.

2. Pathways annotation

We used the KEGG [Kanehisa, et al. 2006] and Biocarta databases available with the GenGen suite [Wang, et al. 2007] (version 2010Apr29, http://openbioinformatics.org/gengen) to assign annotated genes into gene-sets or pathways. To avoid testing too narrowed or too generalized pathways or gene sets [Wang, et al. 2007], we considered only those pathways with number of genes ≥10 and ≤100, resulting in 353 pathways with 3304 genes.

In our data set, 351 of all 353 pathways overlap with other pathways, which means some genes belong to multiple pathways. A specific gene could belong to 1~80 pathways, with an average of 3 pathways, and a median of 2 pathways. While it has been suggested that pathway overlapping is a major factor for biased type-I error rate, either inflated or over-conservative [Schaid, et al. 2012; Wang, et al. 2011], we are not aware of any evaluation demonstrating this point. Our simulation using genome-wide data provides the first opportunity for such evaluation.

3. Genome-wide genetic models

Simulation studies for pathway-based methods are difficult, mainly due to our limited knowledge of the genetic architecture of complex traits. The true underlying genetic model is complex, involving not only individual variants’ effects, but also their interactions and gene by environment interactions as well. Usually, additive models, where the total effect is the cumulative effect of all individual variants, are regarded as an acceptable approximation [Risch 1990]. Here we consider a genome-wide additive model, by which we generate simulation data to distribute the total genetic variance into 40,918 variants

To specify a genome-wide pathway-based genetic model, we not only need to consider the assumptions at variant level, such as the number and the proportion of ‘causal variants’, the variants’ effect sizes and population frequencies, and directions of effects, but we also need to consider the assumptions at the gene and pathway levels, such as the numbers or proportion of genes associated with the trait, the overall direction of effects at the gene level, and overlapping pathway structure.

For simplicity, we use continuous traits in our simulation. As shown in our real data analysis, our approach can also be easily applied to dichotomized traits. We assume that the phenotype vector Y is generated by the following model: Y=Xβ+ε where matrix X is the whole exome sequencing genotype. At each variant j we assumed an additive (versus dominant, recessive, etc) model for sample i and let X_ij= 0, 1 or 2, which represents the number of minor allele. β is the genetic effect coefficient vector for all genotype variants, and ε~N(0,σ²) stands for random noise, which are independent of genetic effect. When generating simulation data, we called any variant j ‘causal’ if β_j deviates from 0. Similarly, ‘causal’ pathways or genes referred to those include any ‘causal’ variants.

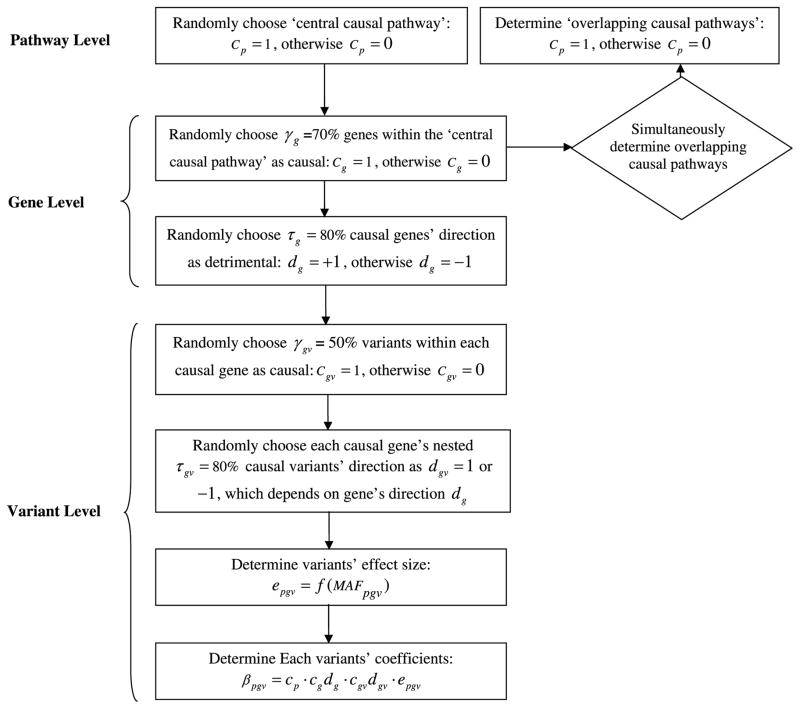
We use a simulation framework that distributes total genetic effects hierarchically into pathways, genes, and eventually individual variants. Formally, the genetic architecture can be written as: β_pgv = C_p · C_gd_g · C_gvd_gv · e_pgv, where binary variables C_p, C_g and C_gv respectively indicates whether a specific pathway p a specific gene g or a specific variant gv within gene g is causal (with value 1) or not (with value 0). First we randomly choose a single causal pathway p among all pathways, which we define as the ‘central causal pathway’ with C_p=1 while other pathways with C_p=0. Within the ‘central causal pathway’ p, we randomly select γ_g=70% genes to be causal, with C_g=1 while C_g=0 for the remaining genes. Since pathways are usually overlapped (described in section 2), we call pathways other than the ‘central causal pathway’ but harboring causal genes as ‘overlapping causal pathways’. Therefore, we update these ‘overlapping causal pathways’ with C_p=1. Nested within each causal gene g, we randomly select γ_gv=50% variants as ‘causal’, with C_gv=1 while other variants with C_gv=0. We next consider the directionality at both gene level and variant level: d_g is the direction of the gene g, while d_gv is the direction of the variant gv Both are dichotomous with −1 (protective) or +1 (detrimental). At the gene level, the direction of a gene refers to the direction of majority of its causal variants. We randomly choose τ_g=80% of all causal genes to be detrimental, with d_g=+1, and 1 − τ_g of all causal genes to be protective, with d_g= −1. For variants nested with each causal gene, we assign τ_gv, a proportion of causal variants to be detrimental, and remaining causal variants to be protective. Effectively, the proportion τ_gv ≥ 50% and here we assign τ_gv =80%. It is noted that τ_gv and τ_g are two independent parameters. The hierarchical structure of generating simulation data is summarized in Figure 1. Moreover, it is possible that more than one ‘central causal pathways’ are associated with trait. Multiple causal pathways will dilute heritability while each gene or pathway’s association will be weakened. To investigate the dilution effect of multiple ‘central causal pathways’, we also simulate the situations with 2 ‘central causal pathways’. In the above simulation framework, we set two ‘central causal pathways’ p and p′ with C_p =1 and C_p′ =1, while keeping remaining steps the same.

Figure 1.

Work flow to simulate genome-wide genetic model. Pathway, gene and variant parameters are specified for each level. The simulation is base on 1000G genome-wide exome sequencing genotype.

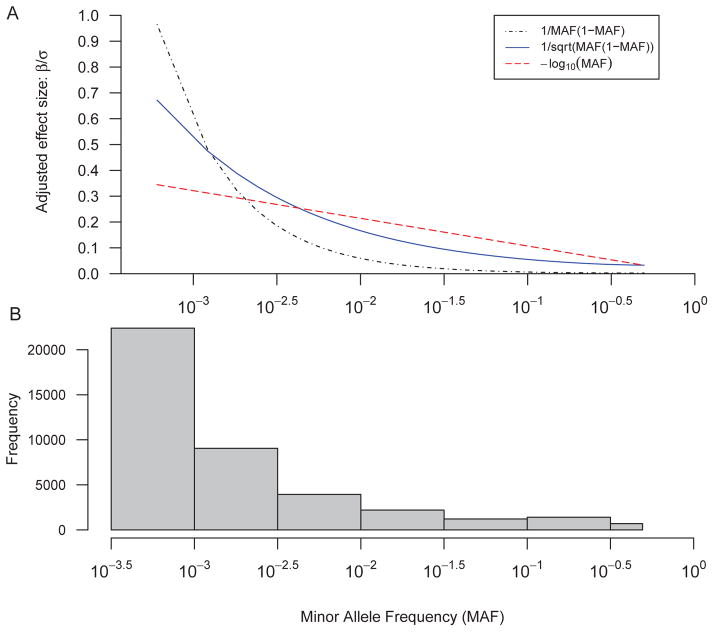
The effect size of individual variants e_pgv has been extensively discussed in existing methodological studies of rare variant associations. Also, there is an ongoing debate as to whether these rare variants called are actually true genetic variants. If these rare variants called have a substantial proportion wrongly called, the downstream association study may suffer reduced power. Most current studies assume that variants of lower Minor Allele Frequency (MAF) have larger effect sizes than variants of higher MAF [Eichler, et al. 2010; Kiezun, et al. 2012; Manolio, et al. 2009], and a variant’s effect size e_pgv is proportional to a function of its MAF: φ (MAF). For example, the weighted-sum test [Kiezun, et al. 2012; Madsen and Browning 2009] assumes that the effect size is proportional to φ(MAF)=1/MAF(1 MAF) while sequence kernel association test (SKAT) [Wu, et al. 2011] assumes the effect size is proportional to φ(MAF) = −log(MAF). As Figure 2 shows, these seemingly similar assumptions actually result in a drastic difference in the effect sizes of variants at very low frequencies (MAF<10⁻³), which are actually abundantly present in real data sets [Li, et al. 2010; Nelson, et al. 2012; Tennessen, et al. 2012b; The 1000 Genomes Project Consortium 2010]. Comparing to effect size proportional to − log(MAF), rare variants with effect size proportional to 1/MAF(1−MAF) have far greater effect size as MAF <10⁻³ while having smaller effect size as MAF>10⁻². To evaluate the influence of effect size determination function φ (MAF), we use 2 different settings in simulation: one is the same with SKAT method: φ(MAF) = −log(MAF), and the other is $\phi (\text{MAF})=1/\sqrt{\text{MAF}(1-\text{MAF})}$. The later choice is similar to the weighted-sum but is easier to interpret: Since the phenotypic variance explained by a variant gv can be written as ${2·\text{MAF}}_{gv}(1-{\text{MAF}}_{gv}){\beta }_{gv}^2$, the latter assumption of effect size conveniently implies that each causal variant has equal contribution to the heritability.

Figure 2.

Comparison of three effect size models. Panel A shows 3 settings to determine the effect size of variants as a function of the variants’ MAF. Different effect sizes are adjusted to keep total heritability constant with h²=20%, where $h^2=\frac{\mathit{Var}(X\beta )}{\mathit{Var}(X\beta )+{\sigma }^2}$, and genotype matrix X comes from 1000G whole-genome exome-sequencing data. As X and h² are fixed, effect size vector β is proportional to σ along different MAF. Panel B shows the MAF distribution of the 1000G genotype data set.

After determining the effect sizes of each variant β_pgv, we set the random noise variation σ² to control the overall heritability. The whole-genome heritability is defined as:

$$h^2=\frac{\text{genetic}\text{effect}\text{on}\text{phenotype}}{\text{genetic}\text{effect}\text{on}\text{phenotype}+\text{random}\text{effect}\text{on}\text{phenotype}}=\frac{\mathit{Var}(X\beta )}{\mathit{Var}(X\beta )+{\sigma }^2}.$$

The heritability of complex traits varies. For many traits such as Type-2 diabetes and breast cancers, previous researches [Czene, et al. 2002; Poulsen, et al. 1999; Schildkraut, et al. 1989] show that their heritabilities are between 20% and 30%. In the simulation, we set the whole genome heritability h² as 20%, to resemble these real data situations. With heritability fixed, the results across different simulated data sets are grossly comparable.

Compared to simulation experiments in the literature, our settings of the parameters specifying variant- and gene-level effect sizes are not novel. The main new feature of our simulation is the specification of pathway-level parameters, such as the central and overlapping causal pathways C_p as well as directionality of genes d_g. We aim to provide a general framework, based on which different pathway methods can be directly compared, rather than making the most accurate models for genome-wide genetic architecture with the most realistic parameters.

4. Evaluating empirical power and type-I error rate

Using the above simulation procedure for the genome-wide genetic model, we generate 1000 data sets with continuous traits for each simulation scenarios. For each data set k,k = 1 ··· 1000, we evaluated 11 different pathway methods (as shown in section 5) and 3 different gene level methods, to evaluate each pathway l out of 353 candidate pathways and obtain their nominal p-values P_kl Most pathway level analyses, especially these competitive tests [Tian, et al. 2005] depend on permutation to summarize statistics’ distribution under null hypothesis. However to achieve genome-wide significance, it is at least 353/0.05 = 7060 permutations for each methods. Following Wang et al.[Wang, et al. 2007], we normalize each pathway’s enrichment score with permutated statistics’ mean and standard deviation, with the aim to adjust pathways’ gene size bias, as well as roughly make different pathways’ enrichment scores comparable. The normalization is important, since we could pool normalized enrichment scores cross 353 pathways in permutation data sets, and then each pathway’s p-value could achieve Bonferroni corrected genome-wide significance level with only a small number of permutations, such as 100 iterations. Since directly applying region-based methods, such as in gene level tests, does not depend on permutation, we directly achieve their p-values for each of 3304 genes.

4.1 Stringent and lenient powers in pathway level study

In our simulation framework, we assume that only genes and their nested variants in the single ‘central causal pathway’ are associated with the trait. However, due to the overlapping structure among pathways, causal genes may also belong to ‘overlapping causal pathways’. To evaluate the power at the pathway level, we could use a stringent criterion, in which we count each of these significant ‘central causal pathways’ as truly positive. Alternatively, we could use a lenient criterion, which considers it a true positive if any of causal pathways, either the central or the overlapping causal pathways, is found significant. This lenient criterion is relevant to a two-step genetic study scenario: where pathway-based method is run first as a filter to narrow down the search, and as a second step, candidate gene association is followed. These two types of power definitions come from pathways’ overlapping structure. In short, we call these two types of power as ‘stringent power’ and ‘lenient power’ respectively.

4.2 Global and local null hypotheses and type-I error in genome-wide association study

Furthermore in our genome-wide simulation, there are two different scenarios to evaluate type-I error rate. The first way is to generate simulation data sets under the ‘global’ null model, in which all genetic effect coefficients are zero, and then to consider any pathways or genes reaching significance level as false positives. In other words, under such a null model, the simulated trait is fully generated by random noise, without any association with genome-wide genotype. The second way is to evaluate “local null hypothesis type I errors” simultaneously with power analysis in our genome-wide association. In the power analysis, these pathways that do not overlap with the central causal pathway are irrelevant of the trait when generating simulation data. We called these pathways ‘non-causal’. Correspondingly, these genes which are irrelevant of the trait when generating simulation data are also called ‘non-causal’. We collect these pathways ‘non-associated’ with trait as ‘local’ null hypothesized, which means although trait is not ‘locally’ associated with these non-causal genes or pathways, causal pathways and genes exist in the whole-genome model. In this scenario, any ‘non-causal’ pathways or genes reaching significance level are considered as false positives. In short, we call these two different scenarios as ‘global null hypothesis type-I error’ and ‘local null hypothesis type-I error’ respectively.

The two type-I errors differ with their application and explanation. The ‘global null hypothesis type-I error’ is naturally used in candidate gene studies, where it is safe to assume that a single gene or region is fully non-associated with trait. However in genome-wide study, it is not realistic to assume that complex traits are totally non-associated with genetic effects. The ‘local null hypothesis type-I error’ is similar to what one would encounter in real data sets, especially in genome-wide study.

To investigate type-I errors, we use Bonferroni correction to control Family-Wise Error Rate (FWER). Since there are overall 353 pathways in this simulation data set, we set the genome-wide threshold α =0.05/353=1.4164e-4 for pathway level tests. For the sake of comparison, we also calculate the gene-level power and type-I error rate. Since there are overall 3304 genes, we set the genome-wide threshold α =0.05/3304=1.5133e-5 for gene level. For each simulation scenario, we generate 1000 simulation datasets and estimate the empirical power as the proportion of datasets for which p-values less than α are observed.

5. Pathway-association methods used in simulation

We consider two categories of methods: extensions of pathway association methods that originally designed for GWAS data, and direct region-based methods that originally designed for gene-level tests.

Many gene set or pathway association tests have been proposed for GWAS analysis [Holden, et al. 2008; Luo, et al. 2010; Wang, et al. 2007; Wang, et al. 2010a; Wang, et al. 2011]. In the context of genome-wide association, Tian et al. [Tian, et al. 2005] formulated two different null hypotheses for these tests: competitive and self-contained. Briefly, competitive null hypotheses assume that the target gene set has the same magnitude of association as that of complement genes in the genome while self-contained null hypotheses solely focus on the target gene set and assume that there is no association between the target gene set and the trait. Therefore, the self-contained null hypothesis does not depend on genes outside the target gene set. For short, we call two classes of methods “competitive” and “self-contained” respectively.

5.1 Competitive methods: Gene Set Enrichment Analysis

Kai Wang’s Gene Set Enrichment Analysis (GSEA) [Wang, et al. 2007] is a typical competitive method. Due to its popularity, we select Kai Wang’s GSEA as the starting point of our evaluation. The GSEA method is based on the single variant association tests in GWAS. In our simulation, we use regular linear regression for single variant test. Afterwards, gene-level statistic for a gene is represented by the strongest associated single variant test statistic within the gene. Then GSEA uses a weighted Kolmogrov-Smirnov (WKS) statistic to calculate a gene set enrichment score. Since WKS statistic is non-parametric, GSEA uses permutation to obtain WKS statistics’ empirical distribution under null hypothesis. To adjust gene size bias of WKS statistics, GSEA normalizes the WKS statistics to make different pathways’ enrichment scores comparable.

A series of works have extended the GSEA method [Holden, et al. 2008; Nam, et al. 2010]. Many of these methods focus on how to summarize individual variants’ information onto the gene level, such as GSA-SNP [Nam, et al. 2010] and SSEA [Weng, et al. 2011]. In GSA-SNP, gene level statistic is summarized with ‘kth best =1,2,3,4,5)’ SNP p-value in each gene while SSEA uses an adaptive rank truncated product method to select representative SNP subset. The gene-level ‘collapsing’ is appropriate in GWAS analyses, since usually only one or a very small number of variants per gene are represented in genotyping microarrays. However, in exome sequencing data, all exonic variants of a gene are profiled, and it is possible that many functional variants in a gene are of moderate effect sizes. In such cases, a collapsed statistic (e.g. the most significant SNP’s statistic or p-value) will likely lose information. Therefore, we consider the non-collapsing idea of GSEA-SNP [Holden, et al. 2008]: treat a pathway as a variants’ set, which is the union of all variants of its genes, and conducting variant-level enrichment score. In doing so, each variant’s information is preserved in pathway association test. Different from GSEA-SNP, we keep using WKS to calculate the enrichment score, instead of trend test [Freidlin, et al. 2002]. With both methods implemented with WKS test statistics, we could directly compare the gene-level collapsing and non-collapsing methods. To highlight the effect of gene-level collapsing, we denote the original GSEA with gene-level collapsing as WKS-MinP method (method 1 in Table A), while denote the method using WKS without gene level collapsing as WKS-Variant method (method 2 in Table A).

Table A.

Summary of 11 pathway level methods used in simulation.

Methods	Hypothesis	Extract SNP information within each gene	Gene set test	Significance assessments
(1) WKS-MinP	Competitive	Most significant SNP’s statistic	Weighted Kolmogrov-Smirnov (WKS) statistic	Sample Permutation
(2) WKS-Variant	Competitive	All SNPs’ statistics	Weighted Kolmogrov-Smirnov (WKS) statistic	Sample Permutation
(3) WKS-WSS	Competitive	Weighed-Sum statistic	Weighted Kolmogrov-Smirnov (WKS) statistic	Sample Permutation
(4) WKS-SS	Competitive	Simple-Sum statistic	Weighted Kolmogrov-Smirnov (WKS) statistic	Sample Permutation
(5) WKS-RV- Collapse	Competitive	First Collapsing rare variants into genetic score; the most significant statistic among all common variants’ statistics and rare variant genetic score statistic	Weighted Kolmogrov-Smirnov (WKS) statistic	Sample Permutation
(6) WKS-RV-CV	Competitive	First collapsing rare variants into a genetic score; All common variants’ statistics and rare variant genetic score statistic	Weighted Kolmogrov-Smirnov (WKS) statistic	Sample Permutation
(7) WKS-SKAT- gene	Competitive	SKAT gene-level statistic	Weighted Kolmogrov-Smirnov (WKS) statistic	Sample Permutation
(8) WKS-SKAT- variant	Competitive	All SNP test statistics calculated with individual variant SKAT tests	Weighted Kolmogrov-Smirnov (WKS) statistic	Sample Permutation
(9) Direct-SKAT	Self- contained	N/A	SKAT	Region-based association
(10) Direct-WSS	Self- contained	N/A	Weighted-Sum	Region-based Association
(11) Direct-SS	Self- contained	N/A	Simple-Sum	Region-based Association

5.2 Extending region-based rare variant association methods to pathway level methods

Recently developed gene- or region-based rare variant association methods provide alternative approaches for summarizing gene-level information. In our evaluation, we include 4 different methods: weighted-sum test [Madsen and Browning 2009], simple-sum test [Morris and Zeggini 2010], collapsing rare variants used in CMC test [Li and Leal 2008], and SKAT test [Wu, et al. 2011]. The general idea of the weighted-sum test is to weight each variant’s effect size according to its estimated standard deviation, and then collapse weighted variants information to a genetic score. In the simple-sum test, the genetic score simply summarizes each gene’s variants with equal weights. CMC test [Li and Leal 2008] collapses rare variants to a genetic score and then apply multivariate methods to test both rare variant genetic score and common variants within a region. Considering the continuous trait in our simulation and the population stratification confounding to be adjusted, we made the following modifications to the algorithm of Weighted-Sum and CMC tests. In the implementation of weighted-sum test, since we are dealing with continuous traits, we use all samples’ minor allele frequency (MAF), instead of the unaffected subjects’ MAF, to estimate variants’ standard deviation as weight. Furthermore, instead of permuting trait status to test the significance of Wilcoxon-type statistic in weighted-sum, we directly use regular linear regression to test the genetic score’s association with trait. In implementation of collapsing rare variants, we use 0.01 as MAF threshold to define rare variants. Then we also use the regular multivariate linear regression to test collapsed genetic information, instead of multivariate logistic regression or Hotelling T² tests for case-control scenario in CMC test. The above tests are known as ‘burden tests’. SKAT method [Wu, et al. 2011] considers the genetic effect as a random effect and uses kernel function in the variance component score test. In the implementation of SKAT, we simply use its default options, such as default weight in weighted linear kernel function.

There are two variations to extend the region-based rare variant association methods described above to pathway level analysis. While these rare variant association methods are originally designed for gene- and region-based tests, these methods can be extended to the pathway level by simply relaxing the definition of regions to all variants nested within whole genes in one pathway, regardless of contiguity. The second one is to run these methods at gene-based level and then rank gene-based p-values to form the WKS-based enrichment score for pathway level analysis. However, we note that these two applications of region-based rare variant methods differ with their null hypotheses: The former tests the self-contained hypothesis and the latter tests the competitive hypothesis.

5.3 Population stratification as covariates in simulation study

In our method implementation, we use regular linear regression to test the phenotypic association of single variants in GSEA and genetic score in rare variant burden tests. All regressions include the top 3 principal components of the genotype matrix to adjust potential population stratification, and thus the regression model is Y = τ_Eig1Eig1+τ_Eig2Eig2+τ_Eig3Eig3+Gβ_G+ε, where Eig1,Eig2 and Eig3 stand for the top 3 eigenvectors as covariates, and τ_Eig1, τ_Eig2 and τ_Eig3 are regression coefficients for these covariates. G stands for a genotype vector in single variant test, or a genetic score vector for weighted-sum or simple-sum of alleles, or a matrix combining common variants and collapsed rare variant genetic score. In SKAT implementation, we consider top 3 eigenvectors as covariates, and fit the null model with them.

Comprehensively, we evaluated 11 different pathway methods in simulation: 8 competitive, WKS-based methods and 3 self-contained, direct region-based methods. All methods used in evaluation are summarized in Table A.

Since it is extremely computationally intensive to run permutation-based association tests for genome-wide exome sequencing data, we use only 100 permutation cycles to generate WKS statistics’ distribution in null hypothesis for 1000 data sets in each simulation scenarios. On average, analyzing one simulation data set with above 11 methods takes 320 CPU hours over computer cluster nodes of 2.66 GHz Intel Xeon processors.

Results

1. Type-I error rates

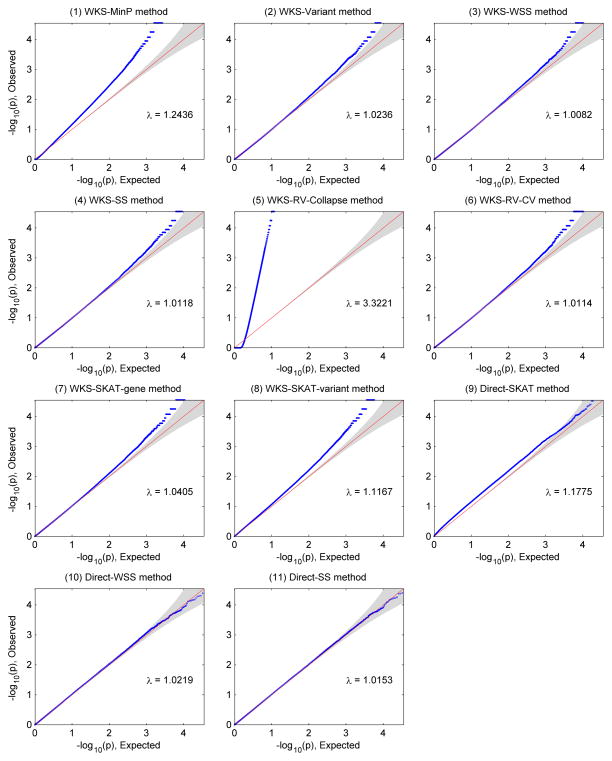
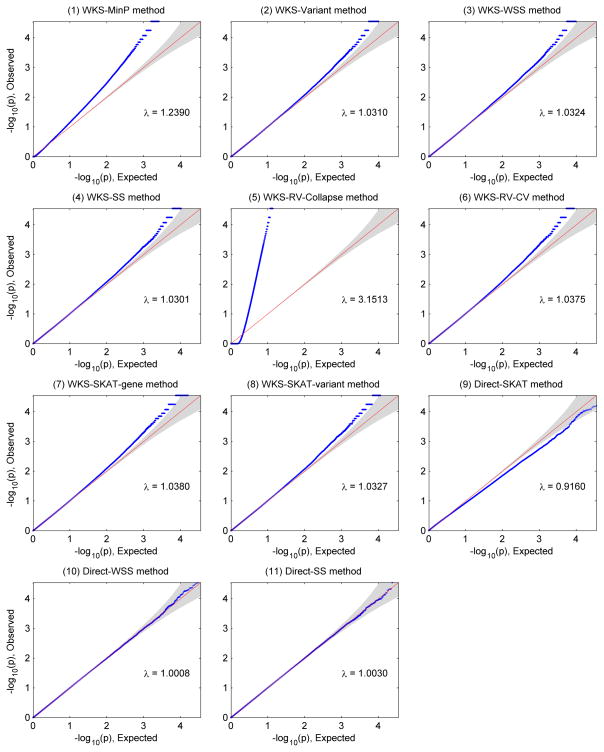
Generally in Figures 3–6, inflations of ‘local null hypothesis type-I errors’ are observed among pathway methods. This kind of type-I error is only well controlled at the genome-wide scale for Direct-WSS method (method 10) and Direct-SS method (method 11) in all 4 simulation scenarios. Most pathway methods control the type-I error rates within a factor of 10 at target genome-wide significance level, except WKS-MinP method (method 1) and WKS-RV-collapse method (method 5). Furthermore, Q-Q plots in Figure 7 shows that most pathway methods’ local null hypothesis type-I errors are slightly inflated. Therefore, strictly controlling type-I errors in genome-wide pathway test remains a challenge.

Figure 3.

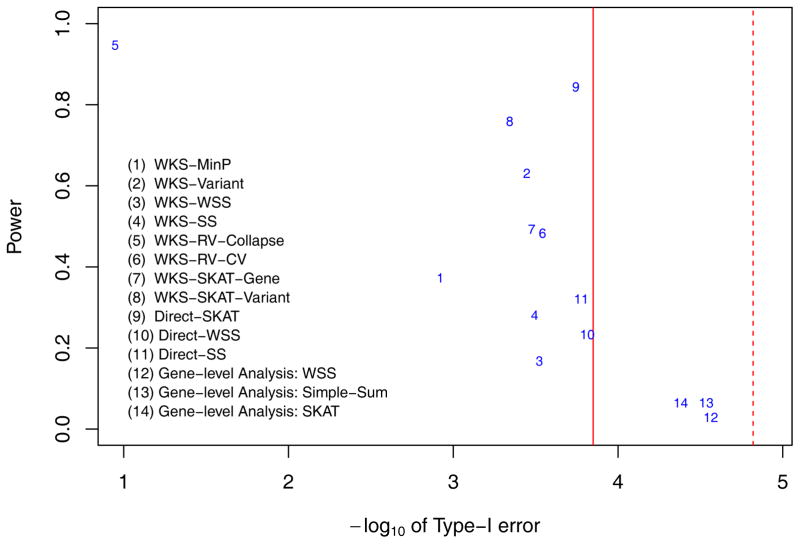
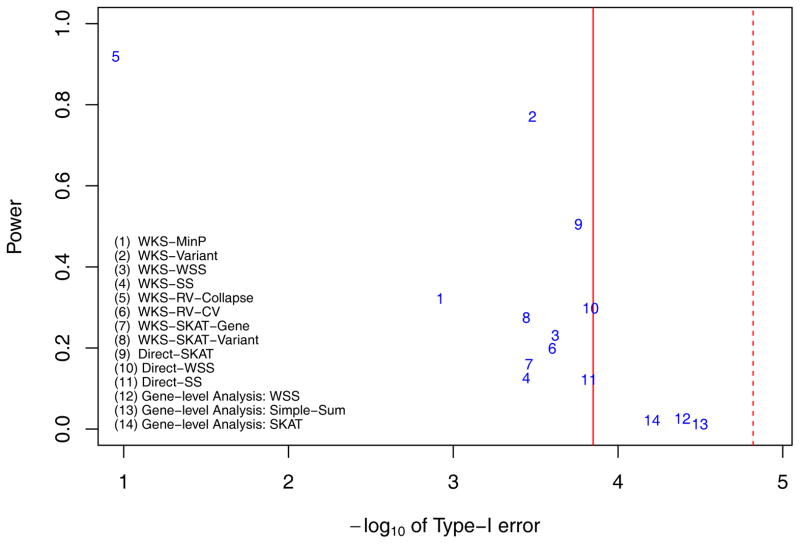
The lenient Powers and local null hypothesis type-I error rates when there is a single ‘Central causal pathway’ while variants’ effect sizes are proportional to −log(MAF). The powers and type-I errors of 11 pathway level methods (methods 1–11) and 3 gene level methods (methods 12–14) are displayed. Among pathway level methods, methods 1–8 belong to competitive tests while methods 9–11 belong to self-contained tests. They are testing different hypotheses. The Red solid line is the genome-wide threshold for pathway level analysis, with α = 0.05/353 = 1.4164e-4. The red dashed line is the genome-wide threshold for gene-level methods, with α = 0.05/3304 = 1.5133e-5.

Figure 6.

The lenient powers and local null hypothesis type-I error rates when there are 2 ‘Central causal pathway’ while variants’ effect sizes are proportional to $1/\sqrt{\text{MAF}(1-\text{MAF})}$. The powers and type-I errors of 11 pathway level methods (methods 1–11) and 3 gene level methods (methods 12–14) are displayed. Among pathway level methods, methods 1–8 belong to competitive tests while methods 9–11 belong to self-contained tests. They are testing different hypotheses. The Red solid line is the genome-wide threshold for pathway level analysis, with α= 0.05/353 = 1.4164e-4; while the red dashed line is the genome-wide threshold for gene-level methods, with α = 0.05/3304 = 1.5133e-5.

Figure 7.

Q-Q plots when we inspect ‘Local null hypothesis type-I errors’ of 11 pathway level methods. Methods 1–8 belong to competitive tests while methods 9–11 belong to self-contained tests. They are testing different hypotheses.

In fact it is also difficult for gene-based tests to control ‘local null hypothesis type-I errors’. As shown in Figures 3–6, all gene-based methods such as weighted-sum test (method 12), simple-sum test (method 13) and SKAT test (method 14) have minor inflated local null hypothesis type-I errors at the genome-wide significance level. However these gene-based tests have well controlled ‘global null hypothesis type-I errors’ (results not shown).

We investigated both ‘global null hypothesis type-I error’ and ‘local null hypothesis type-I error’ in simulation, and found they have similar results for WKS-based competitive pathway methods. That is, they all displayed inflations at the genome-wide significance level (shown in Figures 7–8). However, these two kinds of type-I error rates are different for region-based self-contained pathway methods such as Direct-SKAT method (methods 9). As in Figure 7, Direct-SKAT method (method 9) shows inflated ‘local null hypothesis type-I errors’ while it shows distinct deflation when evaluating ‘global null hypothesis type-I error’ (Figure 8). Meanwhile, Direct-WSS method (method 10) and Direct-SS method (method 11) controls both kinds of type-I errors pretty well and consistently. We summarized two kinds of type-I error rates at both gene-level and pathway-level analysis in Table B.

Figure 8.

Q-Q plots when we inspect ‘global null hypothesis type-I errors’ of 11 pathway level methods. Methods 1–8 belong to competitive tests while methods 9–11 belong to self-contained tests. They are testing different hypotheses.

Table B.

Bias of bonferroni corrected Type-I error rates at genome-wide scale.

	Global Null Hypothesis Type I errors			Local Null Hypothesis Type I errors
	WKS-based methods	Direct-SKAT (method 9)	Direct-WSS (method 10) Direct-SS (method 11)	WKS-based methods	Direct-SKAT (method 9)	Direct-WSS (method 10) Direct-SS (method 11)
Gene-level	NA	0	0	NA	+	+
Pathway-level	+	−	0	+	+	0

Notes: “+” means inflated type-I errors; “−” means deflated type-I errors; ‘0’ means well controlled type-I error estimation; “NA” means that WKS-based method do not apply to gene-level analysis.

For region-based self-contained pathway method such as Direct-SKAT method (method 9), why is the ‘global null hypothesis type-I error’ deflated while ‘local null hypothesis type-I error’ is inflated? We offer the following explanations. When we evaluate ‘global null hypothesis type-I error’, the pathways are not independent due to their overlapping structure. Bonferroni correction, which assumes independent multiple hypotheses, is over-conservative and then results in the type-I error deflation. In the ‘local null hypothesis type-I error’ scenario, there might be correlation due to linkage disequilibrium (LD) between variants inform the ‘causal’ and the ‘non-causal’ genes or pathways. The correlations between ‘causal’ and ‘non-causal’ genes or pathways could make these ‘non-causal’ genes or pathways indirectly associated with the trait, which could inflate the type-I error rate. On the other hand, Direct-WSS method (method 10) and Direct-SS method (method 11) use all variants’ weighted sum or simple sum statistics to construct the tests. These approaches ignore the overlapping structure among pathways as well as the LD among variants, and therefore their type I errors are unaffected by these factors.

2. Simulation power

In general, we found that pathway-based methods indeed provide higher power than gene-based methods. In simulations with genome-wide heritability 20%, the highest power of gene-based tests is 0.065 while the lenient power (details in Materials and Methods section 4) of pathway based methods with well controlled type-I error is 0.844 (method 9 Direct-SKAT shown in Figure 3). The stringent pathway power is lower than lenient power, but also achieves 0.83 (method 9 Direct-SKAT shown in Supplementary Figure S2). Comparing lenient powers in Figures 3–6 with their corresponding stringent powers in Supplementary Figures S2–5, lenient ways to evaluate power always result in higher powers than stringent ways. But both ways clearly show that pathway level methods could achieve higher power than gene-level methods. The increased power highlights the benefit of pathway-based methods compared to gene-based methods in sequencing data analysis.

Specifically we considered gene level methods such as weighted-sum test (method 12), simple-sum test (method 13) and SKAT test (method 14). When we assume that the effect size of a causal variant is proportional to −log(MAF) (Figure 3 and Supplementary Figure S2) and the effects of 80% of causal variants are of the same direction, the SKAT test has the highest power with 0.0649 while simple-sum test has a competitive power of 0.0648; weighted-sum test’s power is 0.0289. The result is consistent with previous simulation results [Wu, et al. 2011]. Since we assume that each causal gene has 50% variants to be causal, SKAT test (method 14) only slightly outperforms methods 12–13 at genome-wide significance level (details as SKAT Supplemental data Figure S2)([Wu, et al. 2011]. These gene level methods’ power is also similar when effect size is proportional to $1/\sqrt{\text{MAF}(1-\text{MAF})}$ (Figure 4 and Supplementary Figure S3).

Figure 4.

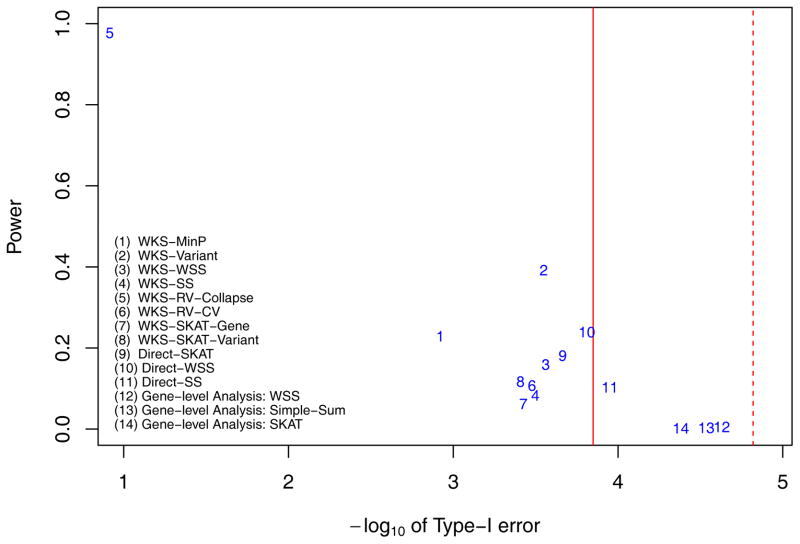
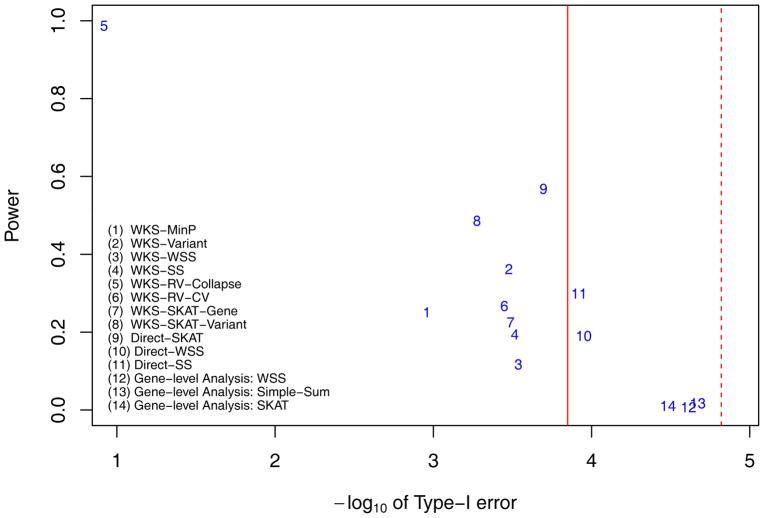
The lenient powers and local null hypothesis type-I error rates when there is a single ‘Central causal pathway’ while variants’ effect sizes are proportional to $1/\sqrt{\text{MAF}(1-\text{MAF})}$. The powers and type-I errors of 11 pathway level methods (methods 1–11) and 3 gene level methods (methods 12–14) are displayed. Among pathway level methods, methods 1–8 belong to competitive tests while methods 9–11 belong to self-contained tests. They are testing different hypotheses. The Red solid line is the genome-wide threshold for pathway level analysis, with α = 0.05/353 = 1.4164e-4. The red dashed line is the genome-wide threshold for gene-level methods, with α = 0.05/3304 = 1.5133e-5.

Among pathway-based methods, no single methods work superiorly to other methods. However, we found that the WKS-Variant method (method 2) consistently provides high power across 4 scenarios (lenient power is 0.631, 0.771, 0.362, and 0.392 respectively) while it controls type-I errors within 3 times the target genome-wide significance level. Secondly, while direct-SKAT method performs superiorly when variant’s effect size is proportional to −log(MAF) (lenient power is 0.844 in Figure 3 and 0.568 in Figure 5) but it does not perform well when variant’s effect size is proportional to $1/\sqrt{\text{MAF}(1-\text{MAF})}$ (lenient power is 0.505 in Figure 4 and 0.181 in Figure 6). This indicates that the SKAT method is sensitive to the effect size allocation assumption (detailed below).

Figure 5.

The lenient Powers and local null hypothesis type-I error rates when there are 2 ‘Central causal pathway’ while variants’ effect sizes are proportional to −log(MAF). The powers and type-I errors of 11 pathway level methods (methods 1–11) and 3 gene level methods (methods 12–14) are displayed. Among pathway level methods, methods 1–8 belong to competitive tests while methods 9–11 belong to self-contained tests. They are testing different hypotheses. The Red solid line is the genome-wide threshold for pathway level analysis, with α = 0.05/353 = 1.4164e-4. The red dashed line is the genome-wide threshold for gene-level methods, with α = 0.05/3304 = 1.5133e-5.

Overall, fully using all SNP information of genes in pathway analysis increases power while better controlling type-I errors. We compared pairs of WKS-based methods: one has gene level collapsing and the other includes all variants nested in genes (methods 1 vs 2, 8 vs 7, and 5 vs 6). From Figures 3–6, WKS-variant method (method 2) has consistently higher power than WKS-MinP method (method 1) which uses only the most significant statistic in each gene. Meanwhile, method 2 controls type-I error better than method 1. The same trend is less clear when comparing WKS-SKAT-variants method (method 8) and WKS-SKAT-genes method (method 7). While method 8 has higher lenient power in all simulation scenarios than method 7, method 8 has a slightly higher type-I error rate than method 7. Comparing two WKS methods with rare variant collapsing (WKS-RV-Collapse, method 5 vs WKS-RV-CV, method 6), WKS-RV-Collapse method (method 5) results in heavily inflated type-I errors, while WKS-RV-CV method (method 6) control type-I error rate much better in all simulation scenarios.

We then compare two variations of region-based methods extended to pathway analysis (method 4 vs 11, 3 vs 10, and 7 vs 9). The first variation is to extend region definition to gene sets and directly apply region based methods to test gene-sets’ effect (method 9, 10 and 11). The other is to use region based tests to extract variants information to gene level and then use weighted KS statistics for further pathway level analysis (method 3, 4 and 7). The power of the Direct-SKAT method (method 9) in pathway analysis is consistently greater than the power of WKS-SKAT-gene method (method 7) in all simulation scenarios. For region-based burden tests, namely weighted-sum test and simple-sum tests, two variations extending to pathway analysis have similar powers (both lenient as Figures 3–6 and stringent as Supplementary Figures S2–5). We noted that power of burden tests is definitely affected by not only the imbalance of damaging and protective variants at the gene-level (80% vs 20% in simulation) and the pathway-level (68% vs 32%), but also the presence of non-causal variants at the gene-level (50%) and pathway-level (65%).

We found that the performance of region-based methods is heavily influenced by the effect size assumption in simulation. These methods put different weights on variants, and their performances in simulation depends on variants’ effect size assumptions [Kiezun, et al. 2012]. In our simulation, Weighted-sum test weighted variant i with $1/\sqrt{n·{\mathit{MAF}}_i(1-{\mathit{MAF}}_i)}$, where n is the genotyped sample size, and MAF_i is variant i’s MAF. Simple-sum tests use constant weight for all variants. In the default option of SKAT, the weight in the weighted linear kernel is $\sqrt{w_i}=\mathit{beta}({\mathit{MAF}}_i,1,25)$. Deviation of effect size assumption affects these methods’ power. For example, the Direct-SKAT method (method 9) results in a lenient power of 0.844 (Figure 3) and stringent power 0.83 (Supplementary Figure S2), when we assume variants’ effect size proportional to −log(MAF). However the lenient power decreases to 0.505 (Figure 4) and stringent power decreases to 0.468 (Supplementary Figure S3) when the effect size violates SKAT’s internal assumptions, and is proportional to $1/\sqrt{\text{MAF}(1-\text{MAF})}$ instead. Both weighted-sum and simple-sum methods show similar effects. Comparing with the effect size proportional to $1/\sqrt{\text{MAF}(1-\text{MAF})}$, the power of directly applying the simple-sum test on pathway (method 11) (both lenient and stringent) is higher when effect size is proportional to −log(MAF), since the latter assumption’s effect size seems more flat than the former. By contrast, since the weighted-sum test puts almost zero weights for MAF >1%, Direct-WSS method (method 10)’s power (both lenient and stringent) is lower when effect size is proportional to −log(MAF). Our results largely agree with evaluations in previous literature [Ladouceur, et al. 2012].

Similar to region-based methods, the WKS-SKAT-Variant method (method 8) still depends on effect size assumption. Comparing WKS-Variant method (method 2), the single SNP test with SKAT has higher power when effect sizes are proportional to −log(MAF) (with both lenient power as Figure 3 and 5, and stringent power as Supplementary Figure S2 and S4), though with a price of higher local null hypothesis type-I error rate. When the simulated effect sizes are proportional to $1/\sqrt{\text{MAF}(1-\text{MAF})}$, the WKS-Variant method (method 2) has higher power (both lenient as Figure 4 and 6 and stringent as Supplementary Figure S3 and S5) than WKS-SKAT-Variant method (method 8).

It is possible that more than one ‘central causal pathways’ are associated with the trait, in which case the total genetic effects are ‘diluted’ into multiple pathways. In our simulations with two central causal pathways, all methods’ powers, both at gene and pathway levels, are indeed decreased. The highest pathway level power is 0.58 (Direct-SKAT in Figure 5). As the heritability is diluted, gene level tests’ powers are also decreased, with highest power 0.017.

3. Real data analysis

We applied pathway methods to an exome sequencing data of chronic obstructive pulmonary disease (COPD), a part of the NHLBI “Grand Opportunity” Exome Sequencing Project.

The phase 1 sequencing study recorded 87K SNPs’ genotype after initial quality control. The pipeline of alignment and genotype calling, as well as quality control procedures are documented in details in their website (http://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/variable.cgi?study_id=phs000291.v1.p1). The dataset includes 47 patients with COPD and 42 lung functional normal controls. These 89 genotyped individuals are all of reported European American descent, and are extracted from 6000 samples in 5 years’ longitudinal Lung Health Study (LHS) [Connett, et al. 1993]. Since smoking has a critical effect on pulmonary function and COPD, all individuals are chosen among smokers to eliminate the covariate’s effect. Besides the affection status and population, the data set includes baseline covariates, such as gender, age, BMI, alcohol consuming status, and asthma affection status.

Similar to genotype processing in simulation, we used ANNOVAR (version 2011JUN21)[Wang, et al. 2010b] with recent hg19 human genome annotation databases to obtain the genomic annotations of these variants. With the original dataset, there are 0.74% genotypes missing. Unlike the simulation data processing, we used BEAGLE (version 3.3.2) [Browning and Browning 2009] to impute the missing genotypes. We repeated the imputation 5 times. After imputation, we applied similar filters as in the simulation and focused only on biallellic SNPs. Next, we used the KEGG [Kanehisa, et al. 2006] and Biocarta databases from GenGen suite [Wang, et al. 2007] (version 2010Apr29, http://openbioinformatics.org/gengen) to assign annotated genes into pathways. Because we are focusing on pathway-based analyses, we excluded genes which do not belong to any of the pathways in KEGG and Biocarta. Finally we have 10,366–10,367 coding variants (different imputations’ results vary slightly), 3159 genes, and 509 pathways for following analysis.

We analyzed the whole-genome exome sequencing data at both the gene and pathway level. In the gene-level analysis, we directly use SKAT test [Wu, et al. 2011] with its default option. In implementation of SKAT, we first fit a null model with all baseline covariates, and then add affection status as phenotype. In pathway level analysis, we implement the WKS-Variant and Direct-SKAT methods, both of which demonstrate high powers with moderately inflated local null hypothesis type-I errors in our simulation scenarios. We use 1000 permutation cycles in the WKS-Variant method. Since the COPD data set is a case-control study, we use logistic regression for single marker estimation adjusting for covariates’ effects. We found that 5 different imputed data sets have similar genotypes (pairwise Pearson correlations > 99.5%), and thus their association results are also similar (the gene level p-values’ Pearson correlations > 99.5%, while pathway level p-values’ correlation > 97.3%). Therefore we only present the result based on the first imputed data set.

One aim of the COPD data analysis is to confirm previously findings. To identify previously confirmed genes associated with COPD from LHS, we searched previous publications related to this study, which include 7 articles as listed in the dbGaP website. Articles [Hansel, et al. 2009; He, et al. 2009; Hersh, et al. 2009; Ogawa, et al. 2007] in LHS report 4 significant genetic associations with COPD (Table C).

Table C.

Information of 4 genes, which are associated with COPD in LHS study previous literatures. We calculate genes’ p-values using SKAT with its default option.

Symbol	Name	Reference	p-value
TGFB1	Transforming growth factor, beta 1	Ogawa et al	0.3079
TGFBR3	Transforming growth factor, beta receptor III	Hersh et al	0.4368
IL6	Interleukin 6	He et al	0.1473
LEPR	Leptin receptor	Hansel et al	0.7798

We further identified 37 pathways which include at least one of these 4 genes. Following the pathway identification, we use the Wilcoxon rank-sum test to test whether these 37 pathways’ p-values are smaller than other complementary pathways’ p-values. WKS-Variant method indeed ranks these 37 pathways’ p-values significantly lower than remaining pathways, with p-value 0.0030. Direct-SKAT method has the same results, with less significant p-value 0.0238. Among these 37 pathways, we list pathways with their p-values < 0.05 in either WKS-Variant or Direct-SKAT pathway analysis in Table D.

Table D.

6 among 37 pathways are significant with either WKS-Variant or Direct-SKAT pathway level analysis (significance level = 0.05). These 6 pathways each includes at least one of 4 genes in Table C. Pathways are accompanied with their p-values with WKS-Variant and Direct-SKAT methods. At last line of table, we combine all 4 genes in one gene-set.

Pathway	Source	Description	Gene Number Within	Gene Number in Table C	p-value (WKS-Va riant)	p-value (Direct-S KAT)
erythPathway	BIOCARTA	Erythrocyte Differentiation Pathway	12	2	0.0476	0.3301
hsa04620	KEGG	Toll-like receptor signaling pathway	58	1	0.4419	0.0278
hsa04630	KEGG	Jak-STAT signaling pathway	99	2	0.4923	0.0064
hsa05210	KEGG	Colorectal cancer	53	1	0.3863	0.0078
hsa05211	KEGG	Renal cell carcinoma	35	1	0.2622	0.0276
hsa05220	KEGG	Chronic myeloid leukemia	44	1	0.2032	0.0062
---	Table C	Combine all 4 genes in Table C	4	4	0.0010	0.2932

In addition, we put these 4 genes together and formed an artificial pathway. Then we used WKS-Variant and Direct-SKAT method to test its association. For this pathway, WKS-Variant method has a p-value 0.0010 while Direct-SKAT has a p-value 0.2932 (Shown in Table D).

Finally, as an agnostic approach, we run tests for all genes and all pathways with the genome-wide significance levels. We found that there are no significant genes or pathways identified after genome-wide Bonferroni correction. These results are not surprising as such a small sample sized study is not likely to be sufficiently powered.

Conclusions and discussion

In this study, we developed, to the best of our knowledge, the first genome-wide simulation framework to evaluate pathway-level association methods for sequencing data. Our framework hierarchically distributes the total genome-wide genetic effect into pathways, genes, and variants. Using exome sequencing genotype data from the 1000 Genomes Project, our simulation provides a platform to directly compare different pathway level methods. With this framework, we identify two type-I errors, based on two definitions of the null hypothesis. Traditional ‘global null hypothesis type-I error’ may not be appropriate to evaluate genome-wide association study, while the ‘local null hypothesis type-I error’ reflects the challenges in real data analyses. In addition, we noticed that LD pattern in real sequencing data will inflate the ‘local null hypothesis type-I error’, while the pathways’ overlapping structure may deflate both kinds of type-I errors. Therefore, accurate control of pathway methods’ type-I error is an overlooked challenge for methodological development of pathway association analysis.

Within the simulation framework, we comprehensively evaluated major ideas for pathway-association that were never systematically tested. By evaluating 11 different pathway methods which include variations from existing GWAS pathway association methods and region-based rare variant tests, we have following results: First, we confirmed that pathway-based methods offer much higher power than gene-based methods with moderately ill-controlled type-I errors. In this sense, pathway analysis is promising to find low effect size genetic regions out of ‘missing heritability’, and helpful to generate new hypotheses. Secondly, fully utilizing all variants’ information in sequencing data, instead of collapsing variant-level information within a gene to gene level, may help to increase the pathway level power. Third, across two different effect size scenarios in our simulation, we found that region based methods are powerful when the effect size distribution is consistent with their internal assumptions, but may severely lack of power when it is not the case. Overall, while no methods demonstrate consistently superior power, a weighted Komogorov-Smirnov (WKS) test over simple regression-based single variant test statistics (WKS-variant method) does not depend on any effect size assumption and achieves consistently high power. Indeed, when analyzing real exome data for COPD, WKS-Variant’s results confirm the association of genes reported in previous literatures, while SKAT and gene-based methods do not confirm these.

As there are no precedents, our genome-wide genetic model framework is designed to be simple. Unavoidably we made many assumptions on the parameters in simulation, such as percentage of causal genes in central causal pathway γ_g, the percentage of causal variants in causal gene γ_gv, as well as directions of gene d_g and variant d_gv. We are making no attempt to justify the choices of our parameter values. One the one hand, our understanding of the genetic architecture of complex traits is very limited, i.e., the ‘missing heritability’. On the other hand, different complex traits vary with their own genetic architectures. As we stated in simulation section, the purpose of our simulation is to provide a general framework, in which different methods can be directly and systematically compared under different genetic architectures.

Accurately controlling type-I errors for pathway level analysis is difficult. Consider the ‘global null hypothesis type-I error’ — Direct-SKAT method is conservative with Bonferroni correction, which indicates the loss of power. However, the WKS based tests are all inflated, which may be attributed to bias in the tests. WKS based methods depend on permutation to generate statistics’ distribution in null hypothesis. Ideally for each pathway, we can achieve p-value’s precision at genome-wide scale with large number of permutation, such as at least 7060 (353/0.05) in our simulation. With limited computation resources, we use normalization to adjust for different pathways’ gene size bias and assume different pathways’ enrichment scores comparable after normalization. In this way, we can achieve p-values’ precision at genome-wide precision with only 100 permutations. However, each pathway’s enrichment score may stem from different statistical distributions, and normalization cannot fully eliminate pathways’ difference. In this sense, the numerical nature of permutation based methods, such as WKS-based methods, could bias the type-I error estimation.

The simulation framework and pathway level analysis methods have been implemented in a Matlab package, feely available at http://www.ssg.uab.edu/wiki/display/~gwu/.