Dynamics of the His79-heme Alkaline Transition of Yeast Iso-1-cytochrome c Probed by Conformationally-gated Electron Transfer with Co(II)bis(terpyridine)

Abstract

Alkaline conformers of cytochrome c may be involved in both its electron transport and apoptotic functions. We use cobalt(II)bis(terpyridine), Co(terpy)₂²⁺, as a reagent for conformationally-gated electron transfer (gated ET) experiments to study the alkaline conformational transition of K79H variants of yeast iso-1-cytochrome c expressed in Escherichia coli, WT*K79H, with alanine at position 72, and Saccharomyces cerevisiae, yK79H, with trimethyllysine (Tml) at position 72. Co(terpy)₂²⁺ is well-suited to the 100 ms to 1 s time scale of the His79-mediated alkaline conformational transition of these variants. Reduction of the His79-heme alkaline conformer by Co(terpy)₂²⁺ occurs primarily by gated ET, which involves conversion to the native state followed by reduction, with a small fraction of the His79- heme alkaline conformer directly reduced by Co(terpy)₂²⁺. The gated ET experiments show that the mechanism of formation of the His79-heme alkaline conformer involves only two ionizable groups. In previous work, we showed that the mechanism of the His73-mediated alkaline conformational transition requires three ionizable groups. Thus, the mechanism of heme crevice opening depends upon the position of the ligand mediating the process. The microscopic rate constants provided by gated ET studies show that mutation of Tml72 (yK79H variant) in the heme crevice loop to Ala72 (WT*K79H variant) affects the dynamics of heme crevice opening through a small destabilization of both the native conformer and the transition state relative to the His79-heme alkaline conformer. Previous pH jump data had indicated that the Tml72→Ala mutation primarily stabilized the transition state for the His79-mediated alkaline conformational transition.

INTRODUCTION

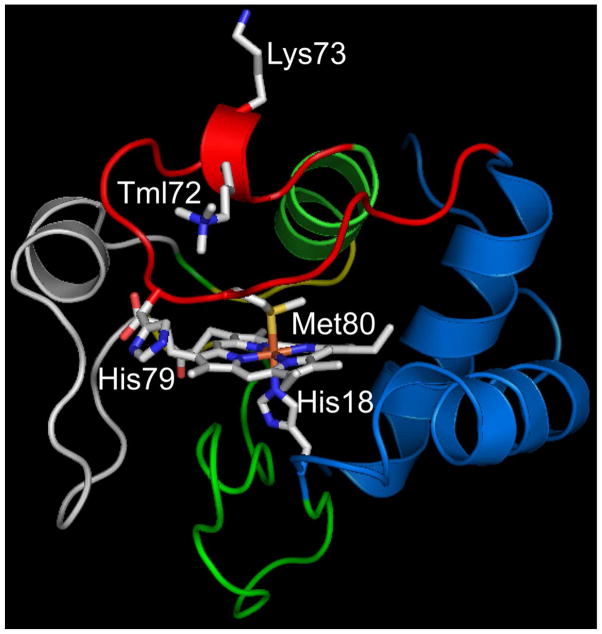
There has been considerable recent interest in characterizing alternate conformers of proteins because they are believed to be important for function.^1–5 In metalloprotions, the interconversion between alternate conformers can be driven by changes in metal ligation.^6–12 One of the most thoroughly studied ligand-mediated conformational changes for a metalloprotein is the alkaline conformational transition of mitochondrial cytochrome c (Cytc).^13,14 The alkaline conformational transition occurs at moderately alkaline pH and involves replacement of the Met80 ligand in the 6^th coordination site of the heme with either Lys73 or Lys79 in the heme crevice loop (residues 70–85, shown in red in Figure 1).^15,16 The Lys73-heme and Lys79-heme alkaline conformers are often assumed to be structurally and functionally equivalent. We apply conformationally-gated electron transfer (gated ET) methods to a K79H variant of yeast iso-1-cytochrome c, iso-1-Cytc, to show that the mechanisms of formation of alkaline conformers with ligands from position 73 versus 79 differ.

Figure 1.

Structure of yeast iso-1-Cytc showing the K79H mutation. The pdb file 2ycc was used and the K79H mutation inserted in silico (HyperChem). The side chains of Lys73 and trimethyllysine 72 (Tml72) and the heme and its native state ligands, His18 and Met80, are shown as stick models colored by element. The heme crevice loop (Ω-loop D, residues 70 to 85) is shown in red.

Since the alkaline transition leads to a drop in the reduction potential of the heme by approximately 0.5 volts,¹⁵ it has been suggested that alkaline conformers could play a role in regulating the function of Cytc in the electron transport chain.^17–19 Cytc also triggers the intrinsic pathway of apoptosis when it is released from mitochondria and binds to Apaf-1 to form the apoptosome.^20–22 More recent work shows that peroxidase activity linked to interaction of Cytc with cardiolipin (CL) in the inner mitochondrial membrane leads to oxidation of CL, which appears to enhance the porosity of the outer mitochondrial membrane.²³ Binding of Cytc to CL leads to loss of Met80-heme ligation,^23,24 and the appearance of multiple conformers,^25,26 such as alkaline conformers and conformers with H₂O or OH⁻ bound in the 6^th coordination site near neutral pH.^27,28

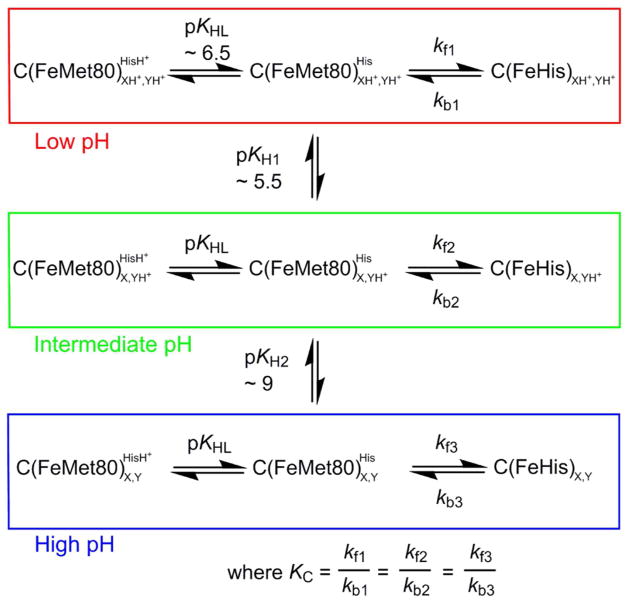
Given the apparent importance of the dynamics of the heme crevice loop and the alkaline conformational transition for Cytc function, a detailed understanding of the alkaline conformational transition is essential. Kinetic studies on the alkaline conformational transition were originally interpreted in terms of a model involving a single ionizable group and a two-state conformational transition.²⁹ However, studies from this laboratory using K73H variants of yeast iso-1-Cytc have shown that three ionizable groups with pK_a’s of ~5.5, ~6.5 and ~9 modulate the dynamics of formation of a His73-heme alkaline conformer, as outlined in Figure 2.^30–33 Furthermore, infrared, electronic and magnetic circular dichroism studies on horse Cytc provide evidence for population of other species besides Lys-heme bound conformers at moderately alkaline pH.^34–36 These species may retain Met80-heme ligation with some structural reorganization³⁴ or could involve replacement of Met80-heme ligation by a nearby buried water molecule.³⁵ Temperature dependent studies also suggest that the alkaline conformational transition involves more species than originally envisioned.^37–40 Our work on K73H variants of iso-1-Cytc shows that species other than the Met80-heme, Lys79-heme and His73-heme conformers exist throughout the pH range 5.0 to 9.5.^30,31 High spin species occur above pH 8 when a K79A mutation is also present.³² The complex distribution of species produced in the alkaline conformational transition suggests both the possibility of metabolic control of electron transport and the availability of coordination states compatible with the peroxidase activity needed in the early stages of apoptosis.

Figure 2.

Kinetic model for the His-heme alkaline transition. C represents Cytc, HisH⁺/His are the protonated and deprotonated forms of the heme ligand (His73 or His79) that replaces Met80 in the His-heme alkaline conformer and FeHis represents a His-heme alkaline conformer of Cytc. XH⁺/X is an ionizable group that deprotonates with pK_H1 ~ 5.5. This ionization changes the rate constants k_f1 and k_b1 for the His-heme alkaline transition to k_f2 and k_b2. YH⁺/Y is an ionizable group that deprotonates with pK_H2 ~ 9. This ionization changes the rate constants k_f2 and k_b2 for the His-heme alkaline transition to k_f3 and k_b3. This mechanism assumes that the incoming His73 or His79 must ionize (pK_HL) for the His73-heme or His79-heme alkaline conformer to form. The simplifying assumption that K_C, the equilibrium constant between the native state and a His-heme conformer when the His is deprotonated, is invariant with pH is generally made when analyzing pH jump data.

NMR studies on horse Cytc first demonstrated that two similar alkaline conformers exist.⁴¹ Mutagenesis studies showed that Lys73 and Lys79 are the contributing ligands for both yeast iso-1-Cytc¹⁵ and horse Cytc.¹⁶ Thermodynamic studies on iso-1-Cytc variants show that the structural rearrangement is smaller for the alkaline conformers formed with a ligand from position 79 versus position 73.^15,42,43 Thus, the nature and properties of these two alkaline conformers may be distinctly different. Our pH jump kinetic studies on a K79H variant of iso-1- Cytc^44,45 did not detect the ionizable group with a pK_a between 5 and 6 (pK_H1 in Figure 2) that affects the dynamics of the His73-heme alkaline transition. Thus, the mechanism of formation of the two alkaline conformers may be qualitatively different.

We have shown for some His73-heme alkaline conformers that there is compensation between forward and backward rate constants as a function of pH which masks the effect of the group that ionizes at low pH (pK_H1 in Figure 2).³¹ Thus, to determine whether or not the apparent lack of an ionizable group affecting the His79-mediated alkaline transition is due to a similar compensation between forward and backward rates below pH 7, we have carried out gated ET studies over the pH range 5 to 8. To accomplish this goal, we introduce bis(2,2′:6,2″-terpyridine)cobalt(II), Co(terpy)₂²⁺, as a reagent for gated ET studies. The slower ET kinetics of this reagent are better tuned to the slower dynamics of the His79-heme alkaline transition^44,45 than hexaammineruthenium(II), a₆Ru²⁺, which we have used in our previous studies on the faster dynamics of the His73-heme alkaline transition.^30,31,46,47

RESULTS AND DISCUSSION

Monitoring Heme Crevice Dynamics with Gated ET

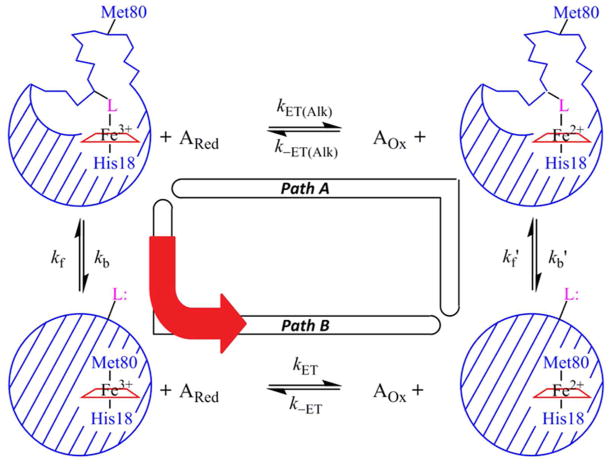
Gated ET, where the redox reaction can potentially occur with either of two conformations of a protein, is usually analyzed with a square-scheme kinetic model (Figure 3). In this model, it is assumed that one conformer (either alkaline or native) is more stable in the reduced state and the other in the oxidized state. For reduction of the protein by a small inorganic reagent, ET can occur along either one of two paths: Path A, reduction followed by the conformational change, or Path B, conformational change followed by reduction. In this case, Path B would correspond to gated ET because the reduction of the heme is gated by the conformational change to the native, Met80-heme ligation state.

Figure 3.

Kinetic square-scheme for conformationally-gated ET between iso-1-Cytc and small inorganic reagents in the reduced, A_Red, and oxidized, A_Ox, states. Iso-1-Cytc can be in either its native state with Met80 bound to the heme or in an alkaline conformer with an alternate ligand, L, bound to the heme. L is either His79 or Lys73 in the current work. In Path A, the Fe³⁺-heme alkaline conformer is reduced first to the Fe²⁺-heme alkaline conformer and then switches the His79 or Lys73 heme ligand for Met80 to form the native conformational state. The reduction of the oxidized alkaline conformer is controlled by the bimolecular rate constants k_ET(Alk) and k_−ET(Alk). The rate constant for converting the reduced alkaline conformer to the reduced native conformer is k_b′ and for converting the reduced native conformer to the reduced alkaline conformer is k_f′. In Path B, gated ET, the Fe³⁺-heme alkaline conformer first exchanges its ligand to reach the Fe³⁺-heme native conformer before it is reduced. The rate constant for converting the oxidized alkaline conformer to the oxidized native conformer is k_b and for converting the oxidized native conformer to the oxidized alkaline conformer is k_f. (This assignment of k_f and k_b matches that typically used with the alkaline conformational transition of Cytc.) The reduction of the oxidized native conformer is controlled by the bimolecular rate constants k_ET and k_−ET. This figure is adapted from reference 14.

Application of the steady-state approximation to the square-scheme model for reduction of a His-heme alkaline conformer of Cytc by an inorganic redox reagent in its reduced state (A_Red) yields eq ^148–50 for the observed ET rate constant, k_ET(obs), under pseudo-first-order conditions,

$$k_{\text{ET}}(\text{obs})=\left(\frac{{k_{\mathrm{b}}}^{\prime }\times k_{\text{ET}(\text{Alk})}[{\mathrm{A}}_{\text{Red}}]}{k_{-\text{ET}(\text{Alk})}[{\mathrm{A}}_{\text{Ox}}]+{k_{\mathrm{b}}}^{\prime }}\right)+\left(\frac{k_{\mathrm{b}}\times k_{\text{ET}}[{\mathrm{A}}_{\text{Red}}]}{k_{\text{ET}}[{\mathrm{A}}_{\text{Red}}]+k_{\mathrm{f}}}\right)$$ (1)

where A_Ox is the oxidized state of the inorganic reagent and the rate constants are defined in Figure 3. The first term on the right side of eq 1 is due to Path A and the second term is due to Path B. In our previous gated ET studies on the His73-heme alkaline conformer,^30,31,51 reduction with A_red = a₆Ru²⁺ goes exclusively by Path B. As long as there is no strong effect on electronic coupling, the exclusive use of Path B is attributable to the unfavorable reduction potential of the His73-heme alkaline conformer (−190 mV versus NHE⁵²) compared to the native state of iso-1- Cytc (290 mV versus NHE¹⁵) because k_ET(obs) is expected to depend strongly on driving force in the Marcus normal region.⁵³ If Path B dominates, eq 1 reduces to eq 2.

$$k_{\text{ET}}(\text{obs})=\frac{k_{\mathrm{b}}\times k_{\text{ET}}[{\mathrm{A}}_{\text{Red}}]}{k_{\text{ET}}[{\mathrm{A}}_{\text{Red}}]+k_{\mathrm{f}}}$$ (2)

Eq 2 predicts that k_ET(obs) will have a hyperbolic dependence on the concentration of A_red. At low concentrations of A_Red (k_f ≫ k_ET[A_Red]), k_ET(obs) increases linearly with A_red concentration because k_ET(obs) ≈ (k_ET/K_C)×[A_Red], where K_C (= k_f/k_b) is the equilibrium constant for formation of the His-heme alkaline conformer from the native (Met80-heme) state (see Figure 2). At high concentrations of A_Red (k_ET[A_Red] ≫ k_f), k_ET(obs) becomes independent of A_Red concentration because k_ET(obs) ≈ k_b.

If the full hyperbolic dependence of k_ET(obs) on A_Red concentration can be observed, then it is possible to extract both microscopic rate constants for the heme crevice dynamics, k_b and k_f, from gated ET data.^31,51 In previous work, we have shown that the k_f obtained from fits of k_ET(obs) versus [A_Red] with eq 2 and k_f obtained by directly fitting kinetic traces to the model in Figure 3 using numerical methods are the same within error.³¹ Thus, within error, the breakdown of the steady-state approximation, which was used to derive Eq 1, at low concentrations of the reducing agent, A_Red, does not affect values of k_f obtained with eq 2. A key factor in the ability to observe a hyperbolic dependence of k_ET(obs) on ARed concentration under pseudo-first-order conditions is the magnitude of k_ET[A_Red] relative to k_f (see eq 2). For a₆Ru²⁺, k_ET is near 50 mM⁻¹s⁻¹ for WT and K73H variants of iso-1-Cytc.^31,47,51 For k_f in the range of 10 to 30 s⁻¹, as is observed for some K73H variants of iso-1-Cytc, a hyperbolic dependence of k_ET(obs) on a₆Ru²⁺ concentration is readily observed while maintaining pseudo-first-order conditions.^31,51 However, the dynamics of the His79-heme alkaline transition for K79H variants of iso-1-Cytc^44,45 observed in pH jump kinetics are slow compared to the His73-heme alkaline transition.^30–33,51 Thus, a redox reagent with a smaller k_ET for reduction of the native conformer of iso-1-Cytc would be more optimal for gated ET studies of the His79-heme alkaline conformer.

Studies on the reduction of horse Cytc by various redox reagents have demonstrated a considerably smaller k_ET of ~1 mM⁻¹s⁻¹ for Co(terpy)₂²⁺,⁵⁴ which should allow the full hyperbolic dependence of k_ET(obs) versus Co(terpy)₂²⁺ concentration to be observed under pseudo-first-order conditions for gated ET with the His79-heme alkaline conformer. The Co^3+/2+ reduction potential of 270 mV versus NHE⁵⁴ also provides for full reduction of the native state of K79H variants of iso-1-Cytc at the molar excess of Co(terpy)₂²⁺ used in gated ET experiments. In the following section, we demonstrate the usefulness of Co(terpy)₂²⁺ for studying the dynamics of heme proteins with slower heme crevice dynamics.

pH Dependence of Gated ET between WT*K79H Iso-1-Cytc and Co(terpy)₂²⁺

The K79H variant used in these studies was expressed from Escherichia coli in the WT* background (WT*K79H variant). The WT* background carries a C102S mutation to prevent disulfide dimerization during physical studies, and a K72A mutation since Lys72 is not trimethylated when yeast iso-1-Cytc is expressed in E. coli.⁵⁵ The K72A mutation prevents formation of Lys72-heme alkaline conformers in addition to the Lys73-heme and Lys79-heme alkaline conformers normally observed for wild-type yeast iso-1-Cytc.^15,55

To focus on the behavior of k_b in the pH range where pK_H1 is expected to affect the kinetics of the alkaline conformational transition, we measured the reduction of WT*K79H iso-1-Cytc with Co(terpy)₂²⁺ from pH 5 to 8 in steps of 0.5. Based on our equilibrium studies on the His79- mediated alkaline transition of WT*K79H,⁴⁴ we expect the Met80-heme native conformer and the His79-heme alkaline conformer to be in equilibrium throughout this pH range. If k_ET[Co(terpy)₂²⁺] ≫ k_f + k_b, then we should see a fast kinetic phase with a rate constant k_obs,1 due to direct bimolecular ET to the Met80-heme native conformer and a slower kinetic phase with a rate constant k_obs,2 due to reduction of the His79-heme conformer after its conversion to the native conformer (gated ET, see Figure 3). Under these conditions, the amplitudes of these phases should reflect the relative proportion of native and His79-heme alkaline conformers.

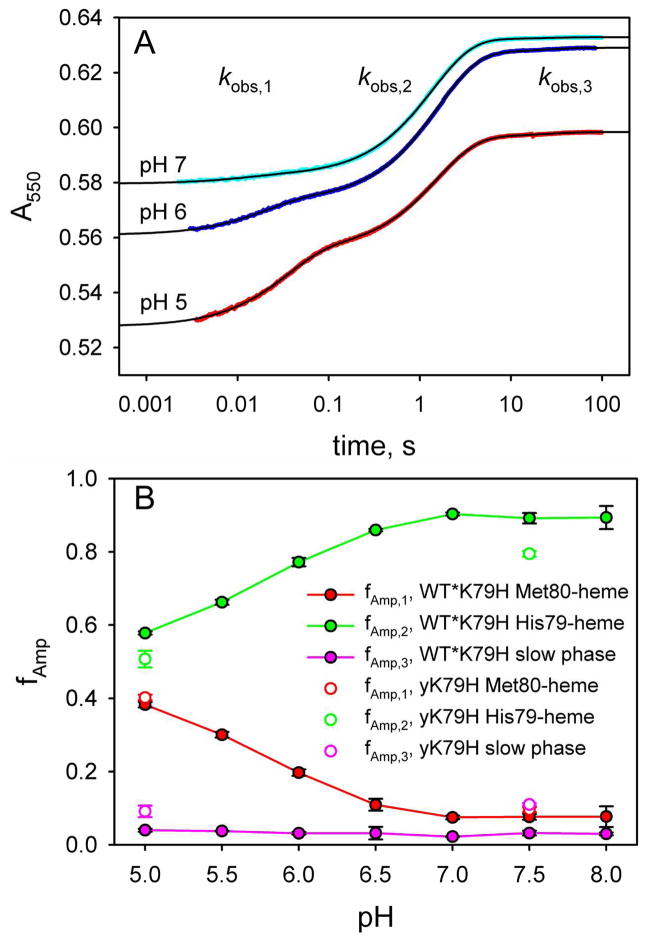
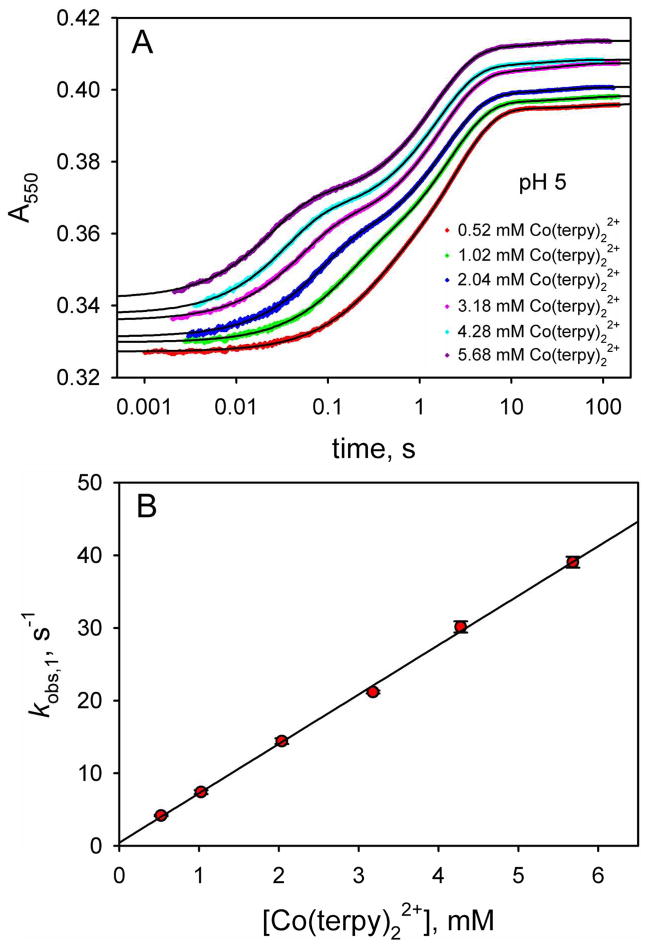
In Figure 4A, we show data at pH 5, 6 and 7 at the high end of the Co(terpy)₂²⁺ concentration range used in our experiments, where k_ET[Co(terpy)₂²⁺] ≫ k_f + k_b holds. At pH 5, the fast phase (k_obs,1) contributes substantially to the overall amplitude. As the pH increases to 6 and 7, the amplitude of the fast phase decreases at the expense of a slower phase on an ~1 s time scale (k_obs,2 in Figure 4A). We also observe a very minor kinetic phase with rate constant, k_obs,3, that occurs on a >10 s time scale (Figure 4A). Figure 4B shows the fractional amplitude, f_Amp, as a function of pH for each of the three kinetic phases at a Co(terpy)₂²⁺ concentration where k_ET[Co(terpy)₂²⁺] ≫ k_f + k_b applies. The fractional amplitude of the fast phase, f_Amp,1, decreases from pH 5 to 6.5 and then remains constant at about 7.5% of the total amplitude from pH 7 to 8. In equilibrium pH titrations of the WT*K79H variant, analogous behavior is observed from pH 5 to 8 for the absorbance at 695 nm, which reports on the presence of the Met80-heme native conformer.⁴⁴ Thus, the fast phase is assigned to direct ET to the native conformer. The fractional amplitude of the ~1 s time scale intermediate phase, f_Amp,2, increases from about 57% of the total amplitude at pH 5 reaching a constant value of ~90% of the total amplitude at pH 7 to 8. This behavior is consistent with the pH dependence expected for the population of the His79-heme alkaline conformer based on equilibrium pH titration measurements over this pH range.⁴⁴ Thus, the kinetic phase corresponding to k_obs,2 is assigned to gated ET to the His79-heme conformer of WT*K79H. The fractional amplitude of the slow phase (k_obs,3 ~ 0.02 to 0.06 s⁻¹, see Tables S1 to S7 in the Supporting Information), f_Amp,3, accounts for ~3% of the total amplitude independent of pH from pH 5 to 8. We discuss assignment of this minor phase later. Our analysis of the gated ET data will focus on the phases assigned to the native state and the His79-heme alkaline conformer.

Figure 4.

Reduction of oxidized WT*K79H iso-1-Cytc by Co(terpy)₂²⁺ at 25 °C in 10 mM buffer and 0.1 M NaCl. (A) Effect of pH on the relative amplitudes of the fast phase due to direct ET to the native conformer (k_obs,1), an intermediate phase due to gated ET to the His79-heme alkaline conformer (k_obs,2) and a slow phase (k_obs,3). The Co(terpy)₂²⁺ concentration is 4.28 mM at pH 5 (red data points), 4.68 mM at pH 6 (blue data points) and 5.14 mM at pH 7 (cyan data points). The solid black lines are fits to triple exponential rise to maximum equations. Reduction is monitored by the increase in absorbance at 550 nm, A₅₅₀, as a function of time, when iso-1-Cytc is reduced by Co(terpy)₂²⁺. The time axis is logarithmic. (B) Fractional amplitudes of the three phases, f_Amp,1, f_Amp,2 and f_Amp,3, for WT*K79H from pH 5 to 8. f_Amp,1, f_Amp,2 and f_Amp,3 are also shown for the yK79H variant at pH 5 and 7.5.

Figure 5A shows gated ET data as a function of Co(terpy)₂²⁺ concentration at pH 5. At low Co(terpy)₂²⁺ concentration, the k_obs,1 (direct reduction of the native state) and k_obs,2 (gated ET to the His79-heme alkaline conformer) phases are poorly separated. But as the Co(terpy)₂²⁺ concentration increases, the k_obs,1 and k_obs,2 phases clearly separate, primarily because of a shift of the fast phase to a progressively faster time scale. The minor k_obs,3 phase on a ~30 s time scale is observed at all Co(terpy)₂²⁺ concentrations. Rate constants and amplitudes for the data in Figure 5A and for similar data at pH 5.5 to 8 are provided in Tables S1 to S7 of the Supporting Information.

Figure 5.

(A) ET from Co(terpy)₂²⁺ to oxidized WT*K79H at pH 5 as a function of time monitored by absorbance at 550 nm, A₅₅₀. The time axis is logarithmic. Data are shown at 6 different Co(terpy)₂²⁺ concentrations. The absolute magnitudes of A₅₅₀ have been adjusted so that the data at different Co(terpy)₂²⁺ concentrations can be compared readily. For data collected with a 10 mm pathlength, the following adjustments were made: 0.52 mM, no adjustment to A₅₅₀; 1.02 mM, observed A₅₅₀ – 0.27; 2.04 mM, observed A₅₅₀ – 0.8. For data collected with a 2 mm pathlength, the following adjustments were made: 3.18 mM, observed A₅₅₀ – 0.06; 4.28 mM, observed A₅₅₀ – 0.19; 5.68 mM, observed A₅₅₀ – 0.30. The solid black curves are fits of each data set to a triple exponential rise to maximum equation. (B) Dependence of k_obs,1 on Co(terpy)₂²⁺ concentration obtained from fits to the data in panel A. The slope of this line yields k_ET = 6.8 ± 0.1. Similar plots at pH values from 5.5 to 8 are given in Figure S1 of the Supporting Information. The k_ET values from fits to a linear equation are collected in Table 1.

Under pseudo-first-order conditions, k_obs,1, due to bimolecular ET from Co(terpy)₂²⁺ to the oxidized native state of WT*K79H, should be a linear function of Co(terpy)₂²⁺ concentration. If k_ET[Co(terpy)₂²⁺] ≫ k_f and k_ET[Co(terpy)₂²⁺] ≫ k_−ET[Co(terpy)₂³⁺] (see Figure 3) then k_obs,1 is given by eq 3.

$$k_{\text{obs},1}=k_{\text{ET}}[\text{Co}{{(\text{terpy})}_2}^{2+}]$$ (3)

A plot of k_obs,1 versus Co(terpy)₂²⁺ concentration at pH 5 is shown in Figure 5B. As expected, k_obs,1 increases linearly with Co(terpy)₂²⁺ concentration with k_ET as the slope. Similar plots are obtained at all pH values (Figure S1 in the Supporting Information). k_ET increases with pH (Table 1) from ~7 mM⁻¹ s⁻¹ to ~14 mM⁻¹ s⁻¹. The pH dependence of k_ET yields a pK_a of 6.1 ± 0.2 (Figure S1 in the Supporting Information), suggesting that the magnitude of k_ET may be affected by the ionization of a histidine. ET between small inorganic reagents and proteins involves an initial binding step followed by ET. Thus, the equilibrium constant for this binding step will affect the magnitude of k_ET.^56,57 Co(terpy)₂²⁺ is positively charged, so deprotonation of a histidine would be expected to enhance its binding to iso-1-Cytc. His79 is located at the heme edge (see Figure 1). Thus, we speculate that deprotonation of His79 in the native state of WT*K79H iso-1- Cytc would increase the Co(terpy)₂²⁺/iso-1-Cytc binding constant and thus k_ET for bimolecular ET from Co(terpy)₂²⁺ to the native state of WT*K79H iso-1-Cytc. A K79A mutation to iso-1- Cytc leads to a significant increase in k_ET for reduction of the native state of iso-1-Cytc by a₆Ru²⁺,^30,46 consistent with this interpretation. We note that previous pH jump experiments and thermodynamic pH titration results yield pK_a’s of ~6.8 and ~6.6, respectively, for His79. However, when our pH titration data are re-fit to account for the fact that the WT*K79H variant is not fully native at pH 5 (Figure 4B), we obtain a pK_a of 6.35 for His79 (Figure S2 and Tables S8 and S9 in the Supporting Information), close to the value we obtain from the pH dependence of k_ET.

Table 1.

Square-scheme Rate Constants from the Reduction of K79H Variants of Iso-1-Cytc by Co(terpy)₂²⁺.

pH	kETa (mM−1 s−1)	Direct ET intercepta (s−1)	kbb (s−1)	kfb (s−1)	kET(Alk)b (mM−1 s−1)
WT*K79H
5.0	6.8 ± 0.1	0.4 ± 0.4	0.49 ± 0.02	0.9 ± 0.2	0.038 ± 0.003
5.5	7.3 ± 0.2	1.2 ± 0.6	0.50 ± 0.02	1.2 ± 0.2	0.029 ± 0.003
6.0	10.0 ± 0.4	1.0 ± 1.5	0.52 ± 0.02	2.1 ± 0.4	0.027 ± 0.004
6.5	11.1 ± 0.2	4.6 ± 0.7	0.56 ± 0.02	3.5 ± 0.4	0.024 ± 0.004
7.0	13.6 ± 0.7	10 ± 2	0.57 ± 0.03	4.1 ± 0.6	0.037 ± 0.005
7.5	14.4 ± 1.0	14 ± 3	0.61 ± 0.04	4.5 ± 0.9	0.047 ± 0.008
8.0	13.3 ± 1.3	19 ± 4	0.70 ± 0.08	6.8 ± 1.8	0.045 ± 0.012
yK79H
5.0	6.0 ± 0.2	−0.1 ± 0.4	0.542 ± 0.003	1.07 ± 0.02	0.024 ± 0.001
7.5	9.7 ± 0.7	9 ± 2	0.76 ± 0.03	4.0 ± 0.3	0.013 ± 0.004

^aReported errors are the standard error of parameters obtained from a fit of k_obs,1 versus Co(terpy)₂²⁺ concentration to a linear equation, as reported by SigmaPlot.

^bReported errors are the standard error of parameters obtained from a fit of k_obs,2 versus Co(terpy)₂²⁺ concentration to eq 4, as reported by SigmaPlot.

In Figure 5B, the intercept on the k_obs,1 axis is zero within error. However, as pH increases, the k_obs,1 intercept increases progressively in magnitude (Table 1 and Figure S1 in the Supporting Information). The non-zero intercept is likely due to conversion of the native Met80-heme conformer to the His79-heme conformer as k_f increases with increasing pH (see below).

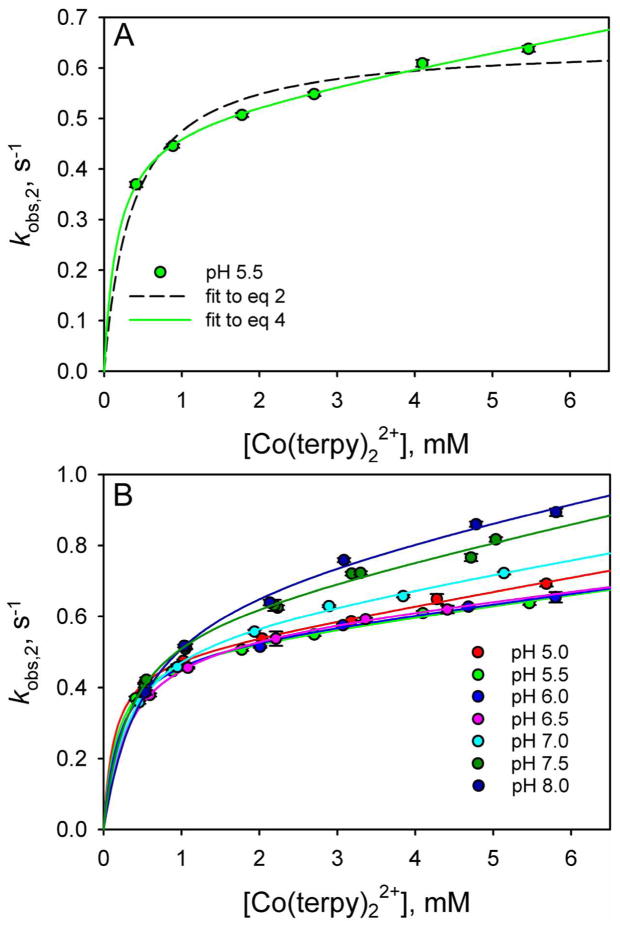
Given that there is a nearly 0.5 V decrease in the reduction potential of iso-1-Cytc when Met80-heme ligation (E^o′ ~ 290 mV versus NHE¹⁵) is replaced by His73-heme ligation (E^o′ ~ −190 mV versus NHE⁵²), we expected that reduction of the His79-heme conformer of WT*K79H iso-1-Cytc by Co(terpy)₂²⁺ would follow Path B exclusively as observed for reduction of the His73-heme conformer by a₆Ru²⁺.^31,51 In Figure 6A, we show the dependence of the rate constant for reduction of the His79-heme alkaline conformer, k_obs,2, on the Co(terpy)₂²⁺ concentration at pH 5.5. The data are fit with eq 2 (dashed line), which assumes gated ET via Path B. The fit to eq 2 is poor and it is clear that k_obs,2 continues to increase slowly at higher Co(terpy)₂²⁺ concentration.

Figure 6.

Rate constants for the intermediate phases, k_obs,2, for reduction of WT*K79H by Co(terpy)₂²⁺ as a function of Co(terpy)₂²⁺ concentration at different pH values. (A) k_obs,2 versus Co(terpy)₂²⁺ concentration data at pH 5.5 showing fits to eq 2 (dashed curve) and eq 4 (solid curve). (B) k_obs,2 versus Co(terpy)₂²⁺ concentration data from pH 5 to 8 fit to eq 4. The values of k_ET used in these fits were derived from fits of the data in Figure 5B and Figure S1 in the Supporting Information to a linear equation. The rate constants k_ET(alk), k_b and k_f in the square-scheme kinetic model (Figure 3), derived from the fits to eq 4, are collected in Table 1.

Therefore, we considered the possibility that both Paths A and B are operative for the reduction of the His79-heme conformer of WT*K79H. Under the condition that k_b′ ≫ k_−ET(Alk)[A_Ox] in Figure 3, eq 1 reduces to eq 4.

$$k_{\text{ET}}(\text{obs})=k_{\text{ET}(\text{Alk})}[{\mathrm{A}}_{\text{Red}}]+\left(\frac{k_{\mathrm{b}}\times k_{\text{ET}}[{\mathrm{A}}_{\text{Red}}]}{k_{\text{ET}}[{\mathrm{A}}_{\text{Red}}]+k_{\mathrm{f}}}\right)$$ (4)

The fit of the data in Figure 6A to eq 4 is considerably better than the fit to eq 2, suggesting that there is slow bimolecular ET between Co(terpy)₂²⁺ and the oxidized His79-heme conformer. Similar behavior is observed at all pHs from 5 to 8 with good fits to eq 4 being obtained (Figure 6B). From pH 5 to 6.5, the k_obs,2 values as a function of Co(terpy)₂²⁺ concentration cluster closely together with the fits to eq 4 yielding similar values for k_b and k_ET(Alk) (Table 1). Above pH 6.5, there is a progressive increase in the magnitude of k_obs,2 at higher Co(terpy)₂²⁺ concentration as pH increases. Fits to eq 4 suggest that this increase in k_obs,2 results from a small increase in k_b (Table 1). The rate constant for formation of the His79-heme conformer from the native state of WT*K79H, k_f, obtained from fits of the data in Figure 6 to eq 4 also increases with pH, consistent with the increasing population of the His79-heme conformer with increasing pH (see Figure 4B).

Interestingly, the intercepts of the plots of k_obs,1 versus Co(terpy)₂²⁺ concentration for direct ET to the native conformer are comparable to k_f obtained from the k_obs,2 versus Co(terpy)₂²⁺ concentration data in Figure 6B up to pH 6.5 (Table 1). This observation appears to indicate that not only reduction of the native conformer but also its conversion to the His79-heme alkaline conformer contribute significantly to the decrease in the concentration of the oxidized native conformer. The rate constant for conversion of the native conformer to the His79-heme alkaline conformer would be independent of Co(terpy)₂²⁺ concentration, yielding k_f as the intercept of a plot of k_obs,1 versus Co(terpy)₂²⁺ concentration (i.e., in lieu of eq 3, k_obs,1 = k_ET[Co(terpy)₂²⁺] + k_f). The match between k_f obtained from fits of the data in Figure 6B to eq 4 and the magnitude of the intercept of k_obs,1 versus Co(terpy)₂²⁺ concentration is poorer above pH 6.5, which may reflect the fact that k_obs,1 is more poorly determined between pH 7 and 8 because of the low population of the native conformer generating the k_obs,1 kinetic phase (see Figure S1 in the Supporting Information).

Our previous work on the reduction of oxidized yK79H iso-1-Cytc with a₆Ru²⁺ showed no evidence of direct bimolecular ET from a₆Ru²⁺ to the His79-heme conformer.⁴⁵ However, previous studies on oxidation and reduction of proteins by small molecule inorganic redox reagents indicate that reagents with hydrophobic aromatic ligands are able to penetrate into the hydrophobic protein interior, whereas hydrophilic reagents like a₆Ru²⁺ cannot.^58–61 The observation that Co(terpy)₂²⁺ can directly reduce the His79-heme conformer despite its lower tendency to give up an electron relative to a₆Ru²⁺ (270 mV versus NHE⁵⁴ for Co(terpy)₂²⁺ compared to 60 mV versus NHE⁶² for a₆Ru²⁺) must result from better electronic coupling in the His79-heme conformer/Co(terpy)₂²⁺ complex than in the His79-heme conformer/a₆Ru²⁺ complex. Thus, the ability of the hydrophobic aromatic terpyridine rings of Co(terpy)₂²⁺ to penetrate closer to the heme of the His79-heme conformer than the hydrophilic ammine ligands of a₆Ru²⁺ apparently leads to an increase in electronic coupling sufficient for k_ET(alk) to be measureable despite the unfavorable driving force for the reaction. Although direct ET to the alkaline conformer appears to occur, k_ET(alk) is still 200–400 fold smaller than k_ET (see Table 1).

Gated ET between yK79H Iso-1-Cytc and Co(terpy)₂²⁺

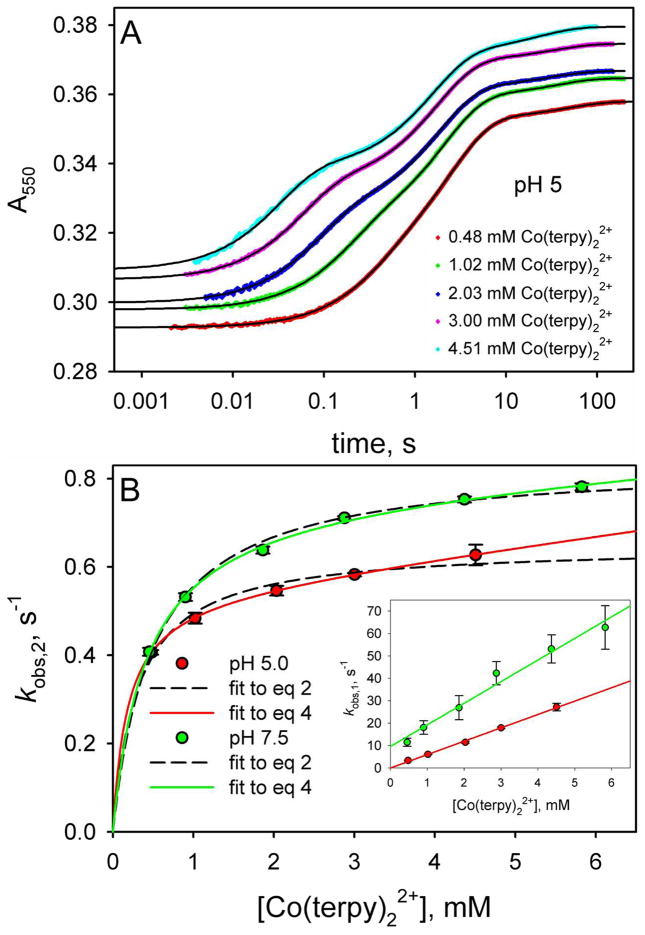
To allow direct comparison with our previously reported studies on the reduction of the yK79H variant expressed in S. cerevisiae, using a₆Ru²⁺ as the reducing reagent, we have measured the reduction of yK79H with Co(terpy)₂²⁺. Figure 7A shows data obtained at pH 5. Consistent with the data on the WT*K79H variants, we observe three kinetic phases (see also Tables S10 and S11 in the Supporting Information). The fractional amplitude of the fast phase, f_Amp,1, corresponding to direct reduction of the native conformer of yK79H is the same as observed for WT*K79H at pH 5 and 7.5 (see Figure 4B). However, the f_Amp of the intermediate phase corresponding to the His79-heme conformer is less for the yK79H variant than for the WT*K79H variant and the f_Amp of the slow phase is greater for the yK79H variant than for the WT*K79H variant (see Figure 4B). Thus, the trimethyllysine72 (Tml72) to alanine substitution in the WT*K79H variant versus the yK79H variant leads a small destabilization of the native conformer relative to the His79-heme conformer (or conversely, a small stabilization of the His79-heme conformer relative to the native conformer). By contrast, the Tml72→Ala substitution destabilizes the conformer responsible for the slow reduction of K79H variants of iso-1-Cytc by Co(terpy)₂²⁺ relative to the native state. We elaborate further on the effects of the Tml72→Ala mutation below.

Figure 7.

Reduction of yK79H iso-1-Cytc as a function of Co(terpy)₂²⁺ concentration. (A) Reduction of oxidized yK79H iso-1-Cytc by Co(terpy)₂²⁺ monitored as a function of time at 550 nm, A₅₅₀. The time axis is logarithmic. Data are shown at 5 concentrations of Co(terpy)₂²⁺. The absolute magnitudes of A₅₅₀ have been adjusted so that the data at different Co(terpy)₂²⁺ concentrations can be compared readily. For data collected with a 10 mm pathlength, the following adjustments were made: 0.48 mM, no adjustment to A₅₅₀; 1.02 mM, observed A₅₅₀ – 0.265; 2.03 mM, observed A₅₅₀ – 0.79. For data collected with a 2 mm pathlength, the following adjustments were made: 3.00 mM, observed A₅₅₀ – 0.06; 4.51 mM, observed A₅₅₀ – 0.21. The solid black curves are fits of each data set to a triple exponential rise to maximum equation. (B) Rate constants for the fast phase, k_obs,1, and intermediate phase, k_obs,2, for reduction of oxidized yK79H by Co(terpy)₂²⁺ as a function of Co(terpy)₂²⁺ concentration. The main panel shows k_obs,2 as a function of Co(terpy)₂²⁺ concentration at pH 5.0 and 7.5, with fits to eq 2 (dashed curves) and eq 4 (solid curves). The inset shows the dependence of k_obs,1 on Co(terpy)₂²⁺ concentration. The slopes of the lines in the inset yield k_ET. The values of k_ET obtained were used in the fits of the k_obs,2 versus Co(terpy)₂²⁺ concentration data in the main panel to eq 2 and eq 4. The rate constants k_ET, k_ET(alk), k_b and k_f in the square-scheme kinetic model (Figure 3), derived from these fits, are collected in Table 1.

In the inset to Figure 7B, plots of the fast phase rate constant, k_obs,1, versus Co(terpy)₂²⁺ concentration are linear as expected for bimolecular ET to the native conformer of yK79H iso-1-Cytc. The magnitude of k_ET obtained from these data is somewhat smaller for the yK79H variant than for the WT*K79H variant (Table 1). Thus, the presence of the positively charged Tml72 appears to slow direct ET to the native state.

The plots of the intermediate phase rate constant, k_obs,2, versus Co(terpy)₂²⁺ concentration in the main panel of Figure 7B are better fit by eq 4, which assumes that slow direct ET from Co(terpy)₂²⁺ to the His79-heme conformer can occur, than by eq 2. However, the improvement in the fit is less pronounced for the yK79H variant than for the WT*K79H variant (compare to Figure 6A). The smaller values for k_ET(Alk) obtained for the yK79H variant are consistent with this observation. Thus, the presence of the positively charged Tml72 also slows direct ET to His79-heme alkaline conformer. The values of the rate constant, k_b, for converting the His79-heme conformer back to the native state, are similar for the yK79H and WT*K79H variants at both pH 5 and 7.5. Reduction of yK79H by a₆Ru²⁺ yielded k_b = 0.65 ± 0.02 at pH 7.5, similar to k_b = 0.76 ± 0.03 obtained using Co(terpy)₂²⁺ to reduce yK79H (Table 1). The uncertainty in evaluating the rate constant, k_f, for converting the native state to the His79-heme conformer is larger. Thus, whether or not k_f is affected by the Tml72→Ala substitution is less clear from the gated ET data. However, based on the amplitude data in Figure 4B and our previous pH jump kinetics results, k_f is increased by the Tml72→Ala substitution (see below).

Distribution of Iso-1-Cytc Species as a Function of pH

In our previous study of the yK79H variant of iso-1-Cytc, we showed that the maximal extinction coefficient at 695 nm for yK79H was considerably less than for WT iso-1-Cytc expressed in yeast.⁴⁵ This result suggested that the Met80-heme conformer was not fully populated near pH 5. However, it is known that the Met80-heme bond may be present even when the 695 nm band disappears,^63,64 suggesting that the extinction coefficient of the 695 nm band, ε₆₉₅, is sensitive to the conformation of the Met80-heme bond.^36,63–65 Thus, it was unclear whether the decrease in ε₆₉₅ could be attributed to the native state not being fully populated at pH 5. In our previous work on the WT*K79H variant, equilibrium data fit with the assumption that the protein was fully native at pH 5 yielded an equilibrium constant for formation of the His79-heme alkaline conformer with a deprotonated His79, K_C(H79), of 4.1 ± 0.7.⁴⁴ A similar value is obtained for yK79H with the same assumption.^44,45 Given the uncertainty about the behavior of ε₆₉₅, the values of K_C(H79) obtained in this way may represent a lower limit for the true magnitude of K_C(H79). In fact, the rate constants, k_f and k_b (see Figures 2 and 3), extracted from fits to pH jump kinetic data for the His79-heme alkaline transition of WT*K79H gave K_C(H79) = 7 ± 1, consistent with the possibility that our previous estimates of K_C(H79) from equilibrium pH titration data are lower limits.⁴⁴ However, even K_C(H79) obtained from k_f and k_b extracted from pH jump kinetic data depends on the assumption that the observed rate constant, k_obs, near pH 5 approaches the magnitude of k_b. If the WT*K79H and yK79H variants are not fully native near pH 5, this assumption breaks down and the rate constants from our pH jump studies will not provide an accurate estimate of K_C(H79).

One of the clear advantages of gated ET methods is that amplitude data (Figure 4B) provide fractional populations of the different species in equilibrium for a given set of solution conditions.^30,31 Thus, the f_Amp data in Figure 4B can be used to obtain the apparent equilibrium constant for formation of the His79-heme alkaline conformer, K_C(H79)_app, as it varies with pH due to the acid dissociation equilibrium of His79. At a specific pH, K_C(H79)_app can be determined by dividing the fractional amplitude for the gated ET phase (f_Amp,2), which corresponds to the equilibrium concentration of the His79-heme alkaline conformer, by the fractional amplitude for the direct reduction (f_Amp,1), which corresponds to the equilibrium concentration of the Met80-heme native conformer (i.e., K_C(H79)_app = f_Amp,2/f_Amp,1).

The f_Amp data from our gated ET experiments in Figure 4B definitively demonstrate that neither WT*K79H nor yK79H are fully native at pH 5 and therefore, the value of K_C(H79) obtained using that assumption in our previous work is inaccurate. At pH 5, K_C(H79)_app = 1.51 ± 0.03 for WT*K79H iso-1-Cytc and K_C(H79)_app = 1.26 ± 0.06 for yK79H iso-1-Cytc (see Table S12 in the Supporting Information). Similar values of K_C(H79)_app are obtained for the two variants for the pH range 5 to 8 using either the f_Amp data or the k_f and k_b values from the gated ET data in Table 1 (K_C(H79)_app = k_f/k_b, see Figure S3 in the Supporting Information). At mildly alkaline pH His79 is almost fully deprotonated, and thus K_C(H79)_app should approach the true value of K_C(H79). Between pH 7 and 8 the amplitude data in Figure 4B yield K_C(H79)_app ~ 12 for WT*K79H iso-1-Cytc and K_C(H79)_app ~ 8 for yK79H iso-1-Cytc (Table S12). These values are considerably larger that the K_C(H79) values obtained from analysis of equilibrium pH titration data assuming the K79H variants are fully native near pH 5.^44,45 However, when we refit our equilibrium pH titration data to account for the fact that the WT*K79H is not fully native at pH 5, we obtain K_C(H79) ~ 11 (see Figure S2 and Table S9 of the Supporting Information), consistent with the value of K_C(H79)_app between pH 7 and 8. It also is evident that K_C(H79)_app is larger for WT*K79H than for yK79H at both pH 5 and 7.5 (Figure 4B, see also Table S12 and Figure S3 in the Supporting Information). Our results indicate that formation of the His79-heme alkaline conformer is ~50% more favorable when Tml72 is mutated to Ala.

The slow ET phase observed in Figures 5A and 7A yields rate constants of 0.03 to 0.06 s⁻¹ (τ ~ 15 to 30 s). Thus, the time scale is consistent with proline isomerization.⁶⁶ For K73H variants of iso-1-Cytc, a peptidyl-prolyl bond isomerizes from trans to cis when the His73-heme alkaline state forms, with about one third of the His73-heme alkaline state having a cis-peptidyl-prolyl bond.^30,32,33 However, f_Amp,3 for the slow phase in Figure 4B does not exhibit the behavior expected for a proline isomerization linked to formation of the His79-heme alkaline conformer. Instead of f_Amp,2 and f_{Amp, 3} initially increasing in synch as the His79-heme alkaline conformer increases in population above pH 5, f_Amp,3 for the slow ET phase remains constant with increasing pH.

At both pH 5 and 7.5, the population of the conformer producing the slow ET phase is larger for the yK79H variant (f_Amp,3 ~0.1) than for the WT*K79H variant (f_Amp,3 ~ 0.03). Our equilibrium studies on the alkaline conformational transition of the yK79H and WT*K79H variants indicate that the Lys73-heme alkaline conformer is more stable for the yK79H variant.^44,45 Thus, it seems possible that the slow phase could be due to a low population of the Lys73-heme alkaline conformer at pH 5. Assuming that this low population conformer is due to the Lys73-heme alkaline conformer, we calculated the apparent equilibrium constant for formation of the Lys73-heme conformer relative to the native state, K_C(K73)_app, for both variants (Table S12 and Figure S3). As pH increases from 5 to 8 for the WT*K79H variant there is only a modest increase in K_C(K73)_app, consistent with equilibrium and kinetic data showing that the Lys73-heme alkaline conformer of WT*K79H iso-1-Cytc only begins to populate significantly above pH 8.⁴⁴ By contrast, K_C(K73)_app increases more rapidly with increasing pH for the yK79H variant (Table S12 and Figure S3 in the Supporting Information), consistent with the observation that the Lys73-heme alkaline conformer begins to populate significantly just above pH 7 for the yK79H variant.⁴⁵ At pH 7.5 the magnitude of K_C(K73)_app is ~3-fold higher for the yK79H variant than for the WT*K79H variant similar to the ~6-fold difference observed in K_C(K73), the equilibrium constant for formation of the Lys73-heme alkaline conformer with a fully deprotonated Lys73, for the yK79H variant versus the WT*K79H variant in our previous work.^44,45 A P76G variant of iso-2-Cytc lowers the apparent pK_a of the alkaline transition to ~6.5.⁶⁷ Thus, a low population of Lys-heme alkaline conformers of cytochrome c near pH 5 has precedent. The side chain of Lys79 is partially buried in iso-1-Cytc.⁶⁸ Thus, the K79H mutation may sufficiently destabilize the native state relative to alkaline conformers to allow a low population of the Lys73-heme conformer at pH 5.

Mechanistic Insights into the Alkaline Transition of Iso-1-Cytc

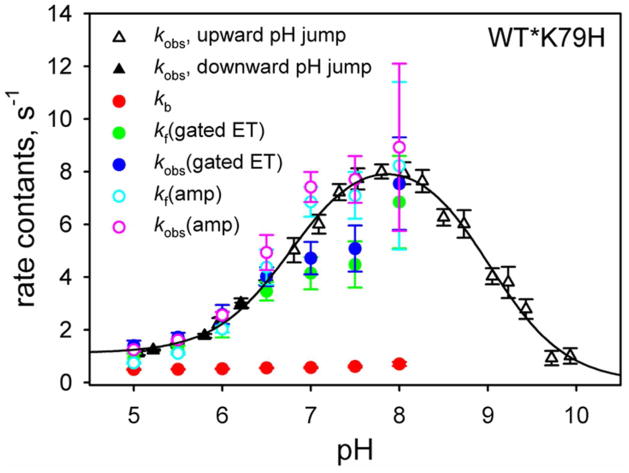
Gated ET allows k_f and k_b for the His79-heme alkaline transition to be extracted from the dependence of k_ET(obs) for gated ET on the concentration of the redox reagent using eq 2 or 4 (Figures 6 and 7). Figure 8 plots k_b and k_f and k_obs (= k_b + k_f) from our gated ET results against k_obs from our published pH jump kinetic data on the His79-heme alkaline transition of the WT*K79H variant.⁴⁴ At pH 6.5 and below, the agreement between the k_obs from gated ET data and from pH jump data is excellent. Above this pH, the agreement is not as good. The poorer agreement between the two estimates of k_obs may be due to the values used for the bimolecular electron transfer rate constant, k_ET, because the direct ET to the native conformer is more poorly defined above pH 6.5. The population of the native conformer is small above pH 6.5 (Figure 4B) and thus the errors in the rate constants used to determine k_ET are large (see Figure S1 in the Supporting Information). Because k_f extracted from fits of the data in Figures 6 and 7 to eq 4 depends on accurate determination of k_ET (see eq 4), k_obs (= k_f + k_b) will be less reliable if k_ET is less well determined.

Figure 8.

Comparison of rate constants for the His79-heme alkaline conformational transition of WT*K79H iso-1-Cytc obtained from gated ET experiments to k_obs for the same conformational transition obtained with pH jump stopped-flow measurements. k_b obtained from gated ET data is shown with filled red symbols. k_f is either obtained from fits to the data in Figure 6 [filled green symbols, denoted k_f(gated ET)] or as k_f = K_C(H79)_app×k_b [open cyan symbols, denoted k_f(amp)] using the amplitude data in Figure 4B to obtain K_C(H79)_app. k_obs(gated ET) (filled blue symbols) is the sum of k_b and k_f(gated ET) and k_obs(amp) (open pink symbols) is the sum of k_b and k_f(amp). Error bars for k_f(amp) are from standard propagation of the errors in k_b and K_C(H79)_app (Table S12 in the Supporting Information). Error bars for k_obs(gated ET), and k_obs(amp) are obtained from standard propagation of the errors in k_b and k_f(gated ET) or k_f(amp). k_obs data from pH jump experiments (solid and open black triangles for downward and upward pH jumps, respectively) are from reference 44. The solid black curve is a fit of the pH dependence of the k_obs data from pH jump experiments to the mechanism in Figure 2, albeit without the pK_H1 ionization.^44,45

Thus, we employed a second method to determine k_f which uses K_C(H79)_app obtained from the amplitude data from the gated ET experiments (Figure 4B, see also Table S12 in the Supporting Information). k_f can be calculated from K_C(H79)_app and k_b (which is well-determined from the plots in Figures 6B and 7B, see Table 1) using k_f = K_C(H79)_app×k_b. k_f and k_obs derived from gated ET amplitude data agree better with the pH jump data above pH 6.5 (Figure 8).

Figure 8 also shows the pH dependence of k_b from pH 5 to 8 for the His79-heme alkaline transition of WT*K79H iso-1-Cytc. k_b is essentially independent of pH. By contrast, pH jump^32,33 and gated ET^31,47 experiments on the His73-heme alkaline transition show a strong pH dependence for k_b between pH 5 and 8 consistent with the ionization of a protein group with a pK_a between 5.5 and 6 modulating the kinetics of the His73 alkaline transition (pK_H1 in Figure 2). Thus, gated ET data provide definitive evidence that the mechanism of the His79-heme alkaline transition is simpler than that of the His73-heme alkaline transition; it does not involve the ionizable group corresponding to pK_H1 in Figure 2. Clearly, the sequence position of the protein ligand mediating the alkaline conformational transition has an important effect on the molecular mechanism of the conformational change. We speculate that the smaller structural perturbation in the His79-heme alkaline conformer versus the His73-heme alkaline conformer does not significantly affect the environment of the ionizable group corresponding to pK_H1.

Although, we only collected gated ET data at pH 5 and 7.5 for yK79H iso-1-Cytc, the data in Table 1 indicate that the conclusions for the mechanism of the His79-heme alkaline transition are the same as for WT*K79H iso-1-Cytc. Thus, the residue at position 72, Tml72 versus Ala72, does not affect the mechanism of the His79-heme alkaline transition.

Effect of the Tml72→Ala Substitution on the Dynamics of the His79-heme Alkaline Transition

In our recent study on the WT*K79H variant using pH jump methods,⁴⁴ we concluded that the primary reason for the increased dynamics of the alkaline transition when Tml72 is replaced by Ala was a lowering of the free energy of the transition state (TS). This conclusion was based on guanidine hydrochloride denaturation experiments which showed that, within error, the Tml72→Ala mutation did not affect the stability of the His79-heme conformer of yK79H iso-1-Cytc relative to WT*K79H iso-1-Cytc.⁴⁴ In addition, analysis of pH jump kinetic data indicated that k_b near neutral pH increased from 0.7 ± 0.2 s⁻¹ for yK79H to 1.1 ± 0.1 s⁻¹ for WT*K79H. In pH jump experiments, k_obs at pH 5 was significantly larger for the WT*K79H variant. The model used to fit the pH dependence of k_obs from pH jump data used the simplifying assumption that k_obs arises solely from k_b at low pH. Therefore, the significantly larger k_obs at pH 5 for the WT*K79H variant relative to the yK79H variant yielded a 60% larger k_b for the WT*K79H variant, consistent with the Tml72→Ala substitution causing a stabilization of the TS by ~0.3 kcal/mol. However, we now know from the gated ET amplitude data that the contribution of k_f to k_obs is still significant at pH 5 (Table 1).

Gated ET measurements allow direct determination of k_b at a given pH with high precision and accuracy (see Table 1). In contrast to our conclusion based on analysis of pH jump data, our gated ET results show that at both pH 5 and 7.5, k_b actually decreases slightly when Tml72 is mutated to Ala. Thus, the gated ET results show that the TS is unaffected or slightly destabilized (by 0.13 ± 0.04 kcal/mol at pH 7.5) relative to the His79-heme alkaline conformer by this mutation.

As discussed above, the inherent error in evaluating k_f from gated ET measurements is larger compared to the relatively precise values that can be obtained for k_b. However, the difference in K_C(H79)_app at pH 7.5 for the yK79H variant versus the WT*K79H variant indicates that the Tml72→Ala mutation destabilizes the native conformer by ~0.2 kcal/mol. Thus, our gated ET results suggest a more modest effect of the Tml72→Ala mutation on heme crevice dynamics than our pH jump results, which indicated that the Tml72→Ala mutation increased k_f by a factor of ~ 2.5 (equivalent to a 0.5 kcal/mol decrease in the barrier to formation of the His79-heme alkaline conformer from the native conformer at 25 °C).⁴⁴ However, we cannot completely rule out the possibility that the smaller k_ET for the yK79H variant versus the WT*K79H variant at pH 7.5 could lead to some systematic decrease in f_Amp,1 and increase in f_Amp,2 via conversion of the native conformer of the yK79H variant to the His79-heme alkaline conformer before is it reduced (i.e., competition between k_f and k_ET, see Figure 3) even at the higher Co(terpy)₂²⁺ concentrations used to evaluate the fractional amplitudes. In this case, K_C(H79)_app for the yK79H variant would be overestimated relative to the WT*K79H variant leading to an underestimation of the destabilization of the native state by the Tml72→Ala mutation. The match between k_obs from pH jump experiments and k_obs(amp) obtained using gated ET amplitude data is reasonable for the WT*K79H variant, suggesting that k_ET effectively outcompetes k_f at the higher Co(terpy)₂²⁺ concentrations. For the yK79H variant, k_obs(amp) obtained with fractional amplitude data is consistently larger than k_obs from pH jump data (Figure S4 in the Supporting Information), suggesting that the fractional amplitude data may be overestimating K_C(H79)_app for the yK79H variant (i.e., k_ET does not adequately outcompete k_f). To be conservative, we estimate the effect of Tml72→Ala mutation on the stability of the native conformer to be 0.2 to 0.6 kcal/mol, the lower limit from gated ET data and the upper limit from pH jump measurements.

CONCLUSION

Using gated ET experiments, we have shown that the alkaline transition of cytochrome c mediated by His79 is mechanistically distinct from that mediated by His73. In particular, only two ionizable groups affect the His79-mediated alkaline transition. Our data provide more exact values for k_b, in particular, which indicate that of the Tml72→Ala substitution in fact slightly destabilizes the TS for the His79-heme alkaline transition rather than stabilizing it. Thus, the enhanced dynamics caused by the Tml72→Ala mutation appear to be primarily attributable to destabilization of the native conformer. Our results also show the power of gated ET methods for extracting mechanistic details on metalloprotein dynamics that are not readily obtained by standard kinetic methods. Finally, Co(terpy)₂²⁺ represents an important addition to the toolbox of reagents for gated ET studies, allowing characterization of metalloprotein dynamics on the 0.1 to 1 second time scale.

EXPERIMENTAL PROCEDURES

Preparation of the WT*K79H and yK79H Variants of Iso-1-Cytc

The WT*K79H variant of iso-1-Cytc was expressed from the pRbs_BTR1 vector⁶⁹ transformed into BL21(DE3) E. coli cells as previously described.⁴⁴ The WT* background carries a C102S mutation to prevent dimerization during physical studies and a K72A mutation to prevent the formation of the Lys72- heme alkaline conformer.⁵⁵

The yK79H variant was expressed from Saccharomyces cerevisiae GM-3C-2 cells⁷⁰ transformed with the pRS/C7.8 shuttle vector⁷¹ carrying iso-1-Cytc with the K79H mutation, as previously described.⁴⁵ Cell lysis was by autolysis with ethyl acetate, as described previously.^72,73 yK79H iso-1-Cytc has the native trimethyllysine at position 72 and carries the C102S mutation to prevent disulfide dimerization during physical studies.

Purification of both proteins was as described previously.^44,72,73 Briefly, cell lysates cleared by centrifugation, were brought to 50% ammonium sulfate and the precipitate was removed by centrifugation. Following dialysis against two changes of 12.5 mM sodium phosphate buffer, pH 7.2, 1 mM EDTA, 2 mM β-mercaptoethanol (β-ME), the dialyzed protein solution was batch-adsorbed onto CM-Sepharose Fast Flow resin equilibrated to 50 mM sodium phosphate buffer, pH 7.2, 1 mM EDTA, 2 mM β-ME followed by elution with a 200 mL linear gradient from 0 to 0.8 M NaCl in 50 mM sodium phosphate buffer, pH 7.2, 1 mM EDTA, 2 mM β-ME. Eluent containing Cytc was concentrated by ultrafiltration, flash frozen and stored at −80 °C in 1.5 mL aliquots containing 3–6 mg of protein. Just before experiments, protein was thawed and purified to homogeneity by HPLC (Agilent 1200 series) using a BioRad UNO S6 column as described previously.⁴⁴

Co(terpy)₂²⁺-mediated Gated ET Measurements

[Co(2,2′:6,2″-terpyridine)₂]²⁺ was produced by the reaction of CoCl₂·6H₂O (Fisher) with 2,2′:6,2″-terpyridine (Fluka) in deionized water using a literature procedure.⁷⁴ The product was precipitated as a microcrystalline solid with sodium trifluoromethane sulfonate (ACROS Organics) and recrystallized from deionized water to which triflouoromethane sulfonate was added after the dissolution of the crude product.⁷⁴ The ¹H NMR spectrum of the product matched that reported in the literature.⁷⁵

Iso-1-Cytc used in gated ET experiments was oxidized with K₃[Fe(CN)₆] as described previously.⁴⁵ Oxidized protein was separated from K₃[Fe(CN)₆] by Sephadex G-25 size exclusion chromatography with the G-25 resin pre-equilibrated to buffer at the pH required for each experiment.

Solid [Co(terpy)₂](CF₃SO₃)₂ was weighed out and dissolved in 10 mM buffer, 0.1 M NaCl and degassed on the vacuum/Ar dual manifold line to produce a 10–12 mM stock solution. This solution was then used to produce additional stock solutions of ~1, 2, 4, 6 and 8–9 mM [Co(terpy)₂](CF₃SO₃)₂ by dilution into degassed buffer. We note that [Co(terpy)₂](CF₃SO₃)₂ displayed poor solubility in aqueous solution in concentrations greater than ~12 mM at 25 °C. Oxidized iso-1-Cytc was diluted into degassed buffer to produce final concentrations of either 10 μM or 50 μM. The degassed buffer was also used to thoroughly flush the Applied Photophysics SX20 stopped-flow spectrometer before performing a mixing experiment.

In 1:1 mixing, the 10 μM iso-1-Cytc stock solution was used with 1, 2 and 4 mM [Co(terpy)₂](CF₃SO₃)₂ stock solutions and the 10 mm pathlength of the flow cell producing final concentrations of approximately 0.5, 1 and 2 mM Co(terpy)₂²⁺ and 5 μM iso-1-Cytc in 10 mM buffer, 0.1 M NaCl. The 50 μM iso-1-Cytc stock solution was used with 6, 8–9 and 10–12 mM [Co(terpy)₂](CF₃SO₃)₂ stock solutions and the 2 mm pathlength of the flow cell, producing final concentrations of approximately 3, 4–4.5 and 5.0–6.0 mM Co(terpy)₂²⁺ and 25 μM iso-1-Cytc in 10 mM buffer, 0.1 M NaCl. At ≥3.0 mM concentration, the absorbance of [Co(terpy)₂]²⁺ at 550 nm is large enough that it is necessary to switch to the shorter pathlength so as not to saturate the detector at 550 nm, the wavelength used to monitor reduction of iso-1-Cytc. The use of a final concentration of 25 μM iso-1-Cytc at the shorter 2 mm pathlength was intended to maintain the same change of absorbance at 550 nm, ΔA₅₅₀, at the 2 mm pathlength as at the 10 mm pathlength (5 μM final iso-1-Cytc concentration) so that there would be no loss in signal-to-noise. At 3 mM Co(terpy)₂²⁺, the ratio of Co(terpy)₂²⁺ to iso-1-Cytc concentration is still >100 and thus pseudo-first-order conditions are maintained. The progress of the experiment was monitored by the growth of an absorbance peak at 550 nm, signifying reduction of the heme iron. All reactions were conducted at 25 °C using a Thermo Neslab RTE7 circulating water bath.

Buffers used in these experiments are as follows: sodium acetate (pH 5, 5.5), sodium 2-(N-morpholino) ethanesulfonate (MES, pH 6, 6.5), sodium phosphate monobasic (pH 7, 7.5) and Tris (pH 8). All buffers contained 0.1 M NaCl and were pH adjusted with NaOH or HCl solutions. The concentrations of all Co(terpy)₂²⁺ solutions were measured spectrophotometrically at 505 nm (ε₅₀₅ = 1404 M⁻¹ cm⁻¹).⁷⁴ Data were collected on a 5 s time scale using pressure hold for fast time scale reduction of iso-1-Cytc. Data were also collected on a 100–200 s timescale to monitor slower time scale reduction of iso-1-Cytc. The absorbance data at 550 nm were fit to two or three exponential functions using SigmaPlot v 7.