Phototropic growth control of nanoscale pattern formation in photoelectrodeposited Se–Te films

Significance

Phototropism, in which plants grow toward a source of illumination, uses dynamic feedback between the light source and photosensitive hormones within the plant to direct the curvature of the plant as it grows. In this manuscript, we describe an adaptive inorganic system that dynamically alters its emergent nanoscale morphology in response to changes in the illumination conditions during growth. Phototropic growth control of nanoscale pattern formation in photoelectrodeposited selenium–tellurium films provides the ability to grow nanostructures of entirely different geometries, periods, and directions abruptly on top of one another, and the ability to change the physical growth direction of the material by changing the direction of the incident light beam.

Abstract

Photoresponsive materials that adapt their morphologies, growth directions, and growth rates dynamically in response to the local incident electromagnetic field would provide a remarkable route to the synthesis of complex 3D mesostructures via feedback between illumination and the structure that develops under optical excitation. We report the spontaneous development of ordered, nanoscale lamellar patterns in electrodeposited selenium–tellurium (Se–Te) alloy films grown under noncoherent, uniform illumination on unpatterned substrates in an isotropic electrolyte solution. These inorganic nanostructures exhibited phototropic growth in which lamellar stripes grew toward the incident light source, adopted an orientation parallel to the light polarization direction with a period controlled by the illumination wavelength, and showed an increased growth rate with increasing light intensity. Furthermore, the patterns responded dynamically to changes during growth in the polarization, wavelength, and angle of the incident light, enabling the template-free and pattern-free synthesis, on a variety of substrates, of woodpile, spiral, branched, or zigzag structures, along with dynamically directed growth toward a noncoherent, uniform intensity light source. Full-wave electromagnetic simulations in combination with Monte Carlo growth simulations were used to model light–matter interactions in the Se–Te films and produced a model for the morphological evolution of the lamellar structures under phototropic growth conditions. The experiments and simulations are consistent with a phototropic growth mechanism in which the optical near-field intensity profile selects and reinforces the dominant morphological mode in the emergent nanoscale patterns.

Photoresponsive materials with chemical or physical properties that change under illumination are enabling for the photolithographic generation of patterns in 2D and 3D structures. In lithography, regions of the photoresist are selectively exposed to light either by physically masking defined areas of the photoresist film or by the formation of a light intensity pattern that varies across the film. Recent extensions of photolithography, such as plasmonic nanolithography and interference lithography, are capable of generating 3D light intensity patterns and thus have been used to fabricate complex structures with feature sizes below 100 nm (1–6). These top-down photopatterning approaches require a different mask design to create each new structure. Maskless techniques have also been developed for patterning surfaces via photoinduced ablation, melting, deposition, and etching. Periodic ripple patterns have been observed during laser-induced damage, melting, and etching of dielectric and metal surfaces as well as for photolytic decomposition of organometallic precursors onto these substrates (7–15). Laser-induced periodic surface structuring (LIPSS) is a stimulated optical phenomena (also referred to as the stimulated Wood’s anomaly) resulting from interference between an intense laser source (i.e., between 10 W/cm² and 10 MW/cm² for continuous laser irradiation or between 75 and 800 mJ/cm² per pulse for pulsed irradiation in the above references) and surface-scattered waves to produce a periodic modulation of the surface profile. Photoanodic etching of n-type Si is another maskless patterning technique in which macroporous etch pits can be produced whose size and shape are controlled by the collection rate of photogenerated minority-carrier holes at the semiconductor surface relative to the mass transport rate of fluoride ions in the etchant solution (16, 17).

Light-directed growth of photoresponsive materials, independent of the optical properties of the growth substrate, could, in turn, enable the design of complex 3D mesostructures such as self-assembled photonic structures (18–20), 3D electrode architectures (21–24), chiral and negative index metamaterials (25–27), as well as optoelectronic devices that exhibit wavelength- and polarization-selective photoconductivity (28, 29). Such processes require dynamic feedback between the illumination conditions and the morphology that develops in response to the optical excitation, and also require a method to control the instantaneous light intensity profile at the growth front of the photoresponsive material. One such example is the plasmon-mediated shape control of silver colloids, which have been observed to transform into larger, triangular nanoprisms when the colloidal particles are irradiated with visible light (30–32). The transformation process has been attributed to the excitation of surface plasmon resonances in the metal nanostructures, such that the particles grow until the frequency of the plasmon resonance matches that of the incident illumination.

Chalcogenide glasses are a technologically important class of materials used in a variety of applications including infrared photodetectors, optical fibers, and as phase-change materials for nonvolatile memory. The structural, mechanical, and optoelectronic properties of both pure chalcogens and chalcogenide compounds, such as selenium, germanium selenide, arsenic sulfide, and arsenic selenide, have been shown to change under visible radiation (33–39). Transient effects under illumination include photoinduced changes in the conductivity, refractive index, and viscosity of the chalcogenide (33–35). In addition, extended exposure times can produce metastable changes to the crystallinity, optical absorption, and surface morphology of these materials (33, 36–39). In the majority of these studies, the chalcogenide film has been grown via vapor deposition and the effects of illumination have been examined after film growth. In contrast, we describe the formation of nanoscale patterns in Se–Te alloys that are deposited electrochemically in the presence of illumination. Solution-phase electrodeposition provides a convenient method to deposit the photoresponsive material and to simultaneously illuminate the growth surface. In the photoelectrochemical growth experiments described herein, the illumination conditions were varied during growth to investigate the dependence of the film morphology on the intensity, wavelength, polarization, and incident angle of the illumination.

Se–Te films were grown via potential-controlled cathodic electrodeposition from an aqueous solution that contained selenium oxide and tellurium oxide (SI Appendix, Text S1, provides a detailed description of the materials and methods). A noncoherent light source, typically a light-emitting diode (LED) was used to illuminate the working electrode during electrodeposition of the Se–Te films. The LEDs had emission wavelengths ranging from 365 to 940 nm with spectral bandwidths between 7 and 37 nm. The illumination intensity produced by the LEDs was varied between 2.8 and 32.5 mW/cm².

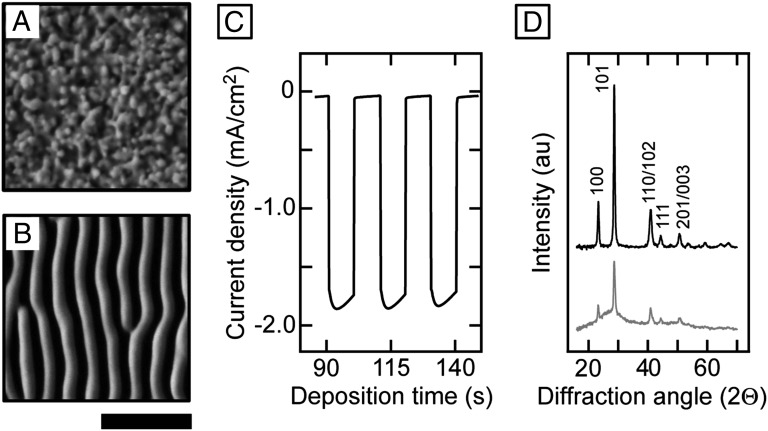
Fig. 1 A and B show scanning electron microscope (SEM) images of Se–Te films electrodeposited on degenerately doped, n-type Si(111) substrates at an applied potential (E) = −0.80 V vs. a standard calomel electrode (SCE) until −1.9 C/cm² of charge had passed between the counter and working electrodes. The film grown in the dark displayed a granular morphology with no long-range morphological order (Fig. 1A). In contrast, the film grown under linearly polarized, 625-nm LED-based illumination with an intensity of 16.9 mW/cm² (Fig. 1B) exhibited a nanoscale lamellar morphology. The lamellae were oriented parallel to the incident light polarization direction, exhibited uniform size and period, and were continuous across the entire substrate (typically 1 cm² in area). The deposition current density was enhanced under illumination compared with growth in the dark. Fig. 1C shows the current density measured during electrodeposition at E = −0.40 V vs. SCE under chopped illumination. At an intensity of 18.2 mW/cm² for 625-nm light, the current density showed a 36-fold enhancement compared with that observed during film deposition in the dark. Similar lamellar patterns were obtained using other illumination sources, including a halogen light bulb as well as a low-intensity He–Ne laser (SI Appendix, Fig. S1).

Fig. 1.

Light-directed pattern formation in electrodeposited Se–Te films. (A) Electrodeposited Se–Te film grown in the dark. (B) Electrodeposited Se–Te film grown under linearly polarized, 625-nm illumination from a noncoherent, LED source with an intensity of 16.9 mW/cm². [Scale bars: 1 µm (for both A and B).] (C) Deposition current density for growth of a Se–Te film under chopped illumination at E = −0.40 V vs. SCE. The current density increased from an average value of −0.05 mA/cm² in the dark to −1.79 mA/cm² under an illumination intensity of 18.2 mW/cm². (D) X-ray diffraction patterns showing Se–Te films grown in the dark (Top trace) and under illumination (Bottom trace). The (hkl) indices were assigned to diffraction peaks according to ref. 40.

Energy-dispersive spectroscopy (EDS) indicated that the films shown in Fig. 1 A and B possessed similar compositions of selenium and tellurium. The Se:Te atomic ratio was 58:42 for the film in Fig. 1A and 57:43 for the film in Fig. 1B. Films that were grown at different applied potentials, on various growth substrates, and under different illumination conditions exhibited Se:Te compositional ratios that ranged from 47:53 to 65:35 (SI Appendix, Fig. S2 and Table S2). X-ray photoelectron spectra (XPS) recorded at various depths through the films showed that the films consisted of elemental Se and Te. The addition of CdSO₄ to the deposition solution improved both film adhesion and the uniformity of the films. XPS depth profiling detected the presence of Cd only at the interface between the Si growth substrate and the Se–Te film (SI Appendix, Text S4 and Figs. S3 and S7). X-ray diffraction (XRD) patterns further indicated that films grown in the dark and under illumination were both composed of a Se–Te alloy with nanocrystalline domains. The diffraction peaks in the patterns were at angles intermediate between that of pure, elemental Se and pure, elemental Te, both with a hexagonal crystal structure, similar to colloidally synthesized Se–Te alloy nanocrystals (Fig. 1D) (40). Debye–Scherrer analysis of the widths of the diffraction peaks was consistent with a crystallite size on the order of tens of nanometers. The film grown under illumination possessed an additional amorphous background. Photovitrification has previously been observed in other chalcogenide compounds such as As–Se and As–S (33, 36). Thus, illumination during electrodeposition of the Se–Te film substantially altered the nanoscale morphology, but produced nearly the same atomic-scale composition and structure as films grown in a dark ambient.

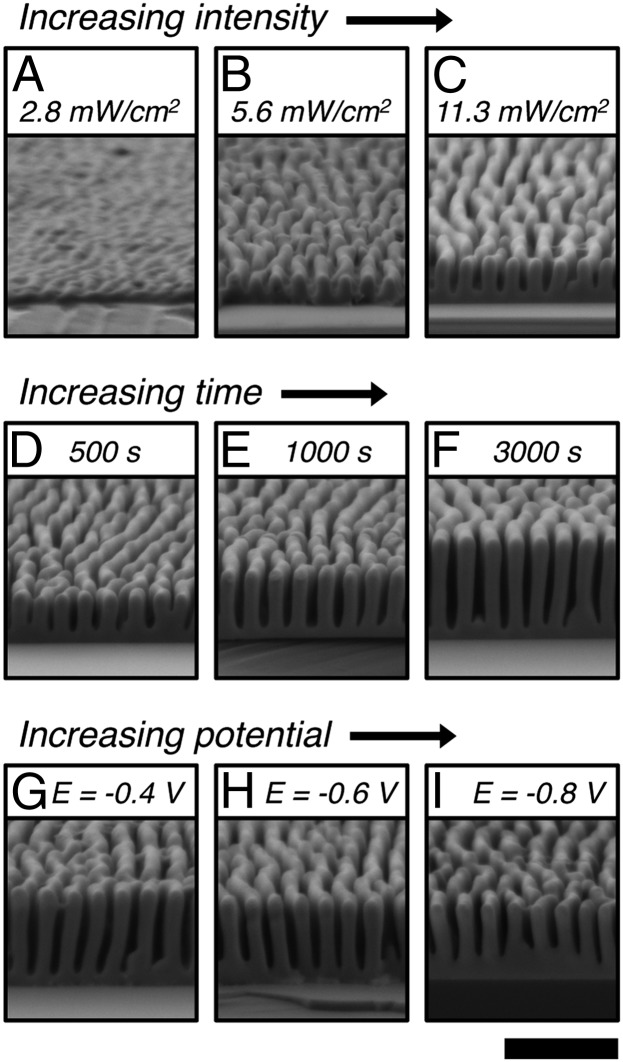
Fig. 2 illustrates how the growth of the lamellar patterns depended on the incident light intensity, deposition time, and applied potential. Cross-sectional SEM images of Se–Te films electrodeposited for 500 s at E = −0.40 V vs. SCE, under linearly polarized, 625-nm light at intensities of 2.8, 5.6, and 11.3 mW/cm², respectively, indicated that increasing the light intensity increased the growth rate (i.e., total amount of material deposited) and increased the height anisotropy (i.e., the peak-to-trough height) of the lamellar features (Fig. 2 A–C). Under constant illumination conditions, the lamellae also grew taller with increasing deposition time (Fig. 2 D–F). For example, at E = −0.40 V vs. SCE under linearly polarized, 625-nm illumination with an intensity between 18.6 and 18.9 mW/cm², the average height of the lamellae at their peaks was 460 ± 28 nm (average ± first SD from 50 measurements) for a film grown for 500 s and was 938 ± 18 nm for a film grown for 3,000 s. At a fixed applied potential during electrochemical deposition, the dark contribution to film growth decreased with time due to the increasing resistance of the Se–Te film. Thus, the deposition current and resulting change in lamellae height slowly decreased with time (SI Appendix, Fig. S4). In contrast, the film thickness of the troughs between lamella remained approximately the same at 122 ± 23 nm for the film grown for 500 s and 116 ± 25 nm for the film grown for 3,000 s. The width of the lamella also remained nearly constant, at 143 ± 10 nm for the film grown for 500 s and 164 ± 9 nm for the film grown for 3,000 s.

Fig. 2.

Effect of light intensity, deposition time, and applied potential on the growth of Se–Te lamellar films. All films were grown under linearly polarized, 625-nm illumination from an LED source. (A–C) Films grown for 500 s at E = −0.40 V vs. SCE with light intensities of (A) 2.8 mW/cm², (B) 5.6 mW/cm², and (C) 11.3 mW/cm². (D–F) Films grown at E = −0.40 V vs. SCE and with a light intensity between 18.6 and 18.9 mW/cm² for deposition times of (D) 500 s, (E) 1,000 s, and (F) 3,000 s. (G–I) Films grown with a light intensity between 18.6 and 18.8 mW/cm² until −1.3 C/cm² of charge had passed at (G) E = −0.40 V, (H) E = −0.60 V, and (I) E = −0.80 V vs. SCE. [Scale bar: 1 µm (applies to all images).]

The relative contributions to the total deposition current density that were produced by the photocurrent and the dark current could be adjusted by changing the light intensity and the applied potential, respectively. Fig. 2 G–I show lamellar films for which the light intensity and total amount of charge passed were held constant, but with values of E = −0.40, −0.60, and −0.80 V vs. SCE, respectively. At a light intensity of 18.6 mW/cm² and E = −0.40 V vs. SCE, the enhancement ratio of the photocurrent to the dark current ratio was 36, whereas under the same light intensity, this ratio decreased to 5 at E = −0.80 V vs. SCE (SI Appendix, Fig. S5 and Table S3). Fig. 2 G–I show that, as the applied potential was made more negative, the lamellar height decreased and the amount of growth at the bottom of the troughs increased. Although more negative potentials and higher light intensities both enhanced the average current density, the dark-current contribution led to nonselective film growth, whereas the photocurrent contribution promoted anisotropic growth of the lamellar features.

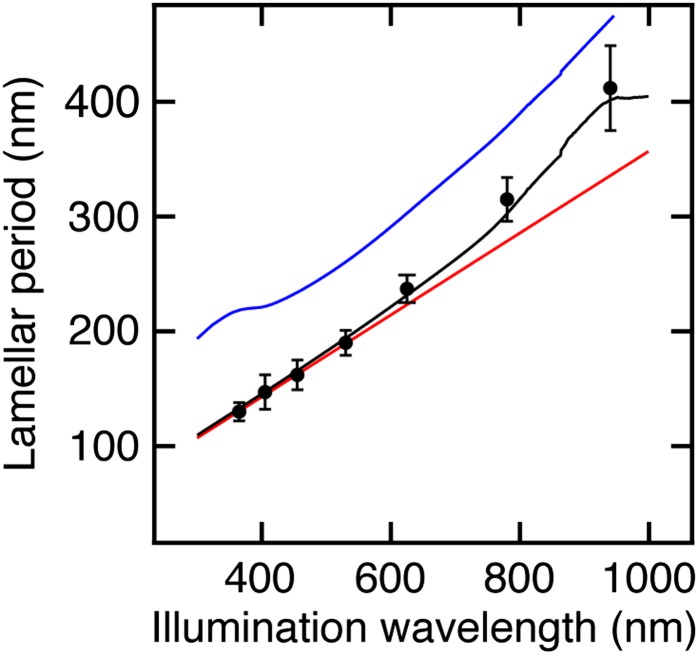
Variations in the polarization, wavelength, and angle of the incident illumination altered the pattern that developed during light-directed growth of the Se–Te films. Fig. 3 A–E shows the effect of polarization on film growth. Under randomly polarized light, the lamellae did not display orientational order (Fig. 3A). However, under linearly polarized illumination, the lamellae grew to be aligned parallel to the electric-field vector of the incident illumination, with the growth pattern evident across the entire substrate (Fig. 3 B and C). When the polarization was changed, further growth of the lamellae occurred with an orientation toward the new direction of the electric field. Woodpile-like nanostructures were therefore created through 90° shifts in the polarization, and spiral structures were produced through continuous rotation of the polarization (Fig. 3 D and E). The period of the lamellae varied from a value of 130 ± 4 nm (average ± first SD from 25 measurements) for UV (365 nm) illumination to 412 ± 19 nm for near-infrared (940 nm) light (Figs. 3 F–I and 4). A change in the illumination wavelength from 940 to 455 nm during growth induced branching in the lamellae in response to the change in lamellar period (Fig. 3J). Thus, complex nanoscale structures in 3D can be produced in a continuous, designed process based on the dynamic response of the evolving film morphology to changes in the incident wavelength and polarization direction.

Fig. 3.

Effect of polarization, wavelength, and angle of the incident light on the growth of Se–Te lamellar films. (A–E) Polarization dependence under normal-incident illumination. Films grown under (A) randomly polarized, 625-nm illumination, (B) linearly polarized, 625-nm illumination with the electric field of the incident light oriented at a 45° angle to vertical, (C) same as B, but with the electric field of the incident light oriented horizontally, (D) growth under 940-nm illumination with the polarizer oriented vertically for 300 s and then horizontally for 300 s, and (E) growth under 940-nm illumination with continuous rotation of the polarization in 5° increments for a total rotation of 550°. (F–J) Wavelength dependence for normal-incident, linearly polarized light. Films grown under illumination wavelengths of (F) 365 nm, (G) 530 nm, (H) 780 nm, (I) 940 nm, and (J) 940 nm until −1.5 C/cm² charge had passed, followed by 455 nm until −1.5 C/cm² charge had passed. (K–O) Dependence on the incident angle for linearly polarized, 625-nm illumination. Films grown under illumination at an angle of (K) 0° from normal, (L) 20° from normal, (M) 40° from normal, (N) 60° from normal, and (O) +60° from normal until −0.9 C/cm² of charge had passed, followed by an angle of −60° from normal until −1.1 C/cm² of charge had passed. [Scale bar: 1 µm (applies to all images).]

Fig. 4.

Comparison of the experimentally observed wavelength dependence of the lamellar period with simulated periods produced by different scattering models. The black circles are the experimentally observed values of the period for lamellae grown under different illumination wavelengths. Each circle represents the average of 25 measurements and the error bars represent 2 SDs in the average value. The red trace is the simulated interference period due to dipole scattering at the surface of a flat Se–Te film. The blue trace is the simulated period due to Bloch mode scattering from a periodically structured Se–Te surface. The black trace is the simulated period combining both scattering modes where the contributions from the surface and Bloch modes are weighted based on the penetration depth of the incident light.

The growth direction of the lamellae changed with the angle of the incident light (Fig. 3 K–O). For example, the lamellae grew normal to the substrate under normal incident illumination (Figs. 2 D–F and 3K), whereas at an angle of 20° from normal, the lamellae appeared to tilt slightly away from the direction of the incident light. However, at more oblique angles of 40° and 60° from normal, respectively, the lamellae grew toward the illumination source. When the angle of illumination was changed from 60° to −60° during growth, some of the lamellae (54% of 200 counted) reoriented to grow toward the new direction of the incident light forming zigzag structures. However, the growth of some lamellae (46%) was stunted, consistent with the shadowing of these lamellae by their neighbors, which inhibited their growth when the incident angle was reversed. Because the growth rate of the Se–Te nanostructures was enhanced under higher illumination intensities, and because the lamellae grew toward the source of illumination, the growth of the inorganic structures can therefore be designated as phototropic, by analogy to the similar phenomenon exhibited by living plants.

The lamellar patterns produced during photoelectrodeposition of the Se–Te alloy resemble qualitatively the ripple patterns formed during LIPSS of metal and dielectric surfaces. Ripple patterns have been observed during laser-induced damage and melting of sodium chloride, silicon, germanium, gallium arsenide, aluminum, brass, as well as other dielectrics and metals (7–12), etching of platinum in a chlorine atmosphere (13), and photolytic decomposition of organometallic cadmium, zinc, aluminum, and copper precursors onto silicon (14, 15). Both processes involve the light-induced formation of a periodic profile on an initially flat surface, but LIPSS and phototropic growth of the Se–Te lamellar patterns arise from fundamentally different phenomena. Experimentally observable differences include the fact that the typical light intensities used for LIPSS are much higher than those used for phototropic growth of the Se–Te films (i.e., between 10 W/cm² and 10 MW/cm² for continuous laser irradiation during LIPSS, whereas the illumination intensities used in this manuscript were less than 50 mW/cm²). LIPSS therefore requires laser irradiation to achieve the necessary intensity, whereas we have demonstrated the formation of lamellar patterns via phototropic growth using a variety of different illumination sources, including LEDs, a halogen light bulb, as well as a low-intensity laser. The ripple patterns formed during LIPSS under normal incident laser irradiation typically run perpendicular to the electric field of the incident laser irradiation with a period of λ/n, where λ is the illumination wavelength and n is the refractive index of the medium above the surface of the substrate. In contrast, phototropic growth produced lamellar patterns that were parallel to the incident electric field with a period of λ/2n at short illumination wavelengths (i.e., <600 nm) but exhibited longer periods at longer wavelengths (Fig. 4). Additionally, phototropic growth is capable of producing structures that cannot be produced by LIPSS, such as dynamically directed growth toward the incident light beam as well as stacked woodpile structures in layers that are optically and physically weakly coupled, or largely uncoupled, from the growth substrate (Fig. 3). (In LIPSS, variations in the angle of the incident laser irradiation only affect the period and orientation of the ripple patterns.) Fundamentally, phototropic growth differs from LIPSS in that the phototropic growth is a property of the growing Se–Te film under noncoherent, low-intensity illumination, as opposed to relying on and exploiting specific optoelectronic properties, using a high-powered laser, of the substrate. Thus, the formation of the initial periodic pattern during phototropic growth, the dependence of the lamellar period and orientation on the wavelength and polarization of the incident illumination, as well as dynamic feedback between the illumination conditions and the evolving nanoscale structure require further examination.

To more fully understand the onset of phototropic pattern formation in the Se–Te material, an optical response model was constructed for a flat Se–Te film with scattering centers at its surface. Full-wave finite-difference time-domain (FDTD) simulations were performed on a 100-nm-thick Se–Te film sandwiched between a Si substrate and a medium with a refractive index of n = 1.4 (i.e., similar to that of the aqueous sulfuric acid solution used in the electrodeposition). The complex dielectric function of the Se–Te material used in the simulations was obtained by fitting spectroscopic ellipsometry data measured for a 170-nm-thick film grown in the dark (SI Appendix, Text S2 and Fig. S9). In the full-wave electromagnetic simulations, dipole radiation sources were used to simulate localized scattering of incident illumination at the surface of a Se–Te film arising from either surface roughness or electronic defects (7, 11). Interference of the scattered light from different points on the surface produced a sinusoidal modulation of the optical intensity at the film surface with a period of λ/2n. (In this model, the intensity pattern was generated by interference between multiple scattering centers, whereas in LIPSS the intensity pattern is due to interference between the incident laser irradiation and surface scattered waves arising from the specific optoelectronic properties of the substrate.) Assuming the growth profile of the Se–Te film is proportional to the intensity of the interference pattern, this scattering model for a flat Se–Te surface produced a simulated period that matched well with the experimentally observed lamellar periods for short illumination wavelengths (Fig. 4). At illumination wavelengths above 600 nm, in which the incident light penetrated more deeply into the Se–Te film, the experimental period deviated to longer values from the periods produced by this dipole scattering model. The addition of a Bloch mode component to the intensity profile arising from the periodically curved Se–Te lamellar surface produced good agreement between the experimental and simulated periods across the entire experimental wavelength range (SI Appendix, Text S3). These results suggest that, although a sinusoidal variation in the surface absorption profile may produce a periodic modulation in the local growth rate of the initially unstructured film, feedback between the evolving nanophotonic structure with the incident radiation guides the growth of the final morphology.

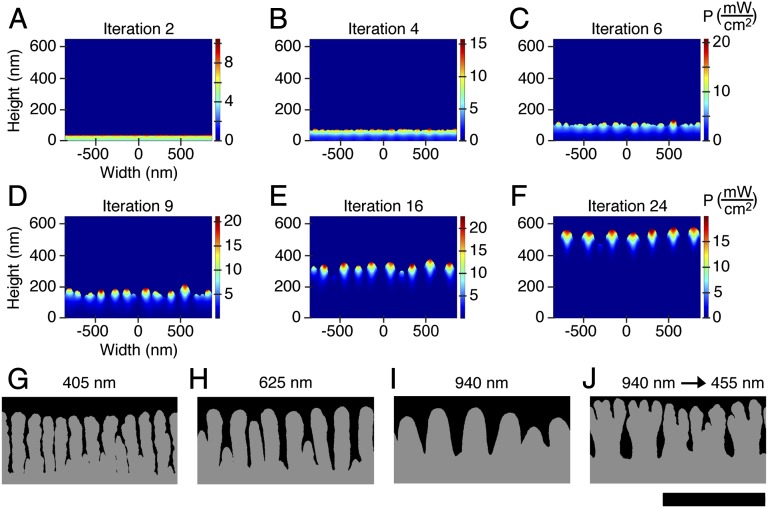
To simulate feedback between the local light intensity and the film growth, an iterative model was used in which the photocarrier generation rate calculated from electromagnetic simulations controlled the probability for mass addition in Monte Carlo simulations of the evolution of the surface. The only input parameters for these simulations were the complex dielectric functions of the Se–Te film and of the surrounding media, as well as estimates of the charge-carrier concentrations and excited-state lifetimes in the material (SI Appendix, Text S3). During the first Monte Carlo iteration, mass was added to a bare Si substrate immersed in water. The local photocarrier generation rate of this initial Se–Te surface layer was calculated under linearly polarized, plane-wave illumination. Mass was then added iteratively to the surface of the same film, with the Monte Carlo probability of mass addition to the surface taken to be proportional to an Arrhenius type of rate constant. The driving force of the rate constant was explicitly related to the local splitting of the electron and hole quasi-Fermi levels in the Se–Te film based on the local power absorbed within the film, which was recalculated for each iteration in the evolving structure. The growth model produced patterns in which the lamellar stripes were parallel to the polarization direction of incident illumination and exhibited periods under a given illumination wavelength that were remarkably similar to those observed in the experimental structures (Fig. 5 A–J).

Fig. 5.

Iterative growth model to simulate feedback between the local absorption profile and phototropic growth of the Se–Te films. (A–F) Simulated absorption profiles at different iterations of growth for Se–Te lamellar patterns under 625-nm normal-incident, plane-wave illumination with the electric field vector of the illumination perpendicular to the plane of the page. The images in A–F have been stretched vertically for clarity and have an aspect ratio of 1.8. (G–J) Simulated structures formed under different illumination wavelengths using the iterative growth model. Films grown under linearly polarized, plane-wave illumination at wavelengths of (G) 405 nm, (H) 625 nm, (I) 940 nm, and (J) in which the illumination wavelength was switched from 940 to 455 nm during the growth simulation. [Scale bar: 1 µm (applies to the images in G–J, which have an aspect ratio of 1).]

Fig. 5 A–F illustrates several stages of growth in the model. During the initial stages of simulated growth, mass was added randomly to the surface, thereby creating a flat Se–Te film with nanoscale surface roughness (Fig. 5A). This roughness, in turn, produced local variations in the photogeneration rate across the surface of the film (Fig. 5 B and C), which caused subsequent deposition preferentially in regions with enhanced absorption. At later stages of growth, the local absorption maxima became periodically spaced, producing a lamellar pattern similar to the pattern that was observed experimentally (Fig. 5 D–F). The period of the simulated structures increased with illumination wavelength and at each simulated wavelength was within 15% of the period observed experimentally (Fig. 5 G–I). Furthermore, the evolving morphology in this iterative growth model dynamically responded to the instantaneous illumination conditions. When the wavelength was changed during the simulations, the lamellae branched to adjust to the new period (Fig. 5J), also in accord with the experimental observations (Fig. 3J).

We have described an adaptive inorganic system that produces predesigned patterns in 3D space from unstructured matter, i.e., in an isotropic solution on an isotropic substrate, directed in space by the properties of a light beam as it interacts with the growing matter. This demonstration of phototropic growth does not arise from any preexisting pattern or classical interference effect in the substrate, but is an emergent phenomenon that occurs dynamically during film growth in response to the incident illumination conditions. Phototropic growth provides the ability to grow structures of entirely different geometries, periods, and directions abruptly on top of one another, and the ability to change the physical growth direction of the material by changing the direction of the incident light beam. A model in which the local optical absorption at the surface of the growing film controlled the probability for mass addition reproduced the experimentally observed nanoscale lamellar patterns and also reproduced their dependence on the wavelength and polarization of the incident illumination. This model required relatively few input parameters as it used only the complex dielectric function of the Se–Te alloy and estimates of the carrier concentration and excited-state carrier lifetimes. Other chalcogenide-based materials possess similar optoelectronic properties to those used as input parameters in the phototropic growth simulations (33–39). The extension of phototropic growth to these material systems could enable a process for dynamic photolithography in which complex 3D structures are built up through temporal variations in the illumination conditions.

Materials and Methods

The Se–Te films were electrodeposited under cathodic bias from aqueous solutions that contained selenium oxide (SeO₂), tellurium oxide (TeO₂), sulfuric acid, and cadmium sulfate (CdSO₄). The experiments were performed using a three-electrode configuration under potential control, with a SCE reference electrode and a platinum mesh counterelectrode. SI Appendix, Text S1, provides details on electrode preparation and the photoelectrochemical setup used to grow the Se–Te films. SI Appendix, Tables S1 and S2, provide the electrochemical and illumination parameters used to grow each film discussed in the manuscript. The Se–Te films were characterized by SEM, EDS, XRD, XPS, and spectroscopic ellipsometry, with details provided in SI Appendix, Text S2. Optical modeling of the Se–Te films was performed using Lumerical FDTD simulation software, and Monte Carlo growth simulations were performed in Matlab. Further details of the modeling and simulations are presented in SI Appendix, Text S3. SI Appendix, Text S4, provides a discussion of the SI figures.