High-throughput DNA sequencing errors are reduced by orders of magnitude using circle sequencing

Significance

This paper presents a library preparation method that dramatically improves the error rate associated with high-throughput DNA sequencing and is substantially more cost-effective than existing error-correction methods. In this strategy, DNA templates are circularized, copied multiple times in tandem with a rolling circle polymerase, and then sequenced on any high-throughput sequencing machine. Each read produced is computationally processed to obtain a consensus sequence of all linked copies of the original molecule. Because it efficiently reduces sequencing error, this method will be broadly enabling in projects where high-throughput sequencing is applied to detect variation in complex samples such as tumors, microbial populations, and environmental communities.

Abstract

A major limitation of high-throughput DNA sequencing is the high rate of erroneous base calls produced. For instance, Illumina sequencing machines produce errors at a rate of ∼0.1–1 × 10⁻² per base sequenced. These technologies typically produce billions of base calls per experiment, translating to millions of errors. We have developed a unique library preparation strategy, “circle sequencing,” which allows for robust downstream computational correction of these errors. In this strategy, DNA templates are circularized, copied multiple times in tandem with a rolling circle polymerase, and then sequenced on any high-throughput sequencing machine. Each read produced is computationally processed to obtain a consensus sequence of all linked copies of the original molecule. Physically linking the copies ensures that each copy is independently derived from the original molecule and allows for efficient formation of consensus sequences. The circle-sequencing protocol precedes standard library preparations and is therefore suitable for a broad range of sequencing applications. We tested our method using the Illumina MiSeq platform and obtained errors in our processed sequencing reads at a rate as low as 7.6 × 10⁻⁶ per base sequenced, dramatically improving the error rate of Illumina sequencing and putting error on par with low-throughput, but highly accurate, Sanger sequencing. Circle sequencing also had substantially higher efficiency and lower cost than existing barcode-based schemes for correcting sequencing errors.

High-throughput DNA sequencing has emerged as a revolutionary force in the study of biological systems. However, a fundamental limitation of these technologies is the high rate of incorrectly identified DNA bases in the data produced (1, 2). For instance, reports in the literature suggest that Illumina sequencing machines produce errors at a rate of ∼0.1–1 × 10⁻² per base sequenced, depending on the data-filtering scheme used (2, 3). These technologies typically produce billions of base calls per experiment, translating to millions of errors. When sequencing a genetically homogenous sample, the effects of erroneous base calls can be largely mitigated by establishing a consensus sequence from high-coverage sequencing reads. However, even high coverage does not eliminate all errors, and attempted verification of detected variants has often revealed the vast majority to be sequencing errors (for example, see refs. 4 and 5). Furthermore, the depth of coverage required for consensus building remains cost-prohibitive for large genomes such as the human genome. As a result, most human studies involving high-throughput sequencing have been limited to only a small fraction of the genetic information, such as the transcriptome, mitochondrial DNA, or a single chromosome. In contexts where rare genetic variants are sought, this error-rate problem presents an even more profound barrier. Examples of rare variant problems include the analysis of mutations in genetically heterogeneous tumors, identification of drug-resistance mutations in microbial populations, and characterizations in immunogenetics (such as B- and T-cell profiling). The mutations of interest in these types of samples may be present at low frequencies, potentially even lower than the sequencing error rate itself. Here, the problem cannot be overcome with high-sequence coverage because a consensus sequence of the heterogeneous sample will mask all variants.

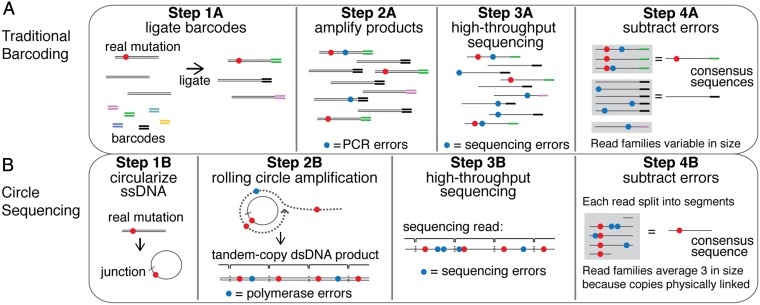
To address this error rate problem, several closely related library preparation protocols have recently been described (6–10). A general schematic for these “barcoding” strategies is shown in Fig. 1A. Each individual DNA molecule in the input material is marked by the ligation of a uniquely identifiable sequence, or barcode (step 1A). Barcoded products are then amplified by PCR (step 2A), and the amplified pool is sequenced (step 3A). Barcode identity is then used to computationally organize sequencing reads into “read families,” where each read family consists of all downstream derivatives of a single starting molecule (step 4A). A consensus sequence is then derived from the reads in each family, with a typical criterion being that the read family must contain at least three members before a consensus sequence is derived (6, 8).

Fig. 1.

Overview of traditional barcoding methods and circle sequencing. (A) In traditional barcoding methods, adapters containing randomized nucleotide regions (barcodes) are ligated to each molecule in the DNA sample (step 1A). The library is then amplified by PCR (step 2A). Products are sequenced on the high-throughput sequencing platform of choice (step 3A). Individual reads containing the same barcode are grouped into read families (gray boxes), and consensus sequences are derived (step 4A). Errors generated during PCR amplification (step 2A, blue circles) and during the sequencing process (step 3A, blue circles) are removed bioinformatically. (B) In circle sequencing, DNA is denatured and single-stranded DNA is circularized (step 1B). Random primers are annealed to circles, and Phi29 polymerase is used to perform rolling circle replication (step 2B). This polymerase has strand-displacement activity so products contain tandemly linked copies of the information in the circle. Random primers and Phi29 polymerase turn long single-stranded copies into double-stranded DNA (step 2B, lower). The tandem copies of information are sequenced using any high-throughput sequencing technology (step 3B). Here, a single long read is shown for simplicity although paired-end reads were used in this study. Each read (or paired-end read pair) is then computationally split into the individual copies of the original circle, grouped into a read family (gray box), and used to generate a consensus sequence (step 4B).

Although barcoding strategies successfully lower the sequencing error rate, these methods have both theoretical and practical limitations that affect the accuracy and cost with which consensus sequences can be produced. First, the members of a read family are not independent copies of the original molecule. Errors that arise during the early stages of PCR, known as jackpot mutations, are amplified exponentially and can appear multiple times in a read family. Second, some templates may be amplified more or less efficiently due to differences in either the barcodes or the target sequences themselves (6). This bias, along with unavoidable variance in the sampling process, results in many read families being much larger or smaller than necessary, reducing efficiency. Third, if identical barcode sequences are ligated to multiple input molecules similar in sequence, incorrect assembly of read families can occur. This issue is especially problematic when sequencing highly similar molecules such as in amplicon libraries. Finally, sequencing errors introduced into barcodes themselves contribute to inefficient formation of read families.

In theory, all of these problems could be avoided if each read family were packaged and delivered as a single molecule, bypassing the need for barcodes to construct read families. Continued advances in the read lengths of major sequencing platforms have made such an approach possible. We have developed a unique library preparation method that (i) eliminates the use of barcodes, (ii) eliminates the effects of jackpot mutations by amplifying DNA templates in a way that does not propagate errors within read families, and (iii) physically links the repeated information comprising each read family so that it comes out of the sequencing process in the optimal proportions needed for efficient error correction. We show that our method produces high-throughput sequencing data with errors at only 8–10 × 10⁻⁶ of base positions sequenced and has an efficiency that is vastly improved over existing barcoding schemes. Our library preparation method, called “circle sequencing,” fits into existing high-throughput sequencing workflows, making it immediately available for a broad range of applications.

Results

Circle Sequencing: Library Preparation.

Our library-preparation method, circle sequencing, is illustrated in Fig. 1B (a full protocol is given in SI Materials and Methods and Fig. S1). The input material for this protocol can be chromosomal DNA, cDNA, amplicons, or any other DNA. The material is size-selected (through amplicon design, shearing followed by gel purification, etc.) such that the size of each fragment averages around 1/3 the anticipated read length from the high-throughput sequencing machine being used. Double-stranded DNA fragments are denatured and the resulting single-stranded DNA is circularized (step 1B). Noncircularized products are eliminated by exonuclease digestion. Random primers are then annealed to the single-stranded circular DNA, and amplification is performed using the Phi29 polymerase. This polymerase possesses single-strand displacement activity that allows it to replicate continuously around the ligated circle, referred to as rolling circle amplification (step 2B). The random primers also anneal to the newly synthesized single-stranded product and allow it to be converted into double-stranded DNA. The resulting double-stranded DNA products (step 2B, lower) are concatamers consisting of multiple tandem copies (brackets) of the information in the original fragment. These products are sequenced (step 3B), and the information in the tandem copies is used to form a read family and a consensus sequence (step 4B). Any genetic variant that existed in the input material (red circle) will be present in all tandem copies whereas errors introduced by the Phi29 polymerase (blue circles in step 2B) or by the sequencing process (blue circles in step 3B) will occur independently and randomly throughout the template.

The rolling circle products generated in circle sequencing can theoretically be sequenced on any high-throughput sequencing platform that offers read lengths long enough to observe multiple repeats within the same product. Illumina technologies currently offer the highest throughput and cost-efficiency, with read lengths of up to 500 bases possible on the MiSeq platform using 2 × 250 paired-end reads. Our bioinformatic pipeline processes circle-sequencing data generated by paired-end reads (full protocol is given in SI Materials and Methods and Figs. S2–S5). This pipeline identifies the repeating units of the original information in each read pair. It then uses these repeats, combined with base call quality scores, to derive a consensus sequence along with a consensus quality score for each consensus base. The pipeline also maps these consensus sequences to a reference genome.

One advantage of circle sequencing is that it is largely resistant to the effects of jackpot mutations that can occur in PCR. Errors will also be made during rolling circle amplification, but will not propagate within a read family because each linked copy is independently derived from the original molecule (illustrated in Fig. S6). An upstream PCR amplification step may be required for some applications of circle sequencing (e.g., for cDNA or amplicon libraries). Circle sequencing will not be able to mitigate the effects of jackpot mutations accumulated before templates are circularized. In such cases, care should be taken to minimize amplification cycles upstream of the circle-sequencing pipeline. Alternately, circle sequencing can also be applied directly to RNA templates (11).

Error Rate of Circle Sequencing.

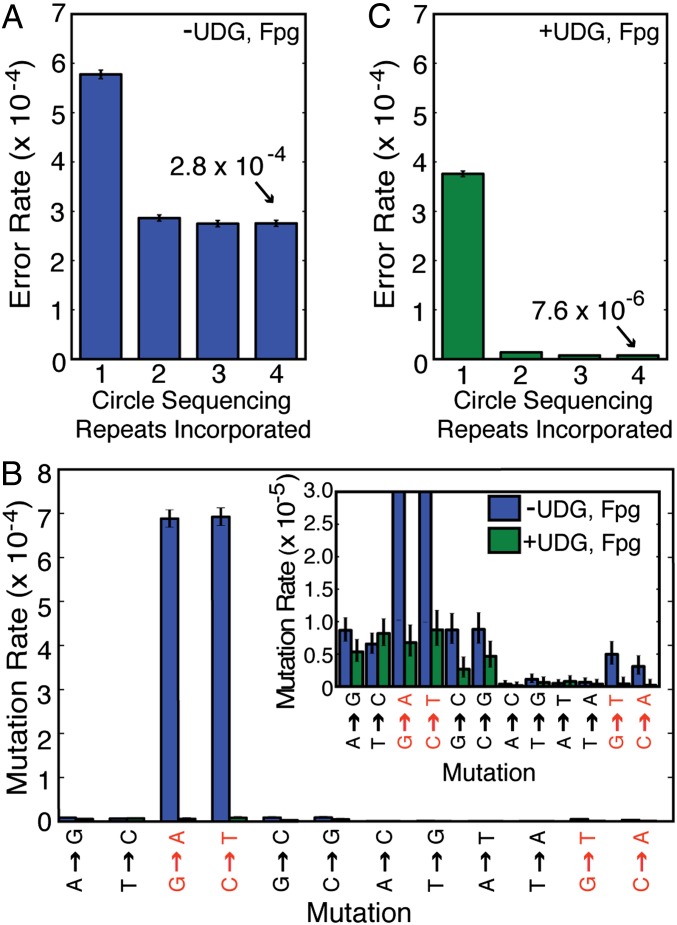
To measure the error rate of this method, we sequenced the ∼12-megabase Saccharomyces cerevisiae genome. First, we used standard Illumina MiSeq sequencing to obtain 51× coverage of a haploid S288C strain. We identified 514 positions at which there is strong evidence that the genome sequence of this strain differs from the published reference S288C sequence. Bases mapping to these questionable sites, or to repetitive sequences, were subsequently ignored throughout this study. Next, we sequenced the strain with circle sequencing and mapped the resulting consensus sequences to the reference genome. Error rates were calculated as the fraction of consensus bases that differed from the reference sequence. As a proof of concept that the circle-sequencing process is capable of eliminating sequencing errors, we calculated the error rates of consensus sequences formed by incrementally incorporating each repeat contained in each read pair. High-quality bases in the first repeat of each sequencing read had an error rate of 5.8 × 10⁻⁴ (Fig. 2A). As expected, this error rate fell as the tandem repeats were used to correct the error in the first repeat. However, the effect was surprisingly small. The inclusion of subsequent tandem copies in our reads reduced this error rate only to 2.9 × 10⁻⁴ with two repeats and 2.7 × 10⁻⁴ with three repeats (Fig. 2A). Because the circularized fragments used in the circle-sequencing pipeline are size-selected, but still vary in size according to a distribution, we recover four and sometimes more repeat units in some of the read pairs. The addition of subsequent repeats beyond three did not lower the error rate further, and the asymptotic value of the error rate achieved (2.8 × 10⁻⁴) was not as small as would be implied by the informational redundancy obtained.

Fig. 2.

Circle sequencing decreases the error rate of high-throughput sequencing. (A) Shown is the error rate of circle sequencing upon incorporation of additional copies of the tandemly duplicated information. When just the first repeat is considered, only bases with quality scores greater than or equal to 30 are used. (B) The profile of the types of errors in circle sequencing consensus sequences (blue bars) reveals a striking signature dominated by G-to-A and C-to-T errors, consistent with base damage due to cytosine deamination. The addition of uracil-DNA glycosylase and formamidopyrimidine-DNA glycosylase during rolling circle amplification (green bars) dramatically eliminates the majority of errors (in red) caused by DNA damage of the types targeted by these enzymes. The lower range is shown in more detail in the Inset. (C) As in A, the graph shows the error rate of circle sequencing upon incorporation of additional copies of the tandemly duplicated information, after the protocol was modified to include DNA repair enzymes.

One barrier to achieving lower error rates using circle sequencing could be DNA damage incurred by sequencing templates during the library preparation protocol. This damage would be especially problematic because, unlike random mutations introduced by the polymerase, a damaged base within the original circular template might be paired with the same incorrect base each time the polymerase replicates around the circle. This process would lead to the propagation of an error in all tandem copies of the circular information. These errors would then be seen as high-confidence base calls and effectively increase the overall error rate. In fact, DNA damage has been identified as a major source of error in standard barcoding-based approaches (8). To examine this possibility further, we analyzed the different types of erroneous base calls produced in circle-sequencing consensus sequences (Fig. 2B). Interestingly, we discovered that a large proportion of mismatches between the consensus sequences and the reference genome were G-to-A and C-to-T mutations. These types of mutations occur when a cytosine base undergoes spontaneous deamination to form uracil. Adenine is incorporated opposite of the uracil during synthesis of the complementary strand, propagating G-to-A and C-to-T transitions. We did not detect a substantial number of G-to-T and C-to-A mismatches indicative of oxidized guanine bases (8-oxo-guanine), the other common type of damage found to affect barcoded samples (8).

Deaminated cytosine and 8-oxo-guanine bases can be excised using the commercially available enzymes uracil-DNA glycosylase (UDG) and formamidopyrimidine-DNA glycosylase (Fpg). To test whether these specific types of damaged bases negatively affect the error rate of our method, these enzymes were included during the rolling circle amplification step. As shown in Fig. 2B, their addition almost completely eliminated damage-induced errors (green bars). We speculate that circular templates that undergo the removal of these damaged bases are precluded from serving as substrates for Phi29 polymerase. We found that treatment of genomic DNA with UDG and Fpg before proceeding with conventional MiSeq library preparation resulted in no change in the mutation profile, suggesting that this damage to DNA is actually incurred during the circle-sequencing library preparation. After modifying our protocol to include these repair enzymes, we reexamined the impact of analyzing one, two, three, and four repeats in consensus building (Fig. 2C). The inclusion of up to four repeats substantially improved the overall error rate from 2.8 × 10⁻⁴ (without enzymes) to 7.6 × 10⁻⁶ (with enzymes). Thus, the error-correcting power of circle sequencing is clear, but care must be taken to address damaged bases that arise during the preparation of these special libraries. It is interesting to note that the extent of DNA damage present in DNA mixtures, and the resultant calling of erroneous bases during downstream sequencing, is only now becoming evident due to the extremely low error rates being achieved by our and other sequencing methods (8). We anticipate that accurate, high-throughput sequencing will provide increased resolution into many types of biological phenomena.

Efficiency of Circle Sequencing and Barcoding.

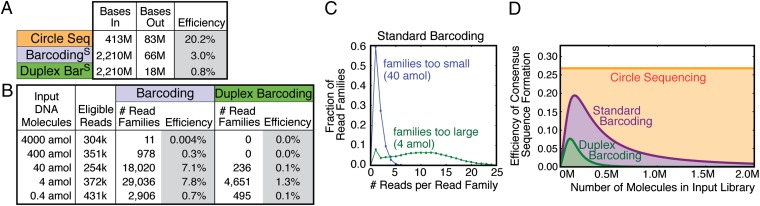
An important metric to consider when selecting an error-correction scheme (i.e., barcoding versus circle sequencing) is cost. Cost is directly related to the efficiency of these methods in turning low-quality data into high-quality data. A major determinant of the overall amount of high-quality data produced by a method is how efficiently the method distributes raw sequencing data across all of the read families produced. The existence of read families that do not contain enough members to produce a consensus, or read families that contain substantially more members than necessary, represents wasted sequencing resources. To analyze this aspect, we define efficiency as the ratio of consensus bases produced to the total number of bases used to produce them. As described above, read families must have at least three members to build consensus sequences. If all read families consist of exactly three members, a perfect efficiency of 33% would be achieved. For circle sequencing, the size of read families is dictated by the lengths of the circularized molecules. To achieve perfect efficiency of 33%, input molecules must be exactly 1/3 the read length. However, any practical size-selection scheme will produce molecules with a distribution of sizes around this desired length. This distribution, and the use of paired end reads (discussed later in this section), results in the actual achieved efficiency being slightly lower than the ideal. In agreement with this reasoning, we achieved an efficiency of 20.2% for circle sequencing (Fig. 3A). One consensus base is produced for every five bases used to build read families.

Fig. 3.

Circle sequencing forms read families more efficiently than barcoding methods. (A) The table shows key metrics of efficiency for the three approaches discussed: circle sequencing, standard barcoding, and duplex barcoding. “Bases in” refers to the total number of bases used to build read families. For the barcoding-based approaches, these are bases in well-formed, uniquely mapping reads. For circle sequencing, these are bases in reads showing clear periodicity. “Bases out” refers to consensus bases. Consensus bases are produced from read families with at least three members (at least three members derived from each strand for duplex barcoding). Efficiency is calculated as the number of consensus bases produced divided by the total number of bases used to produce them (“bases out” divided by “bases in”). Standard and duplex barcoding values (S superscript) are derived from a dataset from ref. 8, which was reanalyzed here. (B) Standard barcoding and duplex barcoding were used to sequence yeast genomic DNA. Tenfold serial dilutions of the input material were made before the library amplification step (Fig. 1A, step 2A), and an 18-cycle PCR was performed. The number of eligible reads refers to the number of reads used to build read families. Also shown are the number of read families consisting of at least three members (standard barcoding) or at least three members from each strand (duplex barcoding), and the efficiency of consensus sequence formation (ratio of read families produced to total eligible reads). (C) The distribution of sizes of read families (number of reads per read family) produced by standard barcoding with 40-attomol input (blue) and 4-attomol input (green). (D) Theoretical efficiency of consensus sequence formation from 1,000,000 sequencing reads using standard barcoding (purple), duplex barcoding (green), and circle sequencing (orange) as a function of the number of unique molecules in the input library.

For comparison, we calculated the efficiency of consensus-sequence formation with barcoding using a dataset from a previously published study by Schmitt et al. (8). This barcoded dataset, derived from the M13mp2 phage genome, produced consensus sequences with an efficiency of 3.0% (Fig. 3A). One consensus base is produced for every 33 bases analyzed. This efficiency is similar to previously reported barcoding efficiencies, which range from 1–8% (6–8). In this particular dataset, the authors used a sophisticated barcoding scheme called duplex barcoding. Here, the forward and reverse strands of each double-stranded input molecule are asymmetrically labeled with barcodes, allowing for the acquisition of either standard barcoding read families or, alternately, more elaborate read families consisting of at least three reads from each strand (i.e., at least six reads total). As would be expected because of the heightened read family criteria, duplex-barcoding consensus sequences were formed with an efficiency of only 0.8% with this dataset, substantially less than the efficiencies of either circle sequencing or standard barcoding.

For barcoding-based approaches, efficiency is dictated by the ratio of barcoded input molecules to total reads produced. If there are too many uniquely barcoded molecules relative to the number of reads produced, read families will tend to be too small for the formation of consensus sequences. Alternately, if there are too few uniquely barcoded molecules relative to the reads produced, read families will be much larger than they need to be, wasting reads. To explore this dependence further, we applied duplex barcodes to sheared yeast genomic DNA and used five different concentrations of input molecules for amplification. Each sample was amplified under identical conditions and sequenced, with the same number of total sequencing reads requested for each. We measured the efficiency with which standard barcoding and duplex barcoding consensus sequences were formed across the five datasets (Fig. 3B). For both standard and duplex barcoding, the efficiency rose, peaked, and declined within the range of library sizes used. The efficiency peaked at a very small library size of 4 attomol for both standard barcoding and duplex barcoding (7.8% and 1.3%, respectively). Although concentration of input DNA is easy to control in setting up these reactions, the optimal library size depends on both barcoding efficiency and the number of reads actually produced in the final dataset. Therefore, the initial input library size must be empirically determined for each experiment.

Next, we looked at the distribution of sizes of read families for the two dilutions producing the highest efficiency (40 and 4 attomol) (Fig. 3B). These datasets produced 18,020 and 29,036 read families with 3 or more members (Fig. 3B). In the 40-attomol library, most read families contained only one or two members (Fig. 3C). In the 4-attomol library, most read families have many more than 3 members, with the average read family size being ∼12 (Fig. 3C). These results clearly demonstrate a direct correlation between input concentration and efficient use of sequencing reads to produce consensus sequences.

To determine the precise expected relationship between input library size and efficiency beyond the five experimental points sampled, we analyzed an idealized theoretical model of the barcoding process. In this model, every barcoded input molecule is massively and uniformly amplified so that each sequencing read produced has an equal and independent chance to sample each of the original input molecules. For simplicity, we assume that exactly 1 million usable sequencing reads are always produced. The expected efficiencies of recovering input molecules at least three times for standard barcoding (Fig. 3D, purple) and recovering both strands of input molecules at least three times each for duplex barcoding (Fig. 3D, green) are plotted as a function of the number of uniquely barcoded input molecules. As discussed above, the idealized perfect efficiency for these approaches would be 33% (or half of this for duplex barcoding). However, unavoidable variance in the distribution of read-family sizes due to the random sampling process caps the efficiency of standard barcoding at 19% and duplex barcoding at 8%. Perhaps more notable is the rapid decline in efficiency observed when the number of barcoded input molecules falls outside a narrow range around these peaks. In practice, precise control over the ratio of barcoded molecules to usable sequencing reads can be difficult to achieve. For instance, inferred estimates of the fraction of input molecules that had barcodes successfully ligated to them varied by a factor of 1.7 across the experiments that we analyzed (Table S1). There is also substantial run-to-run variability in sequencing machine output and in the number of reads wasted on undesired products such as adapter dimers or ill-formed barcodes. In summary, barcoding-based efficiencies are difficult to control and capped at an absolute upper bound of 19%.

We next examined the theoretical efficiency of circle sequencing. The expected efficiency for 150-base circular templates sequenced using 2 × 250 base reads is 27% (Fig. 3D) (see SI Materials and Methods and Fig. S3 for further details of the model). This number is less than the predicted efficiency of 33% because paired end reads are used. Because rolling circle amplification products are sheared randomly and read from either end, each read from a read pair will begin at a different base position within the repeated sequence. This offset introduces some variability in the number of repeats in a read family, with not all repeats being full length (illustrated in Fig. 1, step 4B). Importantly, however, because the repeats within a read family are physically linked and do not need to be recovered from a bulk mixture by sampling, efficiency will not vary with the number of molecules in the input library. Efficiency is therefore a flat line across all input library sizes. This plot demonstrates two key features of circle sequencing: the theoretical peak efficiency is higher than for barcoding-based approaches, and this efficiency is insensitive to experimental conditions, sidestepping a major liability of barcoding-based approaches.

Although the efficiency of consensus sequence formation is critically important, a wide range of other practical issues also affects the total amount of usable data produced. We define yield as the total number of high-quality consensus bases produced divided by the raw number of sequenced bases before any filtering or data processing is performed. This metric considers the overall loss of data in a sequencing project from start to finish, including not only loss due to consensus formation, but also losses due to data filtering and trimming schemes and reads that can't be mapped uniquely to the genome being sequenced. Based on this final point, the parameter of yield will therefore be somewhat genome-specific, as repetitive information and missing regions in genome assemblies can vary from genome to genome. To quantify the cumulative impact of all of these effects on the yield of error correcting methods, we used circle sequencing to sequence a set of yeast genomic libraries that varied in input concentration and/or total reads produced, and compared the data with the set of yeast genomic libraries sequenced with barcoding. The input molecules used and the total sequencing reads obtained for each sample are summarized in Table S2.

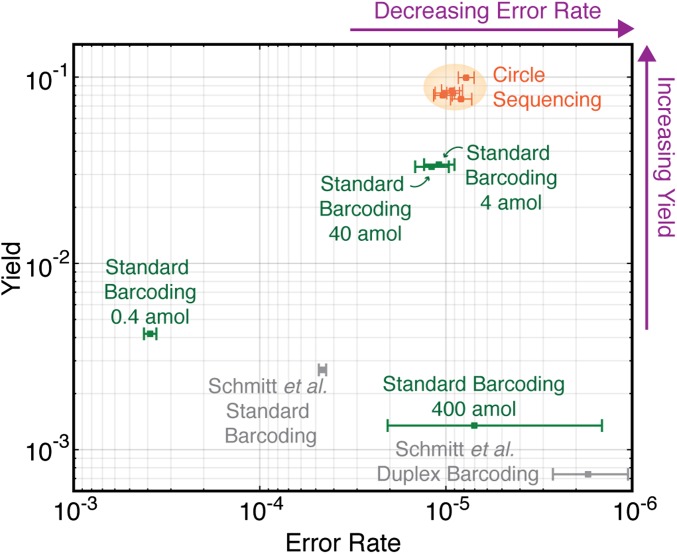
Fig. 4 shows four standard barcoding samples and five circle-sequencing samples on a plot of yield versus error rate. All five of the circle-sequencing samples, regardless of molecules in the original library or reads produced, had a yield and an error rate that clustered within a tight range (orange points). The barcoding libraries were more disperse on this plot, with the samples varying significantly in both yield and error rate (green points). Even the most efficient barcoding samples (4-attomol and 40-attomol libraries) had a yield that was only 1/3 that of the circle-sequencing samples, equating to a cost that would be three times as high for the same amount of high-quality, error-corrected data.

Fig. 4.

Comparison of overall yield and error rate for all error-correction methods. The yeast genome was sequenced with standard barcoding (green points) or circle sequencing (orange points) while varying input DNA concentration and/or reads produced. Error rate (x axis) is defined as the fraction of consensus bases that differ from the reference sequence. Yield (y axis) is the total number of consensus bases produced divided by the raw number of bases sequenced. Circle sequencing produces consistent error rates and yields across a range of experimental conditions (orange shading). Standard barcoding produces highly variable error rates and yields. Another library discussed in the text, from the M13mp2 phage genome generated in ref. 8, was also analyzed (gray points).

Although yields obtained in experiments targeting genomes of different complexities are not directly comparable for the reasons discussed above, we also include values for the barcoded M13mp2 phage genome dataset, which was produced with the Illumina HiSeq machine (8). We find that the metrics of yield and error rate are similar despite differences in the genomes sequenced and sequencing platform used (Fig. 4, gray points). The method that currently produces the lowest error rate is the duplex barcoding method of Schmitt et al. (8). However, the yield of this method is very low, with ∼1 out of 1,000 bases sequenced being recovered as a consensus base. For all sequencing projects, high yield and low error rate are desirable, and so the best methods will fall in the upper right hand corner of the plot in Fig. 4 (purple arrows). Circle sequencing produces high yield and low error rate and is highly robust to experimental design in ways that barcoding approaches are not.

Finally, we considered whether sequence-specific biases affect our library preparation, such as bias in template circularization. This bias could result in nonuniform coverage of the genome being sequenced. As might be expected, we did observe that some degree of template bias is introduced by both barcoding and circle sequencing when each is compared with standard Illumina sequencing. This effect was slightly larger for circle sequencing although the skews in coverage were not extreme in either case (Fig. S7). We also considered that some circular templates might have sequence features that lead to biased amplification during library preparation. This bias could result in many reads deriving from the same circular template. However, we found that greater than 98.8% of the consensus sequences produced in each dataset were derived from unique circular templates, and no single circular template produced more than five consensus sequences.

Discussion

Circle sequencing is a library-preparation method for high-throughput sequencing that achieves low error rate and high efficiency. Its biggest strength is that it is efficient over a range of experimental designs (input library types and reads produced). The choice of library-preparation method will ultimately be dependent on the task at hand. Standard high-throughput sequencing, combined with sufficient read depth, may still be the best choice for genome-sequencing projects. One barcoding approach, duplex barcoding, has an error rate lower than any other method because the inclusion of information from both strands of each DNA duplex helps to eliminate the effects of both jackpot mutations and damaged bases (8). Although this method is highly inefficient, duplex barcoding may be the method of choice in cases where single mutations, such as individual damaged bases in a population of DNA, must be detected (i.e., projects involving the rarest of rare variants). However, for many rare variant problems, circle sequencing would be a better choice than barcoding-based methods. Circle sequencing should be especially powerful in applications related to cancer profiling, immunogenetics, microbial diversity, and environmental sampling.

Superficially, our method appears to resemble the SMRTbell approach of Pacific Biosciences (12). This single-molecule technology also circularizes DNA and uses redundant information produced as a polymerase repeatedly traverses a circular template to reduce error. A key conceptual difference is that our method produces intermediate physical products containing multiple copies of the information in the templates. These products can then be sequenced on platforms that offer dramatically higher throughput and per-base-call accuracy than the single-molecule platform of Pacific Biosciences. We have successfully implemented our method using 2 × 150 base and 2 × 250 base reads on the Illumina MiSeq machine; in principle, appropriately sized circles could be used with 2 × 100 base reads currently available on the higher-throughput HiSeq machine. One technical point to consider in the application of our method is that circle sequencing products, because of the repetitive nature of the information contained, might be especially prone to problems in the clonal amplification that takes place on some high-throughput sequencing machines. Although we did detect this phenomenon, we estimate that the effect is small (further discussed in SI Materials and Methods and Figs. S4 and S5). Finally, as sequencing read lengths increase, it may be possible to construct circularized templates that link together both strands of double-stranded input molecules. By incorporating the key insight of Schmitt et al.'s duplex barcoding method (8), this modification could protect against errors caused by damaged bases in starting templates while retaining the efficiency advantages of circle sequencing.

Materials and Methods

Circle Sequencing.

Genomic DNA was extracted from S. cerevesiae strain S288C, sheared, run on a 1.5% low-melting-point agarose gel, and a narrow slice corresponding to 150 bp was extracted. DNA was phosphorylated and denatured. Three hundred nanograms of DNA (∼3 pmol) was circularized per 20-μL reaction using CircLigase II ssDNA ligase (EpiCentre), and uncircularized DNA was removed with exonuclease. Exonuclease-resistant random primers and varying amounts of DNA circles were annealed and added to the rolling circle reaction consisting of reaction buffer, dNTPs, BSA, inorganic pyrophosphatase, uracil-DNA glycosylase, formamidopyrimidine-DNA glycosylase, and Phi29 DNA polymerase. See SI Materials and Methods for a detailed protocol. Barcoded samples were prepared as in ref. 8.

Bioinformatic Processing.

Our computational pipeline processes circle-sequencing data generated by paired-end reads. The structure of the tandem copies within each read pair is determined by detecting periodicity in each sequence and by aligning the pair of sequences to each other. A consensus sequence is then derived from the copies produced in combination with the base quality scores assigned to each. The junction of circularization in each consensus sequence is identified by performing a rotation-insensitive mapping of the consensus sequence to a reference genome. See SI Materials and Methods for a detailed description.