Accelerated discovery via a whole-cell model

Abstract

Whole-cell modeling promises to facilitate scientific inquiry by prioritizing future experiments based on existing datasets. To test this promise, we compared simulated growth rates with new measurements for all viable single-gene disruption strains in Mycoplasma genitalium. The discrepancies between simulations and experiments led to novel model predictions about specific kinetic parameters that we subsequently validated. These findings represent the first application of whole-cell modeling to accelerate biological discovery.

As next-generation experiments yield data that is high-throughput and complex, there is an increasing need for corresponding computational methods to derive knowledge from the data. Whole-cell models that incorporate every known gene function to make predictions about integrated and complex biological phenomena may address this need. In the 1980s, bacteriologists realized that the simple Mycoplasmas might be tractable for the first comprehensive description of a cell¹, and since that time several groups have worked towards building models of various aspects of Mycoplasma genitalium, the simplest self-replicating organism^2-4. Most recently, our lab constructed a whole-cell model of M. genitalium that incorporates every known gene function to simulate a complete life cycle. The simulations generated by this highly integrated model compared favorably with published data sets including metabolic fluxes, metabolite concentrations, growth rates, and gene and protein expression⁵.

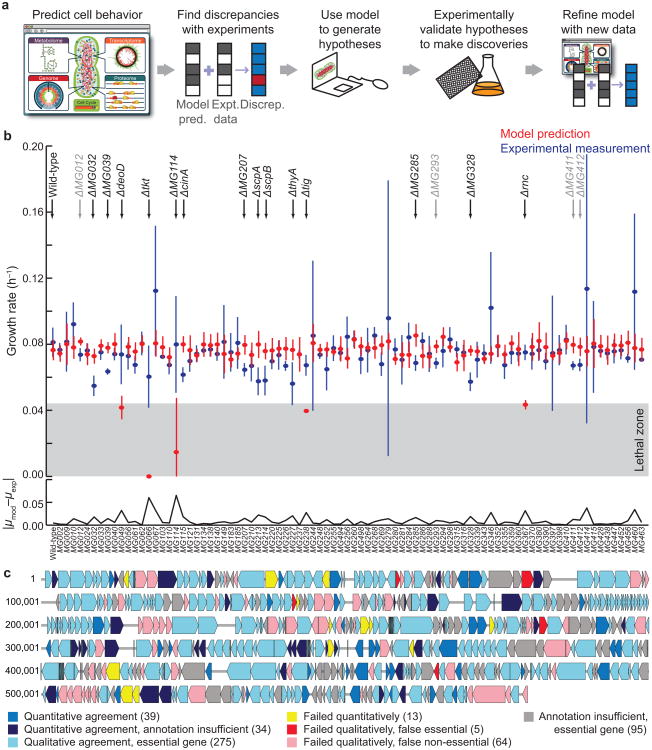
Although these comparisons represented perhaps the broadest validation of any biological model, the most exciting promise of whole-cell modeling—prediction of previously undiscovered cell biology—remains to be fulfilled. In the process of model-driven discovery, for any given complex experiment, the whole-cell model can be used to produce a corresponding simulation, resulting in two sets of data—one computational and one experimental—which can be directly compared to determine how well the model describes observations. Any discrepancy between predictions and observations represents a high-probability opportunity for novel discovery as the discrepancy is resolved, and new discoveries are incorporated back into the model (Fig. 1a).

Figure 1.

Model-driven discovery and the quantitative prediction of growth phenotypes. (a) Schematic of a model-driven discovery pipeline as facilitated by a whole-cell model. (b) Simulated (red, n = 5) and experimentally observed (blue, n = 6, technical and biological replicates) specific growth rates (μ) for 86 non-essential gene disruption strains of M. genitalium. Means ± SD are shown, and the absolute value of the difference between model and experiment is shown below on a separate axis. Eighteen genes exhibited significant (heteroskedastic two-tailed t-test and Wilcoxon rank sum test with P ≤ 0.01, listed in Supplemental Table 2) model-experiment discrepancies (top); four of these were small in magnitude (gray). The “lethal zone” indicates the five extremely slow-growing strains which the model called as non-viable. (c) A chromosome map with comparison between model predictions and experimental observations for all 525 of the M. genitalium genes.

We implemented and tested this model-driven discovery approach using our whole-cell model. We compared model predictions and experimental measurements of the specific growth rates of a non-essential single-gene disruption library of M. genitalium, for all 86 strains for which an experimental rate was determinable^5,6 (Fig. 1b). We also compared our predictions to a metabolic model based on flux-balance analysis⁷, and found that the whole-cell model made more quantitative predictions (Supplementary Fig. 1). We conclude that the presented quantitative specific growth rates and hypotheses required the use of the whole-cell model.

For 84% of the strains, the specific growth rates determined by experiment and simulation were statistically indistinguishable. However, this finding is highly tempered – although our previous analysis showed that the model was able to predict the phenotypes of all 525 gene disruption strains with high accuracy (P < 10⁻⁷)⁵, a null test applied only to the set of 86 viable strains (wherein the null hypothesis is that all viable strains grow at the wild-type rate) would yield a success rate of 94%. In other words, most of the viable strains grow at essentially wild-type growth rates, and some of these are not captured by the model.

Therefore, the greatest value of this dataset is found by considering the discrepancies between model and experiment. By combining these new quantitative measurements and predictions with the qualitative information from our previous work, we produced a detailed map of model-experiment comparisons for all 525 genes in the chromosome (Fig. 1c). This represents the most comprehensive and quantitative comparison of any large-scale cellular model's predictions to growth phenotypic data, as other studies (including our own work) either considered only a small fraction of the total non-essential genes or else made strictly qualitative (growth or no growth) predictions^5,8,9.

Scrutiny of this comparison map highlighted a small group of discrepancies, the resolution of which we hypothesized would be most likely to lead to new discoveries. The model-experiment comparisons fall into seven categories, depending on the nature of the model prediction and whether a gene's function was well-enough annotated for functional inclusion in the model (Supplementary Table 1). Two categories have the richest information content, because of the quantitative nature of the experimental measurements and detailed simulation data. The first group included 13 strains (yellow arrow in Fig. 1c) for which the model was able to predict the qualitative essentiality, but not the quantitative growth rate (p <= 0.01). The second group consisted of five of the strains for which the model failed qualitatively (red arrows), predicting a growth rate that was insufficient to sustain life (the “lethal zone” in Fig. 1b); the corresponding genes were therefore labeled as a “false essential.”

There are 18 strains in these two categories (highlighted at the top of Fig. 1b). For four of the strains, the difference in growth rate between model and experiment was small (<20%, labeled in light gray). Of the remaining 14 strains, five of the corresponding genes are associated with metabolism, two are linked to gene expression, three are involved in chromosome condensation, and the remaining four genes had little or no functional annotation (Supplementary Table 2). For each of these genes, we explored the model's inability to predict the experimental data, looking for a possible mechanism that could explain the discrepancy. A significant aspect of our strategy was to use the whole-cell model and literature to examine the “molecular pathology” of each single-gene disruption, as described in our earlier work⁵. Using this analysis, we were able to hypothesize a previously misrepresented or missing function for each of the hits for which there was a well-characterized gene annotation (Supplementary Material and Supplementary Fig. 2).

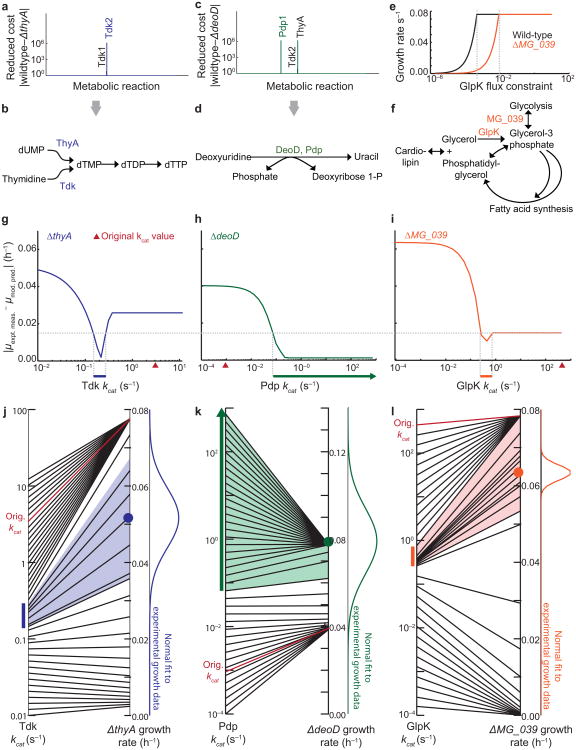
Three “hits” were of particular interest because they were the only ones for which model predictions could be tested using established methods. The three testable hits were metabolic genes: thyA (thymidylate synthase) and deoD (deoxyribose-phosphate aldolase), as previously reported⁵, and MG_039 (glycerol phosphate). For each, we identified an alternate metabolic route that could compensate for the disruption. We employed a strategy based on reduced costs, which are calculated as part of the metabolic sub-model's linear optimization method, to determine the metabolic fluxes which according to the model were limiting cell growth¹⁰. For the thyA strain, only two metabolic reactions were found by reduced cost analysis that did not also appear in the reduced cost analysis of the wild-type strain (Fig. 2a). Interestingly, both reactions were catalyzed by thymidine kinase (Tdk). ThyA and one of the Tdk reactions share a common metabolic product: dTMP, required for DNA replication (Fig. 2b). Reduced cost analysis of the deoD strain led to three candidate reactions, catalyzed by ThyA, Tdk, and pyrimidine-nucleoside phosphorylase (Pdp) (Fig. 2c). Of these, only Pdp was capable of compensating for the production of uracil by DeoD (Fig. 2d). For comparison, we performed the same reduced cost analysis using a simple FBA framework without the additional constraints imposed by the whole-cell model. The stand-alone FBA model was unable to identify notable reduced cost differences between the wild-type and disruption strains (Supplementary Table 3).

Figure 2.

The whole-cell model quantitatively predicts rate constants of metabolic reactions. (a,c) Reduced cost analysis of the metabolic fluxes in the ΔthyA (a) and ΔdeoD (c) single-gene disruption strains. Reduced costs for all of the metabolic fluxes in the model are shown, but only the notable costs are labeled. (b,d) Schematic of metabolic reactions which can compensate for those catalyzed by ThyA (b) and DeoD (d). (e) Plot indicating that constraining the flux of the GlpK reaction reduces the ΔMG_039 specific growth rate (orange) more dramatically than in the wild-type (black). (f) Reaction schematic including the MG_039 and GlpK-catalyzed reactions. (g-i) The magnitude of error between the mean model prediction (n = 6) and the mean experimental measurement (n = 5) of Tdk (g), Pdp (h), and GlpK (i) specific growth rates (μ) changes with the kinetic rates of the reactions. The cutoff for acceptable error (dashed horizontal line) for all strains was constrained by the local minimum observed in the ΔMG_039 strain. The model-predicted ranges are indicated by colored horizontal bars just below the x-axis. (j-l) The mapping of Tdk (j), Pdp (k), and GlpK (l) k_cats (at left) to model-predicted specific growth rates of ΔthyA, ΔdeoD, and ΔMG_039 (at right). The colored bars are the same k_cat ranges shown in (g-i), and the colored region indicates the range of simulated specific growth rates determined by the k_cat range. A normal fit to the experimental specific growth rate data is shown at right for comparison to simulated values, and the original estimate of the k_cat used to train the model, together with its corresponding simulated specific growth rate, is shown in red.

The reduced cost analysis for MG_039, whose product converts dihydroxyacetone phosphate to glycerol-3-phosphate, was unable to highlight compensating reactions to MG_039. We therefore adopted a different approach, reasoning that growth of the disruption strain would be more susceptible than the wild-type strain to the inhibition of any candidate enzyme which could compensate for MG_039. We searched for metabolic reactions which, if constrained in the single-gene disruption, had a stronger effect on the calculated specific growth rate than in the wild-type. Constraining glycerol kinase (GlpK) had the most pronounced difference in effect between the gene disruption strain and the wild-type, sharply reducing the specific growth rate at a flux constraint that was over ten-fold higher (Fig. 2e). Interestingly, GlpK catalyses the production of glycerol-3-phosphate from glycerol as part of a complex fatty acid synthesis network with at least three interlocking cycles (Fig. 2f). The complexity of this sub-network is the most likely reason for the failure of the reduced cost analysis.

In other words, a compensating reaction existed—and was encoded in the model—for each of the three cases, and yet the model had failed to correctly predict the specific growth rates of the corresponding strains. We hypothesized that the failure lied in the kinetic rates of the compensating enzymes. Many of the kinetic parameters required to build the original whole-cell model had not previously been measured in M. genitalium, and had to be approximated from measurements in different organisms. Among these were the parameters for Tdk, Pdp and GlpK. We therefore used the whole-cell model to determine a range for the rate of catalysis (k_cat) for Tdk, Pdp and GlpK, that would reconcile the ΔthyA, ΔdeoD, and ΔMG_039 growth phenotypes, while minimizing the effects on wild-type growth. For each strain, we plotted the absolute value of the difference between the model-predicted and experimentally observed specific growth rates, as a function of k_cat (Fig. 2g–i). We then examined all three plots together to determine a common difference cutoff between experimental and simulated specific growth rates. The cutoff that produced minimum discrepancy for all of the strains was 0.015 h⁻¹ (horizontal dashed line), which corresponds to roughly 20% of the wild-type specific growth rate.

Implementing this cutoff, we observed a single k_cat range that minimized the discrepancy between model and experiment for each enzyme (colored lines). The range for Pdp differed in that the upper limit was unbounded. We confirmed that the predicted range of k_cats mapped well to the distribution of experimental measurements of single-gene disruption strain specific growth rate (Fig. 2j–l).

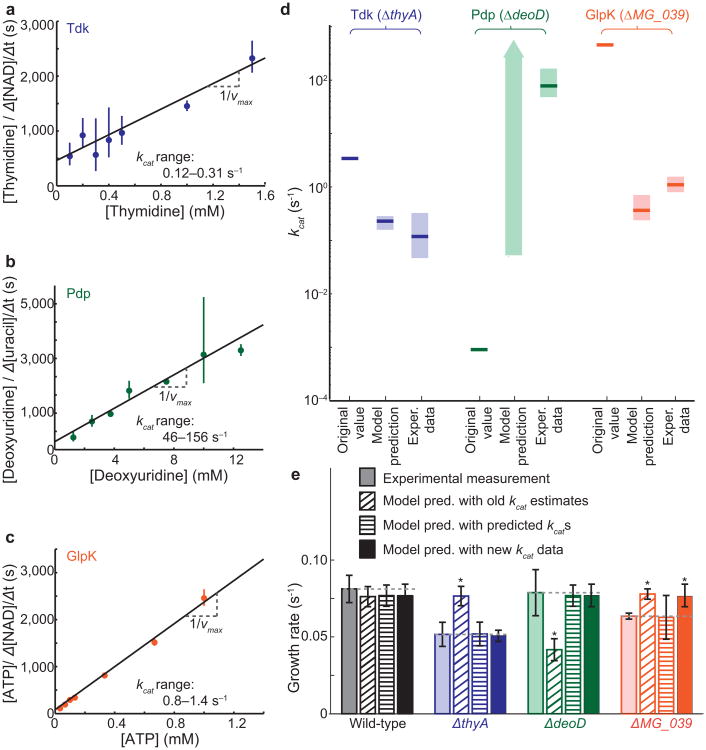
All of these ranges, calculated directly from model predictions, were experimentally testable. We expressed the M. genitalium genes in Escherichia coli, purified the proteins and performed kinetic assays as described in the Online Methods section (Fig. 3a–c and Supplementary Fig. 3). These new measured values corresponded well with the model's predictions, and differed by at least one and up to four orders of magnitude from the values originally used to train the model (Fig. 3d). These results indicate that our model has the ability to make accurate quantitative predictions about previously unmeasured cellular properties.

Figure 3.

Experimental validation of model predictions, and model-driven discovery. (a-c) Hanes-Woolf plots of kinetic assays to measure the v_max of Tdk (a), Pdp (b), and GlpK (c). Error bars represent mean ± SD of three technical replicates per substrate concentration. Linear regression was used to obtain a v_max; k_cat (99% confidence interval indicated on plot) was calculated from the enzyme concentration and v_max. (d) Comparison of k_cat values used to train the model (“Original k_cats” which were estimated from other organisms and not previously measured in M. genitalium⁵), with novel model-based predictions (Fig. 2g–i) and subsequent experimental measurements (Fig. 3a–c). (e) Predicted and measured k_cats were input into the whole-cell model (n = 6) and compared to the experimentally measured specific growth rates and model predictions with original k_cats. P-values were determined by two-tailed t-test, P ≤ 0.01.

As a final step in the discovery process (Fig. 1a), we incorporated all of the newly-determined experimental parameters into the whole-cell model to test whether interactions between these parameters existed which might make the resulting model less predictive than expected. The new parameters led to better predictions of all strains of interest without compromising predictions of the wild-type or other single gene-disruption strains (t-test between model and experimental results, cutoff P ≤ 0.01) (Fig. 3e).

Interestingly, the MG_039 single-gene disruption strain predictions made with the computationally-derived k_cat were more accurate than those made with the experimentally determined k_cat. One reason for this could be that the model prediction for the enzyme concentration, which is multiplied by the k_cat to determine the upper bound on the flux, is incorrect. However, we compared our model predictions for number of proteins per cell with measurements made in the closely-related Mycoplasma pneumoniae by Maier et al.¹¹, and found that the ranges of measured and predicted protein count for all three enzymes are roughly consistent with each other (Supplementary Fig. 4). Another possibility is that GlpK is not the only or most significant flux-limiting enzyme, as calculated. Finally, the whole-cell model calculates the maximal rate of an enzyme as a simple product of the enzyme concentration and k_cat, but in vivo many other parameters and variables, from the substrate concentration and K_m to the limits imposed by allosteric regulation and the like. One can demonstrate that a limiting concentration of intracellular glycerol would be sufficient to reduce the GlpK flux bound to the model-predicted values (Supplementary Fig. 5), and we believe that a better understanding and representation of these other processes in the whole cell model would also increase its predictive power.

In summary, our whole-cell model accurately predicted multiple kinetic parameters based on single-gene disruption strain growth phenotypes. While encouraging, our findings represent only three instances of validation, so more work will be necessary to definitively establish the model's capacity to predict molecular properties. Nevertheless, we were surprised that such detailed, molecular-level predictions could be made based on phenotypic measurements of cellular populations. Such predictions would be impossible without a comprehensive, whole-cell model that explicitly represents both molecular and cellular scales. Overall, these findings represent the first application of whole-cell modeling to accelerate biological discovery.

Online Methods

Single-Gene Disruption Strain Simulations and Growth Assays

M. genitalium single-gene disruption and wild-type strains were obtained from JCVI⁶. Specific growth rates were determined according to the colorimetric protocol described in Karr et al⁵. Simulations were performed as described in Karr et al⁵. Simulation results can be found at SimTK (https://simtk.org/home/wholecell). Simulated cells were modeled in an environment based on Spiroplasma 4 media. At least six experimental replicates and five simulations were run for each disruption strain.

Protein Expression

M. genitalium tdk, pdp, and glpK genes were synthesized by GenScript with E. coli codon optimization. Genes were inserted into pGEX-6P-1 glutathione S-transferase (GST) expression vectors (GE Healthcare) by Gibson assembly¹², and sequence-verified. Resulting vectors were expressed in DH5α E. coli cells. Cells were lysed by sonication, and GST-tagged proteins were pulled-down using glutathione sepharose beads (GE Healthcare). Proteins were cleaved from the beads by PreScission Protease (GE Healthcare), and quantified against a BSA standard by SDS-electrophoresis (Supplementary Fig. 3a–c). Final concentrations: Tdk 1.3 mg ml⁻¹, Pdp 0.2 mg ml⁻¹, GlpK 0.14 mg ml⁻¹.

Kinetic Assays

Tdk activity was measured using a spectrophotometric assay similar to that described in Schelling et al¹³.

Reaction schema:

thymidine + ATP ↔ dTMP + ADP + H+	(catalyzed by Tdk)
ADP + phosphoenolpyruvate + H+ ↔ pyruvate + ATP	(catalyzed by pyruvate kinase)
pyruvate + NADH + H+ ↔ lactate + NAD+	(catalyzed by lactate dehydrogenase)

In a 75 μl reaction volume we added: 0.05 M Tris pH 7.2, 1 mM Dithiothreitol, 2.5 mM MgCl₂, 5mM ATP, 0.18 mM NADH, 0.21 mM phosphoenolpyruvate, 2.4 μg pyruvate kinase, and 1.5 μg lactate dehydrogenase in H₂O (Sigma). Pyruvate kinase and lactate dehrdrogenase were added in excess such that they were not rate limiting (Supplementary Fig. 3e). Thymidine concentrations varied between 0.1 and 1.5 mM, and each reaction consisted of 13 μg of Tdk. Reactions were performed in triplicate. We measured the loss of NADH by A340 measurement at 37°C at 30 s intervals for 10-30 min.

GlpK activity was measured using a spectrophotometric assay similar to that described in Lester et al¹⁴.

Reaction schema:

glycerol + ATP ↔ ADP + glycerol-3-phosphate	(catalyzed by GlpK)
ADP + phosphoenolpyruvate + H+ ↔ pyruvate + ATP	(catalyzed by pyruvate kinase)
Pyruvate + NADH + H+ ↔ lactate + NAD+	(catalyzed by lactate dehydrogenase)

In a 75 μl reaction volume we added: 0.05 M Tris pH 7.2, 3.33 mM glycerol, 0.1 M KCl, 5.25 mM phosphoenolpyruvate, 2.5 mM MgSO₄, 0.2 mM NADH, 2.25 μg pyruvate kinase, 1.125 μg lactate dehydrogenase in H₂O (Sigma). Pyruvate kinase and lactate dehrdrogenase were added in excess such that they were not rate limiting (Supplementary Fig. 3f). ATP concentrations varied between 0.033 and 1 mM, and each reaction consisted of 1.8 μg of GlpK. Reactions were performed in triplicate. We measured the loss of NADH by A340 measurement at 37°C at 30 s intervals for 10-30 min.

Pdp activity was measured using a spectrophotometric assay similar to that described in Leer et al¹⁵.

Reaction schema:

deoxyuridine + phosphate ↔ deoxyribose-1-phosphate + uracil (catalyzed by Pdp)

In a 400 μl reaction volume we added: 10 mM Tris pH 7.3, 10mM phosphate pH7.3, 1 mM EDTA in H₂O. Deoxyuridine (Sigma) concentrations varied between 1.25 and 12.5 mM. Each reaction consisted of 1μg of Pdp and was conducted at 37°C for 9 min. At 45 s intervals, we added 70 μl of 0.5 M NaOH to 30 μl of reaction mix to stop the reaction. We determined uracil production by A290.

Blank controls were performed for all reactions with H₂O instead of enzyme. NADH and uracil concentrations were determined from A340 and A290 measurements respectively using NADH and uracil standard curves. The maximal slope of each reaction curve was used to determine its velocity, and Hanes-Woolf plots were used to determine the v_max and k_cat (Fig. 3a–c). Hanes-Woolf results were compared to Michaelis-Menten non-linear regression results (Supplementary Fig. 3g–h). Both methods yielded comparable results.

Comparison of experimental data and model predictions

The following statistical measures were taken in analyzing the results of Figure 1b and Figure 3e: at least six replicates were performed for each gene disruption specific growth rate measurement, and 15 replicates were performed for the wild-type. At least five simulations were run for each model prediction, and 128 simulations were run for the wild-type. A heteroskedastic two-tailed t-test was performed between each set of experimental measurements and model predictions. We considered experimental and model results to be significantly different if P ≤ 0.01. Due to the small sample size, we wanted to be sure that our results were not biased by the distributions of the data or by extreme outliers. We performed a non-parametric Wilcoxon rank sum test (also with cutoff p ≤ 0.01), which identified the same set of gene “hits”. Finally, from the list of genes with p ≤ 0.01 (18 genes), we only considered those that were over or underpredicted by at least 20% (14 genes).

Linear regression of kinetic assay data

The following statistical measures were taken in computing the results of Figure 3a–c: kinetic reactions were performed in triplicate for seven substrate concentrations for each enzyme. A linear regression was fit to the data, and 99% confidence intervals were determined using the standard error of the slope and a t-distribution obtained using α = 0.01 and degrees of freedom = n − 2 = 19.

Enzyme Quantification and k_cat range calculations

Isolated enzymes were quantified on a SDS-electrophoresis gel against known quantities of BSA. Band volumes were quantified using Quantity One v.4.6.9 software (intensity × area). Linear regressions of the BSA standard curve were used to determine the isolated enzyme concentration. 95% confidence intervals of the linear regressions were determined using the standard errors of the slope and intercept and t-distributions obtained using α = 0.05 and degrees of freedom = n − 2 (Supplementary Fig. 3a–c). The lower enzyme concentration bound and upper v_max bound for each enzyme was used to calculate the upper bound of the k_cat, and the upper enzyme concentration bound and lower v_max bound for each enzyme was used to calculate the lower bound of the k_cat (Supplementary Fig. 3d).

The final values of k_cat used to constrain the whole-cell model were, for predicted values, Tdk = 0.215 s⁻¹, Pdp = 0.5 s⁻¹, and GlpK = 0.46 s⁻¹. For measured values, the k_cats used were Tdk = 0.215 s⁻¹, Pdp = 78.1 s⁻¹ and GlpK = 0.80 s⁻¹ (Fig. 3e). The k_cats were input into the whole-cell model and compared to the experimentally measured specific growth rates and model predictions with original k_cats. P-values were determined by two-tailed t-test, P ≤ 0.01.

Flux Balance Analysis

Flux balance analysis (FBA), has been used to make predictions of cellular growth rates based on a given metabolic network and environmental conditions⁷. However, other studies have noted the difficulty in quantitatively predicting the short-term effects of gene deletion on cell growth using FBA¹⁶. To test FBA's ability to make quantitative predictions of single-gene disruption phenotypes for the M. genitalium metabolic network, we performed a single-gene disruption phenotype analysis of the metabolic genes in the same data set using FBA. We found that these predictions fell into only two categories: either zero or essentially wild-type specific growth rates (Supplementary Fig. 1a). In contrast, the whole-cell model predictions included specific growth rates across the range of zero to 115% of wild-type (Supplementary Fig. 1b).

The distribution was more descriptive than FBA, even in the case where only metabolic genes were considered. This most likely stems from two causes: first, the variation near to the wild-type specific growth rate arises predominantly from the stochastic aspects of the whole-cell model; and second, predicted specific growth rates more distant from the wild-type are due to the substantial constraints on the whole-cell model's metabolic network. Specifically, the metabolic module of the whole-cell model is solved using a similar linear optimization strategy to FBA, but with 63% of the catalysis reactions constrained by rate parameters, as opposed to none of the catalysis reactions typically being constrained in FBA studies^2,5. The tight, detailed constraints on almost every metabolic reaction in the whole-cell model arise from a combination of many cellular processes in the whole-cell framework including transcription, tRNA aminoacylation, translation, protein processing and modification, protein translocation and folding, and macromolecular complexation. Previous studies have shown that the addition of novel constraints to FBA improves predictive ability⁸, and our comparison underscores that such constraints may be essential to make accurate quantitative predictions about cellular growth rates. We conclude that the quantitative specific growth rates and hypotheses presented here required the use of the whole-cell model and would not have been achieved by FBA alone.