Abstract
Recent years, although great efforts have been made to improve its performance, few Histogram equalization (HE) methods take human visual perception (HVP) into account explicitly. The human visual system (HVS) is more sensitive to edges than brightness. This paper proposes to take use of this nature intuitively and develops a perceptual contrast enhancement approach with dynamic range adjustment through histogram modification. The use of perceptual contrast connects the image enhancement problem with the HVS. To pre-condition the input image before the HE procedure is implemented, a perceptual contrast map (PCM) is constructed based on the modified Difference of Gaussian (DOG) algorithm. As a result, the contrast of the image is sharpened and high frequency noise is suppressed. A modified Clipped Histogram Equalization (CHE) is also developed which improves visual quality by automatically detecting the dynamic range of the image with improved perceptual contrast. Experimental results show that the new HE algorithm outperforms several state-of-the-art algorithms in improving perceptual contrast and enhancing details. In addition, the new algorithm is simple to implement, making it suitable for real-time applications.
Keywords: Clipped histogram equalization, Difference of Gaussian, Human visual system, Image enhancement, Perceptual contrast
1. Introduction
In many forms of imaging devices, the quality of images and videos is often affected by a variety of factors including distortion and noise produced by the imaging device, lack of experience in taking images/videos by the operator, and adverse environmental conditions, such as unfavorable illumination. As a result, the captured images or videos may not reveal sufficient details of the true scene and, even worse, may contain artifacts such as washed-outs and unnatural appearances. In these cases, contrast enhancement techniques are useful to produce more visually-pleasing and informative images. Histogram Equalization (HE) is an effective contrast enhancement method with a low computational cost [1]. However, due to problems of brightness variation, washed-out details and over-enhancement, in practice, the standard HE is not usually applied to images directly. Variations of the standard HE algorithm, which can be roughly classified into three classes, have been developed for practical applications.
The first class of HE algorithms focuses on preserving the input brightness. Input histogram is separated into two or more sections before histogram equalization is applied to each section or the target histogram is found before histogram projection. Among these algorithms, the brightness preserving bi-histogram equalization (BBHE) [2] and the dualistic sub-image histogram equalization(DSIHE) [3]divide the input histogram into two parts based on, respectively, the mean (XM) of all intensity values in the input image and the gray level (XE) at which the cumulative probability is equal to 0.5. The mean intensity (brightness) of the output image falls at 0.5(XM + XG) for the BBHE or 0.5(XE + XG) for the DSIHE, where XG is the middle gray level (e.g., XG = 128 for images with 256 gray levels). Similarly, the recursive mean-separate histogram equalization (RMSHE) [4] and the recursive sub-image histogram equalization (RSIHE) [5], respectively, adopt the separations of BBHE and DSIHE recursively to allow scalable brightness preservation. The Brute iteration scheme is used by the minimum mean brightness error bi-histogram equalization (MMBEBHE) [6] to obtain a threshold of gray level which yields the minimum absolute mean brightness error (AMBE). The multipeak histogram equalization with brightness preserving (MPHEBP) [7] applies equalization process separately to each peak of the input histogram. The dynamic histogram equalization (DHE) [8] partitions the input histogram before assigning a new dynamic range for each sub-histogram. Extended from the DHE, the brightness preserving dynamic histogram equalization (BPDHE) [9] improves performance by brightness normalization. The brightness preserving histogram equalization with the maximum entropy (BPHEME) [10] uses a variational approach to find the target histogram which yields output image with the maximum Entropy. Recently, the range limited bi-histogram equalization (RLBHE) [11] was developed. This algorithm adopts Otsus method to obtain an optimal threshold which divides the input histogram into target and background regions. These two regions are then equalized separately so that the contrasts of target and background can both be improved effectively satisfying different criteria. Although brightness can be preserved by those algorithms to avoid over-enhancement, image contrast is poorly enhanced.
The second class of HE algorithms performs equalization on input image locally to improve contrast. The non-overlapped block histogram equalization (NOBHE) [1] divides input image into non-overlapped blocks and performs HE in each block. In order to reduce the blocking artifacts produced by NOBHE, the block overlapped histogram equalization (BOHE) [1] uses overlapped blocks by sliding a window one pixel at a time, which is computationally complex. To speed up computation, the partially overlapped sub-block histogram equalization (POSHE) [12] employs a tradeoff between NOBHE and BOHE. Recently, the non-overlapped sub-block local histogram projection (NOSHP) [13] and multiple layers block overlapped histogram equalization (MLBOHE) [14] algorithms were developed based on the concept of local processing. Although these algorithms can improve local contrast significantly, they often result in local over-enhancement and noise amplification.
The third class of HE algorithms is based on histogram modification to realize contrast improvement without over-enhancement. Manipulation of histogram changes the density function which determines the final dynamic distribution, and thus can improve contrasts in specified dynamic ranges. In addition, they can control the amplification of noise and the enhancement rate by sacrificing a certain amount of contrast. This class includes algorithms such as contrast limited adaptive histogram equalization (CLAHE) [15], histogram equalization with bin underflow and bin overflow (BUBOHE) [16], weighted and thresholded histogram equalization (WTHE) [17], gain-controllable clipped histogram equalization (GC-CHE) [18], and bi-histogram equalization with a plateau level (BHEPL) [19]. Among these algorithms, the CLAHE processes image locally. As a result, the output image may contain unnatural artifacts which are unexpected. The BUBOHE, WTHE, and GC-CHE modify the input histogram using preset parameters. The BHEPL requires no user input; however, it omits the important redistribution process in order to simplify computation.
For performance assessment, the above mentioned HE algorithms usually use the AMBE and the entropy. However, it is found that these two measures which are conducted on image globally may not correspond to a visually-pleasing look of the output image because their results are often poorly correlated to human visual perception (HVP) [20]. In addition, over-enhancement and noise amplification affect local regions of the image differently. Therefore, their effects should be considered locally when an algorithm is designed to enhance image contrast.
In the biological visual system, regardless of the often tremendous range of brightness variation over the day or from place to place, the human visual system (HVS) can perceive objects effectively. One of the primary reasons is that the HVS is more sensitive to edges than brightness [21]. Therefore, in order to improve correlation to the HVS, edge sharpness is often more crucial than brightness enhancement which may causes over-enhancement and noise amplification. Recently, the adaptive height-modified histogram equalization (AHMHE) [22] was developed which upgrades the sharpness of the backlight image for perception by emphasizing edges. It has low computation cost and gives vivid color image. However, frequently, the perceptual contrast is insufficiently represented and some bright regions in image are washed-out [22].
In this paper, motivated by the measure of perceptual contrast [23] [24], a new algorithm for perceptual contrast enhancement with dynamic range adjustment is presented. It is able to enhance the perceptual contrast effectively while avoiding over-enhancement and noise amplification. First, a perceptual contrast map (PCM) is constructed using a modified Difference of Gaussian (DOG) algorithm. The PCM is multiplied with the input image producing a pre-conditioned input for HE to improve perceptual contrast and suppressing high frequency noise in smooth regions. Then, a modified clipped histogram equalization (CHE) is proposed so that details in both dark and bright regions can be revealed without over-enhancement. Our algorithm is applicable to both grayscale and color images. Although it requires several parameters, their default values provide acceptable performance as shown in our experiments. Our tests indicate that the modified CHE is computationally efficient, with only about 30% of the cost required by CLAHE. The efficiency of our algorithm can be further improved because much of the current computing time is utilized for perceptual contrast sharpening using non-optimized Gaussian convolution. After optimizing this convolution, our algorithm may become suitable for real-time applications.
This paper is organized as follows. Section II briefly highlights the DOG and HE concepts related to this study. Section III presents the new HE algorithm in detail. Section IV describes our experimental results. Finally, conclusion is given in Section V.
2. Related concepts
This section briefly highlights the concepts of the perceptual contrast measure based on modified DOG and the histogram modification.
2.1. DOG based perceptual contrast measure [23][24]
The conventional DOG model describes the response of a retinal ganglion cell or a lateral geniculate nucleus neuron as the difference of luminance between a central component and a surrounding component:
| (1) |
where, Rc(x, y) and Rs(x, y) are the central and surrounding components respectively with the midpoint of the receptive-field being at (x, y) of the input image.
Tadmor and Tolhurst [23] conducted analysis of perceptual contrast on the modified DOG model and proposed a division formula for light adaptation in order to make the output of the DOG model dependent on contrast. One scheme is to use the surrounding component of the receptive field as the divisor. The contrast output is thus defined by
| (2) |
.
Motivated by the work presented in [23] and [24], we proposes to use the measure of perceptual contrast, the modified DOG model, as an indication of details need to be enhanced for the input image. Besides, the modified DOG model functions like a band-filter as analyzed in Section III, thus its behavior can be adjusted for properly measuring the desired contrast information.
2.2. Histogram modification [1]
For intensity x of a given image X with dynamic range [X0, XL−1], the probability density function p(x) is defined as
| (3) |
where nx is the number of occurrence of intensity x in the image, N is the total number of pixels in the image. Then, the cumulative density function, c(x), and the final transfer function, f(x), are defined respectively by
| (4) |
| (5) |
.
Then, the output image, Y = {Y (i, j)}, can be expressed as
| (6) |
The c(x) and p(x) are related by
| (7) |
Equation (7) indicates that, by modifying p(x), the shape of c(x) and the rate of enhancement can be controlled. This represents a fundamental concept utilized in the third class of HE algorithms overviewed in Section I.
3. The proposed method
The flow diagram of the new HE algorithm is shown in Fig. 1. The modified DOG model described in Section II is adopted to measure perceptual contrast of the input image. The result is utilized to generate a PCM. Then, the product of the PCM and the input image is computed. Finally, a modified CHE adjusts the dynamic range of the output image.
Fig. 1.
Flow diagram of the proposed method.
3.1. Perceptual contrast sharpening
As mentioned previously, the HVS is more sensitive to edges than brightness. Consequently, edges should be emphasized when an algorithm is designed to improve perception. However, edges normally belong to high frequency components of an image. An overall enhancement on high frequency components often amplifies noise in smooth regions, which is not desirable. Thus, we propose a PCM based on the modified DOG model to extract edge contents in the input image for enhancement. As the DOG model functions as a band-pass filter, the amplitude of the PCM represents the strength of information in the frequency band of interest. Hence, by optimizing the choices of parameters, it becomes feasible to construct a PCM that highlights perceptually important local edges while suppressing high frequency noise in smooth regions.
In order to construct the PCM, the central component (in a (2rc + 1) × (2rc + 1) central mask) and the surrounding component (in a (2rs + 1) × (2rs + 1) surrounding mask) defined previously in (1) are computed by
| (8) |
| (9) |
where I(x, y) is the input image, and Center(x, y) and Surround(x, y) are two Gaussian functions:
| (10) |
| (11) |
Note that, for more flexible mask sizes determined by rc and rs, (10) and (11) are defined differently from those of Tadmor and Tolhurst [23] where mask sizes used are (6rc + 1) × (6rc + 1) and (6rs + 1) × (6rs + 1).
The PCM is defined using the ratio form, i.e.
| (12) |
.
After the PCM is computed, the input image is pre-conditioned by
| (13) |
.
The ratio form of (12) allows a control of DOG output by the mean luminance of the surrounding component of the receptive field. In other words, because the DOG is scaled by the mean luminance, the contrast output becomes independent from the luminance. As a result, the contrast information in both dark and bright regions can be extracted. Besides this scaling property, the relative DOG model in (12) has another important property as a normalized band-pass filter with two cut-off frequencies determined by rc (high-pass cut off) and rs (low pass cut-off) (rc < rs). Different settings of rc and rs result in different emphasis in perceptual contrast. rc enables the suppression of the high frequency noise while preserving perceptual edges. A large rc eliminates more noise, but some perceptual edges are also eliminated. rs helps the compensation of low frequency luminance variation thus emphasizing image contrast, but an excessively large rs may result in unnatural appearances because of the effect of “flat gray”.
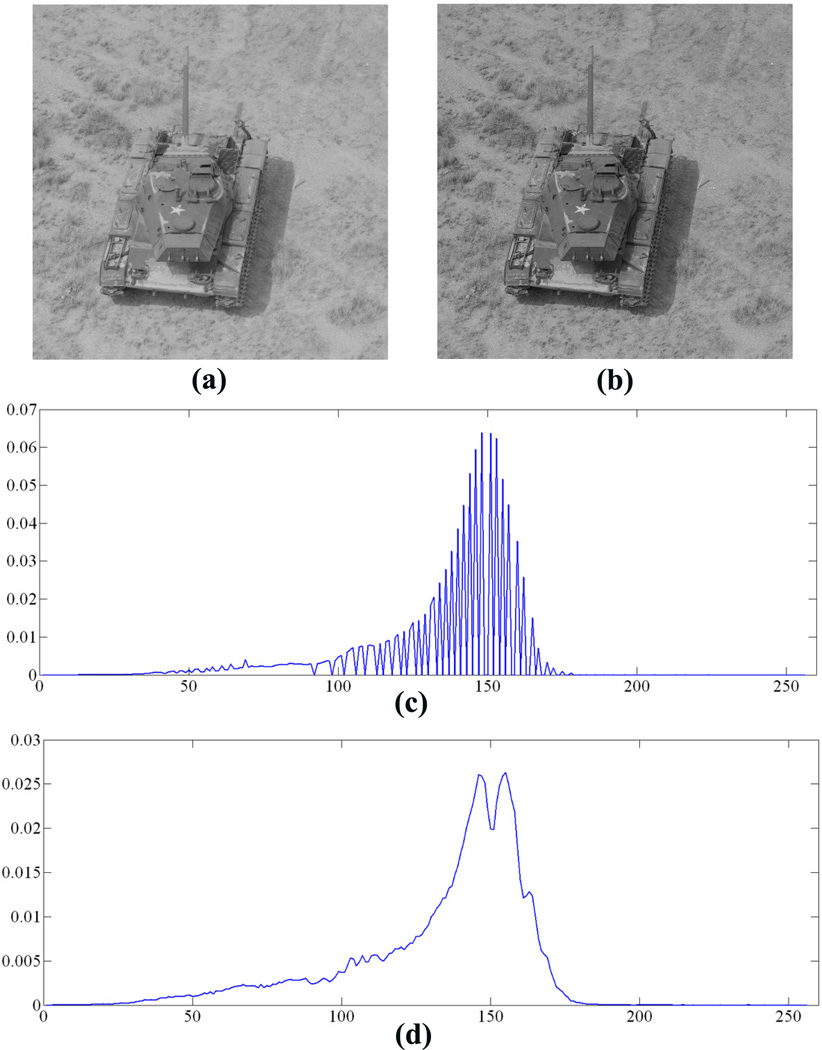
With suitable choices of rc and rs values (to be discussed later), the pre-conditioned image S(x, y) preserves perceptual contrast while suppressing noise in smooth areas. In addition, the empty histogram bins, if any, are likely filled by (13). Fig. 2 illustrates the effect of perceptual contrast sharpening. When compared to the original image (a), the pre-conditioned image (b) has sharper edges, even in shadow regions. The histograms in (c) and (d) indicate that the empty bins in the input histogram are filled and small fluctuations (especially those in dark and bright gray levels which are likely caused by high-frequency noise) are suppressed. Therefore, the preconditioned image has desirable properties of enhancing perceptual contrast and controlling noise.
Fig. 2.
F(a) Original image. (b) Pre-conditioned image by Eq. 13. (c) Histogram of (a). (d) Histogram of (b).
3.2. Dynamic range adjustment
Because the calculation in (12) and (13) may result in an overflow beyond the dynamic range [X0, XL−1] in S, before the subsequent dynamic range adjustment, S is normalized by
| (14) |
where Smax and Smin are respectively the maximum and minimum values of S(x, y).
A modified CHE is proposed here for dynamic range adjustment. Assuming that the noise is nearly white, i.e., the noise is distributed in roughly equal amounts in different histogram bins. Then, the bins with large/small values most likely represent useful information/high frequency noise. Based on this concept, the purpose of histogram modification is to reveal the details in both dark and bright regions of the input image by detecting useful information as follows. For regions in the input image with a narrow dynamic range, large values are assigned in the output histogram bins because more details are there to be emphasized. In contrast, for regions with a wide dynamic range, small values are assigned in the output histogram bins because a less enhancement is desirable in this case to avoid amplifying high frequency noise.
Fig. 3 illustrates an example where the dark region (far left on the x-axis in Fig. 3(a)) occupies a narrower dynamic range compared to the bright region (far-right), so the dark regions is enhanced more for revealing hidden details. On the other hand, the bright region is less enhanced to reduce the effect of noise amplification (Fig. 3(d)). With such dynamic range adjustment, detail enhancement and noise suppression for dark and bright regions can be balanced rationally.
Fig. 3.
Conceptual illustration of the modified CHE. (a) Input histogram of the pre-conditioned signal S and dynamic range detection for dark and bright regions. (b) Setting of the clipping threshold. (c) Histogram Clipping based on the clipping threshold. (d) Clipped portion is redistributed back to the dark and bright regions according to the dynamic ranges detected in (a).
Specifically, given the histogram of the corrected image, hs(x), its maximum, hmax, is found (Fig. 3(b)). The bounders of dark and bright regions, gd and gb, detected using the probability function, ps(x), are defined by
| (15) |
| (16) |
where T is an empirical parameter (to be discussed further at the end of this section) which determines the amount of perceptual contrast expected to be enhanced for dark and bright regions.
The dynamic range of the intermediate region, dr, (Fig. 3(b)) is defined as
| (17) |
Combining with hmax, the clipping threshold, Tc, is determined by
| (18) |
.
Then, as shown in Fig. 3(c), the clipped histogram, hc(x), is
| (19) |
where hs(x) is the input histogram.
The total clipped portion, totalE, is then accumulated with
| (20) |
.
As shown in Fig. 3(d), being inversely proportional to the respectively occupied dynamic range detected by (15) and (16), the totalE is redistributed into two parts for dark and bright regions as defined in (21) and (22).
| (21) |
| (22) |
.
Then, the final histogram, hfinal(x), is expressed in (23).
| (23) |
where:
| (24) |
| (25) |
.
Ultimately, the standard HE described in Section II is applied to map the pre-conditioned and normalized signal Snor into the entire dynamic range, [X0, XL−1].
When compared to other CHE methods, our method has two improvements. First, the clipping threshold is determined by the dynamic range distribution according to (18). Second, the result of clipping is redistributed to only the dark and bright regions with amounts inversely proportional to their respective dynamic ranges. The value of parameter T in (15) and (16) controls the enhancement rate for the output image. As an extremely case, T = 0.5 will make the clipping threshold Tc ≈ 0 and give a modified histogram with most bins having nearly the same height, resulting in an output without dynamic range adjustment. And T = 0 will result in an output image with a similar dynamic range adjustment provided by the standard HE because of none clipping operation.
4. Results and discussion
Experiments have been performed to demonstrate the performance of the proposed algorithm in comparisons to four popular algorithms after analyzing parameter choices.
4.1. Parameters choices
A grayscale image of “Tank” (Fig. 4 and Fig. 5) with size of 512 × 512 was utilized to evaluate the effects of DOG parameters rc, rs, and T. Fig. 4 illustrates the performances of the modified CHE with different settings of T. It can be found that an excessively large T (close to 0.5) causes an ineffective dynamic range control in the input image. A suitable value of T is able to reveal details by adjusting the dynamic range.
Fig. 4.
Evaluation of T. (a) Grayscale transfer functions with different T. (b) Input image of “Tank”. (c) T = 0.45. (d) T = 0.30. (e) T = 0.15. (f) T = 0.05. (g) T = 0.
Fig. 5.
Results with different settings of (rc, rs). (a) (1, 2). (b) (1, 9). (c) (1, 13). (d) (1, 17). (e) (2, 17). (f) (3, 17), (g) (5, 17), (h) (7, 17).
In order to study the effect of DOG model parameters rc and rs, different combinations of these values were evaluated (Fig. 5). In all cases, T = 0.05 was chosen as default. The results shown in (a), (b), (c), and (d) indicate that a larger rs reduces lower frequency brightness variation and the image appears to be flatter. Accordingly, a smaller rc helps the output image preserve more perceptual edges as shown in (e), (f), (g), and (h). A proper pair of rc and rs can effectively emphasize the perceptual contrast while eliminating high frequency noise in smooth regions.
Based on our observations, it was found that rc = 1 and rs = 9 resulting in a 3 × 3 central mask and a 19 × 19 surrounding mask, were effective for images with the resolution of 512 × 512. Although the performance of rc and rs also relies on the dimension of the input image, our experiments indicated that these parameter choices were suitable not only in the particular image, but also in a variety of gray and color images with 512 × 512 and even larger dimensions such as 2000 × 1312. Therefore, these parameters are set as default parameters in our algorithm.
4.2. Performance comparisons
Performance comparisons were carried on both grayscale and color images among CLAHE [15], MMBEBHE [6], BHEPL [19], AHMHE [22], and the new method.
In Fig. 6 and Fig. 7, “Airport” and “Man” are two grayscale images with resolutions of 1024 × 1024 pixels and 512 × 512 pixels respectively. As shown in Fig. 6 and Fig. 7, when compared to BHEPL, MMBEBHE, and AHMHE, CLAHE performs the best for contrast enhancement for all of these images, but it amplifies noise and causes some unnatural look. However, perceptual edges in all images are emphasized by the proposed method without amplifying noise. Output images have much sharper visual appearance. In addition, details in both dark and bright regions are enhanced effectively without affecting the natural appearance or causing over-enhancement.
Fig. 6.
(a) Input image of “Airport”. (b) BHEPL. (c) MMBEBHE. (d) CLAHE. (e) AHMHE. (f) The proposed method.
Fig. 7.
(a) Input image of “Man”. (b) BHEPL. (c) MMBEBHE. (d) CLAHE. (e) AHMHE. (f) The proposed method.
In Fig. 8 and Fig. 9, “Blue-car” and “Garage” are color images with resolutions of 2000 × 1312 pixels and 800 × 524 pixels respectively. All methods mentioned in this section are implemented with the following scheme of color conversions.
| (26) |
where I and O indicate input and output images with subscripts r, g, b, and gray representing their red, green, blue, and grayscale components correspondingly.
Fig. 8.
(a) Input image of “Garage”. (b) BHEPL. (c) MMBEBHE. (d) CLAHE. (e) AHMHE. (f) The proposed method.
Fig. 9.
(a) Input image of “Blue-car”. (b) BHEPL. (c) MMBEBHE. (d) CLAHE. (e) AHMHE. (f) The proposed method.
The luminance component of the input RGB image, Igray, is processed. The result, Ogray, is then combined with input color information, Ir, Ig, and Ib, to form the output RGB image.
As shown in Fig. 8 and Fig. 9, CLAHE can improve local contrast in both dark and bright regions, but the results are unnatural because of over-enhancement. Clearly, MMBEBHE does not reveal details hidden in dark and bright regions sufficiently. BHEPL functions only slightly better than MMBEBHE for enhancing details. Although AHMHE gives the most vivid color images, over-enhancement appearance exists for bright regions and enhancement for details is not sufficient for dark areas. In contrast, the proposed method is more effective in enhancing perceptual contrast and details in both dark and bright regions under different scenes. It also avoids the problems of over-enhancement and noise amplification, as the natural looks of its output images suggest.
Fig. 10 shows cropped regions from the results of “Blue-car” by different algorithms. Girl’s eyes (in dark region) and hair (in bright region) show the problems of artifacts or over-enhancement are caused by CLAHE, MMBEBHE, BHEPL, and AHMHE. However, the proposed method does not bring out those problems. Besides, it emphasizes perceptual contrast and gives much sharper results than the other methods without amplifying high frequency noise.
Fig. 10.
(a) Input image, (b) BHEPL, (c) MMBEBHE, (d) CLAHE, (e) AHMHE, and (f) The proposed method.
4.3. Execution time
Table 1 compares the average execution time of the sample images utilized in our experiments. For clarification, the times, t1 and t2, correspondingly consumed by perceptual contrast sharpening and dynamic range adjustment are listed separately.
Table 1.
Average execution time obtained from sample images.
| Methods | Average execution time (s) | |
|---|---|---|
| BHEPL | 1.6055 | |
| MMBEBHE | 1.5850 | |
| CLAHE | 0.1488 | |
| AHMHE | 7.0279 | |
| t1 | 13.0453 | |
| The Proposed Method | t2 | 0.0512 |
| t1 + t2 | 13.0965 |
It can be observed that although the proposed method consumes more time than BHEPL, MMBEBHE, CLAHE, and AHMHE, the dynamic range adjustment component consumes only a small portion of the total execution time, about 30% of that consumed by CLAHE.
Much of the time is utilized for perceptual contrast sharpening due to the heavy computation burden of non-optimized Gaussian convolutions. For real-time applications, there is already much work presented about efficient computation of the convolution [25][26][27]. Therefore, the computation of the proposed method can be further optimized.
5. Conclusion
A new algorithm for image enhancement is presented. It firstly emphasizes the perceptual contrast by utilizing perceptual contrast measure. Then, a modified CHE is proposed to adjust the dynamic range for revealing details of both dark and bright regions while avoiding the problems of over-enhancement and noise amplification. Although three major parameters are required, default settings of these parameters provide acceptable performance for HVP. Experimental results have shown that the proposed method is effective for both grayscale and color images. The structure of the proposed technique is simple, suitable for implementation in many forms of electronics to enhance their imaging functions. Future work will focus on adaptive parameters selection.
Acknowledgements
This work was supported by National Institutes of Health Grant No.U01HL91736 of the United States.
References
- 1.Gonzalez RC, Woods RE. Digital Image Processing. 2nd ed. Prentice Hall; 2002. [Google Scholar]
- 2.Kim YT. Contrast enhancement using brightness preserving bihistogram equalization. IEEE Trans. Consumer Electronics. 1997 Feb;vol. 43(no. 1):1–8. [Google Scholar]
- 3.Wan Y, Chen Q, Zhang BM. Image enhancement based on equal area dualistic sub-image histogram equalization method. IEEE Trans. Consumer Electronics. 1999 Feb;vol. 45(no. 1):68–75. [Google Scholar]
- 4.Chen SD, Ramli AR. Contrast enhancement using recursive mean-separate histogram equalization for scalable brightness preservation. IEEE Trans. Consumer Electronics. 2003 Nov;vol. 49(no. 4):1301–1309. [Google Scholar]
- 5.Sim KS, Tso CP, Tan YY. Recursive sub-image histogram equalization applied to gray-scale images. Pattern Recognition Letters. 2007 Jul;vol. 28:1209–1221. [Google Scholar]
- 6.Chen SD, Ramli AR. Minimum mean brightness error bi-histogram equalization in contrast enhancement. IEEE Trans. Consumer Electronics. 2003 Nov;vol. 49(no. 4):1310–1319. [Google Scholar]
- 7.Wongsritong K, Kittayaruasiriwat K, Cheevasuvit F, Dejhan K, Somboonkaew A. Contrast enhancement using multipeak histogram equalization with brightness preserving. IEEE Asia-Pacific Conference on Circuits and Systems Proceedings. 1998 Nov 24–27;:455–458. [Google Scholar]
- 8.Wadud MAA, Kabir MH, Dewan MAA, Chae O. A dynamic histogram equalization for image contrast enhancement. IEEE Trans. Consumer Electronics. 2007 May;vol. 53(no. 2):593–600. [Google Scholar]
- 9.Ibrahim H, Kong NSP. Brightness Preserving Dynamic Histogram Equalization for Image Contrast Enhancement. IEEE Trans. Consumer Electronics. 2007 Nov;vol. 53(no. 4):1752–1758. [Google Scholar]
- 10.Wang C, Ye Z. Brightness preserving histogram equalization with maximum entropy: A variational perspective. IEEE Trans. Consumer Electronics. 2005 Nov;vol. 51(no. 4):1326–1334. [Google Scholar]
- 11.Zuo Chao, Chen Qian, Sui Xiubao. Range Limited Bi-Histogram Equalization for image contrast enhancement. Optik. Available online 29 March 2012. [Google Scholar]
- 12.Kim JY, Kim LS, Hwang S-H. An advanced contrast enhancement using partially overlapped sub-block histogram equalization. IEEE Trans. Circuits and Systems for Video Technology. 2001 Apr;vol. 11(No. 4):475–484. [Google Scholar]
- 13.Liu B, Jin W, Chen Y, Liu C, Li L. Contrast enhancement using non-overlapped sub-blocks and local histogram projection. IEEE Trans. Consumer Electronics. 2011 May;vol. 57(no. 2):583–588. [Google Scholar]
- 14.NSPK, Ibrahim H. Multiple layers block overlapped histogram equalization for local content emphasis. Computers&Electrical Engineering. 2011 Sep;vol. 37(no. 5):631–643. [Google Scholar]
- 15.Pizer SM, Amburn EP, Austin JD, Cromartie R, Geselowitz A, Greer T, Romeny BH, Zimmerman JB, Zuiderveld K. Adaptive histogram equalization and its variations. Comp. Vis. Graph. Image Process. 1987 Sep;vol. 39(no. 3):355C368. [Google Scholar]
- 16.Yang S, Oh JH, Park Y. Contrast enhancement using histogram equalization with bin underflow and bin overflow. Proc. Int. Conf. Image Processing. 2003;vol. 1:881C884. [Google Scholar]
- 17.Wang Q, Ward RK. Fast image/video contrast enhancement based on weighted thresholded histogram equalization. IEEE Trans. Consumer Electronics. 2007 May;vol. 53(no. 2):757–764. [Google Scholar]
- 18.Kim T, Paik J. Adaptive contrast enhancement using gain-controllable clipped histogram equalization. IEEE Trans. Consumer Electronics. 2008 Nov;vol. 54(no. 4):1803–1810. [Google Scholar]
- 19.Ooi CH, Kong NSP, Ibrahim H. Bi-histogram with a plateau limit for digital image enhancement. IEEE Trans. Consumer Electronics. 2009 Nov;vol. 55(no. 4):2072–2080. [Google Scholar]
- 20.Chen SD. A new image quality measure for assessment of histogram equalization-based contrast enhancement techniques. Digital Signal Processing. Available online 4 April 2012. [Google Scholar]
- 21.Jayasinghe U, Dharmaratne A. Matching facial images using age related morphing changes. World Academy of Science, Engineering & Technology. 2009;60 [Google Scholar]
- 22.Kang B, Jeon C, Han DK, Ko H. Adaptive height-modified histogram equalization and chroma correction in YCbCr color space for fast backlight image compensation. Image and Vision Computing. 2011 Jul;vol. 29(no. 8):557–568. [Google Scholar]
- 23.Tadmor Y, Tolhurst DJ. Calculating the contrasts that retinal ganglion cells and LGN neurones encounter in natural scenes. Vision Research. 2000 Oct;vol. 40(no. 22):3145–3157. doi: 10.1016/s0042-6989(00)00166-8. [DOI] [PubMed] [Google Scholar]
- 24.Simone G, Pedersen M, Hardeberg JY. Measuring perceptual contrast in digital images. Journal of Visual Communication and Image Representation. 2012 Apr;vol. 23(no. 3):491–506. [Google Scholar]
- 25.Bosi B, Bois G, Savaria Y. Reconfigurable pipelined 2D convolvers for fast digital signal processing. IEEE Trans. on Very Large Scale Integration (VLSI) Systems. 1999 Sep;vol. 7(no. 3):299–308. [Google Scholar]
- 26.Dawood AS, Visser SJ, Williams JA. Reconfigurable FPGAS for real time image processing in space. 14th International Conference on Digital Signal Processing. 2002;vol. 2:845–848. [Google Scholar]
- 27.Tormo FC, Molinet P. Area-efficient 2-D shift-variant convolvers for FPGA-based digital image processing. IEEE Trans. on Circuits and Systems II: Express Briefs. 2006;vol. 53(no. 2):105–109. [Google Scholar]