Multiple constraints on grassland evapotranspiration: implications for closing the energy balance

Abstract

When using the eddy covariance (EC) method for measuring the ecosystem-atmosphere exchange of sensible and latent heat, it is not uncommon to find that these two energy fluxes fall short of available energy by 20-30 %. As the causes for the energy imbalance are still under discussion, it is currently not clear how the energy balance should be closed. The objective of the present paper is to use independent measurements of evapotranspiration (ET) for empirically devising on how to best close the energy balance. To this end ET of a temperate mountain grassland was quantified during two measurement campaigns using both an open- and a closed-path EC system, lysimeters and an approach scaling up leaf-level stomatal conductance to canopy level transpiration. Our study showed that both EC systems underestimated ET measured independently by lysimeters and the up-scaling approach. Best correspondence to independently measured ET was achieved by assigning the entire energy imbalance to ET and by adjusting ET according to the average energy balance ratio during the first and second measurement campaign, respectively. Due to a large spatial variability in ET during the first measurement campaign and given large differences in spatial scale between the EC and the independent methods, we are more confident with the comparison of approaches during the second measurement campaign and thus recommend forcing energy balance closure by adjusting for the average energy balance ratio.

1. Introduction

The energy imbalance, that is the widespread shortfall of measured sensible (H) and latent (λE) heat fluxes with respect to available energy on the order of 20-30 % (Wilson et al., 2002; Foken, 2008), is the thorn in the side of eddy covariance (EC) flux measurements (Baldocchi et al., 1988; Aubinet et al., 2000). Mathematically the energy imbalance may be expressed as

$$\mathrm{Res}={\mathrm{R}}_{\mathrm{n}}-\lambda \mathrm{E}-\mathrm{H}-\mathrm{G}$$ [1]

where Res stands for the residual energy or energy imbalance, R_n for the net radiation, and G for the soil heat flux (Foken, 2008). We note that Eq. [1] neglects other forms of heat fluxes such as biomass storage or metabolic reactions (Meyers and Hollinger, 2004; Jacobs et al., 2008).

Since the causes of the energy imbalance are still under discussion (see Foken, 2008 for a recent synthesis), EC measurements of evapotranspiration (ET) must be suspected of being biased low – in the most extreme case the entire energy imbalance may be attributed to the latent heat flux (Wohlfahrt et al., 2009). The resulting uncertainty may not only be prohibitive for using EC ET measurements for practical applications such as irrigation scheduling (Twine et al., 2000), but poses problems if models, which assume the energy balance to be closed, are to be calibrated with EC flux data (Williams et al., 2009). Along this line, Wohlfahrt et al. (2009) recently showed that surface conductance estimates derived by inverting the Penman-Monteith combination equation (Campbell and Norman, 1998) may differ widely depending on how energy balance closure is forced.

Clearly, elucidating the causes for the energy imbalance should be one of the prime micrometeorological research goals in the near future, also because the energy imbalance, if due to a systematic underestimation of the latent and/or sensible heat flux, may have implications for EC flux measurements of other trace gases (Twine et al., 2000; assuming scalar similarity with heat fluxes). In the meantime, alternative methods of quantifying ET may be used for comparison with ET measured by means of the EC method and thus as a practical approach for correcting for the energy imbalance (Chavez et al., 2009).

The objective of the present paper is to use the EC and two alternative, independent methods to quantify ET of a temperate mountain grassland in Austria and to infer from a comparison of these how to best force energy balance closure with the EC flux data. To this end two measurement campaigns were conducted during which, in addition to both an open-path and closed-path EC system (Haslwanter et al., 2009), ET was measured by weighing lysimeters (Wieser et al., 2008) and an approach by which measurements of leaf-level stomatal conductance were scaled up to canopy-level transpiration.

2. Material and Methods

2.1 Study site and conditions during measurement campaigns

The study site is located at a meadow in the vicinity of the village Neustift (47°07′N, 11° 19′E) in the Stubai Valley (Austria) at an elevation of 970 m a.s.l. in the middle of the flat valley bottom. The fetch is homogenous up to 300 m to the east and 900 m to the west of the instrument tower, the dominant day and night time wind directions, respectively. The average annual temperature is 6.5 °C, average annual precipitation amounts to 852 mm. Further details on soil, vegetation and climate may be found in Hammerle et al. (2008) and Wohlfahrt et al. (2008).

Two measurement campaigns were conducted in June 2009 for determining grassland ET by means of lysimeters and up-scaling: The first campaign took place on 4 June, which was a relatively cool day (daytime average air temperature of 13.5 °C), little evaporative demand (daytime average vapour pressure deficit (VPD) of 6.8 hPa) with alternating periods of sunshine and clouds. The canopy was about 1 m tall and the plant area index amounted to 8.6 m² m⁻². The second campaign took place on 18 June, after the meadow had been cut for the first time this year. This was a sunny (some thin clouds in the afternoon) and warm (daytime average air temperature of 21.3 °C) day with a relatively high evaporative demand (daytime average VPD of 14.5 hPa). Canopy height was 0.15 m and the plant area index amounted to around 2.1 m² m⁻².

2.2 Eddy covariance

ET, which may be converted to the flux of latent heat by multiplication with the latent heat of vaporisation, was measured using the eddy covariance (EC) method (Baldocchi et al., 1988; Aubinet et al., 2000) as part of long-term flux measurements at this site since 2001 (Hammerle et al., 2008; Wohlfahrt et al., 2008; Haslwanter et al., 2009). The three wind components and the speed of sound were measured by a three-dimensional sonic anemometer (R3IA, Gill Instruments, Lymington, UK), H₂O mole densities/fractions by an open-path (OP) (Li-7500, Li-Cor, Lincoln, NE, USA) and a closed-path (CP) (Li-7000, Li-Cor, Lincoln, NE, USA) infrared gas analyser (IRGA). In the CP system air was sucked from the inlet, displaced 0.1 m laterally and 0.1 m below the centre of the sensor volume of the sonic anemometer mounted at 3 m above ground, through a 10 m heated (to 35°C) Teflon tube of 0.004 m inner diameter through a filter (Acro 50, Gelman, Ann Arbor, MI, USA) to the CP IRGA at a flow rate of 9 l min⁻¹ (N035ANE, KNF Neuberger, Freiburg, Germany). The CP IRGA was operated in the absolute mode, flushing the reference cell with dry N₂ from a gas cylinder at 0.1 l min⁻¹. The OP IRGA was displaced 0.3 m laterally and 0.2 m below the centre of the sensor volume of the sonic anemometer and was tilted at an angle of 45° towards North. Both the CP and OP IRGA were arranged approximately at a right angle to the main daytime and nighttime wind direction thereby minimizing longitudinal sensor separation to the sonic anemometer. Raw voltage signals of the H₂O mole fractions/densities from both IRGAs were input at 10 Hz by the analogue input of the sonic, where they were synchronized with the sonic signals, which were output at 20 Hz. All raw data were saved to a hard disc of a personal computer for post-processing using the EdiSol software (University of Edinburgh).

Half-hourly mean eddy fluxes were calculated as the covariance between the turbulent departures from the mean of the vertical wind speed and the H₂O mixing ratios using the post-processing software EdiRe (University of Edinburgh). Means and corresponding turbulent departures were calculated by Reynolds (block) averaging. The tube-induced time delay of the H₂O (0.9 s) signals was determined by optimizing the correlation coefficient with the vertical wind velocity (McMillen, 1988) within a given time window. A fixed lag of 0.3 s was imposed on the OP data through the IRGA software and removed. A three-axis co-ordinate rotation was performed aligning the co-ordinate system’s vector basis with the mean wind streamlines (Kaimal and Finnigan, 1994). Frequency response corrections were applied to raw eddy fluxes accounting for high-pass (block averaging) and low-pass (lateral sensor separation, dynamic frequency response, scalar and vector path averaging, frequency response mismatch and in the case of the CP IRGA the attenuation of concentration fluctuations down the sampling tube) filtering following Moore (1986), Massman (1991) and Aubinet et al. (2000). To this end, a site-specific model cospectrum, described in Wohlfahrt et al. (2005), was employed. Finally density corrections were applied to both CP and OP fluxes based on Webb et al. (1980) – for the CP fluxes only the water vapour effect was corrected for as temperature fluctuations were assumed to have been dampened out by the time when air arrives in the IRGA (Aubinet et al., 2000). Corrections for the effect of self-heating of the OP IRGA (Burba et al., 2006) were not applied as a previous comparison between fluxes measured by the OP and CP IRGA found that this correction decreased the correspondence between both EC systems (Haslwanter et al., 2009).

ET was calculated as the sum of the corrected vertical eddy term and the storage fluxes, the latter being estimated from the time-rate-of-change of the H₂O density at the reference height, which in a previous comparison with a profiling system was found to be sufficiently accurate. Negative fluxes represent transport from the atmosphere towards the surface, positive ones the reverse.

Half-hourly flux data were quality controlled by removal of time periods with (1) the H₂O signal outside a specific range, (2) the coefficient of variation for H₂O concentration and, in the case of the CP IRGA, internal pressure outside a specific range, (3) the third rotation angle exceeding ± 10° (McMillen, 1988), (4) the stationarity test for the H₂O flux exceeding 60% (Foken and Wichura, 1996), (5) the deviation of the integral similarity characteristics larger than 60% (Foken and Wichura, 1996), and (6) the maximum of the footprint function (Hsieh et al., 2000) outside the boundaries of the meadow (cf. Novick et al., 2004).

Similar to Wohlfahrt et al. (2009) we used five scenarios for correcting ET measured by means of the EC method for any energy imbalance:

1. ET_orig: ET as measured by the EC method is assumed correct, i.e. the energy balance is closed each half-hourly period by either attributing the residual energy to H and/or the available energy (i.e. R_n - G);

2. ET_resid: the energy balance is closed each half-hourly period by attributing all the residual energy to λE;

3. ET_β: the energy balance is closed each half-hourly period by attributing the residual energy to both H and λE according to (and thus preserving) the Bowen-ratio (β = H/λE);

4. ET_debc: the energy balance is closed on a daily basis by dividing measured half-hourly H and λE by the daily energy balance ratio, which implies that β is conserved, but also that during each half-hourly period the energy balance may not necessarily be closed; and

5. ET_ltebc: same as scenario (4), but the energy balance is closed on a long-term basis (the entire month of June 2009 in the present case).

2.3 Lysimeter

The lysimeters (six replicates) consisted of 0.19 m deep plastic cylinders (Wieser et al., 2008) with a diameter of 0.2 m that were filled with intact vegetated soil monoliths excavated at the site two weeks before the first measurement campaign. The lysimeters were weighted at hourly (4 June 2009) and half-hourly (18 June 2009) intervals, each measurement lasting less than 30 s. In between the measurements, the lysimeters were returned back into another set of cylinders with a slightly larger diameter that were sunk into the ground so that the upper edge of the lysimeters was level with the soil surface and exposed to an unaltered microclimate by the surrounding, undisturbed canopy (Wieser et al., 2008). ET (mm h⁻¹) was calculated as the (half-)hourly mass difference (kg) divided by the area of the lysimeters (m²) and the time difference between samplings (h).

2.4 Up-scaling

Transpiration of a dry plant canopy (T, mm h⁻¹) was estimated by up-scaling leaf-level stomatal conductance to canopy-level transpiration employing the following equation:

$$T=3600M_w\sum _{p=1}^n\sum _{z=0}^{h}A(p,z)g_l(p,z)\frac{e_s(p,z)-e_a\left(z\right)}{P}$$ [2]

Here M_w refers to the molecular mass of water (0.018 kg mol⁻¹), A to the plant area index (PAI, m² green plant area m⁻² ground area), g_l to the leaf conductance to water vapour (mol m⁻² s⁻¹), e_s and e_a to the saturation and actual water vapour partial pressures (kPa), respectively, and P to the atmospheric pressure (kPa). The index p and z refer to plant species and canopy layer number (i.e. height above ground), over which the summation occurs in Eq. [2]. The PAI was determined in a destructive fashion by stratified clipping of a representative square plot of 0.25 m² (Wohlfahrt et al., 2001). Thickness of the harvested layers ranged between 0.1 and 0.2 m, depending on plant area density (higher resolution in the lower canopy). The harvested plant material was separated into leaves, (green) stems, reproductive organs, dead plant matter and cryptogams. The latter three groups contributed less than 4 % to the total plant area and their evapotranspiration was neglected in Eq. [2]. Leaves and stems were further separated into the dominant herbaceous species (Ranunculus acris, Taraxacum officinale, Trifolium sp.), while leaves and stems of all remaining forbs and grasses were pooled, respectively. The one-sided plant area was determined with an area meter (Li-3100, Li-Cor, Lincoln, NE, USA).

The leaf conductance to water vapour was calculated according to Eq. [3], which makes the reasonable assumption of stomata being distributed just on one (the lower) leaf side:

$$g_l(p,z)=\frac{g_s(p,z)g_b(p,z)}{g_s(p,z)+g_b(p,z)}$$ [3]

Here g_s refers to the stomatal conductance to water vapour (mol m⁻² s⁻¹), which was measured at hourly intervals (three replicates) under the prevailing environmental conditions on one grass (Dactylis glomerata) and three herbaceous (R. acris, T. officinale, Trifolium sp.) species at various levels (species-specific) within the canopy using a portable leaf porometer (Decagon, Pullman, WA, USA).

The leaf boundary layer conductance to water vapour (g_b, mol m⁻² s⁻¹), was calculated according to Campbell and Norman (1998),

$$g_b(p,z)=0.147\frac{u{\left(z\right)}^{0.5}}{d(p,z)}$$ [4]

where u refers to the mean horizontal wind velocity (m s⁻¹) measured at three levels (0.09, 0.35 and 0.90 m) within the canopy by means of hot-wire anemometers (ThermoAir2, Schildknecht, Gossau, Switzerland), and d to the leaf width (m) which was measured with a ruler.

The saturation water vapour partial pressure (e_s, kPa) was calculated as a function of leaf temperature (Campbell and Norman, 1998), which was measured by means of thermocouples (SA1-T, Omega, Stamford, CT, USA) on seven leaves of three species (D. glomerata, T. officinale, Trifolium sp.) at two to three heights (0.06-0.62 m) within the plant canopy. The actual water vapour partial pressure (e_a, kPa) was measured at three heights within/above the canopy (0.09, 0.35 and 2.0 m) with ventilated air temperature and humidity sensors (RFT-2, UMS, Munich, Germany). Atmospheric pressure (P, kPa) was measured with a barometer (CS100 Setra 278, Campbell Scientific, Logan, UT, USA). All of these data, except for stomatal conductance which were saved on the leaf porometer, were logged on a data logger (CR3000, Campbell Scientific, Logan, UT, USA) and saved as half-hourly averages.

In order to apply Eq. [2], measured leaf temperatures, actual water vapour partial pressures, wind speeds and stomatal conductances were linearly interpolated (close to the soil surface and towards the canopy top in some cases also extrapolated) vertically to the grid of the plant area measurements (to the mid-point of each layer). Equation [2] neglects soil evaporation – this is not likely to cause a large systematic bias when the canopy is tall (see Wieser et al., 2008 and references therein), as during the first measurement campaign (4 June 2009). During the second measurement campaign on 18 June 2009, after the first cut, soil evaporation may however contribute a sizeable fraction of total ecosystem ET and therefore we did not conduct the up-scaling experiment during the second measurement campaign.

2.5 Ancillary measurements

Supporting meteorological measurements of relevance to this study included total photosynthetically active radiation (PAR) (BF3H, Delta-T, Cambridge, UK), net radiation (CNR-1, Kipp & Zonen, Delft, Netherlands), air temperature (T_air) and humidity (RH) at 2 m height and soil temperature (T_soil) at 0.05 m depth, measured by the means of a combined temperature/humidity sensor (RFT-2, UMS, Munich, Germany) and a thermocouple (TCAV, Campbell Scientific, Logan, UT, USA), respectively, soil heat flux (G) measured by the means of heat flux plates (3 replicates at 0.05 m depth; HFP01, Hukseflux, Delft, The Netherlands) corrected for the change in heat storage above that depth using the calorimetric method (Sauer and Horton, 2005), volumetric soil water content (ML2x, Delta-T Devices, Cambridge, UK) and precipitation (52202, R. M. Young, Traverse City, MI, USA). All these data were saved as half-hourly averages by a data logger (CR10X, Campbell Scientific, Logan, UT, USA).

3. Results

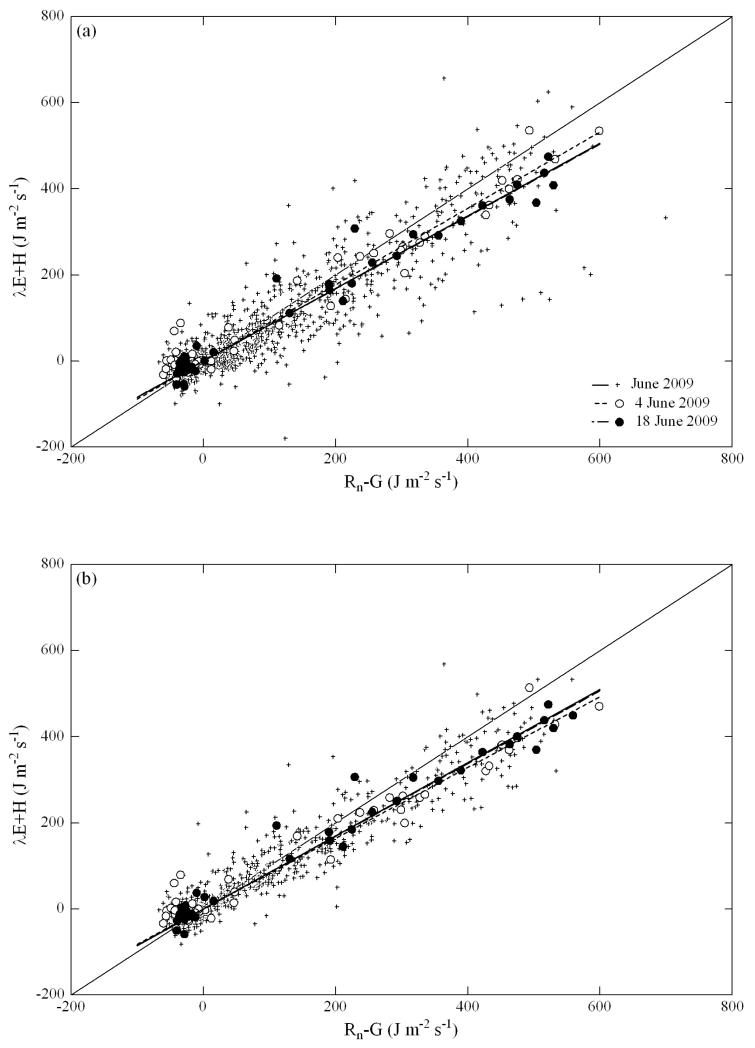
Using all available data from June 2009, the (long-term) energy balance closure amounted to 84 and 85 % with the CP and OP EC system, respectively (linear regressions not significantly different; Fig. 1). Energy balance closure during the two measurement campaigns was very similar to the long-term closure with both systems (linear regressions not significantly different; Fig. 1).

Figure 1. Energy balance closure for the closed-path (a) and open-path (b) eddy covariance system from June 2009 compared against 4 and 18 June 2009.

Linear regressions forced through the origin yielded the following coefficients: closed-path eddy covariance system: 0.84 (entire June), 0.89 (4 June), 0.84 (18 June); open-path eddy covariance system: 0.85 (entire June), 0.82 (4 June), 0.84 (18 June). The thin solid line (1:1 line) indicates perfect energy balance closure.

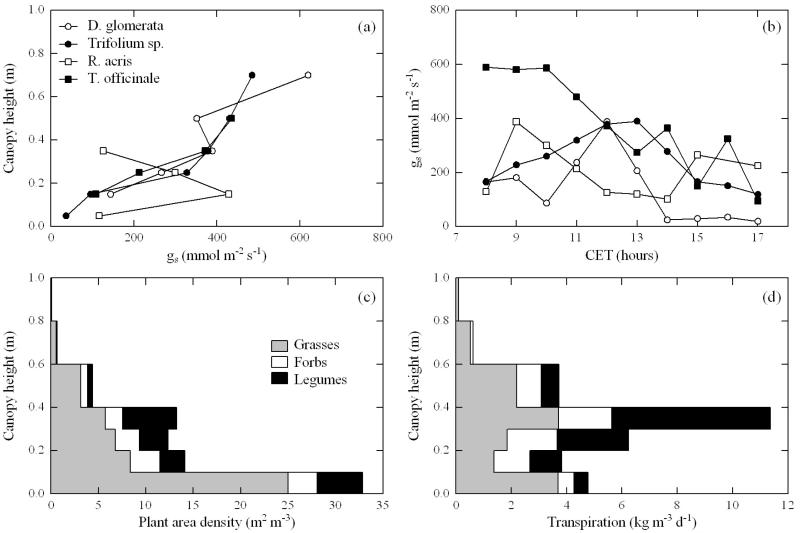
As shown in an exemplary fashion in Figure 2a, stomatal conductance was generally lower close to the soil surface and increased towards the canopy top. Stomatal conductance did not follow a general diurnal trend across species and canopy layers – in some cases maximum conductances were reached around noon, while in other cases conductances tended to be higher in the morning (and afternoon), and in some cases hardly any diel variation was observed (Fig. 2b). Plant area density was highest in the lowermost canopy layer (< 0.1 m) due to a large contribution by grasses, fairly constant above until about 0.4 m, and from there quickly declined towards the canopy top (Fig. 2c). The vertical distribution of transpiration (Fig. 2d) reflected both the vertical distribution of the transpiring plant area (Fig. 2c), as well as the vertical gradient in transpiration per unit plant area (Fig. 2a).

Figure 2. Key results of the up-scaling approach: (a) vertical profile of midday leaf-level stomatal conductance, (b) diurnal course of leaf-level stomatal conductance in the 0.3-0.4 m canopy layer, (c) vertical profile of plant area density, and (d) vertical profile of modelled transpiration.

The various plant species have been pooled into three functional groups in panels (c and d).

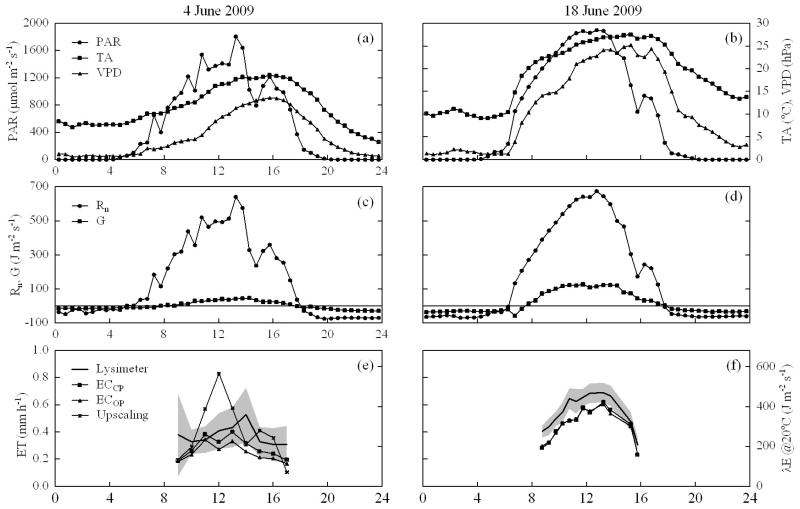
On 4 June, i.e. before the cut, ET measured by both EC systems fell short of both the ET measured by the lysimeters and the up-scaling approach by 24-34 and 29-39 %, respectively (Fig. 3). The up-scaled ET was within one standard deviation of the lysimeter ET (up to 0.2 mm h⁻¹), except for between 11-12 CET (Fig. 3). The best qualitative and quantitative correspondence to the independent ET measurements was achieved when assigning the entire energy imbalance to ET (ET_resid; Table 1). In case of the lysimeter measurements, slopes and y-intercepts of linear regressions with ET measured by the EC method were not statistically significantly different from unity and zero, respectively (Table 1). On 18 June both EC systems underestimated lysimeter ET by 18-19 % (Fig. 3). Because variability in lysimeter ET (up to 0.09 mm h⁻¹ standard deviation) was much lower as compared to the first measurement campaign, ET measured by the EC method was generally below one standard deviation (Fig. 3). The best qualitative and quantitative correspondence with lysimeter ET was achieved by adjusting ET according to the daily or long-term energy imbalance (EC_debc, EC_ltebc; Table 1). Slopes and y-intercepts of linear regressions with ET_debc and ET_ltebc were not statistically significantly different from unity and zero, respectively (Table 1).

Figure 3. Diurnal courses of (a, b) photosynthetically active radiation (PAR, air temperature (TA), vapour pressure deficit (VPD), (c, d) net radiation (R_n), soil heat flux (G) and (e, f) evapotranspiration (ET).

The grey shaded area indicates one standard deviation (n = 6) around the mean of evapotranspiration measured by lysimeters. ET in energy units (λE; assuming an air temperature of 20°C) is shown on the secondary y-axis of the two lowermost panels for reference.

Table 1. Linear regression statistics of evapotranspiration measured by means of eddy covariance (ET_CP … closed-path, ET_OP … open-path) vs. independently measured evapotranspiration (by lysimeters or up-scaling).

Five approaches have been used to close the energy imbalance associated with the eddy covariance method: ET_CP_orig, ET_OP_orig: evapotranspiration without corrections for energy imbalance; ET_CP_resid, ET_OP_resid: evapotranspiration adjusted by attributing the energy imbalance exclusively to evapotranspiration; ET_CP_β, ET_OP_β: evapotranspiration adjusted according to half-hourly bowen-ratio; ET_CP_debc, ET_OP_debc: evapotranspiration adjusted according to the daily energy imbalance ratio; ET_CP_ltebc, ET_OP_ltebc: evapotranspiration adjusted according to the long-term energy imbalance ratio. Slope (k) and y-intercept (d; mm h⁻¹) of the linear regression, coefficient of determination (r²) and root-mean-squared-error (rmse; mm h⁻¹) are reported. Bold numbers indicate the slope and y-intercept are not statistically significantly different from unity and zero, respectively. The number of observations (n) is 9 and 12 for 4 and 18 June 2009, respectively.

	4 June 2009								18 June 2009
	Lysimeter				Up-scaling				Lysimeter
	k	d	r2	rmse	k	d	r2	rmse	k	d	r2	rmse
ETCP_ORIG	0.50	0.10	0.22	0.11	0.26	0.18	0.57	0.20	0.91	−0.05	0.80	0.11
ETCP_resid	0.69	0.07	0.26	0.09	0.31	0.21	0.51	0.17	1.27	−0.16	0.93	0.06
ETCP_β	0.59	0.09	0.25	0.10	0.29	0.19	0.56	0.18	1.23	−0.16	0.94	0.06
ETCP_debc	0.56	0.11	0.22	0.09	0.29	0.20	0.57	0.18	1.08	−0.06	0.80	0.05
ETCP_ltebc	0.59	0.12	0.22	0.09	0.31	0.21	0.57	0.17	1.08	−0.06	0.80	0.05
ETOP_orig	0.34	0.12	0.16	0.15	0.21	0.16	0.54	0.23	0.88	−0.04	0.93	0.11
ETOP_resid	0.68	0.08	0.26	0.09	0.31	0.20	0.51	0.17	1.25	−0.16	0.92	0.06
ETOP_β	0.49	0.11	0.21	0.11	0.26	0.19	0.54	0.20	1.21	−0.15	0.93	0.06
ETOP_debc	0.41	0.14	0.16	0.11	0.25	0.20	0.54	0.20	1.04	−0.04	0.93	0.04
ETOP_ltebc	0.40	0.14	0.16	0.11	0.24	0.19	0.54	0.20	1.04	−0.04	0.93	0.04

4. Discussion

When using the EC method for measuring the ecosystem-atmosphere exchange of sensible and latent heat, it is not uncommon to find that these two energy fluxes fall short of available energy by 20-30 % (Wilson et al., 2002; Foken, 2008). As the causes for the energy imbalance are still under discussion (Foken, 2008), it is currently not clear how the energy balance should be closed (Wohlfahrt et al., 2009). The latter is required if measured sensible and latent heat fluxes are assimilated into or used to validate models which assume the energy balance to be closed (Williams et al., 2009; Wohlfahrt et al., 2009). The objective of this paper is to use independent measurements of ET for empirically devising on how to best close the energy balance. To this end, ET of a temperate mountain grassland was quantified during two measurement campaigns in June 2009 using eddy covariance, lysimeters and an approach scaling leaf-level stomatal conductance up to canopy level transpiration.

In a first step it is instructive to compare differences between the three approaches in terms of their spatial and temporal scale and which water vapour flux they actually quantify (Table 2): The footprint of the EC method is on the order of several hundreds of meters and varies with wind direction and atmospheric conditions (wind speed, atmospheric stability; Schmid, 1997). The source area of the lysimeter measurements amounts to less than a square meter and is, in contrast to the EC method, well defined and constant. The spatial scale of the up-scaling approach ranges from millimetres, the size of the area of the leaf temperature measurements, over centimetres, the size of the leaf area enclosed in the porometer, up to one meter, roughly the spatial scale of the canopy structure measurements. Eddy covariance measurements are made at 20 Hz from which 30 min averages are calculated. The lysimeter ET represents an integral water loss over 30-60 min, while the temporal scale of the up-scaling approach ranges from 30 s, the duration of the leaf conductance measurement, up to 30-60 min, the averaging interval of the driving forces. The EC method and lysimeters quantify both ecosystem evaporation and transpiration, while the up-scaling approach neglects evaporation from the soil surface and any canopy surface water stores.

Table 2. Conceptual comparison of methods used to quantify grassland evapotranspiration.

	Spatial scale	Temporal scale	Vapour flux
Eddy covariance	102 m	50 ms, 30 min average	Evapotranspiration
Lysimeter	100 m	30-60 min integral	Evapotranspiration
Up-scaling	10−2-100 m	30 s, 60 min average	Transpiration

Several causes have been invoked for being responsible for the observed energy imbalance (for a recent synthesis we refer to Foken, 2008) and the scenarios proposed in the present paper for closing the energy balance reflect these:

Assuming that the ET as measured by the EC method is correct (Scenario 1: ET_orig), amounts to assigning the entire energy imbalance to the other terms of the energy balance (Eq. [1]). Indeed, several authors have shown that improving the calculation of some of the non-turbulent energy balance components, e.g. the soil heat flux (Heusinkveld et al., 2004) or the storage term (Meyers and Hollinger, 2004), and/or including commonly neglected terms into the energy balance, e.g. energy flux into photosynthesis (Jacobs et al., 2008), may in some cases greatly reduce the energy imbalance without any adjustment in measured ET. Our study, in accordance with the results obtained by Chavez et al. (2009) over cotton, showed that the EC method underestimated ET measured by lysimeters and the up-scaling approach during both measurement campaigns by 18-39 % (Table 1, Fig. 3) and thus does not support scenario 1. Thereby, only minor differences between the OP and CP EC were found. This is in contrast to Haslwanter et al. (2009), who reported the CP system at our site to yield a 84 mm lower annual ET as compared to the OP system. This difference may be explained by the fact that during the present study the intake line of the CP system was heated to 35°C in order to reduce water vapour interactions with the tube walls (sorption and desorption; Massman and Ibrom, 2008). This measure was taken as Ibrom et al. (2007) have shown that the underestimation of ET by CP systems scales positively with the relative humidity in the intake line. The difference between the CP and OP system reported by Haslwanter et al. (2009) may though also relate to the fact that their study was based on year-round data, while here we have used data from June only when the correspondence between both systems may be generally more favourable. If underestimated or neglected non-turbulent terms in the energy balance contribute significantly to the energy imbalance, one might expect the energy imbalance to differ between the two measurement campaigns, i.e. before and after the cut, because of changes in the contribution of these terms to the energy balance. After the cut the midday G/R_n ratio increased from 0.07 before to 0.18 (Fig. 3; Hammerle et al., 2008) – any error that scales with the measured soil heat flux may thus be expected to be larger after as compared to before the cut. Conversely, errors arising from neglecting heat storage in the biomass may be expected to be quantitatively more important before the cut when the PAI was much higher. Likewise, the error caused by not accounting for the heat flux into photosynthesis must be assumed to be much larger before the cut when gross photosynthesis amounts roughly up to 40 μmol CO₂ m⁻² s⁻¹ (i.e. ca. 20 J m⁻² s⁻¹), while only a few μmol CO₂ m⁻² s⁻¹ are fixed after the cut (Wohlfahrt et al., 2008). As the energy imbalance hardly differed before and after the cut (Fig. 1), this may indicate that either the above-mentioned energy balance components have been quantified correctly or that the changes of the errors into opposite directions actually cancelled out.

Due to the latter possibility and the general uncertainties in quantifying the non-turbulent terms in the energy balance, scenario 2, i.e. assigning the entire energy imbalance to ET (ET_resid), may be considered not very likely as well, as shown by Chavez et al. (2009). This is particularly true if the error in the ET measurement is due to some general shortcoming of the EC method, which would also apply to the sensible heat flux (see also discussion below). Nevertheless, on 4 June 2009 the discrepancy between the EC method and the two independent ET estimates was so large, that assigning the entire energy imbalance to ET turned out to represent the best closure option (Table 1). However, both quantitatively and qualitatively the correspondence was much lower as compared to the best closure approach for the second measurement campaign (Table 1). At this point the issue of spatial scale, which is much smaller for the independent methods as opposed to the EC technique (Table 2), and the heterogeneity within the footprint of the EC measurements, need to be discussed. The standard deviation of the lysimeter ET measurements on 4 June 2009 amounted up to 0.2 mm h⁻¹, which (assuming an air temperature of 20°C) translates into a latent heat flux of ca. 135 J m⁻² s⁻¹. This value is larger than the maximum average energy imbalance, which at noon amounts to around 100 J m⁻² s⁻¹ (Fig. 1). While the footprint of our EC flux system appears homogeneous to the observer, there obviously is some small-scale variability in ET present as evident from the spread in lysimeter measurements (Fig. 3e). If the vegetation patches which are characterised by lower than average ET rates (from lysimeter measurements) make up a significant fraction of the footprint, then the arithmetic average lysimeter ET will be biased high. Ideally, lysimeter ET would be calculated as the average weighted according to the contribution of the various patches to the EC footprint - at present we however lack the small-scale (< 1 m) spatial information that would be necessary to this end. No error bounds have been provided for the up-scaled canopy transpiration as the sources of errors associated with this approach are hard to quantify. Possible errors relate again to the spatial scale of the measurements (Table 2) as opposed to the small-scale heterogeneity of the site, the limited number of replicates, errors in the measurements per se (e.g. the accuracy with which leaf stomatal conductance can be quantified), as well as errors arising from the need to interpolate measurements in both space and time and to integrate measurements over discrete canopy layers. Because of the multitude of error sources, even if most of them are independent and thus do not add linearly (Moncrieff et al., 1996), it is likely that the uncertainty of the up-scaled canopy transpiration is larger than the statistical uncertainty of the lysimeter ET as indicated by the almost twice as high canopy transpiration around noon (up to 600 J m⁻² s⁻¹), which even exceeds net radiation (Fig. 3). The up-scaled canopy transpiration estimates should thus rather be viewed as a conceptual test of our process understanding of canopy transpiration than a practical means for independently corroborating ET estimates measured with the EC method. Finally we would like to mention that scenarios 1 and 2, even if not the most likely ones, are nevertheless useful as they encompass the potential range of possible energy balance closure options and may thus serve as extreme scenarios for any study dealing with the problem of closing the energy imbalance (Wohlfahrt et al., 2009).

Both experimental studies using area-averaging approaches (e.g. scintillometers; Meijninger et al., 2006) and modelling studies using the Large Eddy Simulation technique (LES; e.g. Kanda et al., 2004) suggest the energy imbalance to result from a significant energy flux contribution by large eddies, generated by larger-scale heterogeneities, which are missed by the usual 30 min averaging periods used at most EC sites (Finnigan et al., 2003). According to Foken (2008) it is this scale problem to which the majority of the energy imbalance has to be attributed. As an engineering-type solution (Foken, 2008), which assumes that the bowen-ratio of the energy fluxes carried by these large eddies equals the one measured by the EC method, the energy balance may be closed by assigning the energy imbalance to the sensible and latent heat flux according to the local bowen-ratio (Scenario 3: ET_β). On a regional scale such as the entire Stubai Valley, cutting of grasslands usually occurs within a time window of 2-3 weeks, causing the landscape to become more heterogeneous (i.e. a mix of cut and uncut areas) once cutting has started. If the energy imbalance is indeed to be attributed to large eddies caused by the heterogeneity at the landscape-scale (Foken, 2008), we would thus expect scenario 3 to perform better after the cut. In the present study, however, scenario 3 yielded the poorest correspondence with independently measured ET during both measurement campaigns (Table 1). Possibly, the additional landscape heterogeneity initiated by the onset of the farmers cutting activities, despite fundamentally altering the energy flux partitioning (Hammerle et al., 2008), is not enough to affect the generation of larger eddies, which depends more on roughness changes at forest/non-forest or uban/non-forest transitions, which can be considered static at this time scale. The poor performance of scenario 3 may also have to do with the fact that depending on the size and sign of λE and H, forcing closure according to the bowen-ratio may change ET by unrealistically large amounts (Wohlfahrt et al., 2009).

Another option for closing the energy balance is to use the average energy balance ratio directly for correcting sensible and latent heat fluxes (Twine et al., 2000). This approach likewise conserves the bowen-ratio, but is conceptually different from scenario 3, because during any averaging period the energy balance may not necessarily be closed due to the spread of the half-hourly measurements around the average (Fig. 1). While this approach has been applied in a few studies (e.g. Twine et al., 2000; Morgenstern et al., 2004), it is not yet clear which time frame should be used to determine the average energy balance ratio (Wohlfahrt et al., 2009), which is an issue, if the latter varies temporally. Chavez et al. (2009) have used the average midday Bowen-ration to close the energy balance. In the present paper we have analysed two averaging time frames – daily (Scenario 4: ET_debc) and longer term (i.e. monthly; Scenario 5: ET_ltebc), which in the present case yielded similar results because the daily and monthly energy balance ratios differed only slightly (Fig. 1). Note that the year-round (2001-2006) energy balance closure at this site is lower amounting to 0.76 and 0.78 for the CP and OP system, respectively (Haslwanter et al., 2009). After the cut, on 18 June 2009, adjusting ET for either the daily and long-term energy imbalance resulted in the best correspondence with lysimeter ET (Table 1). In contrast to the first measurement campaign on 4 June 2009, variability in lysimeter ET was much smaller (standard deviation of around 60 J m⁻² s⁻¹), indicating that cutting may have reduced the spatial heterogeneity in ET. Due to the differing spatial scales of the lysimeter and EC measurements (Table 2) we are thus more confident in the comparison between lysimeter and EC ET for the second measurement campaign and thus, in accordance with Chavez et al. (2009), tend to favour scenario 4 and 5 for forcing energy balance closure. We though have to stress, as mentioned above, that these two scenarios may be associated with a residual energy during any half-hourly period which needs to be accounted for in order to fully close the energy balance – to this end scenarios 1 or 3 may be used. Forcing energy balance closure via the longer term energy imbalance was also the option favoured by Wohlfahrt et al. (2009) who used energy balance measurements to derive the surface conductance to water vapour of this grassland and a desert shrub ecosystem.

5. Conclusion

Our study showed that both the OP and CP EC system underestimated ET measured independently by lysimeters and an approach by which leaf-level stomatal conductance is up-scaled to canopy-level transpiration. During two measurement campaigns, however, no single best approach for forcing energy balance closure could be identified. During the first campaign assigning the entire energy imbalance to ET resulted in the best correspondence to independently measured ET, while during the second campaign best correspondence with lysimeter ET was achieved by adjusting EC ET according to the average energy balance ratio. Due to large differences in spatial scale between the EC and the independent methods and a seemingly large spatial variability in ET during the first measurement campaign, we are more confident with the comparison of the approaches during the second measurement campaign and thus conclude that for the present data set forcing energy balance closure by adjusting for the average energy imbalance ratio provided the best correspondence with independently measured ET. But clearly, there is a need for comparisons between ET measured by the EC method and independent approaches for a wider range of ecosystems in order to corroborate our results. In this regard it seems that concurrent measurements of (evapo)transpiration by sap flow and EC methods (e.g. Saugier et al., 1997; Wilson et al., 2001), which are made at quite a few forest sites, have actually been underexploited and may provide ample opportunities to this end.