Performance of Pharmacovigilance Signal Detection Algorithms for the FDA Adverse Event Reporting System

Abstract

Signal detection algorithms (SDAs) are recognized as vital tools in pharmacovigilance. However, their performance characteristics are generally unknown. By leveraging a unique gold standard recently made public by the Observational Medical Outcomes Partnership and by conducting a unique systematic evaluation, we provide new insights into the diagnostic potential and characteristics of SDAs routinely applied to FDAs adverse event reporting system. We find that SDAs can attain reasonable predictive accuracy in signaling adverse events. Two performance classes emerge, indicating that the class of approaches addressing confounding and masking effects benefits safety surveillance. Our study shows that not all events are equally detectable, suggesting that specific events might be monitored more effectively through other sources. We provide performance guidelines for several operating scenarios to inform the trade-off between sensitivity and specificity for specific use cases. We also propose an approach and apply it to identify optimal signaling thresholds given specific misclassification tolerances.

1. Introduction

In order to monitor the safety of drugs during the post-approval phase, the US Food and Drug Administration (FDA) has maintained the Adverse Event Reporting System (AERS) database since 1968¹. AERS contains spontaneous reports of suspected adverse drug events (ADEs) collected from healthcare professionals, consumers, and pharmaceutical companies. Each report includes one or more adverse events that appear to be associated with the administration of a drug, as well as indications and limited demographic information. To date, AERS contains approximately five million reports, and currently receives half a million reports per year.

To identify safety signals of adverse events from spontaneous reports, data mining techniques are increasingly used to supplement the traditional expert review of the reports and to rapidly analyze the large volume of accumulated data. These data mining techniques—commonly known as signal detection algorithms (SDAs)—are used to explore databases of spontaneous reports for concealed associations between drugs and reported adverse events that may evade the scrutiny of manual case assessment. The FDA routinely applies SDAs to AERS in order to monitor, prioritize, and identify new safety signals of ADEs that warrant further attention^{2, 3}. Other regulatory agencies and pharmaceutical companies around the world also apply SDAs to their own spontaneous reports databases.

SDAs are designed to compute surrogate measures of statistical association between drug-event pairs reported in a database. These measures are often interpreted as signal scores, with larger values representing stronger associations, which are assumed more likely to represent true ADEs. A signal score threshold is often used to highlight signals worthy of further review. There are two main types of SDAs: those based on disproportionality analysis (DPA), and those based on multivariate modeling techniques such as logistic regression. DPA methodologies use frequency analysis of 2×2 contingency tables (or stratified versions thereof) to quantify the degree to which a drug-event combination co-occurs disproportionally compared to what would be expected if there were no association⁴. By virtue of being multivariate modeling techniques, approaches in this class can account for potential confounding and masking factors during the analysis of drug-event relationships. Confounding in AERS has been primarily investigated in the context of poly-pharmacy whereby a true association with one drug may bias the estimated association with another drug just because the two drugs tend to be prescribed and reported together. Masking occurs when an increase in background reporting of a specific event disproportionately attenuates measures of true associations toward lower values, thereby masking the true association. The literature has discussed these SDAs in length^5–8

While the value of SDAs has been widely recognized, the performance characteristics of SDAs are not well-understood. This is primarily due to the lack of evaluation guidelines, lack of established gold standards^{7, 9, 10}, and to a certain extent acknowledged shortcomings with the studies that have been conducted^{3, 11–16}. For example, some studies focus mainly on sensitivity rather than on the trade-off between sensitivity and specificity ^{12, 16, 17}. Some use a gold standard of limited size ^{15, 16}. Some are based on one or very few algorithms to evaluate performance^{12, 14–16, 18}. Most have focused on fixed signal qualifying thresholds rather than examine a range of thresholds^{12, 15–17, 19}. Most lack verified true negatives (controls) and focus on positive test cases only. Some cover a limited duration of study^{14, 16, 19}, and some examine a narrow spectrum of drug-event relationships¹⁶.

The Observational Medical Outcomes Partnership (OMOP)^20–22 is a large research initiative that aims to identify the most reliable methods for analyzing large volumes of electronic healthcare data for drug safety surveillance. As part of this ongoing effort, the OMOP investigators have compiled and recently made public an extensive gold standard with which they evaluate their portfolio of methods. The gold standard consists of a total 398 positive and negative test cases, which have been validated to the best of existing knowledge. Each test case represents a drug-event pair. The entire gold standard spans 181 unique drugs, covering NSAIDs, antibiotics, antidepressants, ACE inhibitors, beta blockers, antiepileptics, and glucose lowering drugs. The gold standard focuses on 4 unique events—acute myocardial infarction, acute renal failure, acute liver injury, and gastrointestinal bleeding, which represent four of the most significant drug safety outcomes for a risk identification system²³. The gold standard, though not perfect, is as close as currently exists to a widely recognized and publically available benchmark that can be used to evaluate SDAs.

We use the OMOP gold standard in an effort to systematically evaluate and gain a better understanding of the diagnostic potential and operational characteristics of SDAs that are routinely applied to AERS. Unlike previous studies, we specifically focus on the trade-off between sensitivity and specificity, and separate the intrinsic properties of SDAs from their threshold implementation and their commonly applied adjustments. Additionally, we propose an approach to identify optimal signal qualifying thresholds, which accounts for the relative cost associated with false negative and false positive findings.

Our study makes use of nearly the entire set of AERS reports available to date, and covers five established SDAs in routine use : the Multi-item Gamma Poisson Shrinker (MGPS)²⁴, the Proportional Reporting Ratio (PRR)²⁵, the Reporting Odds Ratio (ROR)²⁶, Logistic Regression (LR)^{27, 28}, and Extended Logistic Regression (ELR)²⁹. Table 1 summarizes the main properties of each SDA. Our evaluation follows similar principles as those used to evaluate the accuracy of clinical diagnostic tests, and is based on performance statistics computed from receiver operating characteristic (ROC) curves. Using the area under the ROC curve (AUC) as a main performance metric, we first examine the diagnostic accuracy of SDAs based on several evaluation categories, and several time snapshots of AERS. We then analyze performance at fixed levels of sensitivity, specificity, and at threshold values likely to be selected in practice. Last, we apply Youden’s weighted index^{30, 31} to identify optimal signal thresholds using different cost schemes.

Table 1.

Signal detection algorithms under evaluation.

	Method name	Description	Signal score computed
Disproportionality Analysis	Multi-item Gamma Poisson Shrinker (MGPS)	Bayesian approach designed to guard against false positive signals due to multiple comparisons. Computes an adjusted value of the observed-to-expected reporting ratio corrected for temporal trends and confounding by age and sex	EBGM (empirical Bayes geometric mean): a centrality measure of the posterior distribution of the true observed-to-expected in the population B05: lower 5th percentile of the posterior observed-to-expected distribution
	Proportional Reporting Ratio (PRR)	Method to compute a measure akin to relative risk to quantify the strength of association between a drug and event. Does not correct for temporal trends and confounding by age and sex	PRR: point estimate (mean) of the relative risk reporting ratio distribution PRR05: lower 5th percentile of the relative risk reporting ratio distribution
	Reporting Odds Ratio (ROR)	Method to compute a measure akin to odds ratio to quantify the strength of association between a drug and event. Does not correct for temporal trends and confounding by age and sex	ROR: point estimate (mean) of the reporting odds ratio distribution RORR05: lower 5th percentile of the reporting odds ratio distribution
Multivariate Modeling	Logistic Regression (LR)	Use of multivariate logistic regression to guard against masking effects and false signals due to confounding by concomitant drugs. Computes odds ratios to quantify the strength of association between a drug and event. Requires the user to select in advance the predictors (drugs and other covariates such as sex and age) to be included in the regression model	LR: point estimate of the odds ratio distribution obtained from logistic regression LR05: lower 5th percentile of the odds ratio distribution obtained from logistic regression
	Extended Logistic Regression (ELR)	Based on logistic regression and designed to produce a better model fit for certain (rare) events by allowing for both additive and multiplicative accumulation of risk factors	ELR: point estimate of the odds ratio distribution obtained from extended logistic regression ELR05: lower 5th percentile of the odds ratio obtained from extended logistic regression

2. Results

Data

Our main evaluation period covered AERS data from 1968 through 2011Q3, totaling 4,784,337 reports. Of the 181 drugs appearing in the gold standard, 163 matched exactly with the drug names that appeared in AERS and 17 drugs were manually matched. One drug (endopeptidases) did not apear in the AERS drugs dictionary, resulting in 4 negative test cases being removed from the gold standard. The remaining 394 test cases were used in this analysis. Of these 394 tests cases, 9 drug-event pairs (3 positive cases) were not reported in AERS. Supplementary Material 1 provides the full set of test cases and the 16 evaluated signal scores associated with each test case.

Effectiveness of SDAs

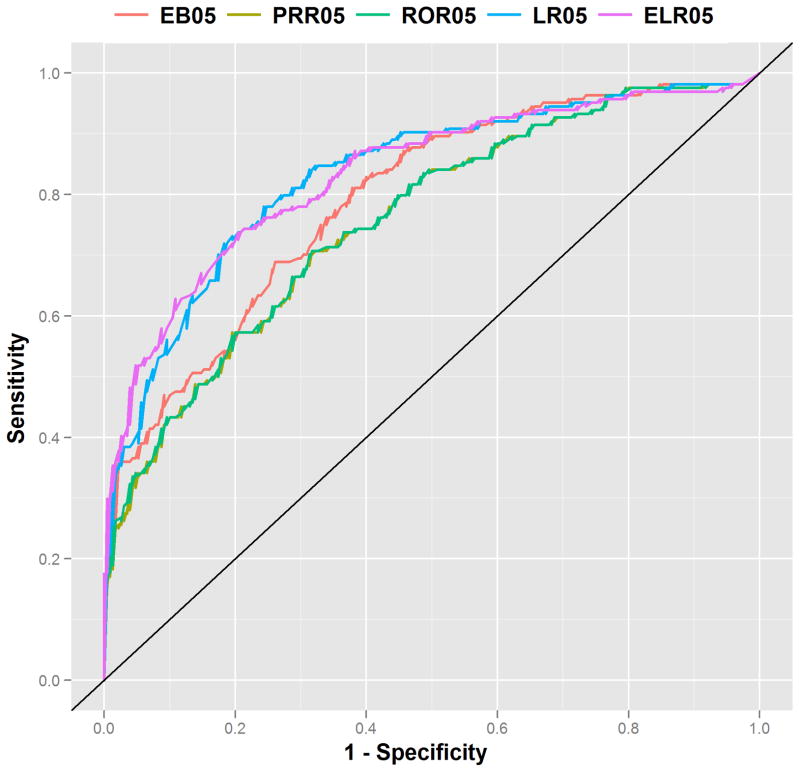
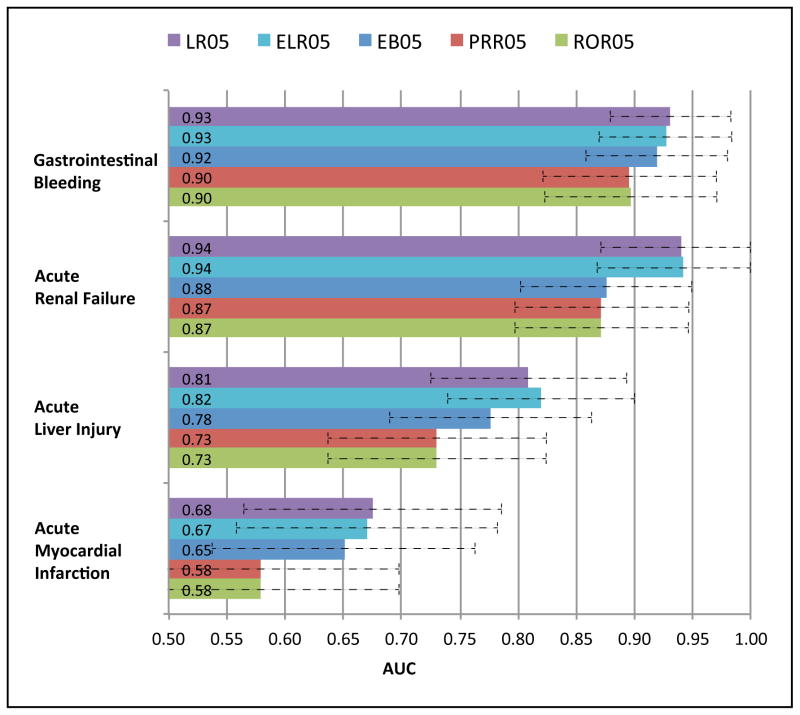
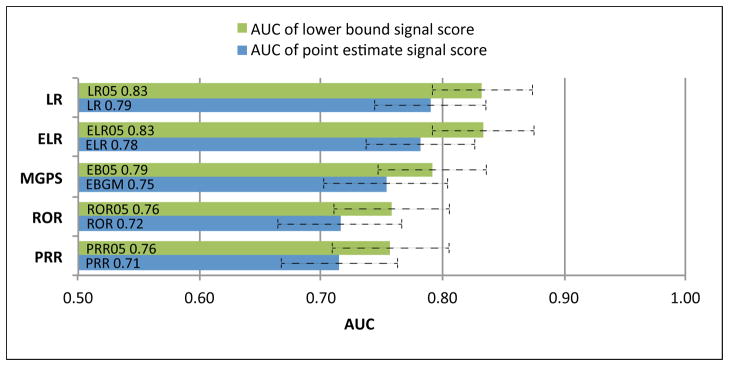
The diagnostic accuracy of SDAs ranges from an AUC=0.71 for PPR to AUC=0.83 for LR05 (Figure 1). Logistic regression (LR)-based approaches outperform DPA approaches (Figures 1 & 2), often by a significant margin, demonstrating their intended purpose to improve upon DPA approaches. The lower bound signal scores (suffixed by 05)—which have been suggested as an adjustment to reduce false signaling²—consistently outperform their corresponding point estimate signal scores across the full range of methods (Figure 1). Among the DPA approaches, MGPS achieved the best performance, with PRR and ROR producing near equivalent performance. P-values (Table 2) indicate that performance differences between the lower bound signal scores are statistically significant at the standard 5% level, except for the relationship between LR05 and ELR05. The ROC curves (Figure 2) display a pattern of containment (no intersection) indicating that there are no levels of sensitivity or specificity for which two methods interchangeably dominate one another. This is especially true for the relationship between DPA and LR based approaches, and implies that LR based approaches are better across all levels of sensitivity/specificity. Examination of AUC by event (Figure 3) reveals that the methods are most effective in discriminating effects when applied to gastrointestinal bleeding and acute renal failure, and least effective in signaling ADEs related to acute myocardial infarction. The event-based differences between best and worst appear to be statistically significant. The figure also shows that the rank ordering of AUCs among the methods is largely preserved even when analyzing each event separately.

Figure 1.

Signal detection algorithm performance based on the Area Under the Receiver Operating Characteristic curves (AUC) metric. LR, Logistic regression; ELR, Extended Logistic Regression; MGPS, Multi-item Gamma Poisson Shrinker; PRR, Proportional Reporting Ratio; ROR, Reporting Odds Ratio. Signal score labels suffixed by ‘05’ (lower bound signal scores) represent the lower 5% of their corresponding point estimate distributions. Error bars reflect AUC 95% confidence intervals.

Figure 2.

Receiver Operating Characteristic (ROC) curves for the EB05, PRR05, ROR05, LR05, and ELR05 signal scores. The pattern of containment between logistic regression and disproportionality based methods imply that the class of logistic regression based approaches provides greater specificity across all levels of sensitivity.

Table 2.

Two-sided P-values for the hypothesis of no difference in performance (AUC) between methods (lower bound signal scores).

	PRR05	ROR05	LR05	ELR05
EB05	<0.00001	0.00001	0.0002	0.0003
PRR05		0.01	<0.00001	<0.00001
ROR05			<0.00001	<0.00001
LR05				0.9

P-values less than 0.00001 are listed at “<0.00001”. P-values show that performance differences between the lower bound signal scores are statistically significant at the standard 5% level, except for the relationship between LR05 and ELR05. P-values are computed using DeLong’s non-parametric approach for correlated ROCs³². AUC, Area Under the Receiver Operating Characteristic curve.

Figure 3.

Signal detection algorithm performance (AUC) classified by event. Error bars reflect AUC 95% confidence intervals. AUC, Area Under the Receiver Operating Characteristic curve.

The next two analyses focus on the EB05 and LR05 signal scores, as the commonly applied representatives of their associated class.

Performance at fixed points

Tables 3 provides performance metrics for fixed levels of sensitivities, specificities, and fixed threshold values likely to be selected in practice. The following are some examples:

Table 3.

Performance metrics for the EB05 and LR05 signal scores based on fixed levels of sensitivity or specificity, or fixed threshold values (left most columns).

	EB05			LR05
Sensitivity	Specificity	PPV	Threshold	Specificity	PPV	Threshold
0.50	0.87	0.73	1.50	0.93	0.83	1.20
0.60	0.79	0.67	1.30	0.87	0.77	1.10
0.70	0.70	0.62	1.10	0.83	0.74	1.00
0.80	0.62	0.60	0.90	0.71	0.67	0.80
0.90	0.47	0.55	0.70	0.55	0.59	0.70
Specificity	Sensitivity	PPV	Threshold	Sensitivity	PPV	Threshold
0.70	0.70	0.62	1.10	0.81	0.66	0.80
0.75	0.65	0.65	1.20	0.78	0.69	0.90
0.80	0.57	0.67	1.30	0.73	0.72	0.90
0.85	0.51	0.71	1.50	0.64	0.75	1.00
0.90	0.47	0.77	1.60	0.56	0.80	1.10
0.95	0.37	0.84	2.00	0.39	0.85	1.40
0.99	0.25	0.95	2.60	0.26	0.95	1.90
Threshold	Sensitivity	Specificity	PPV	Sensitivity	Specificity	PPV
1.00	0.74	0.67	0.62	0.66	0.83	0.73
1.50	0.51	0.85	0.71	0.38	0.97	0.90
2.00	0.36	0.96	0.87	0.24	0.99	0.95
2.50	0.26	0.98	0.91	0.17	1.00	1.00

PPV, positive predictive value.

• At a desired level of at least 0.5 sensitivity, EB05 will result in a specificity of at most 0.87, whereas LR05 would result in a larger specificity of 0.93. The thresholds required to obtain these performance characteristics are 1.5 and 1.2 respectively.

• At a desired level of at least 0.9 specificity, EB05 will result in a sensitivity of at most 0.47, whereas LR05 would result in a sensitivity of 0.56. The thresholds required to obtain these performance characteristics are 1.6, and 1.2 respectively.

• At the commonly cited or suggested threshold value of 2 ^2,32, EB05 will yield a sensitivity of 0.36 and a specificity of 0.96. At the boundary threshold of 1, EB05 and LR05 would result in sensitivities of 0.74/0.66, and specificities of 0.67/0.83 respectively.

Optimal thresholds

Youden’s index is a composite performance measure of sensitivity and specificity that corresponds to a point on the ROC curve, and thus optimal threshold, which maximizes overall correct classification rates while minimizing misclassification rates. Table 4 identifies optimal thresholds for various weighting schemes of Youden’s Index (see methods). Each weighting scheme is characterized by two parameters: c, the cost ratio associated with a false negative as compared with a false positive, and π, the proportion of positive test cases in the gold standard. By giving equal weights to sensitivity and specificity, and not accounting for the prevalence of positive test cases (c=1, π=0.5) the index suggests optimal thresholds around the value 0.9, which produce relatively balanced pairs of sensitivities and specificities in the range 0.62–0.81. Taking into account only the prevalence of positive test cases in the gold standard (c=1, π=0.42) results in larger thresholds, which are naturally shifted towards specificity (since there are more negative test cases). Associating a false positive cost twice as large as the cost associated with false negatives (c=0.5, π=0.42) will result in EB05 being close to its suggested threshold value of 2. Increasing this cost beyond this point did not seem to yield any changes to the optimal threshold for EB05. Likewise assigning more importance to sensitivity did not affect the optimal threshold.

Table 4.

Optimal threshold values for the EB05 and LR05 signal scores based on the weighted Youden index.

	EB05				LR05
Weighting (c, π)	Optimal Threshold	Sensitivity	Specificity	PPV	Optimal Threshold	Sensitivity	Specificity	PPV
(1.00, 0.50)	0.91	0.81	0.62	0.60	0.87	0.78	0.76	0.70
(1.00, 0.42)	1.63	0.47	0.91	0.79	0.95	0.72	0.82	0.74
(1.50, 0.42)	0.91	0.81	0.62	0.60	0.87	0.78	0.76	0.70
(0.50, 0.42)	2.18	0.36	0.98	0.94	1.25	0.49	0.93	0.84
(0.25, 0.42)	2.18	0.36	0.98	0.94	1.69	0.32	0.99	0.95

c, cost ratio associated with a false negative as compared with a false positive; π, proportion of positive test cases in the gold standard.

4. Discussion

With this study we sought to better understand the diagnostic potential and operating characteristics of SDAs routinely applied to AERS. To our knowledge this is the first effort to systematically examine the sensitivity-specificity trade-off and to separate the intrinsic properties of SDAs from their threshold implementation and their commonly applied adjustments. In doing so we examine a large complement of existing SDAs, use a large and diverse reference set of test cases, and examine the majority of AERS reports.

Investigating each signal produced by an SDA involves examining supporting information such as published case reports, biological and clinical plausibility, clinical trials data, and may also require epidemiological studies in healthcare databases^{33, 34}. Consequently, many false alerts may compromise the efficiency of a pharmacovigilance system; and it has been suggested that the specificity or positive predictive value (PPV) of an SDA should be a key consideration^{12, 18, 28}. The appropriate balance between sensitivity and specificity is ultimately a decision that rests with those who use the SDAs. This study informs the choice of balance between sensitivity and specificity (or PPV) based on specific use cases and specific tolerance levels for false positives and false negatives.

Our results suggest that the best performing signal detection algorithms can attain a relatively high degree of accuracy (AUC=0.83) in signaling true ADEs as well as differentiating them from likely spurious ones. Similar levels of accuracy are considered sufficient in widely used diagnostic tests such as those for prostate³⁵ and breast cancers³⁶.

We found that SDAs based on logistic regression are superior to disproportionality analysis, and generally provide greater specificity at a given level of sensitivity. A potential corollary of this finding is that confounding and masking are prevalent in AERS and that methods that adjust for these issues are beneficial to signal detection. Nevertheless, DPA approaches do not require complicated modeling decisions, are faster to compute, and can be applied to AERS as a whole regardless of the event analyzed. Our results also show that there is essentially no difference between LR and ELR in diagnostic accuracy.

The FDA’s main signal detection algorithm, MGPS based on the EB05 score, was found to be the best in its class (DPA), but it appears that stratification plays an important role in its performance. It is also apparent that the family of lower bound signal scores should be preferred over their point estimate counterparts in order to reduce false signaling. For the case of MGPS, the preference of EB05 over the EBGM score has become common practice², albeit with little empirical justification. The equivalent performance of PRR and ROR coincides with an argument presented by Waller et al³⁷.

We examined signal qualifying thresholds at several suggested or commonly cited values and sought to quantitatively identify optimal ones based on a cost or weight attached to sensitivity or specificity. We found that optimal thresholds do not necessarily coincide with those commonly cited (e.g., the value 2) unless a specific tradeoff between sensitivity and specificity is required. We found that at the optimal threshold values SDAs can attain a relatively balanced performance with sensitivity=0.78 and specificity=0.76. By assigning twice as much weight to specificity, SDAs can attain a specificity=0.93 at the expense of dropping sensitivity to 0.50. Under this scenario the optimal threshold is located closer to the commonly cited one.

An important finding is the event-based differential performance of SDAs, which echoes a major result recently reported by OMOP²⁰. That is, in order to maximize the accuracy of a risk identification system through the use of electronic healthcare data, different analytic methods are needed for different health outcomes of interest. Our study is the first to systematically examine event-based differential performance in the context of AERS. The findings suggest that repeating such studies for additional events would enhance the understanding of AERS-based surveillance about the types of outcomes that are best suited for AERS, and those that may need to be surveilled through other sources. For example, it appears that acute myocardial infarction is hard to detect through AERS using existing SDAs (AUC between 0.58–0.67), whereas OMOP has demonstrated that acute myocardial infarction can be detected with much higher accuracy (AUC>0.80) in electronic healthcare data. This finding also supports the general belief that AERS may be better suited for the surveillance of rare events, and less suited for outcomes with a high background rate, such as acute myocardial infarction. However, our results are based on only 4 outcomes and further research is needed before generalizing these findings to other outcomes of interest.

Design choices

A repeated evaluation based on alternative time snapshots of AERS (see methods), indicates that the diagnostic accuracy of SDAs and their rank ordering largely remain stable (AUC difference<0.03). Therefore, our evaluation was not overly sensitive to the time of evaluation on the macro scale. It is likely that with narrower evaluation periods performance may fluctuate, e.g., due to the Weber effect³⁸, publicity biases^{4, 10, 39}, and other reporting patterns that may cause a signal to disappear and reappear over short periods of time.

To examine the sensitivity of the results to the predictors included in the logistic regression models, we reconfigured LR and ELR with fewer and different sets of predictors (see methods). The differences were statistically significant (p-values<0.05) but minimal, e.g., the AUC of LR05 decreased from 0.83 to 0.82 and the same was observed for ELR.

Drug use and the occurrence of adverse events may be correlated with demographic variables such as age and gender or secular variables such as year of report. The importance of stratification to address confounding by these variables, and its influence on the performance of SDAs has been discussed in several reports^{9, 40}. We did not examine performance as a function of all possible stratifications, and used standard starta configurations as defined in the literature. We also examined the unstratified version of MGPS and found that its performance based on the EB05 score worsened (from an AUC=0.79 to AUC=0.76), aligning itself with the performance of PRR05 and ROR05. This finding underscores the notion stratification plays an important role in the performance of SDAs, and that DPA approaches are not that different with respect to diagnostic performance when compared on similar basis. Nonetheless, we stress that it is possible for stratification to adversely impact performance when the number of strata increases and corresponding cell counts become small; producing spurious signals or masking true signals. Therefore, further exploration of stratification is warranted.

The choice of MedDRA groupings to define outcomes and their effect on signal detection have been discussed in several studies with little consensus^{9, 41, 42}. We have used the OMOP definitions as our baseline in an effort to be consistent with OMOP’s gold standard. It is likely that different outcome definitions affect overall performance, but should not affect our comparative findings.

Limitations

The main limitation of this study hinges on the possible correlation between the gold standard and spontaneous reporting. While not directly consulted in the creation of the gold standard, information from spontaneous reporting often contributes to product labeling and the communities’ collective belief of adverse effects, and could have supported the classification of some of the positive test cases used in this study. Moreover, evidence from spontaneous reporting may have contributed to conflicting information in the literature, which may have eliminated some candidate negative controls from consideration. This historical bias suggests that the performance metrics reported here may be biased as it relates to anticipating SDAs’ performance when discriminating future drug-event pairs with unknown effects. Nonetheless, our comparative conclusions should not be affected by this bias.

We did not examine the onset of signals relative to the time an ADE is confirmed or distinguish ADEs associated with acute and chronic drug use. The former however is hard to accurately determine, with some studies providing initial analysis^{12, 14}. We also did not evaluate all existing SDAs. For example, the recently proposed Likelihood Ratio Test⁴³ is currently the only DPA approach that can explicitly control type-I error and false discovery rates associated with multiple comparisons, and it may be instructive to compare the performance of this method with the results presented herein. Furthermore, ROC analysis is only one approach for measuring performance, and other approaches such as those that focus on PPV or false discovery rates could complement this analysis. Last, AERS is subject to several recognized data limitations such as reporting biases, missing or incomplete data, misattributed causal links, and duplicate reporting, which affect the performance characteristics of SDA^{4, 10}. Currently, no SDA is able to overcome all such data quality issues.

4. Methods

Gold Standard

Each drug-event pair is classified as a positive test case or negative test case (control) based on the following criteria:

Positive test cases (41% – 164 of 398 test cases)

• Event listed in Boxed Warning or Warnings/Precautions section of active FDA structured product label.

• Drug listed as ‘causative agent’ in Tisdale et al, 2010: “Drug-Induced Diseases”⁴⁴.

• Literature review identified no powered studies with refuting evidence of effect.

Negative tests cases (59% – 234 of 398 test cases)

• Event not listed anywhere in any section of active FDA structured product label.

• Drug not listed as ‘causative agent’ in Tisdale et al, 2010: “Drug-Induced Diseases”⁴⁴.

• Literature review identified no powered studies with evidence of potential positive association.

The drugs making up the gold standard are specified at the ingredient level, and each event is defined by a group of MedDRA preferred terms (PTs) – a controlled vocabulary developed for ADE applications. OMOP provides alternative definitions for each event ranging from broad to narrow (more specific) definitions. We used the broadest definition for each event. Supplementary material 2 provides the MedDRA grouping for each event, and supplementary material 3 provides a table with the total number of test cases per event.

AERS

We used the public release version of AERS covering the period from 1968 through 2011Q3. From this data we removed duplicate reports, corrected terminological errors, standardized, and normalized drug names at the ingredient level (the same level of drug specificity used by the OMOP gold standard). Events in AERS are coded using MedDRA V14.1. We loaded the preprocessed AERS data into the Empirica Signal V7.3 system (ESS), a drug safety data mining application from Oracle Health Sciences²⁹. Within ESS, we created user-defined (custom) event terms to match the MedDRA PT groups defining each outcome in the gold standard. These user-defined event terms were used to compute reporting frequencies and signal scores for each test case in the gold standard. A spontaneous report was considered to mention a specific outcome if any of the MedDRA PTs defining it was mentioned in the report.

Signal Generation

We used the SDA implementations provided in ESS, and standard configuration parameters as defined in the literature. Signal scores for MGPS were computed based on stratification by age (0–1, 2–4, 5–12, 13–16, 17–45, 46–75, 76–85, >85, unknown), gender (male, female, unknown), and year of report. Unlike DPA methods, LR and ELR are modeled by event (response variable) and require the set of predictors (drugs and strata indicator variables) to be specified in advance. The LR/ELR models we computed included 300 drug predictors, of which 181 were the drugs defining the gold standard and the remaining automatically selected by ESS (based on their co-reported frequency with the event modeled). In addition to these drug predictors we included indicator variables corresponding to same strata used in MGPS. We also reconfigured LR/ELR with same strata as in the main experiment but instead with a set of only 150 drugs, which include only those mentioned with the event in the gold standard and the remaining automatically selected by ESS.

Evaluation

Test cases that were not reported in AERS were assigned a signal score value equal to 0 (lowest possible signal score) so that unreported postive test cases were interpreted as false negatives (becuase they are undetectable) and unreported negative test cases were correctly classifed as true negatives (becuase they are not supposed to be reported).

To examine performance sensitivity to the time of evaluation, we repeated the evaluation with two alternative time periods, 1968–2006 and 1968–2001. For the latter, we removed 32 test cases from the analysis due to 16 drugs approved during or after 2001. None of the drugs in the gold standard were approved after 2006.

Two-sided p-values for the hypothesis of no difference between the performance (AUC) of two SDAs were computed using DeLong’s non-parametric approach for correlated ROCs⁴⁵.

An optimal threshold (T) was identified using a generalizable weighted version of Youden’s index³⁰ proposed by Perkins et al.³¹, and given by:

$$T=\underset{t}{max}\{\mathit{senstivity}(t)+\frac{(1-\pi )}{c·\pi }\mathit{specificity}(t)-1\}$$

Where t is a threshold value, c is the cost ratio associated with a false negative as compared with a false positive, and π is the proportion of positive test cases in the gold standard.

Study Highlights.

What is the current knowledge on the topic?

The performance of signal detection algorithms (SDAs)—which are critical to pharmacovigilance for discovering adverse events—is generally not well understood.

What question this study addressed?

This study characterizes the performance of SDAs routinely applied to the FDA’s adverse event reporting system.

What this study adds to our knowledge?

Overall, SDAs demonstrate reasonable predictive accuracy. The class of approaches that addresses confounding and masking provide improved performance. The study shows that not all events are equally detectable, suggesting that certain events might be surveilled more effectively using other sources. We also propose an approach and apply it to identify optimal signaling thresholds given specific misclassification tolerances.

How this might change clinical pharmacology and therapeutics?

This study provides new insights into the diagnostic potential and characteristics of SDAs to inform future use on and research of SDAs.