The role of the actin cortex in maintaining cell shape

Abstract

Considering that the plasma membrane is host to a variety of mechanical cues in vivo, and the actin cortex is known to support cell shape, it comes as no surprise that the paired membrane-cortex plays a major role in cellular responses to deformation. In a recent study, we applied highly localized forces to HeLa cells in order to examine the deformation response of the membrane and cortex. Direct visualization of the deformation in the loading plane allowed for the characterization of the observed time-dependent strain. Despite large magnitude and long duration loading regimes, the majority of cells recovered their initial pre-deformed morphology within ~2 min. Unexpectedly, perturbed regions above large-volume nuclei were shown to be quite soft and had negligible influence on morphological recovery. The resistance to deformation and ability to recover was found to be largely influenced by the actin network, and dependent upon rho-kinase mediated contractility.

Mechanical cues are well known to influence a variety of cellular functions and processes.^1-3 Key players such as the extracellular matrix, cytoskeleton, and membrane play a concerted response to mechanical perturbations, and numerous studies aim to characterize their roles in mechanotransduction and mechanosensitivity.⁴ The cytoskeleton is well known as the structural edifice of the cell. Actin, in particular, responds dynamically to mechanical deformation by remodelling within a short period of time.⁵ This structurally supportive network must act together with the flexible plasma membrane to resist deformations and also transmit extracellular forces throughout the cell.⁶ Deformation of the membrane leads to chemical rearrangements, protein activation, and intracellular signaling events.^7-12 Moreover, the membrane is linked to the actin cortex, and this membrane-cortex structure plays a major role in governing the mechanical properties of the cell.^13,14 The cortex also plays a key role in controlling cell shape during processes such as mitosis and migration.^14,15 The mechanical properties of these 2 linked cellular constituents clearly influence one another and influence how cells respond to external forces.

In this light, we recently published a study that examined time-dependent deformation of the membrane and cortex of HeLa cells, which we review here (Fig. 1).¹⁶ By applying precise nanonewton forces using an atomic force microscope (AFM) while employing laser scanning confocal microscopy (LSCM), we simultaneously probed and directly visualized the deformation of these cells. The AFM tip was positioned over the center of the nucleus (Fig. 1A), and forces of 5–20nN were applied to the cells for 10 min (Fig. 1B). We observed a viscoelastic cellular response with creeping deformation that demonstrated a linear dependence on force magnitude for the range applied (Fig. 1B, inset). Notably, the majority of cells (80%) recovered at least 50% of their total deformation within 2 min following loading, and most recovered fully (Figs. 1A and 2C). In addition, deformation of the actin cortex was shown to follow that of the membrane, with the majority of the response occurring immediately, and creeping deformation observable during the remainder of loading (Fig. 1B). Although no significant remodelling of F-actin stress fibers was observed in the basal membrane, we cannot rule out possible remodelling of the cortex during or following the deformation.⁵

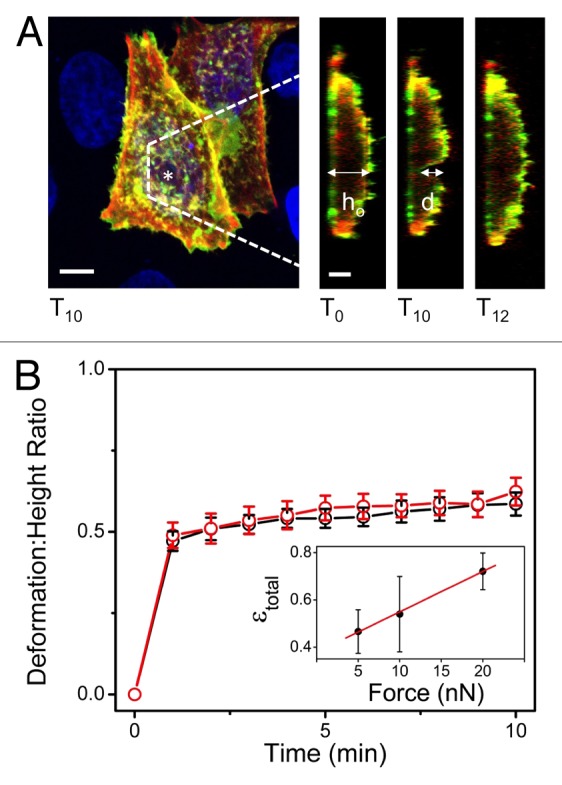
Figure 1. Membrane and cytoskeletal recovery following mechanical perturbation. (A) Both the plasma membrane and underlying cortical actin network recover following mechanical perturbation. Orthogonal YZ images show the undeformed cell height (h_o) prior to deformation (t = 0), the deformation (d) after 10 min of 10-nN applied force (t = 10 min), and the recovered morphology following the removal of the tip (t = 12 – 2 min following loading). This is an example of 1 particular cell that shows in-excess of 50% of cell deformation, but does not reflect the average value of normalized deformation seen in (B). (*) indicates AFM tip position. Green: PH-PLC-δ-EGFP (membrane), Red: LifeAct Ruby (actin cortex), Blue: Hoescht-33342 (nucleus). Scale bars shown are 10μm. (B) Deformation: height ratio (d/h_o) demonstrates creeping behavior of cell deformation over time. Normalized deformation of the membrane (black) vs. actin cortex (red) here shows that the linked cellular components deform simultaneously. Error bars shown are standard error. Inset shows the linear dependence of time-dependent deformation, ε(t) or strain here, on force magnitude for the range tested (5, 10, and 20nN). Error bars for inset are standard deviation. Figure adapted from reference 16.

A test for membrane permeation clearly demonstrated that cells were deformed rather than penetrated from pointed loads.¹⁶ We speculated that the large-volume nucleus may play a role in the observed recovery. To test this hypothesis, the same experiment was performed in regions surrounding the nucleus. Surprisingly, cells perturbed in cytoplasmic regions also recovered (80%). AFM force-maps presented in our previous publication demonstrate that regions above nuclei are softer than peripheral regions, corresponding to their minimal resistance to deformation.¹⁶ In those experiments, force curves were analyzed over a 200-nm indentation in order to isolate the mechanical properties of the cortex and closely underlying nucleus while minimizing substrate effects. Although nuclei are often reported as the stiffest cellular organelle,^17-19 others demonstrate stiffer cytoplasmic regions, consistent with our observations, that likely arise due to an abundance of cytoskeletal filaments in these regions.^20-22 However, our observation is limited to the mechanical properties in a shallow region under the membrane. Young’s modulus measurements performed with deeper indentation will sample different mechanical properties.²³

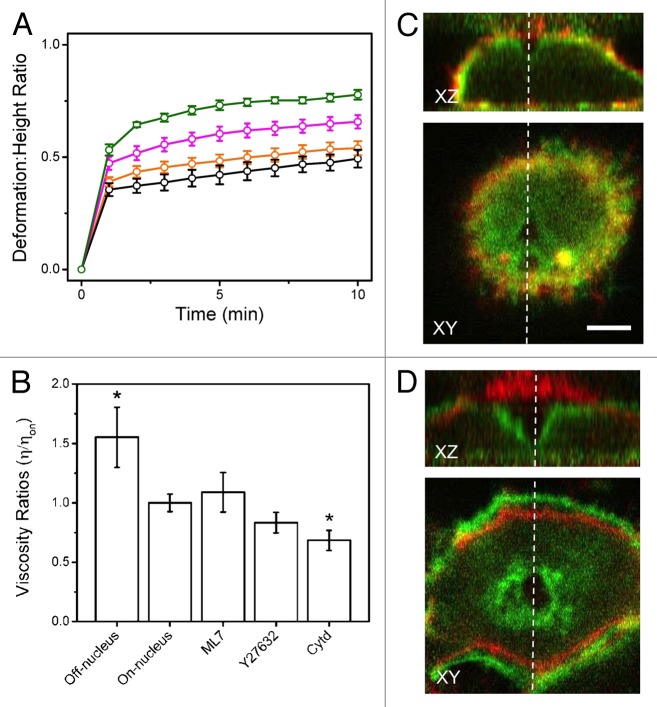
Subsequently, a variety of cytoskeletal inhibitors were employed to examine the role of the cytoskeleton in the deformation/recovery response. Cells were pre-treated with ML7, an inhibitor of myosin light chain kinase (MLCK), Y27632, an inhibitor of rho-kinase (ROCK), and the known actin depolymerizer Cytochalasin d (Cytd). ML7 treatment resulted in no noticeable morphological changes; however, the actin network was partially or completely disrupted by the presence of Y27632 and Cytd, respectively. AFM force-curves (fit to the Hertz model)²⁴ demonstrated a significant decrease (~20%) in stiffness for cells treated with Y27632 and Cytd, in comparison to untreated cells. Reduced stiffness of Y27632- and Cytd-treated cells corresponds with the loss of an intact actin network, and resulted in increased deformation (Fig. 2A). Moreover, cells treated with ML7 displayed a recovery consistent with untreated cells (90%), whereas those treated with Y27632 and Cytd resulted in only 50% and 20% of cells recovering, respectively. The experimental observed time-dependent membrane deformation data was fit with a simple Kelvin-Voigt model using experimentally determined values for Young’s modulus in order to implicitly calculate the viscosity of these cells (Fig. 2B) (see ref. 16 for experimental details). Although there are limitations to this simple model, by comparing viscosity values it was possible to determine that nuclear regions appeared less viscous than surrounding regions, again suggesting the cytoplasm consists of densely packed cytoskeletal filaments resistant to deformation. Moreover, Cytd-treated cells were significantly less viscous than untreated cells and resulted in permanent damage (Fig. 2D), unlike untreated cells (Fig. 2C).

Figure 2. Resistance to deformation is dependent on the cytoskeleton. (A) Deformation: height ratios over time comparing untreated HeLa (orange) to cells treated with ML7 (black), Y27632 (magenta), and Cytd (green). Cells treated with Y27632 and Cytd deformed significantly more than untreated cells. (B) Viscosity ratios derived from Kelvin-Voigt fits of time-dependent strain. Shown are the viscosities of treated cells relative to untreated cells (above the nucleus), as well as the cytoplasmic regions relative to the nuclear region (both untreated). The cytoplasmic regions are more viscous than the nuclear regions, suggesting that they are densely packed with cytoskeletal filaments. As well, cells treated with Cytd are significantly less viscous than untreated cells, indicating that the actin cytoskeleton is mainly responsible for resistance to deformation. Error bars are standard error. (*) indicates p < 0.05 significance compared with on-nucleus results as determined by a t-test. (C) Image overlay of untreated HeLa cells during (after 10 min of 10nN) (green) and prior-to deformation (red). (D) Image overlay of Cytd-treated HeLa cell during (green) and prior-to deformation (red). The deformation is much more pronounced in comparison to untreated cells. Figure adapted from reference 16.

Following up on the results in our previous study,¹⁶ here we report on the role of microtubules (MTs) in governing cortex deformation in HeLa cells by employing Nocodazole (Noco), a known MT inhibitor. As before, a 10-nN force was applied above the cell’s nucleus for 10 min (Fig. 3A). Although MTs were disrupted (Fig. 3B), there was neither a significant change in stiffness or deformation in comparison to untreated cells. We observed 80% recovery of Noco-treated cells, with the majority recovering within 2 min. Both our recent study¹⁶ and the complimentary results shown here demonstrate that actin plays a dominant role in providing mechanical resistance to deformation, for HeLa cells.

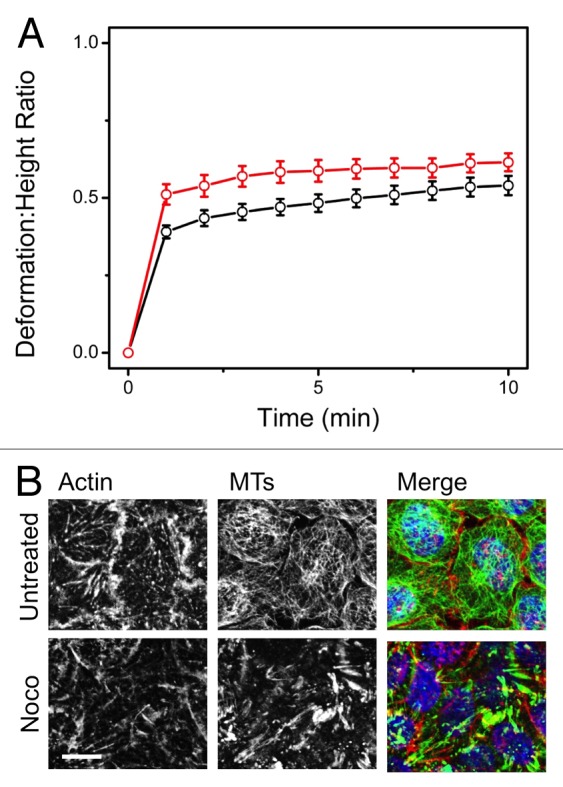
Figure 3. Microtubules are not essential for resisting deformation. (A) Deformation: height ratios over time comparing untreated HeLa (black) to cells treated with Nocodazole (red). Cells were treated with 10mM Noco for 15 min prior to experimentation. Although the average creeping deformation increased from d/h_o = 0.54 for untreated HeLas (n = 26) to d/h_o = 0.61 for Noco-treated cells (n = 10) at t = 10 min of deformation, the increase was insignificant (p > 0.17). This result suggests that the actin network, particularly the cortex, is the key influential cytoskeletal network responsible for the resistance to deformation. Error bars shown are standard error. (B) Immunofluorescent images comparing untreated HeLa to those treated with Noco. Treatment with Noco disrupts the MTs, while leaving the actin network intact. Red: Alexa fluor 564 (actin), Green: Phalloidin (MTs), Blue: Dapi (DNA). Scale bars are 10μm.

Altogether our results demonstrated that the membrane and cortex deform in a unified time-dependent manner, exhibiting near full-recovery within minutes following load-cessation.¹⁶ Surprisingly, large-volume nuclear regions were observed to be highly deformable and do not appear to play a role in cell-shape recovery. This is possibly due to HeLas being a cancerous cell type. AFM force-curves have previously demonstrated that cancer cells and cancer cell nuclei tend to be more deformable than benign cells.^25-28 Moreover, considering that a small number (~20%) of Cytd-treated cells recovered, actin cannot be the sole initiator of cell shape recovery. It is possible that movement of the cytosol, sub-cellular structure, and the dense filamentous networks may also contribute to the observed recovery, in correlation with recently proposed poroelastic models.²⁹ Future studies that characterize the time-dependent mechanical deformations of a variety of sub-cellular structures in multiple cell types will provide further insight into these mechanical responses.

10.4161/cib.26714

Disclosure of Potential Conflict of Interest

No potential conflicts of interest were disclosed.