CAUSAL INFERENCE FOR CONTINUOUS-TIME PROCESSES WHEN COVARIATES ARE OBSERVED ONLY AT DISCRETE TIMES

Abstract

Most of the work on the structural nested model and g-estimation for causal inference in longitudinal data assumes a discrete-time underlying data generating process. However, in some observational studies, it is more reasonable to assume that the data are generated from a continuous-time process and are only observable at discrete time points. When these circumstances arise, the sequential randomization assumption in the observed discrete-time data, which is essential in justifying discrete-time g-estimation, may not be reasonable. Under a deterministic model, we discuss other useful assumptions that guarantee the consistency of discrete-time g-estimation. In more general cases, when those assumptions are violated, we propose a controlling-the-future method that performs at least as well as g-estimation in most scenarios and which provides consistent estimation in some cases where g-estimation is severely inconsistent. We apply the methods discussed in this paper to simulated data, as well as to a data set collected following a massive flood in Bangladesh, estimating the effect of diarrhea on children’s height. Results from different methods are compared in both simulation and the real application.

1. Introduction and motivation

In this paper, we study assumptions and methods for making causal inferences about the effect of a treatment that varies in continuous time when its time-dependent confounders are observed only at discrete times. Examples of settings in which this problem arises are given in Section 1.2. In such settings, standard discrete-time methods such as g-estimation usually do not work, except when certain conditions are assumed for the continuous-time process. In this paper, we formulate such conditions. When these conditions do not hold, we propose a controlling-the-future method which can produce consistent estimates when g-estimation is consistent and which is still consistent in some cases when g-estimation is severely inconsistent.

First, we review the approach of James Robins and collaborators to making causal inferences about the effect of a treatment that varies at discrete, observed times.

1.1. Review of Robins’ causal inference approach for treatments varying at discrete, observed times

In a cross-sectional observational study of the effect of a treatment on an outcome, a usual assumption for making causal inferences is that there are no unmeasured confounders, that is, that conditional on the measured confounders, the data is generated as if the treatment were assigned randomly. Under this assumption, a consistent estimate of the average causal effect of the treatment can be obtained from a correct model of the association between the treatment and the outcome conditional on the measured confounders [Cochran (1965)]. In a longitudinal study, the analog of the “no unmeasured confounders” assumption is that at the time of each treatment assignment, there are no unmeasured confounders; this is called the sequential randomization or sequential ignorability assumption, given as follows.

• (A1)The longitudinal data of interest are generated as if the treatment is randomized in each period, conditional on the current values of measured covariates and the history of the measured covariates and the treatment.

The sequential randomization assumption implies that decision on treatment assignment is based on observable history and contemporaneous covariates, and that people have no ability to see into the future. Robins (1986) has shown that for a longitudinal study, unlike for a cross-sectional study, even if the sequential randomization assumption holds, the standard method of estimating the causal effect of the treatment by the association between the outcome and the treatment history conditional on the confounders can provide a biased and inconsistent estimate. This bias can occur when we are interested in estimating the joint effects of all treatment assignments and when the following conditions hold:

• (c1)conditional on past treatment history, a time-dependent variable is a predictor of the subsequent mean of the outcome and also a predictor of subsequent treatment;
• (c2)past treatment history is an independent predictor of the time-dependent variable.

Here, “independent predictor” means that prior treatment predicts current levels of the covariate, even after conditioning on other covariates. An example in which the standard methods are biased is the estimation of the causal effect of the drug AZT (zidovudine) on CD4 counts in AIDS patients. Past CD4 count is a time-dependent confounder for the effect of AZT on future CD4 count since it not only predicts future CD4 count, but also subsequent initiation of AZT therapy. Also, AZT history is an independent predictor of subsequent CD4 count [e.g., Hernán, Brumback and Robins (2002)].

To eliminate the bias of standard methods for estimating the causal effect of treatment in longitudinal studies where sequential randomization holds but there are time-dependent confounders satisfying conditions (c1) and (c2) (e.g., past CD4 counts), Robins (1986, 1992, 1994, 1998, 2000) developed a number of innovative methods. We focus here on structural nested models (SNMs) and their associated methods of g-testing and g-estimation. The basic idea of the g-test is the following. Given a hypothesized treatment effect and a deterministic model of the treatment effect, we can calculate the potential outcome that a subject would have had if she never received the treatment. Such an outcome is also known as a counterfactual outcome, which is the outcome under a treatment history that might be contrary to the realized treatment history. If the hypothesized treatment effect is the true treatment effect, then this potential outcome will be independent of the actual treatment the subject received conditional on the confounder and treatment history, under the sequential randomization assumption (A1). g-estimation involves finding the treatment effect that makes the g-test statistic have its expected null value. For simplicity, our exposition focuses on deterministic rank-preserving structural nested distribution models; g-estimation also works for nondeterministic structural nested distribution models.

The SNM and g-estimation were developed for settings in which treatment decisions are being made at discrete times at which all the confounders are observed. In some settings, the treatment is varying in continuous time, but confounders are only observed at discrete times.

1.2. Examples of treatments varying in continuous time where covariates are observed only at discrete times

Example 1 (The effect of diarrhea on children’s height)

Diarrheal disease is one of the leading causes of childhood illness in developing regions [Kosek, Bern and Guerrant (2003)]. Consequently, there is considerable concern about the effects of diarrhea on a child’s physical and cognitive development [Moore et al. (2001), Guerrant et al. (2002)]. A data set which provides the opportunity to study the impact of diarrhea on a child’s height is a longitudinal household survey conducted in Bangladesh in 1998–1999 after Bangladesh was struck by its worst flood in over a century in the summer of 1998 [del Ninno et al. (2001), del Ninno and Lundberg (2005)]. The survey was fielded in three waves from a sample of 757 households: round 1 in November, 1998; round 2 in March–April, 1999; round 3 in November, 1999. The survey recorded all episodes of diarrhea for each child in the household in the past six months or since the last interview by asking the families at the time of each interview. In addition, the survey recorded at each of the three interview times several important time-dependent covariates for the effect of diarrhea on a child’s future height: the child’s current height and weight; the amount of flooding in the child’s home and village; the household’s economic and sanitation status. In particular, the child’s current height and weight are time-dependent confounders that satisfy conditions (c1) and (c2), making standard longitudinal data analysis methods biased [see Martorell and Ho (1984) and Moore et al. (2001) for discussion of evidence for and reasons why current height and weight satisfy conditions (c1) and (c2)]. The time-dependent confounders of current height and weight are available only at the time of the interview, and changes in their value that might affect the exposure of the child to the “treatment” of diarrhea, which varies in continuous time, are not recorded in continuous time.

Example 2 [The effect of AZT (Zidovudine) on CD4 counts]

The Multi-center AIDS Cohort Study [MACS, Kaslow et al. (1987)] has been used to study the effect of AZT on CD4 counts [Hernán, Brumback and Robins (2002), Brumback et al. (2004)]. Participants in the study are asked to come semi-annually for visits at which they are asked to complete a detailed interview, including a complete history of their AZT use, as well as to take a physical examination. Decisions on AZT use are made by subjects and their physicians, and switches of treatment might happen at any time between two visits. These decisions are based on the values of diagnostic variables, possibly including CD4 and CD8 counts, and the presence of certain symptoms. However, these covariates are only measured by MACS at the time of visits; the values of these covariates at the exact times that treatment decisions are made between visits are not available.

1.3. A model data generating process

In both the examples of AZT and diarrhea, the exposure or treatment process happens continuously in time and a complete record of the process is available, but the time-dependent confounders are only observed at discrete times. There could be various interpretations of the relationship between the data at the treatment decision level and the data at the observational time level. To clarify the problem of interest in this paper, we consider a model data generating process that satisfies all of the following assumptions:

• (a1)a patient takes a certain medicine under the advice of a doctor;
• (a2)a doctor continuously monitors and records a list of health indicators of her patient and decides the initiation and cessation of the medicine solely based on current and historical records of these conditions, the historical use of the medicine and possibly random factors unrelated to the patient’s health;
• (a3)a third party organization asks a collection of patients from various doctors to visit the organization’s office semi-annually; the organization measures the same list of health indicators for the patients during their visits and asks the patients to report the detailed history of the use of the medicine between two visits;
• (a4)we are only provided with the third party’s data.

Note that in (a2), we assume the sequential randomization assumption (A1) at the treatment decision level.

The AZT example can be approximated by the above data generating process. In the AZT example, (a1) and (a2) approximately describe the joint decision-making process by the patient and the doctor in the real world. (a3) can be justified by reasonably assuming that the staff at the MACS receive similar medical training and use similar medical equipment as the patients’ doctors. In the diarrhea example, the patient’s body, rather than a doctor, determines whether the patient gets diarrhea. Assumption (a3), then, is saying that the third party organization (the survey organization) collects enough health data and that if all the histories of such health data are available, the occurrence of diarrhea is conditionally independent of the potential height.

1.4. Difficulties posed by treatments varying in continuous time when covariates are observed only at discrete times

Suppose our data are generated as in the previous section and we apply discrete-time g-estimation at the discrete times at which the time-dependent covariates are observed; we will denote these observation times by 0,…, K. In discrete-time g-estimation, we are testing whether the observed treatment at time t (t = 0,…, K) is, conditional on the observed treatments at times 0, 1,…, t −1 and observed covariates at times 0,…, t, independent of the putative potential outcomes at times t + 1,…, K, calculated under the hypothesized treatment effect, where the putative potential outcomes considered are what the subject’s outcome would be at times t + 1,…, K if the subject never received treatment at any time point. The difficulty with this procedure is that even if sequential randomization holds when the measured confounders are measured in continuous time [as is assumed in (a2)], it may not hold when the measured confounders are measured only at discrete times. For the discrete-time data, there can be unmeasured confounders. In the MACS example, the diagnostic measures at the time of AZT initiation are missing unless the start of AZT initiation occurred exactly at one of the discrete times that the covariates are observed; the diagnostic measures at the initiation time are clearly important confounders for the treatment status at the subsequent observational time. In the diarrhea example, the nutrition status of the child before the start of a diarrhea episode is missing unless the start of the diarrhea episode occurred exactly at one of the discrete times that covariates are observed; this nutrition status is also an important confounder for the diarrhea status at the subsequent observational time. Continuous-time sequential randomization does not, in general, justify sequential randomization holding for the discrete-time data, meaning that discrete-time g-estimation can produce inconsistent estimates, even when continuous-time sequential randomization holds.

In this paper, we approach this problem from two perspectives. First, we give conditions on the underlying continuous-time processes under which discrete-time sequential randomization is implied, warranting the use of discrete-time g-estimation. Second, we propose a new estimation method, called the controlling-the-future method, that can produce consistent estimates whenever discrete-time g-estimation is consistent and can produce consistent estimates in some cases where discrete-time g-estimation is inconsistent.

Our discussion focuses on a binary treatment and repeated continuous outcomes. We also assume that the cumulative amount of treatment between two visits is observed. This is true for Examples 1 and 2, the AZT and diarrhea studies, respectively. If cumulative treatment is not observed, there will often be a measurement error problem in the amount of treatment, which is beyond the scope of this paper and an issue which we are currently researching.

The organization of the paper is as follows: Section 2 reviews the standard discrete-time structural nested model and g-estimation, describes a modified application when the underlying process is in continuous time and proposes conditions on the continuous-time processes when it works; Section 3 describes our controlling-the-future method; Section 4 presents a simulation study; Section 5 provides an application to the diarrhea study discussed in Example 1; Section 6 concludes the paper.

2. A modified g-estimation for discretely observed continuous-time processes

In this section, we first review the discrete-time structural nested model and the standard g-estimation, and mathematically formalize the setting we described in Section 1.3. Then, with a slight modification and different interpretation of notation, the g-estimation can be applied to the discrete-time observations from the continuous-time model. We will show that under certain conditions, this estimation method is consistent.

2.1. Review of discrete-time structural nested model and g-estimation

To reduce notation for the continuous-time setting, we use a star superscript on every variable in this section.

Assuming that all variables can only change values at time 0, 1, 2,…, K, we use $A_k^{\ast }$ to denote the binary treatment decision at time k. Under the discrete-time setup, $A_k^{\ast }$ is assumed to be the constant level of treatment between time k and time (k + 1). We use $Y_k^{0\ast }$ to denote the baseline potential outcome of the study at time k if the subject does not receive any treatment throughout the study and $Y_k^{\ast }$ to denote the actual outcome at time k. In this paper, we assume that all $Y_k^{0\ast }$’s and $Y_k^{\ast }$’s are continuous variables. Let $L_k^{\ast }$ be the vector of covariates collected at time k. As a convention, $Y_k^{\ast }$ is included in $L_k^{\ast }$.

We consider a simple deterministic model for the purposes of illustration,

$$Y_k^{\ast }=Y_k^{0\ast }+\mathrm{\Psi }\sum _{i=0}^{k-1}{A}_i^{\ast },$$ (1)

where Ψ is the causal parameter of interest and can be interpreted as the effect of one unit of the treatment on the outcome.

Model (1) is known as a rank-preserving model [Robins (1992)]. Under this model, for subjects i and j who have the same observed treatment history up to time k, if we observe Y_k,i < Y_k,j, then we must have $Y_{k,i}^{0\ast }<Y_{k,j}^{0\ast }$. It is also stronger than a more general rank-preserving model since $Y_k^{\ast }$ depends deterministically only on $Y_k^{0\ast }$ and the $A_i^{\ast }$’s.

Causal inference aims to estimate Ψ from the observables, the $A_k^{\ast }$’s and $L_k^{\ast }$’s. One way to achieve the identification of Ψ is to assume sequential randomization (A1). Given this notation and model (1), a mathematical formulation of (A1) is

$$P(A_k^{\ast }\mid {\overline{L}}_k^{\ast },{\overline{A}}_{k-1}^{\ast },{\underset{\_}{Y}}_{k+}^{0\ast })=P(A_k^{\ast }\mid {\overline{L}}_k^{\ast },{\overline{A}}_{k-1}^{\ast }),$$ (2)

where ${\overline{L}}_k^{\ast }=(L_0,L_1,\dots ,L_k),{\overline{A}}_{k-1}^{\ast }=(A_0,A_1,\dots ,A_{k-1})$ and ${\underset{\_}{Y}}_{k+}^{0\ast }=(Y_{k+1}^{0\ast },Y_{k+2}^{0\ast },\dots ,Y_K^{0\ast })$.

For any hypothesized value of Ψ, we define a putative potential outcome,

$$Y_k^{0\ast }(\mathrm{\Psi })=Y_k^{\ast }-\mathrm{\Psi }\sum _{i=0}^{k-1}{A}_i.$$

Then, under (1) and (2), the correct Ψ should solve

$$E[U(\mathrm{\Psi })]\equiv E\left\{\sum _{\begin{array}{c}k<m\le K\\ 1\le i\le N\end{array}}[A_{i,k}^{\ast }-p_k(X_{i,k}^{\ast })]g(Y_{i,m}^{0\ast }(\mathrm{\Psi }),X_{i,k}^{\ast })\right\}=0,$$ (3)

where i is the index for each subject where there are N subjects, $X_{i,k}^{\ast }=({\overline{L}}_{i,k}^{\ast },{\overline{A}}_{i,k-1}^{\ast }),p_k(X_{i,k}^{\ast })=P(A_{i,k}^{\ast }=1\mid X_{i,k}^{\ast })$ is the propensity score for subject i at time k and g is any function. This estimating equation can be generalized, with g being a function of any number of future $Y_{i,m}^{0\ast }(\mathrm{\Psi })$’s and $X_{i,k}^{\ast }$.

To estimate Ψ, we solve the empirical version of (3):

$$U(\mathrm{\Psi })\equiv \sum _{\begin{array}{c}k<m\le K\\ 1\le i\le N\end{array}}[A_{i,k}^{\ast }-p_k(X_{i,k}^{\ast })]g(Y_{i,m}^{0\ast }(\mathrm{\Psi }),X_{i,k}^{\ast })=0.$$ (4)

If the true propensity score model is unknown and is parameterized as $p_k(X_k^{\ast },\beta )$, additional estimating equations are needed to identify β. For example, the following estimating equations could be used:

$$U(\mathrm{\Psi },\beta )=\sum _{\begin{array}{l}k<m\le K\\ 1\le i\le N\end{array}}[A_{i,k}^{\ast }-p_k(X_{i,k}^{\ast })]{[g(Y_{i,m}^{0\ast }(\mathrm{\Psi }),X_{i,k}^{\ast }),X_{i,k}^{\ast }]}^T=0.$$ (5)

The method is known as g-estimation. The efficiency of the estimate depends on the functional form of g. The optimal g function that produces the most efficient estimation can be derived [Robins (1992)]. The formulas for estimating the covariance matrix of (Ψ̂, β̂) are given in Appendix A. A short discussion of the existence of the solution to the estimating equation and identification can be found in Appendix B.

2.2. A continuous-time deterministic model and continuous-time sequential randomization

We now extend the model in Section 2.1 to a continuous-time model and define a continuous-time version of the sequential randomization assumption (A1) as a counterpart of (2).

We now assume that the variables can change their values at any real time between 0 and K. The model in Section 2.1 is then extended as follows:

• {Y_t ; 0 ≤ t ≤ K} is the continuous-time, continuously-valued outcome process;

• {L_t ; 0 ≤t ≤K} is the continuous-time covariate process—it can be multidimensional and Y_t is an element of L_t ;

• {A_t ; 0 ≤t ≤K} is the continuous-time binary treatment process;

• { $Y_t^0$;0 ≤t ≤K} is the continuous-time, continuously-valued potential out-come process if the subject does not receive any treatment from time 0 to time K—it can be thought of as the natural process of the subject, free of treatment/intervention.

As a regularity condition, we further assume that all of the continuous-time stochastic processes are càdlàg processes (i.e., continuous from the right, having limits from the left) throughout this paper.

A natural extension of model (1) is

$$Y_t=Y_t^0+\mathrm{\Psi }{\int }_0^t{A}_{s}ds,$$ (6)

where Ψ is the causal parameter of interest. Ψ can be interpreted as the effect rate of the treatment on the outcome.

In this continuous-time model, a continuous-time version of the sequential randomization assumption (A1) or, equivalently, assumption (a2), can be formalized, although it does not have a simple form similar to equation (2). It was noted by Lok (2008) that a direct extension of the formula (2) involves “conditioning null events on null events.”

Lok (2008) formally defined continuous-time sequential randomization when there is only one outcome at the end of the study. We propose a similar definition for studies with repeated outcomes under the deterministic model (6).

Let $Z_t=(L_t,A_t,Y_t^0)$. Let σ(Z_t) be the σ -field generated by Z_t, that is, the smallest σ -field that makes Z_t measurable. Let σ(Z̄_t) be the σ -field generated by ∪_u≤t σ(Z_u). Similarly, $\sigma ({\overline{Z}}_t,{\underset{\_}{Y}}_{t+}^0)$ is the σ -field generated by $\sigma ({\overline{Z}}_t)\cup \sigma ({\underset{\_}{Y}}_{t+}^0)$, where $\sigma ({\underset{\_}{Y}}_{t+}^0)$ is the σ -field generated by ${\cup }_{u>t}\sigma (Y_u^0)$. By definition, the sequence of σ(Z̄_t), 0 ≤t ≤K, forms a filtration. The sequence of $\sigma ({\overline{Z}}_t,{\underset{\_}{Y}}_{t+}^0)$, 0 ≤t ≤K, also forms a filtration because $\sigma ({\overline{Z}}_t,{\underset{\_}{Y}}_{t+}^0)\subset \sigma ({\overline{Z}}_s,{\underset{\_}{Y}}_{s+}^0)$ for t < s [note that this is true under the deterministic model (6), but not in general].

Let N_t be a counting process determined by A_t. It counts the number of jumps in the A_t process. Let λ_t be a version of the intensity process of N_t with respect to σ(Z̄_t). $M_t=N_t-{\int }_0^t{\lambda }_{s}ds$ will be a martingale with respect to σ(Z̄_t).

Definition 1

With N_t and M_t defined as above, the càdlàg process $Z_t\equiv (L_t,A_t,Y_t^0)$, 0 ≤t ≤K, is said to satisfy the continuous-time sequential randomization assumption, or CTSR, if M_t is also a martingale with respect to $\sigma ({\overline{Z}}_t,{\underset{\_}{Y}}_{t+}^0)$. Or, equivalently, there exists a λ_t that is the intensity of N_t, with respect to both the filtration of $\sigma ({\overline{Z}}_t,{\underset{\_}{Y}}_{t+}^0)$ and the filtration of σ(Z̄_t).

In this definition, given A₀, the counting process ${\{N_t\}}_0^T$ offers an alternative description of the treatment process ${\{A_t\}}_0^T$. The intensity process λ_t, which models the jumping rate of N_t, plays the same role as the propensity scores in the discrete-time model, which models the switching of the treatment process. Definition 1 formalizes assumption (A1) in the continuous-time model, by stating that λ_t does not depend on future potential outcomes.

The definition can be generalized if A_t has more than two levels, where N_t can be a multivariate counting process, each element counts a type of jump of the A_t process and λ_t is the multivariate intensity process for N_t under both the filtration of σ(Z̄_t) and the filtration of $\sigma ({\overline{Z}}_t,{\underset{\_}{Y}}_{t+}^0)$; see Lok (2008).

2.3. A modified g-estimation

In this paper, we assume that the continuous process defined in Section 2.2 can only be observed at integer times, namely, times 0, 1, 2,…, K. We use the same starred notation as in Section 2.1, but interpret instances of this as discrete-time observations from the model in Section 2.2. Specifically:

• { $A_k^{\ast }$, k =0, 1, 2,…, K} denotes the set of treatment assignments observable at times 0, 1, 2,…, K. We use ${\overline{A}}_k^{\ast }$ to denote the observed history of observed discrete-time treatment up to time k, that is, ( $A_0^{\ast },A_0^{\ast },\dots ,A_k^{\ast }$). Additionally, we use cum $A_k^{\ast }={\int }_0^{k-}{A}_{s}ds$ to denote the cumulative amount of treatment up to time k. Note that in the continuous-time model, cum $A_k^{\ast }\ne {\sum }_{k^{\prime }=0}^{k-1}{A}_{k^{\prime }}^{\ast }$, as it would in discrete-time models. We let $\overline{\text{cum}{A}_k^{\ast }}=(\text{cum}{A}_1^{\ast },\text{cum}{A}_2^{\ast },\dots ,\text{cum}{A}_k^{\ast })$. We note that, in practice, people sometimes use ${\stackrel{\sim }{A}}_k^{\ast }=\text{cum}{A}_{k+1}^{\ast }-\text{cum}{A}_k^{\ast }$ as the treatment at time k when applying discrete-time g-estimation to discrete-time observational data. Under deterministic models, such use of g-estimation usually requires stronger conditions than the conditions discussed in this paper. Throughout this paper, we define the treatment at time k as $A_k^{\ast }$.

• We define $L_k^{\ast }$, the observed covariates at time k, to be L_k−, the left limit of L at time k, following the convention that in the discrete model, people usually assume that the covariates are measured just before the treatment decision at time k. $Y_k^{\ast }$ and $Y_k^{0\ast }$ are also defined as Y_k− and $Y_{k-}^0$, respectively, following the same convention. ${\overline{L}}_k^{\ast }$ denotes ( $L_0^{\ast },L_1^{\ast },\dots ,L_k^{\ast }$), and ${\overline{Y}}_k^{\ast }$ and ${\overline{Y}}_k^{0\ast }$ are defined accordingly. ${\underset{\_}{Y}}_{k+}^{0\ast }=(Y_{k+1}^{0\ast },Y_{k+2}^{0\ast },\dots ,Y_K^{0\ast })$.

With this notation and in the spirit of g-estimation, which controls all observed history in the propensity score model for the treatment, we propose the following working estimating equation:

$$U(\mathrm{\Psi })=\sum _{\begin{array}{c}k<m\le K\\ 1\le i\le N\end{array}}[A_{i,k}^{\ast }-p_k(X_{i,k}^{\ast })]g(Y_{i,m}^{0\ast }(\mathrm{\Psi }),X_{i,k}^{\ast })=0,$$ (7)

where $X_{i,k}^{\ast }$ is the collection of ${\overline{L}}_{i,k}^{\ast },{\overline{A}}_{i,k-1}^{\ast }$ and $\overline{\text{cum}{A}_{i,k}^{\ast }},p_k(X_{i,k}^{\ast })=P(A_{i,k}^{\ast }=1\mid X_{i,k}^{\ast })$ and $Y_{i,m}^{0\ast }(\mathrm{\Psi })=Y_{i,m}^{\ast }-\mathrm{\Psi }\text{cum}{A}_{i,k}^{\ast }$.

In practice, $p_k(X_{i,k}^{\ast })$ is unknown and has to be parameterized as $p_k(X_{i,k}^{\ast };\beta )$, and we use different functions g to identify all of the parameters, as in Section 2.1. The covariance matrix of estimated parameters can be estimated as in Appendix A. A discussion of the existence of a solution and identification can be found in Appendix B.

The estimating equation has the same form as (4), except for two important differences. First, the propensity score model in this section conditions on the additional $\overline{\text{cum}{A}_{i,k}^{\ast }}$. In the discrete-time model of Section 2.1, $\overline{\text{cum}{A}_{i,k}^{\ast }}$ would be a transformed version of ${\overline{A}}_{i,k-1}^{\ast }$ and was redundant information. However, with continuous-time underlying processes, $\overline{\text{cum}{A}_{i,k}^{\ast }}$ provides new information on the treatment history. Second, the putative potential outcome $Y_{i,m}^{0\ast }(\mathrm{\Psi })$ is calculated by subtracting the cum $A_{i,k}^{\ast }$ from $Y_{i,m}^{\ast }$, instead of ${\sum }_{l=0}^{k-1}{A}_{i,l}^{\ast }$. We will later refer to the g-estimation in this section as the modified g-estimation (although it is in the true spirit of g-estimation). The justification and limitation of using the modified g-estimation will be discussed in Section 2.4.

We refer to the g-estimation in Section 2.1 as naive g-estimation when it is applied to data from a continuous-time model. When the data come from a continuous-time model, the naive g-estimation can be severely biased, as we will show in our simulation study and the diarrhea application. One source of bias is a measurement error problem, ${\sum }_{l=0}^{k-1}{A}_{i,l}^{\ast }$ is not the correct measure of the treatment; another source of bias is that the important information $\overline{\text{cum}{A}_{i,k}}$ is not conditioned on in the propensity score. Although we would not expect researchers to use naive g-estimation when the true cumulative treatments are available, we present the simulation and real application results using this method as a reference to show how severely biased the estimates would be had we not known the true cumulative treatments and the measurement error problem had dominated.

2.4. Justification of the modified g-estimation

Given discrete-time observational data from continuous-time underlying processes, solving equation (7) provides an estimate for Ψ. For this Ψ estimate to be consistent, an analog to condition (2) is needed:

$$P(A_k^{\ast }\mid {\overline{L}}_k^{\ast },{\overline{A}}_{k-1}^{\ast },\overline{\text{cum}{A}_k^{\ast }},{\underset{\_}{Y}}_{k+}^{\ast 0})=P(A_k^{\ast }\mid {\overline{L}}_k^{\ast },{\overline{A}}_{k-1}^{\ast },\overline{\text{cum}{A}_k^{\ast }}).$$ (8)

Condition (8) is a requirement on variables at observational time points. Its validity for a given study relies on how the data are collected, in addition to the underlying continuous-time data generating process. It is not clear, without conditions on the underlying continuous-time data generating process, how one would go about collecting data in a way such that (8) would hold while the standard ignorability (2) is not true. Here, we will seek conditions at the continuous-time process level that imply condition (8) and hence justify the estimating equation (7). In particular, we consider two such conditions.

2.4.1. Sequential randomization at any finite subset of time points

Recall the data generating process described in Section 1.3. The third party organization periodically (e.g., semi-annually) collects the health data and treatment records of the patients. Suppose that a researcher thinks (8) holds for the time points at which the third party organization collects these data. If the time points have not been chosen in a special way to make (8) hold, then the researcher will often be willing to make the stronger assumption that (8) would hold for any finite subset of time points at which the third party organization chose to collect data. For example, for the diarrhea study, the survey was actually conducted in November, 1998, March–April, 1999 and November, 1999. If a researcher thought (8) held for these three time points, then she might be willing to assume that (8) should also hold if the survey was instead conducted in December, 1998, February, 1999, May, 1999 and October, 1999.

Before formalizing the researcher’s assumption on any finite subset of time points, we make the following observation.

Proposition 2

Under the deterministic model assumption (6), the propensity score has the following property:

$$P(A_k^{\ast }=1\mid {\overline{L}}_k^{\ast },{\overline{A}}_{k-1}^{\ast },\overline{\text{cum}{A}_k^{\ast }})=P(A_k^{\ast }=1\mid {\overline{L}}_k^{\ast },{\overline{A}}_{k-1}^{\ast },{\overline{Y}}_k^{0\ast }).$$ (9)

Proof

Under the deterministic assumption (6) and the correct Ψ, ( ${\overline{L}}_k^{\ast },{\overline{A}}_{k-1}^{\ast },\overline{\text{cum}{A}_k^{\ast }}$) is a one-to-one transformation of ( ${\overline{L}}_k^{\ast },{\overline{A}}_{k-1}^{\ast },{\overline{Y}}_k^{0\ast }$).

Using Proposition 2, we state the sequential randomization assumption at any finite subset of time points as follows.

Definition 3

A càdlàg process $Z_t\equiv (L_t,A_t,Y_t^0)$, 0 ≤t ≤K, is said to satisfy the finite-time sequential randomization assumption, or FTSR, if, for any finite subset of time points, 0 ≤ t₁ < t₂ < ··· < t_n < t_n+1 < ··· < t_n+l ≤K, we have

$$P(A_{t_n}\mid {\overline{L}}_{t_n-},{\overline{A}}_{t_{n-1}},{\overline{Y}}_{t_n-}^0,{\underset{\_}{Y}}_{t_n+}^0)=P(A_{t_n}\mid {\overline{L}}_{t_n-},{\overline{A}}_{t_{n-1}},{\overline{Y}}_{t_n-}^0),$$ (10)

where L̄_tn− = (L_t1−, L_t2−, …, L_tn−), Ā_tn−1 = (A_t1, A_t2, …, A_tn−1), ${\overline{Y}}_{t_n-}^0=(Y_{t_1-}^0,Y_{t_2-}^0,\dots ,Y_{t_n-}^0)$ and ${\underset{\_}{Y}}_{t_n+}^0=(Y_{t_{n+1}-}^0,Y_{t_{n+2}-}^0,\dots ,Y_{t_{n+l}-}^0)$.

It should be noted that for the conditional densities in (9) and (10), and the conditional densities in the following sections, we always choose the version that is the ratio of joint density to marginal density.

The finite-time sequential randomization assumption clearly implies condition (2) and thus justifies the modified g-estimation equation (7). We have also proven a result that shows the relationship between the FTSR assumption and the CTSR assumption.

Theorem 4

If a continuous-time càdlàg process Z_t satisfies finite-time sequential randomization, then, under some regularity conditions, it will also satisfy continuous-time sequential randomization.

Proof

See Appendix C. The regularity conditions are also stated in Appendix C.

The result of Theorem 4 is natural. As mentioned in Section 1.4, the continuous-time sequential randomization does not imply FTSR because, in discrete-time observations, we do not have the full continuous-time history to control. To compensate for the incomplete data problem, some stronger assumption on the continuous-time processes must be made if identification is to be achieved.

2.4.2. A Markovian condition

Given the finite-time sequential randomization assumption described above, two important questions arise. First, Theorem 4 shows that the FTSR assumption is stronger than the continuous-time sequential randomization assumption. It is natural to ask how much stronger it is than the CTSR assumption. Second, the FTSR assumption, unlike the CTSR assumption (A1), is not an assumption on the data generating process itself and so it is not clear how to incorporate domain knowledge about the data generating process to justify it. Is there a condition at the data generating process level which will be more helpful in deciding whether g-estimation is valid?

We partially answer both questions in the following theorem.

Theorem 5

Assuming that the process ( $Y_t^0$, L_t, A_t) satisfies the continuous-time sequential randomization assumption, and that the process ( $Y_{t-}^0$, L_t−, A_t) is Markovian, for any time t and t + s, s > 0, we have

$$P(A_t\mid L_{t-},Y_{t-}^0,{\underset{\_}{Y}}_{t+}^0)=P(A_t\mid L_{t-},Y_{t-}^0),$$ (11)

which implies the finite-time sequential randomization assumption. Here, ${\underset{\_}{Y}}_{t+}^0=(Y_{t_1-}^0,Y_{t_2-}^0,\dots ,Y_{t_n-}^0)$ and t < t₁ < t₂ < ··· < t_n.

Proof

The proof can be found in the Appendix D.

The theory states that the Markov condition and the CTSR assumption together imply the FTSR condition. Therefore, they imply condition (2) and thus justify the modified g-estimation equation (7).

We make the following comments on the theorem.

• The theorem partially answers our first question—the FTSR assumption is stronger than the CTSR assumption, but the gap between the two assumptions is less than a Markovian assumption. The result is not surprising since, with missing covariates between observational time points, we would hope that the variables at the observational time points well summarize the missing information. The Markovian assumption guarantees that variables at an observational time point summarize all information prior to that time point.

• The theorem also partially answers our second question. The CTSR assumption is usually justified by domain knowledge of how treatments are decided. Theorem 5 suggests that the researchers could further look for biological evidence that the process is Markovian to validate the use of g-estimation. The Markovian assumption can also be tested. One could first use the modified g-estimation to estimate the causal parameter, construct the Y⁰ process at the observational time points and then test whether the full observational data of A, L, Y⁰ come from a Markov process. A strict test of whether the discretely observed longitudinal data come from a continuous-time (usually nonstationary) Markov process could be difficult and is beyond the scope of this paper. As a starting point, we suggest Singer’s trace inequalities [Singer (1981)] as a criterion to test for the Markovian property. A weaker test for the Markovian property is to test conditional independence of past observed values and future observed values conditioning on current observed values.

• In the theorem, equation (11) looks like an even stronger version of the continuous-time sequential randomization assumption—the treatment decision seems to be based only on current covariates and current potential outcomes. One could, of course, directly assume this stronger version of randomization and apply g-estimation. However, Theorem 5 is more useful since we are assuming a weaker untestable CTSR assumption and a Markovian assumption that is testable in principle.

• The theorem suggests that it is sufficient to control for current covariates and current potential outcomes for g-estimation to be consistent. In practice, we advise controlling for necessary past covariates and treatment history. The estimate would still be consistent if the Markovian assumption were true and it might reduce bias when the Markovian assumption was not true. As a result, we do control for previous covariates and treatments in our simulation and application to the diarrhea data.

• It is worth noting that the labeling of time is arbitrary. In practice, researchers can label whatever they have controlled for in their propensity score as the “current” covariates, which could include covariates and treatments that are measured or assigned previously. In this case, the dimension of the process that needs to be tested for the Markovian property should also be expanded to include older covariates and treatments.

• Finally, we note that a discrete-time version of the theorem is implied by Corollary 4.2 of Robins (1997) if we set, in his notation, U_ak to be the covariates between two observational time points and U_bk to be the null set.

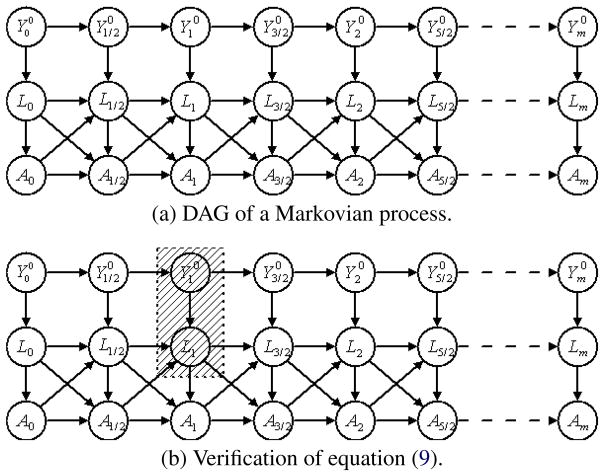
As a discretized example, we illustrate the idea of Theorem 5 by a directed acyclic graph (DAG) in part (a) of Figure 1, which assumes that all variables can only change values at time points 0, 1/2, 1, 3/2, 2,…, m. Note that we do not distinguish the left limits of variables and the variables themselves in all DAGs of this paper, for reasons discussed in Appendix C. We also assume that the process can only be observed at times 0, 1, 2,…, m. It is easy to verify that the DAG satisfies sequential randomization at the 0, 1/2, 1, 3/2, 2,…, m time level. The DAG is also Markovian in time. For example, if we control A₁, L₁, $Y_1^0$, any variable prior to time 1 will be d-separated from any other variable after time 1.

Fig. 1.

Directed acyclic graph.

Part (b) of Figure 1 verifies that A₁ is d-separated from $Y_m^0$, m > 1 by the shaded variables, namely, L₁ and $Y_1^0$, as is implied by equation (9). By Theorem 5, the modified g-estimation works for data observed at the integer times if they are generated by the model defined by this DAG.

It is true that the Markovian condition that justifies the g-estimation equation (7) is restrictive, as will be discussed in the following section. However, our simulation study shows that g-estimation has some level of robustness when the Markovian assumption is not seriously violated.

3. The controlling-the-future method

In this section, we consider situations in which the observational time sequential randomization fails and seek methods that are more robust to this failure than the modified g-estimation given in Section 2.3. The method we are going to introduce was proposed in Joffe and Robins (2009), which deals with a more general case of the existence of unmeasured confounders. It can be applied to deal with unmeasured confounders coming from either a subset of contemporaneous covariates or a subset of covariates that represent past time, the latter case being of interest for this paper. The method, which we will refer to as the controlling-the-future method (the reason for the name will become clear later on), gives consistent estimates when g-estimation is consistent and produces consistent estimates in some cases even when g-estimation is severely inconsistent.

In what follows, we will first describe an illustrative application of the controlling-the-future method and then discuss its relationship with our framework of g-estimation in continuous-time processes with covariates observed at discrete times.

3.1. Modified assumption and estimation of parameters

We assume the same continuous-time model as in Section 2.2. Following Joffe and Robins (2009), we consider a revised sequential randomization assumption on variables at the observational time points

$$P(A_k^{\ast }\mid {\overline{L}}_k^{\ast },{\overline{A}}_{k-1}^{\ast },\overline{\text{cum}{A}_k^{\ast }},{\underset{\_}{Y}}_{k+}^{0\ast })=P(A_k^{\ast }\mid {\overline{L}}_k^{\ast },{\overline{A}}_{k-1}^{\ast },\overline{\text{cum}{A}_k^{\ast }},Y_{k+1}^{0\ast }).$$ (12)

This assumption relaxes (8). At each time point, conditioning on previous observed history, the treatment can depend on future potential outcomes, but only on the next period’s potential outcome. In Joffe and Robins’ extended formulation, this can be further relaxed to allow for dependence on more than one period of future potential outcomes, as well as other forms of dependence on the potential outcomes.

If the revised assumption (12) is true, then we obtain a similar estimating equation as (7). For each putative Ψ, we map $Y_k^{\ast }$ to

$$Y_k^{0\ast }(\mathrm{\Psi })=Y_k^{\ast }-\mathrm{\Psi }\text{cum}{A}_k^{\ast },$$

the potential outcome if the subject never received any treatment under the hypothesized treatment effect Ψ.

Define the putative propensity score as

$$p_k(\mathrm{\Psi })\equiv P(A_k^{\ast }=1\mid {\overline{L}}_k^{\ast },{\overline{A}}_{k-1}^{\ast },\overline{\text{cum}{A}_k^{\ast }},Y_{k+1}^{0\ast }(\mathrm{\Psi })).$$ (13)

Under assumption (12), the correct Ψ should solve

$$U(\mathrm{\Psi })=E\left\{\sum _{\begin{array}{c}1\le i\le n\\ k+1<m\le K\end{array}}[A_{i,k}^{\ast }-p_{i,k}(\mathrm{\Psi })]g(Y_{i,m}^{0\ast }(\mathrm{\Psi }),X_{i,k}^{\ast },h_{i,k}(\mathrm{\Psi }))\right\}=0,$$ (14)

where $X_{i,k}^{\ast }=({\overline{L}}_{i,k}^{\ast },{\overline{A}}_{i,k-1}^{\ast },\overline{\text{cum}{A}_{i,k}^{\ast }}),h_{i,k}(\mathrm{\Psi })=Y_{i,k+1}^{0\ast }(\mathrm{\Psi })$ and g is any function and can be generalized to functions of $X_{i,k}^{\ast },h_{i,k}(\mathrm{\Psi })$, h_i,k(Ψ) and any number of future potential outcomes that are later than time k + 1, for example, $g(Y_{i,k+2}^{0\ast }(\mathrm{\Psi }),Y_{i,k+3}^{0\ast }(\mathrm{\Psi }),X_{i,k}^{\ast },h_{i,k}(\mathrm{\Psi }))$. In most real applications, the model for $p_k(\mathrm{\Psi })=E[A_k^{\ast }\mid X_k^{\ast },h_k(\mathrm{\Psi })]$ is unknown and is usually estimated by a parametric model,

$$p_{i,k}(\mathrm{\Psi };{\beta }_X,{\beta }_h)=E[A_{i,k}\mid X_{i,k}^{\ast },h_{i,k}(\mathrm{\Psi });{\beta }_X,{\beta }_h].$$

We can solve the following set of estimating equations to obtain the estimates of Ψ, β_X and β_h:

$$\begin{array}{l}U(\mathrm{\Psi },{\beta }_X,{\beta }_h)=\sum _{\begin{array}{c}1\le i\le n\\ k+1<m\le K\end{array}}(A_{i,k}^{\ast }-p_{i,k}(\mathrm{\Psi };{\beta }_X,{\beta }_h))\times {[g(Y_{i,m}^{0\ast }(\mathrm{\Psi }),X_{i,k}^{\ast },h_{i,k}(\mathrm{\Psi })),X_{i,k}^{\ast },h_{i,k}(\mathrm{\Psi })]}^T\\ =0.\end{array}$$ (15)

The estimation of the covariance matrix of Ψ, β_X and β_h is similar to the usual standard g-estimation, which is described in Appendix A.

Two important features of estimating equation (15) distinguish it from estimating equation (7). First, in (15), there is a common parameter Ψ in both p_k’s model and $Y_m^{0\ast }(\mathrm{\Psi })$, caused by the fact that the treatment depends on a future potential outcome. Second, in (15), the sum over m and k is restricted to m > k + 1, while in (7), we only need m > k. If we use m = k + 1 in (15), $E\{[A_{i,k}^{\ast }-p_{i,k}(\mathrm{\Psi })]g(Y_{i,k+1}^{0\ast }(\mathrm{\Psi }),X_{i,k}^{\ast },h_{i,k}(\mathrm{\Psi }))\}=0$ usually does not lead to the identification of Ψ, unless certain functional forms of the propensity score model are assumed to be true [see Joffe and Robins (2009)].

3.2. The controlling-the-future method and the Markovian condition

Joffe and Robins’ revised assumption (12) is an assumption on the discrete-time observational data. It relaxes the observational time sequential randomization (8) because (8) always implies (12). At the continuous-time data generating level, (12) allows less stringent underlying stochastic processes than the Markovian process in Theorem 5.

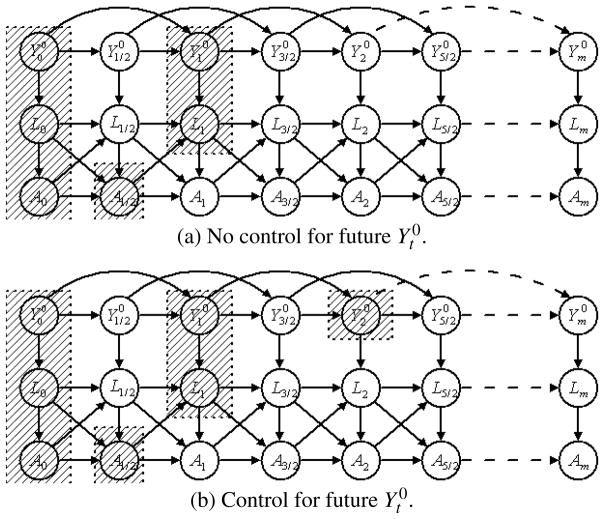
In particular, we identify two important scenarios where the relaxation happens. One scenario is to allow for more direct temporal dependence for the Y⁰ process, which we will refer to as the non-Markovian-Y⁰ case. The other scenario is to allow colliders in L, which we will refer to as the leading-indicator-in-L case. We illustrate both cases by modifying the directed acyclic graph (DAG) example in Figure 1.

The non-Markovian-Y⁰ case

Assume, for example, our data is generated from the DAG in Figure 2, where we allow the dependence of $Y_2^0$ on $Y_1^0$, even if $Y_{3/2}^0$ is controlled. In part (a) of Figure 2, we control for observed covariates (L₀, L₁), treatment (A₀, A_1/2) and current and historical potential outcome ( $Y_0^0,Y_1^0$) for treatment at time 1 (A₁), that is, we have controlled for all historically observed covariates, treatment and cumulative treatment as suggested in the comments accompanying Theorem 5. In this case, the modified g-estimation fails because the paths like $A_1\leftarrow L_{1/2}\leftarrow Y_{1/2}^0\to Y_{3/2}^0\to Y_2^0\to \cdots \to Y_m^0$ are not blocked by the shaded variables. In part (b) of Figure 2, we control for the additional $Y_2^0$. A₁ is not completely blocked from $Y_m^0$, but some paths that are not blocked in part (a) are now blocked, for example, the path of $A_1\leftarrow L_{1/2}\leftarrow Y_{1/2}^0\to Y_{3/2}^0\to Y_2^0\to Y_{5/2}^0\to \cdots \to Y_m^0$. Also, no additional paths are opened by conditioning on $Y_2^0$. We would usually expect that the correlation between A₁ and $Y_m^0$ is weakened. Under the framework of Joffe and Robins (2009), we can control for more than one period of future potential outcomes and expect to further weaken the correlation between A₁ and $Y_m^0$. A modification of assumption (12) that conditions on more future potential outcomes may be approximately true.

Fig. 2.

Directed acyclic graph with non-Markovian $Y_t^0$.

The scenario relates to real-world problems. For instance, in the diarrhea example, $Y_t^0$ is the natural height growth of a child without any occurrence of diarrhea. Height in the next month not only depends on the current month’s height, but also depends on the previous month’s height: the complete historical growth curve of the child provides information on genetics and nutritional status, and provides information about future natural height beyond that of current natural height alone. Therefore, the potential height process for the child is not Markovian. [For a formal argument why children’s height growth is not Markovian, see Gasser et al. (1984).] By the reasoning employed above, g-estimation fails. However, if we assume that the delayed dependence of natural height wanes after a period of time (as in Figure 2), controlling for the next period potential height in the propensity score model might weaken the relationship between current diarrhea exposure and future potential height later than the next period and the assumptions of the controlling-the-future method might hold approximately.

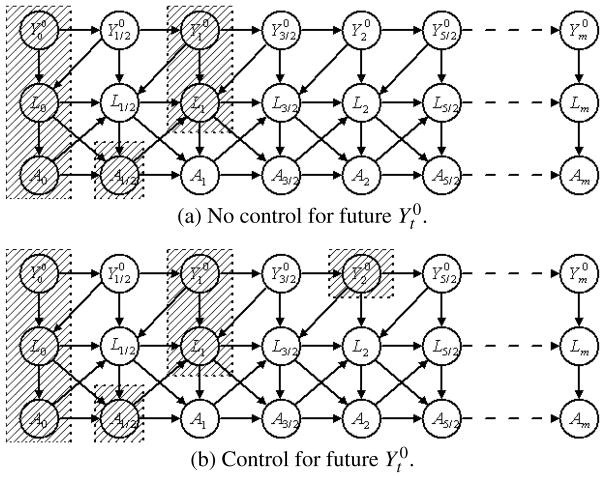
The leading-indicator-in-L case

In Figure 1, we do not allow any arrows from future Y⁰ to previous L, which means that among all measures of the subject, there are no elements in L that contain any leading information about future Y⁰. This means that Y⁰ is a measure that is ahead of all other measures, by which we mean that, for example, $L_2\perp Y_m^0\mid {\overline{Y}}_2^0,{\overline{A}}_{2-},{\overline{L}}_{2-}m>2$. This is not realistic in many real-world problems. In the example of the effect of the diarrhea on height, weight is an important covariate. While both height and weight reflect the nutritional status of a child, malnutrition usually affects weight more quickly than height, that is, the weight contains leading information for the natural height of the child. Figure 1 is thus not an appropriate model for studying the effect of diarrhea on height.

In Figure 3, we allow arrows from $Y_{1/2}^0$ to L₀, from $Y_1^0$ to L_1/2 and so on, which assumes that L contains leading indicators of Y⁰, but the leading indicators are only ahead of Y⁰ for less than one unit of time. Part (a) of Figure 3 shows that controlling for history of covariates, treatment and potential outcomes does not block A₁ from $Y_m^0$. On the path of $A_1\leftarrow L_{1/2}\to L_1\leftarrow Y_{3/2}^0\to Y_2^0\to Y_{5/2}^0\to \cdots \to Y_m^0$, L₁ is a controlled collider. However, in part (b), if we do control for $Y_2^0$ additionally, the same path will be blocked. In general, if we assume that there exist leading indicators in covariates and that the leading indicators are not ahead of potential outcomes for more than one time unit, g-estimation will fail, but the controlling-the-future method will produce consistent estimates.

Fig. 3.

Directed acyclic graph with leading indicator in L_t.

The fact that the controlling-the-future method can work in the leading information scenario can also be related to the discussion of Section 3.6 of Rosenbaum (1984). The main reason for g-estimation’s failure in the DAG example is that L_1/2 is not observable and cannot be controlled. If L_1/2 is observed, it is easy to verify that the DAG in Figure 3 satisfies sequential randomization on the finest time grid. The idea behind the controlling-the-future method is to condition on a “surrogate” for L_1/2. The surrogate should satisfy the property that $Y_m^0$ is independent of the unobserved L_1/2 given the surrogate and other observed covariates [similar to formula 3.17 in Rosenbaum (1984)]. In the leading information case, when m > k + 1 and we have covariates L̄_k that are only ahead of the potential outcome until time at most k + 1, the future potential outcome $Y_{k+1}^0$ is a surrogate. It is easy to check that in Figure 3 ,L_1/2 is independent of $Y_m^0$, given $Y_2^0$, L₁, A₀ and cum A₁ (equivalently, $Y_1^0$).

It is worth noting that we do not need to control for anything except $Y_2^0$ in Figure 3 in order to get a consistent estimate. It is possible to construct more complicated DAGs in which controlling for additional past and current covariates is necessary, which involves more model specifications for the relationships among different covariates and deviates from the main point of this paper.

In Section 4, we will simulate data in cases of non-Markovian- $Y_t^0$ and leading-indicator-in-L_t, respectively, and show that the controlling-the-future method does produce better estimates than g-estimation. However, it is worth noting that when the modified g-estimation in Section 2.3 is consistent, the controlling-the-future estimation is usually considerably less efficient. This is because condition (12) is less stringent than (8). The semiparametric model under (8) is a submodel of the semiparametric model defined by (12). The latter will have a larger semiparamet-ric efficiency bound than the former. Theoretically, the most efficient g-estimation will be more efficient than the most efficient controlling-the-future estimation if the g-estimation is valid. In practice, even if we are not using the most efficient estimators, controlling-the-future estimation usually estimates more parameters, for example, coefficients for h_i,k(Ψ) in the propensity model, and thus is less efficient. For a formal discussion, see Tsiatis (2006).

4. Simulation study

We set up a simple continuous-time model that satisfies sequential ignorability in continuous time, and simulate and record discrete-time data from variations of the simple model. We estimate causal parameters from both the modified g-estimation and the controlling-the-future estimation. We also present the estimates from naive g-estimation in Section 2.1, where we ignore the continuous-time information of the treatment processes, as a way to show the severity of the bias in the presence of the measurement error problem. The results support the discussions in Sections 2.4 and 3.

In the simulation models below, M1 satisfies the Markovian condition in Theorem 5. It also serves as a proof that there exist processes satisfying the conditions of Theorem 5.

4.1. The simulation models

We first consider a continuous-time Markov model which satisfies the CTSR assumption.

• $Y_t^0$ is the potential outcome process if the patient is not receiving any treatment. We assume that

  $$Y_t^0=g(V,t)+e_t,$$
  where g(V, t) is a function of baseline covariates V and time t. Let g(V, t) be continuous in t and let e_t follow an Ornstein–Uhlenbeck process, that is,

  $$d{e}_t=-\theta e_{t}dt+\sigma {dW}_t,$$

  where W_t is the standard Brownian motion.

• Y_t is the actual outcome process and follows the deterministic model (6):

  $$Y_t=Y_t^0+\mathrm{\Psi }{\int }_0^t{A}_{s}ds.$$
• A_t is the treatment process, taking binary values. The jump of the A_t process follows the following formula:

  $$\begin{array}{l}P(A_s\text{jumps}\text{once}\text{from}(t,t+h]\mid {\overline{A}}_t,{\overline{Y}}_t,{\overline{Y}}^0)=s(A_t,Y_t)h+o(h),\\ P(A_s\text{jumps}\text{more}\text{than}\text{once}\text{from}(t,t+h]\mid {\overline{A}}_t,{\overline{Y}}_t,{\overline{Y}}^0)=o(h),\end{array}$$

  where Ā_t and Ȳ_t are the full continuous-time history of treatment and outcome up to time t and Ȳ⁰ is the full continuous-time path of potential outcome from time 0 to time K. By making s(·) independent of Ȳ⁰, we make our model satisfy the continuous-time sequential randomization assumption.

In this model, the only time-dependent confounder is the outcome process itself.

We also consider several variations of the above model (denoted as M1 below):

• Model (M2) extends (M1) to the non-Markovian- $Y_t^0$ case. Specifically, we consider the case where e_t in the model of $Y_t^0$ follows a non-Markovian process, namely an Ornstein–Uhlenbeck process in random environments, which is defined as the following:

  1. J_t is a continuous-time Markov process taking values in a finite set {1,…, m}, which is the environment process;

  2. we have m > 1 sets of parameters θ₁, σ₁,…,θ_m, σ_m;

  3. e_t follows an Ornstein–Uhlenbeck process with parameters θ_j, σ_j, when J_t = j ; the starting point of each diffusion is chosen to be simply the endpoint of the previous one.

• Model (M3) extends (M1) to another setting of non-Markovian- $Y_t^0$ process, where

  $$Y_t^0=g(V,t)+0.8e_{t-1}+0.2e_t.$$

  e_t follows the same Markovian Ornstein–Uhlenbeck process as in M1. Every other variable is the same as in M1.

• Model (M4) considers the case with more than one covariate. In M4, we keep the assumptions on $Y_t^0$ as in (M1) and the deterministic model of Y_t. We add one more covariate, which is generated as follows:

  $$L_t^{-}=0.2Y_t+0.8Y_{t+0.5}^0+0.5{\eta }_t.$$

  η_t follows an Ornstein–Uhlenbeck process independent of the $Y_t^0$ process. In this specification, the covariate $L_t^{-}$ contains some leading information about Y⁰, but it is only ahead of Y⁰ for 0.5 length of a time unit. Here, we use $L_t^{-}$ instead of L_t to denote that it is the covariate excluding Y_t. The simulation model for the A_t process is given in Appendix E.

In all of these models, to simulate data, we use g(V, t) = C (a constant), Ψ = 1, a time span from 0 to 5 and a sample size of 5000. Details of other parameter specifications can be found in Appendix E. We generate 5000 continuous paths of Y_t and A_t (and $L_t^{-}$ in M4), from time 0 to time 5, and record $Y_0^{\ast },A_0^{\ast },Y_1^{\ast },A_1^{\ast },\dots ,Y_4^{\ast },A_4^{\ast },Y_5^{\ast }$ and $\text{cum}{A}_1^{\ast },\dots ,\text{cum}{A}_5^{\ast }$ (and $L_0^{-\ast },\dots ,L_4^{-\ast }$ in M4) as the observed data.

4.2. Estimations and results under M1

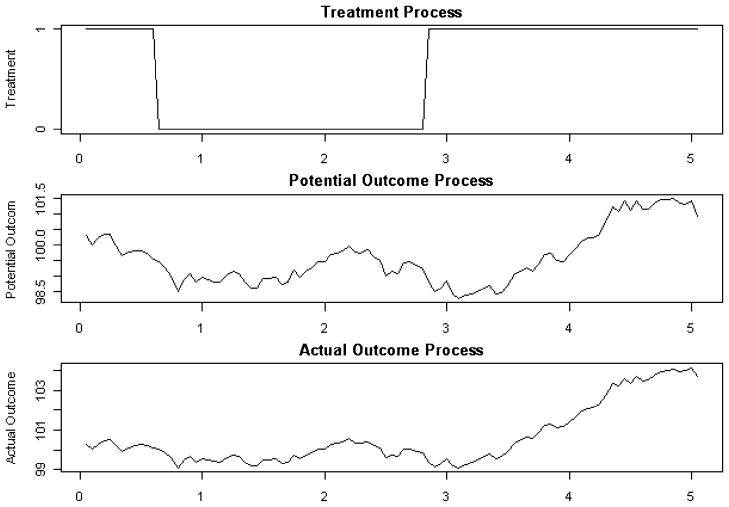
Figure 4 shows a typical continuous-time path of $Y_t^0$, Y_t and A_t. The treatment switches around time 0.7 and time 2.8.

Fig. 4.

Example of continuous-time paths under M1.

We apply three estimating methods on data simulated from M1: the naive discrete-time g-estimation described in Section 2.1, which ignores the underlying continuous-time processes; the modified g-estimation described in Section 2.3, which controls for all the observed discrete-time history; and the controlling-the-future method in Section 3.1 of controlling for the next period’s potential outcome in addition to the discrete-time history.

For estimation, even though we know the data generating process, it is too complicated to use the correct model for the propensity score, that is, the correct functional form for $p_k(\mathrm{\Psi })\equiv P(A_k^{\ast }\mid {\overline{L}}_k^{\ast },{\overline{Y}}_k^{\ast },{\overline{A}}_{k-1}^{\ast },\overline{\text{cum}{A}_k^{\ast }},Y_{k+}^{0\ast }(\mathrm{\Psi }))$. Therefore, we use the following approximations (note that we control for past treatment and covariates as well—see comments for Theorem 5):

1. standard g-estimation ignoring continuous-time processes (naive g-estimation)

   $$\text{logit}(p_k)={\beta }_0+{\beta }_1{A}_{k-1}^{\ast }+{\beta }_2{Y}_{k-1}^{\ast }+{\beta }_3{Y}_k^{\ast };$$
2. g-estimation controlling for all observed history (modified g-estimation)

   $$\text{logit}(p_k)={\beta }_0+{\beta }_1{A}_{k-1}^{\ast }+{\beta }_2{Y}_{k-1}^{\ast }+{\beta }_3{Y}_k^{\ast }+{\beta }_4\text{cum}{A}_k^{\ast };$$
3. the controlling-the-future method, controlling for next period potential outcomes (controlling-the-future estimation)

   $$\text{logit}(p_k(\mathrm{\Psi }))={\beta }_0+{\beta }_1{A}_{k-1}^{\ast }+{\beta }_2{Y}_{k-1}^{\ast }+{\beta }_3{Y}_k^{\ast }+{\beta }_4\text{cum}{A}_k^{\ast }+{\beta }_5{Y}_{k+1}^{0\ast }(\mathrm{\Psi }).$$

We plug these models for the propensity scores into estimation equations (5), (7) and (15) respectively. [Note that in equation (5), $Y_k^{0\ast }(\mathrm{\Psi })=Y_k^{\ast }-\mathrm{\Psi }{\sum }_{l=0}^{k-1}{A}_l^{\ast }$, while in the other two, $Y_k^{0\ast }(\mathrm{\Psi })=Y_k^{\ast }-\mathrm{\Psi }\text{cum}{A}_k^{\ast }$.]

The first panel of Table 1 shows a summary of the estimates of causal parameters for 1000 simulations from M1. The naive g-estimation gives severely biased estimates. Controlling for all observed history and controlling for additional next period potential outcome both give us unbiased estimates. As discussed at the end of Section 3.2, the controlling-the-future method has lower efficiency.

Table 1. Estimated causal parameters from data generated by.

M1–M4

	Naive g-est.	Mod. g-est.	Ctr-future est.
Simulation results from M1, true parameter = 1
Mean estimate†	0.7728	1.0005	0.9988
S.D. of estimates‡	0.0183	0.0191	0.0403
S.D. of the mean estimate*	0.0005	0.0006	0.0013
Absolute bias**	0.2272	0.0005	0.0012
Coverage⋄	0	0.946	0.956
Simulation results from M2, true parameter = 1
Mean estimate†	0.7651	1.0016	1.0000
S.D. of estimates‡	0.0132	0.0158	0.0371
S.D. of the mean estimate*	0.0004	0.0005	0.0012
Absolute bias**	0.2349	0.0016	0.0000
Coverage⋄	0	0.953	0.950
Simulation results from M3, true parameter = 1
Mean estimate†	0.7580	0.9845	1.0026
S.D. of estimates‡	0.0149	0.0180	0.0487
S.D. of the mean estimate*	0.0005	0.0006	0.0015
Absolute bias**	0.2420	0.0155	0.0026
Coverage⋄	0	0.855	0.956
Simulation results from M4, true parameter = 1
Mean estimate†	0.7816	1.0853	1.0085
S.D. of estimates‡	0.0201	0.0289	0.0806
S.D. of the mean estimate*	0.0006	0.0009	0.0025
Absolute bias**	0.2184	0.0853	0.0085
Coverage⋄	0	0.115	0.948

^†Averaged over estimates from 1000 independent simulations of sample size 5000.

^‡Sample standard deviation of the 1000 estimates.

^*Sample $\mathrm{S}.\mathrm{D}./\sqrt{1000}$.

The last row of the first panel in Table 1 shows the coverage rate of the 95% confidence interval estimated from the 1000 independent simulations. Naive g-estimation has a zero coverage rate, while the other two methods have coverage rates around 95%.

4.3. Simulation results under M2 and M3

The results in the second panel of Table 1 are typical for different values of parameters under M2. The naive g-estimation performs badly, while both of the other methods still work well with the data generated from M2. This shows that the modified g-estimation and the controlling-the-future method have some level of robustness to mild violations of the Markovian assumption.

The third part of Table 1 shows the results of simulation from M3, where Y⁰ violates the Markov property more substantially. In this case, we can see that the mean of the modified g-estimates is biased, but the mean of the controlling-the-future estimates is almost unbiased. In the last row of the third panel, the coverage rate for the modified g-estimation drops to 0.855, while the controlling-the-future method still has a coverage rate of 0.956.

4.4. Estimations and results under M4

In M4, we create a covariate $L_t^{-}$ that has leading information about $Y_t^0$. In the data simulated from M4, the observational time sequential randomization (8) no longer holds, although the data are generated following continuous-time sequential randomization. This simulation serves as a numerical proof of the claim that continuous-time sequential randomization does not imply discrete-time sequential randomization.

To show this, we consider the following working propensity score model at time k = 2 and its dependence on the future potential outcome at m = 4:

• not controlling for the next period potential outcome (used in modified g-estimation)

  $$\text{logit}\left(P(A_k^{\ast }=1\mid {\overline{A}}_{k-}^{\ast },{\overline{L}}_k^{-\ast },\overline{\text{cum}{A}_k^{\ast }},{\overline{Y}}_k^{\ast },Y_m^{0\ast })\right)={\beta }_0+{\beta }_1\text{cum}{A}_k^{\ast }+{\beta }_2{L}_{k-1}^{-\ast }+{\beta }_3{L}_k^{-\ast }+{\beta }_4{A}_{k-1}^{\ast }+{\beta }_5{Y}_k^{\ast }+{\beta }_6{Y}_{k-1}^{\ast }+{\beta }_8{Y}_m^{0\ast };$$ (16)
• controlling for the next period potential outcome (used in controlling-the-future estimation)

  $$\text{logit}\left(P(A_k^{\ast }=1\mid {\overline{A}}_{k-}^{\ast },{\overline{L}}_k^{-\ast },\overline{\text{cum}{A}_k^{\ast }},{\overline{Y}}_k^{\ast },Y_{k+1}^{0\ast },Y_m^{0\ast })\right)={\beta }_0+{\beta }_1\text{cum}{A}_k^{\ast }+{\beta }_2{L}_{k-1}^{-\ast }+{\beta }_3{L}_k^{-\ast }+{\beta }_4{A}_{k-1}^{\ast }+{\beta }_5{Y}_k^{\ast }+{\beta }_6{Y}_{k-1}^{\ast }+{\beta }_7{Y}_{k+1}^{0\ast }+{\beta }_8{Y}_m^{0\ast }.$$ (17)

We can use the true values of $Y_{k+1}^{0\ast }$ and $Y_m^{0\ast }$ in the regression to test the discrete-time ignorability since we are simulating the data. Table 2 shows the estimates of β₇ and β₈ in both regression models. The result shows that the coefficient of $Y_m^{0\ast }$, β₈, is significant if we do not control for the future potential outcome and is not significant if we control for the future potential outcome. This shows that observational time sequential randomization (8) does not hold, while the revised assumption (12) holds.

Table 2. Verification of observational time sequential randomization under.

M4

	Reg. model (16)*	Reg. model (17)*
β7		0.1868
p-value		5.56e–05
β8	0.0936	0.0134
p-value	0.0006	0.691

^*Simulation sample size = 10,000.

The estimation results from M4 appear in the fourth panel of Table 1. In applying these methods, we use the following propensity score models separately:

1. g-estimation ignoring the underlying continuous-time processes (naive g-estimation)

   $$\text{logit}(p_k)={\beta }_0+{\beta }_1{A}_{k-1}^{\ast }+{\beta }_2{Y}_{k-1}^{\ast }+{\beta }_3{Y}_k^{\ast }+{\beta }_5{L}_{k-1}^{-\ast }+{\beta }_6{L}_k^{-\ast };$$
2. g-estimation controlling for all observed history (modified g-estimation)

   $$\text{logit}(p_k)={\beta }_0+{\beta }_1{A}_{k-1}^{\ast }+{\beta }_2{Y}_{k-1}^{\ast }+{\beta }_3{Y}_k^{\ast }+{\beta }_4\text{cum}{A}_k^{\ast }+{\beta }_5{L}_{k-1}^{-\ast }+{\beta }_6{L}_k^{-\ast };$$
3. the controlling-the-future method controlling for next period potential outcomes (controlling-the-future estimation)

   $$\text{logit}(p_k(\mathrm{\Psi }))={\beta }_0+{\beta }_1{A}_{k-1}^{\ast }+{\beta }_2{Y}_{k-1}^{\ast }+{\beta }_3{Y}_k^{\ast }+{\beta }_4\text{cum}{A}_k^{\ast }+{\beta }_5{L}_{k-1}^{-\ast }+{\beta }_6{L}_k^{-\ast }+{\beta }_7{Y}_{k+1}^{0\ast }(\mathrm{\Psi }).$$

Both the naive g-estimation and the modified g-estimation give us estimates with severe bias and they have coverage rates of 0 and 0.115, respectively, for the 95% confidence interval constructed from them. It is worth noting that model 3 is misspecified, but, nevertheless, leads to much less biased estimates, and the controlling-the-future method has a coverage rate of 0.948.

5. Application to the diarrhea data

In this section, we apply the different approaches to the diarrhea example mentioned in Section 1 (Example 2). For illustration purposes, we ignore any informative censoring and use a set of 224 children with complete records between ages 3 and 6 from 757 households in Bangladesh around 1998. The outcomes, $Y_k^{\ast }$, are the heights of the children in centimeters, measured at round k of the interviews, for k = 1, 2, 3. The treatment $A_k^{\ast }$ at the inter-view k is defined as $A_k^{\ast }=1$ if the child was sick with diarrhea during the past two weeks of the interview and $A_k^{\ast }=0$ otherwise. The cumulative treatment cum $A_k^{\ast }$ is the number of days that the child suffered from diarrhea from four months before the first interview (July 15th, 1998) to the kth interview. Baseline covariates V include age in months, mother’s height and whether the household was exposed to the flood. Time-dependent covariates other than the outcome, that is, $L_k^{-\ast }$, include mid-upper arm circumference, weight for age z-score, type of toilet (open place, fixed place, unsealed toilet, water-sealed toilet or other), garbage disposal method (throwing away in own fixed place, throwing away in own nonfixed place, disposing anywhere or other method), water purifying process (filter, filter and broil, or other) and source of cooking water (from pond or river/canal, or from tube well, ring well or supply water).

We apply naive g-estimation, modified g-estimation and the controlling-the-future method to this data set. Since we only have three rounds, the actual propensity score models and the estimating equations for the three methods are as follows. Note that these estimating equations are for illustrative purpose and may not be the most efficient estimating equations for this data set.

• Naive g-estimation uses the following propensity score model:

  $$\text{logit}\{P[A_k^{\ast }=1\mid V,L_k^{-\ast },Y_k^{\ast }]\}={\beta }_0+{\beta }_{V}V+{\beta }_L{L}_k^{-\ast }+{\beta }_Y{Y}_k^{\ast },$$

  where k = 1, 2.

• The estimating equations follow the form of (5) in Section 2.1:

  $$\sum _{\begin{array}{c}1\le k<m\le 3\\ 1\le i\le n\end{array}}[A_{k,i}^{\ast }-P(A_{k,i}^{\ast }=1\mid V_i,L_{k,i}^{-\ast },Y_{k,i}^{\ast })]\left(\begin{array}{c}{lY}_{m,i}^{0\ast }(\mathrm{\Psi })\\ V_i\\ L_{k,i}^{-\ast }\\ Y_{k,i}^{\ast }\end{array}\right)=0,$$

  where $Y_{m,i}^{0\ast }(\mathrm{\Psi })=Y_{m,i}^{\ast }-\mathrm{\Psi }{\sum }_{l=1}^{m-1}{A}_l$.

• Modified g-estimation uses this propensity score model:

  $$\text{logit}\{P[A_k^{\ast }=1\mid V,L_k^{-\ast },Y_k^{\ast },\text{cum}{A}_k^{\ast }]\}={\beta }_0+{\beta }_{V}V+{\beta }_L{L}_k^{-\ast }+{\beta }_Y{Y}_k^{\ast }+{\beta }_{\text{cum}A}\text{cum}{A}_k^{\ast },$$

  where k = 1, 2.

• The estimating equations follow the form of (7) in Section 2.3.

  $$\sum _{\begin{array}{c}1\le k<m\le 3\\ 1\le i\le n\end{array}}[A_{k,i}^{\ast }-P(A_{k,i}^{\ast }=1\mid V_i,L_{k,i}^{-\ast },Y_{k,i}^{\ast },\mathit{cum}{A}_{k,i}^{\ast })]\left(\begin{array}{c}{Y}_{m,i}^{0\ast }(\mathrm{\Psi })\\ V_i\\ L_{k,i}^{-\ast }\\ Y_{k,i}^{\ast }\\ \mathit{cum}{A}_{k,i}^{\ast }\end{array}\right)=0,$$

  where $Y_{m,i}^{0\ast }(\mathrm{\Psi })=Y_{m,i}^{\ast }-\mathrm{\Psi }\text{cum}{A}_m$.

• Controlling-the-future estimation uses the following propensity score model:

  $$\text{logit}\{P[A_1^{\ast }=1\mid V,L_1^{-\ast },Y_1^{\ast },\text{cum}{A}_1^{\ast },Y_2^{0\ast }(\mathrm{\Psi })]\}={\beta }_0+{\beta }_{V}V+{\beta }_L{L}_1^{-\ast }+{\beta }_Y{Y}_1^{\ast }+{\beta }_{\text{cum}A}\text{cum}{A}_1^{\ast }+{\beta }_{Y^0}{Y}_2^{0\ast }(\mathrm{\Psi }).$$
  The estimating equations follow (15) in Section 3:

  $$\sum _{1\le i\le n}[A_{1,i}^{\ast }-P(A_{1,i}^{\ast }\mid V_i,L_{1,i}^{-\ast },Y_{1,i}^{\ast },\text{cum}{A}_{1,i}^{\ast },Y_{2,i}^{0\ast }(\mathrm{\Psi }))]\left(\begin{array}{c}{Y}_{3,i}^{0\ast }(\mathrm{\Psi })\\ V_i\\ L_{1,i}^{-\ast }\\ Y_{1,i}^{\ast }\\ \text{cum}{A}_{1,i}^{\ast }\\ Y_{2,i}^{0\ast }(\mathrm{\Psi })\end{array}\right)=0,$$

  where $Y_{3,i}^{0\ast }(\mathrm{\Psi })=Y_{3,i}^{\ast }-\mathrm{\Psi }\text{cum}{A}_3$.

The interpretation of Ψ in the last two models is that one day of suffering from diarrhea reduces the height of the child by Ψ centimeters. For naive g-estimation, the underlying data generating model treats the exposure at the observational time as the constant exposure level for the next six months, which does not make sense in the context. It should be noted that if we apply the naive g-estimation, the estimated Ψ should not be interpreted the same way in the modified g-estimation and the controlling-the-future method. Instead, it be interpreted as the effect of having diarrhea at the time of visits. The effect of the child having diarrhea at any time between the visit and the next visit six months later, but not at the time of the visit, is not described by this Ψ.

The estimating equations are solved by a Newton–Raphson algorithm. The estimated Ψ and its standard deviation are reported in Table 3. Modified g-estimation estimates Ψ̂ = −0.3481, which means that the height of the child is reduced by 0.35 cm if the child has one day of diarrhea. Our controlling-the-future method produces an estimate of Ψ̂ = −0.0840. Although all of the estimates are not significant because of the small sample size, the sign and magnitude of the estimate from the controlling-the-future method are similar to what has been found in other research on diarrhea’s effect on height [e.g., Moore et al. (2001)].

Table 3.

Estimation of Ψ from the diarrhea data set

Method	Estimate	Std. err.
Naive g-est.	−0.3991	0.2469
Modified g-est.	−0.3481	0.2832
Controlling-the-future est.	−0.0840	0.1894

In addition, we note that the standard deviation of the modified g-estimate is higher than that of the controlling-the-future estimate. As discussed at the end of Section 3.2, if the modified g-estimation is consistent, we would expect the controlling-the-future estimation to have larger standard deviation. The standard deviations in Table 3 provide evidence that the modified g-estimation is not consistent.

6. Conclusion

In this paper, we have studied causal inference from longitudinal data when the underlying processes are in continuous time, but the covariates are only observed at discrete times. We have investigated two aspects of the problem. One is the validity of the discrete-time g-estimation. Specifically, we investigated a modified g-estimation that is in the spirit of standard discrete-time g-estimation, but is modified to incorporate the information of the underlying continuous-time treatment process, which we have referred to as “modified g-estimation” throughout the paper. We have shown that an important condition that justifies this modified g-estimation is the finite-time sequential randomization assumption at any subset of time points, which is strictly stronger than the continuous-time sequential randomization. We have also shown that a Markovian assumption and the continuous-time sequential randomization would imply the FTSR assumption. The Markovian condition is more useful than the FTSR assumption, in the sense that it can potentially help researchers decide whether the application of the modified g-estimation is appropriate. The other aspect is the controlling-the-future method that we propose to use when the condition to warrant g-estimation does not hold. The controlling-the-future method can produce consistent estimates when g-estimation is inconsistent and is less biased in other scenarios. In particular, we identified two important cases in which controlling the future is less biased, namely, when there is delayed dependence in the baseline potential outcome process and when there are leading indicators of the potential outcome process in the covariate process.

In our simulation study, we have shown the performance of the modified g-estimation and the controlling-the-future estimation. The results confirm our discussion in earlier sections. The simulation results also indicate the danger of applying naive g-estimation, which is usually severely biased and inconsistent when its underlying assumptions are violated, as in the situations considered.

We have applied the g-estimation methods and the controlling-the-future method to estimating the effect of diarrhea on a child’s height and estimated that its effect is negative but not significant. The real application also provides some evidence that the modified g-estimation is not consistent.

All of the discussion in this paper is based on a particular form of causal model—equation (6). However, all of the arguments could apply to a class of more general rank-preserving models, with necessary adjustments in various equations. If we assume a generic rank-preserving model with $Y_t=f(Y_t^0,h({\overline{A}}_{t-});\mathrm{\Psi })$, where Ā_t− is the continuous-time path of A from time 0 to t−, h is some functional [e.g., in our paper, $h({\overline{A}}_{t-})={\int }_0^t{A}_{s}ds$] and f is some strictly monotonic function with respect to the first argument [e.g., in our paper, f(x, y; Ψ) = x + Ψy], we map $Y_k^{\ast }$ to $Y_k^{0\ast }=f^{-1}(Y_k^{\ast },h({\overline{A}}_{k-});\mathrm{\Psi })$, where f⁻¹ is the inverse of f(x, y; Ψ) with respect to x for any given y. We can then substitute all cum $A_k^{\ast }$’s in this paper by the h(Ā_k−)’s. All of the discussion and formulas in the paper would remain valid under the assumption that we observe all h(Ā_k−)’s, which can be easily satisfied with detailed continuous-time records of the treatment. It should be noted that the argument does not work if a time-varying covariate modifies the effect of treatment. For example, if $Y_t=Y_t^0+\mathrm{\Psi }{\int }_0^t{L}_s^2{A}_{s}ds$, where L_s is a time-varying co-variate, observing the full continuous-time treatment process is not enough. Some imputation for the L_s process is necessary.

The methods considered here have several limitations. These include rank preservation, a strong assumption that the effects of treatment are deterministic. This assumption facilitates the interpretation of models. In other work on structural nested distribution and related models [e.g., Robins (2008)], rank preservation has been shown to be unnecessary in settings in which one is not modeling the joint distribution of potential outcomes under different treatments. We expect that this is also the case here, and work justifying this more formally is in progress. We also require that the cumulative amount of treatment (or the full continuous-time treatment process, if using other causal models mentioned above) between the discrete time points when the covariates are observed is known. Work is in progress on the more challenging case in which the treatment process is only observed at discrete times and the cumulative amount of treatment is measured with error. In addition, we ignore any censoring problem requiring that our data is complete, which might not be satisfied in reality. It will also be interesting to study how to accommodate censored data in our framework in future work.

**Absolute value of (1-mean estimates).

^⋄Coverage rate of 95% confidence intervals for 1000 simulations.

APPENDIX A: ESTIMATING COVARIANCE MATRIX OF ESTIMATED PARAMETERS

The formulas in this appendix can be used to estimate the covariance matrix of the estimated parameters from naive g-estimation of Section 2.1, modified g-estimation of Section 2.3 and the controlling-the-future estimation of Section 3.1. More general results on the asymptotical covariances can be found in van der Vaart (2000).

We write θ = (Ψ, β). In Sections 2.1 and 2.3, β is the parameter in the propensity score model. In Section 3.1, β = (β_X, β_h) is the parameter in the propensity score model. Let U(θ) be the vector on the left-hand side of the estimating equations [equation (5) in Section 2.1, equation (7) in Section 2.3 and equation (15) in Section 3.1, respectively]. We also define

$$U_{i,k,m}(\theta )\equiv \left(A_{i,k}^{\ast }-p_{i,k}(\beta )\right){[g(Y_{i,m}^{0\ast }(\mathrm{\Psi }),X_{i,k}^{\ast }),X_{i,k}^{\ast }]}^T$$

for the naive g-estimation and the modified g-estimation, and

$$U_{i,k,m}(\theta )\equiv \left(A_{i,k}^{\ast }-p_{i,k}(\mathrm{\Psi };{\beta }_X,{\beta }_h)\right){[g(Y_{i,m}^{0\ast }(\mathrm{\Psi }),X_i^{\ast },h_i),X_{i,k}^{\ast },h_{i,k}]}^T$$

for the controlling-the-future estimation. We then have U(θ) = ΣU_i,k,m.

Let $B(\theta )=E[\frac{\partial U(\theta )}{\partial \theta }]$, which can be estimated as

$$\widehat{B}(\theta )=-{\sum _{i,k,m}\left\{\frac{\partial U_{i,k,m}}{\partial \theta }\right\}|}_{\theta =\widehat{\theta }},$$

where θ̂ is the solution from the corresponding estimating equations, k < m in both g-estimations and k < m − 1 in controlling-the-future estimation. The covariance matrix of the estimator θ̂ can then be estimated as

$$\text{Cov}(\widehat{\theta })={\widehat{B}}^{-1}(\theta )\text{Cov}[U(\widehat{\theta })]{\widehat{B}}^{-1}{(\theta )}^{\prime }$$

by the delta method, where Cov[U(θ)] is estimated by

$$\text{Cov}[U(\widehat{\theta })]=\sum _i{U}_i(\widehat{\theta })U_i{(\widehat{\theta })}^{\prime }$$

with U_i = Σ_k,m U_i,k,m(θ̂), k < m in both g-estimations and k < m − 1 in controlling-the-future estimation.

APPENDIX B: EXISTENCE OF SOLUTION AND IDENTIFICATION

The estimating equations in this paper, equation (5) in Section 2.1, equation (7) in Section 2.3 and equation (15) in Section 3.1, are asymptotically consistent systems of equations by definition, if the respective underlying assumptions for each estimating equation hold true. The existence of a solution is guaranteed asymptotically. In addition, we have the same number of equations as the number of parameters in each system. One would usually expect there to exist a solution for the estimating equations, even in a relatively small sample.

However, the asymptotic solution may not be unique, which leads to an identification problem. As a special case from the more general semi-parametric theory [see Tsiatis (2006)], we state the following lemma for identification, following the notation of Appendix A.

Lemma 6

The parameter θ is identifiable under the model

$$E[U(\theta )]=0$$

if both Cov[U(θ₀)] and $B({\theta }_0)\equiv E[\frac{\partial U({\theta }_0)}{\partial \theta }]$ are of full rank. Here, θ₀ is the value of the true parameter.

Proof

The proof is trivial. By Appendix A, the asymptotic covariance matrix of the estimates is given by

$$B^{-1}({\theta }_0)\text{Cov}[U({\theta }_0)]B^{-1}{({\theta }_0)}^{\prime },$$

which will be finite and of full rank when the conditions in the lemma hold true.

APPENDIX C: PROOF THAT FTSR IMPLIES CTSR

We assume that Z_t is a càdlàg process, and everything we discuss is in an a.s. sense.

We first define

$$\begin{array}{c}{\mathcal{H}}_{t-}\equiv \sigma ({\overline{Z}}_{t-1}),\\ {\mathcal{F}}_{t-,t}\equiv \sigma ({\overline{Z}}_{t-},{\underset{\_}{Y}}_{t+}^0).\end{array}$$

Recall that N_t counts the number of jumps in A_t up to time t. We assume that a continuous version of the intensity process of N_t exists, which we denote by η_t. If we define

$$r_t(\delta )=(1-A_{t-})A_{t+\delta }+A_{t-}(1-A_{t+\delta }).$$

Then, under certain regularity conditions [see Chapter 2 of Andersen et al. (1992)], for every t,

$${\eta }_t=\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid {\mathcal{F}}_{t-,t+}]}{\delta }\mathrm{a}.\mathrm{s}.$$

For Theorem 4, we need to show that η_t is also -measurable. This is because if this is true, then

$$\begin{array}{l}E\left[N_{t_0+s}-{\int }_0^{t_0+s}{\eta }_{t}dt|{\mathcal{H}}_{t_0}\right]=E\left[\left(N_{t_0+s}-{\int }_0^{t_0+s}{\eta }_{t}dt\right)-\left(N_{t_0}-{\int }_0^{t_0}{\eta }_{t}dt\right)|{\mathcal{H}}_{t_0}\right]+E\left[\left(N_{t_0}-{\int }_0^{t_0}{\eta }_{t}dt\right)|{\mathcal{H}}_{t_0}\right]\\ =E\left\{E\left[\left(N_{t_0+s}-{\int }_0^{t_0+s}{\eta }_{t}dt\right)-\left(N_{t_0}-{\int }_0^{t_0}{\eta }_{t}dt\right)|{\mathcal{F}}_{t_0-,t_0+}\right]|{\mathcal{H}}_{t_0}\right\}+N_{t_0}-{\int }_0^{t_0}{\eta }_{t}dt\\ =0+N_{t_0}-{\int }_0^{t_0}{\eta }_{t}dt\\ =N_{t_0}-{\int }_0^{t_0}{\eta }_{t}dt.\end{array}$$

The second equality follows because of properties of conditional expectation and the assumption that η_t is -measurable. The third equality holds because η_t is an intensity process of N_t. The last equality shows that η_t is also a intensity process of N_t, which agrees with the definition of CTSR.

Before proving the main result, we assume the following regularity conditions.

1. As stated before, we assume that η_t is continuous. We further assume that η_t is positive, and bounded from below and above by constants that do not depend on t. We also assume that $\frac{E[r_t(\delta )\mid {\mathcal{F}}_{t-,t+}]}{\delta }$ is bounded by a constant for every t within a interval of (0, δ₀].

2. We assume that for any finite sequence of time points, t₁ ≤ t₂ ≤ t₃ ≤ ··· ≤ t_n, the density f(Z_t1 = z₁, Z_t2 = z₂, …, Z_tn = z_n) is well defined and locally uniformly bounded, that is, there exists a constant D and a rectangle B ≡ [t₁ − δ₁, t₁ + δ₁] × [t₂ − δ₂, t₂ + δ₂] × ··· × [t_n − δ_n, t_n + δ_n] such that for any ${(t_1^{\prime },t_2^{\prime },\dots ,t_n^{\prime })}^T\in B$ and any possible value of (z₁, z₂, …, z_n)^T,

   $$f(Z_{t_1^{\prime }}=z_1,Z_{t_2^{\prime }}=z_2,\dots ,Z_{t_n^{\prime }}=z_n)\le D.$$

   For any conditional expectation involving finite sequence of time points, we choose the version that is defined by the joint density.

3. Given any finite sequence of time points, t₁ ≤ t₂ ≤ t₃ ≤ ··· ≤ t_n and any possible value of (z₁, z₂, …, z_n)^T, we assume that the following convergence is uniform in a closed neighborhood of t̃ ≡ (t₁, t₂, t₃, …, t_n):

   $$\begin{array}{l}f(Z_{t_1^{\prime }}=z_1,Z_{t_2^{\prime }}=z_2,\dots ,Z_{t_n^{\prime }}=z_n)\\ =\underset{\mathrm{\Delta }\downarrow 0}{lim}\frac{P(Z_{t_1^{\prime }}\in [z_1,z_1+{\mathrm{\Delta }}_1],Z_{t_2^{\prime }}\in [z_2,z_2+{\mathrm{\Delta }}_2],\dots ,Z_{t_n^{\prime }}\in [z_n,z_n+{\mathrm{\Delta }}_n])}{{\mathrm{\Delta }}_1\times {\mathrm{\Delta }}_2\times \cdots \times {\mathrm{\Delta }}_n},\end{array}$$

   where ${(t_1^{\prime },t_2^{\prime },\dots ,t_n^{\prime })}^T$ is in a neighborhood of t̃.

4. Given any finite sequence of time points, t₁ ≤ t₂ ≤ t₃ ≤ ··· ≤ t_i ≤ ··· ≤ t_n and any possible value of (z₁, z₂, …, z_n)^T, we define

   $$f(\delta )=\frac{P(A_{t_i+\delta }\ne A_{t_i}\mid Z_{t_1}=z_1,Z_{t_2}=z_2,\dots ,Z_{t_n}=z_n)}{\delta }.$$

   We assume that lim_δ↓0 f(δ) exists and is positive and finite. We also assume that f(δ) is finite and is right-continuous in δ, and the continuity is uniform with respect to (δ, t_i) in [0, δ₀] × B(t_i), where B(t_i) is a closed neighborhood of t_i. Further, we assume that the above assumption is true if any of the Z in f is in its left-limit value rather than the concurrent value.

Remark 7

The third regularity condition is needed when we want to prove convergence in density. For example, consider that when δ ↓ 0, we have Z_t2+δ → Z_t2. We can then see that

$$\begin{array}{l}\underset{\delta \downarrow 0}{lim}f(Z_{t_1}=z_1,Z_{t_2+\delta }=z_2,Z_{t_3}=z_3)=\underset{\delta \downarrow 0}{lim}\underset{\begin{array}{l}{\mathrm{\Delta }}_1\downarrow 0\\ {\mathrm{\Delta }}_2\downarrow 0\\ {\mathrm{\Delta }}_3\downarrow 0\end{array}}{lim}\frac{P(Z_{t_1}\in [z_1,z_1+{\mathrm{\Delta }}_1],Z_{t_2+\delta }\in [z_2,z_2+{\mathrm{\Delta }}_2],Z_{t_3}\in [z_3,z_3+{\mathrm{\Delta }}_3])}{{\mathrm{\Delta }}_1{\mathrm{\Delta }}_2{\mathrm{\Delta }}_3}\\ =\underset{\begin{array}{l}{\mathrm{\Delta }}_1\downarrow 0\\ {\mathrm{\Delta }}_2\downarrow 0\\ {\mathrm{\Delta }}_3\downarrow 0\end{array}}{lim}\underset{\delta \downarrow 0}{lim}\frac{P(Z_{t_1}\in [z_1,z_1+{\mathrm{\Delta }}_1],Z_{t_2+\delta }\in [z_2,z_2+{\mathrm{\Delta }}_2],Z_{t_3}\in [z_3,z_3+{\mathrm{\Delta }}_3])}{{\mathrm{\Delta }}_1{\mathrm{\Delta }}_2{\mathrm{\Delta }}_3}\\ =\underset{\begin{array}{l}{\mathrm{\Delta }}_1\downarrow 0\\ {\mathrm{\Delta }}_2\downarrow 0\\ {\mathrm{\Delta }}_3\downarrow 0\end{array}}{lim}\frac{P(Z_{t_1}\in [z_1,z_1+{\mathrm{\Delta }}_1],Z_{t_2}\in [z_2,z_2+{\mathrm{\Delta }}_2],Z_{t_3}\in [z_3,z_3+{\mathrm{\Delta }}_3])}{{\mathrm{\Delta }}_1{\mathrm{\Delta }}_2{\mathrm{\Delta }}_3}\\ =f(Z_{t_1}=z_1,Z_{t_2}=z_2,Z_{t_3}=z_3).\end{array}$$

The interchanging of limits in the second equality is valid because of the third regularity condition. The third equality follows from the fact that probabilities are expectations of indicator functions and that the dominated convergence theorem applies.

We introduce the following lemma for technical convenience.

Lemma 8

If the càdlàg process Z_t follows the finite-time sequential randomization as defined in Definition 3, then the following version of FTSR is also true:

$$P(A_{t_n}\mid {\overline{L}}_{t_{n-1}},L_{t_n-},{\overline{A}}_{t_{n-1}},{\overline{Y}}_{t_{n-1}}^0,Y_{t_n-}^0,{\underset{\_}{Y}}_{t_n+}^0)=P(A_{t_n}\mid {\overline{L}}_{t_{n-1}},L_{t_n-},{\overline{A}}_{t_{n-1}},{\overline{Y}}_{t_{n-1}}^0,Y_{t_n-}^0),$$ (18)

where L̄_tn−1 = (L_t1, L_t2, …, L_tn−1), Ā_tn−1 = (A_t1, A_t2, …, A_tn−1), ${\overline{Y}}_{t_{n-1}}^0=(Y_{t_1}^0,Y_{t_2}^0,\dots ,Y_{t_{n-1}}^0)$ and ${\underset{\_}{Y}}_{t_n+}^0=(Y_{t_{n+1}}^0,Y_{t_{n+2}}^0,\dots ,Y_{t_{n+l}}^0)$.

Remark 9

The difference between (18) and the original definition of FTSR is that in (18), most L’s and Y⁰’s are stated in their concurrent values, while in Definition 3, they are all stated in their left limits. Lemma 8 is only for technical convenience.

Proof of Lemma 8

The result follows directly from the definition of a càdlàg process.

We now consider a discrete-time property.

Lemma 10

Suppose FTSR holds true. If we define

$$\begin{array}{l}\mathcal{F}=\sigma (Z_{t_1},\dots ,Z_{t_{n-1}},Z_{t-},Y_{t_{n+1}}^0,\dots ,Y_{t_{n+l}}^0),\\ \mathcal{H}=\sigma (Z_{t_1},\dots ,Z_{t_{n-1}},Z_{t-}),\end{array}$$

then we have for every t that

$$\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid \mathcal{F}]}{\delta }=\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid \mathcal{H}]}{\delta }a.s.$$ (19)

Proof

First, we note that the limits on both sides of equation (19) exist and are finite. This fact follows from the regularity condition 1. Take ${lim}_{\delta \downarrow 0}\frac{E[r_t(\delta )\mid \mathcal{F}]}{\delta }$, for example:

$$\begin{array}{l}\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid \mathcal{F}]}{\delta }=\underset{\delta \downarrow 0}{lim}\frac{E[E[r_t(\delta )\mid \sigma ({\overline{Z}}_{t-},{\underset{\_}{Y}}_t^0)]\mid \mathcal{F}]}{\delta }\\ =E\left[\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid \sigma ({\overline{Z}}_{t-},{\underset{\_}{Y}}_t^0)]}{\delta }|\mathcal{F}\right]\\ =E[{\eta }_t\mid \mathcal{F}].\end{array}$$

The interchange of limit and expectation is guaranteed by the assumption in regularity condition 1 that $\frac{E[r_t(\delta )\mid \sigma ({\overline{Z}}_{t-},{\underset{\_}{Y}}_t^0)]}{\delta }$ is bounded. The existence is then guaranteed by the dominated convergence theorem and E[η_t | ] is obviously finite.

Given equation (10) and Lemma 8, we always have

$$E[I_{A_t\ne A_{t_n}}\mid {\overline{L}}_{t-},{\overline{A}}_{t_n},{\overline{Y}}_{t-}^0,{\underset{\_}{Y}}_{t+}^0]=E[I_{A_t\ne A_{t_n}}\mid {\overline{L}}_{t-},{\overline{A}}_{t_n},{\overline{Y}}_{t-}^0]\mathrm{a}.\mathrm{s}.,$$ (20)

where L̄_t− = (L_t1, L_t2, …, L_tn−1, L_tn, L_t−)^T, Ā_tn = (A_t1, A_t2, …, A_tn)^T, ${\overline{Y}}_{t-}^0={(Y_{t_1}^0,Y_{t_2}^0,\dots ,Y_{t_n}^0,Y_{t-}^0)}^T$ and ${\underset{\_}{Y}}_{t+}^0={(Y_{t_{n+1}}^0,Y_{t_{n+2}}^0,\dots ,Y_{t_{n+l}}^0)}^T$.

In the regularity conditions, since we assumed the existence of joint density, the usual definition of conditional probability is a version of the conditional expectation defined using σ-fields. In our case, we have

$$\begin{array}{l}\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid \mathcal{F}]}{\delta }=\underset{\delta \downarrow 0}{lim}\frac{P(A_{t+\delta }\ne A_{t-}\mid Z_{t_1},\dots ,Z_{t_{n-1}},Z_{t-},Y_{t_{n+1}}^0,\dots ,Y_{t_{n+l}}^0)}{\delta }\\ =\underset{\delta \downarrow 0}{lim}\underset{t_n\uparrow t-}{lim}\frac{P(A_{t+\delta }\ne A_{t_n}\mid Z_{t_1},\dots ,Z_{t_{n-1}},Z_{t_n},L_{t-},Y_{t-}^0,Y_{t_{n+1}}^0,\dots ,Y_{t_{n+l}}^0)}{\delta +(t-t_n)}\\ =\underset{t_n\uparrow t-}{lim}\underset{\delta \downarrow 0}{lim}\frac{P(A_{t+\delta }\ne A_{t_n}\mid Z_{t_1},\dots ,Z_{t_{n-1}},Z_{t_n},L_{t-},Y_{t-}^0,Y_{t_{n+1}}^0,\dots ,Y_{t_{n+l}}^0)}{\delta +(t-t_n)}\\ =\underset{t_n\uparrow t-}{lim}\frac{P(A_t\ne A_{t_n}\mid Z_{t_1},\dots ,Z_{t_{n-1}},Z_{t_n},L_{t-},Y_{t-}^0,Y_{t_{n+1}}^0,\dots ,Y_{t_{n+l}}^0)}{t-t_n}\\ =\underset{t_n\uparrow t-}{lim}\frac{E[I_{A_t\ne A_{t_n}}\mid {\overline{L}}_{t-},{\overline{A}}_{t_n},{\overline{Y}}_{t-}^0,{\underset{\_}{Y}}_{t+}^0]}{t-t_n}.\end{array}$$

The second equality is guaranteed by the third regularity condition. By Remark 7, we can show that the conditional density in the third line converges to the second line as A_tn and Z_tn converges to A_t− and Z_t−. The (t − t_n) term in the denominator is not needed for the second equality, but is crucial for the interchangeability of limits in the third equality. The interchangeability of limits is guaranteed by the fourth regularity condition. By the fourth regularity condition, the following limit

$$\underset{\delta \downarrow 0}{lim}\frac{P(A_{t+\delta }\ne A_{t_n}\mid Z_{t_1},\dots ,Z_{t_{n-1}},Z_{t_n},Z_{t-},Z_{t_{n+1}},\dots ,Z_{t_{n+l}})}{\delta +(t-t_n)}=\frac{P(A_t\ne A_{t_n}\mid Z_{t_1},\dots ,Z_{t_{n-1}},Z_{t_n},Z_{t-},Z_{t_{n+1}},\dots ,Z_{t_{n+l}})}{t-t_n}$$

is uniform in t_n.

If we integrate out some extra variables, we can get that

$$\underset{\delta \downarrow 0}{lim}\frac{P(A_{t+\delta }\ne A_{t_n}\mid Z_{t_1},\dots ,Z_{t_{n-1}},Z_{t_n},L_{t-},Y_{t-}^0,Y_{t_{n+1}}^0,\dots ,Y_{t_{n+l}}^0)}{\delta +(t-t_n)}=\frac{P(A_t\ne A_{t_n}\mid Z_{t_1},\dots ,Z_{t_{n-1}},Z_{t_n},L_{t-},Y_{t-}^0,Y_{t_{n+1}}^0,\dots ,Y_{t_{n+l}}^0)}{t-t_n}$$

is uniform in t_n.

Therefore, we can interchange the limits in the third equality.

Similarly, we can prove that

$$\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid \mathcal{H}]}{\delta }=\underset{t_n\uparrow t-}{lim}\frac{E[I_{A_t\ne A_{t_n}}\mid {\overline{L}}_{t-},{\overline{A}}_{t_n},{\overline{Y}}_{t-}^0]}{t-t_n}.$$

Therefore, we have

$$\begin{array}{l}\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid \mathcal{F}]}{\delta }=\underset{t_n\uparrow t-}{lim}\frac{E[I_{A_t\ne A_{t_n}}\mid {\overline{L}}_{t-},{\overline{A}}_{t_n},{\overline{Y}}_{t-}^0,{\underset{\_}{Y}}_{t+}^0]}{t-t_n}\\ =\underset{t_n\uparrow t-}{lim}\frac{E[I_{A_t\ne A_{t_n}}\mid {\overline{L}}_{t-},{\overline{A}}_{t_n},{\overline{Y}}_{t-}^0]}{t-t_n}\\ =\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid \mathcal{H}]}{\delta }.\end{array}$$

The second equality comes from (20).

We now prove the final key lemma.

Lemma 11

Given FTSR, η_t is -measurable.

Proof

We prove the result by using the definition of a measurable function with respect to a σ-field.

For any a ∈ , consider the following set:

$$B\equiv \{\omega :{\eta }_t\le a\}.$$

Since η_t is measurable with respect to 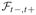, B ∈ .

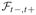By Lemma 25.9 of Rogers and Williams (1994), B is a σ-cylinder and it can be decided by variables from countably many time points. Suppose the collection of these countably many time points is S. S = S₁ ∪ S₂, where t_1,i < t for t_1,i ∈ S₁ and t_2,j > t for t_2,j ∈ S₂.

Let 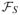denote the σ-field generated by (Z_t1,i, i ∈ 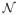; Z_t−; $Y_{t_{2,j}}^0$, j ∈ ). We have augmented the σ-field generated by variables from S with Z_t−.

Next, define the following series of σ-fields:

$$\begin{array}{lll}\hfill {\mathcal{F}}_1& \equiv \hfill & \sigma (Z_{t_{1,1}},Z_{t-},Y_{t_{2,1}}^0),\hfill \\ \hfill {\mathcal{F}}_2& \equiv \hfill & \sigma ({\mathcal{F}}_1,Z_{t_{1,2}},Y_{t_{2,1}}^0),\hfill \\ \hfill & \cdots \hfill & \hfill \\ \hfill {\mathcal{F}}_{\infty }& \equiv \hfill & {\mathcal{F}}_S.\hfill \end{array}$$

Considering the following sets:

$$\begin{array}{lll}\hfill B_1& \equiv \hfill & \{\omega :E[{\eta }_t\mid {\mathcal{F}}_1]\le a\},\hfill \\ \hfill B_2& \equiv \hfill & \{\omega :E[{\eta }_t\mid {\mathcal{F}}_2]\le a\},\hfill \\ \hfill & \cdots \hfill & \hfill \\ \hfill B_S\equiv B_{\infty }& \equiv \hfill & \{\omega :E[{\eta }_t\mid {\mathcal{F}}_S]\le a\}.\hfill \end{array}$$

We have B_k ∈ .

It is easy to see that

$$B_1\supset B_2\supset \cdots \supset B_S$$

because

$$E[E[{\eta }_t\mid {\mathcal{F}}_k]\mid {\mathcal{F}}_{k-1}]=E[{\eta }_t\mid {\mathcal{F}}_{k-1}]$$

and taking conditional expectation preserves the direction of inequality.

Also, with the above definitions, ↑ . Therefore, by Theorem 5.7 from Durrett [(2005), Chapter 4], we know that

$$E[{\eta }_t\mid {\mathcal{F}}_k]\to E[{\eta }_t\mid {\mathcal{F}}_S]\mathrm{a}.\mathrm{s}.$$

It is then easy to see that I_B1 → I_BS a.s. and that

$$B_S=\underset{i=1}{\overset{\infty }{\cap }}{B}_i$$

with difference up to a null set.

We now claim that

$$B_S=B$$ (21)

with difference up to a null set.

Obviously, B ⊂ B_S. Suppose that P(B_S − B) > 0. Since B_S − B ∈ , we have

$${\int }_{B_S-B}{\eta }_{t}P(d\omega )={\int }_{B_S-B}E[{\eta }_t\mid {\mathcal{F}}_S]P(d\omega ).$$

Then

$$\mathit{LHS}>aP(B_S-B)$$

and

$$\mathit{RHS}\le aP(B_S-B).$$

This is a contradiction.

Therefore, $B={\cap }_{i=1}^{\infty }{B}_i$ with difference up to a null set.

Next, we define

$$\begin{array}{ccc}{\mathcal{H}}_1& =& \sigma (Z_{t_{1,1}},Z_{t-}),\\ {\mathcal{H}}_2& =& \sigma ({\mathcal{H}}_1,Z_{t_{1,2}}),\\ & \cdots & \end{array}$$

Given FTSR, by Lemma 10, we have

$$E[{\eta }_t\mid {\mathcal{F}}_k]=E[{\eta }_t\mid {\mathcal{H}}_k].$$

Therefore, every B_k ∈ and thus B_k ∈ .

Since $B={\cap }_{i=1}^{\infty }{B}_i$, B ∈ as well. By the definition of a measurable function, η_t is measurable with respect to .

Combining all of the results in this appendix, we have proven Theorem 4.

APPENDIX D: PROOF OF THEOREM 5

Let ${\mathcal{G}}_t=\sigma (Y_{t-}^0,L_{t-},A_{t-})$. Recall the definition of r_t(δ) = (1 − A_t−)A_t+δ + A_t−(1 − A_t+δ) and that $Z_t={(Y_t^0,L_t,A_t)}^T$. By the Markovian property and the cádlág property, it is easy to show that

$$E[r_t(\delta )\mid \sigma ({\overline{Z}}_{t-})]=E[r_t(\delta )\mid {\mathcal{G}}_t]$$

and that

$$E[r_t(\delta )\mid \sigma ({\overline{Z}}_{t-},Y_{t+s}^0)]=E[r_t(\delta )\mid \sigma ({\mathcal{G}}_t,Y_{t+s}^0)].$$

Note that, without loss of generality, we only consider $Y_{t+s}^0$ in the proof, rather than ${\underset{\_}{Y}}_{t+}^0$.

Therefore, we have a reduced form of continuous-time sequential randomization:

$$\begin{array}{l}\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid \sigma ({\mathcal{G}}_t,Y_{t+s}^0)]}{\delta }=\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid \sigma ({\overline{Z}}_{t-},Y_{t+s}^0)]}{\delta }\\ =\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid \sigma ({\overline{Z}}_{t-})]}{\delta }\\ =\underset{\delta \downarrow 0}{lim}\frac{E[r_t(\delta )\mid {\mathcal{G}}_t]}{\delta }.\end{array}$$

First, we note that if we can prove

$$f(Y_{t+s}^0,A_{t-}\mid Y_{t-}^0,L_{t-})P(A_t\mid Y_{t-}^0,L_{t-})=f(Y_{t+s}^0,A_t\mid Y_{t-}^0,L_{t-})P(A_{t-}\mid Y_{t-}^0,L_{t-}),$$ (22)

then we can conclude (11). The reason is as follows: assuming (22) to be true, we integrate A_t− out on both sides of the equation. We will get

$$f(Y_{t+s}^0\mid Y_{t-}^0,L_{t-})P(A_t\mid Y_{t-}^0,L_{t-})=f(Y_{t+s}^0,A_t\mid Y_{t-}^0,L_{t-}).$$

Dividing the above equation by $f(Y_{t+s}^0\mid Y_{t-}^0,L_{t-})$, we obtain (11).

Consider

$$g({\delta }_1,{\delta }_2)\equiv f(Y_{t+s}^0\mid A_{t+{\delta }_1}=a_1,A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-}),$$

where δ₁ > 0 and δ₂ > 0.

We observe that

$$\begin{array}{l}\underset{{\delta }_1\downarrow 0}{lim}\underset{{\delta }_2\downarrow 0}{lim}g({\delta }_1,{\delta }_2)=\underset{{\delta }_1\downarrow 0}{lim}f(Y_{t+s}^0\mid A_{t+{\delta }_1}=a_1,A_{t-}=a_2,Y_{t-}^0,L_{t-})\\ =\underset{{\delta }_1\downarrow 0}{lim}\frac{f(Y_{t+s}^0,A_{t+{\delta }_1}=a_1\mid A_{t-}=a_2,Y_{t-}^0,L_{t-})}{P(A_{t+{\delta }_1}\mid A_{t-}=a_2,Y_{t-}^0,L_{t-})}\\ =f(Y_{t+s}^0\mid A_{t-}=a_2,Y_{t-}^0,L_{t-})\times \underset{{\delta }_1\downarrow 0}{lim}\frac{P(A_{t+{\delta }_1}=a_1\mid Y_{t+s}^0,A_{t-}=a_2,Y_{t-}^0,L_{t-})}{P(A_{t+{\delta }_1}=a_1\mid A_{t-}=a_2,Y_{t-}^0,L_{t-})}\\ =\{\begin{array}{ll}f(Y_{t+s}^0\mid A_{t-}=a_2,Y_{t-}^0,L_{t-})\times \underset{{\delta }_1\downarrow 0}{lim}\frac{1-P(A_{t+{\delta }_1}\ne A_{t-}\mid Y_{t+s}^0,A_{t-}=a_2,Y_{t-}^0,L_{t-})}{1-P(A_{t+{\delta }_1}\ne A_{t-}\mid A_{t-}=a_2,Y_{t-}^0,L_{t-})},\hfill & \text{if}{a}_1=a_2,\hfill \\ f(Y_{t+s}^0\mid A_{t-}=a_2,Y_{t-}^0,L_{t-})\times \underset{{\delta }_1\downarrow 0}{lim}\frac{P(A_{t+{\delta }_1}\ne A_{t-}\mid Y_{t+s}^0,A_{t-}=a_2,Y_{t-}^0,L_{t-})/{\delta }_1}{P(A_{t+{\delta }_1}\ne A_{t-}\mid A_{t-}=a_2,Y_{t-}^0,L_{t-})/{\delta }_1},\hfill & \text{if}{a}_1\ne a_2.\hfill \end{array}\\ =f(Y_{t+s}^0\mid A_{t-}=a_2,Y_{t-}^0,L_{t-}).\end{array}$$

Here, the validity of taking the limit inside the density is guaranteed by the third regularity condition, and the last equality follows because of the continuous-time sequential randomization assumption.

We also observe that

$$\begin{array}{l}\underset{{\delta }_2\downarrow 0}{lim}\underset{{\delta }_1\downarrow 0}{lim}g({\delta }_1,{\delta }_2)=\underset{{\delta }_2\downarrow 0}{lim}f(Y_{t+s}^0\mid A_{t-{\delta }_2},A_t,Y_{t-}^0,L_{t-})\\ =\underset{{\delta }_2\downarrow 0}{lim}f(Y_{t+s}^0\mid A_t,Y_{t-}^0,L_{t-})=f(Y_{t+s}^0\mid A_t,Y_{t-}^0,L_{t-}).\end{array}$$

The second equality uses the Markov property.

If we can interchange the limits, then we have

$$f(Y_{t+s}^0\mid A_{t-},Y_{t-}^0,L_{t-})=f(Y_{t+s}^0\mid A_t,Y_{t-}^0,L_{t-}).$$

Equation (22) follows from the definition of conditional density.

We now establish the fact that

$$\underset{{\delta }_2\downarrow 0}{lim}\underset{{\delta }_1\downarrow 0}{lim}g({\delta }_1,{\delta }_2)=\underset{{\delta }_1\downarrow 0}{lim}\underset{{\delta }_2\downarrow 0}{lim}g({\delta }_1,{\delta }_2)$$

by showing that lim_δ1↓0 g(δ₁, δ₂) is uniform in δ₂.

If we define g₁(δ₂) = lim_δ1↓0 g(δ₁, δ₂), then

$$\begin{array}{l}\mid g({\delta }_1,{\delta }_2)-g_1({\delta }_2)\mid =\left|\frac{f(Y_{t+s}^0,A_{t+{\delta }_1}=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})}{P(A_{t+{\delta }_1}=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})}-\frac{f(Y_{t+s}^0,A_t=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})}{P(A_t=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})}\right|\\ =f(Y_{t+s}^0\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})\times \left|\frac{P(A_{t+{\delta }_1}=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-},Y_{t+s}^0)}{P(A_{t+{\delta }_1}=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})}-\frac{P(A_t=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-},Y_{t+s}^0)}{P(A_t=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})}\right|.\end{array}$$

Consider the ratio $\frac{P(A_{t+{\delta }_1}=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-},Y_{t+s}^0)}{P(A_{t+{\delta }_1}=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})}$. We claim that it converges to $\frac{P(A_t=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-},Y_{t+s}^0)}{P(A_t=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})}$ uniformly in δ₂.

If a₁ = a₂, then the density $P(A_{t+{\delta }_1}=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})$ is bounded from below by a positive number. By the fourth regularity condition,

$$P(A_{t+{\delta }_1}=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-},Y_{t+s}^0)\to P(A_t=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-},Y_{t+s}^0)$$

and

$$P(A_{t+{\delta }_1}=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})\to P(A_t=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-}),$$

uniformly in δ₂, as δ₁ ↓ 0. When the denominators are bounded from below by a positive number, the ratio also converges uniformly.

If a₁ ≠ a₂, then, by the fourth regularity condition, we have

$$\frac{P(A_{t+{\delta }_1}=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-},Y_{t+s}^0)}{{\delta }_1+{\delta }_2}\to \frac{P(A_t=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-},Y_{t+s}^0)}{{\delta }_2}$$

and

$$\frac{P(A_{t+{\delta }_1}=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})}{{\delta }_1+{\delta }_2}\to \frac{P(A_t=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})}{{\delta }_2},$$

uniformly in δ₂, as δ₁ ↓ 0. Also, the denominator $\frac{P(A_{t+{\delta }_1}=a_1\mid A_{t-{\delta }_2}=a_2,Y_{t-}^0,L_{t-})}{{\delta }_1+{\delta }_2}$ is bounded from below by a positive number. Hence, we establish the uniform convergence of the ratio.

Combining the two cases above, |g(δ₁, δ₂) − g₁(δ₂)| is bounded by O(δ₁), which does not depend on δ₂, so g(δ₁, δ₂) → g₁(δ₂) uniformly in δ₂. Therefore,

$$\underset{{\delta }_2\downarrow 0}{lim}\underset{{\delta }_1\downarrow 0}{lim}g({\delta }_1,{\delta }_2)=\underset{{\delta }_1\downarrow 0}{lim}\underset{{\delta }_2\downarrow 0}{lim}g({\delta }_1,{\delta }_2).$$

By the argument at the beginning of the proof, we have proven the first part of the theorem.

To show that (11) implies FTSR, without of loss of generality, we consider

$$\begin{array}{l}P\left(A_t\mid L_{t-},Y_{t-}^0,A_{t-m},L_{(t-m)-},Y_{(t-m)-}^0,Y_{t+s}^0\right)=\frac{f(A_t,L_{t-},Y_{t-}^0,A_{t-m},L_{(t-m)-},Y_{(t-m)-}^0,Y_{t+s}^0)}{{\sum }_{i=0,1}f(A_t=i,L_{t-},Y_{t-}^0,A_{t-m},L_{(t-m)-},Y_{(t-m)-}^0,Y_{t+s}^0)}\\ =(f(Y_{t+s}^0\mid A_t,L_{t-},Y_{t-}^0)f(A_t,L_{t-},Y_{t-}^0,A_{t-m},L_{(t-m)-},Y_{(t-m)-}^0))/(\sum _{i=0,1}f(Y_{t+s}^0\mid A_t=i,L_{t-},Y_{t-}^0)\times f(A_t=i,L_{t-},Y_{t-}^0,A_{t-m},L_{(t-m)-},Y_{(t-m)-}^0))\\ =\frac{f(Y_{t+s}^0\mid L_{t-},Y_{t-}^0)f(A_t,L_{t-},Y_{t-}^0,A_{t-m},L_{(t-m)-}{Y}_{(t-m)-}^0)}{{\sum }_{i=0,1}f(Y_{t+s}^0\mid L_{t-},Y_{t-}^0)f(A_t=i,L_{t-},Y_{t-}^0,A_{t-m},L_{(t-m)-},Y_{(t-m)-}^0)}\\ =\frac{f(A_t,L_{t-},Y_{t-}^0,A_{t-m},L_{(t-m)-},Y_{(t-m)-}^0)}{{\sum }_{i=0,1}f(A_t=i,L_{t-},Y_{t-}^0,A_{t-m},L_{(t-m)-},Y_{(t-m)-}^0)}\\ =P(A_t\mid L_{t-},Y_{t-}^0,A_{t-m},L_{(t-m)-},Y_{(t-m)-}^0).\end{array}$$

The second equality follows because of the Markov property. The third equality uses equation (11). We have thus proven the second half of the theorem.

APPENDIX E: SIMULATION PARAMETERS

In all simulation models from M1 to M4, we specify the parameters as follows:

• let g(V, t) = C, a constant; let C = 100;

• for M1 (also for M3 and M4), let θ = 0.2 and σ = 1;

• for M2, let m = 2, θ₁ = 0.2, σ₁ = 1 and θ₂ = 1, σ₂ = 0.5. The transition probability of J_t would be P(t) = e^At, where $A=\left(\begin{array}{ll}\hfill -1& \hfill 1\\ \hfill 1& \hfill -1\end{array}\right)$;

• for initial value, e₀ is generated from $N(0,\frac{\sigma }{\sqrt{2\theta }})$;

• the causal parameter Ψ = 1;

• in M1, M2 and M3, s(A_t, Y_t) = e^{α₀ + α₁A_t + α₂Y_t + α₃A_tY_t}; let α₁ = −0.3, α₂ = −0.005, α₃ = 0.007 and α₀ = −0.2;

• in M4, A_t is generated as follows: if Y_t−0.5 > 101 and Y_t > 101, $s(A_t=1,L_t^{\ast })=2.8$; if Y_t0.5 < 99 and Y_t < 99, $s(A_t=0,L_t^{\ast })=2.8$; otherwise, A_t is generated following a model similar to that in M1, except that $s(A_t,L_t^{\ast })=e^{{\alpha }_0+{\alpha }_1{A}_t+{\alpha }_2{L}_t^{\ast }+{\alpha }_3{A}_t{L}_t^{\ast }}$; the values of the α’s are the same as before;

• in M4, η_t follows an Ornstein–Uhlenbeck process with parameters θ = 0.2 and σ = 1;

• for initial value, A₀ is generated from Bernoulli(expit(α₀ + α₂Y₀));

• K = 5 is the number of periods;

• number of subjects n = 5000.