Fast Censored Linear Regression

Abstract

Weighted log-rank estimating function has become a standard estimation method for the censored linear regression model, or the accelerated failure time model. Well established statistically, the estimator defined as a consistent root has, however, rather poor computational properties because the estimating function is neither continuous nor, in general, monotone. We propose a computationally efficient estimator through an asymptotics-guided Newton algorithm, in which censored quantile regression methods are tailored to yield an initial consistent estimate and a consistent derivative estimate of the limiting estimating function. We also develop fast interval estimation with a new proposal for sandwich variance estimation. The proposed estimator is asymptotically equivalent to the consistent root estimator and barely distinguishable in samples of practical size. However, computation time is typically reduced by two to three orders of magnitude for point estimation alone. Illustrations with clinical applications are provided.

1. Introduction

With censored survival data, failure time T is subject to censoring, say, by time C. Consequently, T is not directly observed but through X ≡ T ∧ C and Δ ≡ I(T ≤ C), where ∧ is the minimization operator and I(·) the indicator function. In a regression problem, it is of interest to study the relationship between T and a p × 1 vector of covariates, say Z, using observations of (X, Δ, Z). The accelerated failure time model is the linear regression model on the logarithmic scale along with the conditional independence censoring mechanism:

$$\log T={\beta }^{⊺}\mathrm{Z}+\epsilon ,T╨C\mid \mathrm{Z},$$ (1)

where β is the regression coefficient vector, ε is the random error with an unspecified distribution, and ⫫ denotes statistical independence.

In the extensive literature on model (1), weighted log-rank estimating function (Tsiatis, 1990) has become an accepted and standard estimation method. Despite challenges from discontinuity and, in general, non-monotonicity of the estimating function, the past two decades has seen steady advances, including Tsiatis (1990) and Ying (1993) on the asymptotics; Fygenson & Ritov (1994) and Jin et al. (2003) on consistent root identification; and Parzen et al. (1994), Jin et al. (2001), and Huang (2002) on the interval estimation. Nevertheless, the estimator still has rather poor computational properties with existing algorithms, including the simulated annealing algorithm (Lin & Geyer, 1992), the recursive bisection algorithm (Huang, 2002), the linear programming method (Lin et al., 1998; Jin et al., 2003), the importance sampling method (Tian et al., 2004), and the Markov Chain Monte Carlo approach (Tian et al., 2007). To elaborate on the currently prevailing linear programming method, Lin et al. (1998) showed that the Gehan function can be formulated as a linear program; this is a special monotone weighted log-rank function. Jin et al. (2003) further established that a root to a general weighted log-rank function is the limiting root to a sequence of weighted Gehan functions, provided that the limit exists. They then devised a procedure that iteratively solves weighted Gehan functions via linear programming. However, a (weighted) Gehan function involves pairwise comparisons so that the number of terms in the linear program increases quadratically with the sample size. This explains its computational inefficiency, despite the availability of several well-developed linear programming algorithms including the classical simplex and interior point (cf. Portnoy & Koenker, 1997).

In this article, we propose a novel estimator based on an asymptotics-guided Newton algorithm to achieve good computational properties, for a general weighted log-rank function. Starting from an initial consistent estimate, the algorithm updates the estimation by using a consistent derivative estimate of the limiting estimating function and yields an estimator asymptotically equivalent to a consistent root. Such a Newton-type update is similar to that used in the one-step estimation of Gray (2000). However, the consistency of Gray’s derivative estimate and subsequently the properties of his one-step estimator are not yet established. Furthermore, Gray’s approach uses the Gehan estimator as the initial estimate, which may be computationally intensive in itself. Our proposal is also distinct from the algorithm of Yu & Nan (2006), which targets the Gehan function only. We adopt computationally efficient censored quantile regression as in Huang (2010) to obtain the initial estimate and the derivative estimate. Multiple Newton-type updates are taken for better finite-sample properties. In addition, we develop fast interval estimation with a proposal for sandwich variance estimation. The computational improvement over the linear programming method is tremendous. The proposed asymptotics-guided Newton algorithm is presented in Section 2, and the fast preparatory estimation in Section 3. Section 4 describes new interval estimation methods. Section 5 summarizes simulation results on both statistical and computational properties of the proposal. Illustrations with clinical studies are provided in Section 6. Section 7 concludes with discussion. Technical details and proofs are collected in the Appendices. An R package implementing this proposal is available from the author upon request.

2. Estimation by asymptotics-guided Newton algorithm

The data consist of (X_i, Δ_i, Z_i), i = 1,…, n, as n iid replicates of (X, Δ, Z). Define counting process N_i(t; b) = I(log X_i – b^TZ_i ≤ t)Δ_i and at-risk process Y_i(t; b) = I(log X_i – b^TZ_i ≥ t). The weighted log-rank estimating function is

$$\mathrm{U}\left(\mathrm{b}\right)=n^{-1}\sum _{i=1}^n{\int }_{-\infty }^{\infty }\varphi (s;\mathrm{b})\left\{{\mathrm{Z}}_i-\frac{\sum _{j=1}^n{\mathrm{Z}}_j{Y}_j(s;\mathrm{b})}{\sum _{j=1}^n{Y}_j(s;\mathrm{b})}\right\}{\mathit{dN}}_i(s;\mathrm{b}),$$ (2)

where ϕ(t; b) is a nonnegative weight function; ϕ(t; b) = 1 and $\varphi (t;\mathrm{b})=n^{-1}{\sum }_{i=0}^n{Y}_i(t;\mathrm{b})$ correspond to the log-rank and Gehan functions, respectively. Typically, U(b) is not monotone and can have multiple roots, some of which may not be consistent (e.g., Fygenson & Ritov, 1994). In such a case, the estimator needs to be defined in a shrinking neighborhood of the true value β. On the other hand, U(b) is a step function and a root might not be exact. Nevertheless, an estimator can be defined as a root to

$$\mathrm{U}\left(\mathrm{b}\right)=o_p\left(n^{-1∕2}\right).$$ (3)

With probability tending to 1, such roots exist in a shrinking neighborhood of β and they are all asymptotically equivalent in the order of o_p(n^−1/2) under regularity conditions.

Due to the lack of differentiability, the standard Newton’s method is not applicable. We shall suggest an extension by taking advantage of the asymptotic local linearity of U(b), established by Ying (1993). Write ∥·∥ as the Euclidean norm. Under regularity conditions, for every positive sequence d = o_p(1),

$$\underset{\mathrm{b}:\Vert \mathrm{b}-\beta \Vert \le d}{\sup }\frac{\Vert \mathrm{U}\left(\mathrm{b}\right)-\mathrm{U}\left(\beta \right)-\mathrm{D}(\mathrm{b}-\beta )\Vert }{n^{-1∕2}+\Vert \mathrm{b}-\beta \Vert }=o_p\left(1\right),$$ (4)

for a non-singular matrix D that is the derivative at β of the limiting U(b). This proposed asymptotics-guided Newton algorithm proceeds with the provision of an initial consistent estimate of β and a consistent estimate of D, say ${\widehat{\beta }}^{\left(0\right)}$ and $\widehat{\mathrm{D}}$, respectively. That is, $\Vert {\widehat{\beta }}^{\left(0\right)}-\beta \Vert =o_p\left(1\right)$ and ${\Vert \widehat{\mathrm{D}}-\mathrm{D}\Vert }_{\max }=o_p\left(1\right)$, where ∥·∥_max denotes the maximum absolute value of matrix elements. Note that the above asymptotic local linearity also holds with D replaced by $\widehat{\mathrm{D}}$:

$$\underset{\mathrm{b}:\Vert \mathrm{b}-\beta \Vert \le d}{\sup }\frac{\Vert \mathrm{U}\left(\mathrm{b}\right)-\mathrm{U}\left(\beta \right)-\widehat{\mathrm{D}}(\mathrm{b}-\beta )\Vert }{n^{-1∕2}+\Vert \mathrm{b}-\beta \Vert }=o_p\left(1\right).$$ (5)

Then, Newton-type updates can be made iteratively:

$${\widehat{\beta }}^{\left(k\right)}={\widehat{\beta }}^{(k-1)}-2^{-g}{\widehat{\mathrm{D}}}^{-1}\mathrm{U}\left({\widehat{\beta }}^{(k-1)}\right),k\ge 1.$$ (6)

A standard Newton-type update has the step size of ${\widehat{\mathrm{D}}}^{-1}\mathrm{U}\left({\widehat{\beta }}^{(k-1)}\right)$, corresponding to g = 0. However, over-shooting may occur, in which case the step size is halved repeatedly until the new estimate is an improvement. Thus, g is the smallest non-negative integer such that ${\widehat{\beta }}^{\left(k\right)}$ improves over ${\widehat{\beta }}^{(k-1)}$. We adopt a quadratic score statistic (cf. Lindsay & Qu, 2003) as the objective function for the improvement assessment. Take the variance estimate of Wei et al. (1990):

$$\mathrm{V}\left(\mathrm{b}\right)=n^{-1}\sum _{i=1}^n{\int }_{-\infty }^{\infty }\varphi {(s;\mathrm{b})}^2{\left\{{\mathrm{Z}}_i-\frac{\sum _{j=1}^n{\mathrm{Z}}_j{Y}_j(s;\mathrm{b})}{\sum _{j=1}^n{Y}_j(s;\mathrm{b})}\right\}}^{\otimes 2}{\mathit{dN}}_i(s;\mathrm{b}),$$ (7)

where v^⊗2 ≡ vv^T. By applying the results of Ying (1993), we have ∥V(b) – H∥_max = o_p(1) for any b converging to β in probability, where H is the asymptotic variance of n^1/2U(β). Then, the quadratic score statistic is defined as

$$\Omega \left(\mathrm{b}\right)=n\mathrm{U}{\left(\mathrm{b}\right)}^{⊺}\mathrm{V}{\left(\mathrm{b}\right)}^{-1}\mathrm{U}\left(\mathrm{b}\right).$$ (8)

The use of Ω(b) is justified by its asymptotic local quadraticity, following the asymptotic local linearity (5): For every positive sequence d = o_p(1),

$$\underset{\mathrm{b}:\Vert \mathrm{b}-\beta \Vert \le d}{\sup }\frac{\mid \Omega \left(\mathrm{b}\right)-n{\left\{\mathrm{U}\right(\beta )+\widehat{\mathrm{D}}(\mathrm{b}-\beta \left)\right\}}^{⊺}\mathrm{V}{\left(\mathrm{b}\right)}^{-1}\left\{\mathrm{U}\right(\beta )+\widehat{\mathrm{D}}(\mathrm{b}-\beta \left)\right\}\mid }{{(1+n^{1∕2}\Vert \mathrm{b}-\beta \Vert )}^2}=o_p\left(1\right).$$ (9)

By design, the algorithm dictates $\Omega \left({\widehat{\beta }}^{\left(k\right)}\right)$ to decrease over k.

In our proposal presented later, the initial estimator ${\widehat{\beta }}^{\left(0\right)}$, is n^1/2-consistent. In such a case, ${\widehat{\beta }}^{\left(k\right)}$, for any given k ≥ 1, and also $\widehat{\beta }$, corresponding to the one such that $\Omega \left({\widehat{\beta }}^{\left(k\right)}\right)$ is minimized according to the algorithm, are all asymptotically equivalent to a consistent root of U(b); see Appendix A. Therefore, the one-step estimation is appealing for less computation, as used by Gray (2000). Nevertheless, we shall adopt $\widehat{\beta }$ as our proposed estimator for better finite-sample performance.

In contrast to the linear programming method, this asymptotics-guided Newton algorithm tolerates statistically negligible imprecision. As will be shown, this tolerance has little, if any, effect on the estimator but the gain in computational efficiency can be very large. Meanwhile, the above iteration has a rather different statistical nature from that of Jin et al. (2003) for a non-Gehan function. The sequence of estimates in Jin et al. are not asymptotically equivalent in the first order to each other within a finite number of iterations, and their sequence is not guaranteed to converge. In this regard, our estimator is superior.

3. Fast preparatory estimation via quantile regression

For the initial consistent estimation alone, the Gehan estimator as commonly adopted, e.g., by Jin et al. (2003) and Gray (2000), might not permit fast estimation as explained in Section 1. Furthermore, the consistent estimation of D poses additional challenges; see Gray (2000). We shall approach the preparatory estimation from censored quantile regression, developing further the results of Huang (2010).

3·1 Censored quantile regression

Write the τ-th quantile of log T given Z as Q(τ) ≡ sup{t : Pr(log T ≤ t ∣ Z) ≤ τ} for τ ∈ [0, 1). The censored quantile regression model (Portnoy, 2003) postulates that

$$Q\left(\tau \right)=\alpha \left(\tau \right)+\beta {\left(\tau \right)}^{⊺}\mathrm{Z}\equiv \eta {\left(\tau \right)}^{⊺}\mathrm{S}\forall \tau \in [0,1),T╨C\mid \mathrm{Z},$$ (10)

where quantile coefficient η(τ) ≡ {α(τ),β(τ)^T}^T and S ≡ {1, Z^T}^T. The above model specializes to the accelerated failure time model if β(τ) is constant in τ, i.e., β(τ) = for all τ ∈ [0, 1). On the other hand, in the k-sample problem, the model actually imposes no assumption beyond the conditional independence censoring mechanism and the estimation may be carried out by the plug-in principle using the k Kaplan–Meier estimators. Huang (2010) developed a natural censored quantile regression procedure, which reduces exactly to the plug-in method in the k-sample problem, and to standard uncensored quantile regression of Koenker & Bassett (1978) in the absence of censoring. The estimator $\widehat{\eta }(\cdot )\equiv {\left\{\widehat{\alpha }\right(\cdot ),\widehat{\beta }{(\cdot )}^{⊺}\}}^{⊺}$ is consistent and asymptotically normal. Moreover, the progressive localized minimization (PLMIN) algorithm of Huang (2010) is computationally reliable and efficient.

Nevertheless, η(τ) is only identifiable with τ up to the limit

$$\overline{\tau }=\sup \{\tau :E[{\mathrm{S}}^{\otimes 2}I\{C\ge \eta {\left(\tau \right)}^{⊺}\mathrm{S}\}\left]\text{is nonsingular}\right\},$$

beyond which $\widehat{\eta }\left(\tau \right)$ is, of course, senseless and misleading. However, $\overline{\tau }$ is unknown and, for any given τ > 0, the identifiability of η(τ) cannot be definitively determined in finite sample. We shall establish a probabilistic result on the identifiability, by estimating a conservative surrogate of $\overline{\tau }$. Rewrite

$$\begin{array}{cc}\hfill \overline{\tau }=& \sup \{\tau :\det E[{\mathrm{S}}^{\otimes 2}I\{C\ge \eta {\left(\tau \right)}^{⊺}\mathrm{S}\}]>0\}\hfill \\ \hfill =& \inf \{\tau :\det E[{\mathrm{S}}^{\otimes 2}I\{C\ge \eta {\left(\tau \right)}^{⊺}\mathrm{S}\}]\le 0\}\hfill \\ \hfill =& \inf \left\{\tau :\det E\left({\mathrm{S}}^{\otimes 2}\Delta \left[I\{X\ge \eta {\left(\tau \right)}^{⊺}\mathrm{S}\}-I\{X=\eta {\left(\tau \right)}^{⊺}\mathrm{S}\}{\xi }_{\mathrm{z}}\left(\tau \right)\right]\right)\le 0\right\},\hfill \end{array}$$

where det denotes determinant and ξ_Z(τ) is the τ-th quantile equality fraction (Huang, 2010) of log T given Z. A conservative surrogate ${\overline{\tau }}_{\kappa }$ for $\overline{\tau }$ in the sense that ${\overline{\tau }}_{\kappa }<\overline{\tau }$ is given by

$${\overline{\tau }}_{\kappa }=\inf \{\tau :\det \{E\left({\mathrm{S}}^{\otimes 2}\Delta \right)-\Sigma \left(\tau \right)\}\le \kappa \det E({\mathrm{S}}^{\otimes 2}\Delta \left)\right\}$$ (11)

for given κ ∈ (0, 1], where

$$\Sigma \left(\tau \right)=E\left({\mathrm{S}}^{\otimes 2}\Delta \left[I\{X<\eta {\left(\tau \right)}^{⊺}\mathrm{S}\}+I\{X=\eta {\left(\tau \right)}^{⊺}\mathrm{S}\}{\xi }_{\mathrm{z}}\left(\tau \right)\right]\right).$$

Clearly, ${\overline{\tau }}_{\kappa }\uparrow \overline{\tau }$ as κ ↓ 0. Write

$$\widehat{\Sigma }\left(\tau \right)=n^{-1}\sum _{i=1}^n{\mathrm{S}}_i^{\otimes 2}{\Delta }_i\left[I\{X<\widehat{\eta }{\left(\tau \right)}^{⊺}{\mathrm{S}}_i\}+I\{X=\widehat{\eta }{\left(\tau \right)}^{⊺}{\mathrm{S}}_i\}{\widehat{\xi }}_i\left(\tau \right)\right],$$

where [0, 1]-valued ${\widehat{\xi }}_i\left(\tau \right)$ is the estimated τ-th quantile equality fraction for individual i from the procedure of Huang (2010). We adopt a plug-in estimator for ${\overline{\tau }}_{\kappa }$:

$${\widehat{\tau }}_{\kappa }=\inf \left\{\tau :\det \left\{n^{-1}\sum _{i=1}^n{\mathrm{S}}_i^{\otimes 2}{\Delta }_i-\widehat{\Sigma }\left(\tau \right)\right\}\le \kappa \det \left(n^{-1}\sum _{i=1}^n{\mathrm{S}}_i^{\otimes 2}{\Delta }_i\right)\right\}.$$ (12)

The determinant operator above in the definition and estimation of a conservative surrogate of $\overline{\tau }$ may be replaced by, say, the minimum eigen value. However, determinant involves less computation.

Theorem 1

Suppose that the censored quantile regression model (10) and the regularity conditions of Huang (2010, section 4) hold. For any given κ ∈ (0, 1], ${\widehat{\tau }}_{\kappa }$ is strongly consistent for ${\overline{\tau }}_{\kappa }$.

The regularity conditions of Huang (2010) are mild and typically satisfied in practice. The above result implies that, as the sample size increases, ${\widehat{\tau }}_{\kappa }$ is less than $\overline{\tau }$ with probability tending to 1. In that case, η(τ) is identifiable for $\tau \le {\widehat{\tau }}_{\kappa }$. This result complements those of Huang (2010) to provide a more complete censored quantile regression procedure.

3·2 Initial estimation under the accelerated failure time model

Estimator $\widehat{\beta }\left(\tau \right)$ from the censored quantile regression procedure for any $\tau \in (0,{\widehat{\tau }}_{\kappa }]$, with κ ∈ (0, 1), is consistent for β under the accelerated failure time model. Therefore, choices for the initial estimate abound. We consider one that targets a trimmed mean effect given in Huang (2010):

$$\overline{\beta }={({\widehat{\tau }}_r-{\widehat{\tau }}_l)}^{-1}{\int }_{{\widehat{\tau }}_l}^{{\widehat{\tau }}_r}\widehat{\beta }\left(\tau \right)d\tau$$ (13)

for pre-specified l and r such that 0 < r < l < 1.

Theorem 2

Suppose that the accelerated failure time model (1) holds. Under the regularity conditions of Huang (2010, section 4), $\overline{\beta }$ given by (13) is consistent for β and $n^{1∕2}(\overline{\beta }-\beta )$ is asymptotically normal with mean zero.

In adopting $\overline{\beta }$ as the initial estimate, there is flexibility with the values of l and r. To provide some guideline, we note that det{E(S^⊗2Δ)–Σ(τ)} = τ^p+1 det E(S^⊗2Δ) for quantities in (11) when censoring is absent; recall p is dimension of the covariates. This fact led to the choice of l = 0.95^p+1 and r = 0.05^p+1 in all our numerical studies.

3·3 Derivative estimation

To estimate D, intuitively one would differentiate U(·) at $\overline{\beta }$ However, U(·) is not even continuous. We turn to numerical differentiation instead:

$$\widehat{\mathrm{D}}=\left\{\mathrm{U}(\overline{\beta }+{\mathrm{w}}_1)-\mathrm{U}\left(\overline{\beta }\right)\cdots \mathrm{U}(\overline{\beta }+{\mathrm{w}}_p)-\mathrm{U}\left(\overline{\beta }\right)\right\}{\mathrm{W}}^{-1},$$ (14)

where W ≡ (w₁ … w_p) is a non-singular p × p bandwidth matrix. Clearly, each column of W needs to converge to 0 in probability. However, the convergence rate cannot be faster than O_p(n^−1/2); see equation (4). Furthermore, W⁻¹ needs to behave properly. Specifically, the following conditions are adopted:

$${\Vert \mathrm{W}\Vert }_{\max }=o_p\left(1\right),{\Vert \mathrm{W}\Vert }_{\max }{\Vert {\mathrm{W}}^{-1}\Vert }_{\max }=O_p\left(1\right),{\Vert {\mathrm{W}}^{-1}\Vert }_{\max }=O_p\left(n^{1∕2}\right).$$ (15)

Equivalently, all singular values of W converge to 0 in probability at rates that are of the same order and not faster than O_p(n^−1/2), by the relationship between the max and spectral norms. These conditions are sufficient for the consistency of $\widehat{\mathrm{D}}$, as will be shown, and they permit considerable flexibility for the bandwidth. Nonetheless, some choices of the bandwidth are better than others. Huang (2002) suggested to use a bandwidth comparable to ${\left(\widehat{\beta }\right)}^{1∕2}$, where var(·) denotes the variance and the square root denotes the Cholesky factorization. This could motivate $\widehat{\mathrm{var}}{\left(\widehat{\beta }\right)}^{1∕2}$, where the estimated variance of $\overline{\beta }$ is obtained from the re-sampling method described in Huang (2010). However, computational costs of the re-sampling is not desirable. For this reason, we suggest a different variability measure:

$$\mathrm{M}={({\widehat{\tau }}_r-{\widehat{\tau }}_l)}^{-1}{\int }_{{\widehat{\tau }}_l}^{{\widehat{\tau }}_r}{\left\{\widehat{\beta }\left(\tau \right)-\overline{\beta }\right\}}^{\otimes 2}d\tau ,$$ (16)

and adopt W = M^1/2 as the bandwidth matrix.

Theorem 3

Suppose that the accelerated failure time model (1) and the regularity conditions of Huang (2010, section 4) hold. The conditions given in (15) on the bandwidth matrix are sufficient for ${\Vert \widehat{\mathrm{D}}-\mathrm{D}\Vert }_{\max }=o_p\left(1\right)$, and W = M^1/2 with M given by (16) satisfies these conditions.

Bandwidth M^1/2 is data-adaptive. Our numerical experience shows good performance over a wide range of sample size.

4. Interval estimation

Interval estimation is an integral component of regression analysis. With censored linear regression, the interval estimation shares the challenges for the point estimation and existing methods further aggravate the computational burden beyond the point estimation. Wei et al. (1990) suggested to construct confidence intervals by inverting the test based on the quadratic score statistic, which required intensive grid search. The re-sampling methods of Parzen et al. (1994) and Jin et al. (2001) involve, say, 500 re-samples, each with computation comparable to the point estimation. In comparison, the consistent variance estimator of Huang (2002) is computationally much less demanding. Nevertheless, the computation is still p times that for the point estimation. We now propose new interval estimation techniques.

As a standard and computationally efficient procedure, sandwich variance estimation cannot be readily applied to the weighted log-rank estimating function due to the lack of differentiability. Nevertheless, we suggest to use $\widehat{\mathrm{D}}$ to serve the purpose and the variance of $n^{1∕2}(\widehat{\beta }-\beta )$ can be consistently estimated by

$${\widehat{\mathrm{D}}}^{-1}\mathrm{V}\left(\widehat{\beta }\right){\left({\widehat{\mathrm{D}}}^{-1}\right)}^{⊺},$$ (17)

where V(b) is defined in (7). The computation is trivial beyond the point estimation, even much less than Huang (2002).

We can also develop a procedure to compute the confidence interval of Wei et al. (1990) for each component of β. Write scalar β₁ as a component of β and b₁ as the counterpart in b. The confidence interval of Wei et al. (1990) for β₁ with level 1 – a is given by

$$\left\{b_1:\underset{\mathrm{b}\backslash b_1}{\min }\Omega \left(\mathrm{b}\right)\le {\chi }_1^2\left(a\right),\Vert \mathrm{b}-\beta \Vert =o_p\left(1\right)\right\},$$ (18)

where ${\chi }_1^2\left(a\right)$ is the upper a point of the χ² distribution with 1 degree of freedom. By the asymptotic local quadraticity of (9), the gradient and Hessian of the limiting Ω(b) in a shrinking neighborhood of β are asymptotically equivalent to $2n\mathrm{U}{\left(\mathrm{b}\right)}^{⊺}\mathrm{V}{\left(\mathrm{b}\right)}^{-1}\widehat{\mathrm{D}}$ and $2n{\widehat{\mathrm{D}}}^{⊺}\mathrm{V}{\left(\mathrm{b}\right)}^{-1}\widehat{\mathrm{D}}$, respectively. This approximation permits a Newton’s method to compute the two boundaries that defines the interval given by (18). Specifically, it involves an inner loop to determine min_b/b1 Ω(b) for given b₁ and then an outer loop to locate the two b₁ values such that min_b/b1 $\Omega \left(\mathrm{b}\right)={\chi }_1^2\left(a\right)$. Both loops proceed with the Newton’s method guided by the asymptotic local quadraticity (9).

5. Simulation studies

Numerical studies were carried out to assess statistical and computational properties of the proposal over a wide range of sample size and number of covariates. One series of simulations had the following specification:

$$\log T=\sum _{k=1}^p{Z}_k+\epsilon ,$$

where ε followed the extreme-value distribution, and Z_k, k = 1,…, p, were independently distributed as standard normal. In the presence of censoring, the censoring time C followed the uniform distribution between 0 and an upper bound determined by a given censoring rate.

For comparison, we also computed the estimators of Jin et al. (2003) using the R code downloaded from Dr. Jin’s website (http://www.columbia.edu/~zj7/aftsp.R). For a non-Gehan function, the procedure of Jin et al. (2003) may not converge and we followed their suggestion to run a fixed number of iterations. According to Jin et al. (2003), 3 iterations is adequate and 10 typically renders convergence for practical purposes. More iterations is desirable for statistical performance, but not so for computation.

We focused on two common weighted log-rank functions, Gehan and log-rank. Since its weight is censoring dependent, the Gehan estimator cannot reach the semiparametric efficiency bound. Nevertheless, in the class of weighted log-rank functions, the Gehan function is an exception as being monotone and thus free of inconsistent roots (Fygenson & Ritov, 1994). For this reason, the Gehan estimator plays an important role in identifying a consistent root to a non-Gehan function with existing methods. In fact, the linear programming method of Jin et al. (2003) computes the Gehan estimator as the initial estimate. On the other hand, the log-rank function is a default choice in practice, and its estimator is semiparametrically efficient locally when ε follows the extreme-value distribution (e.g., Tsiatis, 1990).

5·1 Finite-sample statistical performance

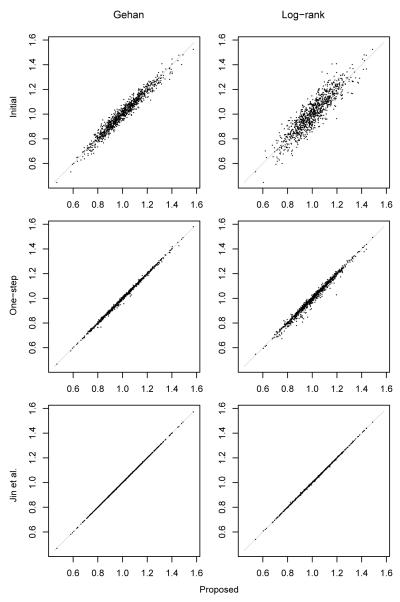
Table 1 reports the summary statistics for the first regression coefficient under sample size of 100 or 200, 2 or 4 covariates, and 0%, 25%, or 50% censoring rate; results for other coefficients were similar and thus omitted. Each scenario involved 1000 simulated samples. In the case of the log-rank function, Jin et al. was the estimator obtained with 10 iterations. Focus on the point estimation first. Across all scenarios considered, the proposed estimator and that of Jin et al. were almost identical in bias and standard deviation up to the reported third decimal point, whereas the one-step estimator showed slight differences. Also, it is interesting to note that the proposed estimator had the smallest average quadratic score statistic, followed by Jin et al. and then the one-step estimator. Figure 1 provides the scatterplots of these estimators as well as the initial estimate under one set-up; plots for other set-ups were similar. The proposed estimator and that of Jin et al. were practically the same, especially in the Gehan function case. The one-step estimator was visibly different, but the initial estimate was much more so. This demonstrates the effectiveness and accuracy of the asymptotics-guided Newton algorithm, even when the sample size was as small as 100.

Table 1.

Simulation summary statistics

		Point estimation									Interval estimation
cen		One-step, ${\widehat{\beta }}^{\left(1\right)}$(1)			Proposed, $\widehat{\beta }$			Jin et al.			SW		TI
	(%)	B	SD	Ω	B	SD	Ω	B	SD	Ω	SE	C	SE	C
size=100, 2 covariates
0	G	−2	124	5764	0	124	37	0	124	68	121	93.6	120	93.3
	L	−7	108	106970	−1	107	1105	−1	107	3328	113	94.2	104	93.6
25	G	5	151	6121	6	151	36	6	151	68	159	96.1	150	95.4
	L	0	138	59858	5	136	800	4	136	2767	146	95.1	132	94.8
50	G	2	206	39234	10	201	45	10	201	97	230	96.7	204	95.3
	L	4	180	51839	10	179	1123	10	179	3839	204	96.3	177	94.6
size=100, 4 covariates
0	G	−5	117	19449	−3	117	93	−3	117	235	123	95.3	119	94.8
	L	−8	107	317532	−2	103	3608	−2	103	10735	119	97.1	103	94.8
25	G	−6	153	20245	−4	153	107	−4	153	273	159	95.1	148	94.2
	L	−7	137	240739	−2	136	9496	−2	136	10739	160	95.6	127	93.3
50	G	−9	206	81991	1	200	173	1	200	435	227	95.3	198	94.2
	L	−4	177	218665	4	175	11634	4	176	22207	217	96.4	166	93.2
size=200, 2 covariates
0	G	−3	83	1789	−3	83	5	−3	83	9	83	94.5	83	94.2
	L	−5	73	38260	−3	72	314	−3	72	1031	75	95.1	72	94.6
25	G	3	103	1446	4	103	4	4	103	9	107	95.9	104	95.7
	L	4	91	20787	6	91	235	6	91	721	96	96.5	92	95.9
50	G	−4	141	14739	−1	138	5	−1	138	11	150	95.8	138	94.6
	L	−1	120	22293	2	120	292	2	120	1548	131	96.4	120	95.8
size=200, 4 covariates
0	G	2	87	4329	2	87	12	2	87	29	84	93.7	83	93.6
	L	−4	75	123051	−1	75	890	−1	75	2824	79	94.9	73	94.2
25	G	2	101	4717	2	100	14	2	100	35	107	96.0	103	95.6
	L	1	89	111116	5	88	1146	5	88	3957	98	96.8	89	95.0
50	G	−1	136	18448	2	134	19	2	134	51	147	96.7	136	95.1
	L	−1	113	112253	4	112	1592	4	112	5194	132	96.6	115	95.0

cen: censoring rate.

G: Gehan estimating function; L: log-rank estimating function.

With the log-rank function, Jin et al. was the estimator with 10 iterations.

For interval estimation, SW: the sandwich variance estimation; TI: the test inversion.

B, SD, SE, and C are all for the first coefficient, where B is bias (×10³), SD standard deviation (×10³),

SE mean standard error (×10³), and C coverage (%) of the 95% confidence interval.

Ω: Mean quadratic score statistic (×10⁶).

Figure 1.

Scatterplots to compare different estimators for the first coefficient with sample size of 100, 2 covariates, and 25% censoring. In the case of the log-rank estimating function, Jin et al. was the estimator with 10 iterations.

Table 1 also reports the performance of the two proposed interval estimation procedures. The 95% Wald confidence interval was constructed for the sandwich variance estimation method. With the test inversion procedure, a standard error was computed as length of the 95% confidence interval given by (18) divided by twice 1.959964. Both standard errors tracked the standard deviation reasonably well. However, the inverted test procedure was superior in the case of smaller sample size, more covariates and heavier censoring. Furthermore, both confidence intervals had coverage probabilities close to the nominal value. For most practical situations, the sandwich variance estimation might be preferred for its minimal computational costs and acceptable performance.

5·2 Computational comparison

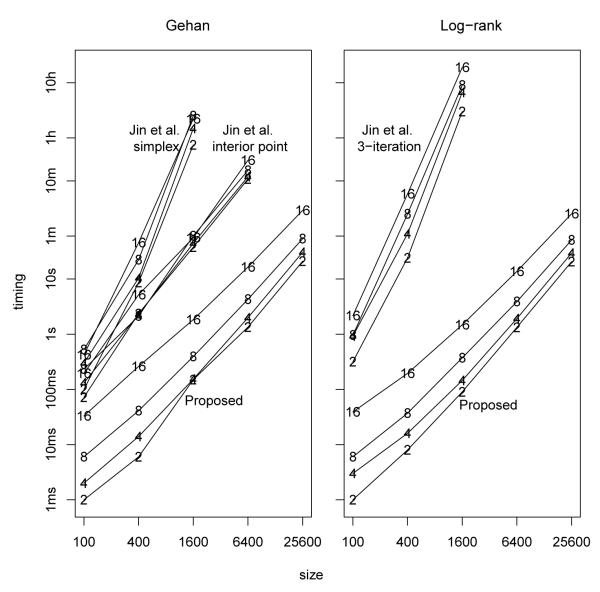
The proposed method was implemented in R with Fortran source code. The R code of Jin et al. (2003) has its core to solve a weighted Gehan function by invoking the rq function from the Quantreg package, which is also written with Fortran source code. To use the point estimation of Jin et al. as a benchmark, we removed their re-sampling interval estimation component. In addition, we modified their code to permit linear programming algorithm options in the rq function. The original code adopts the default Barrodale–Roberts simplex algorithm. In the case of the Gehan function, we also evaluated the timing when using the Frisch–Newton interior point algorithm, known to be more efficient as the size increases (Portnoy & Koenker, 1997). However, the same attempt for the log-rank function gave rise to unexpected estimation results for unknown causes and was thus aborted. The computation was performed on a Dell R710 computer with 2.66 GHz Intel Xeon X5650 CPUs and 64 GB RAM. Sample sizes of 100, 400, 1600, 6400, and 25600 were considered, in combination with 2, 4, 8, and 16 covariates. The censoring rate for all set-ups was approximately 25%.

The left panel of Figure 2 shows the computer times for estimation with the Gehan function. For a given number of covariates, the computer time for the proposed procedure consisting of the point and sandwich variance estimation had a roughly linear increase with the sample size. The timing was within seconds in most cases and, even with the size of 25600 and 16 covariates, it did not exceed 3 minutes. This computational efficiency is extremely impressive in comparison with Jin et al. (2003). The computer time for their point estimation alone was hundreds or even thousands times as long when using the simplex algorithm for linear programming; the computer time became unavailable when the sample size was 6400 or larger since the timing exceeded 1 day. The interior point algorithm speeded up the computation considerably with larger sample sizes, but the computer time was still tens to hundreds times as long. In addition, regardless of the algorithms adopted, the method of Jin et al. (2003) required a computer memory so large that brought the R session to either virtually a halt or crash when the sample size was 25600.

Figure 2.

Timing comparison of the proposed method versus Jin et al. (2003). The timing of the proposed accounted for both the point estimation and the sandwich variance estimation, whereas that of Jin et al. (2003) was for the point estimation alone. The number of covariates, 2, 4, 8, or 16, is marked on each line.

The right panel of Figure 2 corresponds to the log-rank function. In comparison with the case of the Gehan function, the proposed method had comparable computer times. However, the method of Jin et al. (2003) took longer since it required solving weighted Gehan functions iteratively and only the Barrodale–Roberts simplex algorithm was reliable. Thus, the proposed method is even more dominating when a non-Gehan function is adopted.

The proposed method has four components: initial estimation, derivative estimation, Newton iterations, and sandwich variance estimation. To understand their shares, we broke down the computer time in percentages. The estimation function adopted, Gehan or log-rank, made little difference. Initial estimation and derivative estimation were dominating components, whereas the percentage for sandwich variance estimation was always negligible. The percentage for initial estimation increased with sample size and decreased with number of covariates, and derivative estimation followed a reverse trend. For example, in the case of 2 covariates, the percentages of the three point-estimation components were 75%, 20%, and 5% for sample size of 400 and changed to 94%, 5%, and 1%, respectively, for sample size of 25600. When the number of covariates was 16, the corresponding percentages became 21%, 72%, and 7% for sample size of 400, and 54%, 44%, and 2% for sample size of 25600.

As a reviewer noticed from Figure 2, the computer time, however, appeared to increase faster for the proposed method than for the method of Jin et al. (2003), when the number of covariates was scaled up under fixed sample size. Additional simulations confirmed the observation. In an extreme case of 100 covariates with sample size of 1600, the computer times for the proposed method, including both the point estimation and sandwich variance estimation, were 197 and 178 seconds for the Gehan and log-rank functions, respectively. The point estimation of Jin et al. using the interior point algorithm took 499 seconds for the Gehan function. The gap between the two methods shrinks as the number of covariates increases.

6. Illustrations

For illustration, we analyzed two clinical studies using the proposed approach and the method of Jin et al. (2003). For the proposed approach, we adopted the sandwich variance estimation for inference. With Jin et al. (2003), we followed their re-sampling interval estimation with the default re-sampling size of 500.

The first was the well-known Mayo primary biliary cirrhosis study (Fleming & Harrington, 1991, app. D), which followed 418 patients with primary biliary cirrhosis at Mayo Clinic between 1974 and 1984. We adopted the accelerated failure time model for the survival time with five baseline covariates: age, edema, log(bilirubin), log(albumin), and log(prothrombin time). Two participants with incomplete measures were removed. The analysis data consisted of 416 patients, with a median follow-up time of 4.74 years and a censoring rate of 61.5%. The top panel of Table 2 reports the estimation results and their associated computer times. When the Gehan function was used, the point estimators were very similar between the proposed and Jin et al., and their standard errors reasonably close to each other. With the log-rank function, the proposed and Jin et al. with 10 iterations were much closer to each other than they were to Jin et al. with 3 iterations, and the standard errors were again reasonably similar to each other. The quadratic score statistic favored the proposed point estimator over the estimator of Jin et al. for both the Gehan and log-rank functions. The most striking difference between the two methods lied in the computational costs. The proposed method used only tens of milliseconds to complete both the point and interval estimation. In comparison, the point estimation alone of Jin et al. (2003) took from a few seconds up to over a minute, depending on the estimating function, the linear programming algorithm, and the number of iterations. With both their point and interval estimation, the computer time ranged from half an hour to several hours.

Table 2.

Analyses of two clinical studies

	Gehan				Log-rank
							Jin et al.
	Proposed		Jin et al.		Proposed		3-iteration		10-iteration
	Mayo primary biliary cirrhosis study
Estimation
	Est	SE	Est	SE	Est	SE	Est	SE	Est	SE
age	−0.0255	.0061	−0.0255	.0057	−0.0258	.0052	−0.0260	.0052	−0.0257	.0053
edema	−0.9241	.2134	−0.9241	.2837	−0.7108	.2331	−0.7621	.2459	−0.7132	.2492
log(bilirubin)	−0.5581	.0673	−0.5581	.0627	−0.5749	.0580	−0.5725	.0564	−0.5748	.0573
log(albumin)	1.4985	.5142	1.4985	.5229	1.6351	.5170	1.6334	.4492	1.6354	.4572
log(pro. time)	−2.7763	.7773	−2.7761	.7760	−1.8485	.6919	−1.9177	.5481	−1.8435	.5380
Ω	1.238 × 10−6		6.584 × 10−6		3.210 × 10−6		5.344 × 10−2		4.095 × 10−5
Timing, sec
point	—		8 (2)		—		30		81
+ interval	0.035		2667 (1757)		0.028		11609		32258
	ACTG 175 trial
Estimation
	Est	SE	Est	SE	Est	SE	Est	SE	Est	SE
ZDV+ddI	0.3851	.1180	0.3851	.1071	0.3299	.1309	0.3401	na	0.3298	na
ZDV+ddC	0.2396	.1009	0.2396	.1028	0.1853	.1180	0.1940	na	0.1854	na
ddI	0.2857	.1107	0.2857	.1067	0.2612	.1174	0.2684	na	0.2613	na
male	0.0246	.1403	0.0247	.1443	−0.0417	.1383	−0.0303	na	−0.0419	na
age	−0.0107	.0037	−0.0107	.0039	−0.0131	.0041	−0.0125	na	−0.0130	na
white	−0.1500	.0868	−0.1500	.0950	−0.1406	.0836	−0.1432	na	−0.1407	na
homosexuality	−0.0946	.1151	−0.0946	.1205	−0.0104	.1209	−0.0224	na	−0.0101	na
IV drug use	−0.2596	.1108	−0.2596	.1295	−0.1053	.1103	−0.1249	na	−0.1052	na
hemophilia	−0.0835	.1650	−0.0835	.1575	−0.0479	.1758	−0.0495	na	−0.0471	na
HIV symptom	−0.3715	.1000	−0.3715	.0970	−0.3354	.1011	−0.3434	na	−0.3356	na
log(CD4)	1.1004	.1464	1.1004	.1575	1.0917	.1387	1.0941	na	1.0917	na
prior tx, yr	−0.0737	.0255	−0.0737	.0263	−0.0817	.0276	−0.0806	na	−0.0817	na
Ω	4.004 × 10−8		4.941 × 10−7		4.695 × 10−6		7.021 × 10−2		1.824 × 10−4
Timing, sec
point	—		447 (118)		—		2566		7647
+ interval	1.375		na (61083)		1.162		na		na

The interval estimation for the proposed was based on the sandwich variance estimation, and that for Jin et al. was their re-sampling approach with default size of 500.

Under Estimation, Ω: quadratic score statistic; Est: estimate; SE: standard error. Under Timing, the numbers under Jin et al. correspond to the simplex algorithm, except for those in parentheses as for the interior point algorithm. na: not available due to long computer time, being over 1 day.

The second study was the AIDS Clinical Trials Group (ACTG) 175 trial, which evaluated treatments with either a single nucleoside or two nucleosides in HIV-1 infected adults whose screening CD4 counts were from 200 to 500 per cubic millimeter (Hammer et al., 1996). A total of 2467 participants were randomized to one of four treatments: Zidovudine (ZDV), Zidovudine and Didanosine (ZDV+ddI), Zidovudine and Zalcitabine (ZDV+ddC), and Didanosine (ddI). In this analysis, we were interested in time to an AIDS-defining event or death and employed the accelerated failure time model with 12 baseline covariates: ZDV+ddI, ZDV+ddC, ddI, male, age, white, homosexuality, IV drug use, hemophilia, presence of symptomatic HIV infection, log(CD4), and length of prior antiretroviral treatment. Among these covariates, age, log(CD4), and length of prior antiretroviral treatment were continuous and the rest were indicators. The mean follow-up was 29 months and the censoring rate was 87.5%. The estimation results and computer times are summarized in the bottom panel of Table 2. The relative statistical performance of the proposed and Jin et al. (2003) was largely similar to that observed in the previous study. However, the standard error for the log-rank estimator using the re-sampling approach of Jin et al. (2003) might take weeks in computer time and thus was unavailable. In this study of a larger size, the proposed method exhibited more substantial practical advantage in computational efficiency, taking within 2 seconds for both the point and interval estimation. However, it took Jin et al. (2003) over 2 hours for the point estimation alone in the case of log-rank estimating function with 10 iterations.

7. Discussion

Computation is an indispensable element of a statistical method. With censored data, computational burden is perhaps the single most critical impeding factor for practical acceptance of the accelerated failure time model. Existing methods for a weighted log-rank estimating function are computationally too burdensome even for moderate sample size. Our proposal in this article achieves a dramatic improvement and proves feasible in circumstances over a broad range of sample size and number of covariates.

There are alternative estimating functions and methods for censored linear regression. The estimating function of Buckley & James (1979) and its weighted version by Ritov (1990), as an extension of the least squares estimation, would benefit from a similar development. The weighted Buckley–James estimating function is asymptotically equivalent to the weighted log-rank function (Ritov, 1990) and also suffers from discontinuity and non-monotonicity. Parallel to Jin et al. (2003) for the weighted log-rank function, Jin et al. (2006) developed a similar iterative method for the weighted Buckley–James with the Gehan estimator used as the initial estimate. Conceivably, our techniques in this article can be applied to improve the computation. To attain semiparametrically efficient estimation, both the weighted log-rank and weighted Buckley–James require a weight function that involves the derivative of the error density function, which is difficult to estimate and construct. Zeng & Lin (2007) recently developed an asymptotically efficient kernel-smoothed likelihood method. However, as typical for kernel smoothing, their estimator can be sensitive to the choices of kernel and bandwidth in finite sample. Further efforts are needed to achieve both asymptotic efficiency and numerical stability.

Appendix A. Justification of the algorithm in Section 2

Recall that the initial estimate $\widehat{\beta }\left(0\right)$ is n^1/2-consistent. Therefore, $\mathrm{U}\left({\widehat{\beta }}^{\left(0\right)}\right)=O_p\left(n^{-1∕2}\right)$ by equation (5). Write ${\widehat{\beta }}_{g=0}^{\left(1\right)}={\widehat{\beta }}^{\left(0\right)}-{\widehat{\mathrm{D}}}^{-1}\mathrm{U}\left({\widehat{\beta }}^{\left(0\right)}\right)$, corresponding to the one-step estimate with g = 0 in (6). Then, ${\widehat{\beta }}_{g=0}^{\left(1\right)}-\beta =O_p\left(n^{-1∕2}\right)$ and equation (5) implies

$$\mathrm{U}\left({\widehat{\beta }}_{g=0}^{\left(1\right)}\right)=\mathrm{U}\left(\beta \right)+\widehat{\mathrm{D}}({\widehat{\beta }}^{\left(0\right)}-\beta )-\mathrm{U}\left({\widehat{\beta }}^{\left(0\right)}\right)+o_p\left(n^{-1∕2}\right)=o_p\left(n^{-1∕2}\right).$$

Subsequently, $\Omega \left({\widehat{\beta }}_{g=0}^{\left(1\right)}\right)=o_p\left(1\right)$. For the one-step estimate ${\widehat{\beta }}^{\left(1\right)}$, similarly ${\widehat{\beta }}^{\left(1\right)}-\beta =O_p\left(n^{-1∕2}\right)$. Also, since $\Omega \left({\widehat{\beta }}^{\left(1\right)}\right)\le \Omega \left({\widehat{\beta }}_{g=0}^{\left(1\right)}\right),\Omega \left({\widehat{\beta }}^{\left(1\right)}\right)=o_p\left(1\right)$ which in turns implies $\mathrm{U}\left({\widehat{\beta }}^{\left(1\right)}\right)=o_p\left(n^{-1∕2}\right)$. It then follows that ${\widehat{\beta }}^{\left(1\right)}$ is asymptotically equivalent to a consistent root of U(b). The same argument and conclusion apply to ${\widehat{\beta }}^{\left(k\right)}$ for any given finite k ≥ 1.

Before addressing the estimator $\widehat{\beta }$, we first consider $\tilde{\beta }$ as the ${\widehat{\beta }}^{\left(k\right)}$ such that either $\Omega \left({\widehat{\beta }}^{\left(k\right)}\right)$ cannot be further reduced according to the algorithm or the very next Newton-type update would cross the boundary of shrinking neighborhood {b : ∥b – β∥ ≤ n^−a} for some a ∈ (0, 1/2). Note that ${\widehat{\beta }}^{\left(0\right)}$ is inside this neighborhood with probability tending to 1. Since $\Omega \left(\tilde{\beta }\right)\le \Omega \left({\widehat{\beta }}_{g=0}^{\left(1\right)}\right)=o_p\left(1\right)$, $\mathrm{U}\left(\tilde{\beta }\right)=o_p\left(n^{-1∕2}\right)$ and so $\tilde{\beta }$ is asymptotically equivalent to a consistent root of U(b). Consequently, $\tilde{\beta }-\beta =O_p\left(n^{-1∕2}\right)$ and the step size of the next potential Newton-type update is o_p(n^−1/2). They imply that the probability of the next potential Newton-type update across the aforementioned boundary approaches 0. Therefore, $\widehat{\beta }$ is asymptotically equivalent to $\tilde{\beta }$ and so to a consistent root of U(b).

Appendix B. Proofs of theorems in Section 3

Proof of Theorem 1

Note that $\left\{{\mathrm{S}}^{\otimes 2}\Delta I\right(X\le {\mathrm{h}}^{⊺}\mathrm{S}):\mathrm{h}\in {\mathbb{R}}^{p+1}\}$ has a finite number of components and each component is a Donsker class by the same arguments as those in Huang (2010, appendix D). Therefore,

$$\underset{\mathrm{h}\in {\mathbb{R}}^{p+1}}{\sup }{\Vert n^{-1}\sum _{i=1}^n{\mathrm{S}}_i^{\otimes 2}{\Delta }_{i}I(X_i\le {\mathrm{h}}^{⊺}{\mathrm{S}}_i)-E\left\{{\mathrm{S}}^{\otimes 2}\Delta I\right(X\le {\mathrm{h}}^{⊺}\mathrm{S}\left)\right\}\Vert }_{\max }=o\left(1\right)$$

almost surely. Meanwhile, Huang (2010, theorem 2) asserts ${\sup }_{\tau \in [{\tau }_1,{\tau }_2]}\Vert \widehat{\eta }\left(\tau \right)-\eta \left(\tau \right)\Vert =o\left(1\right)$ almost surely for any τ₁ and τ₂ such that $0<{\tau }_1<{\tau }_2<\overline{\tau }$, which implies

$$\underset{\tau \in [{\tau }_1,{\tau }_2]}{\sup }{\Vert {\phantom{\mid }E\left\{{\mathrm{S}}^{\otimes 2}\Delta I\right(X\le {\mathrm{h}}^{⊺}\mathrm{S}\left)\right\}\mid }_{\mathrm{h}=\widehat{\eta }\left(\tau \right)}-E\left[{\mathrm{S}}^{\otimes 2}\Delta I\right\{X\le \eta {\left(\tau \right)}^{⊺}\mathrm{S}\left\}\right]\Vert }_{\max }=o\left(1\right)$$

almost surely. Furthermore, under the regularity conditions, ξ_Z(τ) = 0 and terms involving ${\widehat{\xi }}_i\left(\tau \right)$ are negligible; see Huang (2010, appendix D). Combining these results yields

$$\underset{\tau \in [{\tau }_1,{\tau }_2]}{\sup }{\Vert \widehat{\Sigma }\left(\tau \right)-\Sigma \left(\tau \right)\Vert }_{\max }=o\left(1\right)$$ (19)

almost surely. On the other hand, by definition

$$\begin{array}{cc}\hfill n^{-1}& \sum _{i=1}^n{\Delta }_i\left[I\left\{X<\widehat{\eta }{\left(\tau \right)}^{⊺}{\mathrm{S}}_i\right\}+I\{X=\widehat{\eta }{\left(\tau \right)}^{⊺}{\mathrm{S}}_i\}{\widehat{\xi }}_i\left(\tau \right)\right]\hfill \\ \hfill =& n^{-1}\sum _{i=1}^n{\int }_0^{\tau }\left[I\{X\ge \widehat{\eta }{\left(\nu \right)}^{⊺}{\mathrm{S}}_i\}-I\{X=\widehat{\eta }{\left(\nu \right)}^{⊺}{\mathrm{S}}_i\}\widehat{{\xi }_i}\left(\nu \right)\right]\frac{d\nu }{1-\nu };\hfill \end{array}$$

see Huang (2010, equation (13)). Then, the left-hand side can be made arbitrarily small uniformly in τ ∈ [0, τ₁] for sufficiently small τ₁ > 0, and so is ${\Vert \widehat{\Sigma }\left(\tau \right)\Vert }_{\max }$ since Z is bounded. In the same fashion, ∥Σ(τ)∥_max can be made arbitrarily small. Therefore, equation (19) can be strengthened to

$$\underset{\tau \in [0,{\tau }_2]}{\sup }{\Vert \widehat{\Sigma }\left(\tau \right)-\Sigma \left(\tau \right)\Vert }_{\max }=o\left(1\right)$$ (20)

almost surely.

By the strong law of large numbers, ${\Vert n^{-1}{\sum }_{i=1}^n{\mathrm{S}}_i^{\otimes 2}{\Delta }_i-E\left({\mathrm{S}}^{\otimes 2}\Delta \right)\Vert }_{\max }=o\left(1\right)$ almost surely. Then, we obtain

$$\underset{\tau \in [0,{\tau }_2]}{\sup }\mid \frac{\det \left\{n^{-1}\sum _{i=1}^n{\mathrm{S}}_i^{\otimes 2}{\Delta }_i-\widehat{\Sigma }\left(\tau \right)\right\}}{\det \left\{n^{-1}\sum _{i=1}^n{\mathrm{S}}_i^{\otimes 2}{\Delta }_i\right\}}-\frac{\det \left\{E\right({\mathrm{S}}^{\otimes 2}\Delta )-\Sigma (\tau \left)\right\}}{\det \left\{E\right({\mathrm{S}}^{\otimes 2}\Delta \left)\right\}}\mid =o\left(1\right)$$

almost surely. Since positive definite E(S^⊗2Δ) – Σ(τ) is strictly decreasing with τ ∈ [0, τ₂], so is det{E(S^⊗2Δ)–Σ(τ)}/ det{E(S^⊗2Δ)} by Minkowski’s determinant inequality (cf. Horn & Johnson, 1985). The strong consistency of ${\widehat{\tau }}_{\kappa }$ for ${\overline{\tau }}_{\kappa }$ then follows, upon making ${\tau }_2>{\overline{\tau }}_{\kappa }$.

Proof of Theorem 2

Let

$$\widehat{\mu }={({\overline{\tau }}_r-{\overline{\tau }}_l)}^{-1}{\int }_{{\overline{\tau }}_l}^{{\overline{\tau }}_r}\widehat{\beta }\left(\tau \right)d\tau .$$

From the weak convergence of $\widehat{\beta }(\cdot )$ (Huang, 2010, theorem 2) and Theorem 1, it is easy to establish $\overline{\beta }=\widehat{\mu }+o_p\left(n^{-1∕2}\right)$. The consistency and asymptotic normality of $\overline{\beta }$ follow those of $\widehat{\mu }$.

Proof of Theorem 3

The statement below (15) provides the equivalent conditions in terms of the singular values of W. Therefore,

$$\Vert {\mathrm{w}}_q\Vert =o_p\left(1\right),1∕\Vert {\mathrm{w}}_q\Vert =O_p\left(n^{1∕2}\right),{\forall }_q=1,\cdots p,$$

since ∥w_q∥ is bounded between the maximum and minimum singular values. Then, equation (4) yields

$$\mathrm{U}(\overline{\beta }+{\mathrm{w}}_q)=\mathrm{U}\left(\overline{\beta }\right)+{\mathrm{Dw}}_q+o_p(\Vert {\mathrm{w}}_q\Vert ),q=1,\cdots ,p.$$

Therefore, $\widehat{\mathrm{D}}=\mathrm{D}+o_p\left({\Vert \mathrm{W}\Vert }_{\max }\right){\mathrm{W}}^{-1}=\mathrm{D}+o_p\left({\Vert \mathrm{W}\Vert }_{\max }{\Vert {\mathrm{W}}^{-1}\Vert }_{\max }\right)$, implying the consistency of $\widehat{\mathrm{D}}$.

Matrix M given by (16) is semi-positive definite. Write ${\tau }_q={\widehat{\tau }}_l+q{(p+1)}^{-1}({\widehat{\tau }}_r-{\widehat{\tau }}_l)$ for q = 0,…, p + 1 and ${\overline{\beta }}_q=(p+1){({\widehat{\tau }}_r-{\widehat{\tau }}_l)}^{-1}{\int }_{{\tau }_{q-1}}^{{\tau }_q}\widehat{\beta }\left(\tau \right)d\tau$ for $q=1,\cdots ,p+1$. Then,

$$\begin{array}{cc}\hfill \mathrm{M}=& {({\widehat{\tau }}_r-{\widehat{\tau }}_l)}^{-1}\sum _{q=1}^{p+1}{\int }_{{\tau }_{q-1}}^{{\tau }_q}{\left\{\widehat{\beta }\left(\tau \right)-{\overline{\beta }}_q\right\}}^{\otimes 2}d\tau +{(p+1)}^{-1}\sum _{q=1}^{p+1}{({\overline{\beta }}_q-\overline{\beta })}^{\otimes 2}\hfill \\ \hfill \ge & {(p+1)}^{-1}\sum _{q=1}^p{({\overline{\beta }}_q-\overline{\beta })}^{\otimes 2}.\hfill \end{array}$$

From the weak convergence results in Huang (2010), Peng & Huang (2008), and Theorem 2, it can be verified that $n^{1∕2}{\{{\overline{\beta }}_1^{⊺}-{\beta }^{⊺},\cdots ,{\overline{\beta }}_{p+1}^{⊺}-{\beta }^{⊺}\}}^{⊺}$ converges weakly to a non-degenerate Gaussian distribution with mean zero and so does $n^{1∕2}{\{{\overline{\beta }}_1^{⊺}-{\overline{\beta }}^{⊺},\cdots ,{\overline{\beta }}_p^{⊺}-{\overline{\beta }}^{⊺}\}}^{⊺}$. Therefore, $\det \left\{n{({\overline{\beta }}_1-\overline{\beta },\cdots ,{\overline{\beta }}_p-\overline{\beta })}^{\otimes 2}\right\}$ and subsequently det(nM) are bounded away from 0 in probability. On the other hand, det(nM) = O_p(1), which can be established from convergence of ${\widehat{\tau }}_l$ and ${\widehat{\tau }}_r$ by from asymptotic Theorem 1 and normality of $\widehat{\beta }(\cdot )$ by Huang (2010, theorem 2) and $\overline{\beta }$ by Theorem 2. Therefore, all eigenvalues of nM are bounded both above and away from 0 in probability, and so are the singular values of n^1/2W. The conditions in (15) are then satisfied by the equivalence of the max and spectral norms.