Tuning and Timing in Mammalian Type I Hair Cells and Calyceal Synapses

Abstract

Afferent nerve fibers in the central zones of vestibular epithelia form calyceal endings around type I hair cells and have phasic response properties that emphasize fast head motions. We investigated how stages from hair-cell transduction to calyceal spiking contribute tuning and timing to central (striolar)-zone afferents of the rat saccular epithelium. In an excised preparation, we deflected individual hair bundles with rigid probes driven with steps and sinusoids (0.5–500 Hz) and recorded whole-cell responses from hair cells and calyces at room temperature and body temperature. In immature hair cells and calyces (postnatal days (P)1–P4), tuning sharpened at each stage. Transducer adaptation and membrane-charging time produced bandpass filtering of the receptor potential with best frequencies of 10–30 Hz and phase leads below 10 Hz. For small stimuli, electrical resonances sharply tuned the hair-cell membrane in the frequency range of 5–40 Hz. The synaptic delay of quantal transmission added a phase lag at frequencies above 10 Hz. The influence of spike thresholds at the calyceal spike initiation stage sharpened tuning and advanced response phase. Two additional mechanisms strongly advanced response phase above 10 Hz when present: (1) maturing (P7–P9) type I hair cells acquired low-voltage-activated channels that shortened the rise time of the receptor potential and (2) some calyces had nonquantal transmission with little synaptic delay. By reducing response time, the identified inner-ear mechanisms (transducer adaptation, low-voltage-activated channels, nonquantal transmission, and spike triggering) may compensate for transmission delays in vestibular reflex pathways and help stabilize posture and gaze during rapid head motions.

Introduction

Primary afferents form large calyceal endings on type I hair cells of amniote vestibular epithelia. The calyces contrast with compact bouton endings formed on most hair cells and are the only reported postsynaptic neuronal calyces. Information on how this unique arrangement works is fragmentary and its contribution to vestibular signaling is not understood (for review, see Eatock and Songer, 2011). Here we follow the mechanosensory signal from the hair cell to the afferent calyx in a semi-intact preparation of the immature rat saccular epithelium, addressing the impacts of transduction, voltage-gated channels, the synapse, and afferent spike generation on stimulus processing.

We focus on hair cells and calyceal endings in a central swath within the epithelium (the striola), which differs from the surrounding extrastriola, especially in the activities of innervating nerve fibers (for review, see Goldberg, 1991; Eatock and Songer, 2011). These differences closely parallel differences between central and peripheral zones of semicircular canal epithelia. Striolar and central-zone afferents are larger than extrastriolar and peripheral-zone afferents, with greater conduction speeds (Goldberg and Fernández, 1977; Lysakowski et al., 1995) and more phasic (adapting) response dynamics (Baird et al., 1988; Goldberg et al., 1990a; Hullar et al., 2005). Type I cells and calyces occur in both zones, but are larger and more specialized in striolar and central zones (Baird et al., 1988; Goldberg et al., 1990a), where they often enclose two or more type I hair cells, each with as many as 50 presynaptic ribbons (Lysakowski and Goldberg, 1997). With their accessible sensory receptors, large synapses, and known functions, vestibular epithelia are appropriate models for neurobiological specializations for timing and tuning.

As an approximately vertical linear accelerometer with a broad frequency range, the mammalian saccule detects head tilt, voluntary and passive vertical head motions, bone vibrations, and loud sounds (McCue and Guinan, 1994; Curthoys and Vulovic, 2011). To study vestibular afferent responses to head motions, investigators often move the head sinusoidally at low frequencies (upper limit, 2–30 Hz). By delivering sinusoidal stimuli directly to the hair bundle, we were able to increase the upper frequency limit for a fuller characterization of hair-cell and afferent tuning. To provide time-domain results for comparison with the hair-cell literature, we also applied steps of bundle displacement, voltage, or current, with rise times far shorter than possible in vivo. To investigate the impact of synaptic transmission on the afferent signal, we compared presynaptic (hair cell) and postsynaptic (calyceal) responses to similar stimuli. To reveal the effect of membrane electrical properties, we compared whole-cell recordings of voltage and current to similar stimuli. These are the first reported recordings from mammalian saccular hair cells and from any mammalian vestibular hair cells at body temperature.

We report that in immature saccular epithelia, tuning and timing are strongly affected by transducer adaptation, membrane charging time, synaptic delay of quantal transmission, and spike triggering. Maturational changes in hair cells reduce the impact of membrane charging time. We also provide evidence for nonquantal transmission from type I hair cells to calyces.

Materials and Methods

Preparation.

Animals were handled in accordance with the NIH Guide for the Care and Use of Laboratory Animals and all procedures were approved by the Animal Care Committee at the Massachusetts Eye and Ear Infirmary. Chemicals were obtained from Sigma-Aldrich unless otherwise specified.

Saccules were excised from male and female Long–Evans rats (Charles River), postnatal days (P) 1–P9. At these ages, before the eyes open and cochleas start working, the rat vestibular inner ear exhibits low sensitivity (Curthoys, 1983); it presumably contributes to the righting reflex. Preparation, stimulation, and recording methods resembled our previous descriptions for the rodent utricle (Vollrath and Eatock, 2003; Wooltorton et al., 2007). Briefly, the animal was decapitated and the temporal bone removed and immersed in our standard external solution: Leibovitz-15 (L-15) medium supplemented with 10 mm HEPES-NaOH, pH 7.35 (∼315 mmol/kg). The otic capsule was opened and the saccule plus attached vestibular nerve branches and ganglion were excised and bathed for 10–20 min in L-15 with 100 μg/ml of protease XXIV at ambient temperature (∼25°C). The otolithic membrane was removed and the epithelium plus its innervating ganglion were mounted in an experimental chamber and held flat by glass fibers glued to a coverslip.

Zone and cell identification.

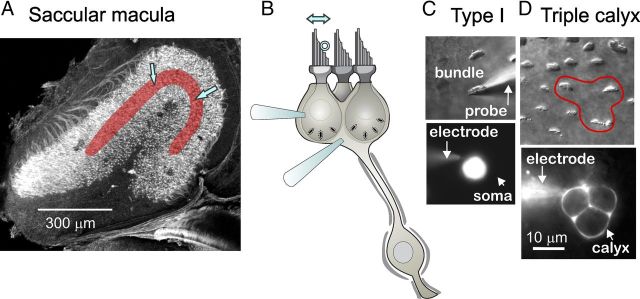
We defined the striola as the zone of prominent complex calyces and large, widely spaced hair bundles (for a full description of the zones, see Eatock and Songer, 2011). In the utricular epithelium, the striola is medial to the line of polarity reversal of hair bundles (Li et al., 2008; Schweizer et al., 2009), but in the saccule it straddles the line of polarity reversal (J. E. Songer and R. A. Eatock, unpublished observations). To avoid mixing striolar and medial extrastriolar data, we focused on striolar cells located within 2 cell widths of the line of polarity reversal. Most recordings were from the area between blue arrows in Figure 1A. Type I hair cells were distinguished from type II cells by their calyces (Fig. 1B,D) and their larger hair bundles (Li et al., 2008). Most calyces in our dataset were complex, meaning that they contacted 2–4 type I hair cells; a triple calyx, around three hair cells, is schematized in Figure 1B and shown in Figure 1D. By filling the calyces with a fluorescent dye in the pipette solution, we were able to determine the number of type I cells enveloped by the calyx, the extent of local branching, and whether the calyx-bearing afferent also made bouton terminals. No evidence for boutons was seen in 17 of 19 filled complex calyces, consistent with expectations based on an anatomical demonstration that virtually all complex calyces belonged to “calyx-only” afferents (Li et al., 2008). The two remaining calyces extended small processes that may or may not have formed nearby boutons. Because these calyces were not extraordinary in terms of their physiology, the data have been pooled. Calyces can also receive synaptic input from adjacent type II hair cells via “outer-face” synapses, but we were only able to evoke calyceal activity by moving hair bundles of type I cells within the calyx, suggesting that the striolar calyces we studied were not receiving significant functional input from outer-face synapses with type II cells. This is consistent with quantitative estimates from another rodent vestibular organ, the chinchilla crista, that such outer-face synapses are rare (Lysakowski and Goldberg, 1997).

Figure 1.

Recording from hair cells and calyceal afferent terminals in the rat saccular epithelium. A, Confocal image of the saccular epithelium excised from a P2 rat (modified from Fig. 2C in Eatock and Songer, 2011). The striolar zone is overlaid with red; most recordings were made from the region between the two blue arrows. The tissue was stained with phalloidin, which labels the actin-based hair bundles, with antibodies to β3-tubulin, which labels all nerve fibers, and with calretinin, which labels type II hair cells and calyx-only striolar nerve fibers. B, Schematic, illustrating a “triple” calyx around three type I hair cells, shows two recording electrodes, one on a hair cell and one on the calyx. Just one recording electrode was used at a time. A stimulus probe (open circle) was positioned against the staircase edge of the hair bundle to deflect it along its most sensitive axis (double arrow above bundle) while recordings were made in whole-cell patch-clamp mode from either the type I hair cell or its postsynaptic calyx. C, Stimulation and recording from a striolar type I hair cell, as viewed from above with differential-interference-contrast or fluorescence optics. Top, The hair bundle was deflected along its sensitive axis with a rigid glass probe. Bottom, The soma below the hair bundle, filled with fluorescent rhodamine diffused in from the recording pipette (electrode). Scale bar in D applies to C. D, Recording from a triple calyx, as viewed from above. Top, The hair bundles of the three type I hair cells within the calyx are outlined (red). Bottom, The recording electrode has filled the triple calyx terminal with rhodamine.

We also recorded from some extrastriolar calyces, which were usually simple (surrounding a single type I cell) and ≥4 cell widths from the line of bundle polarity reversal. In contrast to striolar calyces, fluorescent dye fills showed that the extrastriolar calyces we recorded from were simple calyces connected to afferent processes that branched extensively.

Recordings.

Recordings were usually performed at bath temperatures between 25 and 29°C (mean ∼27°C). In some experiments, we maintained bath temperature at 35–39°C (mean ∼37°C) with a heated platform and temperature controller (TC-344B, Warner Instruments). The standard internal solution contained (in mm) the following: 135 KCl, 0.1 CaCl₂, 3.5 MgCl₂, 3 Na₂ATP, 5 creatine phosphate (Na salt), 0.1 Na-cAMP, 0.1 Li-GTP, 5 EGTA, and 5 HEPES. The solution was brought to pH 7.3 and ∼300 mmol/kg by adding ∼28 mm KOH. We added the fluorescent dye, rhodamine (sulforhodamine 101, 1 mg/100 ml; Invitrogen) to the standard internal solution to label the recorded hair cell or calyx (Fig. 1C,D). In some experiments, a modified internal solution with 10 mm HEPES and 130 mm KCl was used. Because no differences were observed between cells recorded with the different internal solutions, the datasets have been pooled.

Recording pipettes were pulled from R-6 glass (Garner Glass) and had resistances ranging from 3 to 6 MΩ in our standard solutions. Currents or voltages were recorded in the ruptured-patch whole-cell mode with the EPC-10 amplifier with an integrated interface (HEKA), controlled by Patchmaster software (HEKA). Currents were low-pass-filtered with an integrated four-pole Bessel filter (HEKA) set at 2.9 kHz. Potentials are corrected for a liquid junction potential of 5 mV, calculated with JPCalc software (Barry, 1994). Hair cells and calyces were held at −65 mV for voltage-clamp recordings and at resting (zero-current) potential for current-clamp recordings unless otherwise noted. Capacitive currents were electronically nulled with Patchmaster controls.

Mechanical stimulation of the hair bundle.

A stiff glass probe (tip diameter, ∼1 μm) was glued onto a one-dimensional piezoelectric bimorph element (Corey and Hudspeth, 1980), driven with voltages controlled by Patchmaster software and low-pass-filtered with an eight-pole Bessel filter (Frequency Devices). The probe was positioned approximately half-way up the staircase side of the bundle and oriented perpendicular to the axis of maximum sensitivity (Fig. 1B,C). Motions along the sensitive axis and toward the tall edge of the bundle are called “positive.” For typical stimuli (≤±1μm), coupling in both directions appeared good based on visual evaluation as well as response speed. The bimorph was driven with step waveforms [rise time, <800 μs; duration, 400 ms; low-pass filtered at 1 kHz with an 8-pole Bessel filter (Model 902, Frequency Devices)] or a series of sinusoidal “bursts” (as in tone burst) of five cycles each (low-pass filtered at 1.8 kHz with the 8-pole Bessel filter). The frequencies of stimulation were typically 2, 5, 10, 20, 40, 50, 80, and 100 Hz, but in some cases extended down to 0.5 Hz and up to 200 or 500 Hz. Sinusoidal displacements were centered at or near the resting bundle position and had amplitudes of either ±300 nm or between ±600 and ±1000 nm; data collected with stimuli in this larger range, toward the saturating end of the hair cell's operating range (Fig. 2C; see Results), have been pooled. We calibrated probe displacement at both stimulus levels and across all frequencies by projecting the probe image onto the edge of a photodiode. The photodiode output was low-pass filtered at 1800 Hz and digitized at 100 μs. The stimulus probe had a voltage sensitivity of 350 nm/V and a mechanical resonance near 3 kHz, 10-fold above the stimulus frequencies analyzed here. Bode analysis of the photodiode signals showed that the probe motion had stable gain (to within 15 nm) and its phase angle was within 1–2° of the driving voltage from 2 to 100 Hz. The stimulus gain and phase at each frequency and level were calibrated offline by the appropriate photodiode signal.

Figure 2.

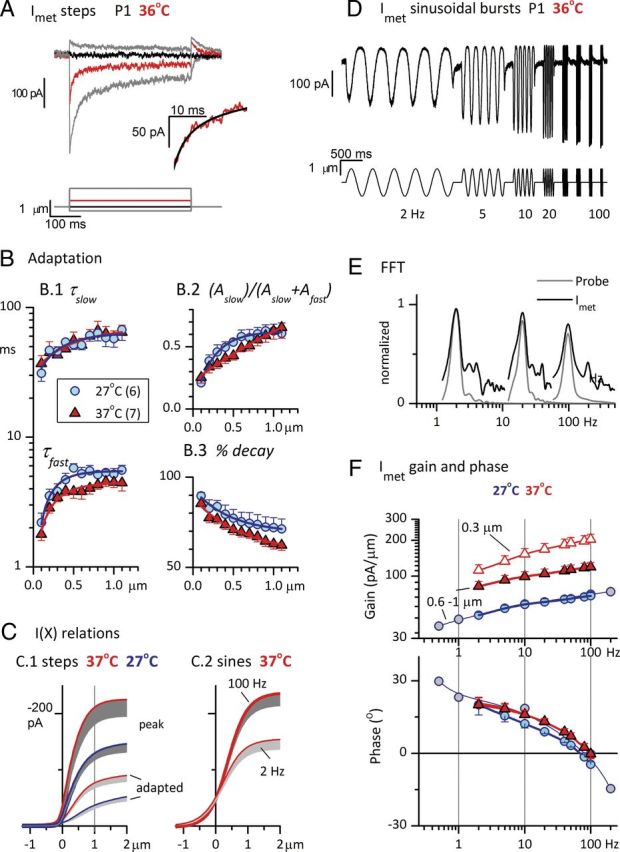
Effects of adaptation and temperature on sensitivity (gain) and timing (phase) of I_met. Data were collected in two temperature ranges: 25–29°C (blue symbols) and 35–39°C (red symbols). For pooled data, we abbreviate these ranges to their midpoints, “27°C” and “37°C”, in this and subsequent figures. A, Step deflections (bottom) of the hair bundle evoked rapidly adapting transduction currents in a P1 striolar type I hair cell at 36°C. Red trace, The response to a step at the midpoint of the operating range, X_1/2. Inset, The first 20 ms following the step to X_1/2. Black curve, Double-exponential fit (Eq. 3; τ_fast = 2.7 ms, τ_slow = 15.9 ms, I_ss = −51 pA, A_slow = −49 pA, A_fast = −72 pA). B, Parameters of adaptation as functions of hair-bundle displacement, at two different temperature ranges. Averages for six striolar type I hair cells at 27°C and seven striolar type I hair cells at 37°C. B.1, Fast and slow time constants from double-exponential fits (Eq. 3; fit shown in A, black curve, inset). τ_fast values were significantly faster at 37°C. B.2, The relative importance of slow adaptation increased with bundle displacement. The amplitude of the slow adaptation term (A_slow, Eq. 3) is divided by the sum of the amplitudes of the fast and slow terms and plotted against bundle displacement. This fraction increased similarly with level at both temperatures; slow adaptation accounted for 20% of the adaptation (decay) at the smallest displacements and 60–70% at the largest displacements. B.3, Percentage decay (extent of adaptation, Eq. 4) at steady state, as estimated by the double-exponential fits, decreased with displacement, and was smaller at every displacement at 37°C than at 27°C. C, Effects of adaptation and temperature on I(X) relations. Averaged I(X) relations were derived from steps (C.1, same cells as in B) and sinusoidal burst data (C.2). Step data (C.1): I(X) relations for peak and steady-state currents were fit with Equation 2 and averaged to produce mean and SEM values (gray shading, −1 SEM) (see Table 1 for fit values). Thick lines with dark shading, Peak (onset) I_met. Thin lines with light shading, Adapted (steady state) responses. Sinusoidal burst data (C.2, same axes): I(X) relations were point-by-point plots of I_met against X for the rising half-cycle of the sinusoidal burst, averaged across all five cycles in the burst. Shown are mean − SEM values of first-order Boltzmann fits (Eq. 1) for 100 Hz fits (thick line, n = 12) and 2 Hz fits (thin line, n = 10) at 35–39°C; see Table 1 for fit values. D, I_met (top, average of 5 traces) from the same P1 striolar type I hair cell as in A, evoked by ±1 μm sinusoidal bundle displacements (2–100 Hz, bottom), 36°C. Adaptation caused high-pass filtering (attenuation of the response at low frequencies). E, Representative FFT analyses of I_met (dark gray, 27°C) and probe motion (light gray) produced by ±1 μm sinusoidal bursts at 2 (left), 20 (middle), and 100 Hz (right). Higher harmonics (2f₀ and 3f₀) are at least 15 dB below the f₀ peak. F, Bode plots of the average gain (top) and phase angle (bottom) of the fundamental (f₀) component of I_met for 27 and 37°C in response to large stimuli (±0.6–1 μm). Responses are also plotted for a smaller stimulus (±0.3 μm) at 37°C. Positive phase angles at low stimulus frequencies and increasing gain with increasing frequency are attributable to adaptation of I_met. Gains and phase leads were higher for both stimulus levels at 37°C (red) than at 27°C (blue); see Table 1 for average values and n's in each condition. Gray circles, Responses of one cell (27°C) to an extended frequency range.

Analysis.

Data were analyzed with Origin 8.1 software (Microcal Software). Results are presented as means ± SEs of the mean. Significance was assessed with the two-tailed Student's t test or ANOVA as implemented by Origin 8.1; all samples were tested for equal variance. Mechanically evoked responses were rejected if there was baseline drift during the measurement period or if the signal-to-noise ratio was small. Data were accepted if maximum values were ≥40 pA/μm for transduction currents (I_met; noise floor, ≤10 pA); ≥10 mV/μm for receptor potentials (RPs; noise floor, ≤1 mV) for immature cells and ≥3 mV/μm for more mature hair cells with a low-voltage-activated conductance that reduces receptor potential gain; ≥5 pA/μm for EPSCs (noise floor, ≤1 pA); ≥1 mV/μm for EPSPs (noise floor, ≤100 μV); and 5 spikes/s/μm for spike rate. The recorded EPSCs and EPSPs may in some cases include both quantal (vesicular) responses and nonquantal responses (see Results; see Figure 5). Both responses, when present, will contribute to the fundamental (f₀) component of the fast Fourier transforms (FFTs) that we plot in Bode plots. Pharmacological separation of quantal and nonquantal components was not done.

Figure 5.

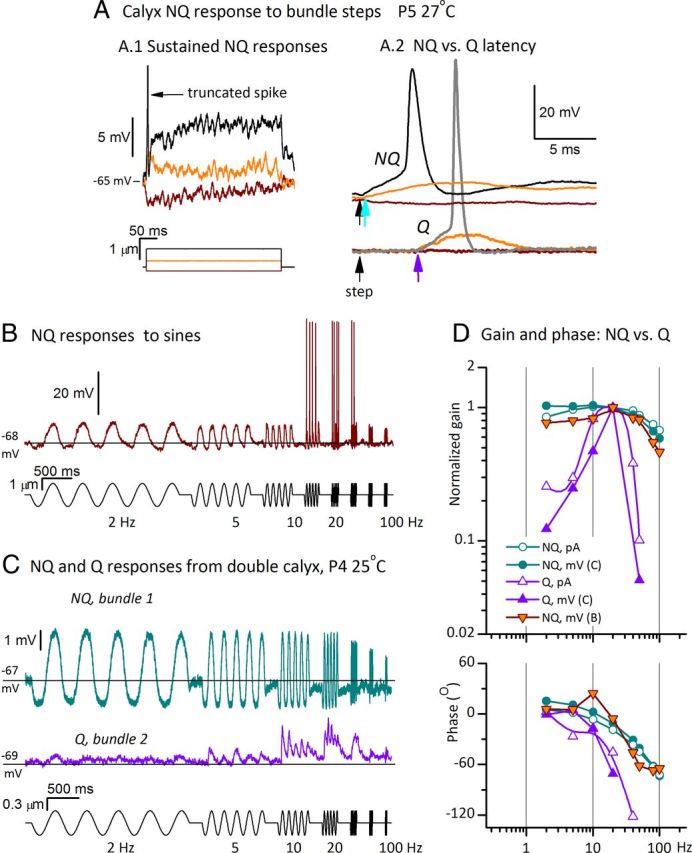
Timing and tuning differ for quantal (Q) and nonquantal (NQ) transmission at calyceal synapses. Data shown are from three exemplar calyces, all in the first postnatal week and recorded at 25–29°C. A, Voltage responses from a double calyx (P5, 27°C) during step stimulation of one of the two hair bundles. A.1, Steps evoked long-lasting (tonic) voltage responses quite different from EPSPs, which are discrete and have a positively skewed shape (examples in Figs. 4B,C.1, 5C). Large stimuli triggered a single spike (black trace). A.2, Nonquantal responses in A.1 are compared, on an expanded time scale and compressed voltage scale, to quantal responses to similar step stimuli recorded in an adjacent double calyx of the same preparation. The two sets of traces are aligned horizontally, with black arrows showing step onset; vertical scaling is the same for both sets of data but vertical alignment is arbitrary. The onset of the nonquantal response (top, cyan arrow) precedes the onset of quantal responses (bottom, purple arrow) by >4 ms. Contrast the discrete EPSP in the quantal response to the sustained depolarization in the subthreshold nonquantal response (orange traces). Note also that the negative step (brown) evoked a hyperpolarizing nonquantal response (expanded in A.1) but no quantal response. B, Voltage response from the calyx of A.1 (single trace) to sinusoidal burst stimuli. From 2–10 and 80–100 Hz, nonquantal potentials were sizeable but subthreshold; at 20, 40, and 50 Hz, they evoked spikes. The nonquantal response to the negative-going phase of the sinusoid dipped below resting potential (black line). C, Different modes of transmission from two hair cells within one striolar double calyx (P4, 25°C, ±300 nm sinusoidal bursts). The two hair bundles were stimulated one at a time in sequence. Stimulating bundle 1 evoked nonquantal transmission (cyan, average of 4 traces); stimulating bundle 2 evoked conventional EPSPs from the same calyx (purple, average of 10 traces). Same voltage scale for both traces. Results were consistent as the probe placement was alternated between the two hair bundles several times. The quantal response was more tuned. Black lines show resting potential; the nonquantal response had a strong hyperpolarizing component but the quantal response did not, as expected for quantal transmission on a baseline of zero spontaneous activity. D, Bode plots of f₀ components of quantal and nonquantal responses. Relative to quantal-response tuning (purple traces), nonquantal tuning for both calyces (cyan and orange symbols) was much broader and, for stimulus frequencies of >5 Hz, had less phase lag (phase angles were less negative). Included are Bode plots for postsynaptic currents from the calyx of C: EPSCs driven by bundle 2 displacements (open purple triangles) and nonquantal currents driven by bundle 1 displacements (open cyan circles). Gain plots were normalized to peak values for ease of comparison.

Membrane capacitance (C_m), membrane resistance (R_m), and series resistance (R_s) were calculated online by the Patchmaster software. Hair cell C_m was 7.9 ± 0.2 pF (38 cells) and did not clearly vary with age between P1 and P9. Uncompensated R_s was 16 ± 1 MΩ (38 cells). Hair-cell input resistance varied with age because type I cells acquire a low-voltage-activated conductance as they mature (Rüsch et al., 1998; see Fig. 10). Capacitance estimates were made for a subset of the calyx data: C_m was 18 ± 5 pF for 10 double complex calyces (each envelopes 2 type I hair cells), 17 ± 10 pF for five triple complex calyces (enveloping three hair cells), and 4.3 and 5.8 pF for two simple calyces, each contacting just one hair cell. In calyceal recordings, space clamp is not always achieved because of long attached afferent fibers, but Patchmaster estimates of the capacitive current are dominated by the fastest (proximate) component (i.e., the calyx).

Figure 10.

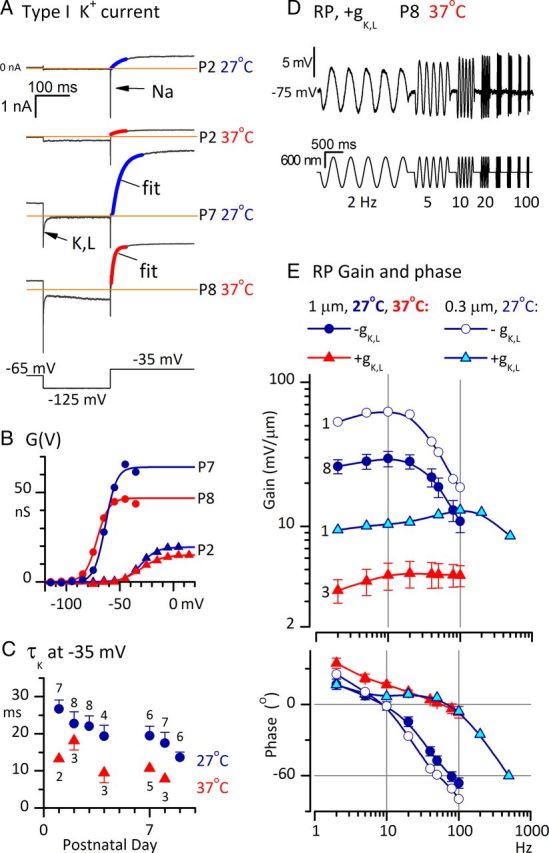
Acquisition of g_K,L by striolar type I hair cells in the first postnatal week greatly broadened receptor potential tuning and reduced phase lags above 5 Hz. A–C, Acquisition of g_K,L with age; effects of temperature. A, Currents evoked in four type I hair cells by the same voltage protocol (bottom). At P2 (both 27 and 37°C), the step from −125 to −35 mV evoked a fast Na⁺ current and an outward current that activated positive to resting potential, as shown by activation curves in B. At P7–P8, type I hair cells had a K⁺ conductance, g_K,L, which was activated at −65 mV, deactivated (arrow, P7 trace) during the step to −125 mV, and reactivated during the step to −35 mV. Colored curves are monoexponential fits to activation. Note the faster activation at 37°C. In the P8 trace (bottom), the gradual increase in inward current during the −125 mV step reflects activation of HCN channels. B, Conductance–voltage (G(V) or activation) curves generated from outward tail currents at −35 mV, as described in Materials and Methods, for the four cells in A. At P2, conductances activated positive to resting potential; at P7–P8, conductances activated negative to resting potential. See Table 3 for average parameters from Boltzmann fits to G(V) curves. C, Activation kinetics of K⁺ current as functions of age and temperature. τ values are from exponential fits of currents evoked by stepping from −125 to −35 mV, as shown in A. N's of averages are shown next to symbols. As activation shifted negatively with age, τ_K at −35 mV decreased. Increasing temperature by 10°C to 37°C also significantly reduced τ_K at −35 mV. D, RP from a type I cell with g_K,L, P8, 37°C (10 traces averaged) in response to ±600 nm sinusoidal bursts. Compared with RP in immature type I cells to similar stimuli (Fig. 3A), RP in cells with g_K,L was smaller and had a broader bandwidth (did not decrease with frequency, at least up to 100 Hz). E, Effects of g_K,L and temperature on gain and phase of RP referenced to bundle displacement. Numbers of cells used for each curve are shown to the left of each gain curve. Cells with g_K,L at 37°C (red) had much lower gains and greater phase leads than cells without g_K,L at 27°C (dark blue circles). Gains were higher for small stimuli than for large stimuli (compare open circles and dark blue circles), as expected from the saturation of V_m(X) relations (Fig. 3E). Extending the frequency range for a cell with g_K,L at 27°C (cyan triangles) revealed the large increase in low-pass corner frequency relative to cells without g_K,L at 27°C (compare with open circles for same stimulus size and temperature). Bottom, Phase plots. In cells lacking g_K,L (open and filled circles), RP lagged bundle displacement (phase was negative) for frequencies >10 Hz; in cells with g_K,L (red and cyan triangles), RP led displacement (phase was positive) up to almost 100 Hz.

I(X) relations were made by plotting I_met against bundle displacement (X) either for positive-going half-cycles of a sinusoidal stimulus or for families of step displacements. The relations were fit with either a first-order Boltzmann function:

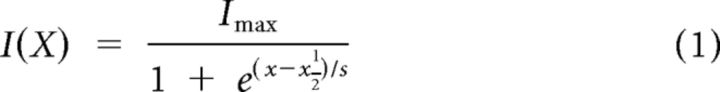where I_max is the maximum current (relative to the current at saturating negative displacements), X_1/2 is the displacement evoking a half-maximal response, and S is the displacement corresponding to an e-fold rise in I_met for X < X_1/2; or a second-order Boltzmann function:

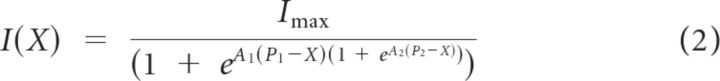where A₁ and A₂ are constants that set the steepness of the second-order Boltzmann and P₁ and P₂ are constants that set its position on the x-axis. Equation 1 was used if Equation 2 did not improve the R² value. From such Boltzmann fits, we calculated the operating range (OR) as the range of displacements over which the response grew from 10% of I_max to 90% of I_max.

Responses to positive step displacements were analyzed to provide the time course of adaptation. We fit the first 250 ms of the response (following the peak) with a double exponential function as shown in Equation 3:

where τ_fast and τ_slow are the short and long time constants, A_fast and A_slow are the amplitudes of the exponential terms, and I_SS is the steady-state current. Goodness of fit was assessed from the coefficient of determination (R² value) and visual inspection of the fit. A double-exponential function fit to the decay during the half-maximal step (X_1/2) yielded time constants that differed by an order of magnitude and provided a significantly better fit than a single-exponential function, as determined by eye and by a significantly improved R² value.

We quantified the extent of adaptation (percentage decay):

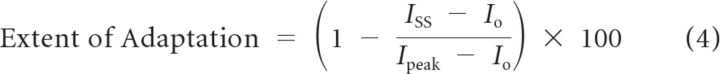where I_o, I_peak, and I_ss are pre-step, peak, and adapted (steady-state) levels of the step-evoked current response at X_1/2.

Sinusoidal responses were analyzed with Matlab 7 (Matlab). To show frequency dependence in a way that can be compared with published afferent data from in vivo studies (Fernández and Goldberg, 1976; Goldberg et al., 1990b; Lasker et al., 2008), we plotted the gain and phase of the fundamental (f₀) component of the response referenced to the f₀ component of the probe motion (Fig. 2E). FFTs were performed on hair-cell transduction currents (I_met), RPs, EPSCs or EPSPs, and the photodiode monitor of stimulus-probe displacement.

In our study, striolar calyceal afferents typically had little to no background firing and spike rates (spikes/cycle or spikes/second) were obtained by counting spikes during sinusoidal bursts (sinusoidal bundle displacements of 5 cycles duration at a specific frequency). These spike rates were divided by the stimulus magnitude to generate transfer functions of either spikes/cycle/micrometer or spikes/second/micrometer. Since all spikes were stimulus-driven and also phase-locked over the stimulus frequency range, it was straightforward to determine the phase angle of each spike relative to stimulus phase. The resulting phase distributions were normal (data not shown), validating this simple method of determining phase. Average phases were reported in the Bode plots. More complex methods are needed when spontaneous rates are significant (Cherif et al., 2008).

Analysis of the voltage dependence of outwardly rectifying current in hair cells.

Conductance–voltage [G(V) or activation] curves were constructed from “tail currents,” currents at the offset of each voltage step in an iterated voltage series. The voltage at the offset of the iterated steps was −35 mV, chosen to minimize contributions from HCN (hyperpolarization-activated, cyclic nucleotide-gated cation) channels, which reverse near −35 mV. To obtain conductance (G), tail currents were divided by driving force V_m − V_rev, where V_rev is the reversal potential of the current. The outwardly rectifying conductance was assumed to comprise one or more K⁺ conductance, for which V_rev was approximated by the K⁺ equilibrium potential (E_K = −84 mV) calculated from K⁺ concentrations in the bath and pipette solutions. The resulting sigmoidal curves were fit with a first-order Boltzmann function (Eq. 5):

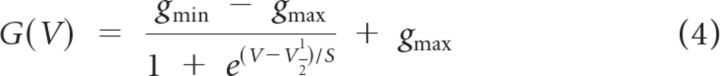where g_min and g_max are the minimum and maximum conductance, V_1/2 is the voltage of half-maximal activation, and S is the voltage range producing an e-fold increase in current at voltages negative to V_1/2. Activation time course was estimated for voltage steps from −125 to −35 mV (∼V_1/2 of the outward current in immature type I hair cells) by fitting the data with the following equation:

where I_SS and I₀ are the steady-state and initial current values and τ_K is the activation time constant for the outward current. Activation of outwardly rectifying K⁺ current in type I cells has previously been fit with more complex equations that introduce a brief delay at the onset (Rüsch and Eatock, 1996). However, the monoexponential Equation 6 provided a good fit to our hair-cell data, possibly because the initial stage of the response was obscured by large, transient, voltage-gated sodium (Na_V) current.

Electrical resonance of immature type I hair cells was quantified by measuring the frequency and decay time of oscillatory voltage responses to depolarizing current steps. The electrical resonance frequency (f_e) was calculated by fitting a damped sinusoid to the voltage response beginning at the initial peak (Fig. 3A.1,D,F, for examples):

where V_SS is the steady-state voltage, V_p is the voltage of the peak response, τ_e is the time constant for the decay of the envelope of the response, and θ is the phase angle. The quality, or sharpness, of electrical tuning was then defined as (Crawford and Fettiplace, 1981):

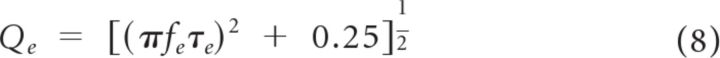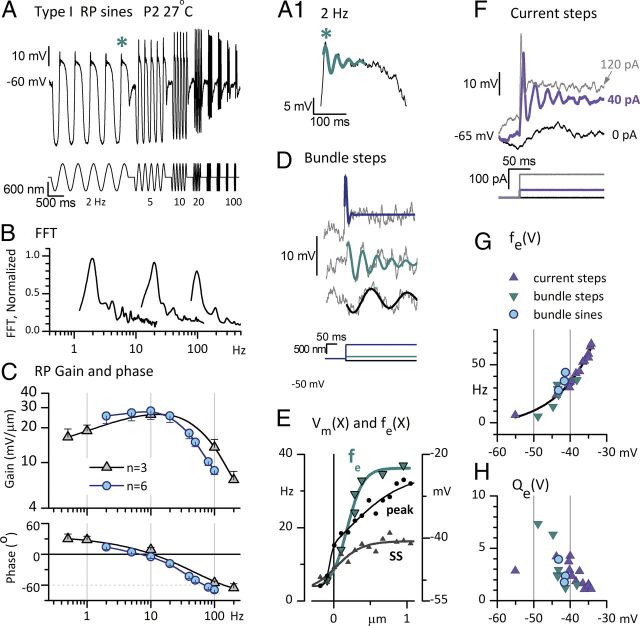
Figure 3.

Membrane properties of immature type I hair cells introduce low-pass filtering and electrical tuning. Data shown are from the same P2 striolar type I hair cell at 27°C, except in C, which are averaged across three or six hair cells. A, RP evoked by the sinusoidal burst series of bundle displacements shows bandpass tuning, with largest peak–peak amplitudes at 10 and 20 Hz. Asterisk, Part of the 2 Hz response is expanded in A.1, revealing voltage oscillations. A.1, Cyan curve, Fit of the oscillations (Eq. 7) used to generate f_e and Q_e (Eq. 8) data in G and H. B, FFT analyses of RP produced by sinusoidal bursts at 2 (left), 20 (middle), and 100 Hz (right), for ±1 μm stimuli. Upper harmonics are at least 15 dB below the f₀ peaks. C, Bode plots of the mean gain and phase angle of the f₀ component of RP as functions of frequency for ±0.6–1 μm sinusoidal burst stimuli. Blue circles, RP averaged from six hair cells providing I_met data at 27°C (Table 1; Fig. 2D). Gray triangles, RP averaged from three hair cells over a wider frequency range (0.5–200 Hz). Low-pass filtering by the hair-cell membrane decreased the phase lead of RP relative to bundle displacement as frequency increased; it became negative (a phase lag) above 10 Hz. D–H, A.1, Electrical tuning of the hair-cell membrane contributed to RP tuning in immature striolar type I hair cells. D, RPs evoked by three step displacements of the hair bundle resonated at different frequencies and qualities: −90 nm step (black): f_e = 5.6 Hz, Q_e = 7.3; +100 nm step (cyan): f_e = 14 Hz, Q_e = 6.3; +670 nm step (gray): f_e = 35 Hz, Q_e = 1. E, f_e and V_m had similar operating ranges of bundle displacement (X), consistent with f_e depending on V_m. Both f_e (cyan, left axis) and steady-state (SS) V_m (gray, right axis) were sigmoidal functions of X, saturating at ∼0.5 μm. At resting bundle position (steady-state V_m, −47 mV), f_e was ∼8 Hz. Peak V_m(X) relation (black circles) had a more sloping saturation. F, Current steps evoked voltage oscillations. A +40 pA current step evoked prominent voltage oscillations (violet). Slower voltage oscillations are visible at resting potential (black). A +120 pA step evoked a faster, more damped oscillation (light gray). G, H, Voltage dependence of resonant frequency (f_e) and tuning sharpness (Q_e) overlapped for bundle displacements and current steps. G, f_e as function of steady-state membrane potential in response to current steps (violet) or bundle steps (dark cyan triangles) or large, low-frequency sinusoidal bundle displacements (bright cyan circles; see A.1). The relation was fit with an exponential function (black curve, R² = 0.93). H, Q_e as a function of steady-state V_m. Symbols as in G. Tuning was sharpest (Q_e largest) near resting potential [i.e., the smallest bundle steps (dark cyan triangles)].

Results

To show how processing in the hair cell and afferent terminal contributes to shaping afferent responses in both the time and frequency domains, we compare the signals evoked at each stage by deflecting the hair bundle (Fig. 1B,C) with step displacements (time domain) or with a series of sinusoidal bursts at frequencies incremented from 2 to 100 Hz (frequency domain). We present whole-cell voltage-clamp and current-clamp recordings from hair cells [transduction currents (I_met) and receptor potentials (RPs)] and calyceal terminals (EPSCs, EPSPs, their nonquantal counterparts, and action potentials or spikes).

Most data were collected from striolar type I hair cells or calyces at room temperature (25–29°C) between P2 and P9, an immature period in which rats lack sight or hearing but do have some vestibular function as shown by righting reflexes. We also show select data at mammalian temperatures (range, 35–39°C). We conclude with data from type I hair cells in the second postnatal week which demonstrate the effects of electrophysiological maturation on the frequency dependence of the receptor potential.

Transducer adaptation

In multiple in vitro preparations (for review, see Eatock, 2000; Fettiplace and Hackney, 2006), hair cells adapt to sustained bundle deflections. We applied step bundle displacements to characterize the time course of adaptation in the rat saccular striola and its influence on the transducer operating range. We applied sine bursts to illustrate the effects of adaptation on frequency tuning and phase. We compare recordings at 25–29°C and 35–39°C to show the temperature dependence of some properties of transduction and adaptation. These results are summarized in Figure 2 and Table 1.

Table 1.

Temperature dependence of transducer I(X) relations and adaptation

Temperature	I(X) parameters					Adaptation at X1/2
	Stimulus (n)	Imax, pA	OR, nm	Po	X1/2, nm	τfast, ms	τslow, ms	Percent decay	Percent Aslow
27°C	Step
	Peak (6)	148 ± 14	1221 ± 161	0.12 ± 0.02	374 ± 45	4.7 ± 0.7	56 ± 9	79 ± 5	45 ± 4
	Steady-state (6)	58 ± 10	1403 ± 247	0.12 ± 0.04	634 ± 172
	0.6–1 μm Sine
	100 Hz (13)	144 ± 12	1056 ± 97	0.16 ± 0.03	405 ± 43
	2 Hz (12)	96 ± 6	1263 ± 66	0.51 ± 0.05	−20 ± 55
37°C	Step
	Peak (7)	233 ± 30, p < 0.03a	902 ± 58	0.13 ± 0.02	311 ± 23	3.6 ± 0.2b	58 ± 6	77 ± 3	36 ± 4
	Steady-state (7)	94 ± 15, p < 0.001c	1244 ± 152	0.13 ± 0.03	437 ± 26
	0.6–1 μm Sine
	100 Hz (12)	241 ± 25, p < 0.001d	1178 ± 59	0.22 ± 0.03	348 ± 42
	2 Hz (10)	155 ± 18, p < 0.003e	1394 ± 129	0.34 ± 0.05, p < 0.03	213 ± 69, p < 0.02

Maximum current (I_max) values^a,c,d,e were larger at 35–39°C (represented by the midpoint “37°C”) than at 25–29°C (“27°C”). Fast adaptation time constants^b were slightly but significantly faster at 37°C when tested across all step displacements (2-way ANOVA). n, number of cells. OR, operating range. P_o, fraction of I_met activated at X = 0 nm. X_1/2, midpoint of sigmoidal fit to I(X) relation. τ_fast, τ_slow, fast and slow adaptation time constants. Percent A_slow, percent of decay attributable to slow adaptation term.

Step-evoked adaptation

In Figure 2A, the hair bundle of a striolar type I hair cell was deflected by a rigid probe in a 36°C bath. Step displacements in the positive direction evoked currents (I_met) that rose rapidly and then adapted (decayed) with two time constants, τ_fast and τ_slow (Eq. 3), differing by approximately an order of magnitude (Fig. 2A, inset; Table 1). Figure 2B shows average parameters from exponential fits (Eq. 3) to adapting step responses of six cells at 25–29°C (designated in figures by the average value, 27°C) and seven other cells at 35–39°C (designated 37°C). τ_fast and τ_slow (Fig. 2B.1), the relative proportions of fast and slow components (Fig. 2B.2), and percentage decay (extent of adaptation, Fig. 2B.3) all changed with stimulus level. While some differences were noted with temperature (next paragraph), trends with stimulus level were similar at the two temperatures. For the smallest displacements (+100 nm), τ_fast and τ_slow averaged ∼2 and 40 ms at 35–39°C and the fast component dominated, producing ∼75% of the total decay. As stimulus level (X, displacement) increased, both time constants increased twofold and the proportion of slow component (Eq. 3, Fig. 2B.2) increased to over ∼60% at X > 1 μm. The extent of adaptation (Fig. 2B.3) also varied with level, decreasing from ∼85% at 100 nm to ∼65% at 1 μm (35–39°C). Table 1 provides average parameters of adaptation at the midpoint (X_1/2) of the peak operating range. At both temperatures, I_met adapted to a steady-state value of ∼20% of the peak (∼80% decay) via fast and slow components, each contributing 40–60% of the total decay and with mean time constants approximately one order of magnitude apart (∼4–5 and ∼60 ms). These immature saccular hair cells behave similarly to mouse utricular hair cells (Géléoc and Holt, 2003; Vollrath and Eatock, 2003).

Temperature effects

At 35–39°C, the fast component of adaptation was slightly but significantly faster (Fig. 2B.1; 2-way ANOVA, p < 0.05 for temperature and level): mean τ_fast values of 4.7 ms (averaged across all levels) at 25–29°C and 3.6 ms at 35–39°C yield a thermal coefficient of 1.3. The extent of adaptation (percentage decay; Fig. 2B.3) decreased with increasing temperature (2-way ANOVA, p < 1.5e–7 for both temperature and level). Pooling the data across 11 displacements, the mean steady-state extent of adaptation (Eq. 4) was 77 ± 2% at 25–29°C and 69 ± 2% at 35–39°C, for a thermal coefficient of 1.12.

Effects of adaptation and temperature on I(X) relations

Adaptation's effects on the relationship between I_met and bundle deflection are summarized in Figure 2C. Figure 2C.1 compares, for the same cell sample of Figure 2B, averaged I(X) relations from peak and steady-state responses to 400 ms displacement steps at 25–29°C [mean (blue) − SE (gray), 6 cells] and 35–39°C (red, 7 cells, different from the sample at 25−29°C). These relations were better fit by a second-order Boltzmann function (Eq. 2) than by a first-order Boltzmann function (Eq. 1), consistent with more than one closed state for the transduction channels. Table 1 gives averaged parameter values from fits of Equation 2, yielding estimates of maximal current (I_max), X_1/2, open probability at the resting bundle position (P_o), and OR. Increasing temperature by 10°C increased both peak and steady-state current 1.5–1.6-fold. Steady-state I_max was ∼40% of peak I_max at both temperatures.

Adaptation's effects in the frequency domain

To study the frequency dependence of I_met, we delivered a series of sinusoidal bundle displacements in bursts of five cycles each, typically incremented from 2 to 100 Hz. Displacements were ±600–1000 nm or, less frequently, ±300 nm.

I_met increased with stimulus frequency (Fig. 2D): this high-pass filtering is attributable to transducer adaptation, which reduces responses at low frequencies. To quantify the effect across multiple hair cells and to also determine phase (timing) as a function of frequency, we generated Bode plots of the fundamental (f₀) component of I_met relative to the stimulus from FFTs (see Materials and Methods). Figure 2E illustrates FFTs of I_met from a striolar type I hair cell during ±600 nm sinusoidal bursts at 2, 20, and 100 Hz, plus FFTs of the corresponding probe motion as monitored by a photodiode (see Materials and Methods). For each burst frequency, the probe motion had one major peak at f₀. I_met also had a large peak at f₀, plus smaller peaks at higher harmonics (2f₀ and 3f₀), which reflect nonlinearities in transduction. Nevertheless, the largest harmonic (2f₀) was at least 15 dB smaller than the f₀ component, indicating that Bode plots of the f₀ component capture much of the frequency dependence of I_met.

The Bode plots in Figure 2F show how average gain (pA/μm) and phase of the f₀ component of I_met varied with sinusoidal burst frequency at different stimulus levels and temperatures. At each frequency, the magnitude of the f₀ component of I_met was divided by the magnitude of the f₀ component of the stimulus, and the phase of the response was referenced to the phase of the stimulus. Positive phase angles correspond to responses that lead the stimulus; negative phase angles correspond to responses that lag the stimulus. For cells held at 35–39°C, responses were measured at two stimulus levels (filled red triangles, ±600–1000 nm; open red triangles, ±300 nm). At 25–29°C, responses were obtained at one stimulus level (±600–1000 nm) averaged across multiple cells for 2–100 Hz (blue circles) and from one cell from 0.5–200 Hz (gray circles). In all cases, as stimulus frequency increased, I_met increased and response phase decreased, from a lead of ∼20° at 2 Hz to 0° (in phase) at ∼100 Hz.

When stimulus level was changed from ±600–1000 to ±300 nm, response gain increased at all frequencies (compare filled and open red triangles). This is expected based on the nonlinear I(X) relations of the hair cells, for which +300 nm is below X_1/2 and +600–1000 nm approaches or reaches positive saturation (Fig. 2C). The phase of I_met relative to the stimulus was relatively insensitive to level in this range (Fig. 2F, bottom; points for different levels overlap in the phase plot).

Increasing temperature increased gain across all frequencies (Fig. 2F, compare filled blue circles and filled red triangles, same stimulus level), consistent with the temperature effect on I_max (Fig. 2C.1, Table 1). Increasing temperature also slightly increased phase leads (Fig. 2F, bottom): the mean phase angle across all frequencies was significantly larger at 37°C (11.7 ± 0.9°, n = 96) than at 27° (8.5 ± 1.0°, n = 80; p = 0.0004, 2-way ANOVA for temperature and stimulus frequency, with Bonferroni's and Tukey's post hoc corrections for multiple comparisons). This phase advance with temperature is consistent with the faster fast adaptation at high temperature (Fig. 2B.1) and may also reflect faster channel activation. The decline in I_met phase with frequency may reflect both a phase lead from transducer adaptation at low frequencies and a phase lag from transducer activation at high frequencies. For comparison, the transducer activation time constants of ∼1 ms in the turtle cochlea (Ricci et al., 2005) would produce significant phase lag above 100 Hz.

The effect of transducer adaptation on sensitivity is illustrated in a different way in Figure 2C.2, with average I(X) relations derived from 100 Hz sinusoidal bursts and 2 Hz sinusoidal bursts at 35–39°C. In contrast to step-evoked I(X) relations, I(X) relations evoked by sinusoidal bursts were well fit by simple first-order Boltzmann functions (Eq. 1), consistent with just two kinetic states (closed and open), and had larger P_o values. I_max values and ORs were similar for the 100 Hz I(X) relation and the peak step-evoked I(X) relation (Fig. 2C.1, Table 1), indicating that at 100 Hz, I_met was not adapted. At 2 Hz, I_met was significantly but not fully adapted, as shown by comparison with steady-state I(X) relations from step stimuli in Figure 2C.1.

In summary, at stimulus frequencies <100 Hz, high-pass filtering by adaptation attenuated responses and introduced a phase lead. Recordings at body temperature yielded larger I_met values and therefore larger gains across all frequencies. The higher temperature also increased high-frequency phase leads, possibly as a combined effect of faster fast adaptation and faster channel activation.

Filtering of the receptor potential by electrical membrane properties

Membrane charging attenuates and slows receptor potentials at high frequencies

I_met depolarizes the hair cell, initiating an RP. In Figure 3A, the sinusoidal burst series evoked RPs from an immature striolar type I cell. Below 10–20 Hz, the RP grew (along with I_met) as a consequence of transducer adaptation. Above 20 Hz, however, the RP fell off as there was insufficient time for I_met to fully charge the membrane cycle by cycle.

In FFTs of the RP from a representative immature striolar type I hair cell (Fig. 3B), most of the response power was centered at f₀. In Figure 3C, the gain and phase of the f₀ component of RP referenced to the hair bundle displacement are plotted against frequency (average from 6 striolar type I hair cells, ±0.6–1 μm stimuli, first postnatal week). The mean best frequency (BF) was 9 ± 2 Hz (range, 4–15 Hz). The high-pass corner frequency, f_HP, was ∼1 Hz, as estimated from the low-frequency roll-off (0.8 ± 0.2 Hz, 5 cells) and as measured in a subset of cells by extending the frequency range to 0.5 Hz (1.1 ± 0.4 Hz, 3 cells; Fig. 3C, gray triangles). This value is in reasonable agreement with the slow adaptation time constant obtained for 0.5–1 μm step displacements at 25–29°C: ∼60 ms, corresponding to a corner frequency [(2πτ)⁻¹] of 3 Hz. Some high-pass filtering (adaptation) may also be mediated by voltage-gated conductances in the hair-cell membrane (Fig. 3F, discussed in the next section). At 2 Hz, I_met and RP had similar phase leads: 22 ± 7° (6 cells, Fig. 2F) and 17 ± 4° (6 cells, Fig. 2C), respectively.

Above 10 Hz, the gain and phase of RP decreased relative to that of I_met (data not shown), consistent with low-pass filtering of I_met as a result of membrane charging time. In immature type I cells stimulated with ±0.6–1 μm sinusoidal bursts (Fig. 3C, filled blue circles), the corner frequency for low-pass filtering, f_LP, was 40 ± 5 Hz (6 cells; range, 24–57 Hz). If this filtering is entirely determined by the membrane time constant, then mean τ_m would be (2πf_LP)⁻¹ or 4 ms, which is close to the mean τ_m (∼7 ms) calculated from input resistance and capacitance for a separate population of 16 immature striolar type I hair cells (R_m = 899 ± 202 MΩ; C_m = 7.7 ± 0.2 pF). For the three cells studied over 0.5–200 Hz (Fig. 3C, gray triangles), a low quality (Q, sharpness) of tuning was measured: Q_{3 dB} = BF/(f_LP − f_HP) = 0.23 ± 0.07.

Thus, for large stimuli, the bandpass filtering of RP is largely attributable to high-pass filtering by adaptation and low-pass filtering by steady-state membrane properties at resting potential.

Electrical resonance of the hair-cell membrane

Bundle displacements sometimes evoked oscillatory RPs. For example, in the 2 Hz data from Figure 3A (see asterisk; replotted on an expanded time scale in Fig. 3A.1), the response at the peak of each cycle oscillated. Oscillations were especially long-lasting for small displacement steps (Fig. 3D). Such oscillations were not seen in I_met (data not shown) indicating that they arise at the RP stage. The frequency (f_e) of the oscillations was a sigmoidal function of step size (Fig. 3E). The operating range of the f_e(X) relation was similar to the operating range of the RP, as illustrated in Figure 3E by overlaying f_e(X) and peak and steady-state V_m(X) curves for the same cell. In this cell, f_e varied almost 10-fold over the operating range of the RP, from ∼4 Hz for a negative displacement to ∼35 Hz for saturating positive displacements.

RP oscillations reflect voltage-dependent (electrical) tuning of the hair-cell membrane, as shown by current-injection experiments that bypass transduction and directly stimulate voltage-sensitive conductances in the hair-cell membrane. Small current steps (Fig. 3F) evoked voltage oscillations similar to those evoked by displacement steps (Fig. 3D). The sharpness, Q_e, of the electrical tuning is proportional to the decay time for oscillations (Eq. 8). f_e and Q_e had similar voltage dependence whether the oscillations were evoked by current steps or by displacement steps (Fig. 3G,H), consistent with a common mechanism. As found in other hair cells (Crawford and Fettiplace, 1981), Q_e had a somewhat bell-shaped dependence on membrane potential, peaking sharply near resting potential.

The mean best f_e (frequency corresponding to the highest Q_e) was 29 ± 4 Hz in seven cells, higher than best frequencies obtained with sinusoidal bursts (∼9 Hz, Fig. 3C). Q_e peaked at 7.5 for a small step displacement (Fig. 3H), a value much higher than the Q_{3 dB} value (∼0.2, Fig. 3C) of Bode plots for sinusoidal bundle displacements. The difference reflects the strong voltage dependence of Q_e (Fig. 3H): the large sinusoidal motion used for the Bode plots in Figure 3C depolarized the hair cell to values positive to −40 mV, where Q_e was low.

Thus, in immature striolar type I hair cells, electrical tuning boosts receptor potentials to stimulus frequencies from several hertz to tens of hertz, with the greatest effect for small transduction currents. Such enhancement may be important in driving transmitter release and downstream activity in the developing vestibular system. As described later in Results, the electrical resonance of the early postnatal period is soon eliminated in type I cells by maturational changes that broaden membrane filtering.

Postsynaptic responses from striolar calyces

Calyceal responses to steps reveal synaptic delay and narrow operating range

Deflecting the hair bundle of a type I hair cell evoked activity in its postsynaptic calyx, which we recorded in voltage clamp as currents (EPSCs) and in current clamp as subthreshold potentials (EPSPs). In Figures 4 and 6, we analyze EPSCs, EPSPs, and spikes from calyces in which the transmission appeared to be predominantly quantal. In Figure 5, we illustrate examples in which a nonquantal response dominates. Figure 4 features quantal events and spikes evoked by step displacements. In a P6 calyx, increasing step size increased the size and decreased the latency of EPSCs (Fig. 4A.1), reaching an asymptote at 7.5 ms (Fig. 4C.4, cyan curve). The distributions of EPSC peak amplitudes from this calyx are plotted in Figure 4A.2 (magenta), superimposed on the pooled distribution of 1424 EPSCs from five calyces at 25–29°C (gray). The EPSCs were collected during trials with hair bundle deflections. For the pooled distribution, mean amplitude was 34.5 ± 0.6 pA, median amplitude was 28 pA, mode was 15 pA, and the largest event was 159 pA. A Gaussian fit to the values between 0 and 33 pA (data not shown) was centered at 19.9 ± 0.6 pA (SEM) with an SD of 8 pA. Adjusting for the reduced driving force in our data (−65 mV) compared with published data from cochlear and vestibular terminals (−80 to −90 mV) yields a modal value of 20 pA, which can be compared with 21 pA in mouse utricular calyces (Dulon et al., 2009), 18 pA for P5–P19 afferents on outer hair cells (Weisz et al., 2009), and 30 pA for P8–P11 afferents on inner hair cells (Grant et al., 2010). If our modal value (15 pA in our conditions) represents the quantal size at these immature rat calyces, then the maximum value of ∼160 pA corresponds to release of 10–11 vesicles, and the median and mean values both correspond to approximately two vesicles.

Figure 4.

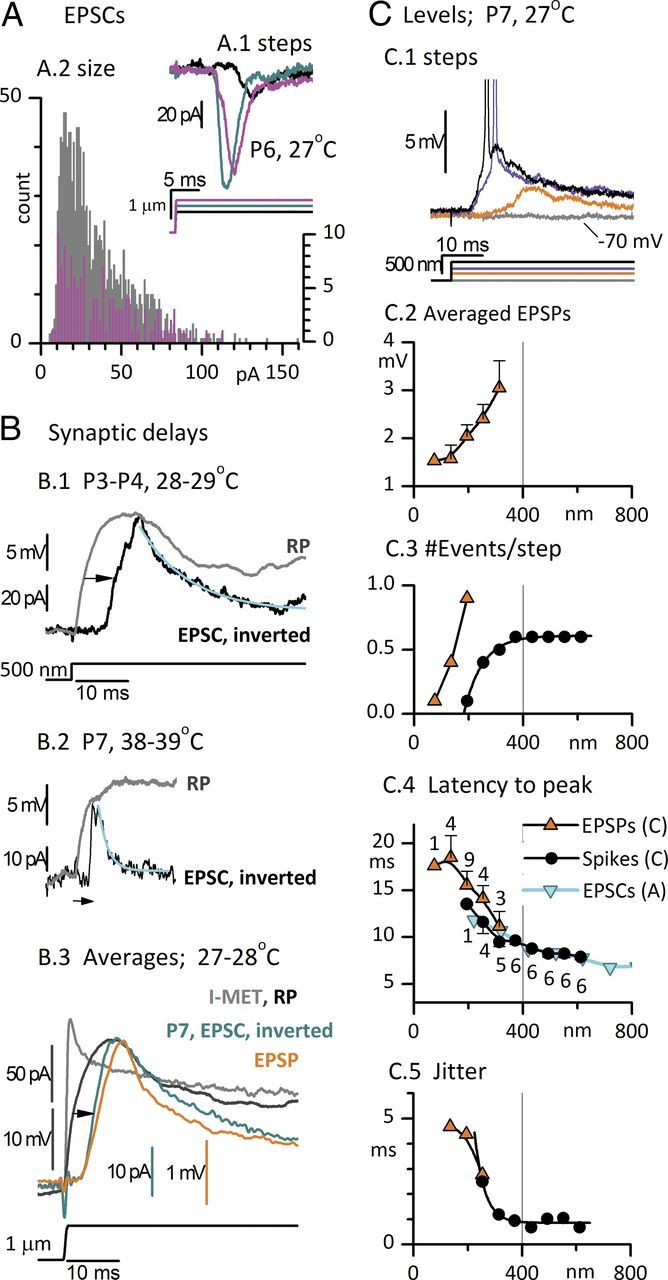
Timing and level dependence of postsynaptic currents, potentials, and spikes recorded from striolar calyces in response to step displacements of type I hair bundles. A, EPSCs. A.1, Responses of a P6 calyx to three positive bundle displacements. Latencies from step onset to onset of first EPSC: 10 ms for the black step; 6.5 ms for the cyan and magenta steps. Latencies to first EPSC are plotted against displacement in F (cyan inverted triangles). A.2, Distributions of EPSC peak sizes from five striolar complex calyces (gray bars, 25–29°C, P4–P7); the distribution for the calyx of A.1 is superimposed (magenta, expanded count scale on right axis). B, Step-evoked RPs from striolar type I hair cells are compared with EPSCs (inverted for comparison) from striolar calyces; records were obtained independently but are matched for stimulus, postnatal age, epithelial zone, and temperature. B.1, Type I: P3, 28°C; calyx: P4, triple, 29°C. The delay of the EPSC relative to the RP (arrow) is 6 ms. EPSC decay time constant (cyan curve) is 9.6 ms. The height of the EPSC (95 pA) suggests summation of five miniature events (vesicles). B.2, P7 type I hair cell at 38°C (with low-voltage-activated conductance, g_K,L; see Fig. 10); P7 double calyx at 39°C. Delay from RP to EPSC (arrow), 2.6 ms. EPSC decay time constant (cyan curve), 1.8 ms. B.3, Averaged EPSCs (inverted, 21 traces) and averaged EPSPs (17 traces) from a P7 double calyx at 27°C in response to +1 μm step deflections of a single hair bundle; compare with I_met and RP of a single type I hair cell (same hair cell as in B.1). Mean peak EPSC and EPSP values are −31 pA and 2.2 mV, corresponding to ∼1.5–2 vesicles (based on size distribution data in A). Synaptic delay from averaged RP to averaged EPSC (arrow), 4.6 ms. Monoexponential fits to the decays of the averaged EPSC and EPSP had time constants of 15.1 and 7.7 ms, respectively (fits not shown). C, Level dependence of EPSPs and spikes evoked in a double calyx by step deflections of one of its input hair bundles (P7, 27°C). C.1, As level (bundle displacement) increased (bottom traces), EPSP latency decreased and EPSP size increased until spike threshold (∼−63 mV in this calyx) was crossed (purple trace). A further increase in bundle displacement reduced spike latency (black trace). C.2–C.5, In mixed EPSP and spike responses (as in C.1), EPSPs (orange triangles) and spikes (black circles) were analyzed separately. EPSP traces that did not give rise to spikes were averaged together (n's for EPSPs for C.4 and C.5 are given in C.4 next to the data points). EPSPs at levels above spike threshold are not shown; instead, spikes are counted. C.2, Average EPSP peak size increased from 1.5 mV (∼1 quantum) at displacements < 200 nm to 3 mV (∼2 quanta) at 300 nm. All EPSPs occurred near the beginning of the step, but because of jitter in their timing (C.5), aligning the averaged traces by the onset of the displacement step reduced the peak relative to an average made by aligning quantal events (data not shown). C.3, Number of events per step. This calyx lacked spontaneous activity; EPSPs were first detected at +75 nm and increased in number per step until they started triggering spikes at +200 nm. C.4, C.5, Latency (C.4, step onset to response peak) and jitter (C.5) declined for both EPSPs and spikes as bundle displacement increased up to ∼300 nm. At higher levels, spike latency (measured at spike peak) and jitter plateaued at 7.9 and 0.7 ms, respectively. C.4, Cyan triangles, First EPSC latencies from the calyx of A.1 show a long minimum latency similar to that for spikes in the calyx featured in C.

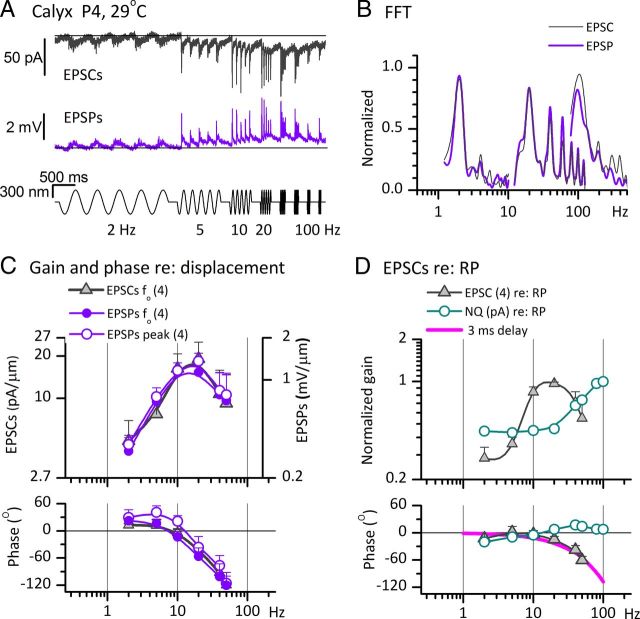
Figure 6.

The frequency dependence of postsynaptic currents and potentials recorded from striolar calyces in response to sinusoidal displacements of type I hair bundles. All signals were evoked by ±300 nm sinusoidal burst series from 2 to 100 Hz. A, EPSCs (top, 5 traces averaged) and EPSPs (bottom, 7 traces averaged) from a P4 triple calyx at 29°C. Black lines aligned with baseline at the start of each trial illustrate the gradual shift in baseline during the trial, consistent with integration or accumulation at synaptic stages. B, FFTs of averaged EPSC and EPSP responses in A at 2, 20, and 100 Hz and ±300 nm. At 2 and 100 Hz, higher harmonics were at least 15 dB below the f₀ component. At 20 Hz (best frequency for this calyx), higher harmonics were significant. C, Bode plots of gain and phase versus burst frequency for ±300 nm stimuli (see A, B). Left axis, EPSCs (f₀ component, n = 4 calyces). For EPSPs (right axis, from the same calyces), we plot the f₀ component of FFTs (filled circles), and peak values of EPSPs (open circles). The phase of peak values leads the phase of the f₀ component (bottom). D, Gain and phase of averaged EPSCs (same data as in C) and nonquantal (NQ) current (1 calyx, from Fig. 5C), both referenced to RP data from a type I hair cell. All measurements are of the f₀ component from FFT analysis of responses to the ±300 nm sinusoidal burst series. The fall-off at high frequencies of the phase lead of EPSCs referenced to RPs (gray triangles) was well fit with a simple delay term of 3 ms (magenta curve), consistent with an average synaptic delay of 3 ms.

For EPSCs from the exemplar calyx in Figure 4A.1, the mean time to peak was 2.9 ± 0.2 ms (n = 20 events) and the mean decay time constant for 16 events with monoexponential decays was 3.1 ± 0.2 ms, in between values from similarly aged mouse utricular calyces (P4–P9; room temperature; time constant, 5–6 ms; Dulon et al., 2009) and the average value for a mature gerbil calyx (1 ms, Rennie and Streeter, 2006). Figure 4B demonstrates that most of the long EPSC latency to the step stimuli in Figure 4A.1 arises at the synapse. We estimated synaptic delay by comparing the presynaptic signal from type I hair cells (the RP) and the postsynaptic signal (EPSC, inverted for comparison) from striolar calyces, matched for stimulus, age range, zone, and temperature. In the P4 calyx of Figure 4B.1, the EPSC lagged the exemplar RP by 6 ms (arrow; delay measured at midpoint of rise). This EPSC was quite slow: its long time to peak (6.5 ms) and decay time constant (15.1 ms) are likely to reflect temporal dispersion of overlapping quanta (synaptic vesicles). Pairing the same RP with the faster EPSCs for the same step size from Figure 4A.1 yields a similar synaptic delay (5.8 ms, data not shown). Immaturity and low temperature are likely to contribute to the long delay, as suggested by a delay of just 2.4 ms in a more mature pairing at body temperature (Fig. 4B.2, arrow). The EPSC time to peak (740 μs) and decay time constant (1.8 ms) were also relatively fast. More data are needed to isolate and quantify the effects of maturation and temperature. Figure 4B.3 compares averaged transduction current and receptor potential from a striolar type I hair cell with averaged EPSC and EPSP responses from a third calyx, older but at 27°C, to saturatingly large (1 μm) steps. Relative to the averaged RP, the averaged EPSC was delayed by 4.0 ms (black arrow). The corresponding averaged EPSP (orange trace) had little additional delay.

In summary, the synaptic delays for quantal transmission (4–6 ms at room temperature) in these immature calyces are not consistent with in vivo data from more mature vestibular afferents. A similar delay characterizes the entire angular vestibulo-ocular reflex (VOR), which involves four synapses, measured in vivo from mature primates (Huterer and Cullen, 2002). Moreover, synaptic delay in mature cat saccular afferents was estimated at <0.5 ms (McCue and Guinan, 1994; see Discussion). It is not surprising, however, to find that synaptic transmission is immature in the rat saccular macula in the first postnatal week. At P9–P11 in the rat cochlea, afferent terminal EPSCs evoked by step depolarizations of inner hair cells also take several milliseconds to peak (Goutman and Glowatzki, 2007). Other hair-cell and synapse properties are immature at this time in rodent vestibular epithelia. During the first two postnatal weeks, calyces of the mouse utricle mature morphologically (Rüsch et al., 1998) and ion channels are added to the hair cells (see Fig. 10) and parent cell bodies in the vestibular ganglion (Kalluri et al., 2010).

In Figure 4C, we examine the level dependence of EPSPs and spikes from a P7 double calyx with no spontaneous activity. Responses for several steps of different size are superimposed in Figure 4C.1. At the low end of the operating range, 50 to 200–300 nm, increasing the bundle deflection increased EPSP peak amplitude (Fig. 4C.2) and EPSP number (Fig. 4C.3), and decreased EPSP latency (Fig. 4C.4) and EPSP jitter (Fig. 4C.5). The smallest EPSPs (mean, 1.5 mV; Fig. 4C.2) may have been “minis” generated by single synaptic vesicles and corresponding to EPSCs of ∼15 pA; maximum subthreshold EPSPs were 3 mV (Fig. 4C.2). In two other calyces (P5, 25–29°C), minimum EPSPs were 2.0 and 1.6 mV and maximum subthreshold EPSPs were 4.4 and 8.4 mV (data not shown). Thus, at this age and temperature, ∼2–3 vesicles were needed to produce a spike.

For bundle displacements between 200 and 400 nm, responses transitioned from EPSPs to spikes (Fig. 4C.1,C.3). The response of this calyx was strongly adapting (phasic), such that just one onset spike was produced at any level. The latency of spike peaks (Fig. 4C.4), however, had a broader level dependence, asymptoting at ∼8 ms for the largest stimuli. This long minimal latency exceeds the synaptic delay (4–6 ms, Fig. 3B), indicating that other processes, such as charging of the presynaptic and postsynaptic membranes, also take significant time in this immature preparation. Between 200 and 400 nm, spike jitter (Fig. 4C.5) fell steeply from ∼5 ms to ∼1 ms. In a model of hair-cell exocytosis (Wittig and Parsons, 2008), jitter depends inversely on the number of readily releasable vesicles, with a jitter of ∼1 ms (similar to the value for >300 nm in Fig. 4C.5) produced by a simulation for two releasable vesicles. Thus, our jitter values together with the evidence for few releasable vesicles (above) are consistent with predictions from the model.

For bundle displacements of >400 nm, spike responses in the calyx of Figure 4C were largely independent of level in number, latency, and jitter. Thus, the spike OR (∼150 nm) was just a fifth of the typical OR for I_met (Table 1), indicating that post-transduction mechanisms compress the OR, consistent with cochlear data (Weiss, 1984; Eatock et al., 1991). These mechanisms may include voltage-dependent properties of the hair-cell and calyceal membranes, synaptic adaptation or fatigue, and refractoriness in the spike generator, any or all of which may be especially pronounced in developing synapses.

Postsynaptic responses to sinusoids reveal nonquantal components and bandpass tuning

To study frequency tuning of EPSCs and EPSPs in calyces, we delivered a series of sinusoidal bursts, usually from 2 to 100 Hz, at a smaller level (±300 nm) than our standard for hair-cell responses (±600–1000 nm). The larger stimuli were needed to map the full I(X) relations in hair cells, whereas the smaller stimuli allowed us to isolate more subthreshold EPSPs in calyces. Calyceal spiking data were collected at both levels.

Quantal and nonquantal components of calyceal responses

Mechanical stimulation sometimes evoked calyceal currents (in voltage clamp) or subthreshold potentials (in current clamp) that appeared to be nonquantal, with different shapes and latencies from quantal (vesicular) events. Nonquantal responses of two calyces are illustrated in Figure 5. Qualitatively similar responses were previously reported in intracellular recordings from chick and turtle calyx-bearing canal afferents stimulated by displacement of canal fluids (Yamashita and Ohmori, 1990; Holt et al., 2007). In the turtle, the nonquantal component occurred together with conventional quantal transmission in individual afferents. Since the turtle afferents may have innervated both type I and type II hair cells, it was not clear whether both forms of transmission occur in the same calyx ending at once. Our results show that nonquantal responses can occur in mammals, at least in the first postnatal week, and that they originate in calyx endings and can occur alone or in combination with quantal responses.

In Figure 5, we highlight nonquantal responses well isolated from quantal responses. Figure 5A shows voltage responses from a calyx to step deflections of the hair bundle of one of its enclosed type I hair cells. Steps evoked sustained voltage changes (Fig. 5A.1) with superimposed voltage noise that did not resemble EPSPs in shape; the largest step evoked a spike at step onset. The sustained voltage responses do not appear to reflect summation of many EPSPs. Further, the latencies of nonquantal responses were much shorter than the latencies of quantal responses, as illustrated on an expanded time scale in Figure 5A.2. The nonquantal response started (cyan arrow) within 0.5 ms after step onset (black arrow). Immediately below are shown, for comparison, quantal responses to similar stimuli from a different calyx; the quantal responses started 5 ms after the step (purple arrow), consistent with quantal latencies in Figure 4A.1. The 10-fold reduction in latency in the nonquantal case argues strongly for a fundamentally more direct mechanism, such as a form of electrical transmission (see Discussion). In Figure 5A.2, the spike evoked by the largest step peaked at 4.6 ms after the step for the nonquantal case, in contrast to 8.2 ms for the quantal case. The quantal spike latency was similar to the lowest spike latencies in a different calyx with quantal transmission (8.3 ms; Fig. 4C.4). Figure 5B shows the response of the nonquantal calyx of Figure 5A to sinusoidal bursts from 2 to 100 Hz. Large quasi-sinusoidal postsynaptic potentials triggered spikes at 20, 40, and 50 Hz with a spike threshold of −56 mV. Consistent with the negative step displacement data in Figure 5A, negative-going phases of the sinusoidal stimuli elicited hyperpolarizations (below resting potential, black line). Hyperpolarization is not expected for a quantal response except through inhibition of a strong background level of quantal summation; in this calyx, there were no spontaneous quantal events.

Quantal and nonquantal transmission can be recorded from one calyx. In the double calyx of Figure 5C, the nature of transmission depended on which of its two type I hair cells was stimulated: deflection of one bundle evoked nonquantal responses (cyan) and deflection of the other bundle evoked quantal responses (purple). This difference in transmission mode was sustained for more than 1 h, during which the stimulus probe was repeatedly switched from one bundle to the other. Again, the large hyperpolarizing component of the nonquantal response (negative to the black line) is difficult to reconcile with a quantal mechanism. For comparison, the entire quantal response is above the line representing resting potential.

In other calyces (data not shown), responses to motion of a single bundle had both nonquantal and quantal components. Both components were always eliminated by moving the stimulus probe slightly off the hair bundle, showing that neither component was an electrical artifact. Possible mechanisms for nonquantal transmission are considered in Discussion.

The frequency dependence of nonquantal and quantal responses from these two calyces are plotted together in Figure 5D. The nonquantal, subthreshold responses of the calyx from A and B, plotted as orange inverted triangles in Figure 5D, had broad filtering with diminishing gain and phase above 20 Hz. For the calyx with both nonquantal and quantal transmission, the nonquantal response [recorded in voltage clamp (cyan open circles) and current clamp (cyan filled circles)] was much more broadly tuned than the quantal response (open and closed purple triangles). The phases of nonquantal responses led the phases of quantal responses, especially above 5 Hz, consistent with the shorter latency of nonquantal responses to steps (Fig. 5A.2).

To recapitulate, some calyceal responses to hair bundle deflections appeared to be quantal (Fig. 4), as expected from other hair-cell synapses. Others appeared to be nonquantal (Fig. 5) because they lacked individual events with the skewed shape of quantal responses, and had much shorter latencies (Fig. 5A.2) and prominent hyperpolarizing components (Fig. 5A–C). In some cases, it appeared possible that the response to a single bundle deflection included both nonquantal and quantal components (data not shown), but confirmation awaits pharmacological experiments to block one or the other component (Holt et al., 2007). Where both components are present, the FFTs that we used to generate Bode plots of gain and phase versus frequency would reflect contributions from both components. FFT analysis is not event-based, unlike many kinds of synaptic analysis, and will therefore agnostically report any stimulus-driven signal. Note also that, in contrast to spontaneous quantal events, there is no signature of nonquantal transmission in the absence of a mechanical or electrical stimulus to the hair cell.

Frequency dependence of EPSCs and EPSPs

Figure 6 further explores the frequency dependence of postsynaptic responses, focusing on responses with less prominent (if any) nonquantal components than in the calyces of Figure 5. In Figure 6A, EPSCs and EPSPs were recorded from a striolar triple calyx in response to ±300 nm sinusoidal bursts applied to one of the three hair bundles; responses to stimulation of a second bundle within this triple calyx were qualitatively similar to those shown. The averaged EPSCs were largest for stimuli between 10 and 40 Hz. During the burst series, there were slow shifts of baseline inward current (in voltage-clamp recording of EPSCs) and depolarization (in current-clamp recording of EPSPs) away from the resting values indicated by black lines in Figure 6A. Such shifts were not seen in receptor potential recordings (Fig. 3A), suggesting accumulation of some factor, such as presynaptic Ca²⁺ or neurotransmitter in the synaptic cleft.

FFTs of the EPSC and EPSP data in Figure 6A are plotted in Figure 6B for 2, 20, and 100 Hz sinusoidal bursts. As expected for quantal responses, these EPSCs and EPSPs were less sinusoidal (more positively skewed) than I_met (Fig. 2), RP (Fig. 3), and nonquantal currents or voltages (Fig. 5). This distortion manifested as additional peaks in the FFTs for EPSCs and EPSPs at frequencies above the fundamental frequency, f₀. Distortion was most prominent for the large, synchronized signals near the best frequency for the calyx (20 Hz; Fig. 6A), with clear FFT peaks at multiple harmonics of f₀.

The Bode plots of the gain and phase of f₀ components of EPSCs and EPSPs referenced to bundle displacement (Fig. 6C) were averaged from four striolar calyces. The gains peak at 20 Hz and at <10 Hz there is a phase lead of 10–15°. Bode plots for EPSCs (filled circles) and EPSPs (open circles) in the same calyces were similar, indicating that the calyceal membrane did not add filtering in this frequency range at this stimulus level. This result is consistent with expression by striolar calyces of low-voltage-activated channels (next section), which decrease membrane filtering in the frequency range of <100 Hz.

By measuring contributions only at f₀ and neglecting the higher harmonics resulting from the skewed shapes of quantal EPSCs and EPSPs (Fig. 6B), our standard Bode analysis may underestimate gains and phase leads of EPSCs and EPSPs. Therefore, we also generated Bode plots of the measured heights and timing of EPSP peaks (Fig. 6C, open circles). The two methods yielded similar gain curves, but peak phases led f₀ phases by about 20° (an expected effect for sinusoidal fits at f₀ of positively skewed events). In computing the phase of spikes relative to EPSPs (next section), we use EPSP phases calculated in both ways.

In Figure 6D, the effect of synaptic mechanisms on response dynamics is revealed by referencing EPSC magnitude and phase to RP data from a type I hair cell matched for age, zone, stimulus level, and temperature. The frequency-dependent phase lag of EPSC relative to RP was well fit by a simple 3 ms delay (Fig. 6D, magenta curve), similar to the 4 ms value for the averaged step data in Figure 4B.3. For comparison, the gain and phase of nonquantal current data from the calyx of Figure 5C were also referenced to RP (cyan open circles; both gain curves are normalized to their peak values). In contrast to the quantal synaptic transfer function, the gain of the nonquantal synaptic transfer function increased with frequency and its phase never fell below zero, consistent with the very short synaptic delay at nonquantal synapses (Fig. 5A.2). The nonquantal and quantal synaptic transfer functions in Figure 6D were calculated with reference to the same type I RP data (chosen from the group characterized in Fig. 3C), but it is possible that the receptor potential input to nonquantal and quantal synapses differs systematically.

Calyceal spiking

K_LV currents, step-evoked firing patterns, and spike regularity

In isolated somata of primary vestibular afferents, the expression of low-voltage activated K⁺ (K_LV) currents is associated with a transient (onset) spike response to depolarizing current steps (Iwasaki et al., 2008; Kalluri et al., 2010). Blocking the K_LV channels converts the firing pattern from the transient response to sustained, highly regular firing, suggesting that K_LV channels are essential to the irregular afferent firing characteristic of striolar and canal central-zone afferents in vivo. This hypothesis is strengthened by recordings illustrated in Figure 7, taken from striolar calyces within several micrometers of the spike initiation zone (Lysakowski et al., 2011), which reveal K_LV currents (Fig. 7A), transient evoked firing patterns (Fig. 7B), and irregular spontaneous activity (Fig. 7C).

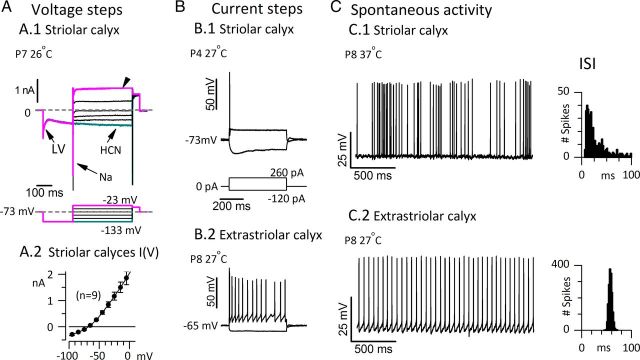
Figure 7.

Striolar calyces had low-voltage-activated K channels, transient firing patterns in response to current steps, and irregular interspike intervals. A.1, Voltage-dependent currents recorded in voltage-clamp mode from a striolar double calyx. A hyperpolarizing prepulse from the holding and resting potential of −73 mV (dashed lines) turned off a low-voltage-activated current (LV, fast decline in inward current) and activated HCN current (cyan, slow increase in inward current). Depolarizing steps activated transient Na⁺ current and a sustained outward current (arrowhead) carried by K_LV channels and likely others. R_m, 48 MΩ; C_m, 7.7 pF. A.2, Averaged I(V) relation, taken 100 ms after step onset, for nine striolar complex calyces: six double calyces (each enveloping 2 type I cells) and three triple calyces (each enveloping 3 type I cells). The slope resistance around the average zero-current potential (−69 mV) was 56 ± 2 MΩ, a low value consistent with the expression of LV and HCN channels, which are activated at resting potential. B, Current steps evoked different firing patterns depending on epithelial location. B.1, Transient (onset) firing in a striolar complex calyx. B.2, Sustained firing in an extrastriolar simple calyx (contacting 1 type I hair cell). C, Spontaneous spike timing was consistent with in vivo data specifying how timing varies with epithelial zone. C.1, A P8 striolar “quadruple” calyx (with 4 type I hair cells) was highly irregular. C.2, P8 extrastriolar simple calyx (same as in B.2) was highly regular. To simplify comparison of spike timing, we chose data with similar mean rates: 19.5 (striolar) and 19.0 (extrastriolar) spikes/s. Right, ISI distributions: coefficient of variation: 1.28 for the irregular striolar calyx, 0.05 for the regular extrastriolar calyx.

In voltage-clamp recordings from nine striolar complex calyces (6 doubles, 3 triples), stepping from −60 or −70 mV to −125 mV (Fig. 7A.1) deactivated a low-voltage-activated (LV) current and activated HCN currents (Meredith et al., 2012). The steady-state I(V) relation, averaged across the nine calyces in Figure 7A.2, had a mean zero-current potential near −70 mV and a mean slope resistance at ∼−70 mV of 50–60 MΩ, a relatively low value consistent with the activated state of many HCN and K_LV channels at resting potential. Depolarizing steps activated rapidly inactivating Na_V current and sustained K⁺ (arrowhead) current. In current-clamp mode (Fig. 7B.1), depolarizing steps evoked transient responses (single spikes at step onset) in all complex calyces (n = 19), half of the simple calyces located in the striola (5 of 10), and one-third of the simple calyces located in the extrastriola (4 of 12). Sustained, regular spiking was evoked in 5 of 10 striolar and 8 of 12 extrastriolar simple calyces (Fig. 7B.2). In total, 24 of 29 striolar calyces and only 4 of 12 extrastriolar calyces had transient firing patterns. Together these results are consistent with previously reported correlations between the striolar zone, irregular firing, and transient firing patterns (Goldberg, 1991, Kalluri et al., 2010).

At 25–29°C, spontaneous spiking occurred in just 1 of 19 complex striolar calyces recorded in current clamp. All 19 were capable of spiking, as revealed by injecting depolarizing current steps (Fig. 7B.1). Four of 10 simple striolar calyces fired spontaneously at 25–29°C. The five spontaneously firing striolar calyces (1 complex and 4 simple) were all from P7 or P8 animals, raising the possibility that spike activity increases with maturation. They had irregular interspike intervals (Table 2), like striolar afferents in vivo (for review, see Goldberg, 2000).

Table 2.

Variation in spike rate and regularity with temperature and epithelial zone

Zone	°C	n	Age, days	Spikes/s	CV	FF, spikes/s
Striola	25–29	5	7.4 ± 0.2	6.3 ± 2.1	1.14 ± 0.25	0.24 ± 0.06
Extrastriola	25–29	9	6.3 ± 0.2	15.3 ± 2.0, p < 0.014a	0.22 ± 0.08, p < 9.5e–4c	0.013 ± 0.008, p < 1.8e–4d
Striola	35–39	4	6.5 ± 0.9	19.8 ± 3.7, p < 0.013b	1.59 ± 0.53	0.14 ± 0.07

Relative to striolar afferent spike rates at 25–29°C, mean spike rates were significantly higher for extrastriolar afferents at 25–29°C^a and for striolar afferents at 35–39°C^b. CV^c and Fano factor (FF)^d were both significantly lower for extrastriolar afferents than for striolar afferents (comparison shown for 25–29°C).

In nine striolar calyces recorded at 35–37°C, three of seven complex calyces and two of two simple calyces fired spontaneously (Fig. 7C.1, Table 2). Comparison of mean firing rates for the samples recorded at 25–29 and 35–39°C yielded a Q₁₀ temperature coefficient of 3. As expected for striolar afferents in vivo, firing was irregular, and this was the case at both temperatures, with comparable coefficient of variation values (SD/mean) and Fano factors (variance/mean) [Fig. 7C.1, interspike interval (ISI) histogram; Table 2].

Relative to striolar calyces, extrastriolar calyces had significantly higher spontaneous rates and greater spike timing regularity at 25–29°C (Fig. 7C.2, ISI histogram; Table 2). The differences persisted when comparisons were made at similar spike rates, as illustrated by the examples in Figure 7C, suggesting that in vivo differences in spike regularity are preserved in our excised preparation. These differences may be related to frequency tuning if, as hypothesized (Sadeghi et al., 2007), spike regularity influences the frequency dependence of mutual information density in vestibular afferents.

Spike generation influences timing and tuning of afferent signals

Experiments in which vestibular afferents were driven with sinusoidal extracellular currents suggested that spike-generating mechanisms do not contribute to the differences in response dynamics of regular and irregular afferents (Goldberg et al., 1982; Goldberg, 2000). For stimuli coming through the hair cell, however, we find that spike generation influences response dynamics, as illustrated in Figure 8. Fig. 8A,B shows EPSPs and spikes evoked in one calyx by sinusoidal hair-bundle displacements. EPSPs and spikes occurred together in Fig. 8A.2,A.3; in Figure 8A.1, EPSPs were isolated by hyperpolarizing the membrane below spike threshold. EPSPs at <5 Hz and >40 Hz were present but subthreshold; as a result, the tuning of spikes was sharper than the tuning of EPSPs. Comparing the timing of spikes and EPSPs (Fig. 8B) shows that spikes can cross threshold (arrowheads) or even peak before EPSPs peak (cyan arrows), producing a phase advance.

Figure 8.

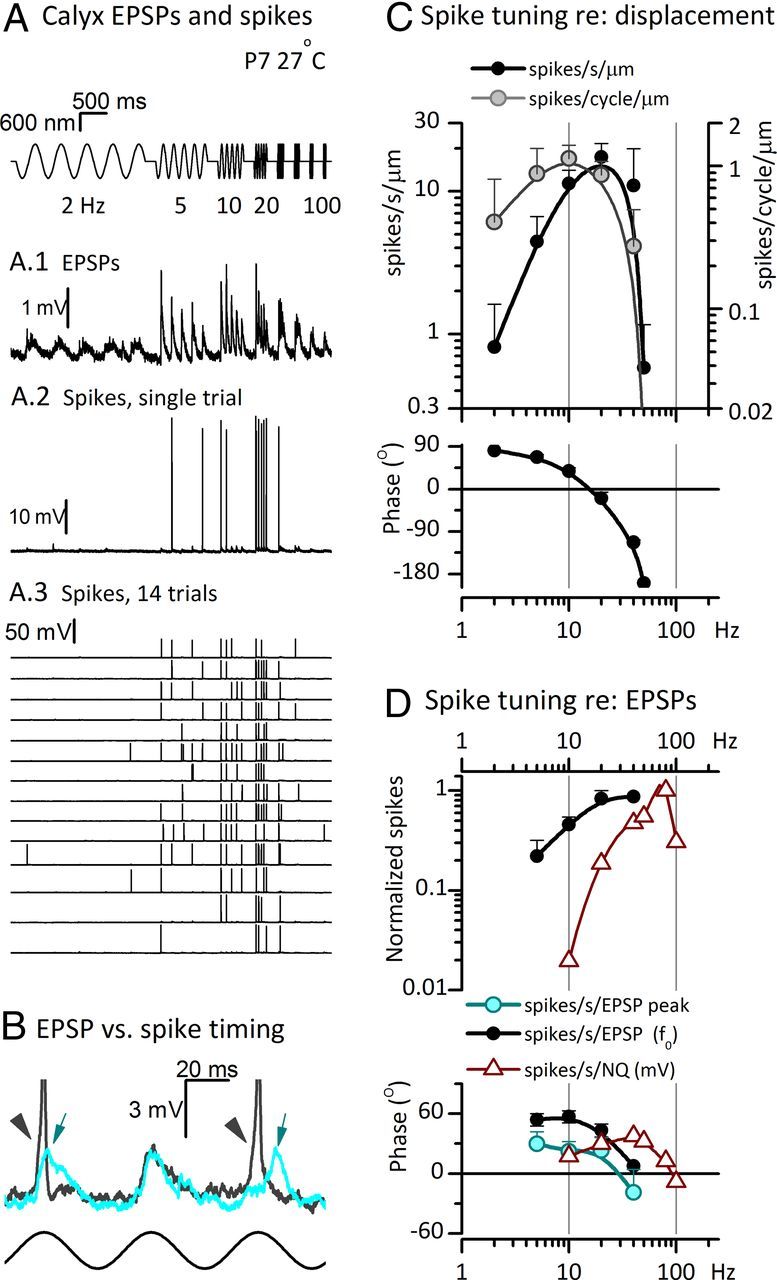
Spike generation sharpened tuning and increased phase lead (reduced latency) of the afferent signal. A, B, Current-clamp records from a striolar double calyx (P7, 27°C) during sinusoidal stimulation of one hair bundle. In sequence from the top are the ±600 nm stimulus, (A.1) EPSPs averaged from three sweeps obtained without spikes from a resting potential of −71 mV, (A.2) a single trace showing spiking from the same cell (which began when the cell spontaneously depolarized to −66 mV), (A.3) 14 sequential sweeps. Strong phase-locking produced near coincidence of spikes in different sweeps. The 20 Hz sinusoidal burst evoked the most spikes. B, Two sweeps of the 20 Hz response at high temporal resolution, showing both spikes and EPSPs. As shown by arrows, spikes often precede the peaks of EPSPs (i.e., spikes phase-lead EPSPs at 20 Hz). C, Gain and phase of spikes/cycle (gray circles) and spikes/second (black circles) referenced to bundle displacement expressed in micrometers. Averaged from five calyces, including the calyx in A. The number of spikes per cycle is more analogous to the sizes of RPs, EPSCs, and EPSPs plotted in Figures 3C and 6C; the number of spikes per second can be compared with in vivo afferent data. D, Transfer functions for spikes/second referenced to EPSPs for the quantal data in C (solid black) and for the nonquantal (NQ) data in Figure 5B (open brown triangles). By comparing spike rate with EPSPs, these plots show the additional tuning at the spike-generation stage; failure to trigger spikes at outlying frequencies significantly sharpens the spike-tuning curve. Bottom, Phase difference between spikes and EPSPs (spike phase minus EPSP phase), with EPSP phase measured in two ways for the quantal data: from the f₀ FFT component of EPSPs (black circles) or from the voltage peak (cyan circles; see B, arrows). Below 30 Hz, spikes had a substantial phase lead in either case, but the lead was smaller when peak EPSP was measured. For the nonquantal calyx in Figure 5B (open brown triangles), spikes held a phase lead relative to the f₀ component of nonquantal postsynaptic potentials up to higher frequencies (100 Hz).

The frequency dependence of calyceal spiking is shown in Figure 8C, with gain plotted either as spikes/cycle/micrometer or as spikes/second/micrometer. The number and phase of spikes relative to hair-bundle displacement were averaged across five calyces for ±300 nm displacements. The measurement of spikes/cycle is more analogous to the measures we used at earlier stages (I_met, RP, EPSC, and EPSP were all expressed as amplitude/cycle) but spikes/second is commonly used for in vivo afferent data. The direct comparison in Figure 8C illustrates how normalizing by time (spikes/second) rather than stimulus cycle shifts the curve toward higher frequencies. Phase angle (timing relative to the stimulus) is the same in both cases. The averaged phase angle was high at low frequencies (90° at 2 Hz) but fell steeply with frequency, crossing zero to become a phase lag above 20 Hz.

The transfer function between spike rate and EPSP amplitude (Fig. 8D, black circles), averaged over the same five calyces, directly shows the influence of spike-generating mechanisms. The tuning of gain by spike-generating mechanisms was stronger than can be shown because the ∼0 spike rate below 5 Hz and above 40 Hz (Fig. 8A.2,A.3) cannot be represented on the logarithmic axis. In phase plots of spikes associated with the f₀ component of EPSPs (bottom graph, black circles), spikes had a large phase lead (50° at 5 Hz). If spike times are instead compared with the times of EPSP peaks (cyan circles; Fig. 6C, cyan arrows), spikes have a smaller but still substantial phase advance of ∼30° at 5 Hz, indicating that spikes can trigger during the rising phase of EPSPs. Thus, quantal transmission and the spike generator both contribute to the large phase advance of afferent spiking at low stimulus frequencies (<40 Hz).

For comparison, Figure 8D includes (open triangles) the transfer function from postsynaptic potential to spike rate for the nonquantal synapse of Figure 5B. Spike rate was more sharply tuned and phase advanced relative to the nonquantal postsynaptic potential.

Summary of tuning in immature striolar type I cells and calyces at room temperature

Figure 9 summarizes the incremental loss of bandwidth as the mechanically evoked signal advances through the immature type I hair cell and calyceal terminal (25–29°C). Stimuli were ±600–1000 nm displacements of the hair bundle, the larger of the two sinusoidal levels used in this study. Figure 9A shows data from two exemplar cells, both striolar, P7, and recorded at 27°C: I_met and RP are from a striolar type I cell in a double calyx, and EPSCs, EPSPs, and spikes are from the double calyx also featured in Figure 4C. Figure 9B shows Bode plots of gain and phase of each signal referenced to the stimulus: calyceal data are from the exemplar calyx in A and the I_met and RP data are averaged data from several cells (replotted from Figs. 2F and 3C, respectively).

Figure 9.

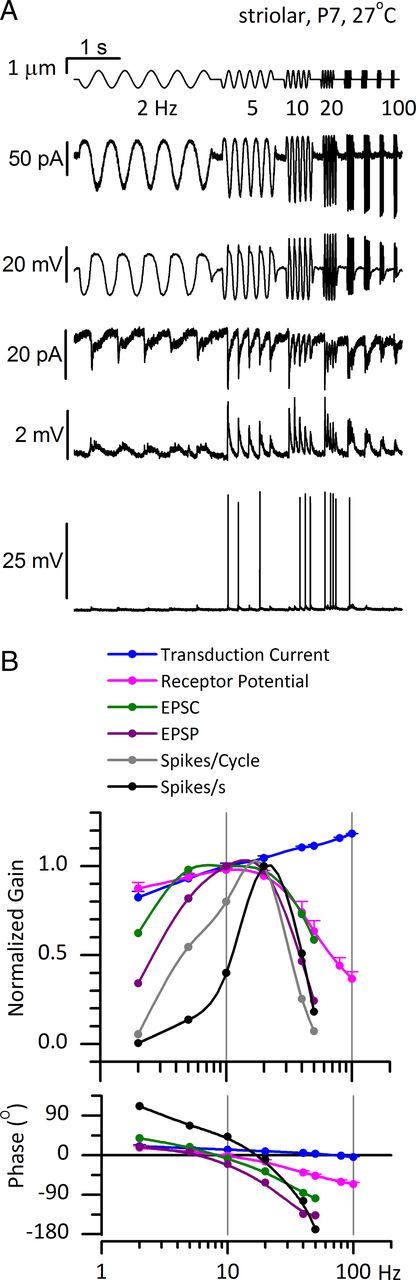
Summary of tuning by type I hair cells and calyces in the rat saccular epithelium (P2–P9) for ±600–1000 nm stimuli at 25–29°C. Gains are normalized by the peak response. The type I cell data summarized here were immature in that they lacked the signature conductance of mature type I cells, g_K,L (Fig. 10). Tuning got progressively sharper as the signal advanced from the transduction channels to the afferent spike generator. A, Exemplar responses to sinusoidal bursts are aligned for a type I hair cell from a complex calyx (I_met and RP) and for a double calyx (EPSCs, EPSPs, and spikes); both cells were from P7 striolar zones and recorded at 27°C. From top to bottom: Sinusoidal bursts (2, 5, 10, 20, 40, 50, 80, and 100 Hz), I_met, RP, EPSCs, EPSPs, and spikes. B, Response gain and phase referenced to bundle displacement. Hair-cell data (I_met, RP) are the same averaged data shown in Figure 3C. Calyx data (EPSC, EPSP, spikes/cycle, and spikes/second) are from the exemplar calyx of A. FFTs were used to calculate gains and phases at each stage except spiking.

Best frequencies at each stage are between 10 and 50 Hz. Low-frequency gain and phase are strongly influenced by transducer adaptation, synapse adaptation, and spike generation. High-frequency gain and phase are strongly influenced by the hair-cell membrane charging time (τ_m) and the delay across the synapse. For these relatively large stimuli, a single-pole filter with a corner frequency of (½πτ_m) closely approximates the transfer function of RP relative to I_met; recall that smaller stimuli excite electrical resonance in the immature hair-cell membrane (Fig. 3), which sharpens RP tuning. A progressive phase lag accumulates at high frequencies. The phase lag of EPSCs relative to RP suggests a 3 ms synaptic delay (Fig. 6D). In this exemplar calyx, the quantal response was prominent (Fig. 9A), and the timing data (Fig. 4C.4, step latencies; Fig. 9B, phase data) suggest that any nonquantal component was not significant.

Maturation and physiological temperature affect tuning and timing of the receptor potential

The strong low-pass filtering of the receptor potential by the membrane of immature type I hair cells depends on their high input resistances. It is well known, however, that as type I cells mature, they acquire large numbers of low-voltage-activated K channels, collectively called g_K,L, which reduce R_in and electrical tuning (Correia and Lang, 1990; subsequent publications are reviewed in Eatock and Songer, 2011). In this section we show how g_K,L changed hair-cell tuning and timing.

Striolar type I hair cells in the rat saccule gradually acquire g_K,L with age, as previously described for the utricles of mice (Rüsch et al., 1998; Géléoc et al., 2004) and rats (Hurley et al., 2006). Figure 10 compares voltage-gated currents (A) and conductance–voltage curves (B) in exemplar P2 and P7–P8 striolar type I cells at 25–29°C (“27°C”) and 35–39°C (“37°C”). P7–P8 cells had a large conductance (g_K,L) at the holding potential of −65 mV, which was deactivated by stepping to −125 mV, then reactivated with steps positive to −100 mV (Fig. 10A). In contrast, the K⁺ conductance of P2 cells activated positive to resting potential and was much smaller (Fig. 10A). G(V) curves in Figure 10B illustrate the large difference in steady-state activation ranges and maximum conductance at the two ages. Between P3 and P9, the average half-activation value in a sample of 63 striolar type I cells fell from ∼−30 to ∼−70 mV and g_max tripled. Table 3 shows strong effects of age (P2–P4 vs P7–P9) on activation midpoint, maximal conductance, and activation kinetics, which is accounted for by the acquisition of g_K,L.

Table 3.

Changes in electrophysiological parameters of striolar type I hair cells with age and temperature

Temperature	t test	Membrane properties				Boltzmann parameters of activation						τK, −35 mV (ms)
		Rm (MΩ)		Cm (pF)		V1/2 (mV)		gK (nS), −35 mV		S (mV)
		P1–P4	P7–P9	P1–P4	P7–P9	P1–P4	P7–P9	P1–P4	P7–P9	P1–P4	P7–P9	P1–P4	P7–P9
27°C		899 ± 202 (16)	294 ± 100 (17)	7.7 ± 0.2 (16)	7.3 ± 0.5 (17)	−35 ± 2 (27)	−63 ± 4 (19)	16 ± 1 (27)	35 ± 5 (19)	9.4 ± 0.4 (27)	8.2 ± 0.5 (19)	23 ± 1 (27)	17 ± 1 (19)
	Age effect, p value	<0.01a		NS		<1e–8b		<4e–4c		NS		<0.01d
37°C		570 ± 128 (7)	54 ± 17 (5)	8.3 ± 0.3 (7)	8.9 ± 0.2 (2)	−39 ± 4 (9)	−62 ± 5 (8)	17 ± 1 (9)	39 ± 9 (8)	9.3 ± 0.5 (9)	7.8 ± 0.4 (8)	14 ± 2 (9)	10 ± 2 (8)
	Age effect, p value	<0.02a		NS		<7e–3b		<0.01c		NS		NS
	Temperature effect	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	<4e–3e	<0.05

Significance was tested with one-way ANOVA; differences were considered significant at p < 0.05 and are provided when significant. NS, not significant. The reduced R_m^a, more negative V_1/2^b, increased maximum g_K^c, and decreased activation time course of outward current at −35 mV (τ_K)^d of P4–P7 cells reflect the increased expression of g_K,L. Increasing temperature also decreased τ_K^e.

Figure 10 also shows the effect of increasing temperature on activation of outward currents, as illustrated with activation curves (Fig. 10B, Table 3) and activation time course (Fig. 10C, Table 3). In contrast to a previous report on mouse utricular type I hair cells (Rüsch and Eatock, 1996), we found no significant temperature-induced shift in steady-state activation at either age. In the previous study, individual cells were followed as temperature was shifted, whereas we are comparing two populations held at different temperatures. Monoexponential fits of the current evoked by a step from −125 to −35 mV yielded activation time constants (τ_K) with mean values that decreased at higher temperatures (Fig. 10C) with a thermal coefficient of 1.6–1.7 (calculated from values in Table 3).

Adding g_K,L and increasing temperature had a dramatic combined effect on receptor potentials, as illustrated in Figure 10D for one type I cell responding to sinusoidal displacements. The RP was much smaller and less tuned than for type I cells lacking g_K,L and at 27°C (Fig. 3A). These effects are quantified and averaged across several cells in Bode plots (Fig. 10E). Striolar type I cells without g_K,L at 25–29°C (blue filled circles) had larger gains than striolar type I cells with g_K,L at mammalian temperature (red triangles) and had much larger phase lags above 2 Hz. Thus, the combination of higher temperature and g_K,L flattened tuning and strongly increased phase over most of the frequency range. A significant effect of g_K,L alone is predicted by its well known effect on low-pass corner frequency (Correia et al., 1996), and individual examples support this prediction. In Figure 10E, data from two cells at the same temperature (27°C), one with g_K,L (cyan triangles) and one without g_K,L (blue open circles), suggest that g_K,L may decrease gain ∼5-fold and increase the low-pass corner frequency ∼10-fold. Cells with g_K,L also, as expected, lacked electrical resonance (data not shown).

Thus, by inserting many low-voltage-activated channels in its membrane, the developing type I hair cell sacrifices gain and sharpness of electrical tuning in return for faster timing. This maturational specialization is consistent with the known emphasis of striolar and central zones of vestibular epithelia on phasic signals and high conduction velocity (Goldberg, 1991).

Discussion

In immature saccular epithelia, tuning was typically centered between 10 and 50 Hz and sharpened at each afferent stage (Fig. 9). Electrical tuning was a prominent feature of the receptor potential at small stimulus levels (Fig. 3). Thus, immature vestibular hair cells, like immature cochlear hair cells (Kennedy, 2012), have mechanisms to amplify small mechanoelectrical signals at early stages of development. With maturation, type I cells lose gain but add bandwidth and speed, possibly reflecting a need to supply fast, linear representations of head motions to reflex pathways.

VORs can have near ideal performance over a wide frequency range. For head-motion frequencies from <5 to ≥25 Hz, the angular VOR has a gain (eye motion per head motion) near 1 and phase near zero (Huterer and Cullen, 2002). This reflex pathway involves four synapses from hair cell to ocular muscle. The flat frequency performance of the reflex requires that neurobiological mechanisms introduce phase leads to compensate for phase lags incurred by conduction and transmission times along the pathway. We have identified several inner-ear mechanisms that advance response phase: adaptation of mechanoelectrical transduction, addition of K_LV channels to the hair-cell membrane, nonquantal transmission, and spike generation in the primary afferent terminal. Although the angular VOR is mediated by semicircular canals, our saccular data are relevant given the striking morphological and physiological parallels between canals and otolith organs (Goldberg, 1991; Eatock and Songer, 2011). In vivo data from mature vestibular afferents (Hullar et al., 2005; Ramachandran and Lisberger, 2006; Lasker et al., 2008) show high-pass filtering for frequencies up to 20 Hz or more, which is qualitatively consistent with our data. Maturational changes in the calyx may further enhance response speed: striolar calyces, like type I hair cells, add K_LV channels past the first postnatal week (Hurley et al., 2006; Kalluri et al., 2010).

Mechanoelectrical adaptation

In mammalian cochlear hair cells, reducing external Ca²⁺ from perilymph levels (millimolar) to the low levels in mature cochlear endolymph (20 μm) doubled adaptation time constants (Beurg et al., 2010). The smaller difference between mature vestibular endolymphatic levels [∼200–250 μm (Sterkers et al., 1988)] and our external Ca²⁺ (1.3 mm) should have a smaller impact on adaptation time constants. These considerations and our results suggest that, at physiological Ca²⁺ and body temperature, transducer adaptation in mammalian vestibular hair cells may have time constants of 50–100 and 5–10 ms, with corresponding high-pass corner frequencies of 1–3 and 15–30 Hz, well positioned to influence vestibular signals. An important effect of adaptation is the phase lead in I_met relative to bundle displacement at frequencies of <100 Hz (35−39°C).

Voltage responses of striolar type I hair cells

Frog saccular and turtle cochlear hair cells have high-quality electrical resonances that support tuning to vibrations and sound, respectively (Art and Fettiplace, 1987; Hudspeth and Lewis, 1988; Catacuzzeno et al., 2004). Here we report that immature striolar type I cells from the rat saccule also have sharp (Q_e > 5) electrical tuning matched to the mechanical tuning of the receptor potential (Fig. 3). Like other immature hair cells in rodents (Rüsch and Eatock, 1997; Marcotti et al., 2003; Géléoc et al., 2004; Wooltorton et al., 2007), immature striolar type I cells of the rat saccule have sizeable Na_V conductances (Fig. 10A), which may contribute to electrical tuning or spiking, as in cochlear hair cells (Marcotti et al., 2003). The enhanced excitability of immature hair cells is thought to drive development of the immature auditory and vestibular systems (Kennedy, 2012). In preparation for mature function, neonatal striolar type I hair cells lose Na_V channels (Géléoc et al., 2004; Wooltorton et al., 2007) and gain g_K,L (Fig. 10) and consequently are no longer electrically resonant. The impact of g_K,L on tuning and timing of the RP is expected to be felt at downstream stages, but this remains to be demonstrated.

K_LV channels in neurons reduce response times (Rothman and Manis, 2003), but the rationale for g_K,L in vestibular hair cells has not been clear. If most head-motion energy is at frequencies <10 Hz, membrane-charging times in hair cells without g_K,L (type II cells) should suffice. Why add g_K,L and suffer the reduced gain? The answer may be that natural stimuli do include frequencies well above 10 Hz (Armand and Minor, 2001). Otolith striolar afferents respond to bone vibrations (Curthoys and Vulovic, 2011), phase-lock to acoustic tones at hundreds of hertz (McCue and Guinan, 1994), and have remarkably short acoustic latencies, as discussed in the next section. These capabilities may require the improvement in RP response time that accompanies g_K,L (Fig. 10E).

Synaptic transmission

The envelopment of type I hair cells by the vestibular calyx has long prompted interest in the possibility of nonquantal transmission. Given the abundant evidence for quantal transmission at these synapses (e.g., Lysakowski and Goldberg, 1997, Schessel et al., 1991; Bonsacquet et al., 2006; Rennie and Streeter, 2006; Dulon et al., 2009), any nonquantal transmission must coexist with quantal mechanisms. We provide evidence for both. The graded responses illustrated in Figure 5 are unlikely to reflect the summation of quanta, based on their short latencies, the absence of individual quanta, and hyperpolarizing responses to negative bundle deflections.

The mechanism of nonquantal transmission is not known. Fluorescent dye did not pass between hair cell and calyx in our experiments, consistent with earlier evidence that gap junctions are not involved (Gulley and Bagger-Sjöbäck, 1979; Ginzberg, 1984; Yamashita and Ohmori, 1991). Pharmacological experiments on turtle crista afferents suggest that only a minor component of nonquantal activity is attributable to glutamate accumulation (Holt et al., 2007). Other possibilities include ephaptic transmission and K⁺ changes in the synaptic cleft (Goldberg, 1996; Lim et al., 2011; Contini et al., 2012).

In recordings from afferent fibers at sites distant from the terminals and stimulated by cupular motion (Holt et al., 2007), quantal and nonquantal components occur together, but might arise at different afferent terminals. Our methods revealed that nonquantal responses alone can trigger spikes (Fig. 5B) and that both quantal and nonquantal components can be present within individual calyces (Fig. 5C). Given that an individual calyx can generate both kinds of responses, the difference in transmission modes may have a presynaptic origin, such as a difference in hair-cell ion channels. Type I hair cells may acquire g_K,L channels (Fig. 10) at different rates or differentially express BK (big potassium) channels (Schweizer et al., 2009). Nonquantal transmission could be an immature property in our tissue but it also occurs in more mature calyx-bearing afferents of turtles (Holt et al., 2007) and chicks (Yamashita and Ohmori, 1990).

Nonquantal transmission may reduce response latency (Figs. 5, 6D). Quantal synaptic delays, which averaged 3–4 ms at 27°C (Figs. 4B, 8D), are likely to be much reduced at body temperature and following maturation, as demonstrated at other synapses (Wang et al., 2009). Nevertheless, for striolar afferents in the cat saccular nerve, estimated synaptic delays to loud acoustic clicks (∼300 μs; McCue and Guinan, 1994) are even shorter than cochlear delays, leading McCue and Guinan (1994) to speculate that transmission at the type I-calyx synapse is electrical (i.e., nonquantal). While nonquantal transmission is fast, quantal transmission affords amplification via biochemical cascades, one-way directionality, and tuning (amplification at frequencies of interest) (Schnee et al., 2005; Rutherford and Roberts, 2006). Having both mechanisms could make calyceal transmission more versatile through differences in their level and frequency dependence or in their sensitivity to transmitters released from efferent terminals on calyces.

Afferent spiking

Differences in response dynamics of striolar and extrastriolar afferents (Goldberg et al., 1990a) have previously been attributed to mechanical and hair-cell stages, whereas differences in spike timing were attributed to afferent properties (Goldberg, 2000). We observed, however, that postsynaptic spike-generating mechanisms in the afferent sharpened tuning and enhanced phase leads relative to EPSPs. Thus, differences in ion-channel expression between central-zone and peripheral-zone calyces (Lysakowski et al., 2011) may contribute to zonal differences in afferent response dynamics.

The phase leads of afferent spikes relative to bundle displacement plateaued near +80° at 2 Hz (Fig. 8C), higher than phase leads (∼45°) of vestibular afferents relative to head motion at 2 Hz (Goldberg et al., 1990b; Lasker et al., 2008). Factors in this difference might include the transformation from head motion to bundle deflection and differences in developmental stage and Ca²⁺ levels.

Recordings from isolated parent cell bodies of vestibular afferents suggested that the irregular firing of striolar afferents requires K_LV channels (Kalluri et al., 2010); this hypothesis assumed that ion channels in the cell bodies resemble those at spike initiation zones in distal afferent terminals. In the striola, spiking is likely to initiate at the afferent heminode immediately below the calyx, and both the calyx and heminodes are strongly immunoreactive for K_LV subunits from the K_V1 and K_V7 channel families (Lysakowski et al., 2011). Our evidence for K_LV current and irregular spiking in striolar calyces (Fig. 7) strengthens the evidence linking striolar irregular spike timing to K_LV channel expression.