Causal Inference in Occupational Epidemiology: Accounting for the Healthy Worker Effect by Using Structural Nested Models

Abstract

In a recent issue of the Journal, Kirkeleit et al. (Am J Epidemiol. 2013;177(11):1218–1224) provided empirical evidence for the potential of the healthy worker effect in a large cohort of Norwegian workers across a range of occupations. In this commentary, we provide some historical context, define the healthy worker effect by using causal diagrams, and use simulated data to illustrate how structural nested models can be used to estimate exposure effects while accounting for the healthy worker survivor effect in 4 simple steps. We provide technical details and annotated SAS software (SAS Institute, Inc., Cary, North Carolina) code corresponding to the example analysis in the Web Appendices, available at http://aje.oxfordjournals.org/.

Mortality rates in occupational cohorts have long been observed to differ from those in the general population (1, 2). Comparisons of mortality rates in occupational cohorts with those observed in the general population to estimate the effects of occupational exposures are subject to what has been termed the “healthy worker effect.” Kirkeleit et al. (3) assessed the potential for the healthy worker effect in a large cohort of Norwegian workers. In this commentary, we provide some background on the concept, define it by using causal diagrams, and provide a simplified example of how to use methods aimed at resolving the problems it poses for occupational epidemiologists, as we (4) and others (5) have recently demonstrated.

Since the mid-1970s, a number of studies have suggested that the healthy worker effect was composed of at least the following 2 distinct processes: the selection of healthy individuals into the workplace and the early termination of workers with poor prognosis (6–9). The former process, known as the healthy worker selection effect (or healthy hire effect), is the focus of the work by Kirkeleit et al. As noted by the authors, this component of the healthy worker effect can be classified as confounding of the exposure-outcome relationship due to work status at study entry (3, p. 1223). It is for this reason that many occupational cohort studies rely on internal referent groups to estimate exposure effects among workers with different exposure levels (9, p. 86). The latter process, known as the healthy worker survivor effect, poses more difficult problems for estimating the effect of an occupational exposure on a given outcome.

Although recognized for more than 40 years, only a few strategies exist that are meant to address the healthy worker survivor effect. Two of these arose in the late 1970s and are commonly encountered as ostensible solutions to the problem (1, 10, 11). In 1976, Fox and Collier (6) argued that doing their analysis in the subcohort of individuals who were alive 15 years after study entry stratified by work status would minimize the selection effect and significantly reduce the survivor effect (6, p. 228). Gilbert and Marks (12) proposed a related approach in 1979 by using regression adjustment for work status.

A few years later, exposure lagging was informally proposed as a solution to the healthy worker survivor effect (13). With this method, recent exposures are ignored because exposures nearest to the event could only have been acquired by the “survivors” who are at the root of the healthy worker survivor effect (11). Thus, it was thought that discarding exposure information from the survivors can put those who survive longer on a more equal exposure footing with those who do not survive as long.

In a seminal paper, Robins (8) was the first to show a fundamental problem with each of these approaches. Over time, for a deleterious exposure, individuals more susceptible to the outcome leave the workplace and are thus removed prematurely from exposure in part because of their exposure history. Yet work status is also related to subsequent exposure status; once an individual has left work, there is often no chance of incurring subsequent work-based exposures. Because of this feedback between exposure and work status, the healthy worker survivor effect is not amenable to solutions involving regression adjustment, stratification, or restriction (8). In this commentary, we use causal diagrams (14, 15) to show how the healthy worker survivor effect is an example of a more general type of bias, known as time-varying confounding affected by prior exposure (henceforth, time-varying confounding). We briefly discuss a commonly used method to deal with this type of bias (inverse probability-weighted marginal structural models) and show why it is not generally applicable to the problem encountered in the healthy worker survivor effect. Finally, we illustrate the use of G-estimation of a structural nested failure time model in a simple simulated example and include detailed SAS software (SAS Institute, Inc., Cary, North Carolina) code for implementing the procedure (Web Appendix 2, available at http://aje.oxfordjournals.org/).

CAUSAL DIAGRAMS

Figure 1 is a causal diagram representing the healthy worker effect. The graph should be read from left to right, indicating the passage of time. For simplicity, we let the subscripts denote time (e.g., year) on study for a hypothetical 2-year occupational cohort study. For an observation at time m ∈ {0,1}, we let W₀ denote an indicator of baseline work status and X_m denote an occupational exposure under study. W₁ represents work status at time 1. For example, W₁ can be a binary indicator of employment status or the time since hire (e.g., in years) for an observation at time 1. We let T represent the survival time for the event under study. Finally, U represents some unmeasured common cause (or causes) of work status and survival time that can be a time-varying or time-fixed scalar (or a vector of time-varying and/or time-fixed components). For example, U can represent unmeasured smoking status and/or some latent measurement of individual prognosis. Figure 1 is a simplified representation of the healthy worker effect. Other diagrams with identical ramifications have been outlined in the literature (15, 16).

Figure 1.

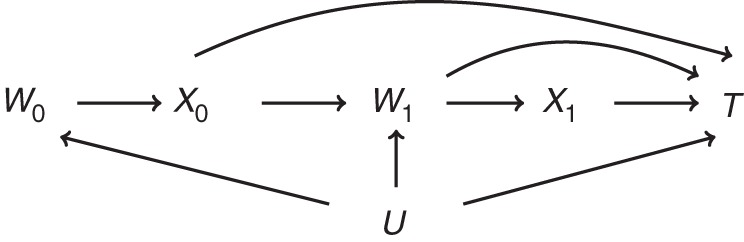
Simplified causal diagram representing the healthy worker effect. W₀, work status at baseline; X₀, exposure status at baseline; W₁, work status at time 1; X₁, exposure status at time 1; T, time to event; U, unmeasured variable.

The use of an internal referent population is equivalent to restricting the analysis to W₀ = 1, which blocks the biasing path X₀ ← W₀ ← U → T and thus resolves the problem posed by the healthy worker selection effect. However, because work status W₁ is both a mediator and a collider on the path from X₀ to T, any method that involves conditioning (e.g., regression adjustment, stratification) on work status W₁ to estimate the magnitude of the arrows in Figure 1 emanating from (X₀, X₁) creates 2 problems. First, it may induce collider-stratification bias by creating a noncausal association between prior exposure X₀ and the survival time T through the path X₀ → W₁ ← U → T (15, 17, 18). Second, it will block any indirect effect of X₀ on T via W₁. However, not adjusting for work status results in a biased path between subsequent exposure X₁ and the survival time T through the path X₁ ← W₁ ← U → T and, thus, a confounded exposure-effect estimate. Were this the only issue encountered in the healthy worker survivor effect, it could easily be resolved with inverse probability-weighted marginal structural models (MSMs) (19, 20). However, as we explain in the next section, because individuals who leave work have no chance of incurring subsequent work-based exposure, inverse probability-weighted MSMs are not a tenable solution for the healhty worker survivor effect (20). Instead, structural nested models can be used. In the remainder of this commentary, we use simulated data generated from Figure 1 for 2 time points to illustrate the problem of using MSMs to address the healthy worker survivor effect, and we show how structural nested models can be used to account for this bias.

We generated 3,000 observations following Figure 1 by using the algorithm outlined by Young et al. (21) for 2 time points. For each observation i, generate the potential survival time under no exposure 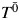from an exponential distribution with a rate parameter λ = 5. For time point 0, W₀ = 1 for all individuals, and X₀ was generated from a Bernoulli distribution with

For time point 1, W₁ was generated from a Bernoulli distribution with

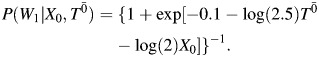X₁ was generated from a Bernoulli distribution with

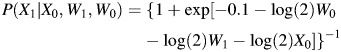if W₁ = 1 and was set to 0 if W₁ = 0. Finally, we let the observed survival time T be minimum of 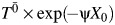(corresponding to an event that would have occurred at t < 1 under the observed exposure), 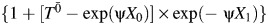(corresponding to an event that would have occurred at 1 ≤ t < 2 under the observed exposure), or 2 (corresponding to administrative censoring at t = 2).

Table 1 shows the data for 3 observations generated by using this approach. In these data, X₀, X₁, and T are as explained previously; W_m is a binary indicator of whether observation i was classified as employed during time m; Y is an event indicator equal to 0 if the observation was administratively censored at the second time point. We use these data to give context to our discussion of causal inference and the use of marginal structural and structural nested models in occupational cohort studies.

Table 1.

Three Observations From the Simulated Example Data (n = 3,000)

ID	W1a	X0b	X1c	Td	Ye
10	0	1		0.645	1
32	1	1	1	1.758	1
359	1	0	1	1.908	1

Abbreviation: ID, observation-level identifier.

^a W₁ represents work status at time 1.

^b X₀ represents exposure status at time 0.

^c X₁ represents exposure status at time 1.

^d T represents observed survival time.

^e Y represents event indicator.

Causal effects are usually defined in terms of potential outcomes, often denoted 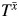, where 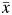denotes exposure history. In our simulated setting, 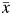can take on 1 of the following 4 distinct values: (0, 0), (0, 1), (1, 0), or (1, 1). 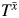thus represents the survival time that would have been observed under exposure 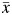(22). Several identifiability assumptions are required to use empirical data to estimate quantities reflecting potential outcomes. These include treatment variation irrelevance (23), positivity (24), noninterference (25), and conditional exchangeability (26). Treatment variation irrelevance (also known as counterfactual consistency) requires that an individual's observed outcome be the potential outcome the individual would have had under the observed exposure. For a binary exposure, positivity requires exposed and unexposed individuals in all confounder strata at all time points. Noninterference requires that an individual's potential outcome does not depend on another individual's exposure status. The conditional exchangeability assumption is also known as the sequential ignorability assumption (27) and the condition of no unmeasured confounding (28).

In the presence of confounding, an individual's exposure status is predictive of his or her outcome irrespective of the exposure's actual effect on the outcome. When there is no measured or unmeasured confounding, an individual's exposure status is independent of his or her baseline prognosis (or potential outcome). Thus, under no measured or unmeasured confounding, the coefficient for the potential outcome in a regression model for the exposure will be equal to 0. For example, when fitting the model

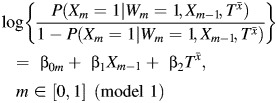to our simulated data, a statistical test of the hypothesis that β₂ = 0 will fail to reject if W_m is the only confounder. Of course, we never have data on 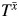. However, we outline below how relevant information in 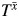can be obtained by using structural nested models when the aforementioned identifiability assumptions hold.

Importantly, identifiability assumptions, including conditional exchangeability, are not a unique requirement of a particular set of methods. Rather, the assumptions must hold for any statistical model parameter to correspond to a causal exposure contrast. Indeed, the array of methods available to epidemiologists (e.g., randomization, regression, standardization, matching, propensity score methods, instrumental variables) are meant, in large part, to satisfy the conditional exchangeability assumption. To interpret model parameters as policy-relevant (i.e., causal) effects, epidemiologists must (when applicable) collect information on a sufficient set of confounders and use methods that can properly adjust for these confounders to render conditional exchangeability as close to true as possible. For occupational epidemiologists, this means collecting sufficient information on relevant confounders (including time-varying work status) and using methods that can account for the time-varying confounding that characterizes the healthy worker survivor effect.

MARGINAL STRUCTURAL MODELS

Marginal structural models (fit by inverse probability weights) are often used for dealing with time-varying confounding. As in other forms of standardization to control confounding, these models estimate exposure effects in a “pseudo-population” obtained by weighting the observed data by the inverse of the probability of the observed exposure conditional on measured confounders (19, 20). If the set of measured confounders is sufficient to adjust for confounding, the conditional exchangeability assumption is met in the pseudo-population created by weighting.

To fit these models to our simulated data would require an estimate of the probability of exposure conditional on work status at time 1. However, as can be seen in Table 2, in the stratum of observations of those who left work at time 1, there are no exposed individuals. Thus, the probability of being exposed is 0, and the inverse probability weight (being 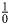) is undefined. This problem, known as a violation of the positivity assumption, is the reason that “MSMs should not be used in occupational cohort studies” (20, p. 557). Despite their inability to account for time-varying confounding under positivity violations (20, 29, 30), studies have been conducted in which inverse probability-weighted MSMs were used to try to account for the healthy worker survivor effect (31, 32). Other estimation methods for marginal structural models exist that, in principle, may be used to account for the healthy worker survivor effect. These include general MSMs (33) or MSMs estimated by using the G formula (34). This latter class of MSMs has been used to estimate the effect of hypothetical interventions on permissible asbestos exposure levels in a cohort of textile factory workers in the United States (35).

Table 2.

Contingency Table of Work Status by Exposure Status

Work Statusa	Exposure Status
	Time 0		Time 1
	Unexposed	Exposed	Unexposed	Exposed	Total
Left work			693	0	693
At work	927	2,073	285	2,022	5,307
Total	927	2,073	978	2,022	6,000

^a All individuals at work at time 0.

STRUCTURAL NESTED MODELS

In the absence of positivity, structural nested accelerated failure time (AFT) models are a useful alternative to estimate effects of occupational exposures (4, 5). Parameters for these models are estimated by using G-estimation. Joffe (29) reviewed a number of strengths and limitations of this approach compared with more common MSMs. These include the fact that structural nested models can estimate interactions between 2 or more time-varying covariates (whereas MSMs are limited to estimating interactions between a time-varying and time-fixed covariates). Additionally, G-estimation can be used when the set of measured confounders is sufficient to render exchangeability true, even if only in a subset of the person-time under study. Thus, with G-estimation, one can restrict estimation to the subset of at-work person-time, whereas the structural nested model itself specifies the relationship between the exposure and survival time over all available person-time. For this reason, structural nested AFT models can be used to account for the healthy worker survivor effect.

Generally, structural nested AFT models are a mapping between the failure time that would have been observed under no exposure 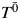, the failure time that would have been observed under some arbitrary exposure 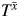, and some unknown parameter ψ: 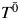= h(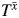, ψ) (36). This mapping is most often of the form

where X(t) = X₀ for t < 1 and X(t) = X₁ for 1 ≤ t < 2, and where {X₀, X₁} denote the observed exposures and, thus, (by treatment variation irrelevance) T is the observed outcome. This single equation cannot be solved because there are 2 unknowns, 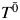and ψ. However, if we assume that the measured confounders are sufficient to adjust for all confounding, then, by the definition of conditional exchangeability provided in model 1, we know that the exposure X_m is independent of the potential outcomes 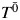. With this second equation (model 1), and 1 last issue to address, we can solve for ψ. The last issue is known as artificial censoring.

To estimate parameters for structural nested models (as explained below), we use the observed survival time T and the observed exposure X to impute the unknown potential outcome 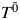. Yet, because of administrative censoring (due to the end of follow-up), not all survival times will be observed. This results in a bias that must be accounted for by artificially censoring some individuals whose event times were observed. To make our explanation concrete, we illustrate the implementation of structural nested AFT models in 4 steps by using the 3 observations from our simulated data listed in Table 1. These 4 steps can be summarized as follows:

1. Define 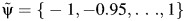, a set of candidate ψ values likely to include the true value of ψ and its 95% confidence intervals.

2. For each value in the set defined by 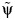, impute 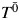by using the structural nested model. To make the dependence of the imputed potential outcome on 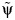clear, we denote it as .

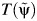3. Artificially censor the imputed potential outcomes to obtain a Δ indicator, defined as 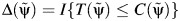, where I{•} is the indicator function, which takes a value of 1 if {•} is true (0 otherwise), and 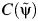is the artificial censoring time defined in Web Appendix 1.

4. Use model 1 to test whether 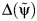(instead of T^x) is independent of the exposure. The value of 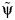that renders the Z statistic for β₂ in model 1 equal to 0 is selected as the parameter estimate .

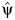This method of estimating the parameter of a structural nested AFT model is known as the grid-search method. This approach is subject to limitations, and alternative options are available, which we discuss in Web Appendix 1. By using the grid-search method, we obtain confidence intervals for 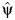by 1) computing the standard error as 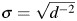, where d is the slope of a local linear regression of 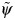on the Z statistic for the parameter in model 1 (37); 2) assuming the Z statistic for the parameter in model 1 follows a standard normal distribution and choosing the values of 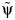that correspond to Z-statistic values of ±1.96 for upper and lower 95% confidence intervals (38); or 3) implementing the bootstrap (39). In Web Appendix 1, we provide a detailed procedure on how to implement these steps in our example data. In Web Appendix 2, we provide the annotated SAS software (SAS Institute, Inc.) code used to generate the example data and to implement each of these steps.

INTERPRETATION

After carrying out steps 1–4 (detailed in Web Appendix 1), we obtain a Z statistic for the test that β₂ = 0 (as outlined in step 4 above) for each of the candidate values in the set 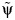, which are plotted in Figure 2. These Z statistics cross 0 on the y-axis at the point estimate value of 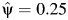. We obtain 95% slope-based confidence intervals with lower and upper bounds of 0.08 and 0.42, respectively. Taking 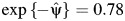(95% slope-based confidence interval: 0.65, 0.92) gives a relative time (or survival time ratio) for the effect of exposure on survival time. This number can be interpreted as the ratio of the survival time that would have been observed under exposure at all time points (always exposed) relative to the survival time that would have been observed under no exposure at any time point (never exposed). Thus, in our simulated setting, we would say that being exposed at both time points decreases survival by (1 − 0.78) × 100 = 22.0% relative to being unexposed at both time points.

Figure 2.

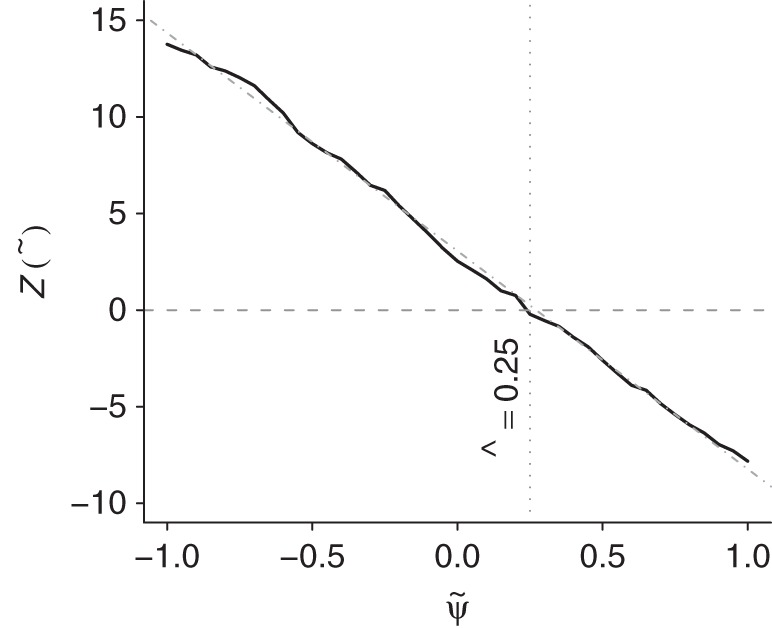
Plot of the test statistic 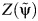by 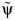obtained by using 3,000 simulated observations from the example data set. The horizontal dashed line represents 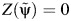; the vertical dotted line represents 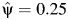; and the diagonal dashed-dotted line represents slope of a linear regression of 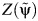on .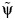

In occupational epidemiology, the contrast of always exposed versus never exposed may not always be realistic. Often, only a very small proportion of person-time in an occupational cohort study is classified as “at work.” An alternative approach would be to estimate a contrast corresponding to “exposed in the first m years” relative to “never exposed.” Details on how to do this are available in the literature (5, Web Appendix).

CONCLUSION

The healthy worker survivor effect is a well-known bias in occupational epidemiology, and one that can be accounted for with structural nested models. G-estimation of a structural nested AFT model was proposed more than 20 years ago yet, to our knowledge, it has only been used twice to estimate exposure effects in occupational cohort studies (4, 5). The scarcity of its use may partly be the result of key challenges and limitations encountered when implementing the method. These limitations can become problematic when the exposure is continuous, and more so when the number of parameters in the structural nested AFT model is large (≥3), and they are currently the subject of ongoing biostatistical research (29, 40). However, G-estimation of a structural nested AFT model has already proven useful in the context of occupational epidemiology, where researchers are often interested in estimating the effect of a single exposure. Although quantifying the potential for the healthy worker effect is an important contribution (3), more important still is the unbiased estimation of exposure effects in occupational epidemiology. Hopefully, this illustration will enable occupational epidemiologists to implement structural nested models on a more routine basis.