Biomechanics of superior oblique Z-tenotomy

Abstract

Background

A recent report suggests that 70%-80% Z-tenotomy of the superior oblique tendon is necessary to effectively treat A-pattern strabismus associated with over depression in adduction. To clarify the clinical effect, we compared the biomechanics of Z-tenotomy on the superior oblique tendon, superior rectus tendon, and isotropic latex material.

Methods

Fresh bovine superior oblique tendons were trimmed to 20 mm × 10 mm dimensions similar to human superior oblique tendon and clamped in a microtensile load cell under physiological conditions of temperature and humidity. Minimal preload was applied to avoid slackness. Tendons were elongated until failure following Z-tenotomies, made from opposite tendon sides, spaced 8 mm apart and each encompassing 0%, 20%, 40%, 50%, 60%, or 80% tendon width. Digitally sampled failure force was monitored using a precision strain gauge. Control experiments were performed in similar-sized specimens of bovine superior rectus tendon and isotropic latex.

Results

Progressively increasing Z-tenotomy of latex caused a linearly graded reduction in force. In contrast, Z-tenotomy of up to 50% in superior oblique and superior rectus tendons caused nonlinear reduction in force transmission that reached a negligible value at 50% tenotomy and greater.

Conclusions

Z-tenotomy up to 50% progressively reduces extraocular tendon force transmission, but Z-tenotomy of ≥50% is biomechanically equivalent in vitro to complete tenotomy.

The superior oblique muscle is the longest and thinnest of the six extraocular muscles, and it has a broad scleral insertion. One principal role of the superior oblique muscle is infraduction, which is maximal in adduction. Overdepression in adduction is associated with A-pattern strabismus, often treated by superior oblique weakening surgery. Several surgical techniques have been advocated for superior oblique lengthening and weakening, including recession^1-3; tenectomy^4,5; tendon-lengthening using a silicone tendon expander,^6-8 nonabsorbable suture,⁹ or autologous fascia¹⁰; tenotomy^11-14; and marginal Z-tenotomy.^15-18 A recent report advocated Z-tenotomy for treating mild to moderate A-pattern strabismus associated with overdepression in adduction.¹⁹ This report claimed that 70%-80% superior oblique Z-tenotomy is required to collapse A-pattern strabismus and normalizes versions. However, the biomechanical effects of Z-tenotomy have been heretofore uncharacterized.

Biomechanical characterization can define the behavior of tissue for clinical or research purposes. Theoretical models have been developed to describe the mechanical behavior of tissues, including artery,²⁰ brain,²¹ heart muscle,²² kidney,²³ liver,²⁴ ligament and tendon,^25-29 and skin.³⁰ Several different mechanical techniques and modeling methods have been applied to various tissues, such as extraocular muscle,^31-33 orbital connective tissue and fat,³⁴ cornea,³⁵ and sclera.³⁶ Most relevant to strabismus, a recent biomechanical study by Shin and colleagues³⁷ has helped interpret the novel functional anatomical finding that intramuscular innervation of horizontal rectus muscles is segregated into superior and inferior (transverse) compartments.^38,39 Transverse mechanical coupling between extraocular muscle compartments has been shown to be low, suggesting potential independent compartmental action.³⁷ The complex internal structure of extraocular muscle and tendon contrasts with the isotropic structure of a uniform elastic material such as latex rubber, which is uniform in all directions.

Z-tenotomy is performed by making overlapping incisions, spaced some distance apart, from opposite sides of the tendon. For Z-tenotomy exceeding 50% from each opposite margin, no tendon fibers remain continuous across the two tenotomy incisions, implying that any postoperative force transmission by the tendon would be due to transverse coupling between tendon fiber bundles. The study of Shin and colleagues predicts that even 50% Z-tenotomy would reduce transmitted force maximally. In this light, it is puzzling that a greater superior oblique Z-tenotomy, 70%-80%, is reported necessary to treat A-pattern strabismus associated with overdepression in adduction.³⁷ The present study aimed to understand this question by investigating the biomechanical effect of various doses Z-tenotomy of the superior oblique tendon in a bovine tendon model.

Methods

Custom Microtensile Load Cell Testing

A custom, horizontally mounted microtensile load cell was constructed using heavy aluminum and steel hardware on a 12.5 mm thick aluminum foundation plate so that the structure did not deform measurably during tissue loading. A servocontrolled electromagnetic linear motor (Ibex Engineering, Newbury Park, CA) capable of high speed (controllable to 100 mm/s maximum) and 20 nm resolution was mounted in line with an S-shaped semiconductor strain gauge (FUTEK Advanced Sensor Technology, Irvine, CA) having 5 mN force resolution (equivalent to 1.962 gram force), providing precise control of both position and speed. The strain gauge was attached to a 127 mm long stainless steel tensile shaft that passed into a closed physiologic chamber through a frictionless air bearing that served as its mechanical support. Inside the physiologic chamber the tensile shaft was attached to a serrated stainless steel compression clamp to engage one end of the specimen under test. The other specimen end was similarly clamped to a tensile shaft fixed to the opposite end of the load cell. When the linear motor displaced the tensile shaft, the strain gauge indicated the corresponding force.

Specimens under test were enclosed in a physiologic chamber with transparent walls whose lower portion contained a water bath heated under feedback control to maintain 100% humidity and 37°C temperature in the overlying air, as measured by a thermocouple. A high-resolution video camera with 50 mm macro lens (Canon EOS 5D Mark II, Japan) was mounted to photograph the specimen from above through a transparent cover that was coated with an anticondensation compound to inhibit fogging during photography of the specimen. Figure 1 illustrates the photograph of the load cell and components.

FIG 1.

Microtensile load cell. Photograph of apparatus. A strain gauge (2) attached to the linear motor (1) was connected to the specimen clamp (5) through a tensile shaft (4) that was supported by a frictionless air bearing (3).

Specimen Preparation

Fresh heads of cows aged 20-30 months were obtained immediately after slaughter from a nearby abattoir (Manning Beef LLC, Pico Rivera, CA). Transport time from abattoir to laboratory was approximately one hour, and one hour additionally elapsed for dissection and preparation of specimens in the laboratory. After extraction, specimens were maintained in lactated Ringer’s solution at 37°C. To minimize axial damage to tendon fibers, each specimen was initially reduced to dimensions 25 mm × 10 mm, by cutting the margin of the longer dimension parallel to fibers. This left 2.5 mm long margin for clamping at each end, so that the actual testing dimension was 20 mm × 10 mm.

Experimental Procedure

Preloading was applied to superior oblique tendons to avoid slackness. Tensile testing was performed under the physiological conditions by subjecting specimens to increasing tension until every tendon ruptured. Force at failure represents the ability of the tendon to withstand tensile force applied to it. Before tensile loading, Z-tenotomy was performed by making two transverse incisions, each from opposite sides of the specimen, spaced 8 mm apart (Figure 2A). In different specimens, Z-tenotomy was performed from each tendon margin at 0%, 20%, 40%, 50%, 60%, and 80% tendon width. Figure 2B illustrates 20% Z-tenotomy. Control experiments were performed in similar-sized specimens of bovine superior rectus muscle tendon, and isotropic latex.

FIG 2.

Experimental approach. A, Schematic drawing of Z-tenotomy experiment. Extraocular tendons were clamped in both ends and pre-loading was applied for avoiding slackness. Then, specimen was cut from two opposite direction with different portion (20, 40, 50, 60, and 80% width). The distance between two cuts was 8 mm. B, 20% Z-tenotomy experiment of superior oblique tendon. After clamping the specimen (top), 20% of tendon width was incised from both margins with 8 mm longitudinal spacing (bottom).

Results

Z-tenotomy with Control Material Isotropic Rubber

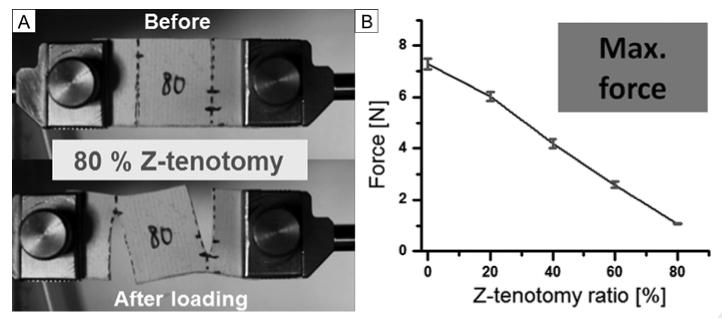
Isotropic latex rubber (Abrasion-resistant natural latex rubber 1/16 inch thick, McMaster-Carr, Santa Fe Springs, CA) was used a control material. Specimens were prepared measuring 30 mm long, and 20 mm wide. Unlike tendon specimens, only 20% elongation was applied in latex tensile testing since this is well characterized, linearly elastic material, and force behavior is linear like a spring, so that maximum force transition for various Z-tenotomy ratios should correspond to failure force transition of extraocular muscle. Each of three specimens was tested for 5 different Z-tenotomy ratios progressively increased from 0, 20, 40, 60, 80% tendon width at 1 mm/s loading rate. Representative specimen photographs and result data according to 5 different Z-tenotomy ratios are illustrated in Figure 3. As may be seen in Figure 3A, the latex between incisions became distorted to slanted by path by shear force. There was a linear trend of decreasing maximum force with increasing percentage Z-tenotomy, as shown in Figure 3B. This reflects the combined effect of tensile and shear forces. Theoretically, as tenotomy percentage increases, tensile force would be expected to decrease and reaches to zero at 50% Z-tenotomy, because of decreasing cross section area for tensile loading. However, this effect is offset by shear force that increases and peaks at 50% Z-tenotomy, before decreasing progressively for greater tenotomy. Consequently, the experimental data, reflecting the sum of tensile and shear forces, exhibited a linearly decreasing, isotropic coupling effect. The graph in Figure 3B extrapolates to nearly zero force at about 90% Z-tenotomy.

FIG 3.

Z-tenotomy of latex. A, Photographs of 80% z-tenotomy tensile testing (before and after elongation). Middle part of specimen was distorted affected by the shear force caused by Z-tenotomy and following tensile loading. B, Maximum force transition from 0 to 80% Z-tenotomy tensile testing results. Linear trend was monitored according to the Z-tenotomy ratio. Error bars indicate SD.

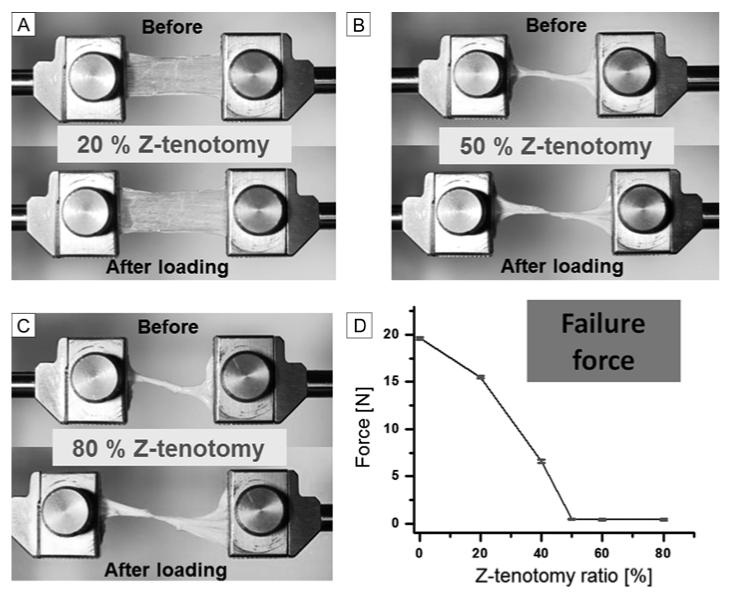
Superior oblique Z-tenotomy Tensile Testing

A total of 30 superior oblique specimens were elongated until failure at 1 mm/s loading rate, including 6 different Z-tenotomy ratios. Representative specimen photographs before and after loading, and failure force data for each Z-tenotomy ratio are illustrated in Figure 4. Tendon failure force exhibited two significant trends varying with the amount of Z-tenotomy (Figure 4D). For less than 50% superior oblique Z-tenotomy, tendon failure force declined with a parabolic shape, rather than linearly as observed for latex rubber. In more striking contrast, for more than 50% Z-tenotomy, superior oblique force transmission was reduced to a roughly constant value of nearly zero (0.46, 0.42, and 0.42N at 50%, 60%, and 80% Z-tenotomy, resp.). Consequently, the superior oblique tendon showed a parabolic response to increasing Z-tenotomy until 50%, but virtually no tensile force after 50% Z-tenotomy. Although tensile forces in latex rubber were all measured at 20% elongation from initial length rather than at failure for the same range of Z-tenotomies as employed in tendons (Figure 3B), comparison between the linear trend in rubber and nonlinear pattern in muscle is valid since force transition in linear elastic rubber should be similar at any elongation point up to failure.

FIG 4.

Tensile Testing after superior oblique Z-tenotomy. A, 20% Z-tenotomy (before and after elongation). B, 50% Z-tenotomy. C, 80% Z-tenotomy. D, Failure force transition from 0 to 80% Z-tenotomy results. Error bars indicate SD.

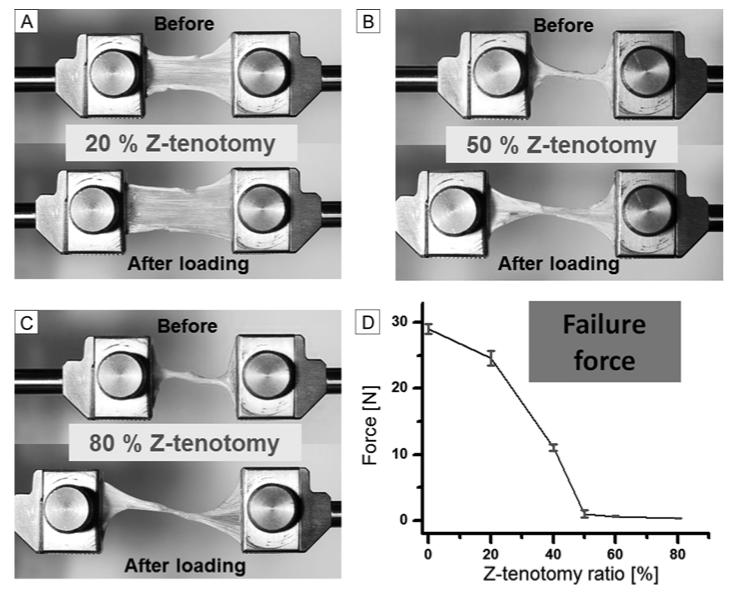
Superior Rectus Z-tenotomy

Tensile testing of the superior rectus tendon was performed identically to that for superior oblique tendons. Representative specimen photographs before and after loading, and failure force are illustrated in Figure 5. As may be seen by comparing Figures 4D and 5D, Z-tenotomy had similar effect for both the superior oblique and superior rectus tendons. In both cases, tensile testing to failure demonstrated progressively steep, nonlinear decline for less than 50% Z-tenotomy, and almost zero residual force for more than 50%.

FIG 5.

Z-tenotomy of superior rectus tendon. A, 20% Z-tenotomy before and after elongation. B, 50% Z-tenotomy before and after elongation. C, 80% Z-tenotomy before and after elongation. D, Failure force transition from 0 to 80% Z-tenotomy results. Failure force was reduced to near zero for 50% or greater Z-tenotomy. Error bars indicate SD.

Discussion

These biomechanical experiments confirm that Z-tenotomy incisions weaken both artificial material and extraocular tendon in graded fashion. However, the effect depends strongly on the structure of the material. A control experiment using isotropic rubber demonstrated a decline of maximum force that varied linearly with the dose of Z-tenotomy. As the Z-tenotomy dose increased, tensile force decreased as the amount of intact latex became reduced. At the same time, a coupling effect developed and progressively increased in the latex specimen, converting force transmission from pure axial along the axis of elongation to an increasing Z-shaped slant. Since latex rubber has an isotropic structure throughout, shear force is efficiently transferred through the part of the specimen between the two “tenotomy” incisions. It is therefore intuitive that linear reduction of maximum force as a function of Z-tenotomy ratio occurs as a result of isotropic coupling effect.

Surgical advocates of Z-tenotomy appear to have implicitly assumed that extraocular tendon is an isotropic material like latex because tenotomy percentages substantially exceeding 50% have been advised for effective superior oblique weakening.¹⁹ But in these experiments neither superior oblique nor superior rectus tendon exhibited mechanical responses to progressively increasing Z-tenotomy that resembled latex. For both tendons, failure force declined at an accelerating rate with progressive tenotomy until at or above 50%, at which point there was hardly any force transmission at all. Putting it another way, Z-tenotomy or 50% or more is mechanically very nearly the same as complete, unguarded tenotomy. The difference in biomechanics reflects the internal structure of extraocular tendon.

The biomechanics of extraocular tendon differ from the behavior of isotropic latex because tendon does not have an isotropic structure. An isotropic structure is the same in all directions. Tendon is orthotropic, meaning that it is the same in one direction—along the length of the tendon—but differs transverse to the length of the tendon. Unlike latex rubber, extraocular tendon is composed of strong parallel fibers aligned longitudinally, thinly woven with sparse, thin transverse fibers and a small amount of viscous extrafibrillar matrix filled between fiber bundles in the transverse direction. Our measurements by atomic force microscopy indicate that the individual longitudinal fibers behave with pure elasticity of high stiffness, without significant viscosity.⁴⁰ Dual-channel load cell experiments have demonstrated that tensile elongation of any arbitrary proportion of tendon or muscle fibers within any extraocular muscle results in only about 5% coupling force transmission to the remainder of the tendon or muscle fibers.³⁷ Poor transfer of shear force in extraocular tendon causes substantial force decoupling between transverse layers and represents the greatest biomechanical difference from a material such as isotropic latex. These findings are especially relevant for Z-tenotomy exceeding 50%. A 50% or greater Z-tenotomy renders discontinuous all of the stiff tendon fibers that normally transmit longitudinal force, leaving the minimal mechanism of shear force coupling as the only means of force transmission. It is particularly notable that transverse force coupling in extraocular tendon and muscle, which is low even for static elongations, declines even further in the dynamic case for elongations of increasing speed.³⁷ Of course, the current experiments were performed in vitro and deliberately isolated the tendons from sheaths and other tissues that would be present in vivo so that tendon biomechanics could be studied without compounding by these other tissues. Nevertheless, the current results demonstrate that the in vivo biomechanical effect of Z-tenotomy of 50% or more would be similar to complete, unguarded tenotomy, in both cases being limited to the incidental tensile force of tendon sheaths and adjacent tissues. Since 70%-80% Z-tenotomy of the superior oblique tendon has been advocated as necessary surgical technique,¹⁹ the current data indicate that the operation as performed is mechanically equivalent to 50% tenotomy or even to total, unguarded, tenotomy. The latter is likely to be technically simpler and faster to perform.